2011全国各地中考数学试题分类汇编考点24 三角形全等2份打包)

2011全国中考真题全等三角形的性质与判定一、选择题1.（2011•江苏宿迁，7，3）如图，已知∠1=∠2，则不一定能使△ABD≌△ACD的条件是（）A、AB=ACB、BD=CDC、∠B=∠CD、∠BDA=∠CDA2.（2011南昌，10，3分）如图，在下列条件中，不能证明△ABD≌△ACD的是（）A.BD=DC，AB=ACB.∠ADB=∠ADC，BD=DCC.∠B=∠C，∠BAD=∠CADD.∠B=∠C，BD=DC3.（2011年山东省威海市，6，3分）在△ABC中，AB＞AC，点D、E分别是边AB、AC的中点，点F在BC边上，连接DE，DF，EF，则添加下列哪一个条件后，仍无法判定△BFD与△EDF全等（）A、EF∥AB B、BF=CF C、∠A=∠DFE D、∠B=∠DEF4.（2011年江西省，7，3分）如图，在下列条件中，不能证明△ABD≌△ACD的是（）A.BD=DC，AB=ACB.∠ADB=∠ADC，BD=DCC.∠B=∠C，∠BAD=∠CADD.∠B=∠C，BD=DC5. （2011安徽省芜湖市，6,4分）如图，已知△ABC 中，∠ABC =45°，F 是高AD 和BE 的交点，CD =4，则线段DF 的长度为（ ）A、B 、4C、D、6. （2011浙江金华，9，3分）如图，西安路与南京路平行，并且与八一街垂直，曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口，准备去书店，按图中的街道行走，最近的路程约为（ ）A.600mB.500mC.400mD.300mEDCBA7. （2011梧州，12，3分）如图，点B、C 、E 在同一条直线上，△ABC 与△CDE 都是等边三角形，则下列结论不一定成立的是（ ）A 、△ACE ≌△BCDB 、△BGC ≌△AFCC 、△DCG ≌△ECFD 、△ADB ≌△CEA8.（2011广西百色，8，4分）如图，在△ABC中，AB=AC，∠ABC．∠ACB的平分线BD，CE相交于O点，且BD交AC于点D，CE交AB于点E．某同学分析图形后得出以下结论：①△BCD≌△CBE；②△BAD≌△BCD；③△BDA≌△CEA；④△BOE≌△COD；⑤△ACE≌△BCE；上述结论一定正确的是（）A．①②③B．②③④C．①③⑤D．①③④9.（2011•恩施州9,3分）如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为50和39，则△EDF的面积为（）A、11B、5.5C、7D、3.510.（2011湖北十堰，6，3分）工人师傅常用角尺平分一个任意角。

2011年上海市中考数学试卷（解析版）锦元数学工作室编辑满分150分考试时间100分钟一、选择题（本大题共6题，每题4分，共24分）1．（上海4分）下列分数中，能化为有限小数的是(A) 13；(B) 15；(C) 17；(D) 19．【答案】B。

【考点】有理数。

【分析】∵15＝0．2，故选B。

2．（上海4分）如果a＞b，c＜0，那么下列不等式成立的是(A) a＋c＞b＋c；(B) c－a＞c－b；(C) a c＞b c；(D) a bc c >．【答案】Ａ。

【考点】不等式的性质。

【分析】根据不等式的性质，得(A) a＞b有a＋c＞b＋c，选项正确；(B)由a＞b有－a＜－b，从而c－a＜c－b，选项错误；(C) 由a＞b，c＜0有a c＜b c，选项错误；(D) 由a＞b，c＜0有a b<c c。

故选Ａ。

3．（上海4分）下列二次根式中，最简二次根式是(A)15；(B) 0.5；(C) 5(D) 50．【答案】B。

【考点】最简二次根式。

【分析】155120.522504525⨯，∴15，0.550都不是最简二次根式。

故选B。

4．（上海4分）抛物线y＝－(x＋2)2－3的顶点坐标是(A) （2，－3）；(B) （－2，3）；(C) （2，3）；(D) （－2，－3）．【答案】Ｄ。

【考点】二次函数的顶点坐标。

【分析】由二次函数的顶点式表达式y ＝－(x ＋2)2－3直接得到其顶点坐标是（－2，－3）。

故选Ｄ。

5．（上海4分）下列命题中，真命题是．(A)周长相等的锐角三角形都全等； (B) 周长相等的直角三角形都全等； (C)周长相等的钝角三角形都全等； (D) 周长相等的等腰直角三角形都全等． 【答案】D 。

【考点】命题与定理，全等三角形的判定。

【分析】根据全等三角形的判定方法，逐一判断：A 、周长相等的锐角三角形的对应角不一定相等，对应边也不一定相等，假命题；B 、周长相等的直角三角形对应锐角不一定相等，对应边也不一定相等，假命题；C 、周长相等的钝角三角形对应钝角不一定相等，对应边也不一定相等，假命题；D 、由于等腰直角三角形三边之比为1：1：2 ，故周长相等时，等腰直角三角形的对应角相等，对应边相等，故全等，真命题。

第22章 全等三角形一、选择题1. （2011安徽芜湖，6，4分）如图，已知ABC △中，45ABC ∠= ， F 是高AD 和BE 的交点，4CD =，则线段DF 的长度为（ ）. A ．22B ． 4C ．32D ．42【答案】B2. （2011山东威海，6，3分）在△ABC 中，AB ＞AC ，点D 、E 分别是边AB 、AC 的中点，点F 在BC 边上，连接DE ,DF ,EF .则添加下列哪一个条件后，仍无法判定△BFD 与△EDF 全等（ ）． A ． EF ∥ABB ．BF =CFC ．∠A =∠DFED ．∠B =∠DFE【答案】C3. （2011浙江衢州，1,3分）如图，OP 平分,MON PA ON ∠⊥于点A ，点Q 是射线OM 上的一个动点，若2PA =，则PQ 的最小值为（ ）A.1B.2C.3D. 4（第6题）AONM QP【答案】B4. （2011江西，7，3分）如图下列条件中，不能．．证明△ABD≌△ACD的是（）.A.BD=DC，AB=ACB.∠ADB=∠ADCC.∠B=∠C，∠BAD=∠CADD.∠B=∠C，BD=DC【答案】D5. （2011江苏宿迁,7,3分）如图，已知∠1＝∠2，则不一定．．．能使△ABD≌△ACD的条件是（▲）A．AB＝AC B．BD＝CD C．∠B＝∠C D．∠BDA＝∠CDA【答案】B6. （2011江西南昌，7，3分）如图下列条件中，不能．．证明△ABD≌△ACD的是（）.A.BD=DC，AB=ACB.∠ADB=∠ADCC.∠B=∠C，∠BAD=∠CADD.∠B=∠C，BD=DC【答案】D7. （2011上海，5，4分）下列命题中，真命题是（）．(A)周长相等的锐角三角形都全等；(B) 周长相等的直角三角形都全等；(C)周长相等的钝角三角形都全等；(D) 周长相等的等腰直角三角形都全等．【答案】D8. （2011安徽芜湖，6,4分）如图，已知ABC △中，45ABC ∠= ， F 是高AD 和BE 的交点，4CD =，则线段DF 的长度为（ ）. A ．22B ． 4C ．32D ．42【答案】B二、填空题1. （2011江西，16，3分）如图所示，两块完全相同的含30°角的直角三角形叠放在一起，且∠DAB=30°。

2011 年全国各地 100 份中考数学试卷分类汇编第 21章三角形的边与角一、选择题1. （2011福建福州，10，4 分）如图3, 在长方形网格中, 每个小长方形的长为2,宽为1, A 、B 两点在网格格点上,若点则知足条件的点C 个数是（C 也在网格格点上）, 以A、B、C 为极点的三角形面积为 2 ,A．2 B．3 C．4 D． 5BA图 3【答案】 C2. （2011山东滨州，5，3 分）若某三角形的两边长分别为 3 和4,则以下长度的线段能作为其第三边的是( )A. 1B. 5C. 7D.9【答案】 B3.（ 2011 山东菏泽， 3，3 分）一次数学活动课上，小聪将一副三角板按图中方式叠放，则∠等于A． 30°B．45°C． 60°D． 75°45°30°【答案】 D4. （2011山东济宁，形是（）A.直角三角形C.钝角三角形3，3 分）若一个三角形三个内角度数的比为B.锐角三角形D.等边三角形2︰ 7︰ 4，那么这个三角【答案】 B5.（2011 浙江义乌， 2，3 分）如图， DE 是△ ABC 的中位线，若 BC 的长是 3cm，则 DE 的长是（）AD EB CA． 2cm B． 1.5cm C． 1.2cm D．1cm【答案】 B6. （ 2011 台湾台北，23）如图 (八 )，三边均不等长的ABC ，若在此三角形内找一点O，使得OAB 、OBC 、OCA 的面积均相等。

判断以下作法何者正确？A．作中线AD ，再取AD 的中点OB．分别作中线AD 、BE ，再取此两中线的交点OC．分别作AB 、BC 的中垂线，再取此两中垂线的交点OD．分别作 A 、 B 的角均分线，再取此两角均分线的交点O【答案】 B7.（ 2011 台湾全区， 20）图 (五 )为一张方格纸，纸上有一灰色三角形，其极点均位于某两网格线的交点上，若灰色三角形面积为21平方公分，则此方格纸的面积为多少平方公分？4A ．11B． 12C． 13D． 14【答案】Ｂ8. （2011 江苏连云港，5，3 分）小华在电话中问小明：“已知一个三角形三边长分别是4，9，12，怎样求这个三角形的面积？小明提示说：“可经过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的选项是（）【答案】 C9.（ 2011 江苏苏州， 2,3 分）△ ABC的内角和为A.180 °B.360 °C.540 °D.720 °【答案】 A10．（2011 四川内江， 2，3 分）如图，把一块直角三角板的直角极点放在直尺的一边上，如果∠ 1=32°，那么∠ 2 的度数是A． 32°B． 58°C． 68°D． 60°21【答案】 C11.（2011 湖南怀化， 2， 3 分）如图 1 所示，∠ A、∠ 1、∠ 2 的大小关系是A. ∠ A>∠ 1>∠ 2 C. ∠ A>∠ 2>∠1B. ∠ 2>∠ 1>∠ A D. ∠ 2>∠A>∠ 1【答案】 B12.（ 2011 江苏南通， 4， 3 分）以下长度的三条线段，不可以构成三角形的是A. 3，8，4B. 4， 9，6C. 15， 20， 8 D . 9， 15， 8【答案】 A13. （2011 四川绵阳5， 3）将一副惯例的三角尺按如图方式搁置，则图中∠AOB的度数为BOAA．75°B． 95°C． 105 °D． 120 °【答案】 C14.（2011 四川绵阳 6， 3）王师傅用 4 根木条钉成一个四边形木架，如图 .要使这个木架不变形，他起码要再钉上几根木条 ?A．0 根 B.1 根 C.2 根 D.3 根【答案】 B15.（ 2011 广东茂名， 2， 3 分）如图，在△ ABC 中， D、Ｅ分别是 AB、 AC的中点，若 DE＝5，则 BC＝A．6 B． 8 C． 10 D． 12【答案】 C16. （2011山东东营，5，3分）一副三角板,以下图叠放在一同,则图中∠的度数是（）A．75B．60C．65D．55【答案】 A17. （2011河北，10，3分）已知三角形三边长分别为2，x，13，若x 为正整数，则这样的三角形个数为（）A． 2 B．3 C． 5 D． 13【答案】 B18.（ 2010 湖北孝感， 8，3 分）如图，在△ ABC中， BD、 CE是△ ABC的中线， BD与 CE订交于点O,点F、G分别是BO、CO的中点，连接AO.若AO=6cm，BC=8cm，则四边形DEFG的周长是( )A.14cmB.18cmC.24cmD.28cm【答案】 A19.20．21.22.23.24.25.二、填空题1.（2011浙江金华，12，4分）已知三角形的两边长为4，8，则第三边的长度能够是（写出一个即可） .【答案】答案不独一，如2. （2011浙江省舟山，5、6 等14， 4 分）如图，在△ABC 中， AB=AC， A 40 ，则△ ABC的外角∠ BCD＝度．BA C D（第 14 题）【答案】 1103.（2011 湖北鄂州， 8， 3 分）如图，△ ABC 的外角∠ ACD 的均分线 CP 的内角∠ ABC 均分线BP 交于点 P，若∠ BPC=40°，则∠ CAP=_______________．A PB C D第 8 题图【答案】 50°4. （2011宁波市，17，3分）如图，在ABC 中， AB＝ AC， D、E 是分∠ BAC，∠ EBC＝∠ E＝ 60°，若 BE＝ 6cm， DE＝ 2cm，则 BC＝ABC 内两点，cmAD 平【答案】 85. （2011浙江丽水，12，4分）已知三角形的两边长为4，8，则第三边的长度能够是(写出一个即可 ).【答案】答案不唯一，在4<x<12 之间的数都可6.（2011 江西， 13，3 分）如图，在△ ABC中，点 P 是△ ABC的心里，则∠ PBC+∠ PCA+∠ PAB =度 .第 13题图【答案】 907.（ 2011 福建泉州， 15，4 分）如图，在四边形ABCD中，P是对角线BD的中点，E，F分别是 AB， CD 的中点 AD BC，PEF 18 ，则PFE 的度数是．FDCPBA E（第 15 题）【答案】 188.（ 2011 四川成都， 13,4 分）如图，在△ ABC中，D、E 分别是边 AC、BC 的中点，若 DE=4,则AB= .CD EA B【答案】 8.9.（2011 四川内江，加试 2，6 分）如图，在△ ABC中，点 D、 E 分别是边 AB、 AC的中点DF 过 EC的中点 G 并与 BC的延伸线交于点F，BE 与 DF 交于点 O。

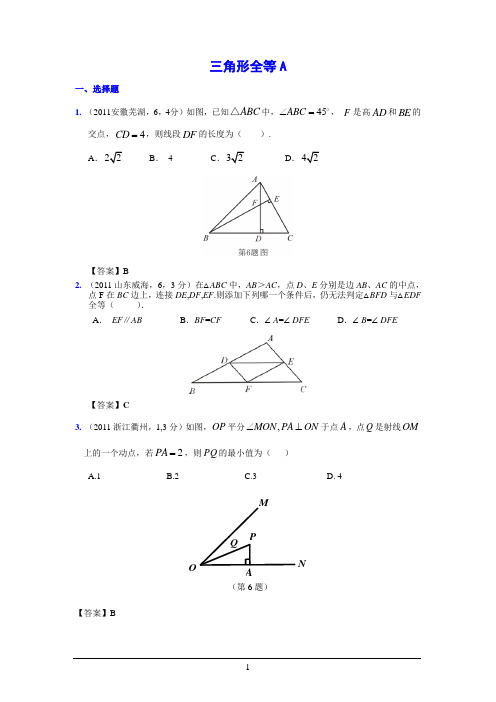
三角形全等A一、选择题1. （2011安徽芜湖，6，4分）如图，已知ABC △中，45ABC ∠= ， F 是高AD 和BE 的交点，4CD =，则线段DF 的长度为（ ）. A．B ． 4 C．D．【答案】B2. （2011山东威海，6，3分）在△ABC 中，AB ＞AC ，点D 、E 分别是边AB 、AC 的中点，点F 在BC 边上，连接DE ,DF ,EF .则添加下列哪一个条件后，仍无法判定△BFD 与△EDF 全等（ ）．A ． EF ∥ABB ．BF =CFC ．∠A =∠DFED ．∠B =∠DFE【答案】C3. （2011浙江衢州，1,3分）如图，OP 平分,MON PA ON ∠⊥于点A ，点Q 是射线OM 上的一个动点，若2PA =，则PQ 的最小值为（ ）A.1B.2C.3D. 4【答案】BON4. （2011江西，7，3分）如图下列条件中，不能．．证明△ABD≌△ACD的是（）.A.BD=DC，AB=ACB.∠ADB=∠ADCC.∠B=∠C，∠BAD=∠CADD.∠B=∠C，BD=DC第7题图【答案】D5. （2011江苏宿迁,7,3分）如图，已知∠1＝∠2，则不一定．．．能使△ABD≌△ACD的条件是（▲）A．AB＝AC B．BD＝CD C．∠B＝∠C D．∠BDA＝∠CDA【答案】B6. （2011江西南昌，7，3分）如图下列条件中，不能．．证明△ABD≌△ACD的是（）.A.BD=DC，AB=ACB.∠ADB=∠ADCC.∠B=∠C，∠BAD=∠CADD.∠B=∠C，BD=DC第7题图【答案】D7. （2011上海，5，4分）下列命题中，真命题是（）．(A)周长相等的锐角三角形都全等；(B) 周长相等的直角三角形都全等；(C)周长相等的钝角三角形都全等；(D) 周长相等的等腰直角三角形都全等．【答案】D8. （2011安徽芜湖，6,4分）如图，已知ABC △中，45ABC ∠= ， F 是高AD 和BE 的交点，4CD =，则线段DF 的长度为（ ）.A ．B ． 4C ．D ．【答案】B 二、填空题2. （2011广东湛江19,4分）如图，点,,,B C F E 在同一直线上, 12∠=∠,BC FE =,1∠ （填“是”或“不是”） 2∠的对顶角，要使ABC DEF ∆≅∆，还需添加一个条件，这个条件可以是 （只需写出一个）．【答案】AC DF = 三、解答题1. （2011广东东莞，13，6分）已知：如图，E,F 在AC 上，AD ∥CB 且AD =CB ，∠D ＝∠B . 求证：AE =CF.【答案】∵AD ∥CB ∴∠A=∠C又∵AD=CB ，∠D=∠B ∴△ADF ≌△CBE ∴AF=CE ∴AF+EF=CE+EF 即AE=CF2. （2011山东菏泽，15（2），6分）已知：如图，∠ABC =∠DCB ，BD 、C A 分别是∠ABC 、∠DCB 的平分线．求证：AB =DC证明：在△ABC 与△DCB 中(A B C D C B A C B D B C B C B C ∠=∠⎧⎪∠=∠⎨⎪=⎩已知）（公共边）（∵AC 平分∠BCD ，BD 平分∠ABC ）∴△ABC ≌△DCB∴AB =DC3. （2011浙江省，19，8分）如图，点D ，E 分别在AC ，AB 上． (1) 已知，BD=CE ，CD=BE ，求证：AB=AC ；(2) 分别将“BD=CE”记为①，“CD=BE” 记为②，“AB=AC”记为③．添加条件①、③，以②为结论构成命题1，添加条件②、③以①为结论构成命题2．命题1是命题2的 命题，命题2是 命题．（选择“真”或“假”填入空格）．【答案】(1) 连结BC，∵ BD=CE，CD=BE，BC=CB．∴△DBC≌△ECB （SSS）∴∠DBC =∠ECB∴ AB=AC(2) 逆，假；4. （2011浙江台州，19,8分）如图，在□ABCD中，分别延长BA，DC到点E，使得AE=AB，CH=CD，连接EH，分别交AD，BC于点F,G。

2011年全国各地100份中考数学试卷分类汇编第30章解直角三角形一、选择题1. （2011湖北武汉市，10，3分）如图，铁路MN和公路PQ在点O处交汇，∠QON=30°．公路PQ上A处距离O点240米．如果火车行驶时，周围200米以内会受到噪音的影响．那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时，A处受噪音影响的时间为A．12秒． B．16秒． C．20秒． D．24秒．【答案】B2. （2011湖南衡阳，9，3分）如图所示，河堤横断面迎水坡AB的坡比是1，堤高BC=5m，则坡面AB的长度是（）A．10m B．C．15m D．【答案】A3. （2011山东东营，8，3分）河堤横断面如图所示，堤高BC＝5米，迎水坡AB的坡比1：（坡比是坡面的铅直高度BC与水平宽度AC之比），则AC的长是（）A．米B．10米C．15米D．米【答案】A4. （2010湖北孝感，10，3分）如图，某航天飞船在地球表面P点的正上方A处，从A处观测到地球上的最远点Q，若∠QAP=α，地球半径为R，则航天飞船距离地球表面的最近距离AP，以及P、Q两点间的地面距离分别是（）A.sin R α，180Rπα B. sin R R α-，()90180R απ- C. sin R R α-，()90180R απ+ D. cos RR α-，()90180R απ- 【答案】B5. （2011宁波市，9，3分）如图，某游乐场一山顶滑梯的高为h ，滑梯的坡角为a ，那么滑梯长l 为A ． h sin aB ． h tan aC ． hcos a D ． h ·sin a【答案】A6. （2011台湾台北，34）图(十六)表示一个时钟的钟面垂直固定于水平桌面上，其中分针上有一点A ，且当钟面显示3点30分时，分针垂直于桌面，A 点距桌面的高度为10公分。

如图(十七)，若此钟面显示3点45分时，A 点距桌面的高度为16公分，则钟面显示3点50分时，A 点距桌面的高度为多少公分？A ．3322－B ．π＋16C ．18D ．19【答案】D7. （2011山东潍坊，10，3分）身高相等的四名同学甲、乙、丙、丁参加风筝比赛，四人放出风筝的线长、线与地面的夹角如下表（假设风筝线是拉直的），则四名同学所放的风筝中最高的是（ ）同学 甲 乙 丙 丁 放出风筝线长 140m 100m 95m 90m 线与地面夹角 30° 45° 45° 60° A.甲 B.乙 C.丙 D.丁 【答案】D8. （2011四川绵阳10，3）周末，身高都为1.6米的小芳、小丽来到溪江公园，准备用她们所学的知识测算南塔的高度.如图，小芳站在A 处测得她看塔顶的仰角α为45°，小丽站在B 处测得她看塔顶的仰角β为30°.她们又测出A 、B 两点的距离为30米。

广东2011年中考数学试题分类解析汇编专题9：三角形一、选择题1. （茂名3分）如图，在△ABC 中，D 、E 分别是AB 、AC 的中点，若DE=5，则BC=A 、6B 、8C 、10D 、12【答案】C 。

【考点】三角形中位线定理。

【分析】利用三角形的中位线定理求得BC 即可。

故选C 。

2.（茂名3分）如图，已知：45°＜A ＜90°，则下列各式成立的是 A 、sinA=cosA B 、sinA ＞cosAC 、sinA ＞tanAD 、sinA ＜cosA【答案】B 。

【考点】锐角三角函数的定义，三角形的边角关系。

【分析】∵45°＜A ＜90°，∴BC ＞AC 。

而sinA=BC AB ，cosA=ACAB ，∴sinA ＞cosA 。

又∵C=900，∴AB ＞BC ＞AC 。

而tanA=BCAC，∴sinA ＜tanA 。

故选B 。

3.（深圳3分）如图，小正方形边长均为1，则下列图形中三角形(阴影部分)与△ABC 相似的是【答案】B 。

【考点】相似三角形的判定。

【分析】如B图△EFG和△ABC中，∠EFG=∠ABC=1350，AB 2CB 22 , 2 EF 1GF 2====，AB CB EF GF∴=。

EFG ABC ∴∆∆∽。

实际上， A ，C ，D 三图中三角形最大角都小于∠ABC ，即可排它，选B 即可。

4.（深圳3分）如图，△ABC 与△DEF 均为等边三角形，O 为BC 、EF 的中点，则AD ：BE的值为A.3:1 B. 2:1 C.5:3 D.不确定【答案】A 。

【考点】等边三角形的性质，相似三角形的判定和性质。

【分析】连接AO ，DO 。

设等边△ABC 的边长为a ，等边△ABC 的边长为b 。

∵O 为BC 、EF 的中点，∴AO 、DO 是BC 、EF 的中垂线。

∴∠AOC=∠DOC=900，∴∠AOD=1800—∠COE 。

某某某某2011年中考数学试题分类解析汇编专题9：三角形 一、选择题 1.（某某某某3分）如图，在Rt△ABC 中，∠ACB=90°，BC=3，AC=15，AB 的垂直平分线ED 交BC 的延长线与D 点，垂足为E ，则sin∠CAD=A 、14B 、13 C 、154 D 、1515【答案】A 。

【考点】锐角三角函数的定义，线段垂直平分线的性质，勾股定理。

【分析】设AD=x ，则CD=x －3，在直角△ACD 中，（x －3）2+ (15)2=x 2，解得，x=4。

∴CD=4－3=1，∴sin∠CAD=CD 1AD 4=。

故选A 。

2.（某某某某3分）如图，矩形OABC 的边OA 长为2，边AB 长为1，OA 在数轴上，以原点O 为圆心，对角线OB 的长为半径画弧，交正半轴于一点，则这个点表示的实数是A 、2.5B 、22C 、3D 、5【答案】D 。

【考点】勾股定理，实数与数轴。

【分析】本题利用实数与数轴的关系及直角三角形三边的关系（勾股定理）解答即可：由勾股定理可知，∵OB=22215+=，∴这个点表示的实数是5。

故选D 。

3.（某某某某3分）如图，已知AB ＝AC ，∠A＝︒36，AB 的中垂线MD 交AC 于点D 、交AB 于点M 。

下列结论：①BD 是∠ABC 的平分线；②△BCD 是等腰三角形；③△ABC∽△BCD；④△AMD≌△BCD，正确的有( )个A 、4B 、3C 、2D 、1【答案】B 。

【考点】相似三角形的判定，全等三角形的判定，线段垂直平分线的性质，等腰三角形的判定和性质，三角形内角和定理。

【分析】首先由AB 的中垂线MD 交AC 于点D 、交AB 于点M ，求得△ABD 是等腰三角形，即可求得∠ABD 的度数，又由AB=AC ，即可求得∠ABC 与∠C 的度数，则可求得所有角的度数，可得△BCD 也是等腰三角形，则可证得△ABC∽△BCD：∵AB 的中垂线MD 交AC 于点D 、交AB 于点M ，∴AD=BD。

全国2011年中考数学试题分类解析汇编(181套）专题29：三角形全等一、选择题1．（某某某某3分）如图，在△ABC中，AB=AC，∠ABC、∠ACB的平分线BD，CE相交于O点，且BD交AC于点D，CE交AB于点E.某同学分析图形后得出以下结论：①△BCD≌△CBE，②△BAD≌△BCD，③△BDA≌△CEA，④△BOE≌△COD，⑤△ACE≌△BCE。

上述结论一定正确的是A. ①②③B. ②③④C. ①③⑤D. ①③④【答案】D。

【考点】全等三角形的判定。

【分析】根据全等三角形的判定定理，可知①由ASA可证△BCD≌△CBE；②△BAD≌△BCD不一定成立；③由AAS可证△BDA≌△CEA；④由AAS可证△BOE≌△COD；⑤△ACE≌△BCE不一定成立。

故选D。

2.（某某某某3分）如图，在△ABC中，∠ACB＝90º，∠A＝15º，AB＝8，则AC·BC的值为A．14 B．16 3 C．415 D．16【答案】D。

【考点】全等三角形的判定和性质，锐角三角函数。

【分析】延长BC到点D，使CD＝CB，连接AD，过点D作DE⊥AB，垂足为点E。

则知△ACD≌△ACB，从而由已知得∠CAD＝∠A＝15º，AD＝AB。

因此，在Rt△ADE中，AD＝8，∠BAD＝30º，∴DE＝AD·sin30º＝4。

从而S△ADE＝12·AB·DE＝16，又S△ADE＝12·BD·AC＝12·2BC·AC＝AC·BC，即AC·BC＝16。

3.（某某宿迁3分）如图，已知∠1＝∠2，则不一定．．．能使△ABD≌△ACD的条件是A．AB＝AC B．BD＝CD C．∠B＝∠C D．∠ BDA＝∠CDA【答案】B。

【考点】全等三角形的判定。

【分析】条件A构成SAS，条件C构成AAS，条件D构成ASA，根据全等三角形的判定定理，它们都能使△ABD≌△ACD。