5、对偶单纯形法

对偶单纯形法的原理和应用一、原理介绍对偶单纯形法是线性规划的一种求解方法，通过对原问题的对偶问题进行迭代求解，来达到求解原问题的目的。

下面详细介绍对偶单纯形法的原理。

1. 线性规划问题的对偶性在线性规划问题中，我们常常需要求解最小化或最大化线性目标函数的问题，同时满足一系列线性约束条件。

对于这样的问题，可以通过定义对偶问题来求解。

2. 对偶问题的定义对于原问题的最小化形式，可以定义对偶问题的最大化形式。

对于原问题的最大化形式，可以定义对偶问题的最小化形式。

对偶问题和原问题之间具有很强的对称性。

3. 对偶单纯形法的基本思想对偶单纯形法的基本思想是通过迭代求解对偶问题来达到求解原问题的目的。

在每一次迭代中，首先确定最优解是否已经找到，如果找到最优解，则结束算法；否则，确定要改进的变量，通过计算改变最变量之前对应的对偶变量的值，然后再进行下一次迭代。

二、应用场景对偶单纯形法在实际应用中有着广泛的应用场景。

下面列举几个典型的应用场景。

1. 生产计划问题在生产计划问题中，常常需要确定各个生产线的产量，以最小化总成本或最大化总利润。

对偶单纯形法可以应用于该问题的求解，通过定义对偶问题，并通过迭代求解对偶问题，来确定生产线的产量。

2. 项目调度问题在项目调度问题中，需要确定各个项目的开始时间和结束时间，以最小化总工期或最大化资源利用率。

对偶单纯形法可以应用于该问题的求解，通过定义对偶问题，并通过迭代求解对偶问题，来确定项目的调度方案。

3. 运输问题在运输问题中，需要确定各个供应商到各个销售点的运输量，以最小化总运输成本。

对偶单纯形法可以应用于该问题的求解，通过定义对偶问题，并通过迭代求解对偶问题，来确定每个供应商和销售点的运输量。

4. 资源分配问题在资源分配问题中，需要确定各个资源的分配比例，以最大化总效益或最小化总成本。

对偶单纯形法可以应用于该问题的求解，通过定义对偶问题，并通过迭代求解对偶问题，来确定资源的分配比例。

对偶单纯形法例题详细步骤
对偶单纯形法是一种常用的解除线性规划问题的数学方法，由美国数学家鲍门士（George B. Dantzig）在1950年提出，早期更多用于研究管理科学问题，现在广泛用于线性规划问题的求解。

先来回顾一下线性规划的定义：给定线性约束条件和目标函数，要求寻找这样一组变量使目标函数极值化，称为线性规划问题，其中的线性约束条件主要可以分为等于约束和不等于约束，可以分为最大化型和最小化型。

由于线性规划问题本身涉及到多个变量约束严格，可能由于几何等原因不容易采取直接解决，而且有可能会涉及到多目标求解，因此对偶单纯形法是一种更为合理的求解方法。

该方法的目标是建立一个对偶问题，该问题只有一个变量，可以用单纯形法解决。

通过构建相应的对偶问题，将多个目标变量整合为一个，用一个变量来表示即可，这样只需解决一个线性规划问题，就可以根据对偶变量的极值情况，求出原始变量的最优解。

具体到此例来说，我们的目标就是要找出最优解。

我们先要把问题抽象为一个线性规划问题，它包括等式约束条件和不等式约束。

接下来我们可以根据问题性质来分析模型，确定问题的类型，然后找出原始最优解，剩余的就是利用对偶单纯形法求解，方法往往是把原始的规划问题转换为对偶的单纯形问题，求出对偶变量的最优解，再把它转换成原始问题的最优解。

总之，对偶单纯形法是一种非常灵活有效的求解线性规划问题的数学方法，其安全可靠性被广泛应用于解决众多线性规划问题。

对偶单纯形法的条件
首先，对偶单纯形法的条件包括：
1. 对偶可行性条件，对偶单纯形法要求原始问题和对偶问题都是可行的。

也就是说，原始问题的约束条件和对偶问题的变量非负条件都必须满足。

2. 对偶非退化条件，这个条件要求对偶单纯形表中的对偶变量都是非负的，且对偶问题的最优解是非退化的。

3. 对偶互补松弛条件，这个条件指的是原始问题的最优解和对偶问题的最优解之间存在一种互补关系，即原始问题的最优解和对偶问题的最优解必须满足一组互补松弛条件。

其次，对偶单纯形法的条件还涉及到对偶单纯形表的构建和迭代计算的条件：
1. 对偶单纯形表的构建需要满足对偶问题的约束条件和非负条件，通过构建对偶单纯形表，可以进行对偶单纯形法的迭代计算。

2. 对偶单纯形法的迭代计算需要满足一定的迭代规则和条件，
包括选择合适的进入变量和离开变量，进行主元素的换入换出操作，更新对偶单纯形表等操作。

最后，对偶单纯形法的条件还包括了对原始问题和对偶问题的
理解和转化能力：
1. 需要理解原始问题和对偶问题之间的对偶关系，以及如何通
过对偶问题来求解原始问题的最优解。

2. 需要具备将原始问题转化为对偶问题的能力，以及对对偶问
题的理解和求解能力。

总的来说，对偶单纯形法的条件涉及到对原始问题和对偶问题
的理解、对偶单纯形表的构建和迭代计算条件，以及对偶问题的可
行性、非退化性和互补松弛条件的满足。

这些条件是对偶单纯形法
顺利求解线性规划问题的基础，需要严格满足和理解。

对偶单纯形法详解一、对偶单纯形法的基本概念1. 对偶单纯形法呀，就像是单纯形法的一个“双胞胎兄弟”，但是又有自己独特的地方。

我们知道单纯形法是从一个基本可行解开始，逐步迭代找到最优解。

可对偶单纯形法呢，它是从一个满足对偶可行性的基本解开始。

啥叫对偶可行性呢？就是对应的对偶问题的解是可行的。

说白了，这就像是走了一条和单纯形法不太一样的路，但是目标都是找到那个最优解。

2. 比如说，我们有一个线性规划问题，它的标准形式是有目标函数，还有一系列的约束条件。

对偶单纯形法在处理这个问题的时候，会关注对偶问题的一些特性。

就好比我们看一个东西，不能只看表面，还要看它背后的影子一样，对偶单纯形法就是把目光投向了对偶问题这个“影子”，通过这个来找到原问题的最优解。

二、对偶单纯形法的计算步骤1. 第一步，要先确定一个初始的对偶可行基本解。

这个可不像随便找个数字就行，它是有要求的。

就像我们搭积木，每一块积木的位置都很重要。

这个初始解要满足对偶可行性的条件。

如果不满足，那后面的计算就像是在歪歪扭扭的地基上盖房子，肯定不行。

2. 第二步，检查这个基本解对应的检验数。

这检验数就像是一个小裁判，告诉我们这个解是不是朝着最优解的方向去的。

如果检验数都满足一定的条件，那说明我们离最优解已经很近了，就像我们快到山顶了，能看到山顶的风景了。

3. 第三步，如果检验数不满足条件，那就得进行换基操作。

这换基就像是换火车轨道一样，要小心翼翼的。

要选择合适的变量进基和出基，这样才能保证我们换了之后朝着最优解的方向前进。

而且这个过程要不断重复，直到找到那个最优解为止。

就像我们在迷宫里找出口，不断尝试不同的路，直到找到正确的出口。

三、对偶单纯形法的优势1. 对偶单纯形法在处理一些特殊类型的线性规划问题的时候特别有用。

比如说当我们的线性规划问题的约束条件系数矩阵比较特殊的时候，它可能比单纯形法更高效。

这就好比在不同的路况下，有的车适合走平坦的公路，有的车适合走崎岖的山路，对偶单纯形法就是适合某些特殊“路况”的方法。

41第2章对偶理论与灵敏度分析即y 是对偶问题（D ）的一个可行解。

条件式（2-21）称为对偶可行性条件，即最优性条件式（2-20）与对偶可行性条件式（2-21）是等价的，因此，如果一个原始可行基B 是原问题（P ）的最优基，则1=B y c B -就是对偶问题（D ）的一个可行解，此时对应的目标函数值1B w=yb =c B -，等于原问题（P ）的目标函数值，可知1=B y c B -也是对偶问题（D ）的最优解。

若原问题（P ）的一个基本解1=0B b x ⎛⎞⎜⎟⎝⎠-对应的检验数向量满足条件式（2-20），即 =(,)=0,0B N N B σσσc c B N -1（-）≤则称x 为（P ）的一个正则解。

于是可知，原问题（P ）的正则解x 与对偶问题（D ）的可行解y 是一一对应的，它们由同一个基B 所决定，我们称这一基为正则基。

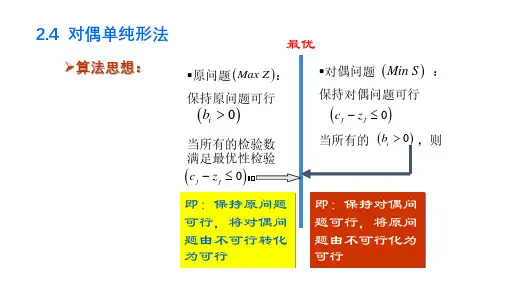
因此，我们可以设想另一条求解思路，即在迭代过程中，始终保持对偶问题解的可行性，而原问题的解由不可行逐渐向可行性转化，一旦原问题的解也满足了可行性条件，也就达到了最优解。

也即在保持正则解的正则性不变条件下，在迭代过程中，使原问题解的不可行性逐步消失，一旦迭代到可行解时，即达到了最优解。

这正是对偶单纯形法的思路，这个方法并不需要把原问题化为对偶问题，利用原问题与对偶问题的数据相同（只是所处位置不同）这一特点，直接在反映原问题的单纯形表上进行运算。

2.3.2 对偶单纯形法的计算步骤求解如下标准形式线性规划问题：max =z cx s.t.0Ax =bx ⎧⎨⎩≥对偶单纯形法的计算步骤如下：（1）找一个正则基B 和初始正则解(0)x ；将原问题化为关于基B [不妨设12=(,,,)m B P P P ]的典式，列初始对偶单纯形表，如表2-5所示。

表2-5 对偶单纯形表12 1 2 12121c 1x 1'b 1 0 … 0 1+1'm a 1+2'm a … 1'n a 2c 2x 2'b 01 02+1'm a 2+2'm a … 2'n am c m x'm b 0…1 +1'mm a +2'mm a … 'mn a c j -z j0 0 0+1m σ+2m σ…n σ（2）若1=b'B b -≥0，则停止计算，当前的正则解1=x B b -，即为原问题的最优解；否则转下一步。