一维随机变量及其分布习题

(A) P{X ≤ 0} = P{X ≥ 0} = 0.5
(B) f (x) = f (−x)
(C) P{X ≤ 1} = P{X ≥ 1} = 0.5
(D) F (x) = 1 − F (−x)
5. 设随机变量 X 的密度函数为ϕ(x) ，且ϕ(−x) = ϕ(x) ， F (x) 是 X 的分布函数，
一元件损坏仪器即停止工作，求仪器正常工作 1000 小时以上的概率。
解：设 Ai 表示第 i 个元件的寿命( i = 1,2,",5 )，则 Ai 相互独立，且
{ } P
Ai
> 1000
=
∫+∞
1000
f
(x)dx
=
∫+∞
1000
1 1000
e −x 1000 dx
=
−e −x 1000
+∞ 1000
上海交通大学概率论与数理统计学习指导与课外习题第二章第二章第二章一维随机变量及其分布一维随机变量及其分布一内容提要与大纲要求一内容提要与大纲要求内容提要内容提要1
上海交通大学《概率论与数理统计》学习指导与课外习题 第二章
第二章 一维随机变量及其分布
一、内容提要与大纲要求
内容提要
1. 随机变量及其概率分布； 2. 随机变量分布函数的概念及性质； 3. 离散型随机变量的分布； 4. 连续型随机变量的概率密度； 5. 常见随机变量的概率分布； 6. 随机变量函数的概率分布。
= 1 − 0.98400 − 400 × 0.02 × 0.98399 ≈ 0.997165 。
或：用泊松近似， λ = np = 8 ，
P{X ≥ 2} = 1− P{X < 2} = 1− (P{X = 0}+ P{X = 1})

第⼆章⼀维随机变量及其分布第⼆章⼀维随机变量及其分布⼀、填空题1.已知F （x ）=P {}X x ≤,则P {}a2.设随机变量 X 的分布函数为,()0,x A Be F x -?+=?00x x >≤ 则A= ,B= （A,B 均为常数）3.设X 的分布函数为0,11,116()1,1221,2x x F x x x <--≤≤则{}1P X <= ，{}12P X <<= . 4.当常数C= 时，{},1,2,(1)CP X n n n n ===+ 为X 的分布律.5.设X 的密度函数为2,()0,x ke f x -?=??00x x >≤则{}12P X -<<= . 6.设X 服从参数为λ的泊松分布，且{}{}122p X P X ===，则{}3P X == . 7.设(1,4)X N ，则{}1P X <= .8.设X 的分布律为101211114436X -??，则2X 的分布律为 .9.设X 服从[]0,1上的均匀分布，则21Y X =-的密度函数为 .10.设X 的密度函数为f(x)，则XY e-=的密度函数为 .⼆、选择题1.设连续型随机变量X 的密度函数为f(x)，分布函数为F （x ），则下列结论正确的是（）<+=()D 当12x x <时，12()()F x F x <2.设X 的分布函数为F(x)，则下列函数中，仍为分布函数的是( )()(21)A F x - ()(1)B F x -3()()C F x ()1()D F x --3.设X 的分布函数为20,()F x x b c ??=-，，x a a x x ≤<≤>则常数a,b,c 的值为( )()A -1,1,1. ()B 1,1,1. ()C 1,0,1. ()D 1,1,0.4.设离散型随机变量X 的分布律为{},1,2,kP X k b k λ=== ，则常数b,λ应满⾜( )()A b>0 ()B 0<λ<1 ()C b=11λ-- ()D 以上都应满⾜5.设X 服从参数为λ的泊松分布，s 表⽰X 取偶数的概率，t 表⽰X 取奇数的概率，则有( )()A s=t ()B st ()D s 与t 的⼤⼩关系不定6.某公司汽车站从上午6点起，每15分钟有⼀班车⽤过，若某乘客到达该站的时间在 8:00到9:00服从均匀分布，则他候车的时间少于5分钟的概率是( )()A 13 ()B 23 ()C 14 ()D 127.设2X N(0,)σ，则对任⼀实数λ，下列结论正确的是( ){}{}()1A P X P x λλ<=-<- {}{}()B P X P X λλ<=> 22()X (0,)C N λλσ 22()(,)D X N λλλσ++8.设22()x xf x CeB ()C ()D9.设X 在[],a b 上服从均匀分布，,λµ的任意两实数，则下列命题正确的是( )()A X 服从均匀分布 ()B 2X 服从均匀分布()C 2(1)X λµ++服从均匀分布 ()D 2(1)X λµ-+服从均匀分布10.设X 为⼀随机变量，Y 为X 的单值函数，则下列命题不正确的是( )()A 若X 为连续型时，Y 未必为连续型 ()B 若X 为连续型时，Y 未必为离散型 ()C 若X 为离散型时，Y 未必为连续型 ()D 若X 为离散型时，Y 未必为离散型三、解答题1．盒中有4只⽩球1只⿊球，现⼀只⼀只地将球取出来，取出后不放回，设X 表⽰取到⿊球的取球次数，求X 的分布律. 2.设甲，⼄，丙三⼈同时向⼀⽬标射击⼀次，命中率分别为0.4，0.5，0.7，设X 表⽰击中，⽬标的⼈数，求X 的分布律. 3.设1cos ,0221()sin ,0220,x x f x x x ππ-≤其它试问f(x)是否为某随机变量X 的密度函数？如果是，求X 的分布函数. 4.设X 的密度函数为2(),0,k xf x Ae k x -=>-∞<<+∞,试求：(1)常数A (2){}(1,0)P X ∈- (3)X 的分布函数()F x5.设X 服从参数为1的泊松分布，{}{}2,50Y X P Y k P Y k ===+≠，k 为某⾮负整数.求{}{}5P Y k P Y k =-=+.⾍卵是否发育成幼⾍是相互独⽴的.证明昆⾍所产的幼⾍数η服从参数为p λ的泊松分布.7.设X 是[]0,1上的连续型随机变量， {}0.290.75,1P X Y X ≤==-，试决定y ，使得{}0.25P Y y ≤=.8.某班有40名学⽣，某次考试的成绩()72,64X N ,已知⼀学⽣成绩为80分.问该学⽣在全班⼤概排到多少位？9.某⼚⽣产的电⼦管寿命()()2N 1600X σ以⼩时计，，若电⼦管寿命在1200⼩时以上的概率不⼩于0.96，求σ的范围.10.已知某电⼦管元件的寿命(X ⼩时）的概率密度为110001,0()10000,0e xf x x -?>?=??≤?求 (1)这种元件能使⽤1200⼩时以上的概率； (2)5个这种元件中⾄少有3个能使⽤1200⼩时以上的概率.11.已知测量误差N 7.5,100X （⽶）（），问必须测量多少次才能使⾄少有⼀次误差的绝对值不超过10⽶的概率⼤于0.9？12设13,3X B ??，Y 服从[]0,3上的均匀分布，且X 与Y 独⽴，问⾏列式1102011X X Y -->的概率是多少？ 13.设连续型随机变量X 的密度函数为(),()0,x a x b e f x -?-=??00x x >≤期中,a b 为常数，已知曲线()y f x =在2x =时取得拐点. (1)求,a b 的值;(2)设{}()1(0)g t P t X t t =<<+>，问t 为何值时，()g t 取得最⼤值？ 14.(1)设ξ服从参数为λ的泊松分布，证明当[]k λ=时，{}P k ξ==最⼤； (2)设(,)B n p ξ，证明当[](1)k n p =+时，{}P k ξ=最⼤. 15.设X 服从指数分布，证明当,0s t >时，{}{}P X s t X s P X t >+>=>.16.设连续型随机变量X 的密度函数()f x 为偶函数，()F X 为X 的分布函数，证明()(),02x F x f t dt x -=->?.17.设X 的分布律为{}1,1,2,2k P X k k === ，求sin 2Y X π=的分布律.18对圆⽚直径进⾏测量，测量值X 在[]5,6上服从均匀的分布，求圆⽚⾯积Y 的概率密度()Y f y .19.设2(,)X N µσ ,求Y X =的概率密度()Y f y .20.设X 在[]0,2π上服从均匀分布，求Y sinX =的密度函数()Y f y21.设X 在[],a b 上服从均匀分布，Y cx d =+(0)c ≠，证明Y 仍服从均匀分布. 22.设连续型随机变量X 的分布函数为()F x ，若对任意{},(),(,)0a b a b P X a b <∈>，证明()Y F X =服从[]0,1上的均匀分布.23.设Z 为连续型随机变量，分布函数为()Z F z ，且对任意{},(),(,)0a b a b P Z a b <∈>，X 服从[]0,1上的均匀分布，证明1()Z Y F X -=与Z 同分布.24.设X 与Y 独⽴，X 的密度函数为()f x ，1ab Y p p ?? ?-??，证明X Y +的密度函数为()()(1)()h x p x a p f x b =-+--.第⼆章习题答案⼀、填空题1.(0)(),()(0)F b F a F b F a ----.2.1,1A B ==-.3.由题意可得X 的分布律为112111632X -??，故116P X ??<=，{}120X <<=4.由111(1)n cc n n ∞==?=+∑ 5.由20()12x f x dx ke dx k +∞+∞12()21x P X f x dx e dx e ---<<===-??6.12211!2!e e λλλλλ--=?=.{}1136P X e -==7.{}{}111110(0)(1)2X P X P X φφ-?<=-<<==-<<=--[]1111(1)(1)0.84130.3413222φφ=--=-=-= 8.24011176412X ?? ? ?9.2(1)Y X =-服从[]0,2上的均匀分布，故有：1, 02()20,Y y f y ?≤≤?=其他10.1(ln ),0()0,0Y f y y yf y y ?->?=??≤?⼆、选择题1.C6.A7.A8.B9.C 10.D 三、解答题 1.设A i 表⽰第i 次取到⿊球，1,2,3,4,5.i ={}111()5P X P A ==={}{}()()()()()()112112341213124123512344112()()()545543211154325P X P A A P A A A P X P A A A A AP A P A A P A A A P A A A A P A A A A A ====?======所以X 的分布律为X 1 2 3 4 5P15 15 15 15 152.设,,A B C 分别表⽰甲，⼄，丙击中⽬标，由题意知,,A B C 相互独⽴，则{}{}{}{}00.50.30.091230.40.50.70.14P X P ABC P A P B P C P X P ABC ABC ABC P X P ABC ABC ABC P X P ABC ==??===++==+==??=（）=（）（）（）=0.6(）=0.36（+）=0.41（）=所以X 的分布律为X 0 1 2 3 P 0.06 0.36 0.41 0.143.显然()f x ⾮负可积，且2201111()cos sin 12222f x dx xdx xdx ππ+∞故()f x 可为某随机变量X 的密度函数220202()()(),210cos ,022110cos sin ,022210,2xx x x xF x f t dtf t dt x dt tdt x dt tdt tdt x dt x ππππππππ-∞-∞--∞---∞-+∞=?<-+-≤-≥0,21sin ,0221cos ,021,2x x x x x x ππ<-+?-≤4.(1)由()1f x dx +∞-∞=?，得21k xAAedx k+∞--∞==?，所以A k =(2){}0022111(1,0)()(1)2k xk P X f x dx kedx e ----∈-===-??(3)20220,0()(),x kt xxktkt ke dt x F x f t dtp ke dt ke dt x -∞-∞--∞=??+≥221,0211,0kx e x e x -?-≥5.由题意知2k m =，25k n +=，,m n 为两个⾮负整数，225m n -=.()()5n m n m +-=.进⽽得5,1n m n m +=-=.解得3n =，2m =.即有4k =. {}{}{}{}{}{}54923P Y k P Y k P Y P Y P X P X =-=+==-===-=2311111112!3!33e e e e---=-==. 6.{},0,1,2!rP r e r r λλξ-==={}(1),0k k r k r P k r C p p r k ηξ-===-≥≥由全概率公式可得{}{}{}(1)!rk k r k r r kr kP k P r P k r e C p p r λληξηξ∞∞--========-∑∑(1)!(1)!!()!!()!r k rk k r k k r kr kp r e p p e p r k r k k r k λλλλλ-∞∞---==??-??=-=--∑∑(1)()(),0,1,2,!!k k p p p p e e e k k k λλλλλ---===即η服从参数为p λ的泊松分布.7.{}{}{}110.25P Y y P X y P X y ≤=-≤=≥-=.有对⽴事件的概率公式8.{}72807287280111888X P X P P --->=>==-≤1(1)10.84130.1587φ=-=-=400.1587 6.348?= 因此该学⽣在全班排在⼤约第七位.9.{}16001200160040012000.96X P X P σσσ--??>=>=-≥?16004004000.04,()0.04X P φσσσ-??≤-≤-≤?，即得400400400()0.96,1.75228.61.75φσσσ≥≥?≤≈ 10.(1){}6100051200112000.30121000x P X e dx e --+∞>==≈?(2)5个元件中⾄少有3个能使⽤1200⼩时以上的概率为6618612555555553()(1)101560.1674iiii C ee ee e -----=??-=-+≈∑ 11.设测量n 次，则有{}1(17.510)0.9n P X ---≤>解得2n >，故n ⾄少取3.12.{}1120(1)(2)0101XX P Y P X Y ?-->=-->{}{}{}{}{}{}223300333310,2010,201212121112223(()())()()333333381P X Y P X Y P X P Y P X P Y C C C =->->+-<-<=>>+<<=++=13.(1)当0x >时，()(1),()(2)x x f x a b x e f x a x b e --'''=+-=--，由当2x =时，()y f x =取得拐点知(2)0f ''=，得0b =.⼜()11x f x a xe dx a +∞+∞--∞=?==?，即 1a =所以,0,()0,0.x xe x f x x -?>=?≤?(2)111()()()t t t x tttg t f x dx f x dx xe dx +++-===?[](1)(1)()(1)1(1)tt tg t t e t e ee t -+--+'=+-=-- 令()0g t '=，得11t e =-，且易知当11t e =-时，()g t 取得最⼤值.14.{}{}11,(1)1,!(1)!11,kk k P k ee k k k P k k k λλλξλλλλξλ--->?表明{}P k ξ=随着k 的增⼤，由递增变成递减，若λ为整数，则k λ=及1λ-时，{}P k ξ=最⼤；若λ不为整数，则[]k λ=时，{}P k ξ=最⼤. (2)⽅法同上.15.设X 的密度函数为,()0,x e f x λλ-?=??00x x >≤{}{}{}{}{},P X s t X s P X s t P X s t X s P X s P X s >+>>+>+>==>>()x s t t s t s x se dxe e e e dxλλλλλλλ+∞--+-++∞--===??{}x t tP X t e dx e λλλ+∞-->==?所以{}{}P X s t X s P X t >+>=> 16.(1)()()()x xF x f t dt t uf u du --∞+∞-==---?()1()1()x xf u du f t dt F x +∞-∞==-=-?所以 ()()1F x F x +-=(2)01()()()()()2xx xF x f t dt f t dt f t dt f t dt --∞-∞--==-=-?17.由于1,sin 0,21,n π-??=??412241n m n m m =-==+故Y 只取1,0,1-三个值.{}{}{}{}{}41121121412151102232181115315m m mm P Y P X m P Y P X m P Y ∞-=∞==-==-=========--=∑∑所以Y 的分布律为Y 1- 0 1P215 13 81518.2224X Y X ππ??==,且X 在[]5,6上服从均匀分布.{}2()4Y F y P Y y P X y π??=≤=≤.当254y π<时，()0Y F y =；当9y π>时，()1Y F y =；当2594y ππ<<时，()55Y F y P X P X =-≤≤=≤≤=??2594()()0,Y Y y f y F y ππ<<'==?其他19.{}{}{}()X Y F y P Y y P y P y X y =≤=≤=-≤≤ 当0y ≤时，()0Y F y =；当0y >时，()Y y X y y y F y P µµµµµσσσσσ-------=≤≤=Φ-Φ?? ? ???????，1,0()()0,0Y Y y y y f y F y y µµ??σσσ??---?+>? ? ???'==???≤20.{}{}()sin Y F y P Y y P X y =≤=≤. 当1y ≤-时，()0Y F y =；当1y ≥时，()1Y F y = 当1a y ≤<时，arcsin 20arcsin 111()(2arcsin )222yY y F y dx dx y ππππππ-=+=+?；当10y -<<时，2arcsin arcsin 11()(2arcsin )22yY yF y dx y πππππ+-==+?.11()()0,Y Y y F y F y -<<'==?其他22.由(){},0P X a b ∈>知，()F x 单增，进⽽有反函数.由于0()1F x ≤≤，故当0y <时，()0Y F y =；当1y >时，()1Y F y =；01y ≤≤时，{}11()()(()).Y F y P X F y F F y y --=≤==1,01()()0,Y y y F y F y ≤≤?'==?其他23.本题只须证明Z ()()Y F y F y =.{}{}{}1Z ()(X)()()Y Z Z F y P Y y P F y P X F y F y -=≤=≤=≤=.24.{}{}{},,P X Y x P Y a X Y x P Y b X Y x +≤==+≤+=+≤{}{}{}{}{}{},,()(1)()x a x bP Y a X x a P Y b X x b P Y a P X x a P Y b P X x b p f t dt p f t dt ---∞-∞==≤-+=≤-==≤-+=≤-=+-?求导便得X Y +的密度函数为()()(1)()h x pf x a p f x b =-+--.。

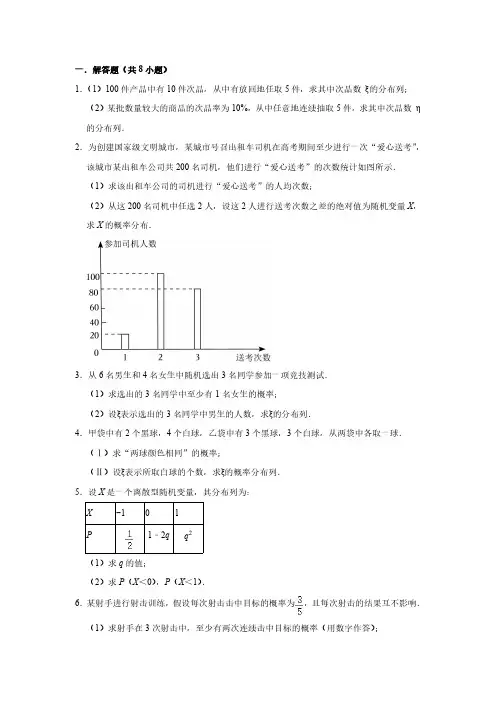
一．解答题（共8小题）1．（1）100件产品中有10件次品，从中有放回地任取5件，求其中次品数ξ的分布列；（2）某批数量较大的商品的次品率为10%，从中任意地连续抽取5件，求其中次品数η的分布列．2．为创建国家级文明城市，某城市号召出租车司机在高考期间至少进行一次“爱心送考”，该城市某出租车公司共200名司机，他们进行“爱心送考”的次数统计如图所示．（1）求该出租车公司的司机进行“爱心送考”的人均次数；（2）从这200名司机中任选2人，设这2人进行送考次数之差的绝对值为随机变量X，求X的概率分布．3．从6名男生和4名女生中随机选出3名同学参加一项竞技测试．（1）求选出的3名同学中至少有1名女生的概率；（2）设ξ表示选出的3名同学中男生的人数，求ξ的分布列．4．甲袋中有2个黑球，4个白球，乙袋中有3个黑球，3个白球，从两袋中各取一球．（Ⅰ）求“两球颜色相同”的概率；（Ⅱ）设ξ表示所取白球的个数，求ξ的概率分布列．5．设X是一个离散型随机变量，其分布列为：X−101P1﹣2q q2（1）求q的值；（2）求P（X＜0），P（X＜1）．6．某射手进行射击训练，假设每次射击击中目标的概率为，且每次射击的结果互不影响．（1）求射手在3次射击中，至少有两次连续击中目标的概率（用数字作答）；（2）求射手第3次击中目标时，恰好射击了4次的概率（用数字作答）；（3）设随机变量ξ表示射手第3次击中目标时已射击的次数，求ξ的分布列．7．袋中有3个红球，4个黑球，从袋中任取4个球．（1）求红球个数X的分布列；（2）若取到一个红球得2分，取到一个黑球得1分，求得分不小于6分的概率．8．从5名男生和3名女生中任选2人去参加学校组织的“低碳杯”知识抢答赛，用ξ表示选出的女生的人数．（1）求随机变量ξ的分布列；（2）求事件“选出的2学生至少有一女生”的概率．参考答案与试题解析一．解答题（共8小题）1．（1）100件产品中有10件次品，从中有放回地任取5件，求其中次品数ξ的分布列；（2）某批数量较大的商品的次品率为10%，从中任意地连续抽取5件，求其中次品数η的分布列．【解答】解：（1）由题意知ξ的可能取值为0，1，2，3，4，5，每次取出次品的概率为：，相当于5次独立重复实验，ξ～B（5，），P（ξ＝0）＝＝0.59059，P（ξ＝1）＝＝0.32805，P（ξ＝2）＝＝0.07329，P（ξ＝3）＝＝0.0081，P（ξ＝4）＝＝0.00045，P（ξ＝5）＝＝0.00001，∴ξ的分布列为：ξ012345P0.590590.328050.07290.00810.000450.00001（2）由题意知η的可能取值为0，1，2，3，4，5，且η～B（5，0.1），∴η的分布列为：η012345P0.590590.328050.07290.00810.000450.000012．为创建国家级文明城市，某城市号召出租车司机在高考期间至少进行一次“爱心送考”，该城市某出租车公司共200名司机，他们进行“爱心送考”的次数统计如图所示．（1）求该出租车公司的司机进行“爱心送考”的人均次数；（2）从这200名司机中任选2人，设这2人进行送考次数之差的绝对值为随机变量X，求X的概率分布．【解答】解：（1）由统计图得200名司机中送考1次的有20人，送考2次的有100人，送考3次的有80人，∴该出租车公司的司机进行“爱心送考”的人均次数为；（2）从该公司任选两名司机，记“这两人中﹣人送考1次，另一人送考2次”为事件A，“这两人中一人送考2次，另一人送考3次“为事件B，“这两人中﹣人送考1次，另一人送考3次”为事件C，“这两人送考次数相同”为事件D，由题意知X的所有可能取值为0，1，2，，，，所以X的分布列为：X012P3．从6名男生和4名女生中随机选出3名同学参加一项竞技测试．（1）求选出的3名同学中至少有1名女生的概率；（2）设ξ表示选出的3名同学中男生的人数，求ξ的分布列．【解答】解：（1）由意可知，选出的3名同学全是男生的概率为＝，∴选出的3名同学中至少有1名女生的概率为P＝1﹣＝．（2）根据题意，ξ的可能取值为0，1，2，3，P（ξ＝0）＝＝，P（ξ＝1）＝＝，P（ξ＝2）＝＝，P（ξ＝3）＝＝，∴ξ的分布列为：ξ0123P4．甲袋中有2个黑球，4个白球，乙袋中有3个黑球，3个白球，从两袋中各取一球．（Ⅰ）求“两球颜色相同”的概率；（Ⅱ）设ξ表示所取白球的个数，求ξ的概率分布列．【解答】解：（I）从甲中取出黑球的概率为，取出白球的概率为，从乙中取出黑球的概率为，取出白球的概率为，故“两球颜色相同”的概率P＝．（II）由题意可得，ξ所有可能取值为0，1，2，P（ξ＝0）＝＝，P（ξ＝1）＝，P（ξ＝2）＝，故ξ的分布列为：ξ012P5．设X是一个离散型随机变量，其分布列为：X−101P1﹣2q q2（1）求q的值；（2）求P（X＜0），P（X＜1）．【解答】解：（1）依题意，得，解得或（舍去），所以．（2）由（1）得，，所以，．6．某射手进行射击训练，假设每次射击击中目标的概率为，且每次射击的结果互不影响．（1）求射手在3次射击中，至少有两次连续击中目标的概率（用数字作答）；（2）求射手第3次击中目标时，恰好射击了4次的概率（用数字作答）；（3）设随机变量ξ表示射手第3次击中目标时已射击的次数，求ξ的分布列．【解答】解：（1）设事件该射手第i次射击，击中目标为A i，i＝1，2，3，则，所以，事件射手在3次射击中，至少有两次连续击中目标可表示为，因为事件，，A1A2A3互斥，所以又事件A1，A2，A3相互独立，所以＝＝；（2）事件射手第3次击中目标时，恰好射击了4次等于事件前3次中恰好击中两次目标且第四次击中目标，又各次击中目标的概率为，所以前3次中恰有两次击中目标的概率为，第四次击中目标的概率为，所以事件射手第3次击中目标时，恰好射击了4次的概率；（3）由已知ξ的取值有3，4，5，⋅⋅⋅，n，⋅⋅⋅，又，，，⋅⋅⋅，，所以随机变量ξ的分布列为：ξ345…n…P……7．袋中有3个红球，4个黑球，从袋中任取4个球．（1）求红球个数X的分布列；（2）若取到一个红球得2分，取到一个黑球得1分，求得分不小于6分的概率．【解答】解：（1）由题意可得，X可能取值为0，1，2，3，P（X＝0）＝，P（X＝1）＝，P（X＝2）＝，P（X＝3）＝，故X的分布列为：X0123P（2）设得分为Y，则得分Y可以取4，5，6，7，分别对应4个黑球，3黑1红，2黑2红，1黑3红四种情况，P（Y≥6）＝P（Y＝6）+P（Y＝7）＝，故得分不小于6分的概率为．8．从5名男生和3名女生中任选2人去参加学校组织的“低碳杯”知识抢答赛，用ξ表示选出的女生的人数．（1）求随机变量ξ的分布列；（2）求事件“选出的2学生至少有一女生”的概率．【解答】解：（1）由题意得ξ的可能取值为0，1，2，P（ξ＝0）＝＝，P（ξ＝1）＝＝，P（ξ＝2）＝＝，∴随机变量ξ的分布列为：ξ012P（2）事件“选出的2学生至少有一女生”的概率为：P＝P（ξ＝1）+P（ξ＝2）＝＝．。

第 2 章一维随机变量及其分布一、选择题1．设 F(x)是随机变量X的分布函数，则以下结论不正确的选项是（A）若 F(a)=0 ，则对任意 x≤a 有 F(x)=0（B）若 F(a)=1 ，则对任意 x≥a 有 F(x)=1（C）若 F(a)=1/2 ，则 P( x≤a)=1/2（D）若 F(a)=1/2 ，则 P( x≥a)=1/22．设随机变量 X 的概率密度 f(x) 是偶函数，分布函数为 F(x) ，则（A）F(x)是偶函数（B）F(x) 是奇函数（C）F(x)+F(-x)=1（D）2F(x)-F(-x)=1 3．设随机变量 X1, X 2的分布函数、概率密度分别为 F1 (x) 、F2 (x) ，f 1 (x)、f 2 (x) ，若 a>0, b>0, c>0，则以下结论中不正确的选项是（A）aF (x)+bF2(x)是某一随机变量分布函数的充要条件是a+b=11（B）cF1(x) F 2(x)是某一随机变量分布函数的充要条件是c=1（C）af 1(x)+bf2(x)是某一随机变量概率密度的充要条件是a+b=1（D）cf 1(x) f 2(x)是某一随机变量分布函数的充要条件是c=14．设随机变量 X1, X2是任意两个独立的连续型随机变量，它们的概率密度分别为 f 1 (x)和 f 2 (x) ，分布函数分别为 F1 (x) 和 F2 (x) ，则（A）f 1 (x) +f 2 (x)必为某一随机变量的概率密度（B）f 1(x) f 2(x)必为某一随机变量的概率密度（C）F1(x)+F 2(x)必为某一随机变量的分布函数（D）F1(x)F 2 (x)必为某一随机变量的分布函数5．设随机变量 X 遵从正态分布N (1,12)，Y遵从正态分布N (2,22) ，且P(|X1| 1) P(|Y 2| 1) ，则必有（A）1 2（B）1 2（C）1 2（D）1 26．设随机变量 X 遵从正态分布N ( ,2 ) ，则随σ的增大，概率P(|X|)（A）单调增大（B）单调减小（C）保持不变（D）增减不定7．设随机变量 X1,X2的分布函数分别为 F1 (x) 、F2(x) ，为使 aF1 (x) －bF2 (x)是某一随机变量分布函数，在以下给定的各组数值中应取（A）a3 , b2（B）a2 , b2（C）a1 , b3（D）a1 , b3 553322228．设 f(x)是连续型随机变量 X 的概率密度，则 f(x)必然是（A）可积函数（B）单调函数（C）连续函数（D）可导函数9．以下陈述正确的命题是（A）若P(X1) P(X 1), 则 P(X 1)12（B）若 X~b(n, p),则 P(X=k)=P(X=n-k), k=0,1,2,,n（C）若 X 遵从正态分布 , 则 F(x)=1-F(-x)（D）lim [ F (x) F ( x)]1x10．假设随机变量X遵从指数分布，则随机变量Y=min{X,2} 的分布函数（A）是连续函数（B）最少有两其中止点（C）是阶梯函数（D）恰好有一其中止点二、填空题1．一实习生用同一台机器连接独立的制造了 3 个同种零件，第i个零件不合格的概率为 p i1个零件中合格品的个数，则 P X2i 1,2,3 ，以 X 表示3i12．设随机变量X的概率密度函数为 f x2x0 x 1以 Y 表示对 X 的三次重复观察中0其他事件 X 1出现的次数，则 P Y2 23．设连续型随机变量X的分布密度为 f x axe 3x x 0，则 a，X的分布0x0函数为4．设随机变量的分布函数b , x0, 则 a =， b =，cF ( x)ax) 2(1c,x 0,=。

第2章一维随机变量 习题2一. 填空题：1.设 离 散 型 随 机 变 量 的 分 布 函 数 是 (){}x P x F ≤=ξ， 则 用 F (x) 表 示 概 {}0x P =ξ = __________。

解：()()000--x F x F 2.设 随 机 变 量 的 分 布 函 数 为 ()()+∞<<∞-+=x arctgx x F π121 则 P{ 0<<1} = ____14_____。

解： P{ 0<<1} = =-)0(F )1(F 143.设 服 从 参 数 为 的 泊 松 分 布 ， 且 已 知 P{ = 2 } = P{ = 3 }，则 P{ = 3 }= ___2783e - 或 。

4.设 某 离 散 型 随 机 变 量 的 分 布 律 是 {}⋅⋅⋅===,2,1,0,!k k C k P Kλξ，常 数 >0， 则 C 的 值 应 是 ___ e _____。

解：{}λλλλξ-∞=∞=∞==⇒=⇒=⇒=⇒==∑∑∑e C Ce k C k Ck P KK KK K 11!1!105 设 随 机 变 量 的 分 布 律 是 {}4,3,2,1,21=⎪⎭⎫⎝⎛==k A k P kξ则 ⎭⎬⎫⎩⎨⎧<<2521ξP = 。

解：()A A k P k 161516181412141=⎪⎭⎫ ⎝⎛+++==∑=ξ 令15161A = 得 A =1615()()212521=+==⎪⎭⎫ ⎝⎛<<ξξξp p P 8.041211516=⎥⎦⎤⎢⎣⎡+=6.若 定 义 分 布 函 数 (){}x P x F ≤=ξ， 则 函 数 F(x)是 某 一 随 机 变 量 的 分 布 函 数 的 充 要 条 件 是F ( x ) 单 调 不 减 ， 函 数 F (x) 右 连 续 ， 且 F (- ) = 0 ， F ( + ) = 17. 随机变量) ,a (N ~2σξ，记{}σ<-ξ=σa P )(g ，则随着σ的增大，g()σ之值 保 持 不 变 。

函数 x h( y)，则Y g(X )是连续性随机变量．其密度函数
为
fY
(
y)
f
X
[h( y)] 0
|
h(
y)
|
当 y
其他
其中 min{g(), g()}， max{g(), g()}．
第17页/共19页
•作业 •第63页 10
第18页/共19页
感谢您的观看！
第19页/共19页
Y X 3的概率密度．
解： X 的密度函数为
ex 当 x 0
f (x) 0
当x0
因为函数 y x3是严格单调
增函数，其反函数为 x 3 y ，由
X 的密度函可数直接求得Y 的 密度函数.
fY ( y)
f (3 0
y )( 3
y ) 当 y 0 ,
当y0
即
fY
(
y)
1 3
e
3
y
第3章 连续型随机变量
3.2 一维连续型随机变量函数的分布
例3.6
定理3.2
例3.7
例3.8
同步练习
小结
第2页/共19页
第3章 连续型随机变量
3.2 一维连续型随机变量函数的分布
例 3.6 设随机变量 X 有
解：设 Y 的分布函数为 FY ( y)，
概率密度
则
x
f
X
(
x)
8
0
当0 x 4 其他
Y 2X 1的密度函数为
fY
( y)
y1 e 2 (
y 1) 2
,
y
1，
0
, y 1
即
fY
(

【参考答案】
A 7.设随机变量ξ 服从 0-布,又知ξ 取 1 的概率为它取 0 的概率的一半,则p{ξ = 1} 是( )。
1 密 A. 3
B.0 1
C. 2 D.1 【参考答案】
A
8.离散型随机变量ξ 的分布律为P (ξ = k) = bλk ,(k = 1,2,⋯),的充分必要条件是( )。
A.b >0且0 < λ <1
)。 【参考答案】 空（1）: 0.0455
3.设随机变量ξ
的分布函数为F (x) =
⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪
1−
k2 x2 + 2kx + 2 2
e −kx,x
≥0
⎪
⎪ ⎪ ⎪ ⎩
0,
x <0
,则p
⎧ ⎪⎪⎨⎪− ⎪ ⎩
1 k
≤ξ
≤
1 k
⎫ ⎮ ⎮ ⎬ ⎮ ⎮ ⎭
=
( )。 【参考答案】
空（1）:
线
【参考答案】
ξ 的概率密度为φ (x) =
1
− (x −1) 2
e8
2 2π
【参考答案】
ξ 的概率密度φ (x) =
⎧ ⎪⎪ ⎪ ⎨ ⎪⎪ ⎪ ⎩
λe −λx 0
x >0 x ≤0
y = 1 x3+2的反函数x = h (y) = 3 3(y−2) 3
⎧⎪
1
⎪
h '(y) =
−2
(3y−6) 3
,φ
⎥
⎦
x 0
= 1 − 1 e −x+ 1 =1− 1 e −x
22
2
2
⎧⎪ ⎪ ⎪ ⎪
1 ex

概率论与数理统计练习题系第二章专业班姓名随机变量及其分布（一）学号一．选择题：1 ．设X是失散型随机变量，以下可以作为X的概率分布是[B]X x1x2x3x4X x1x2x3x4（ A）1111（B）1111 p p248162488X x1x2x3x4（D）X x1x2x3x4（ C）1111p1111 p23412234122 ．设随机变量ξ的分布列为X0123C ] p0.10.30.4F ( x) 为其分布函数，则 F ( 2) = [0.2（ A）（B）（ C）（D）1二、填空题：1 ．设随机变量X的概率分布为X012，则 a = p a0.20.52 ．某产品 15 件，其中有次品 2 件。

现从中任取3 件，则抽得次品数X 的概率分布为P(X 0)C13366， P( x1)C21 C13236， P( xC22 C1313 C153105C1531052)105C1533 ．设射手每次击中目标的概率为, 连续射击10 次，则击中目标次数X 的概率分布为P( X k ) C10k(0.7)k (0.3)10 k(k0,1, 2,L ,10)三、计算题：1 ．同时掷两颗骰子，设随机变量X为“两颗骰子点数之和”求：（ 1）X的概率分布；（2）P( X3) ；（3）P( X12)解：（1）P( X2)1P( X3)2P( X4)3P(X 5)4，，，，36363636P( X6)5，P( X7) 6 ， P( X5 436 8)， P(X 9)363636P( X10)3 ，P( X11)2 ，P( X 1363612)36所以 X 的概率分布列：X 2 34 5 6 7 89 10 11 12P12 34 5 6 5 4 3 2 1363636363636 3636363636（2） P(X3) 336（ 3） P(X>12)=02 ．产品有一、 二、三等品及废品四种， 其中一、 二、三等品及废品率分别为 60%，10%，20%及 10%，任取一个产品检查其质量，试用随机变量X 描述检查结果。

第二章 《随机变量及其分布》练习题一、选择题1．任意抛掷三枚均匀硬币，恰有2枚正面朝上的概率为( )A ．34 B ．38 C ．13 D ．142．在4次独立重复试验中，事件A 发生的概率相同，若事件A 至少发生1次的概率为6581，则事件A 在1次试验中发生的概率为( )A ．13 B ．25 C ．56 D ．343．若X ～B (10,0.8)，则P (X ＝8)等于( )A ．C 810×0.88×0.22B ．C 810×0.82×0.28 C ．0.88×0.22D ．0.82×0.284．若X 是一个随机变量，则E (X －E (X ))的值为( )A ．无法求B ．0C ．E (X )D ．2E (X )5．某人从家乘车到单位，途中有3个交通岗．假设在各交通岗遇到红灯的事件是相互独立的，且概率都是0.4，则此人上班途中遇红灯次数的均值为( ) A ．0.4 B ．1.2 C ．0.43D ．0.66．已知随机变量ξ的概率分布如下表所示：且η＝2ξ＋3，则E (η)等于( )A.35 B.65 C.215 D.1257．随机变量ξ的分布列为则ξ的数学期望是( )A ．2B ．2.1C ．2.3D ．随m 的变化而变化8．某班有14的学生数学成绩优秀，如果从班中随机地找出5名学生，那么其中数学成绩优秀的学生数ξ～B ⎝⎛⎭⎫5，14，则E (－ξ)的值为( ) A.14 B ．－14 C.54 D ．－549．有10张卡片，其中8张标有数字2,2张标有数字5，从中任意抽出3张卡片，设3张卡片上的数字之和为X ，则X 的数学期望是( )A ．7.8 B ．8 C ．16 D ．15.6 10．设随机变量ξ的分布列如下表：且E (ξ)＝1.6，则a －b 等于( D ．－0.411．设一随机试验的结果只有A 和A 且P (A )＝m ，令随机变量ξ＝⎩⎪⎨⎪⎧1，A 发生0，A 不发生，则ξ的方差D (ξ)等于( )A ．mB ．2m (1－m )C ．m (m －1)D ．m (1－m )12．由以往的统计资料表明，甲、乙两运动员在比赛中得分情况为：D ．无法确定 13．已知随机变量ξ，η满足ξ＋η＝8，且ξ服从二项分布ξ～B (10,0.6)，则E (η)和D (η)的值分别是( )A ．6和2.4B ．2和2.4C ．2和5.6D ．6和5.614.随机变量X 的分布列如下：若E (X )＝158，则D (X )等于( ) A.732 B.932 C.3364 D.556415．若随机变量ξ的分布列为P (ξ＝m )＝13，P (ξ＝n )＝a ，若E (ξ)＝2，则D (ξ)的最小值等于( )A ．0B ．2C ．4D ．无法计算16．某班举行了一次“心有灵犀”的活动，教师把一张写有成语的纸条出示给A 组的某个同学，这个同学再用身体语言把成语的意思传递给本组其他同学．若小组内同学甲猜对成语的概率是0.4，同学乙猜对成语的概率是0.5，且规定猜对得1分，猜不对得0分，则这两个同学各猜1次，得分之和X (单位：分)的数学期望为( )A ．0.9 B ．0.8 C ．1.2 D ．1.117.有10张卡片，其中8张标有数字2,2张标有数字5，从中任意抽出3张卡片，设3张卡片上的数字之和为X ，则X 的数学期望是( )A ．7.8 B ．8 C ．16 D ．15.6二、填空题1．一射手对靶射击，直到第一次命中为止，每次命中的概率为0.6，现有4颗子弹，命中后的剩余子弹数目X 的期望为________．2．袋中装有6个红球，4个白球，从中任取1个球，记下颜色后再放回，连续摸取4次，设X 是取得红球的次数，则E (X )＝________.3．随机变量ξ的取值为0,1,2.若P (ξ＝0)＝15，E (ξ)＝1，则D (ξ)＝________.4.节日期间，某种鲜花的进价是每束2.5元，售价是每束5元，节后对没有卖出的鲜花以每束1.6元处理．根据前5年节日期间对这种鲜花需求量ξ(束)的统计(如下表)，若进这种鲜花500束在今年节日期间销售，则利润的均值是________元.三、解答题1．某师范大学志愿者支教团体有6名男同学，4名女同学．在这10名同学中，3名同学来自数学系，其余7名同学来自物理、化学等其他互不相同的七个系．现从这10名同学中随机选取3名同学，到希望小学进行支教活动（每位同学被选到的可能性相同）． （Ⅰ）求选出的3名同学来自互不相同的系的概率；（Ⅱ）设X 为选出的3名同学中女同学的人数，求随机变量X 的分布列和数学期望．2.现有甲、乙两个靶，某射手向甲靶射击一次，命中的概率为34；向乙靶射击一次命中的概率为23，该射手每次射击的结果相互独立．假设该射手进行一次测试，先向甲靶射击两次，若两次都命中，则通过测试；若两次中只命中一次，则再向乙靶射击一次，命中也可通过测试，其它情况均不能通过测试．(1)求该射手通过测试的概率；(2)求该射手在这次测试中命中的次数X 的分布列及数学期望．3．在“出彩中国人”的一期比赛中，有6位歌手(1～6)登台演出，由现场的百家大众媒体投票选出最受欢迎的出彩之星，各家媒体独立地在投票器上选出3位出彩候选人，其中媒体甲是1号歌手的歌迷，他必选1号，另在2号至6号中随机的选2名；媒体乙不欣赏2号歌手，他必不选2号；媒体丙对6位歌手的演唱没有偏爱，因此在1至6号歌手中随机的选出3名．(1)求媒体甲选中3号且媒体乙未选中3号歌手的概率；(2)用X表示3号歌手得到媒体甲、乙、丙的票数之和，求X的分布列及数学期望．4.某学校举行知识竞赛，第一轮选拔共设有A、B、C、D四个问题，规则如下：①每位参加者计分器的初始分均为10分，答对问题A、B、C、D分别加1分、2分、3分、6分，答错任一题减2分；②每回答一题，计分器显示累计分数，当累计分数小于8分时，答题结束，淘汰出局；当累计分数大于或等于14分时，答题结束，进入下一轮；当答完四题，累计分数仍不足14分时，答题结束，淘汰出局；③每位参加者按问题A、B、C、D顺序作答，直至答题结束．假设甲同学对问题A、B、C、D回答正确的概率依次为34、12、13、14，且各题回答正确与否相互之间没有影响．(1)求甲同学能进入下一轮的概率；(2)用ξ表示甲同学本轮答题结束时答题的个数，求ξ的分布列和数学期望E(ξ)．第二章 《随机变量及其分布》练习题一、选择题1．任意抛掷三枚均匀硬币，恰有2枚正面朝上的概率为( )A ．34 B ．38 C ．13 D ．14[解析] 抛一枚硬币，正面朝上的概率为12，则抛三枚硬币，恰有2枚朝上的概率为P ＝C 23⎝⎛⎭⎫122×12＝38. 2．在4次独立重复试验中，事件A 发生的概率相同，若事件A 至少发生1次的概率为6581，则事件A 在1次试验中发生的概率为( )A ．13 B ．25 C ．56 D ．34[解析] 事件A 在一次试验中发生的概率为p ，由题意得1－C 04p 0(1－p )4＝6581，所以1－p ＝23，p ＝13， 3．若X ～B (10,0.8)，则P (X ＝8)等于( )A ．C 810×0.88×0.22B ．C 810×0.82×0.28 C ．0.88×0.22D ．0.82×0.28[解析] ∵X ～B (10,0.8)，∴P (X ＝k )＝C k 100.8k (1－0.8)10－k ，∴P (X ＝8)＝C 8100.88·0.22，故选A ． 4．若X 是一个随机变量，则E (X －E (X ))的值为( )A ．无法求B ．0C ．E (X )D ．2E (X )[解析] 只要认识到E (X )是一个常数，则可直接运用均值的性质求解．∵E (aX ＋b )＝aE (X )＋b ，而E (X )为常数，∴E (X －E (X ))＝E (X )－E (X )＝0. [答案] B5．某人从家乘车到单位，途中有3个交通岗．假设在各交通岗遇到红灯的事件是相互独立的，且概率都是0.4，则此人上班途中遇红灯次数的均值为( )A ．0.4B ．1.2C ．0.43D ．0.6[解析] ∵途中遇红灯的次数X 服从二项分布，即X ～B (3,0.4)，∴E (X )＝3×0.4＝1.2. [答案] B 6．已知随机变量ξ的概率分布如下表所示：且η＝2ξ＋3，则E (η)等于( )A.35 B.65 C.215 D.125解析：E (ξ)＝0×715＋1×715＋2×115＝35，E (η)＝E (2ξ＋3)＝2E (ξ)＋3＝2×35＋3＝215.答案：C7．随机变量ξ的分布列为则ξ的数学期望是( )A ．2B ．2.1C ．2.3D ．随m 的变化而变化解析：∵0.2＋0.5＋m ＝1，∴m ＝0.3，∴E (ξ)＝1×0.2＋2×0.5＋3×0.3＝2.1.答案：B8．某班有14的学生数学成绩优秀，如果从班中随机地找出5名学生，那么其中数学成绩优秀的学生数ξ～B ⎝⎛⎭⎫5，14，则E (－ξ)的值为( )A.14 B ．－14 C.54 D ．－54 解析：∵E (ξ)＝5×14＝54，∴E (－ξ)＝－E (ξ)＝－54，故选D.9．有10张卡片，其中8张标有数字2,2张标有数字5，从中任意抽出3张卡片，设3张卡片上的数字之和为X ，则X 的数学期望是( )A ．7.8 B ．8 C ．16 D ．15.6解析：X 的取值为6,9,12，P (X ＝6)＝C 38C 310＝715，P (X ＝9)＝C 28C 12C 310＝715，P (X ＝12)＝C 18C 22C 310＝115.E (X )＝6×715＋9×715＋12×115＝7.8.答案：A10．设随机变量ξ的分布列如下表：且E (ξ)＝1.6，则a －b 等于( D ．－0.4解析：根据题意，⎩⎪⎨⎪⎧ 0.1＋a ＋b ＋0.1＝1，0×0.1＋a ＋2×b ＋3×0.1＝1.6，解得⎩⎪⎨⎪⎧a ＝0.3b ＝0.5.所以a －b ＝－0.2.答案C11．设一随机试验的结果只有A 和A 且P (A )＝m ，令随机变量ξ＝⎩⎪⎨⎪⎧1，A 发生0，A 不发生，则ξ的方差D (ξ)等于( )A ．mB ．2m (1－m )C ．m (m －1)D ．m (1－m ) 解析：依题意ξ服从两点分布，∴D (ξ)＝m (1－m )，故选D.12．由以往的统计资料表明，甲、乙两运动员在比赛中得分情况为：A ．甲B ．乙C ．甲、乙均可D ．无法确定解析：E (ξ1)＝E (ξ2)＝1.1，D (ξ1)＝1.12×0.2＋0.12×0.5＋0.92×0.3＝0.49，D (ξ2)＝1.12×0.3＋0.12×0.3＋0.92×0.4＝0.69，∴D (ξ1)<D (ξ2)，即甲比乙得分稳定，选甲参加较好，故选A.13．已知随机变量ξ，η满足ξ＋η＝8，且ξ服从二项分布ξ～B (10,0.6)，则E (η)和D (η)的值分别是( )A ．6和2.4 B ．2和2.4 C ．2和5.6D ．6和5.6解析：由已知E (ξ)＝10×0.6＝6，D (ξ)＝10×0.6×0.4＝2.4.∵ξ＋η＝8，∴η＝8－ξ.∴E (η)＝－E (ξ)＋8＝2，D (ξ)＝(－1)2D (ξ)＝2.4.答案：B 14.随机变量X 的分布列如下：若E (X )＝158，则D (X )等于( ) A.732 B.932 C.3364 D.5564解析：由⎩⎪⎨⎪⎧1×0.5＋2x ＋3y ＝158，0.5＋x ＋y ＝1，得⎩⎨⎧x ＝18，y ＝38.所以D (X )＝⎝⎛⎭⎫1－1582×12＋⎝⎛⎭⎫2－1582×18＋⎝⎛⎭⎫3－1582×38＝5564. 答案：D15．若随机变量ξ的分布列为P (ξ＝m )＝13，P (ξ＝n )＝a ，若E (ξ)＝2，则D (ξ)的最小值等于( )A ．0B ．2C ．4D ．无法计算解析：由于分布列中，概率和为1，则a ＋13＝1，a ＝23. ∵E (ξ)＝2，∴m 3＋2n3＝2.∴m ＝6－2n .∴D (ξ)＝13×(m －2)2＋23×(n －2)2＝23×(n －2)2＋13×(6－2n －2)2＝2n 2－8n ＋8＝2(n －2)2.∴n ＝2时，D (ξ)取最小值0.答案：A16．某班举行了一次“心有灵犀”的活动，教师把一张写有成语的纸条出示给A 组的某个同学，这个同学再用身体语言把成语的意思传递给本组其他同学．若小组内同学甲猜对成语的概率是0.4，同学乙猜对成语的概率是0.5，且规定猜对得1分，猜不对得0分，则这两个同学各猜1次，得分之和X (单位：分)的数学期望为( )A ．0.9 B ．0.8 C ．1.2D ．1.1[解析] X 的取值为0、1、2，P (X ＝0)＝(1－0.4)(1－0.5)＝0.3， P (X ＝1)＝0.4×(1－0.5)＋(1－0.4)×0.5＝0.5， P (X ＝2)＝0.4×0.5＝0.2，∴E (X )＝0×0.3＋1×0.5＋2×0.2＝0.9. [答案] A17.有10张卡片，其中8张标有数字2,2张标有数字5，从中任意抽出3张卡片，设3张卡片上的数字之和为X ，则X 的数学期望是( )A ．7.8 B ．8 C ．16 D ．15.6[解析] X 的取值为6、9、12，P (X ＝6)＝C 38C 310＝715，P (X ＝9)＝C 28C 12C 310＝715，P (X ＝12)＝C 18C 22C 310＝115. E (X )＝6×715＋9×715＋12×115＝7.8. [答案] A二、填空题1．一射手对靶射击，直到第一次命中为止，每次命中的概率为0.6，现有4颗子弹，命中后的剩余子弹数目X 的期望为________．解析：X 的可能取值为3,2,1,0，P (X ＝3)＝0.6；P (X ＝2)＝0.4×0.6＝0.24；P (X ＝1)＝0.42×0.6＝0.096；P (X ＝0)＝0.43＝0.064.所以E (X )＝3×0.6＋2×0.24＋1×0.096＋0×0.064＝2.376.2．袋中装有6个红球，4个白球，从中任取1个球，记下颜色后再放回，连续摸取4次，设X 是取得红球的次数，则E (X )＝________.解析：每一次摸得红球的概率为610＝35，由X ～B ⎝⎛⎭⎫4，35，则E (X )＝4×35＝125. 3．随机变量ξ的取值为0,1,2.若P (ξ＝0)＝15，E (ξ)＝1，则D (ξ)＝________.解析：由题意设P (ξ＝1)＝p ，则ξ的分布列如下由E (ξ)＝1，可得p ＝35，所以D (ξ)＝12×15＋02×35＋12×15＝25. 答案：254.节日期间，某种鲜花的进价是每束2.5元，售价是每束5元，节后对没有卖出的鲜花以每束1.6元处理．根据前5年节日期间对这种鲜花需求量ξ(束)的统计(如下表)，若进这种鲜花500束在今年节日期间销售，则利润的均值是________元.解析：节日期间这种鲜花需求量的均值为E (ξ)＝200×0.20＋300×0.35＋400×0.30＋500×0.15＝340(束)．设利润为η，则η＝5ξ＋1.6×(500－ξ)－500×2.5＝3.4ξ－450， 所以E (η)＝3.4E (ξ)－450＝3.4×340－450＝706(元)． 三、解答题1．某师范大学志愿者支教团体有6名男同学，4名女同学．在这10名同学中，3名同学来自数学系，其余7名同学来自物理、化学等其他互不相同的七个系．现从这10名同学中随机选取3名同学，到希望小学进行支教活动（每位同学被选到的可能性相同）． （Ⅰ）求选出的3名同学来自互不相同的系的概率；（Ⅱ）设X 为选出的3名同学中女同学的人数，求随机变量X 的分布列和数学期望． 解：（Ⅰ）3A 设“选出的名同学来自互不相同的系”为事件，1203373731049()60C C C C P A C346310()(0,1,2,3)k k c c p xk k c （Ⅱ）随机变量X 的所有可能值为0，1，2，3.随机变量X 的分布列为数学期望113161236210305E X ．2.现有甲、乙两个靶，某射手向甲靶射击一次，命中的概率为34；向乙靶射击一次命中的概率为23，该射手每次射击的结果相互独立．假设该射手进行一次测试，先向甲靶射击两次，若两次都命中，则通过测试；若两次中只命中一次，则再向乙靶射击一次，命中也可通过测试，其它情况均不能通过测试．(1)求该射手通过测试的概率；(2)求该射手在这次测试中命中的次数X 的分布列及数学期望．[解析] (1)设“该射手通过测试”为事件A ，“向甲靶射击两次都命中”为事件B ，“向甲靶射击两次中只命中一次，则再向乙靶射击一次，命中”为事件C ．事件B ，C 互斥，且A ＝B ＋C ．所以该射手通过测试的概率P (A )＝P (B )＋P (C )＝⎝⎛⎭⎫342＋C 12·34·⎝⎛⎭⎫1－34·23＝1316. (2)由题意知，X ＝0,1,2. P (X ＝0)＝⎝⎛⎭⎫1－342＝116；P (X ＝1)＝C 12·34·⎝⎛⎭⎫1－34·⎝⎛⎭⎫1－23＝18；P (X ＝2)＝P (A )＝1316. 所以该射手在这次测试中命中的次数X 的分布列为该射手在这次测试中命中的次数X 的数学期望为E (X )＝0×116＋1×18＋2×1316＝74.3．在“出彩中国人”的一期比赛中，有6位歌手(1～6)登台演出，由现场的百家大众媒体投票选出最受欢迎的出彩之星，各家媒体独立地在投票器上选出3位出彩候选人，其中媒体甲是1号歌手的歌迷，他必选1号，另在2号至6号中随机的选2名；媒体乙不欣赏2号歌手，他必不选2号；媒体丙对6位歌手的演唱没有偏爱，因此在1至6号歌手中随机的选出3名．(1)求媒体甲选中3号且媒体乙未选中3号歌手的概率；(2)用X 表示3号歌手得到媒体甲、乙、丙的票数之和，求X 的分布列及数学期望．[分析] (1)设A 表示事件：“媒体甲选中3号歌手”，B 表示事件“媒体乙选中3号歌手”，C 表示事件“媒体丙选中3号歌手”，由等可能事件概率公式求出P (A )，P (B )，由此利用相互独立事件的概率乘法公式和对立事件的概率公式能求出媒体甲选中3号歌手且媒体乙未选中3号歌手的概率．(2)先由等可能事件概率计算公式求出P (C )，由已知得X 的可能取值为0,1,2,3，分别求出相应的概率，由此能求出X 的分布列及数学期望．[解析] (1)设A 表示事件“媒体甲选中3号歌手”，B 表示事件“媒体乙选中3号歌手”，C 表示事件“媒体丙选中3号歌手”， P (A )＝C 14C 25＝25，P (B )＝C 24C 35＝35，媒体甲选中3号且媒体乙未选中3号歌手的概率为P (A B )＝P (A )(1－P (B ))＝25×(1－35)＝425.(2)P (C )＝C 25C 36＝12，由已知得X 的可能取值为0,1,2,3，P (X ＝0)＝P (A B C )＝(1－25)(1－35)(1－12)＝325，P (X ＝1)＝P (A B C )＋P (A B C )＋P (A B C )＝25(1－35)(1－12)＋(1－25)×35×(1－12)＋(1－25)(1－35)×12＝1950， P (X ＝2)＝P (AB C )＋P (A B C )＋P (A BC )＝25×35×(1－12)＋25(1－35)×12＋(1－25)×35×12＝1950，P (X ＝3)＝P (ABC )＝25×35×12＝325，∴X 的分布列为E (X )＝0×325＋1×1950＋2×1950＋3×325＝32.114.某学校举行知识竞赛，第一轮选拔共设有A 、B 、C 、D 四个问题，规则如下：①每位参加者计分器的初始分均为10分，答对问题A 、B 、C 、D 分别加1分、2分、3分、6分，答错任一题减2分；②每回答一题，计分器显示累计分数，当累计分数小于8分时，答题结束，淘汰出局；当累计分数大于或等于14分时，答题结束，进入下一轮；当答完四题，累计分数仍不足14分时，答题结束，淘汰出局；③每位参加者按问题A 、B 、C 、D 顺序作答，直至答题结束．假设甲同学对问题A 、B 、C 、D 回答正确的概率依次为34、12、13、14，且各题回答正确与否相互之间没有影响．(1)求甲同学能进入下一轮的概率；(2)用ξ表示甲同学本轮答题结束时答题的个数，求ξ的分布列和数学期望E (ξ)．[解析] 设A 、B 、C 、D 分别表示甲同学能正确回答第一、二、三、四个问题的事件，A －、B －、C －、D－分别为A 、B 、C 、D 的对立事件(例如A －表示甲同学第一题回答错误)．由题设条件知，P (A )＝34，P (B )＝12，P (C )＝13，P (D )＝14，P (A －)＝14，P (B －)＝12，P (C －)＝23，P (D －)＝34. (1)记“甲同学能进入下一轮”为事件W ，则由题设条件知W ＝ABC ＋AB C －D ＋A B －CD ＋A －BCD ＋A－B C －D ，∵A 、B 、C 、D 各事件相互独立，∴P (W )＝P (A )·P (B )·P (C )＋P (A )·P (B )·P (C －)·P (D )＋P (A )·P (B －)·P (C )·P (D )＋P (A －)·P (B )·P (C )·P (D )＋P (A －)·P (B )·P (C －)·P (D )＝34×12×13＋34×12×23×14＋34×12×13×14＋14×12×13×14＋14×12×23×14＝14. (2)由题意知，ξ的可能取值为2、3、4，则P (ξ＝2)＝P (A －B －)＝P (A －)·P (B －)＝14×12＝18， P (ξ＝3)＝P (ABC ＋A B －C －)＝P (A )P (B )P (C )＋P (A )P (B －)P (C －)＝34×12×13＋34×12×23＝38. P (ξ＝4)＝1－P (ξ＝2)－P (ξ＝3)＝1－18－38＝12， ∴ξ的分布列为∴E (ξ)＝2×18＋3×38＋4×12＝278.。

随机变量及其概率分布练习题(共90分)一．选择题(每题2分共20分)2．F(X)是随机变量X 的分布函数，则下列结论不正确的是（ ）A.≤0F(x )1≤B.F(x )=P{X=x }C.F(x )=P{X x ≤}D.F(∞+)=1, F(∞-)=03．设随机变量X 的分布律为如下表格：F(x)为其分布函数，则F(5)=( ) X0 2 4 6 P 0.1 0.2 0.3 0.4A.0.3B.0.5C.0.6D.0.44．下列函数可以作为随机变量分布函数的是（ ） 4x 01≤≤x 2x 10<≤xA.F(x)=B.F(x)=1 其它2 其它-1 x<0 0 x<0C.F(x)= 2x 10<≤xD.F(x)= 2x 5.00<≤x 1 其它 1 x ≥0.54x 31<<-x 5．设X 的密度函数为f(x)= 则P{-2<x<2}=( ) 0, 其它A. 0B.83C. 43D. 856. 以下函数可作为随机变量X 的概率密度的是（ ）A.f(x)=.;11,0,其它<<-⎩⎨⎧x xB.f(x)=.;11,,02其它<<-⎩⎨⎧x xC.f(x)=.;11,0,21其它<<-⎪⎩⎪⎨⎧x D.f(x)=.;11,0,2其它<<-⎩⎨⎧x7.设随机变量X~N(1，4)，5.0)0(,8413.0)1(=Φ=Φ，则事件{13X ≤≤}的概率为（） A.0.1385 B.0.2413 C.0.2934 D.0.34138．已知随机变量X 的分布函数为（ ）F(x)= ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥<≤<≤<313132102100x x x x ，则P }{1X ==A ． 61B ．21C ．32D ．19．已知连续型随机变量X 服从区间[a ，b ]上的均匀分布，则概率=⎭⎬⎫⎩⎨⎧+<32b a X P ( )A ．0B ．31C ．32D ．110、设随机变量X 在区间[2，6]上服从均匀分布，则P{2<x<4}=( )A.P{5<x<7}B.p{1<x<3}C.P{3<x<5}D.P{4.5<x<6.5}二．填空题(每题2分共20分)2．设连续型随机变量X 的分布函数为如下F(x), 则X 的概率密度)(x f 为（ ） 0 x<0F(x)= 2x, 5.00<≤x1 x ≥0.53．设随机变量X 的分布为P{X=k}=10k，k=0,1，2,3,4,则P{0.5<X ≤2}=( )4．设随机变量X ～N(2,9)，已知标准正态分布函数值=Φ)1(0.8413，为使P{X<a}<0.8413,则常数a<( )5．某人掷五次骰子，则在五次中得到点为6的次数X 的分布率为P{X=i}=( ) i=0,1,2,3,4,56．设随机变量X 服从区间[]10,0上的均匀分布，则P （X>4）=_ _．7．在[]T ,0内通过某交通路口的汽车数X 服从泊松分布，且已知P{X=4}=3P{X=3}，则在[]T ,0内至少有一辆汽车通过的概率为_ _．8.已知随机变量X 的分布函数为F(x)=⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤<≤<3x 13x 1321x 0210x 0 则P{2<X ≤4}=_ _．9.已知随机变量X 的概率密度为f(x)=ce -|x|，-∞<x<+∞，则c=_ _．10．设随机变量X 的概率分布为F (x )为其分布函数，则F (3)=_ _．三．计算题。

y 8 用 X 代替2 X +8 y 2
概率论
用

y X
y 代替 X y
2

这样做是为了利用已知的 X的分布，从而求出相应的概率.
这是求r.v.的函数的分布的一种常用方法.
概率论 定理: 设 X是一个取值于区间 [a, b], 具有概率密度 f(x)的连续型随机变量, 又设 y=g(x)处处可导, 且对于任意 x, 恒有 g'(x)>0 或恒有 g'(x)<0, 则 Y=g(X)是一个连续型随机变量，它的概率密度为：
y
f X ( x)
1

( x ) 2
2
2
概率论
2
1
e
,
x
yb fY ( y ) fX , a a
y
2
即：fY ( y )
1 a
1 2

yb a 2
2
e

dh( y ) , f X [h( y )] fY ( y ) dy 0,
a x b
y
其它
其中， min g ( x ), max g ( x ),
a x b
x=h(y) 是 y=g(x) 的反函数 .
概率论 2x 2 0 x 例4: 设随机变量X的概率密度为: f X ( x ) 求 Y = sinX 的概率密度. 1 Y 1 0 其它 解: 当 0 x 时, 0 y 1 FY y P Y y
当 y 0时，FY ( y ) 0,
当 y 1时，FY ( y ) 1，

1 19 P (Y ≥ 1) = 1 − P (Y = 0) = 1 − (1 − )3 = 3 27
(8)
Y = 2X +1， 各值互不相等， Y 的概率分布为 P(Y = −1) = 0.5, P(Y = 3) = 0.5 。
⎧0 ⎪ 其分布函数为 FY ( y ) = ⎨0.5 ⎪1 ⎩
y < −1 −1 ≤ y < 3 y≥3
, Y = g(X ) 为 X
= g ( xi ) 各值互不相等，则 Y 的分布为 P (Y = yi ) = pi , i = 1, 2, = g ( xi ) 各值不是互不相等， 则 Y 的分布为： P (Y = yi ) =
g ( x j ) = yi
∑
P( X = x j )
2、若 X 为连续型随机变量，其概率密度为 概率密度
x<a a≤ x<b x≥b
⎧λ e − λ x 5、 指数分布， 密度函数 f ( x) = ⎨ ⎩ 0
三、随机变量函数的分布
⎧1 − e− λ x x>0 ， 分布函数 F ( x) = ⎨ x≤0 ⎩ 0
= xi ) = pi , i = 1, 2,
x>0 x≤0
1、若 X 为离散型随机变量，概率分布为 P ( X 的函数，求 Y 的分布。 (1) 若 yi (2) 若 yi
y 2 + Xy + 1 = 0 有实根的概率
为
。 (7) 设 随 机 变 量
X ~ B(2, p), Y ~ B(3, p)
， 若
P ( X ≥ 1) =
5 ， 则 9
P(Y ≥ 1) =
。
(8) 给定 X 的分布 P( X ，Y 的分布函数为

概率论
第二节 离散型随机变量
离散型随机变量及其分布律 离散型随机变量表示方法 三种常见分布
一、离散型随机变量及其分布律
例1 从中任取3 个球 取到的白球数X是一个随机变量 . (1) X 可能取的值是0,1,2 ; (2) 取每个值的概率为:
3 P { X 0} 3 5 1 3 10 5 6 3 10 5 3 3 10
2) 二项分布的泊松近似
定理(泊松定理)：在n重伯努利试验中，
概率论
事件A在每次试验中发生的概率为p， 如果n 时，np ( 0为常数 )， 则对任意给定的非负整数k，有： n k n k lim p 1 p = e n k k!
k 3 k
3 k
, k 0,1,2,3
=0.104
3. 泊松分布(Poisson Distribution)
1) 设随机变量X所有可能取的值为0 , 1 , 2 , … , 且概率分布为：
P( X k )
概率论

k
e

,
k 0,1,2,,
k!
其中 λ>0 是常数, 则称 X 服从参数为 λ 的泊松分布,记作X~π(λ).
概率论
随机变量 X 只可能取 0 与 1 两个值，其分布律为：
PX k p 1 p
k 1 k
,
k 0,1
0
p 1
或
X
0
q
1
p
pk
称 X 服从（0-1）分布或两点分布 或
X ~ b(1, p)
概率论
对于一个随机试验，如果它的样本空间只包含两个元 素，即 W {1 , 2 }，我们总能在W上定义一个服从 （0－1）分布的随机变量．

第七章随机变量及其分布目录第七章随机变量及其分布 27.1条件概率与全概率公式 27.1.1条件概率 27.1.2全概率公式 3习题7.1 47.2离散型随机变量及其分布列 5习题7.2 67.3离散型随机变量的数字特征 77.3.1离散型随机变量的均值 77.3.2离散型随机变量的方差 9习题7.3 107.4二项分布与超几何分布 117.4.1二项分布 117.4.2超几何分布 13习题7.4 147.5正态分布 15习题7.5 16复习参考题7 17随机变量及其分布7.1条件概率与全概率公式7.1.1条件概率思考原理一般地,设A,B为两个随机事件,且P(A)>0,我们称P(B∣A)=P(AB) P(A)为在事件A发生的条件下,事件B发生的条件概率,简称条件概率(conditional probability ).思考原理由条件概率的定义,对任意两个事件A与B,若P(A)>0,则P(AB)=P(A)P(B∣A)我们称上式为概率的乘法公式(multiplication formula).1在5道试题中有3道代数题和2道几何题，每次从中随机抽出1道题，抽出的题不再放回.求：(1)第1次抽到代数题目第2次抽到几何题的概率；(2)在第1次抽到代数题的条件下，第2次抽到几何题的概率.2已知3张奖券中只有1张有奖，甲、乙、丙3名同学依次无放回地各抽一张.他们中奖的概率与抽奖的次序有关吗？3银行储蓄卡的密码由6位数字组成.某人在银行自助取款机上取钱时，忘记了密码的最后1位数字，求：(1)任意按最后1位数字，不超过2次就按对的概率；(2)如果记得密码的最后1位是偶数，不超过2次就按对的概率.练习1.设A⊆B，且P(A)=0.3，P(B)=0.6.根据事件包含关系的意义及条件概率的意义，直接写出P(B∣A)和P(A∣B)的值再由条件概率公式进行验证.2.从一副不含大小王的52张扑克牌中，每次从中随机抽出1张扑克牌，抽出的牌不再放回.已知第1次抽到A牌，求第2次抽到A牌的概率.3.袋子中有10个大小相同的小球，其中7个白球，3个黑球.每次从袋子中随机摸出1个球，摸出的球不再放回.求：(1)在第1次摸到白球的条件下，第2次摸到白球的概率；(2)两次都摸到白球的概率.7.1.2全概率公式探究公式一般地,设A 1,A 2,⋯,A n 是一组两两互斥的事件,A 1∪A 2∪⋯∪A n =Ω,且P A i >0,i =1,2,⋯,n ,则对任意的事件B ⊆Ω,有P (B )=ni =1 P A i P B ∣A i .我们称上面的公式为全概率公式(t otalprobability formula ).4某学校有A ，B 两家餐厅，王同学第1天午餐时随机地选择一家餐厅用餐.如果第1天去A 餐厅，那么第2天去A 餐厅的概率为0.6；如果第1天去B 餐厅，那么第2天去A 餐厅的概率为0.8.计算王同学第2天去A 餐厅用餐的概率.5有3台车床加工同一型号的零件，第1台加工的次品率为6%，第2，3台加工的次品率均为5%，加工出来的零件混放在一起.已知第1，2，3台车床加工的零件数分别占总数的25%，30%，45%.(1)任取一个零件，计算它是次品的概率；(2)如果取到的零件是次品，计算它是第式£=1，2，3)台车床加工的概率.探究公式贝叶斯公式(Bayes formula )：设A 1,A 2,⋯,A n 是一组两两互斥的事件,A 1∪A 2∪⋯∪A n =Ω,且P A i >0,i =1,2,⋯,n ,则对任意的事件B ⊆Ω,贝叶斯公式是由英国数学家贝叶斯(T .Bayes ,1702-1761)发现的,它用来描述两个条件概率之间的关系.P (B )>0,有P A i ∣B =P A i P B ∣A iP (B )=P A i P B ∣A ink =1P A k P B ∣A k,i =1,2,⋯,n6在数字通信中心信号是由数字0和1组成的序列.由于随机因素的干扰，发送的信号0或1有可能被错误地接收为1或0.已知发送信号0时，接收为0和1的概率分别为0.9和0.1；发送信号1时，接收为1和0的概率分别为0.95和0.05.假设发送信号0和1是等可能的.(1)分别求接收的信号为0和1的概率；(2)已知接收的信号为0，求发送的信号是1的概率.练习1.现有12道四选一的单选题，学生张君对其中9道题有思路，3道题完全没有思路.有思路的题做对的概率为0.9，没有思路的题只好任意猜一个答案，猜对答案的概率为0.25.张君从这12道题中随机选择1题，求他做对该题的概率.2.两批同种规格的产品，第一批占40%，次品率为5%；第二批占60%，次品率为4%.将两批产品混合，从混合产品中任取1件.(1)求这件产品是合格品的概率；(2)已知取到的是合格品，求它取自第一批产品的概率.习题7.1复习巩固1.为了研究不同性别学生患色盲的比例，调查了某学校2000名学生，数据如下表所示.男女合计色盲60262非色盲11407981938合计12008002000从这2000人中随机选择1个人.(1)已知选到的是男生，求他患色盲的概率；(2)已知选到的学生患色盲，求他是男生的概率.2.从人群中随机选出1人，设B=“选出的人患有心脏病”，C=“选出的人是年龄大于50岁的心脏病患者”，请你判断P(B)和P(C)的大小，并说明理由.3.甲、乙两人同时向一目标射击，已知甲命中目标的概率为0.6，乙命中目标的概率为0.5.已知目标至少被命中1次，求甲命中目标的概率.4.甲和乙两个箱子中各装有10个球，其中甲箱中有5个红球、5个白球，乙箱中有8个红球、2个白球.掷一枚质地均匀的骰子，如果点数为1或2，从甲箱子随机摸出1个球；如果点数为3，4，5，6，从乙箱子中随机摸出1个球.求摸到红球的概率.5.在A、B、C三个地区爆发了流感，这三个地区分别有6%、5%、4%的人患了流感假设这三个地区的人口数的比为5:7:8，现从这三个地区中任意选取一个人.(1)求这个人患流感的概率；(2)如果此人患流感，求此人选自A地区的概率.6.已知P(A)>0，P(B)>0，P(B∣A)=P(B)，证明：P(A∣B)=P(A).综合运用7.一批产品共有100件，其中5件为不合格品.收货方从中不放回地随机抽取产品进行检验，并按以下规则判断是否接受这批产品：如果抽检的第1件产品不合格，则拒绝整批产品；如果抽检的第1件产品合格，则再抽1件，如果抽检的第2件产品合格，则接受整批产品，否则拒绝整批产品.求这批产品被拒绝的概率.8.在孟德尔豌豆试验中，子二代的基因型为DD、Dd、dd，其中D为显性基因，d为隐性基因，且这三种基因型的比为1:2:1.如果在子二代中任意选取2颗豌豆作为父本杂交，那么子三代中基因型为dd的概率是多大？9.证明条件概率的性质(1)和(2).拓广探索10.证明：当P(AB)>0时，P(ABC)=P(A)P(B∣A)P(C∣AB).据此你能发现计算P A1A2⋅⋅⋅A n的公式吗？7.2离散型随机变量及其分布列思考原理一般地,对于随机试验样本空间Ω中的每个样本点ω,都有唯一的实数X (ω)与之对应,我们称X 为随机变量(random var iable ).思考原理可能取值为有限个或可以一一列举的随机变量,我们称为离散型随机变量(discrete random var iable ).通常用大写英文字母表示随机变量,例如X ,Y ,Z ;用小写英文字母表示随机变量的取值,例如x ,y ,z .思考原理一般地,设离散型随机变量X 的可能取值为x 1,x 2,⋯,x n ,我们称X 取每一个值x i 的概率P X =x i =p i ,i =1,2,⋯,n为X 的概率分布列(list of probability distribution ),简称分布列.探究公式对于只有两个可能结果的随机试验,用A 表示“成功”,A表示“失败”,定义X =1,A 发生,0,A发生.如果P (A )=p ,则P (A)=1-p ,那么X 的分布列如表7.2-3所示.表7.2-3X 01P1-pp我们称X 服从两点分布(two -po int distribution )或0-1分布.1一批产品中次品率为5%，随机抽取1件，定义X =1,抽到次品,0,抽到正品. 求X 的分布列.2某学校高二年级有200名学生，他们的体育综合测试成绩分5个等级，每个等级对应的分数和人数如表7.2-4所示.表7.2-4等级不及格及格中等良优分数12345人数2050604030从这200名学生中任意选取1人，求所选同学分数X 的分布列，以及P (X ≥4).3一批笔记本电脑共有10台，其中A 品牌3台，B 品牌7台.如果从中随机挑选2台，求这2台电脑中A 品牌台数的分布列.练习1.举出两个离散型随机变量的例子．2.下列随机试验的结果能否用离散型随机变量表示？若能，请写出各随机变量可能的取值，并说明这些值所表示的随机试验的结果．(1)抛掷2枚骰子，所得点数之和；(2)某足球队在5次点球中射进的球数；(3)任意抽取一瓶标有1500mL的饮料，其实际含量与规定含量之差．3.篮球运动员在比赛中每次罚球命中得1分，不中得0分．已知某运动员罚球命中的概率为0.7，求他罚球1次的得分的分布列．4.抛掷一枚质地均匀的硬币2次，写出正面向上次数X的分布列．习题7.2复习巩固1.张同学从学校回家要经过4个红绿灯路口，每个路口可能遇到红灯或绿灯．(1)写出随机试验的样本空间；(2)设他可能遇到红灯的次数为X，写出X的可能取值，并说明这些值所表示的随机事件．2.某位同学求得一个离散型随机变量的分布列为：X0123P0.20.30.150.45试说明该同学的计算结果是否正确．3.在某项体能测试中，跑1km时间不超过4min为优秀．某位同学跑1km所花费的时间X是离散型随机变量吗？如果只关心该同学是否能够取得优秀成绩，应该如何定义随机变量？4.某位射箭运动员命中目标的环数X的分布列为：X678910P0.050.150.250.350.20如果命中9环或10环为优秀，那么他一次射击成绩为优秀的概率是多少？综合运用5.老师要从10篇课文中随机抽3篇让学生背诵，规定至少要背出其中2篇才能及格，某同学只能背诵其中的6篇，试求：(1)抽到他能背诵的课文的数量的分布列；(2)他能及格的概率．6.某种资格证考试，每位考生一年内最多有3次考试机会．一旦某次考试通过，便可领取资格证书．不再参加以后的考试，否则就继续参加考试，直到用完3次机会．李明决定参加考试，如果他每次参加考试通过的概率依次为0.6，0.7，0.8，且每次考试是否通过相互独立，试求：(1)李明在一年内参加考试次数X的分布列；(2)李明在一年内领到资格证书的概率．7.3离散型随机变量的数字特征7.3.1离散型随机变量的均值探究公式一般地,若离散型随机变量X的分布列如表7.3-2所示,表7.3-2X x1x2⋯x nP p1p2⋯p n则称E(X)=x1p1+x2p2+⋯+x n p nn=x i p ii=1为随机变量X的均值(m ean)或数学期望(mathematical exp ectation),数学期望简称期望.1在篮球比赛中，罚球命中1次得1分，不中得0分．如果某运动员罚球命中的概率为0.8．那么他罚球1次的得分X的均值是多少？2抛掷一枚质地均匀的骰子，设出现的点数为X，求X的均值．3猜歌名游戏是根据歌曲的主旋律制成的铃声来猜歌名．某嘉宾参加猜歌名节目，猜对每首歌曲的歌名相互独立，猜对三首歌曲A，B，C歌名的概率及猜对时获得相应的公益基金如表7.3-3所示．表7.3-3歌曲A B：C 猜对的概率0.80.60.4获得的公益基金额/元100020003000规则如下：按照A，B，C的顺序猜，只有猜对当前歌曲的歌名才有资格猜下一首．求嘉宾获得的公益基金总额X的分布列及均值．探究公式一般地,下面的结论成立:E(aX+b)=aE(X)+b.4根据天气预报，某地区近期有小洪水的概率为0.25，有大洪水的概率为0.01，该地区某工地上有一台大型设备，遇到大洪水时要损失60600元，遇到小洪水时要损失10000元．为保护设备，有以下3种方案：方案1运走设备，搬运费为3800元；方案2建保护围墙，建设费为2000元，但围墙只能防小洪水；方案3不采取措施．工地的领导该如何决策呢？练习1.已知随机变量X的分布列为：X12345P0.10.30.40.10.1(1)求E(X)；(2)求E(3X+2)．2.抛掷一枚硬币，规定正面向上得1分，反面向上得-1分，求得分X的均值．3.甲、乙两台机床生产同一种零件，它们生产的产量相同，在1h内生产出的次品数分别为X1，X2其分布列分别为：甲机床次品数的分布列X10123P0.40.30.20.1乙机床次品数的分布列X2012P0.30.50.2哪台机床更好？请解释你所得出结论的实际含义？7.3.2离散型随机变量的方差探究公式我们称D (X )=x 1-E (X ) 2p 1+x 2-E (X ) 2p 2+⋯+x n -E (X ) 2p n=ni =1 x i -E (X ) 2p i为随机变量X 的方差(va r iance ),有时也记为V ar (X ),并称D (X )为随机变量X 的标准差(s ta n dard deviation ),记为σ(X ).探究公式在方差的计算中,利用下面的结论经常可以使计算简化.D (X )=ni =1 x i -E (X ) 2p i=n i =1 x 2i -2E (X )x i +(E (X ))2p i=ni =1x 2i p i -2E (X )ni =1x i p i +(E (X ))2ni =1p i=ni =1x 2i p i -(E (X ))2.5抛掷一枚质地均匀的骰子，求掷出的点数X 的方差．6投资A ，B 两种股票，每股收益的分布列分别如表7.3-9和表7.3-10所示．表7.3-9股票A 收益的分布列收益X /元-102概率0.10.30.6表7.3-10股票B 收益的分布列收益Y /元012概率0.30.40.3(1)投资哪种股票的期望收益大？(2)投资哪种股票的风险较高？练习1.已知随机变量X 的分布列为：X 1234P0.20.30.40.1求D (X )和σ(2X +7)．2.若随机变量X 满足P (X =c )=1，其中c 为常数，求D (X )．3.甲、乙两个班级同学分别目测数学教科书的长度，其误差(精确到1cm )X 和Y 的分布列如下：甲班的目测误差分布列X-2-1012P0.10.20.40.20.1乙班的目测误差分布列Y-2-1012P0.050.150.60.150.05先直观判断X和Y的分布哪一个离散程度大，再分别计算X和Y的方差，验证你的判断．!习题7.3复习巩固1.某品牌手机投放市场，每部手机可能发生按定价售出、打折后售出、没有售出而收回三种情况．按定价售出每部利润100元，打折后售出每部利润0元，没有售出而收回每部利润-300元．据市场分析，发生这三种情况的概率分别为0.6，0.3，0.1.求每部手机获利的均值和方差．2.现要发行10000张彩票，其中中奖金额为2元的彩票1000张，10元的彩票300张，50元的彩票100张，100元的彩票50张，1000元的彩票5张．1张彩票可能中奖金额的均值是多少元？3.随机变量X的分布列为P(X=0)=0.2，P(X=1)=a，P(X=2)=b，若E(X)=1，求a和b．4.在单项选择题中，每道题有4个选项，其中仅有一个选项正确．如果从四个选项中随机选一个，选对的概率为0.25．请给选对和选错分别赋予合适的分值，使得随机选择时得分的均值为0．5.证明：D(aX+b)=a2D(X)．综合运用6.有A和B两道谜语，张某猜对A谜语的概率为0.8，猜对得奖金10元；猜对B谜语的概率为0.5，猜对得奖金20元，规则规定：只有在猜对第一道谜语的情况下，才有资格猜第二道．如果猜谜顺序由张某选择，他应该选择先猜哪一道谜语？7.甲、乙两种品牌的手表，它们的日走时误差分别为X和Y(单位：s)，其分布列为：甲品牌的走时误差分布列X-101P0.10.80.1乙品牌的走时误差分布列Y-2-1012P0.10.20.40.20.1试比较甲、乙两种品牌手表的性能．拓广探索8.设E(X)=μ，a是不等于μ的常数，探究X相对于μ的偏离程度与X相对于a的偏离程度的大小，并说明结论的意义．7.4二项分布与超几何分布7.4.1二项分布思考原理我们把只包含两个可能结果的试验叫做伯努利试验(Bernoulli trials ).思考原理我们将一个伯努利试验独立地重复进行n 次所组成的随机试验称为n 重伯努利试验.显然,n 重伯努利试验具有如下共同特征：(1)同一个伯努利试验重复做n 次;(2)各次试验的结果相互独立.探究公式一般地,在n 重伯努利试验中,设每次试验中事件A 发生的概率为p (0<p <1),用X 表示事件A 发生的次数,则X 的分布列为P (X =k )=C k n p k (1-p )n -k ,k =0,1,2,⋯,n如果随机变量X 的分布列具有上式的形式,则称随机变量X 服从二项分布(binomialdistribution ),记作X ∼B (n ,p ).1将一枚质地均匀的硬币重复抛掷10次，求：(1)恰好出现5次正面朝上的概率；(2)正面朝上出现的频率在0.4,0.6 内的概率.2如图是一块高尔顿板的示意图.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木钉，小木钉之间留有适当的空隙作为通道，前面挡有一块玻璃.将小球从顶端放入，小球下落的过程中，每次碰到小木钉后都等可能地向左或向右落下，最后落入底部的格子中.格子从左到右分别编号为0，1，2，⋯，10，用X 表示小球最后落入格子的号码，求X 的分布列.3甲、乙两选手进行象棋比赛，如果每局比赛甲获胜的概率为0.6，乙获胜的概率为0.4，那么采用3局2胜制还是采用5局3胜制对甲更看利？归纳一般地,确定一个二项分布模型的步骤如下:(1)明确伯努利试验及事件A的意义,确定事件A发生的概率p;(2)确定重复试验的次数n,并判断各次试验的独立性;(3)设X为n次独立重复试验中事件A发生的次数,则X∼B(n,p).探究公式一般地,可以证明:如果X∼B(n,p),那么E(X)=np,D(X)=np(1-p).练习1.将一枚质地均匀的硬币连续抛掷4次，X表示“正面朝上”出现的次数.(1)求X的分布列；(2)E(X)=，D(X)=.2.鸡接种一种疫苗后，有80%不会感染某种病毒.如果5只鸡接种了疫苗，求：(1)没有鸡感染病毒的概率；(2)恰好有1只鸡感染病毒的概率.3.判断下列表述正确与否，并说明理由：(1)12道四选一的单选题，随机猜结果，猜对答案的题目数X~B(12,0.25)；(2)100件产品中包含10件次品，不放回地随机抽取6件，其中的次品数Y~B(6,0.1).4.举出两个服从二项分布的随机变量的例子.7.4.2超几何分布探究公式一般地,假设一批产品共有N件,其中有M件次品.从N件产品中随机抽取n件(不放回),用X 表示抽取的n件产品中的次品数，则X的分布列为P(X=k)=C k M C n-k N-kC n N,k=m,m+1,m+2,⋯,r其中n,N,M∈N∗,M≤N,n≤N,m=max{0,n-N+M},r=min{n,M}.如果随机变量X的分布列具有上式的形式,那么称随机变量X服从超几何分布(hypergeometric distribution).探究公式随机变量X服从超几何分布，则E(X)=nM N4从50名学生中随机选出5名学生代表，求甲被选中的概率.5一批零件共有30个，其中有3个不合格.随机抽取10个零件进行检测，求至少有1件不合格的概率.6一个袋子中有100个大小相同的球，其中有40个黄球、60个白球，从中随机地摸出20个球作为样本.用X表示样本中黄球的个数.(1)分别就有放回摸球和不放回摸球，求X的分布列；(2)分别就有放回摸球和不放回摸球，用样本中黄球的比例估计总体中黄球的比例，求误差不超过0.1的概率：练习1.一箱24罐的饮料中4罐有奖券，每张奖券奖励饮料一罐，从中任意抽取2罐，求这2罐中有奖券的概率.2.学校要从12名候选人中选4名同学组成学生会，已知有4名候选人来自甲班.假设每名候选人都有相同的机会被选到，求甲班恰有2名同学被选到的概率.3.举出两个服从超几何分布的随机变量的例子.习题7.4复习巩固1.抛掷一枚骰子，当出现5点或6点时，就说这次试验成功，求在30次试验中成功次数X的均值和方差.2.若某射手每次射击击中目标的概率为0.9，每次射击的结果相互独立，则在他连续4次的射击中，恰好有一次未击中目标的概率是多大.3.如图，一个质点在随机外力的作用下，从原点0出发，每隔1s等可能地向左或向右移动一个单位，共移动6次.求下列事件的概率.(1)质点回到原点；(2)质点位于4的位置.4.从一副不含大小王的52张扑克牌中任意抽出5张，求至少有2张A牌的概率(精确到0.00001).综合运用5.某射手每次射击击中目标的概率为0.8，共进行10次射击，求(精确到0.01)：(1)恰有8次击中目标的概率；(2)至少有8次击中目标的概率.6.有一个摸奖游戏，在一个口袋中装有10个红球和20个白球，这些球除颜色外完全相同，一次从中摸出5个球，至少摸到3个红球就中奖.求中奖的概率(精确到0.001).7.一个车间有3台车床，它们各自独立工作.设同时发生故障的车床数为X，在下列两种情形下分别求X的分布列.(1)假设这3台车床型号相同，它们发生故障的概率都是20%；(2)这3台车床中有A型号2台，B型号1台，A型车床发生故障的概率为10%，B型车床发生故障的概率为20%.拓广探索8.某药厂研制一种新药，宣称对治疗某种疾病的有效率为90%.随机选择了10个病人，经过使用该药治疗后，治愈的人数不超过6人，你是否怀疑药厂的宣传.7.5正态分布思考原理取值往往充满某个区间甚至整个实轴,但取一点的概率为0,我们称这类随机变量为连续型随机变量(continuous random var iable).思考原理对任意的x∈R,f(x)>0,它的图象在x轴的上方.可以证明x轴和曲线之间的区域的面积为1.我们称f(x)为正态密度函数,称它的图象为正态密度曲线,简称正态曲线,如图7.5-4所示.若随机变量X的概率分布密度函数为f(x),则称随机变量X服从正态分布(normal distribution ),记为X∼Nμ,σ2.特别地,当μ=0,σ=1时,称随机变量X服从标准正态分布.思考原理由X的密度函数及图象可以发现,正态曲线还有以下特点:(1)曲线是单峰的,它关于直线x=μ对称;(2)曲线在x=μ处达到峰值1;σ2π(3)当|x|无限增大时,曲线无限接近x轴.探究公式若X∼Nμ,σ2,则E(X)=μ,D(X)=σ2.1李明上学有时坐公交车，有时骑自行车．他各记录了50次坐公交车和骑自行车所花的时间，经数据分析得到：坐公交车平均用时30min，样本方差为36；骑自行车平均用时34min，样本方差为4．假设坐公交车用时X和骑自行车用时Y都服从正态分布．(1)估计X，Y的分布中的参数；(2)根据(1)中的估计结果，利用信息技术工具画出X和Y的分布密度曲线；(3)如果某天有38min可用，李明应选择哪种交通工具？如果某天只有34min可用，又应该选择哪种交通工具？请说明理由．练习1.设随机变量X~N(0,1)，则X的密度函数为，P X≤0≈，P X ≤1≈，P X≤1≈，P(X>1)≈．(精确到0.0001．)2.设随机变量X~N0,22，随机变量Y~N0,32，画出分布密度曲线草图，并指出P(X≤-2)与P(X≤2)的关系，以及P(|X|≤1)与P(|Y|≤1)之间的大小关系．3.举出两个服从正态分布的随机变量的例子．习题7.5复习巩固1.对某地区数学考试成绩的数据分析，男生成绩X服从正态分布N72,82，女生成绩Y服从正态分布N74,62．请你从不同角度比较男、女生的考试成绩．2.某市高二年级男生的身高X(单位：cm)近似服从正态分布N170,52，随机选择一名本市高二年级的男生，求下列事件的概率：(1)165<X≤175；(2)X≤165；(3)X>175．3.若X~Nμ,σ2，则X位于区域[μ,μ+σ]内的概率是多少？综合运用4.袋装食盐标准质量为400g，规定误差的绝对值不超过4g就认为合格．假设误差服从正态分布，随机抽取100袋食盐，误差的样本均值为0，样本方差为4．请你估计这批袋装食盐的合格率．复习参考题7复习巩固1.举例说明P(B)与P(B∣A)没有确定的大小关系．2.抛掷两枚质地均匀的骰子，求：(1)两个点数都出现偶数的概率；(2)已知第一枚骰子的点数是偶数的条件下，第二枚骰子的点数也是偶数的概率．3.假设有两箱零件，第一箱内装有10件，其中有2件次品；第二箱内装有20件，其中有3件次品．现从两箱中随意挑选一箱，然后从该箱中随机取1个零件．(1)求取出的零件是次品的概率；(2)已知取出的是次品，求它是从第一箱取出的概率．4.已知离散型随机变量X的分布列如下表所示：X012P0.361-2q q2求：(1)常数q的值；(2)E(X)和D(X)．5.已知随机变量X取可能的值1，2，⋯，n是等可能的，且E(X)=10，求n的值．6.已知每门大炮击中目标的概率都是0.3，现存n门大炮同时对某一目标各射击一次．(1)当n=10时，求恰好击中目标3次的概率(精确到0.001)；(2)如果使目标至少被击中一次的概率超过95%，至少需要多少门大炮？综合运用7.长时间玩手机可能影响视力．据调查，某校学生大约40%的人近视，而该校大约有20%的学生每天玩手机超过1h，这些人的近视率约为50%．现从每天玩手机不超过1h的学生中任意调查一名学生，求他近视的概率．8.某商场要在国庆节开展促销活动，促销活动可以在商场内举行，也可以在商场外举行．统计资料表明，每年国庆节商场内的促销活动可获得利润2万元；商场外的促销活动，如果不遇到有雨天气可获得利润8万元，如果遇到有雨天气则会带来经济损失3万元．9月30日气象台预报国庆节当地的降水概率是40%，商场应该选择哪种促销方式？9.一份某种意外伤害保险费为20元，保险金额为50万元．某城市的一家保险公司一年能销售10万份保单，而需要赔付的概率为10-5．利用计算工具求(精确到0.0001)：(1)这家保险公司亏本的概率；(2)这家保险公司一年内获利不少于100万元的概率．拓广探索10.甲、乙、丙三人相互做传球训练，第1次由甲将球传出，每次传球时，传球者都等可能地将球传给另外两个人中的任何一人，求n次传球后球在甲手中的概率．11.某单位有10000名职工，想通过验血的方法筛查乙肝病毒携带者．假设携带病毒的人占5%，如果对每个人的血样逐一化验，就需要化验10000次.统计专家提出了一种化验方法：随机地按5人一组分组，然后将各组5个人的血样混合再化验．如果混合血样呈阴性，说明这5个人全部阴性；如果混合血样呈阳性，说明其中至少有一人的血样呈阳性，就。

求分布函数 F ( x ).
设随机变量X的分布函数为 例 设随机变量 的分布函数为
A / 2e x , x≤0 F ( x ) = 0.5, 0 < x ≤ 1 B + Ce −( x −1) , x > 1 求A，B，C的值 .
A 设随机变量X有密度 例 设随机变量 有密度 f ( x ) = x , x ∈ R, −x e +e
面积为 F ( x )
f ( x)
O
x
x
连续型随机变量的分布函数的性质： 连续型随机变量的分布函数的性质： 1) 0 ≤ F ( x ) ≤ 1；
F 2)F(x)单调不减，即当 x1 ≤ x2 时， ( x1 ) ≤ F ( x2 ); 单调不减， 单调不减
3) F ( −∞ ) = xlim F ( x ) = 0, F ( +∞ ) = xlim F ( x ) = 1; → −∞ → +∞ 4)F(x)右连续，即对任意实数 x , F ( x + 0) = F ( x ). 右连续， 右连续
密度函数一定连续吗？ 问题 (1) 密度函数一定连续吗？ (2) 对于一个给定的连续型随机变量， 对于一个给定的连续型随机变量， 其密度函数唯一吗？ 其密度函数唯一吗？ (3) 连续型随机变量与离散型随机变量 的本质区别是什么? 的本质区别是什么
连续型随机变量与离散型随机变量的本质 区别在于： 区别在于：连续型随机变量取单个值的概率 为零，也离散型不一定， 为零，也离散型不一定，这主要是由于积分 的性质.由此，便有下列的等价形式： 的性质 由此，便有下列的等价形式： 由此
d F ( x ) = f ( x ). dx
设连续型随机变量X有分布函数 例 设连续型随机变量 有分布函数