下载文档原格式
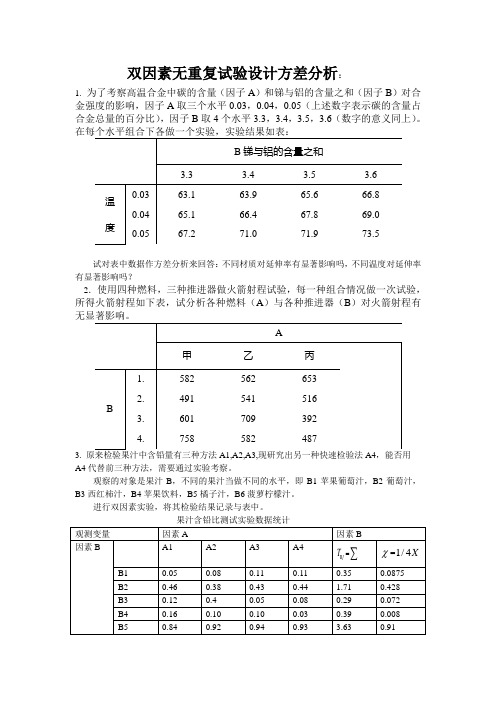
双因素无重复试验设计方差分析：1.为了考察高温合金中碳的含量（因子A）和锑与铝的含量之和（因子B）对合金强度的影响，因子A取三个水平0.03，0.04，0.05（上述数字表示碳的含量占合金总量的百分比），因子B取4个水平3.3，3.4，3.5，3.6（数字的意义同上）。
试对表中数据作方差分析来回答：不同材质对延伸率有显著影响吗，不同温度对延伸率有显著影响吗？2．使用四种燃料，三种推进器做火箭射程试验，每一种组合情况做一次试验，所得火箭射程如下表，试分析各种燃料（A）与各种推进器（B）对火箭射程有3.A4代替前三种方法，需要通过实验考察。
观察的对象是果汁B，不同的果汁当做不同的水平，即B1苹果葡萄汁，B2葡萄汁，B3西红柿汁，B4苹果饮料，B5橘子汁，B6菠萝柠檬汁。
进行双因素实验，将其检验结果记录与表中。
4.原来检验果汁中含铅量有三种方A1,A2,A3,现研究出另一种快速检验法A4,能否用A4代替前三种方法，需要通过实验考查。
观察的对象是果汁B，不同的果汁当做不同的水平，即B1苹果葡萄汁，B2葡萄汁，B3西红柿汁，B4苹果饮料，B5桔子汁，B6菠萝柠檬汁.进行双因素交错搭配实验，即用四种方法同时检验每一种果汁，将其检验结果记录于表5.六个水稻品种（A1、A2、A3、A4、A5和A6）种在四种不同的土壤类型（B1、B2、B 3和B 4）中，产量数据如表7.26所示，如果品种和土壤类型都是固定效应，试对资料进行适当的分析。
表7.26 例7.9的产量资料及数据整理6.B ）对合金强度的影响，因子A 取3个水平0.03，0.04，0.05（上述数字表示碳的含量占合金总量的百分比），因子B 取4个水平3.3，3.4，3.5，3.6（数字的意义7. 将落叶松苗木栽在4块不同苗床上，每块苗床上苗木又分别使用3种不同的肥料以观察肥效差异，一年后于每一苗床的各施肥小区内用重复抽样方式各取苗木若干株测其平均高，8. 某企业需采购大宗原材料，共有4家企业生产这些原材料，每家均有、、、四种类型的原材料，该企业决策机构对每个企业的每种样品进行试验，的数据如下：９．A 1:0.34~0.74,A 2:0.48~0.52,A 3:0.53~0.56及三种不同的加荷速度（单位：10-1N/cm 3·min ）B 1:600,B 2:2400,B 3:4200. １０．将土质基本相同的一块耕地，分成均等大小的5个地块，没每个地块又分成均等的四个小区；有四个品种的小麦，在每一地块内，随机地分种在四个小区上，每一小区种任一种小麦同样多的用种量。
双因素方差分析一、无交互作用下的方差分析设A 与B 是可能对试验结果有影响的两个因素，相互独立，无交互作用。
设在双因素各种水平的组合下进行试验或抽样，得数据结构如下表：表中每行的均值.i X （i=1,2,…r ）是在因素A 的各个水平上试验结果的平均数；每列的均值jX .(j=1,2,…,n)是在因素B 的各种水平上试验的平均数。
以上数据的离差平方和分解形式为：SST=SSA+SSB+SSE （6.13） 上式中：∑∑-=2)(X X SST ij(6.14)∑-=∑∑-=2.2.)()(X X n X XSSA i i (6.15)∑-=∑∑-=2.2)()(X Xr X XSSB j j（6.16）∑+-∑-=2..)(X X X X SSE ji ij(6.17)SSA 表示的是因素A 的组间方差总和，SSB 是因素B 的组间方差总和，都是各因素在不同水平下各自均值差异引起的；SSE 仍是组内方差部分，由随机误差产生。
各个方差的自由度是：SST 的自由度为nr-1，SSA 的自由度为r-1，SSB 的自由度为n-1，SSE 的自由度为nr-r-n-1=（r-1）(n-1)。
各个方差对应的均方差是：对因素A 而言： 1-=r SSA MSA （6.18） 对因素B 而言： 1-=n SSB MSB （6.19）对随机误差项而言：1---=n r nr SSEMSE （6.20）我们得到检验因素A 与B 影响是否显著的统计量分别是：)]1)(1(,1[~---=n r r F MSE MSA F A （6.21）)]1)(1(,1[~---=n r n F MSE MSBF B （6.22）【例6-2】某企业有三台不同型号的设备，生产同一产品，现有五名工人轮流在此三台设备上操作，记录下他们的日产量如下表。
试根据方差分析说明这三台设备之间和五名工人之间对日产量的影响是否显著？（α=0.05）。
