第五章同时博弈与序贯博弈转换

基于同时博弈和序贯博弈的寡头市场古诺均衡比较分析作者：王贵民来源：《经济研究导刊》2014年第21期摘要：根据国内外在古诺模型研究上的缺陷，分别从古诺假定、产品差异、成本差异以及非线性市场需求等方面对垄断市场结构中厂商之间同时博弈与序贯博弈两种情况的均衡状况进行比较分析，得出寡头垄断市场中厂商之间的均衡与产品质量、成本状况、市场需求以及博弈的顺序等因素有关的结论，从而为中国相关行业的决策提供理论依据。

关键词：古诺均衡；同时博弈；序贯博弈；寡头垄断市场中图分类号：F0 文献标志码：A 文章编号：1673-291X（2014）21-0003-06引言古诺模型作为分析寡头市场的一种理论结构，假定两家企业的产品完全相同、二者的边际成本都等于0，并且需求函数也是一样的线性函数。

同时，还假定企业在考虑产量时都把其他企业有可能的反应考虑在内。

自从1938年法国经济学家古诺提出该模型以后，国内外理论界对此模型展开了多种多样的扩展。

如Bischi等人加进了线性成本的条件，Agiza等人引入了非线性成本，Terrance等加进了信息不对称的前提，Scherer等研究了产品差别的情况。

中国学者张明善、闫安等人引入了动态分析的多头垄断，聂规划等研究了无限重复博弈，李天政等加进了需求价格弹性为常数的条件，而秦玉峰则对古诺均衡与斯塔克里贝格均衡进行了比较分析。

这些成果对古诺模型的发展做出了积极贡献，但它们缺乏对寡头企业之间博弈顺序不同所造成的均衡状态差异进行比较分析。

因此，本文试图从同时博弈和序贯博弈两个方面对古诺模型的均衡及其扩展进行比较分析。

一、基于初始假定的同时博弈和序贯博弈均衡比较如前所述，古诺在研究双寡头垄断市场结构时，假定市场上两企业生产完全相同的产品，它们面临共同的线性需求曲线，并且它们的边际成本相等。

下面首先对在这种假定条件下企业间博弈顺序不同造成的均衡结果进行分析。

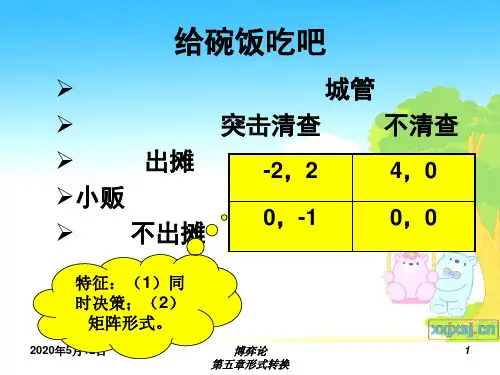
（一）同时博弈条件下的均衡分析如果某一市场存在A、B两家企业，其生产的产品完全相同，产量用qA、qB表示，它们面临的需求函数是相同的，P=a-bQ。

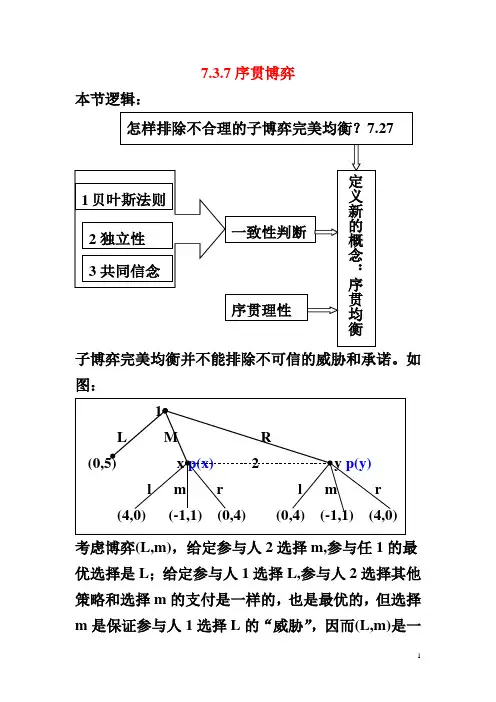
7.3.7序贯博弈本节逻辑：子博弈完美均衡并不能排除不可信的威胁和承诺。

如图：考虑博弈(L,m)，给定参与人2选择m,参与任1的最优选择是L；给定参与人1选择L,参与人2选择其他策略和选择m的支付是一样的，也是最优的，但选择m是保证参与人1选择L的“威胁”，因而(L,m)是一个纳什均衡，而且这个博弈只有自身一个子博弈， 因而也是子博弈完美均衡。

但这不是博弈的真实结果，因为参与人2选择m 不是一个可信的威胁。

考虑参与人1没有选择L 。

这样参与人2对于博弈进行到x,y 的信念分别是p(x),p(y),p(x)+p(y)=1.这时，选择纯策略m 的期望收益是：p(x)*1+p(y)*1=1。

混合策略（0.5，0.5）选择（l,r ）的期望收益是： p(x)(0.5*0+0.5*4)+p(y)(0.5*4+0.5*0)=2>1。

因而如果参与人1真的没有选择L ，那么参与人1也不会选择m ，威胁是不可信的，（L,m ）不是真实的博弈结果。

那么，如何排除m 这些不可信的威胁或承诺？方法：1、引进完美贝叶斯均衡；2、引进序贯均衡概念。

7.3.7.1信念信念体系p （x ）是指在在信息集I(x)上的一个概率分布，该概率分布描述了该信息集上的参与人)(x 关于博弈进入该信息集上每一个决策结的的概率（后验概率）。

显然，这些概率和=1。

如上例里p(x)+p(y)=1。

判断/状态（p,b ）是一对信念体系/行为策略有序组合，给定状态（p,b ），信念p 可解释为给定行为策略b 已被采取时，参与人所持有的信念。

在一个合理的状态中，信念体系p 应当是应用贝叶斯法则从既定的行为策略b 中推导出来的——当这样做是可行的，也就是在信息集在均衡路径上：∈=Iy b x P b x P x p )()()( 如图7.283/115/515/115/315/3)(=++=αP 。

贝叶斯法则：信念必定是利用贝叶斯法则由策略中推出的——当这样做是可行的。

Chapter06序贯博弈和同时博弈的结合序贯博弈和同时博弈的结合Combining Sequential and Simultaneous Moves第6章Chapter 6序贯博弈和同时博弈的结合Combining Sequential and Simultaneous Moves博弈类型Game Type概念Concepts分析技术Techniques of Analysis博弈树(扩展形式) Game Trees (Extensive form)收益表(策略形式) Payoff tables (Strategic form) 纯粹序贯博弈反转均衡Purely Sequential- Rollback move games equilibrium纯粹同时博弈Purely Simultaneousmove games纳什均衡Nash equilibriumSlide 2序贯博弈和同时博弈的结合Combining Sequential and Simultaneous Moves在现实中，许多策略环境包含了这两种相互作用的成分。

In reality, many strategic situations contain elements of both types of interaction.而且，我们还可以使用扩展形式或策略形式分析任何一种博弈(可以交叉使用)。

Also, we can use either extensive form or strategic form for any type of game.Slide 3内容提要Outline兼具同时和序贯行动的博弈Games with both simultaneous and sequential moves改变博弈中的行动顺序Changing the order of moves in a game !改变分析方法Change in the method of analysis *三人博弈Three-player gamesSlide 4 兼具同时和序贯行动的博弈Games with Both Simultaneous and Sequential Moves典型的例子一般都是博弈者在一段比较长的时间内相互作用。

同时博弈与序贯博弈深圳大学中国经济特区研究中心 章平题1•有两个参与人，A和B，他们轮流选择一个介于2和10之间的整数（可以重复）。

A先选。

随着博弈的进行，不断将两个所选的数字合起来累加。

当累计总和达到100的时候，博弈结束。

这时候判所选数字恰好使累计总和达到100的局中人为胜者。

请问：•谁将赢得这场博弈？•完整行动计划是什么？•根据逆推归纳法，当累计接近100时，得到88[100-(3+9)]的人会赢，问题变为抢 88。

•同理，问题可变为抢76,64,52,40,28,16,4,继续逆推（100-12n，当n=8时余4），就是先抢到4的人会赢。

•A，先选4，则A胜出。

•子博弈精炼纳什均衡为上述报法。

•有两个参与人，A和B，他们轮流选择一个介于2和10之间的整数（可以重复）。

A先选。

随着博弈的进行，不断将两个所选的数字合起来累加。

当累计总和达到或者超过100的时候，博弈结束。

这时候判所选数字首先使累计总和达到或者超过100的参与人为输家。

请问：•谁将赢得这场博弈？•完整的行动计划是什么？•根据逆推归纳法，当累计接近100时，得到97[100-3]的人会赢，问题变为抢 97。

•同理，问题可变为抢85,73,61,49,37,25,13,1继续逆推，就是先抢到1，会赢。

•A，先选1，则A胜出。

•子博弈精炼纳什均衡。

博弈树转换成矩阵型表述•确定可供参与人选择的纯策略数目，从而确定表格大小•每个策略组合对应的个子中，按照约定填入收益题2•考虑下面两个超级大国争霸的博弈：有两个超级大国，1和2。

在第一阶段，1首先行动，它可以选择发展核武器或不发展核武器。

在第二阶段，2观察到1的选择后，决定自己是发展核武器还是不发展核武器。

这个博弈的具体支付情况如下：如果双方都发展核武器，则双方都不会获得额外的好处，我们用0和0来表示这种情形。

如果一方发展而另一方不发展，则发展的一方会赢得军备优势，从而称霸世界。

我们用发展的一方得5，不发展的一方的—1来表示这种情形。

序贯博弈名词解释
嘿，你知道啥是序贯博弈不？序贯博弈啊，就好比是一场精彩的棋局！想象一下，两个人在下棋，一个人先走一步，然后另一个人再根
据对方的走法来决定自己的下一步。

这就是序贯博弈啦！比如说，你
和朋友玩猜拳游戏，你先出拳，这就是序贯博弈中的第一步呀。

序贯博弈可不简单哦！它涉及到很多策略和决策呢。

就好像你在走
一条充满选择的路，每一步都得深思熟虑。

比如说在商业竞争中，一
家公司先推出一款产品，另一家公司就得根据这个来决定自己要不要
跟进，推出类似的产品或者采取其他策略，这多有意思啊！
它也像是一场心理战呢！你得去猜对方会怎么做，然后根据这个来
调整自己的行动。

比如你和小伙伴玩捉迷藏，你找的时候，就得想想
他可能会藏在哪里，这就是在进行序贯博弈呀！
而且哦，序贯博弈中先后顺序很重要呢！先行动的一方可能会有一
些优势，但也不一定哦，后行动的一方也可能通过观察和分析来找到
更好的策略。

这就好像跑步比赛，先跑的人不一定就能赢，后面的人
也可能奋起直追呢！
在生活中，序贯博弈无处不在呀！找工作面试的时候，你先展示自己，然后面试官根据你的表现来决定要不要录用你，这也是序贯博弈呀！还有谈恋爱的时候，你先表达自己的感情，对方再决定怎么回应，这同样是序贯博弈。

序贯博弈就是这样，充满了策略、智慧和不确定性。

它让我们的生活变得更加丰富多彩，也让我们不断地去思考和决策。

所以啊，可别小瞧了序贯博弈哦，它真的很重要呢！我的观点就是，序贯博弈就像生活中的一场大冒险，每一步都充满挑战和惊喜，我们要好好去感受和应对它呀！。

信息经济学作业：P157第16、17、18、20、、21、23题 16、1、该游戏有先动优势，又A 先选择，故A 将赢得这场博弈。

2、A 将赢得这场博弈，故A 有最优策略为:A 先选择数字4或者5，之后A 根据B 的选择，每次使得其选择数字与B 选择数字之和为12，按照此策略，A 将赢得最终博弈，具体如下图——按照理论B 将没有可能在该比赛规则下赢得比赛，但博弈中存在颤抖手现象，B 唯一获胜的希望即在A 出现颤抖手——失误时。

17、1、该游戏依旧具有先动优势，又A 先选择，故A 仍赢得这场博弈。

2、A 将赢得这场博弈，故A 有最优策略为:A 先选择数字2或者3，之后A 根据B 的选择，每次使得其选择数字与B 选择数字之和为12，按照此策略，A 将赢得最终博弈，具体如下图——按照理论B 将没有可能在该比赛规则下赢得比赛，但博弈中存在颤抖手现象，B 唯一获胜的希望即在A 出现颤抖手——失误时。

18、 将条件“轮流选择一个介于2和10之间的整数”改为“轮流选择一个介于1和5之间的整数”后，对整体最有策略思路没有影响，依旧是最终A 赢得博弈。

只是影响了博弈次数和数字选择。

如图——AB B B A A A 84=12*7 96=12*8A A AB B B20、按照倒推法，B 最后选择结束的收益为100，选择不结束的收益也100，对B 而言结束不结束收益相等，可以合理假设B 选择结束不结束的概率为50%，50%，倒退一步，A 选择结束的收为99，选择不结束的收益50%可能为98，50%的可能为100（其选择不结束的期望收益=98*50%+100*50%=99）。

A 的选择有赖于对B 的推断，而B 的选择有赖于 推断A 是一个冒险者还是一个保守者 若A 是冒险者，A 会推断B 不结束，A 也选择继续，此时A 、B 的收益分别为100、100。

若A 是保守者，A 会推断B 结束，A 也选择结束，以此类推，A 、B 收益分别为1、1. 21、A B B B AA A 90=6*15 96=6*16A A AB B B (99,99) (98,100)(1,1) (0,3) (2,2) (1,4) (3,3)如上图所示，A 先选择收益最大为（2，0），B 先选择收益最大为（1，1） 对A 而言，先动收益2大于后动收益1，故A 具有先动优势；同理，对B 而言，先动收益1，大于后动收益0，故B 也具有后动优势。

关于博弈论的课程设计一、课程目标知识目标：1. 学生能理解博弈论的基本概念，掌握博弈论的基本原理。

2. 学生能运用博弈论分析日常生活中的竞争与合作问题，解释相关现象。

3. 学生了解博弈论在不同领域中的应用，如经济学、政治学、心理学等。

技能目标：1. 学生具备运用博弈论模型进行问题分析和解决的能力。

2. 学生能通过小组讨论、案例分析等形式，提高团队协作和沟通能力。

3. 学生掌握运用博弈论软件进行简单模拟实验的方法。

情感态度价值观目标：1. 学生认识到竞争与合作的重要性，树立正确的竞争观念。

2. 学生在团队协作中学会尊重他人，培养合作精神。

3. 学生通过博弈论的学习，提高对社会现象的观察和思考能力，培养批判性思维。

课程性质：本课程为选修课程，旨在帮助学生运用博弈论分析现实生活中的问题，提高问题解决能力。

学生特点：高中生具备一定的逻辑思维能力和自主学习能力，对新鲜事物充满好奇心。

教学要求：结合学生特点，注重理论与实践相结合，鼓励学生积极参与讨论，培养实际操作能力。

通过本课程的学习，使学生能够将博弈论知识运用到实际生活中，提高分析问题和解决问题的能力。

同时，注重培养学生的团队协作和沟通能力，提升其情感态度价值观。

教学过程中，将目标分解为具体的学习成果，以便进行教学设计和评估。

二、教学内容1. 博弈论基本概念：博弈、博弈论、博弈参与者、博弈策略、支付函数等。

2. 博弈论基本类型：静态博弈、动态博弈、完全信息博弈、不完全信息博弈等。

3. 博弈论分析方法：均衡分析、序贯均衡、重复博弈、贝叶斯均衡等。

4. 博弈论应用实例：囚徒困境、鹰鸽博弈、公共物品供给问题、市场竞争等。

5. 博弈论软件操作：介绍博弈论软件的使用方法，进行简单模拟实验。

教学大纲安排：第一周：博弈论基本概念及分类第二周：博弈论分析方法（一）第三周：博弈论分析方法（二）第四周：博弈论应用实例分析第五周：博弈论软件操作与实践第六周：课程总结与拓展教材章节关联：第一章：博弈论导论第二章：静态博弈分析第三章：动态博弈分析第四章：不完全信息博弈第五章：博弈论应用实例第六章：博弈论软件操作教学内容注重科学性和系统性，结合课程目标，按照教学大纲安排，有序进行。

序贯博弈问题一、序贯博弈到底是什么？你有没有听过“博弈”这个词？不是打牌那种博弈，指的是一种决策上的游戏，参与者之间的互动决定了每个人的选择与结果。

这就好比你和朋友去吃火锅，火锅店菜单上有各种菜品。

你点了一个菜，等着对方点菜。

可对方不急，先看你点了啥，准备做出反应。

这个过程中，谁先动手，谁后行动，都得影响到最终结果。

大家都在试图猜测对方的想法，自己能得到什么好处。

你以为自己点的牛肉最划算，结果对方一看，“牛肉不行，还是羊肉好”，再调整策略。

你们俩这一来一回的“反应”，就构成了一个典型的序贯博弈。

再想象一下，假设你和朋友去参加一个选秀节目。

节目组规定，选手只能按照先后顺序选择道具，先选的选手能占得先机，但后选的可以看到前面选了什么，再做决定。

这个就类似于序贯博弈的模式。

每一位参与者的决策，都不仅仅是独立的，而是会受到前一个人决策的影响。

在这样的情况下，谁先动手，谁就能占得先机，这个先后顺序决定了最后的胜负。

二、谁先出手更有利？在序贯博弈中，先出手的玩家不一定就能稳赢，但他们肯定比后出手的更占优势。

为什么呢？因为先出手的人往往能掌控局面，虽然选择的范围有限，但可以设置一些“陷阱”，让后出手的人不得不按自己的节奏来。

有点像是你在打麻将时，摸到一张牌，感觉对自己有利，但是如果你不出这个牌，对方可能会“碰”了，结果变得一团乱。

所以，谁先出手，谁就能为自己争取更多的空间。

想象一下，如果你是第一个选择道具的人，你可以挑选最适合自己或者最具战略性的道具，不管其他选手怎么选，你都可以稍微有些预判。

而如果你是第二个选手，虽然知道了对方的选择，但你却没法直接“修正”自己的策略，因为对方的选择可能已经给你造成了一些限制。

这种情况放到生活中也一样。

比如你想约一个朋友去看电影，如果你是先提出邀请的人，你可以选择一部自己感兴趣的电影。

如果对方是先出手的，他就能决定电影的类型，虽然你可以根据他的选择做出反应，但你心里总有些“被动”的感觉。