序贯决策博弈

序贯博弈纳什均衡序贯博弈是博弈论中一种重要的博弈形式，也是实际生活中的普遍存在。

在序贯博弈中，参与者的行动是有先后顺序的，并且每个参与者的行动都会对自己和其他参与者的收益产生影响。

其中，纳什均衡是对于序贯博弈的一种重要的分析方法和结果。

序贯博弈可以分成两种情形：完全和不完全信息序贯博弈。

在完全信息的序贯博弈中，参与者可以获得游戏的所有信息，并且可以推导出所有参与者的策略和结果。

而在不完全信息的序贯博弈中，参与者只能知道一部分信息，并且需要进行一定的推断和猜测。

每个参与者的策略和结果都是不确定的。

不过，无论是完全信息还是不完全信息的序贯博弈，都可以利用纳什均衡来求解。

纳什均衡是序贯博弈中确定最优策略的一种方法。

纳什均衡指的是在博弈中所有参与者都遵循自己的最优策略时，达到的均衡状态。

也就是说，任何一方都不能通过单独改变自己的策略来获得更好的结果。

纳什均衡的概念是由约翰·纳什提出的，并且被广泛应用于博弈论中，是对于博弈问题的一种比较普遍的解决方法。

在序贯博弈中，纳什均衡可以通过反复应用最优化原理来求解。

最优化原理指的是，每个参与者都会选择一种最优策略，以尽可能地获得最好的结果。

也就是说，每个参与者都会根据自己的利益来做出决策。

通过比较不同的策略组合的结果，可以对于最终结果进行分析和预测。

如果某个策略组合成为纳什均衡，就意味着这个组合对于所有参与者都是最好的决策。

举一个例子，假设有两个商人X和Y，他们都出售同样的产品，并且都有两种售价可供选择。

如果两个人的售价不同，则会影响另一个商人的收益。

他们在某个时候进行交易，Y先决定自己的售价，然后X再根据Y的售价来决定自己的售价。

如果X的售价高于Y，则X会获得更高的利润，但Y就会失去他的订单，反之亦然。

这是一个典型的不完全信息的序贯博弈。

为了找到最好的策略组合，可以使用最优化原理和纳什均衡。

首先，假设Y选择售价为a，那么X的最优策略是选择一个更低的售价b，这样他就能获得更高的利润。

决策理论与方法多属性决策多目标及序贯决策多属性决策是指在决策过程中考虑多个属性或指标，通过对这些属性进行量化和比较，找出最优选择的决策方法。

在实际决策中，我们常常需要考虑多个属性因素，而这些因素往往是相互矛盾甚至相互制约的。

多属性决策的关键是建立合理的评价指标体系，将不同属性进行量化，再通过合适的决策模型或方法进行计算和比较。

常用的多属性决策模型包括加权法、层次分析法和灰色关联法等。

多目标决策是指在决策过程中存在多个决策目标，且这些目标往往是相互冲突或无法同时达到的。

多目标决策的目标是找到一个最佳的折衷方案，使得各个决策目标能够得到尽可能满足。

多目标决策的关键是建立合理的决策模型，将各个决策目标进行量化和比较，再通过适当的优化方法或规划方法寻找最优解。

常用的多目标决策方法包括线性规划、整数规划、动态规划和遗传算法等。

序贯决策是指在决策过程中需要根据不完全的信息和不确定的环境进行连续的决策，即通过一系列的决策步骤逐渐完善和调整决策方案。

序贯决策的关键是建立适当的决策模型，将决策过程分解为多个连续的阶段，每个阶段根据已有的信息和条件做出决策，并根据反馈信息不断调整和优化决策方案。

常用的序贯决策方法包括马尔可夫决策过程、博弈论和贝叶斯决策等。

在实际应用中，多属性决策、多目标决策和序贯决策往往会相互结合使用。

例如，在制定企业的发展战略时，需要考虑多个因素，如市场需求、竞争环境和资源能力等，这涉及到多属性决策的内容。

同时，为了实现企业的长远目标，需要考虑多个决策目标，如利润最大化、成本最小化和风险最小化等，这也涉及到多目标决策的内容。

而在制定战略的实施方案时，可能需要根据不断变化的市场和竞争环境进行序贯的决策，这涉及到序贯决策的内容。

综上所述，多属性决策、多目标决策和序贯决策是决策理论与方法中常用的三个重要方法。

它们分别从不同的角度和需求出发，帮助人们在复杂和不确定的决策环境中做出最佳决策。

这些方法在实际应用中相互结合，能够提供更全面和准确的决策支持。

同时博弈与序贯博弈深圳大学中国经济特区研究中心 章平题1•有两个参与人，A和B，他们轮流选择一个介于2和10之间的整数（可以重复）。

A先选。

随着博弈的进行，不断将两个所选的数字合起来累加。

当累计总和达到100的时候，博弈结束。

这时候判所选数字恰好使累计总和达到100的局中人为胜者。

请问：•谁将赢得这场博弈？•完整行动计划是什么？•根据逆推归纳法，当累计接近100时，得到88[100-(3+9)]的人会赢，问题变为抢 88。

•同理，问题可变为抢76,64,52,40,28,16,4,继续逆推（100-12n，当n=8时余4），就是先抢到4的人会赢。

•A，先选4，则A胜出。

•子博弈精炼纳什均衡为上述报法。

•有两个参与人，A和B，他们轮流选择一个介于2和10之间的整数（可以重复）。

A先选。

随着博弈的进行，不断将两个所选的数字合起来累加。

当累计总和达到或者超过100的时候，博弈结束。

这时候判所选数字首先使累计总和达到或者超过100的参与人为输家。

请问：•谁将赢得这场博弈？•完整的行动计划是什么？•根据逆推归纳法，当累计接近100时，得到97[100-3]的人会赢，问题变为抢 97。

•同理，问题可变为抢85,73,61,49,37,25,13,1继续逆推，就是先抢到1，会赢。

•A，先选1，则A胜出。

•子博弈精炼纳什均衡。

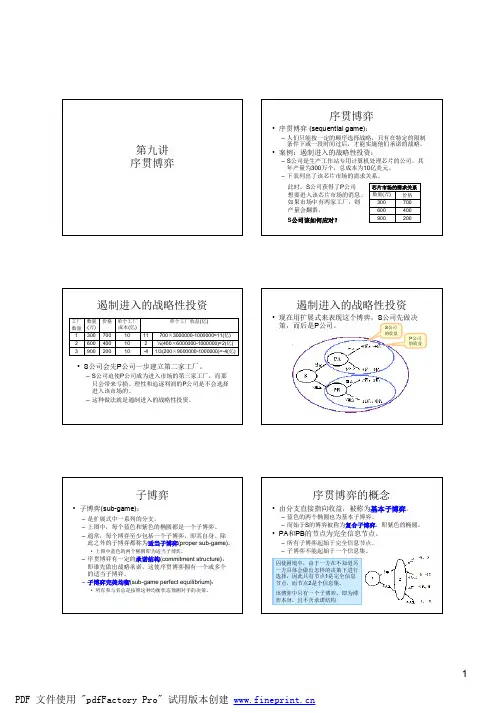
博弈树转换成矩阵型表述•确定可供参与人选择的纯策略数目，从而确定表格大小•每个策略组合对应的个子中，按照约定填入收益题2•考虑下面两个超级大国争霸的博弈：有两个超级大国，1和2。

在第一阶段，1首先行动，它可以选择发展核武器或不发展核武器。

在第二阶段，2观察到1的选择后，决定自己是发展核武器还是不发展核武器。

这个博弈的具体支付情况如下：如果双方都发展核武器，则双方都不会获得额外的好处，我们用0和0来表示这种情形。

如果一方发展而另一方不发展，则发展的一方会赢得军备优势，从而称霸世界。

我们用发展的一方得5，不发展的一方的—1来表示这种情形。

博弈论基础课程教学大纲课程名称：博弈论基础英文名称：Game Theory课程编号：X4080251学时数：32其中实验（实训）学时数：0课外学时数：0学分数：2适用专业：金融学一、课程的性质和任务本课程是经济类专业选修课程之一。

本课程的任务是使学生从应用角度出发，在理论和实践上掌握博弈论的基本概念和基本方法，使学生具有应用博弈论的方法分析实际问题的初步能力。

二、课程教学内容的基本要求、重点和难点1.博弈的基本理论基本要求：理解策略形式的博弈，掌握博弈三要素和博弈的基本分类，理解囚徒困境、“抓钱博弈”。

重点和难点：博弈要素、囚徒困境2.同时决策博弈基本要求：掌握纳什均衡的定义，理解优势策略均衡，理解纳什均衡的应用。

重点和难点：纳什均衡3.混合策略纳什均衡基本要求：理解混合策略与期望支付，了解反响函数法，掌握纳什定理和奇数定理，了解多重纳什均衡及其甄别。

重点和难点：纳什定理4.序贯决策博弈基本要求：掌握序贯决策博弈与博弈树，理解策略与行动，了解序贯博弈的纳什均衡, 了解倒推法。

重点和难点：序贯决策博弈与博弈树5.同时博弈与序贯博弈基本要求：掌握正规型表示与展开型表示，理解同时决策与序贯决策的混合博弈，了解树型博弈的子博弈，了解子博弈精炼纳什均衡重点和难点：同时博弈与序贯博弈的正规型表示与展开型表示6.重复博弈和策略性行动基本要求：理解囚徒困境的有限次重复，理解囚徒困境的无限次重复，掌握重复次数不确定的情形，.掌握策略性行动的分类。

重点和难点：囚徒困境的有限次、无限次重复7.零和博弈基本要求：掌握零和博弈与非零和博弈，了解最小最大方法、直线交叉法，理解零和博弈的线性规划解法，了解霍特林模型。

重点和难点：零和博弈与非零和博弈，零和博弈的线性规划解法三、教学方式及学时分配四、课程其它教学环节的要求本课程以教师讲课为主，并适当安排课堂讨论，以学生课后实践为辅，同时鼓励学生参与经济实践与经济讨论的活动如举行经济辩论、撰写小论文等。

序贯博弈名词解释
嘿，你知道啥是序贯博弈不？序贯博弈啊，就好比是一场精彩的棋局！想象一下，两个人在下棋，一个人先走一步，然后另一个人再根
据对方的走法来决定自己的下一步。

这就是序贯博弈啦！比如说，你
和朋友玩猜拳游戏，你先出拳，这就是序贯博弈中的第一步呀。

序贯博弈可不简单哦！它涉及到很多策略和决策呢。

就好像你在走
一条充满选择的路，每一步都得深思熟虑。

比如说在商业竞争中，一
家公司先推出一款产品，另一家公司就得根据这个来决定自己要不要
跟进，推出类似的产品或者采取其他策略，这多有意思啊！
它也像是一场心理战呢！你得去猜对方会怎么做，然后根据这个来
调整自己的行动。

比如你和小伙伴玩捉迷藏，你找的时候，就得想想
他可能会藏在哪里，这就是在进行序贯博弈呀！
而且哦，序贯博弈中先后顺序很重要呢！先行动的一方可能会有一
些优势，但也不一定哦，后行动的一方也可能通过观察和分析来找到
更好的策略。

这就好像跑步比赛，先跑的人不一定就能赢，后面的人
也可能奋起直追呢！
在生活中，序贯博弈无处不在呀！找工作面试的时候，你先展示自己，然后面试官根据你的表现来决定要不要录用你，这也是序贯博弈呀！还有谈恋爱的时候，你先表达自己的感情，对方再决定怎么回应，这同样是序贯博弈。

序贯博弈就是这样，充满了策略、智慧和不确定性。

它让我们的生活变得更加丰富多彩，也让我们不断地去思考和决策。

所以啊，可别小瞧了序贯博弈哦，它真的很重要呢！我的观点就是，序贯博弈就像生活中的一场大冒险，每一步都充满挑战和惊喜，我们要好好去感受和应对它呀！。

序贯博弈纳什均衡序贯博弈是博弈论中的一种重要形式，指的是参与者在不同时间点依次做出决策的博弈过程。

而纳什均衡则是博弈论中的一个重要概念，指的是在博弈中，各参与者通过选择策略使得自己的收益最大化，并且其他参与者无法通过改变策略获得更好的收益。

本文将从序贯博弈和纳什均衡两个方面展开讨论。

序贯博弈是一种动态博弈形式，参与者在不同时间点做出决策，每个决策都会影响后续的决策和收益。

在序贯博弈中，每个参与者的决策都是基于先前的决策和当前的信息来进行的。

这种博弈形式常见于现实生活中的许多情景，比如商业谈判、国际政治等。

纳什均衡是指在博弈中，每个参与者选择的策略组合使得自己的收益最大化，而其他参与者无法通过改变策略获得更好的收益。

换句话说，纳什均衡是一种稳定状态，任何一个参与者都没有动机单方面改变自己的策略。

纳什均衡是博弈论中的一个核心概念，被广泛应用于经济学、政治学、社会学等领域。

在序贯博弈中寻找纳什均衡是一个复杂而困难的问题。

因为参与者的决策是基于先前的决策和当前的信息，而且每个参与者都在追求自身的最大化收益。

在序贯博弈中，参与者需要考虑对手可能的行动和自己的收益，以及对手对自己的行动的反应，从而做出最优的决策。

为了寻找序贯博弈的纳什均衡，可以使用博弈树来表示博弈的过程和参与者的决策。

博弈树是一个树状结构，每个节点表示一个决策点，每个边表示一个决策的结果。

通过遍历博弈树，可以确定每个参与者的最优策略，并找到纳什均衡。

在博弈树上，每个参与者都有一个决策节点，表示他们在该节点处做出的决策。

每个决策节点有多个子节点，表示参与者在不同决策下的选择。

通过遍历博弈树，可以确定每个参与者的最优策略。

最优策略是指在当前节点下，使得参与者的收益最大化的决策。

当所有参与者都选择了最优策略后，就可以确定博弈的纳什均衡。

纳什均衡是一种稳定状态，任何一个参与者都没有动机单方面改变自己的策略。

在博弈树上，纳什均衡可以通过遍历博弈树，并找到每个参与者的最优策略来确定。