江西省高安中学2017-2018学年高二1月月考数学(文)试题 Word版 含答案

江西省高安中学2017-2018学年上学期期末考试高二年级数学（文）试题一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．复数iiz +=2（i 为虚数单位）的虚部为（ ） A ．2- B ．i C ．i 2- D ．12．如图所示的程序框图，运行相应的程序，输出的n 的值为( ) A ．4 B ．3 C ．2 D ．13．已知双曲线方程为x 2－3y 2＝6，则双曲线的离心率等于( ) A. 3 B ．233C. 2 D ．34．2017年8月1日是中国人民解放军建军90周年，中国人民银行为此 发行了以此为主题的金银纪念币.如图所示是一枚8克圆形金质纪念币，直径22mm ，面额100元.为了测算图中军旗部分的面积，现用 1粒芝麻向硬币内投掷100次，其中恰有30次落在军旗内，据此可估 计军旗的面积大约是（ ）A.27265mm π B. 23635mm π C. 236310mm π D. 236320mm π5．“q p ∨是真命题”是“p 为真命题”的（ ）A ．必要不充分条件B ．充分不必要条件C ．充要条件D ．既不充分也不必要条件6．若关于x 的不等式|x －2|＋|x －1|≥a 在R 上恒成立，则a 的最大值是( ) A ．0 B ．1 C ．－1 D ．27．在－20到40之间插入8个数，使这10个数成等差数列，则这10个数的和为( ) A.200B.100C.90D.708．已知变量x 与变量y 之间具有相关关系，并测得如下一组数据则变量x 与y 之间的线性回归方程可能为（ ）A ．0.710.3y x =-+B ．0.7 2.3y x =-C ．10.30.7y x =-+D ．10.30.7y x =-9．已知变量y x ,满足约束条件⎪⎩⎪⎨⎧≤-≥+≤112y x y x y ，则y x z +=3的最大值为（ ）A ．12B ．11C ．3D ．1- 10．已知不等式2201x m x ++>-对一切(1)x ∈+∞，恒成立，则实数m 的取值范围是（ ） A ．8m <- B ．8m >- C. 6m <- D ．6m >-11．设函数4y x ax b =++在1x =处的切线方程为y x =，则,a b 的值是( )． A ．3,3a b == B ．3,3a b ==- C ．3,3a b =-= D ．3,3a b =-=-12．设数列{}n a 前n 项和为n S ，已知145a =，112,0,2121,1,2n n n n n a a a a a +⎧≤≤⎪⎪=⎨⎪-<≤⎪⎩则2018S 等于（ ）A ．50445B ．50475 C. 50485 D ．50495二、填空题（每题5分，满分20分，将答案填在答题纸上）13．某品牌空调在元旦期间举行促销活动，所示的茎叶图表示某专卖店 记录的促销期间8天的销售量情况(单位：台)，则销售量的中位数是 ．14．已知抛物线方程为22y x =，则抛物线上的点),23(0y P 到焦点F 的距离为 ． 15．设ABC ∆的内角C B A ,,所对边分别为c b a ,,，若()()a b c a b c ab +-++=，则角=C .16．若函数32()4f x x x ax =+--在区间(1,1)-内恰有一个极值点，则实数a 的取值范围为 ．三、解答题 （本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．（本小题满分10分）在极坐标系中，圆C 的极坐标方程为：cos sin ρθθ=+．以极点为原点，极轴为x 轴的正半轴建立平面直角坐标系，直线l 的参数方程为：2,221,2x t y t ⎧=⎪⎪⎨⎪=+⎪⎩(t 为参数).(1)求圆C 的直角坐标方程和直线l 的普通方程；(2)当θ∈(0，π)时，求直线l 与圆C 的公共点的极坐标．18．（本小题满分12分）在ABC ∆中，c b a ,,分别为内角C B A ,,所对的边，且满足c b a <<，B a b sin 2=.（1）求A 的大小；（2）若32,2==b a ，求ABC ∆的面积.19. （本小题满分12分）随着资本市场的强势进入，互联网共享单车“忽如一夜春风来”，遍布了一二线城市的大街小巷.为了解共享单车在A 市的使用情况，某调查机构借助网络进行了问卷调查，并从参与调查的网友中抽取了200人进行抽样分析，得到表格：（单位：人）经常使用 偶尔或不用 合计 30岁及以下 70 30 100 30岁以上 60 40 100 合计 13070200（1）根据以上数据，能否在犯错误的概率不超过0.15的前提下认为A 市使用共享单车情况与年龄有关？（2）现从所抽取的30岁以上的网友中利用分层抽样的方法再抽取5人. （i ）分别求这5人中经常使用、偶尔或不用共享单车的人数；（ii ）从这5人中，再随机选出2人赠送一件礼品，求选出的2人中至少有1人经常使用共享单车的概率.参考公式： ()()()()()22n ad bc K a b c d a c b d -=++++，其中n a b c d =+++.参考数据：()20P K k ≥ 0.15 0.10 0.05 0.025 0.0100k2.072 2.7063.841 5.024 6.63520．（本小题满分12分）已知数列{}n a 是公差不为0的等差数列，12a =且234,,1a a a +成等比数列． (1)求数列{a n }的通项公式；(2)设2(2)n n b n a =+，求数列{}n b 的前n 项和n S .21.（本小题满分12分）已知椭圆22221(0)x y a b a b+=>>的离心率e ＝32，连接椭圆的四个顶点得到的菱形的面积为4. (1)求椭圆的方程；(2)设直线l 过椭圆的左端点A ，与椭圆的另一个交点为B.，AB 的垂直平分线交y 轴于点0(0,)Q y ，且QA →·QB →＝4，求0y 的值．22．（本小题满分12分）已知函数21()(22)4ln 2f x x a x a x =+--. (1)讨论()f x 的单调性；(2)设1a =，若存在12,(2,)x x ∈+∞，且12x x ≠,使不等式1212|()()||ln ln |f x f x k x x -≤-成立，求实数k 的取值范围.江西省高安中学2017-2018学年上学期期末考试高二年级数学（文）试题答案一、选择题：1-6 ACBCAB 7-12 BABDCB 二、填空题：13. 15 14. 2 15.32π16. [1,5) 三、解答题：17.解：(1)圆C ：cos sin ρθθ=+，即2cos sin ρρθρθ=+，故圆C 的直角坐标方程为220x y x y +--=.直线l 的普通方程为10x y -+=.……………(5分)(2)由(1)知圆C 与直线l 的直角坐标方程，将两方程联立220,10,x y x y x y ⎧+--=⎨-+=⎩解得0,1,x y =⎧⎨=⎩即圆C 与直线l 在直角坐标系下的公共点为(0,1)，将(0,1)转化为极坐标为(1,)2π，即为所求.(10分)18.解：（1）∵B a b sin 2=，∴由正弦定理化简得：B A B sin sin 2sin =， ∵0sin ≠B ，∴21sin =A ，∵c b a <<，∴A 为锐角，则6π=A ；……………(5分) （2）∵2=a ，32=b ，23cos =A ，∴由余弦定理得：A bc c b a cos 2222-+= 即233221242⨯⨯⨯-+=c c ，整理得：0862=+-c c 解得2=c （舍去）或4=c ，则322143221sin 21=⨯⨯⨯==A bc S .……………(12分) 19.解：（1）由列联表可知，()2220070406030 2.19813070100100K ⨯⨯-⨯=≈⨯⨯⨯.因为2.198 2.072>，所以能在犯错误的概率不超过0.15的前提下认为A 市使用共享单车情况与年龄有关. （2）（i ）依题意可知，所抽取的5名30岁以上的网友中，经常使用共享单车的有6053100⨯=（人），偶尔或不用共享单车的有4052100⨯=（人）. （ii ）设这5人中，经常使用共享单车的3人分别为a ， b ， c ；偶尔或不用共享单车的2人分别为d ， e .则从5人中选出2人的所有可能结果为(),a b ， (),a c ， (),a d ， (),a e ， (),b c ， (),b d ，(),b e ， (),c d ， (),c e ， (),d e 共10种.其中没有1人经常使用共享单车的可能结果为(),d e 共1种， 故选出的2人中至少有1人经常使用共享单车的概率1911010P =-=. 20. (1)设数列{a n }的公差为d ，由12a =且234,,1a a a +成等比数列，得(2＋2d)2＝(2＋d)(3＋3d)，解得d ＝－1或d ＝2. 当d ＝－1时，a 3＝0，这与a 2，a 3，a 4＋1成等比数列矛盾，舍去．所以d ＝2， 所以a n ＝a 1＋(n －1)d ＝2n ，即数列{a n }的通项公式为a n ＝2n ，(n ∈N*)．……………(6分) (2)2111(22)(1)1n b n n n n n n ===-+++，所以12111111(1)()()1223111n n nS b b b n n n n =++=-+-+-=-=+++……………(12分) 21.解：(1)由e ＝c a ＝32，得3a 2＝4c 2.再由c 2＝a 2－b 2，得a ＝2b.由题意可知12×2a×2b ＝4，即ab ＝2.解方程组⎩⎪⎨⎪⎧a ＝2b ，ab ＝2，得a ＝2，b ＝1.所以椭圆的方程为2214x y +=.……………(5分) (2)由(1)可知A(－2,0)．设B 点的坐标为11(,)x y ，直线l 的斜率为k ，则直线l 的方程为(2)y k x =+．于是A ，B 两点的坐标满足方程组22(2),1,4y k x x y =+⎧⎪⎨+=⎪⎩ 由方程组消去y 并整理，得2222(14)161640k x k x k +++-=.由212164214k x k --=+，得2122814k x k -=+.从而12414ky k =+. 设线段AB 的中点为M ，则M 的坐标为22282(,)1414k kk k -++． 以下分两种情况：①当k ＝0时，点B 的坐标为(2,0)，线段AB 的垂直平分线为y 轴，于是QA →＝(－2，－y 0)，QB →＝(2，－y 0)．由QA →·QB →＝4，得y 0＝±2 2.②当k≠0时，线段AB 的垂直平分线方程为222218()1414k k y x k k k-=-+++． 令x ＝0，解得02614ky k =-+，由QA →＝(－2，－y 0)，QB →＝(x 1，y 1－y 0)．QA →·QB →＝－2x 1－y 0(y 1－y 0)＝2422222222(28)6464(16151)()414141414(14)k k k k k k k k k k k --+-++==+++++， 整理得7k 2＝2，故k ＝±147.所以y 0＝±2145.综上，y 0＝±22或y 0＝±2145.……………(12分) 22.解:(1)∵f ′(x)=x+(2a-2)- 4a x = x 2+(2a-2)x-4a x = (x+2a)(x-2)x (x ＞0).令f ′(x)=0得x=2或x=-2a.∴①当-2a=2,即a=-1时, f ′(x)≥0在x ＞0时恒成立,即f(x)在(0,+∞)上单调递增. ②当-2a ＞2,即a ＜-1时,f(x)在(0,2)和(-2a,+∞)上单调递增,在(2,-2a)上单调递减. ③当0＜-2a ＜2,即-1＜a ＜0时,f(x)在(0,-2a)和(2,+∞)上单调递增,在(-2a,2)上单调递减 ④当-2a ≤0,即a ≥0时,f(x)在(0,2)上单调递减,在(2,+∞)上单调递增. ………(6分) (2)由(1)知,当a=1时,f(x)在(2,+∞)上单调递增,不妨设x 2＞x 1＞2, 则不等式|f(x 1)-f(x 2)|≤k |lnx 1-lnx 2|可化为f(x 2)-f(x 1)≤klnx 2-klnx 1f(x 1)-klnx 1≥f(x 2)-klnx 2,令g(x)=f(x)-klnx,则g(x)在(2,+∞)上存在单调递减区间. ∴g ′(x)= f ′(x) - k x ＜0 在区间(2,+∞)有解,即(x+2)(x-2)x - kx ＜0在x ∈(2,+∞)上有解，∴k ＞x 2-4, x ∈(2,+∞),故k ＞0. ……………(12分)。

江西省高安市2017-2018学年高一数学1月月考试题（重点班，无答案）一．选择题（5×12＝60分）1．设集合}{21A x x m =≤- ，集合}{12B x x =≤≤，若B A ⊆，则实数m 的取值范围是（ ） A ． 31,2⎡⎤⎢⎥⎣⎦B ．(,1]-∞C ．3(,]2-∞D ．3[,]2+∞ 2．函数1y ax =+在R 上是单调递减，则2()(43)g x a x x =-+的增区间是（ ）A ．[2,)+∞B ．[2,)-+∞C ．(,2]-∞D ．(,2]-∞- 3．已知函数23 0()log 0x x x f x x ⎧≤⎪=⎨>⎪⎩，则1()2f f ⎡⎤⎢⎥⎦⎣的值是（ ） A ．－3B ．3C ．13D ．13- 4．下列函数中不能用二分法求函数零点的是（ ） A ．25y x =- B ．ln 29y x x =-+C ．244y x x =++D ．lg 5y x =+ 5．在四面体A BCD -的棱AB 、BC 、CD 、DA 上分别取E 、F 、G 、H 四点，如果EF 与HG 交于点M ，则（ ）A ．M 一定在直线AC 上B ．M 一定在直线BD 上C ．M 可能在直线AC 上，也可能在直线BD 上D ．M 既不在直线AC 上，也不在直线BD 上6．已知函数x y e =的反函数为()y f x =，则（ ）A ．2(2)()x f x e x R =∈B ．(2)ln 2ln (0)f x x x =>C ．(2)2()x f x e x R =∈D ．(2)ln ln 2(0)f x x x =+> 7．如图平面α⋂平面PQ β=、EG ⊥平面α，FH ⊥平面α，垂足分别为G 、H ，为使PQ ⊥GH ，则需要增加一个条件是（ ）A ．EF ⊥平面αB ．EF ⊥平面βC ．PQ ⊥GED ．PQ ⊥FH8．函数()f x 的图象向右平移1个单位长度，所得到的图象与曲线x y e =关于y 轴对称，则()f x ＝（ ）A ．1x e +B ．1x e -C ．1x e -+D ．1x e --9．函数2()2x f x x =-的零点个数为（ ）A ．1B ．2C ．3D ．4 10．设奇函数()f x 在(,0)-∞上是增函数，且(1)0f -=，则不等式()()0f x f x x -->的解集为（ ）A ．(1,0)(1,)-⋃+∞B ．(,1)(0,1)-∞-⋃C ．(,1)(1,)-∞-⋃+∞D ．(1,0)(0,1)-⋃ 11．已知函数()21,x f x a b c =-<<，且()()()f a f c f b >>，则下列结论中一定成立的是（ ）A ．0a <0b <0c <B ．0a <0b ≥0c >C ．22a c -<D ．222a c +< 12．如图，当A α∈，点B α∈，点P α∉PB ⊥α，C 是α内异于A 和B 的动点，且PC⊥AC ，则动点C 在平面α内组成的图形是（ ）A ．一条线段，但要去掉两个点B ．一个圆，但要去掉两个点C ．两条平行直线D ．半圆，但要去掉两个点二．填空题13．若幂函数135()mf x x -=在(,0)-∞上单减，在(0,)+∞上单增，则最大的整数m =________.14．已知函数2230()0x x x f x x a x ⎧+-<=⎨+≥⎩ 的增区间为[1,)-+∞，则实数a 的取值范围是_______.15．直四棱柱1111ABCD A B C D -的底面是边长为1的正方形，侧棱长1AA =，则异面直线11A B 与1BD 所成角的大小为________.16．一个圆锥的侧面展开图是中心角为90，面积为1S 的扇形，若该圆锥的表面积为2S ，则21S S ＝__________.三．解答题17．设集合}{}{2222log (612)log (32),24xm x A x x x x B x -=+≥++=< （1）当3m =时，求()R A C B ⋂；（2）若(1,4)A B ⋂=-，求实数m 的值.18．已知函数2220()00 0x x x f x x x mx x ⎧-+>⎪==⎨⎪+<⎩ 是奇函数（1）求实数m 的值；（2）若函数()f x 在区间[1,2]a --上单增，求实数a 的取值范围.19．如图，在正方体1111ABCD A B C D -中，M 、N 、P 分别是1AD 、BD 、1B C 的中点.求证：（1）MN ∥平面11CC D D ；（2）平面MNP ∥平面11CC D D .20．如图，已知三棱锥,90,P ABC ACB D -∠=为AB 的中点，且PDB ∆是正三形，PA ⊥PC（1）求证：PA ⊥平面PBC ；（2）求证：平面PAC ⊥平面ABC .21．已知四棱锥P ABCD -的直观图与三视图如图所示，其中主视图与左视图为直角三角形，俯视图为正方形，已知该几何体的体积为23. （1）求实数a 的值；（2）将PAB ∆绕PB 旋转一周，求所得旋转体的体积.22．已知函数2211()log (),()()168x f x mx x m g x =-+= （1）若函数()y f x =的定义域为R ，求实数m 的取值范围；（2）在（1）的条件下，若对于任意1x R ∈，存在2(,0]x ∈-∞，使得12()()f x g x >，求实数m 的取值范围.。

一、选择题：（本题包括12小题，共60分，每小题只有一个选项符合题意） 1.抛物线2y x =在点11,24M ⎛⎫⎪⎝⎭的切线的倾斜角是（ ） A ．30° B ．45° C ．60° D ．90° 2.定积分⎰+1)sin (dx x x 的值为（ ）A ．1cos 23-B ．122+π C ．π D ．213.函数)(x f 在定义域R 内可导，若)2()(x f x f -=，且当()1,∞-∈x 时，0)()1(<'-x f x ，设)2(),23(),1(f c f b f a ==-=则（ ）A. c b a <<B. a c b <<C. b c a <<D. b a c <<4.已知函数x x ax x f 33)(23+-=，若)(x f '存在唯一的零点0x ，且00>x ，则a 的值是( )A. 12或B.0C. 01或D. 15．设()()()201,212,x x f x x x ⎧≤<⎪=⎨-≤≤⎪⎩则()20f x dx ⎰等于( )A.34 B.45 C.56D ．不存在 6.设函数)40)(cos (sin )(π≤≤-=x x x e x f x，则函数的所有极大值之和为（ ） A. π4eB. ππ3ee + C. ππ3ee - D. πe7．设函数y=xsinx+cosx 的图象在点(t,f(t))处切线斜率为k ,函数k=g(t)的部分图象为（ ）8．已知函数()f x 与()f x '的图像如下图所示，则函数()()xf xg x e =的递减区间为（ )A ．()0,4B ．()4,1,,43⎛⎫-∞ ⎪⎝⎭ C ． 40,3⎛⎫⎪⎝⎭D ．()()0,1,4,+∞ 9．已知函数2()ln log 1f x a x b x =++，3)2017(=f ，则)20171(f 等于（ ） A. 1- B. 2 C. 2- D. 4110.已知函数)(x f 的导数)(x f '，)(x f 不是常数函数，且0)()()1(≥'++x f x x f x ，对[)+∞∈,0x 恒成立，则下列不等式一定成立的是（ ）A. )2()1(f ef <B. 0)1(<fC. )2(2)(f e ef <D. )2(2)1(ef f <11．已知函数()()221xf x ae x a x =--+，若函数()f x 在区间()0,ln 2上有最值，则实数a 的取值范围是（ ）A ．(),1-∞-B ．()1,0- C. ()2,1-- D ．()(),00,1-∞12．已知函数()()2ln 1f x a x x =+-在区间()0,1内任取两个实数p ，q ，且p q ≠，不等式2)1()1(>---+qp q f p f 恒成立，则实数a 的取值范围为（ ）A ．(]12,30B ．(],18-∞C ．[)18,+∞D ．(]2,18-二、填空题：（本题包括4小题，共20分）13.若函数()()32'123f x f x x =-+，则()'1f 的值为 . 14.曲线3y x =与 .15.已知函数)100)...(2)(1()(+++=x x x x x f ，则=')0(f .16.已知()xf x xe =，2()(1)g x x a =-++，若12,x x R ∃∈，使得21()()f x g x ≤成立，则实数a 的取值范围是 ．三、解答题：（本题包括6小题，共70分）17．（10分））已知函数x x x f 3)(3-=及)(x f y =上一点)2,1(-p ，过点p 作直线l .（1）求使直线l 和)(x f y =相切且以p 为切点的直线方程；（2）求使直线l 和)(x f y =相切且切点异于p 的直线方程．18．（12分）已知()xkx bf x e +=． （1）若()f x 在0x =处的切线方程为1y x =+，求k 与b 的值； （2）求x xd e x ⎰-1119．(12分)已知曲线42:2-=x y C . （1）求曲线C 在点)2,3(A 处的切线方程；（2）过原点O 作直线l 与曲线C 交于B A ,两不同点，求线段AB 的中点M 的轨迹方程．20.（12分)已知函数)(1ln )(R a x x a x f ∈+-=. （1）求)(x f 的单调区间；（2）若0)(≤x f 在),0(+∞上恒成立，求所有实数a 的值；21．（12分）设函数xxe x f =)(. （1） 求)(x f 的单调区间与极值；（2）是否存在实数，使得对任意的),(21+∞∈a x x 、，当21x x <时恒有ax a f x f a x a f x f -->--1122)()()()(成立．若存在，求a 的范围，若不存在，请说明理由．22.（12分）设函数)(x f y =，对任意实数y x ,都有xy y f x f y x f 2)()()(++=+. （1）求)0(f 的值；（2）若1)1(=f ，求)4(),3(),2(f f f 的值；（3）在（2）的条件下，猜想))((*N n n f ∈的表达式并证明。

第Ⅰ卷一、选择题：共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合U R =，集合{1A x x =<-或}4x >，{}23B x x =-≤≤，那么阴影部分表示的集合为（ ）A ．{}24x x -≤<B ．{3x x ≤或}4x ≥C ．{}21x x -≤≤-D ．{}13x x -≤≤2．设复数12,z z 在复平面内的对应点关于实轴对称，11z i =+，则12z z =（ ）A ．2-B ．2C ．1i -D ．1i +3．右图所示的程序运行后输出的结果是（ ）A ．5-B ．3-C ．0D ．14．如图所示的数阵中，每行、每列的三个数均成等差数列，如果数阵中所有数之和等于63，那么52a =（ ）A ．2B ．8C ．7D ．4414243515253616263a a a a a a a a a ⎛⎫ ⎪ ⎪ ⎪⎝⎭5．“吸烟有害健康，吸烟会对身体造成伤害”，哈尔滨市于2012年5月31日规定室内场所禁止吸烟．美国癌症协会研究表明，开始吸烟年龄()X 分别为16岁、18岁、20岁和22岁，其得肺癌的相对危险度()Y 依次为15.10、12.81、9.72、3.21；每天吸烟()U 10支、20支、30支者，其得肺癌的相对危险度()V 分别为7.5、9.5和16.6．用1r 表示变量X 与Y 之间的线性相关系数，用2r 表示U 与V 之间的线性相关系数，则下列说法正确的是（ ）A ．12r r =B ．120r r >>C ．120r r <<D ．120r r <<7．设α为平面，a 、b 为两条不同的直线，则下列叙述正确的是（ ）A ．若,a b αα ，则a bB ．若,a a b α⊥ ，则b α⊥C ．若,a a b α⊥⊥，则b αD ．若,a a b α⊥ ，则b α⊥8．在平面直角坐标系xOy 中，已知ABC ∆的顶点()0,3A 和()0,3C -，顶点B 在椭圆2211625x y +=上，则()sin sin sin A C A C+=+（ ） A ．35 B ．45 C ．54 D ．539．已知点()()*,n n a n N ∈在x y e =的图象上，若满足12ln ln ln n n T a a a k =++⋅⋅⋅+>是n 的最小值为5，则k 的取值范围是（ ）A ．15k <B ．10k <C ．1015k ≤<D ．1015k <<10．如图网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则这个几何体的体积为（ ）A ．2B ．3C ．4D ．511．已知点P 在直线320x y +-=上，点Q 在直线360x y ++=上，线段PQ 的中点为()00,M x y ，且002y x <+，则00y x 的取值范围是（ ） A ．1,03⎡⎫-⎪⎢⎣⎭ B ．1,03⎛⎫- ⎪⎝⎭ C ．1,3⎛⎫-+∞ ⎪⎝⎭ D ．()1,0,3⎛⎫-∞-+∞ ⎪⎝⎭12．已知函数()()23,0ln 1,0x x x f x x x ⎧-+<⎪=⎨+≥⎪⎩，若()f x ax ≥，则a 的取值范围是（ ）A ．(],0-∞B ．(],1-∞C ．[]3,0-D ．[]3,1-第Ⅱ卷（非选择题，共90分）本卷包括必考题和选考题两个部分．第13题~第21题为必考题，每个考生都必须作答，第22题~第24题为选考题，考生根据要求作答．二、填空题：本大题共4小题，每题5分，共20分．13．已知双曲线22221x y a b-=的离心率为2，那么该双曲线的渐近线方程为______． 14．在某次数学考试中，甲、乙、丙三名同学中只有一个人得了优秀．当他们被问到谁得到了优秀时，丙说：“甲没有得优秀”；乙说：“我得了优秀”；甲说：“丙说的是真话”，事实证明：在这三名同学中，只有一人说的是假话，那么得优秀的同学是______．15．某高中准备租用甲、乙两种型号的客车安排900名学生去冰雪大世界游玩．甲、乙两种车辆的载客量分别为36人/辆和60人/辆，租金分别为400元/辆和600元/辆，学校要求租车总数不超过21辆，且乙型车不多于甲型车7辆，则学校所花租金最少为______元．16．已知点O 是ABC ∆外心，4,3AB AO ==，则AB AC ⋅ 的取值范围是______．三、解答题：解答应写出文字说明、证明过程或演算步骤．17．（本小题满分12分）已知函数())()1cos cos ,02f x x x x x R ωωωω=+-∈>．若()f x 的最小正周期为4π． （1）求函数()f x 的单调递增区间；（2）在ABC ∆中，角,,A B C 的对边分别是,,a b c ，且满足()2cos cos a c B b C -=，求函数()f A 的取值范围．18．（本小题满分12分）如图，四棱锥S ABCD -中，SD ⊥底面ABCD ，,,1,2AB DC AD DC AB AD DC SD ⊥==== ，,M N 分别为,SA SC 的中点，E 为棱SB 上的一点，且2SE EB =．（1）证明：MN 平面ABCD ；（2）证明：DE ⊥平面SBC 的大小．19．（本小题满分12分）现有甲、乙、丙、丁4个学生课余参加学校社团文学社与街舞社的活动，每人参加且只能参加一个社团的活动，且参加每个社团是等可能的．（1）求文学社和街舞社都至少有1人参加的概率；（2）求甲、乙同在一个社团，且丙、丁不同在一个社团的概率．20．（本小题满分12分） 已知椭圆()2222:10,0x y C a b a b+=>>的两焦点与短轴的一个端点的连线构成等边三角形，直线10x y ++=与以椭圆C 的右焦点为圆心，以椭圆的长半轴长为半径的圆相切．（1）求椭圆C 的方程；（2）设点,,B C D 是椭圆上不同于椭圆顶点的三点，点B 与点D 关于原点O 对称．设直线,,,CD CB OB OC 的斜率分别为1234,,,k k k k ，且1234k k k k =．（ⅰ）求12k k 的值；（ⅱ）求22OB OC +的值．21．（本小题满分12分）已知函数()2ln 2f x x ax a =--+．（,a Ra ∈为常数）． （1）讨论函数()f x 的单调性；（2）若存在(]00,1x ∈，使得对任意的(]2,0a ∈-，不等式()00ame f x +>（其中e 为自然对数的底数）都成立，求实数m 的取值范围．请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分．22．（本小题满分10分）选修4-1：几何证明选讲如图，圆M 与圆N 交于,A B 两点，以A 为切点作两圆的切线分别交圆M 和圆N 于C 、D 两点，延长DB 交圆M 于点E ，延长CB 交圆N 于点F ．已知5,10BC DB ==．（1）求AB 的长；（2）求CF DE．23．（本小题满分10分）选修4-4：坐标系与参数方程已知曲线C 的极坐标方程是4cos ρθ=．以极点为平面直角坐标系的原点，极轴为x 轴的正半轴，建立平面直角坐标系，直线l 的参数方程是1cos sin x t y t αα=+⎧⎨=⎩（t 为参数）． （1）将曲线C 的极坐标方程化为直角坐标方程；（2）若直线，与曲线C 相交于A 、B 两点，且AB =α的值．24．（本小题满分10分）选修4-5：不等式选讲已知函数()f x =M ．（1）求实数M 的值；（2）求关于x 的不等式x x M +≤的解集．。

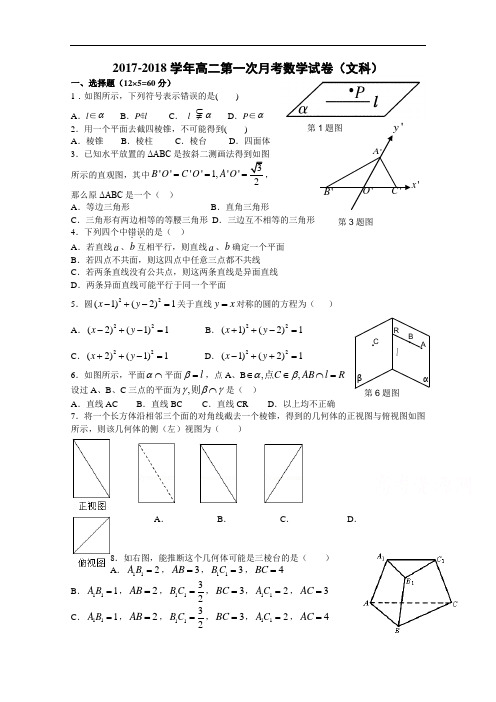
α· ·AB ·C β lR2017-2018学年高二第一次月考数学试卷（文科）一、选择题（12×5=60分）1．如图所示，下列符号表示错误的是( ) A ．l ∈α B ．P ∉l C ． l ⊂≠α D ．P ∈α 2．用一个平面去截四棱锥，不可能得到( )A ．棱锥B ．棱柱C ．棱台D ．四面体 3．已知水平放置的ΔABC 是按斜二测画法得到如图所示的直观图，其中''''1,''2B OC O A O ===，那么原ΔABC 是一个（ ）A ．等边三角形B ．直角三角形C ．三角形有两边相等的等腰三角形D ．三边互不相等的三角形 4．下列四个中错误．．的是（ ） A ．若直线a 、b 互相平行，则直线a 、b 确定一个平面 B ．若四点不共面，则这四点中任意三点都不共线C ．若两条直线没有公共点，则这两条直线是异面直线D ．两条异面直线可能平行于同一个平面5．圆22(1)(2)1x y -+-=关于直线y x =对称的圆的方程为（ ） A ．22(2)(1)1x y -+-= B ．22(1)(2)1x y ++-=C ．22(2)(1)1x y ++-=D ．22(1)(2)1x y -++=6．如图所示，平面α⋂平面l β=，点A 、B ,,C AB l R αβ∈∈⋂=点 设过A 、B 、C 三点的平面为,γβγ⋂则是（ ） A ．直线AC B ．直线BC C ．直线CR D ．以上均不正确7．将一个长方体沿相邻三个面的对角线截去一个棱锥，得到的几何体的正视图与俯视图如图所示，则该几何体的侧（左）视图为（ ）A ．B ．C ．D ．8．如右图，能推断这个几何体可能是三棱台的是（ ） A ．112A B =，3AB =，113B C =，4BC =B ．111A B =，2AB =，1132B C =，3BC =，112AC =，3AC = C ．111A B =，2AB =，1132B C=，3BC =，112AC =，4AC = '第1题图第3题图第6题图D ．11AB A B =，11BC B C =，11CA C A =9．将半径为1的圆分割成面积之比为1:2:3的三个扇形作为三个圆锥的侧面，设这三个圆锥底面半径依次为1r ，2r ，3r ，那么123r r r ++的值为（ ） A ．B ．2C ．D ．110．已知,,P Q R 是圆22280x y x +--=上不同三点，它们到直线:70l x +=的距离分别为123,,x x x ，若123,,x x x 成等差数列，则公差的最大值为（ ） A ．1B ．2C ．3D ．411．用若干块相同的小正方体搭成一个几何体，从两个角度 观察得到的图形如图，则搭成该几何体最少需要的小正方体 的块数是（ ）块？ A ．8 B ．7 C ．6 D ．512．若直线10()ax y a a R +-+=∈与圆224x y +=交于A 、B 两点（其中O 为坐标原点），则AO AB ⋅的最小值为（ ）A ．1B ．2C ．3D ．4 二、填空题（4×5=20分）13．如果OA //O A ''，OB //O B ''，那么AOB ∠和A O B '''∠ 的关系为 14．y ＝|x |的图象和圆x 2＋y 2＝4所围成的较小的面积是 15．若实数x 、y 满足221x y +=，则21y x ++的取值范围是________ 16．如下图是正方体的平面展开图，则在这个正方体中： ①BM 与ED 平行 ②CN 与BE 是异面直线 ③CN 与BM 成60o 角 ④DM 与BN 是异面直线以上四个中，正确的序号是________2018届高二年级第一次月考数学试卷（文科）答题卡13、14、15、16、三、解答题 17．（10分）一木块如图所示，点P 在平面VAC 内，过点P 将木块锯开，使截面平行于直线VB 和AC ，应该怎样画线？第8题图P ·18．（12分）已知圆心(2,3)-，一条直径的两个端点恰好在两坐标轴上，求这个圆的方程。

2017-2018学年江西省宜春市高安中学高二（下）期末数学试卷（文科）一、选择题：（本大题共12个小题，每小题5分，共60分.每小题给出的四个选项中只有一项是符合题目要求的）1．（5分）设集合A＝{﹣1，0，1，2}，B＝{x|2﹣x≥0，x∈N}，则A∩B＝（）A．{0，1}B．{0，1，2}C．{0，2}D．{1，2}2．（5分）若复数z满足z•（1+i）＝1﹣i（i是虚数单位），则z的共轭复数＝（）A．i B．﹣i C．1+i D．1﹣i3．（5分）函数f（x）＝lnx+3x的零点个数为（）A．0B．1C．2D．34．（5分）若，且，则sin2α＝（）A．B．C．D．5．（5分）已知某居民小区户主人数和户主对户型结构的满意率分别如图1和图2所示，为了解该小区户主对户型结构的满意程度，用分层抽样的方法抽取20%的户主进行调查，则样本容量和抽取的户主对四居室满意的人数分别为（）A．100，8B．80，20C．100，20D．80，86．（5分）已知x，y满足约束条件则z＝x+2y的最大值是（）A．﹣3B．﹣1C．1D．37．（5分）若抛物线y2＝2px（p＞0）的准线经过双曲线x2﹣y2＝1的左焦点，则p＝（）A．1B．C．D．28．（5分）执行如图所示的程序框图，输出的S值为（）A．2B．C．D．9．（5分）某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为（）A．3B．2C．2D．210．（5分）在△ABC中，角A，B，C所对的边分别为a，b，c，若b cos C＝a，，则△ABC的面积为（）A．B．C．D．11．（5分）已知函数f（x）＝（ω＞0，|φ|＜，a∈R）在区间[﹣3，3]上的图象如图所示，则可取（）A．4πB．2πC．πD．12．（5分）已知函数f（x）是定义在上的偶函数，f'（x）为其导函数，若，且，则f（x）＜0的解集为（）A．B．C．D．二、填空题：本大题共四小题，每小题5分，共20分13．（5分）已知函数，若f（a）＝3，则实数a的值为．14．（5分）若函数f（2x+1）＝x2﹣2x，则f（3）＝．15．（5分）已知各项皆为正数的等比数列{a n}（n∈N*），满足a7＝a6+2a5，若存在两项a m、a n使得＝4a1，则+的最小值为．16．（5分）在△ABC中，角A、B、C所对的边分别是a、b、c，若2sin A、sin C、2sin B成等比数列且角C为锐角，则的取值范围为．三、解答题：解答应写出必要的文字说明，证明过程或演算步骤17．（12分）记等差数列{a n}的前n项和为S n，若a3＝6，S7＝56．（1）求数列{a n}的通项公式a n；（2）若数列{b n}的首项为1，且，求数列{b n}的前n项和T n．18．（12分）如图所示：在三棱柱ABC﹣A1B1C1中，BB1⊥B1C1，D，E分别为A1C1，A1B1的中点，且A1B1⊥BD，BB1＝BA1＝BD＝A1B1＝2（1）求证：A1B1⊥平面BDE；（2）求四棱锥C1﹣ABB1A1的体积．19．（12分）某厂准备在甲、乙两位工人中派一名工人参加省活动技能大赛，为此安排甲、乙两位工人在厂实习基地现场进行加工直径为30mm的零件测试，他俩各加工10个零件，甲、乙两个人加工这10个零件的数据（单位：mm）用如下的数表所示：注：表格中第一列表示的意义是：甲、乙现场加工第一个零件的数据分别是30.0和30.2，第二列表示的意义是：甲、乙现场加工第二个零件的数据分别是30.0和29.8，…，其它列，以此类推．（1）若考虑平均数与完全符合要求的个数，你认为谁的成绩好些？（2）计算甲、乙两个人的方差，考虑平均数与方差，说明谁的成绩好一些？（3）根据上表，在给出的坐标纸（详见答题卡）上画出甲、乙两个人加工零件的数据的折线图．若竞赛时加工零件的个数远远超过10个，请根据折线图的趋势，你认为派谁去更合适？简述理由．20．（12分）已知椭圆C：（a＞b＞0）的离心率为，短轴一个端点到右焦点的距离为．（Ⅰ）求椭圆C的方程；（Ⅱ）设直线l与椭圆C交于A、B两点，坐标原点O到直线l的距离为，求△AOB面积的最大值．21．（12分）已知函数f（x）＝e x﹣ax（a＞0），且f（x）在x＝a处的切线与直线x+（e﹣1）y＝0垂直．（1）求f（x）的极值；（2）若不等式（m﹣x）f（x）＜x+1在x∈（0，+∞）上恒成立，求整数m的最大值．请考生在第22、23题中任选一题作答，如果多做，按所做的第一题计分，作答时请用2B 铅笔填涂题号．[选修4-5：不等式选讲]22．（10分）在极坐标系中，已知直线l的方程为：3ρsinθ＝ρcosθ+2，直角坐标系中，曲线C的参数方程为：（t为参数）（1）写出直线l与曲线C的直角坐标方程；（2）设直线l与曲线C的公共点为M，N，F为曲线C的焦点，求△FMN的周长．[选修4-4：坐标系与参数方程]23．设函数f（x）＝|x﹣a2|+|x+b2|（a、b∈R）．（1）若a＝1，b＝0，求f（x）≥2的解集；（2）若f（x）的最小值为6，求a+b的最大值．2017-2018学年江西省宜春市高安中学高二（下）期末数学试卷（文科）参考答案与试题解析一、选择题：（本大题共12个小题，每小题5分，共60分.每小题给出的四个选项中只有一项是符合题目要求的）1．【解答】解：∵集合A＝{﹣1，0，1，2}，B＝{x|2﹣x≥0，x∈N}＝{x|x≤2，x∈N}＝{0，1，2}，∴A∩B＝{0，1，2}．故选：B．2．【解答】解：设z＝a+bi，因为（a+bi）（1+i）＝1﹣i，即a﹣b+（a+b）i＝1﹣i，所以，解得a＝0，b＝﹣1，所以z＝﹣i，所以＝i．故选：A．3．【解答】解：函数f（x）＝lnx+3x在（0，+∞）递增，由f（）＝ln+1＝1﹣ln3＜0，f（1）＝ln1+3＝3＞0，由函数零点存在定理，可得f（x）在（，1）只有一个零点．故选：B．4．【解答】解：若，且＝﹣sinα，即sinα＝﹣，cosα＝＝，∴sin2α＝2sinαcosα＝﹣，故选：C．5．【解答】解：样本容量为：（150+250+100）×20%＝100，∴抽取的户主对四居室满意的人数为：100×．故选：A．6．【解答】解：x，y满足约束条件的可行域如图：目标函数z＝x+2y经过可行域的A时，目标函数取得最大值，由：解得A（﹣1，2），目标函数的最大值为：﹣1+2×2＝3．故选：D．7．【解答】解：抛物线y2＝2px（p＞0）的准线为x＝﹣，双曲线x2﹣y2＝1的左焦点为（﹣，0），则由题意可得＝，可得p＝2．故选：D．8．【解答】解：当k＝0时，满足进行循环的条件，执行完循环体后，k＝1，S＝2，当k＝1时，满足进行循环的条件，执行完循环体后，k＝2，S＝，当k＝2时，满足进行循环的条件，执行完循环体后，k＝3，S＝，当k＝3时，不满足进行循环的条件，故输出结果为：，故选：C．9．【解答】解：由三视图可得直观图，再四棱锥P﹣ABCD中，最长的棱为P A，即P A＝＝＝2，故选：B．10．【解答】解：在△ABC中，∵b cos C＝a，∴由余弦定理可得：cos C＝＝，可得：a2+c2＝b2，可得：B＝90°，∵，∴可得：ac＝2，∴△ABC的面积S＝ac sin B＝＝．故选：A．11．【解答】解：由图象可知f（x）是偶函数，∴φ＝kπ，又|φ|＜，∴φ＝0．令f（x）＝0得cosωx＝0，∴ωx＝+kπ，解得x＝+，k∈Z．∵ω＞0，∴f（x）的最小正零点为，由图象可知f（x）的最小正零点为1，故＝1，解得ω＝，∴f（x）＝，由图象f（0）＝2，故＝2，∴a＝，∴＝π．故选：C．12．【解答】解：设g（x）＝，x∈，∴g′（x）＝，∵f′（x）+tan x•f（x）＞0，x∈（﹣，0），∴cos x•f′（x）+sin x•f（x）＞0，∴g′（x）＞0在（﹣，0）上恒成立，∴g（x）在（﹣，0）上单调递增，∵f（x）为偶函数，∴g（x）也为偶函数，∴g（x）在（0，）上单调递减，∵f（x）＜0，f（）＝0，∴＜0，∴g（x）＜0＝g（），∴|x|＞，∴﹣＜x＜﹣或＜x＜，故选：D．二、填空题：本大题共四小题，每小题5分，共20分13．【解答】解：函数，若f（a）＝3，可得a≤0时，，解得a＝﹣1；a＞0时，log3a＝3，解得a＝27．综上实数a的值为：﹣1或27．故答案为：﹣1或27．14．【解答】解法一：（换元法求解析式）令t＝2x+1，则x＝则f（t）＝﹣2＝∴∴f（3）＝﹣1解法二：（凑配法求解析式）∵f（2x+1）＝x2﹣2x＝∴∴f（3）＝﹣1解法三：（凑配法求解析式）∵f（2x+1）＝x2﹣2x令2x+1＝3则x＝1此时x2﹣2x＝﹣1∴f（3）＝﹣1故答案为：﹣115．【解答】解：设各项皆为正数的等比数列{a n}的公比为q＞0（n∈N*），∵a7＝a6+2a5，∴＝a5q+2a5，化为q2﹣q﹣2＝0，解得q＝2．∵存在两项a m、a n使得，∴＝4a1，∴2m+n﹣2＝24，∴m+n＝6．则＝＝≥＝，当且仅当n＝2m ＝4时取等号．∴的最小值为．故答案为：．16．【解答】解：∵2sin A、sin C、2sin B依次成等比数列，则：sin2C＝4sin A sin B，利用正弦定理，得：c2＝4ab，又C为锐角，∴0＜cos C＜1，∴1，∴＜1，化为：＜8，∴＜＜2，∴＜＜．故的取值范围是．故答案为：．三、解答题：解答应写出必要的文字说明，证明过程或演算步骤17．【解答】解：（1）设等差为d的等差数列{a n}的前n项和为S n，若a3＝6，S7＝56．由已知得：，又因为：a1+a7＝2a4，得a4＝8，所以公差d＝2，故a n＝6+（n﹣3）•2＝2n（2）由（1）知：，故，所以数列{b n}是以1为首项，2为公比的等比数列∴18．【解答】证明：（1）在△A1B1B中，BB1＝BA1＝A1B1∵E为A1B1的中点，A1B1⊥B1E，A1B1⊥BD，BE∩BD＝B，∴A1B1⊥平面BDE．（2）∵DE⊥A1B1，DE∥B1C1，得B1C1⊥A1B1，B1C1⊥B1B1，A1B1∩BB1＝B1⇒B1C1⊥平面ABB1A1BB1＝BA1＝BD＝A1B1＝2在，∴DE＝1，∴B1C1＝2，，∴．19．【解答】解：（1）根据表中数据可得：，，∴两人的平均数相等，但甲的完全符合要求的个数为5个，而乙为2个，∴甲的成绩好些．（2）∵且∴s乙2＞s甲2，即在平均数相同的情况下，甲的波动性小，∴甲的成绩好些．（3）画出折线图（如右上图），由其走势可知，尽管乙的成绩前面起伏大，但后来逐渐稳定，误差小，预测乙的潜力大，虽然甲比较稳定，但潜力小，∴派乙参加．20．【解答】解：（Ⅰ）设椭圆的半焦距为c，依题意∴b＝1，∴所求椭圆方程为．（Ⅱ）设A（x1，y1），B（x2，y2）．（1）当AB⊥x轴时，．（2）当AB与x轴不垂直时，设直线AB的方程为y＝kx+m．由已知，得．把y＝kx+m代入椭圆方程，整理得（3k2+1）x2+6kmx+3m2﹣3＝0，∴，．∴|AB|2＝（1+k2）（x2﹣x1）2＝＝＝＝＝．当且仅当，即时等号成立．当k＝0时，，综上所述|AB|max＝2．∴当|AB|最大时，△AOB面积取最大值．21．【解答】解：（1）由f（x）＝e x﹣ax，得f'（x）＝e x﹣a，∴f'（a）＝e a﹣a，又∵f（x）在x＝a处的切与直线x+（e﹣1）y＝0垂直，∴f'（a）＝e﹣1，即e a﹣a＝e﹣1且a＞0，∴a＝1，即∴f'（x）＝e x﹣x，∴f'（x）＝e x﹣1，令f'（x）＝0得：x＝0，当x∈（﹣∞，0）时，f'（x）＜0，f（x）为减函数，当x∈（0，+∞）时，f'（x）＞0，f（x）为增函数，∴x＝0时，f（x）取到极小值f（0）＝1，无极大值．（2）由（1）知：f（x）＝e x﹣x，故原不等式可化为：（m﹣x）（e x﹣x）＜x+1，由（1）知，当x＞0，e x﹣x＞0，∴，令，则m＜g（x）min，又∵，令h（x）＝e x﹣x﹣2，则h'（x）＝e x﹣1，∵x＞0，∴h'（x）＞0，∴h（x）在（0，+∞）为递增，又h（1）＜0，h（2）＞0，∴h（x）在（0，+∞）上存在唯一零点，设为x0，则x0∈（1，2），则当x∈（0，x0）时，g'（x）＜0，当（x0，+∞）时g'（x）＞0，∴，又∵，将，代入得：g（x0）＝x0+1，由x0∈（1，2），得：g（x0）∈（2，3），∴整数k的最大值为2．请考生在第22、23题中任选一题作答，如果多做，按所做的第一题计分，作答时请用2B 铅笔填涂题号．[选修4-5：不等式选讲]22．【解答】解：（1）由（t为参数），消t得：y2＝x又∵x＝ρcosθ，y＝ρsinθ，∴直线l的直角坐标方程为：x﹣3y+2＝0（2）由（1）得，，消x得：y2﹣3y+2＝0，∴y1＝1，y2＝2，不妨设M（1，1），N（4，2），，[选修4-4：坐标系与参数方程]23．【解答】解：（1）因为a＝1，b＝0，所以f（x）＝|x﹣1|+|x|，当x＜0时，1﹣x﹣x≥2，x≤﹣，∴x≤﹣，当0≤x＜1时，1﹣x+x≥2，x∈φ当x≥1时，，综上：；（2）∵|x﹣a2|+|x+b2|≥|x﹣a2﹣x﹣b2|＝a2+b2，∴a2+b2＝6成立，即∵，∴．。

江西省高安市2017-2018学年高二数学1月月考试题 理一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知命题p q 、，“p ⌝为真”是“p q ∧为假”的（ ）.A 必要不充分条件 .B 充分不必要条件 .C 充要条件 .D 既不充分也不必要条件2.双曲线9322=-y x 的虚轴长是（ ）4.已知甲、乙两组数据如图茎叶图所示，若它们的中位数相同，平均数也相同，则图中的n m ,的比值=m（ ）.A 方程02=++b ax x 的两根的绝对值存在一个小于1 .B 方程02=++b ax x 的两根的绝对值至少有一个大于等于1 .C 方程02=++b ax x 没有实数根.D 方程02=++b ax x 的两根的绝对值都不小于16.函数32)(23++-=x x x x f 的单调递减区间为（ ）7.已知直线l 过点)1,0(-，且与曲线x y ln =相切，则直线l 的方程为（ ）9.《九章算术》上有这样一道题：“今有垣厚若干尺，两鼠对穿，大鼠日一尺，小鼠也日一尺，大鼠日自倍，小鼠日自半，问何日相逢，各穿几何？”题意是：“有两只老鼠从墙的两边打洞穿墙，大老鼠第一天进一尺，以后每天加倍；小老鼠第一天也进一尺，以后每天减半.”假设墙厚16尺，现用程序框图描述该问题，则输出n =（ ）.A 2 .B 4 .C 6 .D 810.已知点)0,3(M ，椭圆1422=+y x 与直线)3(+=x k y 交于点A 、B ，则ABM ∆的周长为（ ）.A 4 .B 8 .C 12 .D 1611.“已知实数x ，y 满足1)1()1(22=-+-y x ，求22y x +的最大值”时，可理解为在以点)11(，为圆心，以1为半径的圆上找一点，使它到原点距离最远问题，据此类比到空间，试分析：已知实数x ，y ，z 满足1)1()1()1(222=-+-+-z y x ，求222z y x ++的最大值是( )12.定义在R 上的函数()f x 满足：()()1f x f x '+>，()04f =，则不等式()3x x e f x e >+（其中e 为自然对数的底数）的解集为（ ）.A ),3()0,(+∞-∞ .B ),0(+∞.C ),3(+∞ .D ),0()0,(+∞-∞二、填空题:(本大题共4小题,每小题5分,共20分,把答案填在答卷纸的相应位置上) 13.函数x x y sin 21-=在区间]2,0[π的极值为________.14.已知实数,x y 满足，则y x z 23+=的最大值___________.15.在正三棱柱111C B A ABC -中，所有棱长均为1，则点1B 到平面1ABC 的距离为________. 16.双曲线与抛物线()220y px p =>有相同的焦点F ，且相交于,A B 两点，AB 连线经过焦点F ，则双曲线的离心率为．三、解答题:(本大题共6小题,共70分,解答应写出文字说明，证明过程或演算步骤）. 17.（10分）已知命题p ：0342≤+-x x ，命题q ：0242≤--mx x ． （1）若2=m ，q p ∨为真命题，q p ∧为假命题，求实数x 的取值范围； （2）若p 是q 的充分条件，求实数m 的取值范围.18.（12分）在ABC ∆中，内角,,A B C 的对边分别为,,a b c ，且满足.（1）求角C 的大小；（2）若2=c ，求ABC ∆的面积的最大值.19.（12分）设{}n a 是公差不为零的等差数列，22222345a a a a +=+，n S 为其前n 项和，77S =.（1）求{}n a 的通项公式； （2）设431++=n n n a a b ，数列}{n b 的前n 项和为n T ，若对于任意的+∈N n 都有3a T n <，求a 的最小值.20.如图，在四棱锥ABCD P -中，ABCD PD 平面⊥，底面ABCD 为正方形，2==CD PD ，E ，F 分别是AB ，PB 的中点． （1）求证：CD EF ⊥；（2）求BD 与平面DEF 所成角的正弦值．21.已知椭圆C ：（0a b >>）的离心率为，过右焦点且垂直于x 轴的直线1l与椭圆C 交于A ，B 两点，且||AB =2l ：()y k x m =-)43,(>∈m R m 与椭圆C 交于M ，N 两点.（1）求椭圆C 的标准方程；（2）已知点)0,45(R ，若⋅是一个与k 无关的常数，求实数m 的值. 22.设函数．（1）当0=b 时，求函数()f x 的单调区间； （2）令（23x ≤≤）其图象上任意一点00(,)P x y 处切线的斜率恒成立，求实数a 的取值范围；（3）当0a =，1b =-时，方程()f x mx =在区间内有唯一实数解，求实数m 的取值范围.江西省高安中学2019届高二年级上学期第三次考试 数学（理科）试题(答案)一．选择题（本大题共12小题，每小题5分，共60分）.二、填空题（本大题共4小题,每小题5分,共20分）. 13.236-π14.23 15.72116.21+ 三、解答题:(本大题共6小题,共70分).17.（10分）（1）若p 真：31≤≤x ，若q 真：46x -≤≤， 由已知，p 、q 一真一假. ①若p 真q 假，则⎩⎨⎧>-<≤≤6431x x x 或，无解；②若p 假q 真，则⎩⎨⎧≤≤-><6431x x x 或，∴x 的取值范围为]6,3()1,4[ -.（2）对于p ：31≤≤x ，由已知,对任意]3,1[∈x ，0242≤--mx x 恒成立， 故xx m 24-≥，故5-≥m 18.（12分）解：（1）∵，∴由正弦定理可得：sin sin sin cos B A C C A =+，又∵()sin sin sin sin cos sin B A C A C A C =+=+，sin sin cos A C A C =， ∵sin 0A ≠，∴解得：，∵()0,C π∈， ∴.（2）∵2c =，，∴由余弦定理可得：，即：，当且仅当a b =时等号成立，∴，当且仅当a b =时等号成立，即ABC ∆的面积的最大值为2 19.（12分）（1）设数列{}n a 的公差为(0)d d ≠因为22222345a a a a +=+，所以42423535()()()()a a a a a a a a -+=-+，即342222(0)d a d a d ⋅=-⋅≠ 所以34a a =- 又因为，所以431,1a a ==-，2d =。

江西省高安市2017-2018学年高一数学1月月考试题（创新班）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设全集U ＝R ，M ＝{x |x ≥1}，N ＝{x |0≤x <5}，则(∁U M )∪(∁U N )为( )A ．{x |x ≥0)B ．{x |x <1或x ≥5}C ．{x |x ≤1或x ≥5}D ．{x |x <0或x ≥5}2.．下列叙述中不正确的是( )A ．若直线的斜率存在，则必有倾斜角与之对应B ．每一条直线都有唯一对应的倾斜角C ．与坐标轴垂直的直线的倾斜角为0°或90°D ．若直线的倾斜角为α，则直线的斜率为tan αU U 与命题P ⊆Q 等价的有( )A ．1个B ．2个C ．3个D ．4个5.已知函数f (x )＝⎩⎪⎨⎪⎧e x－1 x ≤1，ln x x >1，)那么f (ln2)的值是( )A ．0B ．1C ．ln(ln2)D ．26.已知某几何体的三视图如图所示，则该几何体的体积是( )A ．108cm 3B ．100cm 3C ．92cm 3D ．84cm 37.已知函数，若f (a )＞f (－a )，则实数a 的取值范围是( )A ．(－1,0)∪(0,1)B ．(－∞，－1)∪(1，＋∞)C ．(－1,0)∪(1，＋∞)D ．(－∞，－1)∪(0,1)8.已知a ，b 为两个不相等的实数，集合M ＝{a 2－4a ，－1}，N ＝{b 2－4b ＋1，－2}，映射f ：x →x 表示把集合M 中的元素x 映射到集合N 中仍为x ，则a ＋b 等于( )A ．1B ．2C ．3D ．4 9.具有下列性质的三棱锥中，哪一个是正棱锥？( )A ．顶点在底面的射影到底面各顶点的距离相等B ．底面是正三角形，且侧面都是等腰三角形C ．相邻两条侧棱间的夹角相等D ．三条侧棱相等，侧面与底面所成角也相等10.以等腰直角三角形ABC 的斜边BC 上的高AD 为折痕，把△ABD 和△ACD 折成互相垂直的两个平面后，某学生得出下列四个结论：①BD ⊥AC ；②△BCA 是等边三角形；③三棱锥D ­ABC 是正三棱锥④平面ADC ⊥平面ABC .其中正确的是( )A.①②④B.①②③C.②③④D.①③④11.定义域为R 的函数，若关于x 的方程0)()(2=++c x bf x f 恰有3个不同的实数解321,,x x x ，则)(321x x x f ++等于（ ） A ．0B ．lC ．3lg2D ．2lg2二、填空题：（本题共4小题，每小题5分，共20分．）13.直线ax ＋2y －1＝0与x ＋(a －1)y ＋2＝0平行，则a 等于．14.对于直线l 和平面α，β，下列说法中正确的是______．(把所有正确答案填在横线上)①若α∥β且l∥β，则l∥α ②若l β且α⊥β，则l⊥α ③若l⊥β且α⊥β，则l∥α ④若l⊥β且α∥β，且l⊥α15.已知P 是圆22:(4)1C x y +-=外一点，过点P 作圆C 的切线，切点为A 、B ．记四边形PACB 的面积为()f P ，当P 在圆22:(4)(1)4D x y ++-=上运动时，()f P 的取值范围为．16.对于函数错误！未找到引用源。

高安中学2019届高二年级上学期第一次段考文科数学试卷一、选择题：（本大题共12小题，每小题5分，共60分．在每小题给出的四处备选项中，只有一项是符合题目要求的．)1.如果p是真命题，q是假命题，则（）A。

qp∧是真命题 B.qp∨是假命题 C.p⌝是真命题D。

q⌝是真命题2。

高安市为了了解三年级、六年级、九年级这三个年级的学生视力是否存在显著差异,拟从这三个年级中按人数比例抽取部分学生进行调查，则最合理的抽样方法是（)A. 系统抽样法B。

分层抽样法C。

抽签法D。

随机数法3．一部3卷文集随机地排在书架上，卷号自左向右为1,2,3顺序的概率是（）A.16B.31 C.12D。

324.不等式0)1)(2)(1(>+--xxx的解集是（）A. ()()+∞-,21,1 B. ()()2,11,-∞-C。

()()+∞-∞-,21, D.()()2,11,1-5.在区间[]4,4-上随机的取一个数x，则x满足220x x+-<的概率为( ）A．12B．38C．58D．06．口袋内装有一些大小相同的红球、白球和黑球,从中摸出1个球，摸出红球的概率是0。

42,摸出白球的概率是0.28，那么摸出黑球的概率是（)A.0。

42 B。

0.28 C。

0。

3 D。

0.797。

下图是输出数据15的程序框图,则判断框内应填入的条件是A.3>iB. 4i≤C。

3i≤D。

i＞48.下表是某厂1至4月份用水量（单位：百吨）的一组数据:月份x1234用水量y 4.543 2.5由散点图可知，用水量y与月份x之间有较好的线性相关关系，其线性回归直线方程是0.7y x a=-+，则a等于（）A。

10。

5 B。

5。

15 C.5.2D.5。

259．已知等比数列na 满足13a，13521aa a ，则357aa a 等于( ）A ．21B ．42C ．63D ．8410.已知不等式,012>+-mx mx对任意实数x 都成立，则m 的取值范围（ ）A ． ()[)+∞-∞-,04,B ．[)4,0 C.(]()+∞∞-,40, D ．[)0,4- 11．已知△ABC 中，∠ACB=90°，BC=3，AC=4，P 是AB 上一点，则点P 到AC 、BC 的距离乘积的最大值是( ) A 。