【解析】福建安徽版02期2014届高三名校数学理试题分省分项汇编专题09圆锥曲线原卷版Word版无答案

2014高考圆锥曲线真题汇总（理科）1．（满分14分）如图在平面直角坐标系x o y 中，12,F F 分别是椭圆顶点B 的坐标是(0,)b ，连接2BF 并延长交椭圆于点A ，过点A 作x 轴的垂线交椭圆于另一点C ，连接1FC .（1）若点C 的坐标为（2）若1FC AB ⊥，求椭圆离心率e 的值.2．已知点A ()02-，,椭圆F 是椭圆E 的右焦点，直线AF O 为坐标原点 （I ）求E 的方程；（II ）设过点A 的动直线l 与E 相交于P,Q 两点。

当OPQ ∆的面积最大时，求l 的直线方程.3．已知椭圆C （0a b >>）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形.（1）求椭圆C 的标准方程；（2）设F 为椭圆C 的左焦点，T 为直线3x =-上任意一点，过F 作TF 的垂线交椭圆C 于点P ，Q.（i ）证明：OT 平分线段PQ （其中O 为坐标原点）；（ii T 的坐标. 4．（本题满分16分）本题共3个小题，第1小题满分3分，第2小题满分5分，第3小题满分8分.在平面直角坐标系xoy 中，对于直线l ：0ax by c ++=和点),,(),,(22211y x P y x P i 记1122)().ax by c ax by c η=++++（若η<0，则称点21,P P 被直线l 分隔.若曲线C 与直线l 没有公共点，且曲线C 上存在点21P P ，被直线l 分隔，则称直线l 为曲线C 的一条分隔线.⑴ 求证：点），（），（012,1-B A 被直线01=-+y x 分隔； ⑵若直线kx y =是曲线1422=-y x 的分隔线，求实数k 的取值范围；⑶动点M 到点）（2,0Q 的距离与到y 轴的距离之积为1，设点M 的轨迹为E ，求证：通过原点的直线中，有且仅有一条直线是E 的分割线.5．如图，曲线C 由上半椭部分抛物线22:1(0)C y x y =-+≤连接而成，12,C C 的公共点为,A B ，其中1C 的离心率为（1）求,a b 的值；（2）过点B 的直线l 与12,C C 分别交于,P Q （均异于点,A B ），若AP AQ ⊥，求直线l 的方程. 6．（本小题满分14分）已知抛物线2:2(0)C y px p =>的焦点为F ，A 为C 上异于原点的任意一点，过点A 的直线l 交C 于另一点B ，交x 轴的正半轴于点D ，且有||||FA FD =.当点A 的横坐标为3时，ADF ∆为正三角形. （Ⅰ）求C 的方程；（Ⅱ）若直线1//l l ，且1l 和C 有且只有一个公共点E ，（ⅰ）证明直线AE 过定点，并求出定点坐标；（ⅱ）ABE ∆的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由. 7．（本小题满分13分）如图，已知双曲线()1,2,,2,2n n N n *⋅⋅⋅∈≥的右焦点1a ,点2a 分别在1b 的两条渐近线上，1b 轴，2112,a a b b ξη=-=-∥3n =(ξ为坐标原点）.（1）求双曲线ξ的方程；（2）过η上一点()p c 的直线与直线()p c 相交于点N ，证明点P 在C 上移动时，. 8（1）求椭圆C 的标准方程；（2）若动点()00,P x y 为椭圆外一点，且点P 到椭圆C 的两条切线相互垂直，求点P 的轨迹方程. 9．（本小题满分13分）的两条渐近线分别为x y l x y l 2:,2:21-==.（1）求双曲线E 的离心率；（2）如图，O 为坐标原点，动直线l 分别交直线21,l l 于B A ,两点（B A ,分别在第一，四象限），且OAB ∆的面积恒为8，试探究：是否存在总与直线l 有且只有一个公共点的双曲线E ？若存在，求出双曲线E 的方程；若不存在，说明理由.10的左、右焦点分别为12,F F ，点D 在椭圆上，112DF F F ⊥，，12DF F ∆的面积为 （1）求该椭圆的标准方程；（2）设圆心在y 轴上的圆与椭圆在x 轴的上方有两个交点，且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点，求圆的半径..11动直线l 与椭圆C 只有一个公共点P ，且点P 在第一象限.（１）已知直线l 的斜率为k ，用k b a ,,表示点P 的坐标；（２）若过原点O 的直线1l 与l 垂直，证明：点P 到直线1l 的距离的最大值为b a -.12．（0a b >>）的左、右焦点为12,F F ，右顶点为A ，上顶点为B ．已1232F F （1）求椭圆的离心率；（2）设P 为椭圆上异于其顶点的一点，以线段PB 为直径的圆经过点1F ，经过原点O 的直线l 与该圆相切，求直线13．设1F ,2F 分别是椭圆M 是C 上一点且2MF与x 轴垂直，直线1MF 与C 的另一个交点为N. （1）若直线MNC 的离心率；（2）若直线MN 在y 轴上的截距为2a,b.14．圆224x y +=的切线与x 轴正半轴，y 轴正半轴围成一个三角形，当该三角形面积最小时，切点为P （如图）P（1）求1C 的方程；（2）椭圆2C 过点P 且与1C 有相同的焦点，直线l 过2C 的右焦点且与2C 交于A ，B 两点，若以线段AB 为直径的圆心过点P ，求l 的方程.15．如图,O 为坐标原点,的左右焦点分别为12,F F ,离心率为1e ;双曲左右焦点分别为34,F F ,离心率为2e ,已知(1)求12,C C 的方程;(2)过1F 点作1C 的不垂直于y 轴的弦AB ,M 为AB 的中点,当直线OM 与2C 交于,P Q 两点时,求四边形APBQ 面积的最小值.16．在平面直角坐标系xOy 中，点M 到点()1,0F 的距离比它到y 轴的距离多1，记点M 的轨迹为C .（1）求轨迹为C 的方程；（2）设斜率为k 的直线l 过定点()2,1p -，求直线l 与轨迹C 恰好有一个公共点，两个公共点，三个公共点时k 的相应取值范围.17．已知抛物线C ：22(0)y px p =>的焦点为F ，直线4y =与y 轴的交点为P ，与C的交点为Q （1）求C 的方程； （2）过F 的直线l 与C 相交于A ，B 两点，若AB 的垂直平分线l '与C 相较于M ，N 两点，且A ，M ，B ，N 四点在同一圆上，求l 的方程. 18．已知椭圆C ：2224x y +=. （1）求椭圆C 的离心率；（2）设O 为原点，若点A 在椭圆C 上，点B 在直线2y =上，且OA OB ⊥，试判断直线AB 与圆222x y +=的位置关系，并证明你的结论.19．如图，已知两条抛物线()02:1121>=p x p y E 和()02:2222>=p x p y E ，过原点O的两条直线1l 和2l ，1l 与21,E E 分别交于21,A A 两点，2l 与21,E E 分别交于21,B B 两点. （1）证明：;//2211B A B A（2）过原点O 作直线l （异于1l ，2l ）与21,E E 分别交于21,C C 两点.记111C B A ∆与222C B A ∆的面积分别为1S 与2S ,.参考答案1．（1（2【来源】2014年全国普通高等学校招生统一考试数学（江苏卷带解析）【解析】试题分析：（1）求椭圆标准方程，一般要找到关系,,a b c的两个等量关系，本题中椭圆过点，可把点的坐标代入标准方程，得到一个关于,,a b c 的方程，另外（2）要求离心率，就是要列出关于,,a b c 的一个等式，题设条件是1FC AB ⊥，即11F C AB k k ⋅=-，求1F C k ，必须求得C 的坐标，由已知写出2BF 方程，与椭圆方程联立可解得A 点坐标11(,)x y ，则11(,)C x y -，由此1F C k 可得，代入11F C A Bk k⋅=-可得关于,,a b c 的等式，再由可得e 的方程，可求得e . 试题解析：（1）由题意，2(,0)F c ，(0,)B b，，解得1b =．∴椭圆方程为 （2）直线2BF 方程为联立方程组，解得A 点坐标为，则C 点坐标为又，由1F C A B ⊥得，即4223b a c c =+，∴22222()3a c a c c -=+，化简得【考点】椭圆标准方程，椭圆离心率，直线与直线的位置关系．2．（I （II 【来源】2014年全国普通高等学校招生统一考试理科数学（新课标Ⅰ带解析）【解析】试题分析：（I ）由直线AF 求得2a =，再利用222b a c =-求b ，进而可确定椭圆E 的方程；（II ）依题意直线l 的斜率存在，故可设直线l 方程为2y kx =-，和椭圆方程联立得22(14k )x 16120kx +-+=．利用弦长公式表示利用点到直线l 的距离求OPQ ∆的高从而三角形OPQ ∆的面积可表示为关于变量k 的函数解析式()f k ，再求函数最大值及相应的k 值，故直线l 的方程确定．试题解析：（I ）设右焦点(c,0)F ，由条件知，，所以2a =，222b ac =-1=．故椭圆E 的方程为（II ）当l x ⊥轴时不合题意，故设直线:l 2y kx =-，1122(x ,y ),Q(x ,y )P ．将2y kx =-得22(14k )x 16120kx +-+=．当216(4k 3)0∆=->，即又点O 到直线PQ 的距离d =所以OPQ ∆的面积则0t >，，当且仅当2t =时，0∆>．所以，当OPQ ∆的面积最大时，l 的方程为 【考点定位】1、椭圆的标准方程及简单几何性质；2、弦长公式；3、函数的最值．3．（2）(3,0)T - 【来源】2014年全国普通高等学校招生统一考试理科数学（四川卷带解析）【解析】试题分析：（1）因为焦距为4，所以2c =，由此可求出,a b 的值，从而求得椭圆的方程.（2）椭圆方程化为2236x y +=.设PQ 的方程为2x my =-，代入椭圆方程得：22(3)420m y my +--=.（ⅰ）设PQ 的中点为00(,)M x y ，求出,OM OT k k ，只要O M O T k k=，即证得OT 平分线段PQ.（ⅱ）可用m 表示出PQ ，TF 可得：再根据取等号的条件，可得T 的坐标.试题解答：（1）2c =，又（2）椭圆方程化为2236x y +=.（ⅰ）设PQ 的方程为2x my =-，代入椭圆方程得：22(3)420m y my +--=. 设PQ 的中点为00(,)M x y ，则又TF 的方程为0(2)y m x -=-+，则3x =-得y m =，OT 过PQ 的中点，即OT 平分线段PQ.当1m =±时取等号，此时T 的坐标为(3,1)T -±.【考点定位】1、椭圆的方程；2、直线与圆锥曲线；3、最值问题.4．(1)证明见解析；（2（3）证明见解析. 【来源】2014年全国普通高等学校招生统一考试理科数学（上海卷带解析） 【解析】试题分析：本题属于新定义问题，（1）我们只要利用题设定义求出η的值，若0η<，则结论就可得证；（2）直线y kx =是曲线2241x y -=的分隔线，首先直线与曲线无交点，即直线方程与曲线方程联立方程组2241x y y kx⎧-=⎨=⎩，方程组应无实解，方程组变形为22(14)10k x --=，此方程就无实解，注意分类讨论，按二次项系数为0和不为0分类，然后在曲线上找到两点位于直线y kx =的两侧．则可得到所求范围；（3）首先求出轨迹E 的设其方程为y kx =，这个方程有无实数解，直接判断不方便，可转化为判断函数22()(1)44F x k x kx =+-+与的图象有无交点，而这可利用函数图象直接判断．()y F x =是开口方向向上的二次函数，()y G x =是幂函数，其图象一定有交点，因此直线y kx =不是E 的分隔线，过原点的直线还有一条就是0x =，它显然与曲线E 无交点，又曲线E 上两点(1,2),(1,2)-一定在直线0x =两侧，故它是分隔线，结论得证．试题解析：（1）由题得，2(2)0η=⋅-<，∴(1,2),(1,0)A B -被直线10x y +-=分隔. （2）由题得，直线y kx =与曲线2241x y -=无交点即222241(14)10x y k x y kx⎧-=⇒--=⎨=⎩无解 ∴2140k -=或221404(14)0k k ⎧-≠⎨∆=-<⎩，∴ 又对任意点(1,0)和(1,0)-在曲线2221x y -=上，满足20k η=-<，被直线y kx =分隔，所以所求k 的范围是（3）由题得，设(,)M x y ，∴ 化简得，点M 的轨迹方程为222[(2)]1x y x +-⋅= ①当过原点的直线斜率存在时，设方程为y kx =. 联立方程，2222432[(2)]1(1)4410x y x k x kx x y kx⎧+-⋅=⇒+-+-=⎨=⎩.令2432()(1)441F x k x kx x =+-+-，因为2(0)(2)(1)[16(1)15]0F F k =-⋅-+<， 所以方程()0F x =有实解，直线y kx =与曲线E 有交点．直线y kx =不是曲线E 的分隔线． ②当过原点的直线斜率不存在时，其方程为0x =.显然0x =与曲线222[(2)]1x y x +-⋅=没有交点，又曲线E 上的两点(1,2),(1,2)-对于直线0x =满足110η=-⋅<，即点(1,2),(1,2)-被直线0x =分隔．所以直线0x =是E 分隔线．综上所述，仅存在一条直线0x =是E 的分割线. 【考点】新定义，直线与曲线的公共点问题.5．（1）2a =，1b =；【来源】2014年全国普通高等学校招生统一考试理科数学（陕西卷带解析） 【解析】试题分析：（1）由上半椭圆和部分抛物22:1(0)C y x y =-+≤公共点为,A B ，得1b =，设2C 的半焦距为c ，由2221a c b -==，解得2a =；（2）由（1）知，上半椭圆1C 的方程为，(1,0)B ，易知，直线l 与x 轴不重合也不垂直，故可设其方程为(1)(0)y k x k =-≠，并代入1C 的方程中，整理得：2222(4)240k x k x k +-+-=，，又(1,0)B ，得得点P 的坐标同理，由2(1)(0)1(0)y k x k y x y =-≠⎧⎨=-+≤⎩得点Q 的坐标为2(1,2)k k k ----，最后由0AP AQ ⋅=u u u r u u u r ,故直线l试题解析：（1）在1C 方程中，令0y =，得(,0),(,0)A b B b - 在2C 方程中，令0y =，得(1,0),(1,0)A B - 所以1b =设2C 的半焦距为c ，由及2221a c b -==，解得2a = 所以2a =，1b =（2）由（1）知，上半椭圆1C 的方程为，(1,0)B 易知，直线l 与x 轴不重合也不垂直，设其方程为(1)(0)y k x k =-≠ 代入1C 的方程中，整理得：2222(4)240k x k x k +-+-= （*）设点P 的坐标(,)P P x y又(1,0)B ，得所以点P 的坐标为同理，由2(1)(0)1(0)y k x k y x y =-≠⎧⎨=-+≤⎩得点Q 的坐标为2(1,2)k k k ---- ，(1,2)AQ k k =-+u u u rAP AQ ⊥Q0AP AQ ∴⋅=u u u r u u u r ,0k ≠Q ，4(2)0k k ∴-+=，解得故直线l 的方程为考点：椭圆和抛物线的几何性质；直线与圆锥曲线的综合问题.6．（I ）24y x =.（II ）（ⅰ）直线AE 过定点(1,0)F .（ⅱ）ABE ∆的面积的最小值为16. 【来源】2014年全国普通高等学校招生统一考试理科数学（山东卷带解析） 【解析】试题分析：（I 解得3t p =+或3t =-（舍去）.得2p =.抛物线C 的方程为24y x =. （II ）（ⅰ）由（I ）知(1,0)F ，设0000(,)(0),(,0)(0)D D A x y x y D x x ≠>，可得02D x x =+，即0(2,0)D x +，直线AB 根据直线1l和直线AB 平行，可设直线1l 的方程为直线AE 恒过点(1,0)F .注意当204y =时，直线AE 的方程为1x =，过点(1,0)F ，得到结论：直线AE 过定点(1,0)F .（ⅱ）由（ⅰ）知，直线AE 过焦点(1,0)F ， 设直线AE 的方程为+1x my =，根据点00(,)A x y 在直线AE 上， ，再设11(,)B x y ，直线AB应用点B 到直线AE从而得到三角形面积表达式，应用基本不等式得到其最小值. 试题解析：（I设(,0)(0)D t t >，则FD因为||||FA FD =， 解得3t p =+或3t =-（舍去）. ，解得2p =. 所以抛物线C 的方程为24y x =. （II ）（ⅰ）由（I ）知(1,0)F ，设0000(,)(0),(,0)(0)D D A x y x y D x x ≠>， 因为||||FA FD =，则0|1|1D x x -=+， 由0D x >得02D x x =+，故0(2,0)D x +， 故直线AB 因为直线1l 和直线AB 平行，设直线1l 的方程为设(,)E E E x y ，则当204y ≠时， 可得直线AE由2004y x =，直线AE 恒过点(1,0)F .当204y =时，直线AE 的方程为1x =，过点(1,0)F ，所以直线AE 过定点(1,0)F .（ⅱ）由（ⅰ）知，直线AE 过焦点(1,0)F ，设直线AE 的方程为+1x my =， 因为点00(,)A x y 在直线AE 上，设11(,)B x y ，直线AB由于00y≠，所以点B到直线AE的距离为则ABE∆的面积即01x=时等号成立.所以ABE∆的面积的最小值为16.考点：抛物线的定义及其几何性质，直线与抛物线的位置关系，点到直线的距离公式，基本不等式的应用.7．（12【来源】2014年全国普通高等学校招生统一考试理科数学（江西卷带解析）【解析】试题分析：（1）求双曲线ξ的方程就是要确定a的值，用a,c表示条件：1b轴，2112,a a b b ξη=-=-∥3n =，即可得：直线OBOAAB ⊥OB ，解得23a =，故双曲线C2）本题证.分别用坐标表示直线l 与AF及直线l 与直线的交点为)，并利用化简.： 试题解析：（1）设(,0)F c ，因为1b =，所以直线OB又直线OA又因为AB ⊥OB ，解得23a =，故双曲线C （2）由（1，则直线l 的方程为因为直线AF 的方程为2x =，所以直线l 与AF直线l 与直线因为是C考点：双曲线方程，直线的交点8．（1（2）220013x y +=.【来源】2014年全国普通高等学校招生统一考试理科数学（广东卷带解析）【解析】 试题分析：（1）利用题中条件求出c 的值，然后根据离心率求出a 的值，最后根据a 、b 、c 三者的关系求出b 的值，从而确定椭圆C 的标准方程；（2）分两种情况进行计算：第一种是在从点P 所引的两条切线的斜率都存在的前提下，设两条切线的斜率分别为1k 、2k ，并由两条切线的垂直关系得到121k k =-，并设从点()00,P x y 所引的直线方程为()00y k x x y =-+，将此直线的方程与椭圆的方程联立得到关于x 的一元二次方程，利用0∆=得到有关k 的一元二次方程，最后利用121k k =-以及韦达定理得到点P 的轨迹方程；第二种情况是两条切线与坐标轴垂直的情况下求出点P 的坐标，并验证点P 是否在第一种情况下所得到的轨迹上，从而得到点P 的轨迹方程. 试题解析：（1解得2b =，因此椭圆C 的标准方程为（2）①设从点P 所引的直线的方程为()00y y k x x -=-，即()00y kx y kx =+-， 当从点P 所引的椭圆C 的两条切线的斜率都存在时，分别设为1k 、2k ，则121k k =-， 将直线()00y kx y kx =+-的方程代入椭圆C 的方程并化简得()()()222000094189360kx k y kx x y kx ++-+--=，()()()2220000184949360k y kx k y kx ⎡⎤∆=--⨯+--=⎡⎤⎣⎦⎣⎦， 化简得()2200940y kx k ---=，即()()22200009240x k kx y y --+-=，则1k 、2k 是关于k 的一元二次方程()()22200009240x k k x y y --+-=的两根，则化简得220013x y +=；②当从点P 所引的两条切线均与坐标轴垂直，则P 的坐标为()3,2±±，此时点P 也在圆2213x y +=上.综上所述，点P 的轨迹方程为2213x y +=.【考点定位】本题以椭圆为载体，考查直线与圆锥曲线的位置关系以及动点的轨迹方程，将直线与二次曲线的公共点的个数利用∆的符号来进行转化，计算量较大，从中也涉及了方程思想的灵活应用，属于难题. 9．存在【来源】2014年全国普通高等学校招生统一考试理科数学（福建卷带解析） 【解析】试题分析：(1) 已知双曲线的两条渐近线分别为x y l x y l 2:,2:21-==,(2)首先分类讨论直线l 的位置..再讨论直线l 不垂直于x 轴,由OAB ∆的面积恒为8,由直线与双曲线方程联立以及韦达定理,即可得到直线l 有且只有一个公共点.试题解析：(1)因为双曲线E 的渐近线分别为和2,2y x y x ==-.所以从而双曲线E (2)由(1)知,双曲线E设直线l 与x 轴相交于点C.当l x ⊥轴时,若直线l 与双曲线E 有且只有一个公共点,又因为OAB ∆的面积为8,此时双曲线E 的方程为 若存在满足条件的双曲线E,则E 以下证明:当直线l 不与x 轴垂直时，双曲线E.设直线l 的方程为y kx m =+,依题意,得k>2或k<-2.记1122(,),(,)Ax y Bx y .由2y x y kx m=⎧⎨=+⎩,得,同理得.由得,由得, 222(4)2160k x kmx m ----=.因为240k -<,所以22222244(4)(16)16(416)k m k m k m ∆=+-+=---,又因为224(4)m k =-.所以∆=,即l 与双曲线E 有且只有一个公共点.因此,存在总与l 有且只有一个公共点的双曲线E,且E考点：1.双曲线的性质.2.直线与双曲线的位置关系.3. 三角形的面积的表示.10．（1（2【来源】2014年全国普通高等学校招生统一考试理科数学（重庆卷带解析）【解析】试题分析：（1）由题设知()()12,0,,0F c F c -其中222c ab =- 结合条件12DF F ∆的面积为，可求c 的值，再利用椭圆的定义和勾股定理即可求得,a b 的值，从而确定椭圆的标准方程；（2）设圆心在y 轴上的圆与椭圆在x 轴的上方有两个交点为()()111222,,,P x y P x y 由圆的对称性可知1212,x x y y =-=，利用()()111222,,,P x y P x y 在圆上及11220PF P F ⋅=u u u u r u u u u r确定交点的坐标，进而得到圆的方程.解：（1）设()()12,0,,0F c F c -，其中222c a b =-，故1c =.，由112DF F F ⊥得（2）如答（21）图，设圆心在y 轴上的圆C 与椭圆相交，()()111222,,,P x y P x y 是两个交点，120,0y y >>，11F P ,22F P 是圆C 的切线，且11F P ⊥22F P 由圆和椭圆的对称性，易知2112,x x y y =-=由（1）知()()121,0,1,0F F -，所以()()111122111,,1,F P x y F P x y =+=--u u u u r u u u u r ，再由11F P ⊥22F P得()221110x y -++=，即211340x x +=，10x =.当10x =时，12,P P 重合，此时题设要求的圆不存在. 时，过12,P P 分别与11F P ,22F P 垂直的直线的交点即为圆心C . 由11F P ,22F P 是圆C 的切线，且11F P ⊥22F P ，知21CP CP ⊥，又12||||CP CP =故圆C 的半考点：1、圆的标准方程；2、椭圆的标准方程；3、直线与圆的位置关系；4、平面向量的数量积的应用.11．（1）点P 的坐标为（2）详见解析． 【来源】2014年全国普通高等学校招生统一考试理科数学（浙江卷带解析） 【解析】试题分析：（1）已知直线l 的斜率为k ，用k b a ,,表示点P 的坐标，由已知椭圆动直线l 与椭圆C 只有一个公共点P ，可设出直线l 的方程为()0y kx m k =+<，结合椭圆方程，得，消去y 得，()22222222220ba kxa kmx a m ab +++-=，令0∆=，得22220b m a k -+=，即2222b a k m +=，代入原式得点P 的坐标为，再由点P 在第一象，可得点P 的坐标为（2）点P 到直线1l 的距离的最大值为b a -，由直线1l 过原点O 且与l 垂直，得直线1l 的方程为0x ky +=，利用点到直线距离公式可得，即，由式子特点，需消去k 即可，注意到即可证明．（1）设直线l 的方程为()0y k x m k =+<，由，消去y 得，()22222222220ba kxa kmx a m ab +++-=，由于直线l 与椭圆C 只有一个公共点P ，故0∆=，即22220b m a k -+=，解得点P 的坐标为，由点P 在第一象限，故点P 的坐标为 （2）由于直线1l 过原点O ，且与l 垂直，故直线1l 的方程为0x ky +=，所以点P 到直线1l 的距离，整理得，因为时等号成立，所以点P 到直线1l 的距离的最大值为b a -.点评：本题主要考查椭圆的几何性质，点单直线距离，直线与椭圆的位置关系等基础知识，同时考查解析几何得基本思想方法，基本不等式应用等综合解题能力。

一．基础题组1。

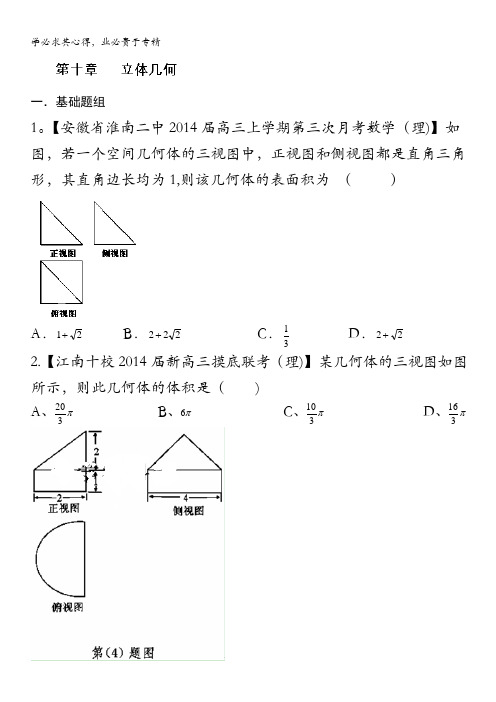
【安徽省淮南二中2014届高三上学期第三次月考数学（理)】如图，若一个空间几何体的三视图中，正视图和侧视图都是直角三角形，其直角边长均为1,则该几何体的表面积为（）A．21+B．222+C．13D．22+2.【江南十校2014届新高三摸底联考（理)】某几何体的三视图如图所示，则此几何体的体积是（)A、203πB、6πC、103πD、163π3.【2013合肥二模（理）】某几何体的三视图如图（其中侧视图中的圆弧是半圆）,则该几何体的表面积为（ ）4。

【2013合肥二模（理）】设m ，n 是不同的直线，α,β，γ是不同的平面,有以下四个命题：①②③④其中，真命题是（ ）A ．①④ B ． ②③ C ． ①③ D ． ②④ 5。

【安徽淮北一中2014届高三第三次月考数学理试题】已知,m n 为两条不同直线,,αβ为两个不同平面,给出下列命题:①//m n m n αα⊥⎧⇒⎨⊥⎩ ②//m m n n ββ⊥⎧⇒⎨⊥⎩ ③//m m ααββ⊥⎧⇒⎨⊥⎩ ④////m n m n αβαβ⊂⎧⎪⊂⇒⎨⎪⎩其中的正确命题序号是( ）A ．③④B ．②③C ．①②D ．①②③④ 6。

【安徽省寿县第一中学2014届高三上学期第二次月考数学(理)试卷（实验A 班月考)】已知n m ,为异面直线,⊥m 平面α，⊥n 平面β。

直线l 满足,,,l m l n l l αβ⊥⊥⊄⊄,则（ ) A ．βα//,且α//lB ．βα⊥，且β⊥lC ．α与β相交，且交线垂直于lD ．α与β相交，且交线平行于l 7。

【安徽省示范高中2014届高三上学期第一次联考数学理试题】已知一几何体的三视图如图所示，则该几何体的体积为____8.【安徽涡阳四中2014届高三第三次质量检测(理）】如图,正方体ABCD —A 1B 1C 1D 1的棱长为1，E,F 分别为线段AA 1，B 1C 上的点，则三棱锥D 1—EDF 的体积为____________。

第十章立体几何一．基础题组1.【2014某某涡阳蒙城】如图⑴、⑵、⑶、⑷为四个几何体的三视图，根据三视图可以判断这四个几何体依次分别为（）A．三棱台、三棱柱、圆锥、圆台B．三棱台、三棱锥、圆锥、圆台C．三棱柱、正四棱锥、圆锥、圆台D．三棱柱、三棱台、圆锥、圆台2.【2014某某南安一中】下列图形中不一定是平面图形的是（）A. 三角形B. 四边相等的四边形C. 梯形D.平行四边形【答案】B3.【2014某某南安一中】如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（ ）A ．π9B ．π10C ．π11D ．π124.【2014某某南安一中】ABC ∆的斜二侧直观图如图所示，则ABC ∆的面积为（ ）A ．1B ．2C ．22D ．2【答案】B【解析】试题分析：根据斜二测画法的原则可知ABC ∆的底为2，高为2，所以面积为2.考点：本题考查空间几何体的直观图及画法（斜二测画法），原则“横不变、纵减半，平行性不改变”.5．【2014某某四地六校高三第三次月考数学文】如图，一个简单空间几何体的三视图其主视图与侧视图都是边长为2的正三角形，俯视图轮廓为正方形，则此几何体的表面积是A ．443+B ．12C ．43D ．8【答案】B【解析】 6.【2014某某南安一中】设m n 、是两条不同的直线，,,αβγ是三个不同的平面，给出下列四个命题：①若m α⊥，//n α，则m n ⊥ ②若//αβ，//βγ，m α⊥，则m γ⊥ ③若//m α，//m β，n αβ⋂=，则//m n ④若αγ⊥，βγ⊥，m αβ⋂=，则m γ⊥ 正确命题的个数是( )A ．1B ．2C ．3D ．4俯视图 主视图 侧视图考点：本题考查直线与平面平行与垂直的判定、平面与平面的平行与垂直的判断，考查空间想象能力，逻辑思维能力．7．【2014某某四地六校高三第三次月考数学文】已知n m ,是两条不同的直线，γβα,,是三个不同的平面，下列命题正确的是( )（A ）若αα//,//n m ，则n m //．（B ）若γαβα⊥⊥,，则γβ//．（C ）若βα//,//m m ，则βα//．（D ）若βα⊥⊥m m ,，则βα//．8.【2014皖西七校联合考试数学文】已知,m n 是两条不重合的直线，,αβ是两个不重合的平面，给出下列命题：①若m α⊥，n β⊥，且m n ⊥，则αβ⊥；②若m α⊥，//n β，且m n ⊥，则αβ⊥；③若//m α，//n β，且//m n ，则//αβ；④若m α⊥，//n β，且//m n ，则//αβ.其中正确命题的个数是（ ）A .0B .1C .2D .3【答案】B【解析】①利用当两个平面的法向量互相垂直时，这两个平面垂直，可以知道①正确； ②由题意画出反例图为：9.【2014皖西七校联合考试数学文】一个几何体的三视图如图,则该几何体的表面积为.10.【2014某某南安一中】已知一个球的表面积为264cm π，则这个球的体积为3cm 。

一．基础题组1.【安徽省淮南二中2014届高三上学期第三次月考数学(理）】在极坐标系中，曲线1)sin cos 2(:1=+θθρC与曲线)0(,:2>=a a C ρ的一个交点在极轴上，则a 的值为 。

2。

【福建莆田一中2014段考(理）】（1）（本小题满分7分)选修4-2：矩阵与变换曲线221:1C x y +=在矩阵0(0,0)0a M a b b ⎛⎫=>> ⎪⎝⎭的变换作用下得到曲线222:14x C y +=．（Ⅰ）求矩阵M ;（Ⅱ)求矩阵M 的特征值及对应的一个特征向量．3。

【福建莆田四中2014高三上期中考试(理）】（1)“选修4—2矩阵与变换"已知()(1)ab y f x Acd ⎛⎫==⎪⎝⎭的图象如图经作用后变换为曲线C （如图2）.（I ）求矩阵A ；（II ）求矩阵A 的特征值.4。

【福建莆田四中2014高三上期中考试(理）】(2）“选修4—4坐标系与参数方程”已知极点与原点重合，极轴与x 轴的正半轴重合．若曲线1C 的极坐标方程为:2253cos280ρ-ρθ-=，直线的参数方程为：x 13ty t ⎧=-⎪⎨=⎪⎩（t 为参数）。

（I)求曲线1C 的直角坐标方程;（II ）直线上有一定点(1,0)P ,曲线1C与交于M,N 两点,求PN PM •的值。

【解析】（1）由2253cos280ρ-ρθ-=得222253(cos sin )80ρ-ρθ-θ-= 即2222253cos 3sin 80ρ-ρθ+ρθ-=，从而22225(x y )3x 3y 80+-+-=，整理得2214x y += ……………………………3分（2）把直线的参数方程代入到曲线1C 的直角坐标方程，得272330t t --=，1237t t ⋅=-.由t 的几何意义知()()1212227PM PN t t ⋅=⋅=…………………………………………………7分二．能力题组5。

一．基础题组1。

【福建长乐二中等五校2014届高三上期中联考（理）】已知全集R U =，集合},12|{},0|{2Z n n x x N x x x M ∈+===-=，则N M 为（)A ．{}0B ．}1{C ．{0，1｝D ．φ2。

【福建莆田一中2014段考（理）】已知集合}2|{≤=x x A ,}0)3(|{<-=x x x B ，则B A =（ ） A ．}20|{≤<x x B ．}0|{<x x C ．2|{≤x x ，或}3>x D ．0|{<x x ，或}2≥x3。

【安徽省毫州市涡阳四中2014届高三上学期第二次月考数学（理)】已知集合(){}214,M x x x N=-<∈∣,{}1,0,1,2,3P =-,则M ∩P =( ）A 。

{}0,1,2B 。

{}1,0,1,2-C 。

{}1,0,2,3-D 。

{}0,1,2,3 【答案】A4。

【江南十校2014届新高三摸底联考（理)】已知集合A＝｛y｜y＝2,x x R∈}，B＝｛x|y＝22log2xx-+}，则A∩B＝（）A、［0，2)B、［1，2）C、（－∞,2）D、(0，2)5.【安徽省淮南二中2014届高三上学期第三次月考数学(理）】已知函数()()lg1f x x=-的定义域为M，函数1yx=的定义域为N，则M N=（）A。

{}10x x x<≠且 B . {}10x x x≤≠且C。

{}1x x>D。

{}1x x≤6。

【安徽省毫州市涡阳四中2014届高三上学期第二次月考数学（理）】实数x，条件p：2x x<，条件q：11≥x，则p是q的( ）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件7.【安徽省毫州市涡阳四中2014届高三上学期第二次月考数学（理）】下列命题：（1）若“22b a<，则b a <”的逆命题;（2）“全等三角形面积相等"的否命题；（3）“若0a ≥，则0322>++-a ax ax 的解集为R ”的逆否命题;（4）“若)0(3≠x x 为有理数，则x 为无理数”．其中正确的命题是（ ）A ．（3）（4）B ．（1）（3）C ．（1）(2）D ．（2)（4)8.【安徽省望江四中2014届高三上学期第一次月考数学理】若集合{|0}1xA x x =≤-,2{|2}B x x x =<,则A B =（ ）A.{|01}x x <<B.{|01}x x ≤<C.{|01}x x <≤D.{|01}x x ≤≤ 答案:A解析：集合A ＝｛|x 01x ≤<｝,A ＝｛|x 02x <<｝，所以，AB ={|01}x x <<9。

一．基础题组1. 【2014福建三明】若()1cos 3πα+=-，则cos α的值为（ ）A ．13 B ．13- C ．3 D ．3-2. 【2014福建三明】函数sin 2y x =是（ ）A ．周期为π的奇函数B ．周期为π的偶函数C ．周期为2π的奇函数D ．周期为2π的偶函数3.【2014年“皖西七校”高三年级联合考试理】若||2,||1==a b ，且a 与b 的夹角为60 ，当||x -a b 取得最小值时，实数x 的值为（ ）A .2B .2-C .1D .1- 【答案】C【解析】22222||224x x x x x -+=-=+-a b a a b b ，因此当 1x =时，2||x -a b 最小，所以当1x =时，||x -a b 最小 ，故选C .考点：1.向量的模、数量积；2.二次函数的最值.4.【“华安、连城、永安、漳平一中，龙海二中，泉港一中”六校联考2013-2014学年上学期第三次月考】三角形ABC 中,a=15,b=10,A=︒60,则=B cos （ ）A ．322±B ．－36 C ．36±D ．365.【“华安、连城、永安、漳平一中，龙海二中，泉港一中”六校联考2013-2014学年上学期第三次月考】将函数1sin 2cos 222y x x =+的图象向_________单位可得到函数cos(2)3y x π=+的图象。

A ．向左平移4π B ．向右平移2π C ．向右平移3πD ．向左平移8π6.【“华安、连城、永安、漳平一中，龙海二中，泉港一中”六校联考2013-2014学年上学期第三次月考】已知函数,sin )(x x x f -= R x ∈，则)4(π-f 、)1(f 、)3(πf 的大小关系（ ） A ．)3(πf >)4(π-f >)1(f B ． )4(π-f >)1(f >)3(πfC ．)1(f >)3(πf >)4(π-f D ．)3(πf >)1(f >)4(π-f7. 【2014福建三明】已知函数()2()cos 1f x x m =-+在cos 1x =-时取得最大值，在cos x m =时取得最小值，则实数m 的取值范围是（ ）A ．1m ≤-B ．1m ≥C ．0m 1≤≤D ．10m -≤≤8．【2014福建安溪八中12月月考数学理】为了得到函数)62sin(π-=x y 的图象，可以将函数x y 2cos =的图象( ) A.向右平移6π个单位长度 B. 向右平移3π个单位长度 C.向左平移6π个单位长度 D. 向左平移3π个单位长度【答案】B 【解析】试题分析：因为2sin(2)cos((2))cos(2)6263x x x ππππ-=--=-.又因为余弦函数是偶函数.所以22cos(2)cos(2)cos 2()333x x x πππ-=-=-.所以为了得到函数)62sin(π-=x y 的图象可以由函数x y 2cos =的图象右平移3π的单位.即选B.考点：1.正弦函数与余弦函数的相互转化.2.三角函数的平移问题. 9. 【2014福建安溪八中12月月考数学理】 设向量(cos55,sin55),(cos25,sin 25)a b =︒︒=︒︒ ，若t是实数，则||a tb -的最小值为( ) A.22B.21C. 1D. 210. 【2014福建安溪八中12月月考数学理】 已知cos sin 6παα⎛⎫-+= ⎪⎝⎭7sin 6πα⎛⎫+⎪⎝⎭的值是( )A ． C ．45- D ． 45考点：1.角的和差公式.2.三角函数的化一公式.3.三角函数的诱导公式.11.【2014宿州一模】设向量(sin 2a α= 的模为2，则cos 2α=（ ）A.2B. 12C. 12-D. 14-填空题12. 【2014福建三明】已知A 为ABC ∆的内角，且1sin 2A =，则A = .13.【2014年“皖西七校”高三年级联合考试理】已知21sin()34πα-=，则sin()3πα+= .【答案】14-【解析】221sin()sin[()]sin()3334πππααπα+=-+=--=-.考点：正弦函数的诱导公式.14．【2014福建安溪八中12月月考数学理】已知函数()2sin()f x x ωϕ=+的图像如右图所示，则(0)f = ．解答题15. 【2014福建三明】（本小题满分6分）已知tan 2α=，求下列各式的值： ①tan 4πα⎛⎫+⎪⎝⎭②sin cos sin cos αααα+-.21312+==--…………9分 ②原式tan 1tan 1αα+=-…………11分21321+==-…………12分. 考点：1.对数的运算；2.两角和的正切公式；3.同角三角函数的基本关系式.16.【2014年“皖西七校”高三年级联合考试理】（本小题满分12分）已知函数1()sin cos (0,0)2f x x x λωωλω=>>的部分图象如图所示，其中点为最高点，点为图象与轴的交点，在ABC ∆中，角,,A B C 对边为,,a b c ，b c ==，且满足(2)cos cos 0c B A =.（Ⅰ）求ABC ∆的面积；（Ⅱ）求函数()f x 的单调递增区间.试题解析：（Ⅰ）由(2)cos cos 0c B A =，得6B π=……3分在ABC ∆中，BC 边上的高sin h c B ==，故12ABC S BC h ∆=⨯⨯=……6分17. 【2014福建四地六校第三次月考数学理】（本题满分13分）设三角形ABC 的内角,,A B C 所对的边长分别为,,a b c ,)3,23(),cos ,(cos a b c C A -== ,且⊥. (Ⅰ)求角A 的大小;（Ⅱ）若ＡＣ＝ＢＣ，且BC 边上的中线AM 求ABC ∆的面积.（2）由（1）知Ａ＝6π，又ＡＣ＝ＢＣ，所以C=32π………………7分设ＡＣ＝x,则ＭＣ＝x 21AMC ∆中，由余弦定理得 222cos 2AM C MC AC MC AC =⋅-+……………………………9分即222)7(32cos 22)2(=⋅-+πx x x x解得x=2……………………………………………………………………11分 故332sin 2212=⋅⋅=∆πABC S …………………………………………13分 考点：1.向量的垂直坐标形式的表示.2.余弦定理.3.三角恒等变换. 18. 【2014福建安溪八中12月月考数学理】(本题满分13分) 已知11tan tan -=-αα，求下列各式的值： （I ）ααααcos sin cos 3sin +-；（II ）2)cos()sin()2(cos 2++--+απαπαπ.19.【2014宿州一模】（本小题满分12分）在ABC ∆中，,,a b c 分别为角,,A B C 的对边，ABC ∆的面积S 满足cos 2S A = (Ⅰ)求角A 的值;(Ⅱ)若a =设角B 的大小为x,用x 表示c,并求c 的取值范围.二．能力题组20. 【2014福建三明】（本小题满分12分）已知向量()sin ,2a α=- 与()1,cos b α=，其中0,2πα⎛⎫∈ ⎪⎝⎭.（1）问向量,a b能平行吗？请说明理由；（2）若a b ⊥，求sin α和cos α的值；（3）在（2）的条件下，若cos 0,2πββ⎛⎫=∈ ⎪⎝⎭，求αβ+的值.三．拔高题组21.【2014宿州一模】函数tan()(04)42x y x ππ=-<<的图像如图所示，A 为图像与x 轴的交点,过点A 的直线l 与函数的图像交于C 、B 两点.则()OB OC OA +⋅=（ ）A.-8B.-4C.4D.8【答案】D 【解析】试题分析：因为函数tan()(04)42x y x ππ=-<<可化为cot 4xy π=-，所对称中心是(24,0)k π+.所以A 点的坐标是（2,0）.因为A 点是对称中心，所以点A 是线段BC 的中点，所以2OC OB OA += .所以()OB OC OA +⋅= 222()248OA OA OA ⋅==⨯= .故选D.考点：1.正切函数的诱导公式.2.函数的对称性.3.向量的加法.4.向量的数量积. 22. 【2014福建三明】函数()sin y x x R π=∈的部分图像如图所示，设O 为坐标原点，P是图像的最高点，B 是图像与x 轴的交点，则tan OPB ∠的值为 （ ）A ．10B ．8C ．87 D ．4723. 【2014福建三明】已知sin15cos15a =︒︒，22cos sin 66b ππ=-，2tan 301tan 30c ︒=-︒，则,,a b c 的大小关系是（ ）A ．a b c <<B ．a b c >>C ．c a b >>D ．a c b <<24. 【2014福建三明】（本小题满分12分）已知函数()()sin 0f x x x ωωω=>.的周期为π.（1）若[)0,x ∈+∞，求它的振幅、初相；（2）在给定的平面直角坐标系中作出该函数在[]0,x π∈的图像；（3）当[]0,x π∈时，根据实数m 的不同取值，讨论函数()()g x f x m =-的零点个数.试题解析：（1）化为()2sin 3f x x πω⎛⎫=+⎪⎝⎭…………1分 由T π=得，2ω=即()2sin 23f x x π⎛⎫=+ ⎪⎝⎭…………2分 （1）函数的振幅是2A =，初相为3πϕ=…………4分（2）列表。

2014年福建高考理科数学试题逐题详解（解析版）一、选择题：本大题共10小题，每小题5分，共50分．在每个题给出的四个选项中，只有一项是符合要求的．【2014年福建卷（理01）】复数z=（3﹣2i）i的共轭复数等于（）A．﹣2﹣3i B．﹣2+3i C． 2﹣3i D． 2+3i【答案】C【解析】∵z=（3﹣2i）i=2+3i，∴．故选：C【2014年福建卷（理02）】某空间几何体的正视图是三角形，则该几何体不可能是（）A．圆柱B．圆锥C．四面体D．三棱柱【答案】A【解析】圆柱的正视图为矩形，故选：A【2014年福建卷（理03）】等差数列{a n}的前n项和为S n，若a1=2，S3=12，则a6等于（）A．8 B．10 C．12 D．14【答案】C【解析】由题意可得S3=a1+a2+a3=3a2=12，解得a2=4，∴公差d=a2﹣a1=4﹣2=2，∴a6=a1+5d=2+5×2=12，故选：C．【2014年福建卷（理04）】若函数y=log a x（a＞0，且a≠1）的图象如图所示，则下列函数图象正确的是（）A．B．C．D．【答案】B【解析】由题意可知图象过（3，1），故有1=log a3，解得a=3，选项A，y=a﹣x=3﹣x=单调递减，故错误；选项B，y=x3，由幂函数的知识可知正确；选项C，y=（﹣x）3=﹣x3，其图象应与B关于x轴对称，故错误；选项D，y=log a（﹣x）=log3（﹣x），当x=﹣3时，y=1，但图象明显当x=﹣3时，y=﹣1，故错误．故选：B．【2014年福建卷（理05）】阅读如图所示的程序框图，运行相应的程序，输出的S的值等于（）A．18 B．20 C．21 D．40【答案】B【解析】由程序框图知：算法的功能是求S=21+22+…+2n+1+2+…+n的值，∵S=21+22+1+2=2+4+1+2=9＜15，S=21+22+23+1+2+3=2+4+8+1+2+3=20≥15．∴输出S=20．故选：B【2014年福建卷（理06）】直线l：y=kx+1与圆O：x2+y2=1相交于A，B 两点，则“k=1”是“△OAB的面积为”的（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分又不必要条件【答案】A【解析】若直线l：y=kx+1与圆O：x2+y2=1相交于A，B 两点，则圆心到直线距离d=，|AB|=2，若k=1，则|AB|=，d=，则△OAB的面积为×=成立，即充分性成立．若△OAB的面积为，则S==×2×==，解得k=±1，则k=1不成立，即必要性不成立．故“k=1”是“△OAB的面积为”的充分不必要条件．故选：A【2014年福建卷（理07）】已知函数f（x）=，则下列结论正确的是（）A.f（x）是偶函数B． f（x）是增函数C． f（x）是周期函数D． f（x）的值域为[﹣1，+∞）【答案】D【解析】由解析式可知当x≤0时，f（x）=cosx为周期函数，当x＞0时，f（x）=x2+1，为二次函数的一部分，故f（x）不是单调函数，不是周期函数，也不具备奇偶性，故可排除A、B、C，对于D，当x≤0时，函数的值域为[﹣1，1]，当x＞0时，函数的值域为值域为（1，+∞），故函数f（x）的值域为[﹣1，+∞），故正确．故选：D【2014年福建卷（理08）】在下列向量组中，可以把向量=（3，2）表示出来的是（）A．=（0，0），=（1，2）B．=（﹣1，2），=（5，﹣2）C．=（3，5），=（6，10）D．=（2，﹣3），=（﹣2，3）【答案】B【解析】根据，选项A：（3，2）=λ（0，0）+μ（1，2），则 3=μ，2=2μ，无解，故选项A不能；选项B：（3，2）=λ（﹣1，2）+μ（5，﹣2），则3=﹣λ+5μ，2=2λ﹣2μ，解得，λ=2，μ=1，故选项B能．选项C：（3，2）=λ（3，5）+μ（6，10），则3=3λ+6μ，2=5λ+10μ，无解，故选项C 不能．选项D：（3，2）=λ（2，﹣3）+μ（﹣2，3），则3=2λ﹣2μ，2=﹣3λ+3μ，无解，故选项D不能．故选：B【2014年福建卷（理09）】设P，Q分别为圆x2+（y﹣6）2=2和椭圆+y2=1上的点，则P，Q两点间的最大距离是（）A．5B．+C．7+D．6【答案】D【解析】设椭圆上的点为（x，y），则∵圆x2+（y﹣6）2=2的圆心为（0，6），半径为，∴椭圆上的点与圆心的距离为=≤5，∴P，Q两点间的最大距离是5+=6．故选：D【2014年福建卷（理10）】用a代表红球，b代表蓝球，c代表黑球，由加法原理及乘法原理，从1个红球和1个蓝球中取出若干个球的所有取法可由（1+a）（1+b）的展开式1+a+b+ab 表示出来，如：“1”表示一个球都不取、“a”表示取出一个红球，而“ab”则表示把红球和蓝球都取出来．以此类推，下列各式中，其展开式可用来表示从5个无区别的红球、5个无区别的蓝球、5个有区别的黑球中取出若干个球，且所有的蓝球都取出或都不取出的所有取法的是（）A．（1+a+a2+a3+a4+a5）（1+b5）（1+c）5 B．（1+a5）（1+b+b2+b3+b4+b5）（1+c)5 C．（1+a）5（1+b+b2+b3+b4+b5）（1+c5） D．（1+a5）（1+b）5（1+c+c2+c3+c4+c5）【答案】A【解析】所有的蓝球都取出或都不取出的所有取法中，与取红球的个数和黑球的个数无关，而红球篮球是无区别，黑球是有区别的，根据分布计数原理，第一步取红球，红球的取法有（1+a+a2+a3+a4+a5），第二步取蓝球，有（1+b5），第三步取黑球，有（1+c）5，所以所有的蓝球都取出或都不取出的所有取法有（1+a+a2+a3+a4+a5）（1+b5）（1+c）5，二、填空题：本大题共5小题，每小题4分，共20分．把答案填在答题卡的相应位置【2014年福建卷（理11）】若变量 x，y满足约束条件，则z=3x+y的最小值为_________ ．【答案】1【解析】作出不等式对应的平面区域如图，由z=3x+y，得y=﹣3x+z，平移直线y=﹣3x+z，由图象可知当直线y=﹣3x+z，经过点A（0，1）时，直线y=﹣3x+z的截距最小，此时z最小．此时z的最小值为z=0×3+1=1，故答案为：1【2014年福建卷（理12）】在△ABC中，A=60°，AC=4，BC=2，则△ABC的面积等于．【答案】【解析】∵△ABC中，A=60°，AC=4，BC=2，由正弦定理得：，∴，解得sinB=1，∴B=90°，C=30°，∴△ABC的面积=．故答案为：【2014年福建卷（理13）】要制作一个容器为4m3，高为1m的无盖长方形容器，已知该容器的底面造价是每平方米20元，侧面造价是每平方米10元，则该容器的最低总造价是（单位：元）【答案】160【解析】设池底长和宽分别为a，b，成本为y，则∵长方形容器的容器为4m3，高为1m，故底面面积S=ab=4，y=20S+10[2（a+b）]=20（a+b）+80，∵a+b≥2=4，故当a=b=2时，y取最小值160，即该容器的最低总造价是160元，故答案为：160【2014年福建卷（理14）】如图，在边长为e（e为自然对数的底数）的正方形中随机撒一粒黄豆，则它落到阴影部分的概率为_________ ．。

2014年普通高等学校招生全国统一考试（安徽卷） 数学（理科）试卷第I 卷（选择题 共50分）一．选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的.（1）设i 是虚数单位，z 表示复数z 的共轭复数. 若,1i z +=则zi z i+⋅=（ ） 2- B. i 2- C. 2 D. i 220<x ”是“0)1ln(<+x ”的（ ）充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 【答案】B 【解析】试题分析：因为0)1ln(<+x ，所以ln(1)ln1x +<，即10x -<<，因而“0<x ”是“0)1ln(<+x ”的必要而不充分条件考点：1.对数的运算；2.充要条件.如图所示，程序框图（算法流程图）的输出结果是（ ） A. 34 B. 55 C. 78 D. 89【答案】B以平面直角坐标系的原点为极点，x 轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位，已知直线l 的参数方程是13x t y t =+⎧⎨=-⎩（t 为参数），圆C 的极坐标方程是θρcos 4=，则直线l 被圆C 截得的弦长为（ ）14B.142C.2D.22y x ,满足约束条件⎪⎩⎪⎨⎧≥+-≤--≤-+02202202y x y x y x ，若ax y z -=取得最大值的最优解不唯一．．．，则实数a 的值为（ ） A,121-或 B.212或 C.2或1 D.12-或 【答案】D 【解析】试题分析：题中的约束条件表示的区域如下图，将ax y z -=化成斜截式为y ax z =+，要使其取得最大值的最优解不唯一，则y ax z =+在平移的过程中与20x y +-=重合或与220x y -+=重合，所以2a =或1-.考点：1.线性规划求参数的值.设函数))((R x x f ∈满足.sin )()(x x f x f +=+π当π<≤x 0时，0)(=x f ，则=)623(πf （ ） 21 B. 23 C.0 D.21-一个多面体的三视图如图所示，则该多面体的表面积为（ ）A.21+3B.18+3C.21D.18考点：多面体的三视图与表面积.8.从正方体六个面的对角线中任取两条作为一对，其中所成的角为60 的共有（）A.24对B.30对C.48对D.60对考点：1.直线的位置关系；2.异面直线所成的角.9.若函数()12f x x x a =+++的最小值为3，则实数a 的值为（ ） A.5或8 B.1-或5 C.1-或4- D.4-或810.在平面直角坐标系xOy 中，已知向量,,1,0,a b a b a b ==⋅=点Q 满足2()OQ a b =+.曲线{cos sin ,02}C P OP a b θθθπ==+≤≤，区域{0,}P r PQ R r R Ω=<≤≤<.若C Ω为两段分离的曲线，则( )A.13r R <<<B.13r R <<≤C.13r R ≤<<D.13r R <<< 【答案】A第I I 卷（非选择题 共100分）二. 选择题:本大题共5小题，每小题5分，共25分. 11.若将函数()sin 24f x x π⎛⎫=+ ⎪⎝⎭的图像向右平移ϕ个单位，所得图像关于y 轴对称， 则ϕ的最小正值是________.10d +=，∴1q =.考点：1.等差，等比数列的性质.设n a ,0≠是大于1的自然数，na x ⎪⎭⎫⎝⎛+1的展开式为n n x a x a x a a ++++ 2210.若点)2,1,0)(,(=i a i A i i 的位置如图所示，则______=a .【答案】3 【解析】试题分析：由图易知0121,3,4a a a ===，则12212113,()4n n a C a C a a ====，即23(1)42na n n a ⎧=⎪⎪⎨-⎪=⎪⎩，解得3a =.考点：1.二项展开式的应用.设21,F F 分别是椭圆)10(1:222<<=+b by x E 的左、右焦点，过点1F 的直线交椭圆E 于B A ,两点，若x AF BF AF ⊥=211,3轴，则椭圆E 的方程为__________已知两个不相等的非零向量,,b a 两组向量54321,,,,x x x x x 和54321,,,,y y y y y 均由2个a 和3个b 排列而成.记5544332211y x y x y x y x y x S ⋅+⋅+⋅+⋅+⋅=，min S 表示S 所有可能取值中的最小值.则下列命题的是_________（写出所有正确命题的编号）. ①S 有5个不同的值. ②若,b a ⊥则min S a .③若,b a ∥则min S 与b 无关. ④若a b 4>，则0min >S . ⑤若2min ||2||,8||b a Sa ==，则a 与b 的夹角为4π三．解答题：本大题共6小题，共75分.解答应写出文子说明、证明过程或演算步骤.解答写在答题卡上的指定区域内. （16）（本小题满分12分）设ABC 的内角,,A B C 所对边的长分别是,,a b c ，且3,1,2.b c A B === （1）求a 的值； （2）求sin()4A π+的值.故sin()sin coscos sin444A A A πππ+=+2221242()32326-=⨯+-⨯=.（17）（本小题满分12分）甲乙两人进行围棋比赛，约定先连胜两局者直接赢得比赛，若赛完5局仍未出现连胜，则判定获胜局数多者赢得比赛，假设每局甲获胜的概率为23，乙获胜的概率为13，各局比赛结果相互独立. 求甲在4局以内（含4局）赢得比赛的概率；记X 为比赛决出胜负时的总局数，求X 的分布列和均值（数学期望）.k 局乙获胜”.则2()3k P A =，1(),1,2,3,4,53k P B k ==. 121231234()()()()P A P A A P B A A P A B A A =++121231234()()()()()()()()()P A P A P B P A P A P A P B P A P A =++2222122125633333381⎛⎫⎛⎫⎛⎫=+⨯+⨯⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.X 的可能取值为2,3,4,5.121212125(2)()()()()()()9P X P A A P B B P A P A P B P B ==+=+=. 1231231231232(3)()()()()()()()()9P X P B A A P A B B P B P A P A P A P B P B ==+=+=123412341234123410(4)()()()()()()()()()()81P X P A B A A P B A B B P A P B P A P A P B P A P B P B ==+=+=8(5)1(2)(3)(4)81P X P X P X P X ==-=-=-==. X 2 345P59 29 1081 8814a ≥时，21x ≥，由（1）知，()f x 在[0,1]上单调递增，所以()f x 在0x =和1x =处分别取得最小值和最大值.②当04a <<时，21x <.由（1）知，()f x 在2[0,]x 上单调递增，在2[,1]x 上单调递减，因此()f x 在21433ax x -++==处取得最大值.又(0)1,(1)f f a ==，所以当01a <<时，()f x 在1x =处取得最小值；当1a =时，()f x 在0x =和1x =处同时取学科网得最小只；当14a <<时，()f x 在0x =处取得最小值.考点：1.含参函数的单调性；2.含参函数的最值求解. (本小题满分13分)如图，已知两条抛物线()02:1121>=p x p y E 和()02:2222>=p x p y E ，过原点O 的两条直线1l 和2l ，1l 与21,E E 分别交于21,A A 两点，2l 与21,E E 分别交于21,B B 两点.证明：;//2211B A B A过原点O 作直线l （异于1l ，2l ）与21,E E 分别交于21,C C 两点.记111C B A ∆与222C B A ∆的面积分别为1S 与2S ,求21S S 的值.（20）(本题满分13分)如图，四棱柱1111D C B A ABCD -中，A A 1⊥底面ABCD .四边形ABCD 为梯形，BC AD //,且BC AD 2=.过D C A ,,1三点的平面记为α，1BB 与α的交点为Q . 证明：Q 为1BB 的中点；求此四棱柱被平面α所分成上下两部分的体积之比；若A A 14=，2=CD ，梯形ABCD 的面积为6，求平面α与底面ABCD 所成二面角大小.【答案】（1）Q 为1BB 的中点；（2）117；（3）4π.解法2如第（20）题图2，以D 为原点，1,DA DD 分别为x 轴和z 轴正方向建立空学科网间直角坐标系.（本小题满分13分）设实数0>c ，整数1>p ，*N n ∈.（1）证明：当1->x 且0≠x 时，px x p+>+1)1(；（2）数列{}n a 满足pc a 11>，pn n n a pc a p p a -++-=111，证明：p n n c a a 11>>+.综合①②可得，当1->x 且0≠x 时，对一切整数1p >，不等式px x p +>+1)1(均成立.证法1：先用数学归纳法证明1pn a c >.①当1n =时，由题设11pa c >知1pn a c >成立.②假设(1,*)n k k k N =≥∈时，不等式1pk a c >成立.由111p n n n p c a a a p p-+-=+易知0,*n a n N >∈.当1n k =+时，1111(1)p k k p k ka p c ca a p p p a -+-=+=+-.。

一．基础题组1．【安徽涡阳四中2014届高三第三次质量检测(理)】已知向量(2,1)a =-,10a b ⋅=,5a b -=,则b =（ ）A ．20B ．C ．D ． 40 【答案】B2．【福建漳州芗城中学2014届高三11月月考（理）】若AB =(1,1),AC =(3,8),AD =(0,1),BC CD +=(a,b),则a+b=( )(A)-1 (B)0 (C)1 (D)2 【答案】A3．【福建莆田四中2014高三上期中考试(理)】已知直线a y x =+与圆222=+y x 交于A 、B两点，O 是原点，C 是圆上一点，若OC OB OA =+，则a 的值为（ ） A ．1± B ．2± C ．3± D ．2±【答案】A ．4．【安徽省芜湖市沈巷中学2014届高三一轮复习测试（一）数学理试题】点O 在ABC ∆所在平面内,给出下列关系式:(1)0=++OC OB OA ; (2)OA OC OC OB OB OA ⋅=⋅=⋅;(3)0=⎫⎛-⋅=⎫⎛-⋅BA BC AB AC ;(4)0)()(=⋅+=⋅+BC OC OB AB OB OA ． 则点O 依次为ABC ∆的 （）A ．内心、外心、重心、垂心B ．重心、外心、内心、垂心C ．重心、垂心、内心、外心D ．外心、内心、垂心、重心【答案】C5．【安徽省芜湖市沈巷中学2014届高三一轮复习测试（一）数学理试题】已知向量,,a b c 满足++=0a b c ,且a 与c 的夹角为60,|||=b a ,则tan ,<>=a b （ ）A BC ．D ．【答案】C6．【安徽省屯溪一中2014届高三上学期期中考试数学（理）试题】已知ABC ∆所在的平面内一点P 满足02=++PC PB PA ,则=∆∆∆PBC PAC PAB S S S ::.)(A 3:2:1 .)(B 1:2:1 .)(C 1:1:2 .)(D 2:1:1【答案】B7．【安徽省淮北一中2014届高三第三次月考数学理试题】ABC ∆中,60,A A ∠=︒∠的平分线AD 交边BC 于D,已知AB=3,且1()3AD AC AB R λλ=+∈,则AD 的长为 （ ）A ．1BC ．D ．3【答案】C8．【安徽省皖南八校2014届高三10月第一次联考数学(理)试题】已知ABC ∆为等边三角形,2AB =,设,P Q 满足,(1)()AP AB AQ AC R λλλ==-∈,若32BQ CP ⋅=-,则λ等于 （）A ．12B C D9．【安徽省皖南八校2014届高三10月第一次联考数学(理)试题】已知向量a 、b 满足||1,()(2)0a a b a b =+⋅-=,则||b 的取值范围为（） A ．[1,2]B ．[2,4]C ．11[,]42D ．1[,1]210．【安徽省屯溪一中2014届高三上学期期中考试数学（理）试题】已知点O 、N 、P 在ABC ∆所在的平面内,==,=++,⋅=⋅=⋅,则点O 、N 、P 依次ABC ∆是的_____、_____、____．__ 【答案】外心、重心、垂心11．【安徽省屯溪一中2014届高三上学期期中考试数学（理）试题】已知向量)1,3(=a ,)1,0(-=b ,)3,(k c =,若2+与共线,则=k ___________【答案】3-=k12．【安徽省寿县第一中学2014届高三上学期第二次月考数学（理）试卷（实验A 班月考）】已知直线:1()l y ax a a R =+-∈．若存在实数a 使得一条曲线与直线l 有两个不同的交点,且以这两个交点为端点的线段长度恰好等于a ,则称此曲线为直线l 的“绝对曲线”．下面给出四条曲线方程:①21y x =--;②2y x =;③22(1)(1)1x y -+-=;④2234x y +=;则其中直线l 的“绝对曲线”有_______________【答案】②③④13．【安徽省寿县第一中学2014届高三上学期第二次月考数学（理）试卷（实验A 班月考）】在平面直角坐标系中,O 是坐标原点,若两定点,A B 满足2OA OB OA OB ==⋅=,则点集{}R ,,2,|∈≤++=μλμλμλP 所表示的区域的面积是_______________．【答案】14．【安徽省芜湖市沈巷中学2014届高三一轮复习测试（一）数学理试题】12,e e 是两个不共线的向量,已知122AB e ke =+,123CB e e =+,122CD e e =-,且D B A ，，三点共线,则实数k =_______;【答案】8-1．【安徽省皖南八校2014届高三10月第一次联考数学(理)试题】若(1,2),(1,0)a b ==-,则2a b -=_________．【答案】(3,4) 2a-b=(2,4)-(-1,0)=(3,4)．15．【江南十校2014届新高三摸底联考(理)】向量a ，b 满足则a 与b 的夹角为 ．16．【安徽涡阳四中2014届高三第三次质量检测(理)】已知向量(1,2),(1,0),(3,4)===a b c ．若λ为实数，()λ+a b ∥c ，则λ的值为 ．【答案】12． 17．【福建漳州芗城中学2014届高三11月月考（理）】设向量a =（1，cos θ）与b =（1-，2cos θ）垂直，则cos2θ等于_______【答案】0．18．【福建漳州芗城中学2014届高三11月月考（理）】正方形ABCD 的边长为l ，点E 是AB 边上的动点．则DE CB ⋅的值为 【答案】1．19．【福建莆田四中2014高三上期中考试(理)2==，2)()2(-=-∙+b a b a ，则与的夹角为 ． 【答案】3π．20． 【安徽省芜湖市沈巷中学2014届高三一轮复习测试（一）数学理试题】若向量(1,2),(2,1),a b →→==-,k t 为正实数．且211(1),x a t b y a b k t→→→→→→=++=-+,(1)若x y →→⊥,求k 的最大值;(2)是否存在,k t ,使//x y ?若存在,求出k 的取值范围;若不存在,请说明理由．二．能力题组21．【安徽省淮南二中2014届高三上学期第三次月考数学（理）】ABC ∆中，60,A A∠=︒∠的平分线AD 交边BC 于D ，已知3=AB ，且1()3AD AC AB R λλ=+∈，则AD 的长为( )A ．1BC ．D ．322．【福建漳州芗城中学2014届高三11月月考（理）】给出下列4个命题:①非零向量，a b 满足||==-a b a b ，则+与a a b 的夹角为30°; ②“b a ⋅＞0”是“a 与b 的夹角为锐角”的充要条件;③函数y=|x+1|图象按向量a =(-1,0)平移，得到的对应函数表达式为y=|x+2|;④在△ABC 中，若0=⎪⎭⎫⎝⎛-⋅⎪⎭⎫ ⎝⎛+→→→→AC AB AC AB 则△ABC 为等腰三角形．其中正确的命题是________ 【答案】①③④．23．【福建莆田四中2014高三上期中考试(理)】如右图，在△OAB 中，C 为OA 上的一点，且2,3OC OA D =是BC 的中点，过点A 的直线l ∥OD，P 是直线l 上的动点，12OP OB OC l l =+，则21l l -= ． 【答案】-23． 24．【安徽涡阳四中2014届高三第三次质量检测(理)】（本小题满分12分）已知向量)2cos ,(cos ),1,sin 2(x x x =-=，定义函数)(x f ⋅=（Ⅰ）求函数)(x f 的表达式，并指出其最大最小值；（Ⅱ） 在锐角ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，且,8,1)(==bc A f 求ABC ∆ 的面积S 。

一．基础题组1.【福建莆田一中2014段考(理)】已知抛物线243xy =的准线过双曲线2221x y m-=-的一个焦点，则双曲线的离心率为（ )A.324B 。

62C.3 D 。

332.【2013合肥二模（理）】过双曲线﹣=1(a ＞0，b ＞0）的左焦点F （﹣c,0）(c ＞0)，作倾斜角为的直线FE 交该双曲线右支于点P ，若=（+），且•=0则双曲线的离心率为（ ） A ． B ． +1 C ．D ．3。

【福建莆田四中2014高三上期中考试(理）】设双曲线的一个焦点为F ，虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近垂直,那么此双曲线的离心率为( ） 2 3 31+51+ 4.【安徽省寿县第一中学2014届高三上学期第二次月考数学（理)试卷(实验A 班月考）】设12,F F 是双曲线2222:1(0,0)x y C a b a b-=>>的两个焦点,P是C 上一点,若a PF PF 6||||21=+，且12PF F ∆的最小内角为30,则C 的离心率为（ )A ．2B ．23C ．3D ．26 5.【安徽省望江二中2014届高三复习班上学期第一次月考数学(理）试题】若抛物线22y px =的焦点与双曲线22122x y -=的右焦点重合，则p 的值为（ ） A ．2-B ．2C ．4D ．4-6。

【安徽省江南十校2014届新高三摸底联考数学理试题】双曲线的左、右焦点分别为F 1、F 2，点P 在右支上,且PF 1与圆x 2+y 2=a 2相切,切点为PF 1的中点,F 2到一条渐近线的距离为3，则的面积为（ ）A ．9B ．3C ．3D ．17。

【安徽省阜阳一中2014届高三上学期第一次月考数学（理）试题】抛物线2x y =上的任意一点到直线02=--y x 的最短距离为（ ）A ．2B ．827C ．22D ．以上答案都不对8.【安徽省池州一中2014届高三第一次月考数学（理)试题】若双曲线()222103x y a a -=>的离心率为2，则a 等于( ）A ．2B 3C ．32D ．19。