中国人口增长预测-数学建模
- 格式:doc
- 大小:949.13 KB
- 文档页数:22

中国人口增长预测模型的建立与分析摘要针对我国人口发展过程中出现的老龄化进程加快,出生人口性别比持续升高,乡村人口城镇化的新特点,我们基于LESLIE 矩阵,着重考虑城镇与乡村间的人口迁移及女性人口比例变化对我国人口增长的影响,经过两次改进建立了便于计算机求解的差分方程模型,对我国2005年以后45年的人口增长进行了预测。
随后利用时间段参数设置法,对差分方程模型又进行了一次改进。
然后运用等维灰色系统预测法对该差分方程模型的中短期预测进行了检验,同时根据2001年人口基本数据运用此模型对2001年~2005年进行了预测,并用实际数据对预测结果进行了检验。
我们将预测区间分为2006~2020年、2021~2035年、2036~2050年三个区间,以量化短期、中期与长期。
通过调整模型中相关参数及输入条件,定量地分析了男女性别比例、老龄化和乡村人口城镇化对我国人口增长的影响。
预测结果表明,从短期来看,我国的出生性别比变化不明显,将在短期内维持基本不变,老龄化进程在15年内在上升了8个百分点,人口扶养比持续升高,这将加重我国的人口压力,乡村人口城镇化水平进展缓慢;从中期来看,总人口性别比将保持在1与1.1之间,老龄化进程将呈线性增加趋势,乡村人口城镇化水平将持续发展;从长期来看,老龄化进程将在2035到2045年经历老龄人口高峰平台,老龄人口比重在0.3以上,育龄妇女人数持续下降,总人口数将在2023年达到峰值14.05亿。
关键词:LESLIE矩阵,人口预测,性别比例,城镇化,老龄化,灰色系统预测一、问题的重述人口问题是中国社会发展的重要问题,对中国人口的中长期预测有助于政府制定相应的政策保持中国的长治久安。
现需要解决的问题如下:1.主要根据2001~2005年的人口统计数据,对中国人口增长的中短期和长期趋势作出预测,特别要关注老龄化,出生人口性别比及乡村人口城镇化等因素。
2.指出所建模型的优点和不足之处。

数学建模之中国人口增长的预测和人口结构的简析随着社会经济的发展,人口增长一直是一个备受关注的问题。
数学建模是研究人口增长和人口结构的重要方法之一、本文将对中国人口增长的预测和人口结构进行简析,并利用数学建模方法进行预测分析。
首先,中国人口增长的情况是众所周知的。
随着中国的经济快速发展,人民生活水平的提高,医疗水平的提高以及计划生育政策的实施,中国的人口增长率逐渐放缓。
根据国家统计数据,自2024年以来,中国的总人口增长率一直在下降,其中在2024年总人口为14亿人,增长率仅为0.35%。
根据这一趋势,可以推断出未来的人口增长率可能会进一步下降。
在进行人口增长预测时,可以运用数学建模方法中的指数增长模型。
指数增长模型是描述人口增长的一种常用方法,其基本形式为:N(t)=N0*e^(r*t)其中,N(t)表示时间t时刻的人口数量,N0表示初始人口数量,r表示人口增长率,e表示自然对数的底数。
利用指数增长模型可以对未来的人口增长进行预测。
但要注意的是,由于人口增长受到多种因素的影响,例如政策调整、经济发展、文化变迁等,所以对于人口的精确预测是一项复杂而困难的任务。
因此,在进行人口预测时,应结合实际情况,综合考虑人口增长的多个因素。
另外,人口结构是指人口在不同年龄段的分布情况。
人口结构反映了一个地区或国家的经济、社会、教育等方面的发展状况。
中国的人口结构表现为老龄化趋势和少子化现象。
根据国家统计数据,中国的老龄化人口比例逐年提高,同时生育率呈下降趋势。
这种人口结构的变化将对中国的社会、经济等多个方面产生深远的影响。
为了分析人口结构的变化,可以利用数学建模中的人口金字塔。
人口金字塔以年龄为横轴,人口数量为纵轴,通过金字塔的形状和比例来反映人口的结构情况。
通过观察人口金字塔的变化,可以了解人口的年龄分布情况,判断人口的变化趋势,为相关政策和规划提供依据。
总之,中国人口增长的预测和人口结构的分析是一个复杂的问题,数学建模可以提供一种客观、科学的方法来分析这些问题。

全国大学生数学建模比赛论文人口预测模型 The manuscript was revised on the evening of 2021中国人口预测模型摘要:人口数量的变化,关系到一个国家的未来。
认识人口数量的变化规律,建立人口模型,能够较准确的预报,是有效控制人口增长的前提。
本文对人口预测的数学模型进行了研究。
首先,建立人口指数模型、Logistic模型及灰度预测模型。
对我国2005年以后45年的人口增长进行了预测,根据1982年人口基本数据运用模型对1982年~2005年进行了预测,并用实际数据对预测结果进行了检验。
我们将预测区间分为2006~2030年、2030~2050年两个区间,以量化未来我国短中期与长期的人口变化。
关键词:人口数量的变化人口指数模型 Logistic模型灰度预测模型MATLAB Excel目录第一部分问题重述 (3)第二部分问题分析 (3)第三部分模型的假设 (3)第四部分定义与符号说明 (3)第五部分模型的建立与求解 (3)模型一 (3)模型二 (8)模型三 (12)第六部分对模型的评价 (14)第七部分参考文献 (15)第八部分附表 (15)一、问题重述人口问题始终是制约我国发展的关键因素之一。
本题要求根据已知数据,运用数学建模的思想对我国人口做出分析和预测。
具体问题如下:从中国的实际情况和人口增长的特点,例如我国老龄化进程加快、出生人口性别比持续升高、乡村人口城镇化等,利用参考附录中所提供的数据,建立中国人口增长的数学模型,由此对中国人口增长的中短期和长期趋势做出预测,并指出模型的优缺点。
二、 模型假设1、假设题目所给的数据真实可靠;2、假设不考虑我国人口大规模的朝国外迁移,也不考虑外国人大量涌入我国;3、假设不考虑战争、自然灾害、疾病对人口数目和性别比的影响;4、假设在本世纪中叶前,我国计划生育政策稳定。
5、假设中短期内生育率和死亡率保持相对稳定6、假设相同年龄段人口性别比基本稳定。

中国人口增长预测数学建模引言中国作为世界上人口最多的国家之一,人口增长一直是一个备受关注的问题。
人口数量的增长对于国家的经济、社会、环境等方面都有着重要的影响。
因此,预测中国人口的增长趋势对于未来的发展规划具有重要意义。
本文将介绍一种基于数学建模的方法,用于预测中国人口的增长情况。
方法数据收集为了进行人口增长预测的数学建模,我们需要收集一系列历史人口数据。
这些数据可以从各种统计年鉴、人口普查、政府发布的数据等渠道获取。
通常,我们需要收集的数据包括中国的总人口数量、出生率、死亡率、迁入率和迁出率等。
建立数学模型基于收集到的数据,我们可以建立一个数学模型来描述中国人口的增长情况。
常用的数学模型包括指数增长模型、Logistic增长模型等。
在本文中,我们以Logistic增长模型为例。
Logistic增长模型基于以下假设: 1. 人口增长率与当前人口数量成正比; 2. 当人口数量接近一定的上限时,人口增长率会逐渐减小。
Logistic增长模型的公式可以表示为:dP/dt = r*P*(1-P/K)其中,P表示人口数量,t表示时间,r表示人口增长率,K表示人口的上限。
参数估计为了应用Logistic增长模型进行人口预测,我们需要估计模型中的参数。
参数估计可以通过拟合历史数据来完成。
常用的参数估计方法包括最小二乘法、最大似然估计等。
模型验证一旦完成参数估计,我们可以使用模型预测未来的人口变化情况。
为了验证模型的准确性,我们可以将预测结果与实际观测数据进行比较。
如果预测结果与实际观测数据较为接近,说明模型具有较好的预测能力。
预测未来人口增长利用建立的数学模型和参数估计,我们可以进行未来人口增长的预测。
通过不同的假设和参数值,我们可以探讨不同因素对人口增长的影响。
例如,我们可以考虑不同的出生率和死亡率情况下的人口增长,或者研究不同人口政策下的人口增长趋势。
结论本文介绍了一种基于数学建模的方法,用于预测中国人口的增长情况。

中国人口增长预测本题是一个人口发展预测的问题。
人口发展与一般种群增长一样,是由自然增长率决定的。
然而,人类个体是一种社会的个体,所以人口发展有自己的特点。
想到人口的迁移,性别比例,城镇化等。
同时,人口发展受政策的影响,例如计划生育;也要受到人们意识的影响,像生育意识等。
但是从社会层面上看,生育意识在整个社会上体现为妇女的生育模式,进而可以特别地去考虑。
思考方法:首先,数据的处理。
在经过EXCEL分析和验证后,适当修正题中的个别有误数据后,利用有效数据进行建模求解,在此过程中,我们提取出死亡率、生育率等感念,且把人的一生按年龄分为青年期、衰老期等阶段。
这是求解人口增长模型的必要过程和方法。
其次,模型建立。
和一般的预测模型一样,本模型也是个预测模型,所以考虑到用题目所给的五年的信息,来推测今后几十年的人口的总数和结构情况。
对此,我们选用差分方程模型和数据参数拟合等方法。
同时,将死亡率与出生率分开分别计算和拟合,通过五年的实际数据拟合出相应函数的参数,再利用此函数进行评估和预测。
最后,利用已有信息以及上述所求出的对应函数和方程,对中短期与长期进行估计和预测,进而得出人口结构、人口比例、人口数量等一系列的相关数据。
以下是解答过程:1.数据说明:x:表示最大的年龄;mi=1,2,3,4,5,6 其中1表示市男性,2表示市女性,3表示镇男性,4表示镇女性,5表示乡男性,6表示乡女性;A :表示婴儿性别比例矩阵;* :表示点乘;P(x,t):表示t时刻年龄为x的人口数量;ibir(x,t):表示t时刻年龄为x的出生率;i)(,i dea x t:表示t时刻年龄为x的死亡率;)(i t k:表示t时刻婴儿的死亡率;tra(x,t):表示t时刻年龄为x的人口迁出率;i2.假设条件1. 假设国内社会环境稳定,无异常大量死亡或出生情况发生,人口比例,人口总数不会出现突变状况; 2. 假设只存在乡向城镇迁出,不存在其他迁移方式,且不同年龄段迁移率相同; 3. 假设不考虑国家之间的迁入与迁出,把中国内部看为一个封闭的模型; 4. 对于90岁以上的人都按照90岁处理; 5. 假设只存在乡向城镇迁出,不存在其他迁移方式,且不同年龄段迁出率相同,按照0.6%均匀增长。
中国人口增长的预测和人口结构的简析摘要本文根据过去数十年的人口数据,通过建立不同的数学模型,对中国人口的增长进行了短期和中长期的预测。
模型一:从中国统计年鉴—2008,查找得到2000-2007年的人口数据,然后用灰色模型进行人口的短期(2008-2017)预测。
这里,我们采用两种算法进行人口总数的预测。
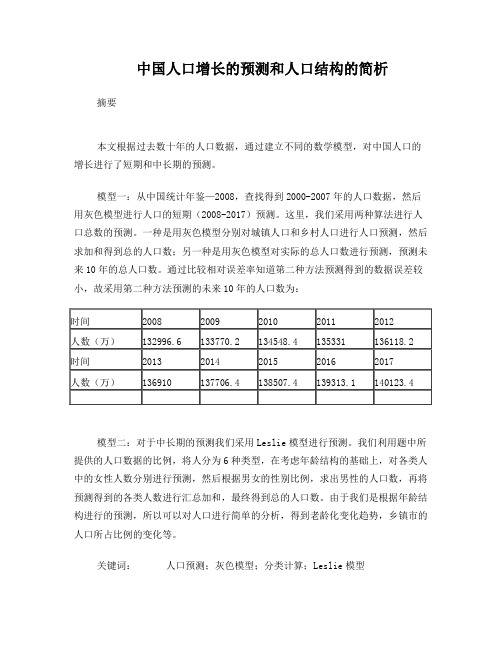
一种是用灰色模型分别对城镇人口和乡村人口进行人口预测,然后求加和得到总的人口数;另一种是用灰色模型对实际的总人口数进行预测,预测未来10年的总人口数。
通过比较相对误差率知道第二种方法预测得到的数据误差较小,故采用第二种方法预测的未来10年的人口数为:模型二:对于中长期的预测我们采用Leslie模型进行预测。
我们利用题中所提供的人口数据的比例,将人分为6种类型,在考虑年龄结构的基础上,对各类人中的女性人数分别进行预测,然后根据男女的性别比例,求出男性的人口数,再将预测得到的各类人数进行汇总加和,最终得到总的人口数。
由于我们是根据年龄结构进行的预测,所以可以对人口进行简单的分析,得到老龄化变化趋势,乡镇市的人口所占比例的变化等。
关键词:人口预测;灰色模型;分类计算;Leslie模型一、模型假设模型一的假设:1、不考虑国际迁移,认为国家内部迁移不改变人口总量;2、不考虑自然灾害、疾病等因素对人口数量的影响;3、文中短期预测到2017年4、大面积自然灾害、疾病的发生以及人们的生育观念等因素会对当年的生育率和人口数量产生影响,认为这些因素在预测误差允许的范围内.模型二的假设:1、每一年龄组的女性在每一个时间段内有相同的生育率和死亡率;2、在预测的时间段内男女的性别比例保持现状不变;3、不考虑人口的迁入和迁出;4、不考虑空间等自然因素的影响,不考虑自然灾害对人口数量的影响。
二、问题分析中国是一个人口大国,随着经济的不断发展,生产力达到较高的水平,现在的问题已不是仅仅满足个人的需要,而是要考虑社会的需要。
中国未富先老,对经济的发展产生很大的影响。
中国人口增长预测摘要本文从中国人口的实际情况和人口增长的特点出发,根据题目和中国统计年鉴中的相关数据,建立了两个关于中国人口增长的数学模型,并对中国人口做出了分析和预测。
模型一:利用中国统计年鉴中 2000—2005 年人口的数据,运用灰色理论的基本原理建立 GM(1,1) 模型。
该模型利用离散数据列进行生态处理,建立动态的微分方程,对我国近5年、10年、20年的总人口分别进行了预测。
又根据中国人口城乡分布不同且总趋势也不同的特点,把全国人口分为城市人口、城镇人口、乡村人口三部分分别进行灰色预测。
结果表明,该模型较好的反映并预测中国人口短中期和长期的变化情况。
模型二:按人口年龄结构特征,将人口分为幼年(0—14岁)男女、中年(15—49岁)男女、老年(50岁以上)男女。
各年龄段的人口变化是由出生率、死亡率和转化为其他年龄段的转化人数决定的。
根据各年龄段人口数量变化特点,对各年龄段转化人数引入转化因子,改进马尔萨斯模型,附带出生率、死亡率、生育率、出生性别比率等约束条件,建立了新的具有年龄结构的人口增长模型。
结合我国人口的特点,运用已知数据和利用微分方程的数值解,预测出男性和女性幼年、中年、老年的人口数量。
可反映中国不同年龄结构的人口分布情况。
关键词:灰色预测;小误差频率;微分方程组;人口模型;转移因子一.问题重述中国是一个人口大国,人口问题始终是制约我国发展的关键因素之一。
因此人口预测的科学性、准确性是至关重要的。
英国人口学家马尔萨斯的人口指数增长模型和荷兰生物学家的Logistic模型都是经典的人口预测模型。
但是,影响中国人口的因素较多,人口结构较复杂,这些模型对人口预测很粗略,甚至是不准确的。
因此,我们要根据我国具体的人口结构现状(如老龄化进程加速)、人口的分布现状(如乡村人口城镇化)、人口比率现状(如出生人口性别比持续升高)等特点,来较准确、较具体地对中国人口进行预测,建立人口增长的数学模型,由此对中国人口中短期和长期增长趋势做出预测。
关键字:人口数平衡点方程模型运动预测曲线稳定增长人口一题目:请在人口增长的简单模型的基础上。
" (1)找到现有的描述人口增长,与控制人口增长的模型;" (2)深入分析现有的数学模型,并通过计算机进行仿真验证;" (3)选择一个你们认为较好的数学模型,并应用该模型对未来20年的某一地区或国家的人口作出有关预测;" (4)就人口增长模型给报刊写一篇文章,对控制人口的策略进行论述。
二摘要:本次建模是依照已知普查数据,利用Logistic模型,对中国人口的增长进行预测。
首先假设人口增长符合Logistic模型,即引入常数,用来表示自然环境条件所能容许的最大人口数。
并假设净增长率为,即净增长率随着人口数N(t)增长而减小,当N(t) 时,净增长率趋于零。
按照这个假设,。
用参数=3.0,r=0.0386, =1908, =14.5。
画出N=N(t)的图像,作为人口增长模型的一种近似。
做微分方程解的定性分析,求出N=N(t)的驻点和拐点,按照函数作图方法列出定性分析表,作出相轨迹的运动图。
当初始人口<时,方程的解单调递增到地趋向,这意味着如果使用Logistic模型描述人口增长,则人口发展地总趋势是渐增到最大人口数,因此可作为人口的预测值,也称谓平衡点。
用导数做稳定分析,为判断平衡点是否为稳定,可在平面上绘制f(x)的图象,然后像函数绘图那样,用导数进行定性分析,通过图看出人口数N(t)按时间是递增的,当人口数未达到饱和状态的时候,将逐渐地趋向,这意味着是稳定的平衡点。
按该模型,未来人口的数量将随着时间的演化,从初始状态出发达到极限状态,这样就给出了人口的未来预测。
三问题的提出1. Malthus模型英国统计学家Malthus(1766-1834)发现人口增长率是一个常数。
设t时刻人口为N(t),因为人口总数很大,可近似把N(t)当作连续变量处理。
Malthus的假设是:在人口的自然增长过程中,净相对增长率(出生率减去死亡率)是常数,即单位时间内人口的增长量与人口总数成正比。
中国人口增长的预测和人口的结构分析摘要本文是在已知国家政策和人口数据的前提下对未来人口的发展进行预测和评估,选择了两种模型分别对人口发展的短期和长期进行预测。
模型一中我们在人口阻滞增长模型logistic模型的基础上进行改进,弥补了logistic原始模型仅仅能表示环境对人口发展趋势影响的缺陷,加入了社会因素的影响作为改进,保证了logistic改进模型的有效性和短期预测的正确性。
多次运用拟合的方法(非线性单元拟合,线性多元拟合)对数据进行整合,得到的改进模型对短期预测具有极高的准确性,证明了我们的修正方式与模型改进具有一定的正确性。
模型二中我们分别考虑了城、乡、镇人口的发展情况,利用不同年龄段存活率和死亡率的不同,采用迭代的方式也就是Leslie矩阵的方式对人口发展进行预测,迭代的方式不同于拟合,具有逐步递进的准确性,在参数正确的前提下,能够保证每一年得到的人口都有正确性,同时我们分男女两方面来考虑模型,不仅仅用静态的男女比例来估算人口总数,具有更高的准确性。
然而Leslie模型涉及的参数较多,如果采用动态模型的方式,计算量过大,我们首先用均值的方式对模型进行简化,同样得到迭代矩阵后的人口数值,发展趋势与预测相同,能够很好的预测中国人口的长期发展,同时,由于Leslie矩阵涉及多个参数,所以我们用最终的结果来表征老龄化程度,城乡比,抚养比等多个评价社会发展的参数,得到了较好的估计值,使模型在估算人口的基础上得到了推广和应用。
通过logistic改进模型和Leslie模型我们分别对中国人口发展进行短期和中长期预测,均能得到很好的效果,说明了我们的模型在适用范围内的准确性和实用性。
关键词:人口发展预测;logistic模型改进;参数拟合;Leslie迭代模型;一、问题重述中国是世界上人口最多的发展中国家, 人口问题始终是制约我国发展的关键因素之一,人口众多、资源相对不足、环境承载能力较弱是中国现阶段的基本国情,短时间内难以改变。
关于计划生育政策调整对人口数量、结构及其影响的研究【摘要】本文着重于讨论两个问题:1、从目前中国人口现状出发,对于中国未来人口数量进行预测。
2、针对深圳市讨论单独二胎政策对未来人口数量、结构及其对教育、劳动力供给与就业、养老等方面的影响。
对于问题1从中国的实际情况和人口增长的特点出发,针对中国未来人口的老龄化、出生人口性别比以及乡村人口城镇化等,提出了 Logistic 、灰色预测、等方法进行建模预测。
首先,本文建立了 Logistic 阻滞增长模型,在最简单的假设下,依照中国人口的历史数据,运用线形最小二乘法对其进行拟合, 对 2014 至 2040 年的人口数目进行了预测, 得出在 2040 年时,中国人口有 14.32 亿。
在此模型中,由于并没有考虑人口的年龄、 出生人数男女比例等因素,只是粗略的进行了预测,所以只对中短期人口做了预测,理 论上很好,实用性不强,有一定的局限性。
然后, 为了减少人口的出生和死亡这些随机事件对预测的影响, 本文建立了 GM(1,1) 灰色预测模型,对 2014 至 2040 年的人口数目进行了预测,同时还用 2002 至 2013 年的 人口数据对模型进行了误差检验,结果表明,此模型的精度较高,适合中长期的预测, 得出 2040 年时,中国人口有 14.22 亿。
与阻滞增长模型相同,本模型也没有考虑年龄 一类的因素,只是做出了人口总数的预测,没有进一步深入。
对于问题2针对深圳市人口结构中非户籍人口比重大,流动人口多这一特点,我们采用了灰色GM(1,1)模型,通过matlab 对深圳市自2001至2010年的数据进行拟合,发现其人口变化近似呈线性增长,线性相关系数高达0.99,我们就此认定其为线性相关并给出线性方程。
同理,针对其非户籍人口,我们进行matlab 拟合发现,其为非线性相关,并得出相关函数。
并做出了拟合函数0.0419775(1)17255.816531.2t X t e ⨯+=⨯-。
中国人口增长的预测和人口的结构分析摘要本文是在已知国家政策和人口数据的前提下对未来人口的发展进行预测和评估,选择了两种模型分别对人口发展的短期和长期进行预测。
模型一中我们在人口阻滞增长模型logistic模型的基础上进行改进,弥补了logistic原始模型仅仅能表示环境对人口发展趋势影响的缺陷,加入了社会因素的影响作为改进,保证了logistic改进模型的有效性和短期预测的正确性。
多次运用拟合的方法(非线性单元拟合,线性多元拟合)对数据进行整合,得到的改进模型对短期预测具有极高的准确性,证明了我们的修正方式与模型改进具有一定的正确性。
模型二中我们分别考虑了城、乡、镇人口的发展情况,利用不同年龄段存活率和死亡率的不同,采用迭代的方式也就是Leslie矩阵的方式对人口发展进行预测,迭代的方式不同于拟合,具有逐步递进的准确性,在参数正确的前提下,能够保证每一年得到的人口都有正确性,同时我们分男女两方面来考虑模型,不仅仅用静态的男女比例来估算人口总数,具有更高的准确性。
然而Leslie模型涉及的参数较多,如果采用动态模型的方式,计算量过大,我们首先用均值的方式对模型进行简化,同样得到迭代矩阵后的人口数值,发展趋势与预测相同,能够很好的预测中国人口的长期发展,同时,由于Leslie矩阵涉及多个参数,所以我们用最终的结果来表征老龄化程度,城乡比,抚养比等多个评价社会发展的参数,得到了较好的估计值,使模型在估算人口的基础上得到了推广和应用。
通过logistic改进模型和Leslie模型我们分别对中国人口发展进行短期和中长期预测,均能得到很好的效果,说明了我们的模型在适用范围内的准确性和实用性。
关键词:人口发展预测;logistic模型改进;参数拟合;Leslie迭代模型;一、问题重述中国是世界上人口最多的发展中国家, 人口问题始终是制约我国发展的关键因素之一,人口众多、资源相对不足、环境承载能力较弱是中国现阶段的基本国情,短时间内难以改变。
人口问题始终是制约我国发展的关键因素之一. 无论是对我国目前发展的认识还是对未来发展的预测,人口问题的研究都有着非常重要的意义. 从我国的实际情况和人口特点出发,认识人口数量的变化规律,建立人口模型,做出较准确的预测是控制人口增长的前提,而预测中国人口的变化趋势,是一切政策和方案实施的前提,所以,结合材料和背景,根据中国人口变化的趋势预测中国未来人口的变化是我们需要去研究的课题。
二、问题分析材料中给出了《中国人口年鉴》来提供人口变化趋势,同时给出了《中国人口发展战略报告》来为我们提供中国人口的控制方案和方向,结合材料我们得到,最初未进行计划生育期间,人口数量大幅度上升,出生率远远大于死亡率,导致当下中国具有极大的人口基数,即使已经实施了计划生育政策,我们每年的新生婴儿数量仍然非常巨大,归根究底,都是因为过去的几十年里累计的巨大人口基数导致的。
而当下,由于计划生育的实施以及时代的发展,大量的家庭几乎只有一个孩子甚至不生孩子,由此带来的是零增长甚至负增长,所以,结合当下我国人口基数大,然而生育率已经骤减等现况,结合经典人口预测模型对我国人口进行预测,是我们对问题的解决方案。
(1)首先我们要对人口的短期变化趋势进行预测,对当前和短期内的人口分布,人口现状进行定性的描述。
虽然不同算法具有局限性,然而短期预测时,大量算法如:灰色预测,拟合预测都能够一定程度接近地对人口变化趋势进行表征而不产生较大误差,但是为了能够精准预测,我们选择对logistic模型进行改进,使其在进行短期预测时能够更加准确减少误差。
(2)在对人口的短期预测结束后,我们要对人口发展进行长期的预测,而材料中给出了城乡镇三类地区的人口分布,也帮助我们细化不同地区的人口发展,同时也能更加准确地对全国人口的人口发展进行长期预测,为此我们引入Leslie模型,利用矩阵迭代的方式进行长期的人口预测,在稳态下保证Leslie模型对长期预测就有准确性。
三、模型建立1)符号说明r——人口增长率x i——人口数量下角标表示不同情况下的人口数量g=g(t)——修正因子k——年代,时间b——生育率s——存活率d——死亡率2)模型假设1.假设社会稳定发展,不考虑意外发生的战争瘟疫等造成人口产生突变的因素。
2.由于社会发展的稳定性,假设年代不是影响出生率,死亡率等计算因子的主要因素,可以认为出生率,存活率,死亡率等因子是关于年龄的单元函数。
3.假设当前政策长久进行,女性生育年龄分布和生育模式保持当前情况不变,由此我们可以认为各年龄段的女性和男性生育率是一个固定分布。
3)模型建立模型一、利用logistic模型的改进来预测短期人口的变化我们知道,普通的人口阻滞增长模型将额外的环境条件等限制人口增长的因素考虑进来,并认为人口数量越大阻滞作用越明显,将人口的增长率r看作一个关于人口数量的函数而不认为是一个定值,此时r=r(x),所以人口变化趋势可以用微分方程来表示:我们引入人口容量设为,则r()=0,此时r(x)=r(1-)由此解得:x(t)=综上,我们得到了原始的logistic模型,代表了环境容纳量一定的情况下人口发展的情况,然而我们单单考虑了环境因素而没有考虑社会因素的影响,这是导致logistic模型产生误差的原因,所以我们引入修正因子作为社会因素的影响修正,引入g()作为修正项,得到改进后的logistic函数:x(t)=+g()此时,我们通过数据研究,引入主要影响的三个因素,分别为城镇人口比例,男女比例以及老龄人口比例作为影响因素,于是我们得到g=g(),随后移项可得影响因子的关系函数g()= x(t)-由于假设中提到了社会稳定的问题,所以我们认为城乡比,男女性别比例等一系列因素仅仅是时间的函数,随年份的改变而改变,所以g=g()=g(t)我们利用01年到05年的数据对logistic模型进行拟合(拟合函数见附录),得到x m和r的值,得到简单的logistic模型参数,附曲线如图X m=14.1990396292082;r=0.069311514967144;得到logitic原始模型为x(t)=图:logistic原始模型拟合——人口随时间变化从图中我们虽然没有发现人口的S型增长,但是我们预见到峰值将会出现在2050年左右,符合人口发展的趋势,这里没有出现我们希望的S型增长,可能是因为我们的人口增长趋势已经进入S型增长的后半部分,或者中国人口基数过大或者模型简单考虑环境因素并没有很好解释人口发展,所以我们认为该图仍具有正确性,并以此为基础进行修正因子加入的改进。
而后我们对修正因子进行估算,通过数据,我们得到x(t)以及logistic模型的数值,代入可以得到g(t)的值,我们取2001-2005年城镇人口比例男女性别比例老龄化人口比例分别为x1 x2 x3作为影响因素,代入t=0、1、2、3,分别得到G1=g()=g(0)=0.0091G2=g()=g(1)=0.0042G3=g()=g(2)=-0.0021G4=g)=g(3)=-0.0012G5=g)=g(4)=-0.003我们进行多参拟合,因为三个影响因素的比重相差不多,我们不考虑层次分析简单地认为三个影响因素权重相同,为此我们引入多参变量的一次拟合方式:g(t)=a+bx1+cx2+dx3代入01年到04年的数据进行多参拟合得到t 城镇比重男女比例老龄人口比重实际人口原始logistics数据Ф2001 0 0.371655 1.1532 7.18202 127627 127536 0.0091 2002 1 0.387097 1.1932 7.52601 128453 128411 0.0042 2004 3 0.411789 1.1928 8.18121 130000 130021 -0.0021 2003 2 0.412354 1.69 7.86589 129227 129239 -0.0012 2005 4 0.448427 1.1846 8.65496 130756 130759 -0.0003由于假设中我们提出,男女比例,城乡比,老龄化比重等因素不会因为年代的改变而发生突变,所以我们认为这些因子都是关于时间的函数,此后我们分别用二次拟合的方式对城镇人口比例,老龄化比例和男女比例进行二次拟合(拟合程序见附录):x1 =0.0022823 t^3 - 0.01251 t^2 + 0.032717 t + 0.37025x2=0.0026833 t^3 - 0.093986 t^2 + 0.34086 t + 1.1113x3 =0.013545 t^3 - 0.064487 t^2 + 0.40946 t + 7.1791随后我们利用g(t)=a+bx1+cx2+dx3作为目标函数进行多参数拟合利用f=x(t)-得到的表格中的数据进行拟合得到:a,b,c,d的数值如下:a=0.303466672b=-0.015436071206309c=-0.021475121184176d=0.067720279因此我们可以得到g()= 0.303466672X1-0.01543607X2-0.021475121X3+0.067720279代入修正因子,我们得到改进后的logistic函数:x(t)=+0.303466672X1-0.01543607X2-0.021475121X3+0.067720279分别代入拟合后的三个修正因子关于t的函数关系得到最终的logistic改进模型:x(t)=+ 0.303466672*(0.0022823 t^3 - 0.01251 t^2 + 0.032717 t + 0.37025)-0.01543607(0.0026833 t^3 - 0.093986 t^2 + 0.34086 t + 1.1113)-0.021475121(0.013545 t^3 - 0.064487 t^2 +0.40946 t + 7.1791)+0.067720279利用这个函数我们重新预测短期内的人口发展如下:表:利用logistic改进模型对未来人口预测年份估计值年份估计值年份估计值2006 13.21323 2024 13.9473 2042 14.173522007 13.27887 2025 13.96824 2043 14.179722008 13.34071 2026 13.98784 2044 14.185522009 13.39893 2027 14.00617 2045 14.190932010 13.45372 2028 14.02333 2046 14.195982011 13.50524 2029 14.03937 2047 14.20072012 13.55367 2030 14.05436 2048 14.20512013 13.59918 2031 14.06839 2049 14.209222014 13.64192 2032 14.0815 2050 14.213062015 13.68204 2033 14.09375 2051 14.216642016 13.71968 2034 14.10521 2052 14.219982017 13.755 2035 14.11591 2053 14.223112018 13.78811 2036 14.12591 2054 14.226022019 13.81915 2037 14.13526 2055 14.228742020 13.84824 2038 14.14399 2056 14.231282021 13.8755 2039 14.15214 2057 14.233652022 13.90102 2040 14.15976 2058 14.235862023 13.92492 2041 14.16687 2059 14.23793图:logistic改进模型关于总人口的预测从图中我们可以看出,我国人口在未来的20年内平稳增长并在2030年附近达到峰值并可能长期保持这个趋势,在政策不变社会稳定的前提下,我国人口将平稳发展不会产生较大的改变。