吉林省长春市十一高中2020至2021学年高二下学期期中考试 数学

吉林省长春市市第十一中学2020年高二数学文联考试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 已知的（）A．充分不必要条件B．必要不充分条件C．充要条件 D．既不充分也不必要条件参考答案：B2. 已知直线是的切线，则的值为（）Ａ．Ｂ．Ｃ．Ｄ．参考答案：A3. 当时，函数在上是增函数，则实数的取值范围是（）A. B. C. D.参考答案：B4. 经过椭圆的一个焦点作倾斜角为45°的直线，交椭圆于A、B两点．设O为坐标原点，则( )A．B． C．或D．参考答案：B5. 正方体中,分别为的中点，则与平面夹角的正弦值为（）参考答案：B略6. 设函数的导函数，则的值等于( )A. B. C. D.参考答案：A略7. 直线x－y＋m＝0与圆x2＋y2－2x－1＝0有两个不同的交点的一个充分不必要条件为()．A．m＜1 B．－3＜m＜1 C．－4＜m＜2D．0＜m＜1参考答案：D略8. 定义在R上的函数f（x）使不等式恒成立，其中f'（x）是f（x）的导数，则（）A．B．f（2）＞2f（0）＞4f（﹣2）C．D．f（2）＜2f（0）＜4f（﹣2）参考答案：B【考点】63：导数的运算．【分析】构造函数g（x）=，求出函数的单调性，从而求出函数值的大小即可．【解答】解：构造函数g（x）=∴g′（x）=，∵恒成立，∴2f′（2x）＞ln2f（2x）恒成立，∴g′（x）＞0，∴g（x）在R上为增函数，∴g（1）＞g（0）＞g（﹣1），∴＞＞，∴f（2）＞2f（0）＞4f（﹣2），故选：B9. 已知函数，若存在唯一的零点，且，则的取值范围是参考答案：B10. “，”是“双曲线的离心率为”的（）A. 充要条件B. 必要不充分条件C. 既不充分也不必要条件D. 充分不必要条件参考答案：D【分析】当时，计算可得离心率为，但是离心率为时，我们只能得到，故可得两者之间的条件关系.【详解】当时，双曲线化为标准方程是，其离心率是；但当双曲线的离心率为时，即的离心率为，则，得，所以不一定非要.故“”是“双曲线的离心率为”的充分不必要条件.故选D. 【点睛】充分性与必要性的判断，可以依据命题的真假来判断，若“若则”是真命题，“若则”是假命题，则是的充分不必要条件；若“若则”是真命题，“若则”是真命题，则是的充分必要条件；若“若则”是假命题，“若则”是真命题，则是的必要不充分条件；若“若则”是假命题，“若则”是假命题，则是的既不充分也不必要条件.二、填空题:本大题共7小题,每小题4分,共28分11. 函数的单调递增区间是___________________________。

吉林省长春市十一高中高二下学期期中考试（数学理）一、选择题（每题4分，共48分）1. 设a 是实数，且211i i a +++是实数，则=a ( ) A.21 B.1 C.23 D.22. 设随机变量ξ~(),,p n B 且6.1=ξE ，28.1=ξD ，则（ ） A .2.0,8==p n B. 4.0,4==p nC. 32.0,5==p nD. 45.0,7==p n3. ()101i -(i 为虚数单位)的二项展开式中第7项为（ ）A . 210- B. 210 C.i 120- D.i 120 4. ()5223++x x的展开式中，x 的系数为（ ）A .160 B.240 C.360 D. 8005. 函数⎪⎩⎪⎨⎧≤≤<≤-+=)20(cos 2)02(2)(πx x x x x f 的图象与x 轴所围成的封闭图形的面积为（ ）A . 23 B. 1 C. 4 D. 216.已知线性回归方程,1ˆbx y +=若,9,2==y x 则=b （ ）A.4B.4-C.18D. 0 7. 英文单词“office ”中的6个字母排成一列，方法数有（ ）种A.66A B.55A C. 6621A D. 4422A A8. 从编号为10,...,3,2,1的10个大小相同的球中任取4个，则所取4个球的最大号码是6的概率为（ ）A.841B.211C.52D. 539. 6名旅客，安排在3个客房里，每个客房至少安排1名旅客，则不同方法有（ ）种A .360 B.240 C.540 D. 21010.4名男生和4名女生排成一排，女生不排在两端，不同的排法数为（ ）A .4424AA B. 4444AA C. 6624AA D. 88A11. ()()()()(),2...22121111122192+++++++=++xaxaxaaxx则=++++1121...aaaa（）A .2- B.1- C.1 D. 212.由左图中的规律可判断右图问号处的图形应是（）二、填空题（每题4分，共16分）13. 若()51-ax的展开式中，3x的系数是-80，则a=____________14. 在某项测量中，测量结果ξ~()2,1σN,若ξ在()2,0内取值的概率为,8.0则ξ在(]2,∞-内取值的概率为___________15.从10,...,3,2,1这10个数中取4个，使它们的和为奇数，有__________种取法。

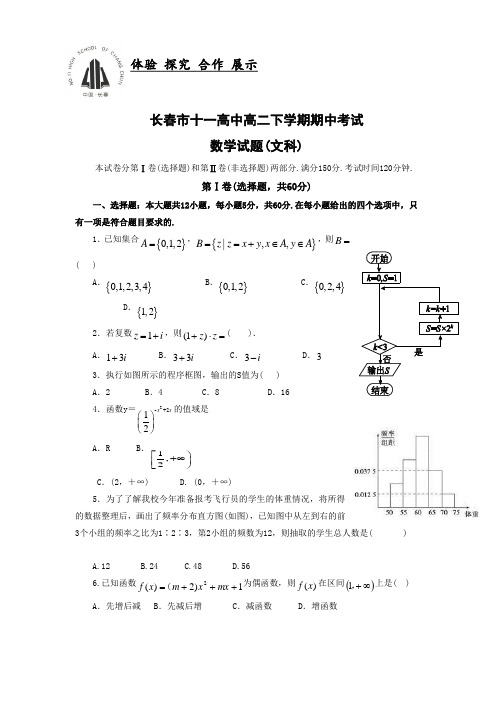
长春市十一高中高二下学期期中考试数学试题(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.第Ⅰ卷(选择题，共60分)一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合{}0,1,2A =，{}|,,B z z x y x A y A ==+∈∈，则B =( )A ．{}0,1,2,3,4 B ．{}0,1,2 C ．{}0,2,4D ．{}1,22．若复数1z i =+，则(1)z z +⋅=( )．A ．13i +B ．33i +C ．3i -D ．3 3．执行如图所示的程序框图，输出的S 值为( ) A ．2 B ．4 C ．8 D ．16 4．函数y ＝2-+212x x⎛⎫ ⎪⎝⎭的值域是A ．RB ．1,2⎡⎫+∞⎪⎢⎣⎭C ．(2，＋∞) D. (0，＋∞)5．为了了解我校今年准备报考飞行员的学生的体重情况，将所得的数据整理后，画出了频率分布直方图(如图)，已知图中从左到右的前3个小组的频率之比为1∶2∶3，第2小组的频数为12，则抽取的学生总人数是( )A.12B.24C.48D.566.已知函数1)2)(2+++=mx x m x f （为偶函数，则)(x f 在区间()∞+，1上是( ) A ．先增后减 B ．先减后增 C ．减函数 D ．增函数体验 探究 合作 展示7．同时投掷两个骰子，则向上的点数之差的绝对值为4的概率是( ) A.181 B.121 C.91 D.618．下表是某厂1—4月份用水量(单位：百吨)的一组数据：y＝－0．7x ＋a ，则a 等于( )A ．10．5B ．5．15C ．5．2D ．5．259．用反证法证明命题“设b a ,为实数，则方程02=++b ax x 至少有一个实根”时，要做的假设是( )A.方程02=++b ax x 没有实根B.方程02=++b ax x 至多有一个实根C.方程02=++b ax x 至多有两个实根D.方程02=++b ax x 恰好有两个实根 10．在区间[1,1]-上随机取一个数x ，cos2x π的值介于0到12之间的概率为A ．12B ．2πC ．13D ．2311．若1>>b a ，)2lg(),lg (lg 21,lg lg b a R b a Q b a P +=+==，则下列不等式成立的是( )A ．Q P R <<B ．R Q P <<C ．R P Q <<D ．Q R P <<12．已知函数()f x 的定义域为()()0,,f x '+∞为()f x 的导函数，且满足()()f x xf x '<-，则不等式()21(1)(1)f x x f x +>--的解集是( )A ． ()1,+∞B ．()2,+∞C ．(1,2)D ． ()0,1第Ⅱ卷(非选择题，共90分)二、填空题:本大题共4小题，每小题5分，共20分.13．已知{1,2,3,4}A ⊆，且A 中至少有一个偶数，则这样的A 有_______________个. 14．某班级有50名学生，现要采取系统抽样的方法在这50名学生中抽出10名学生，将这50名学生随机编号1～50号，并分组，第一组1～5号，第二组6～10号，…，第十组46～50号，若在第三组中抽得号码为12的学生，则在第八组中抽得号码为 的学生．15．若不等式220x ax b ++<的解集为{}32x x -<<，则=a 16．已知2()2'(1)f x x xf =+，则)0('f = ．三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤. 17．(本题满分10分) 已知函数2()sin 22cos 2f x x x x =+⋅．(1)求()f x 的最小正周期；(2)若[,]84x ππ∈，且()1f x =，求x 的值． 18.(本题满分12分) 已知等比数列{}n a 的各项均为正数，11a =，公比为q ；等差数列{}n b 中，13b =，且{}n b 的前n 项和 为n S ，233227,S aS q a +==.(1)求{}n a 与{}n b 的通项公式；(2)设数列{}n c 满足92nncS =，求{}n c 的前n 项和n T .19.(本题满分12分)已知函数()|2||23|f x x a x =-++，()|1|2g x x =-+． (1)解不等式|()|5g x <；(2)若对任意1x R ∈，都存在2x R ∈，使得12()()f x g x =成立，求实数a 的取值范围．20．(本题满分12分)大家知道，莫言是中国首位获得诺贝尔奖的文学家，国人欢欣鼓舞.某高校文学社从男女生中各抽取50名同学调查对莫言作品的了解程度，结果如下：(2)对莫言作品阅读超过75篇的则称为“对莫言作品非常了解”，否则为“一般了解”.根据题意完成下表，并判断能否有75%的把握认为对莫言作品的非常了解与性别有关？附：()()()()d b c a d c b a bc ad n K ++++-=2221.(本题满分12分) 已知椭圆C ：2222x y a b +＝1(a>b>0)的焦点为F 1(－1，0)，F 2(1，0)，且经过点P(1，32)．(1)求椭圆C 的方程；(2)设过F 1的直线l 与椭圆C 交于A 、B 两点，问在椭圆C 上是否存在一点M ，使四边形AMBF 2为平行四边形，若存在，求出直线l 的方程，若不存在，请说明理由．22．(本题满分12分)已知函数2()2ln ().f x x x a x a R =++∈ (1)当4a =-时，求()f x 的最小值；(2)若函数()f x在区间(0，1)上为单调函数，求实数a的取值范围长春市十一高中高二下学期期中考试数学答案(文科)一．选择13. 12 ；14. 37；15. 2；16. - 4三．解答题17.解：(1)1cos4()2cos22xf x x x-=⋅1cos442xx-=1sin(4)62xπ=-+． 3分因为242Tππ==，所以()f x的最小正周期是2π． 5分(2)由(1)得，因为()1f x=，所以1sin(4)62xπ-=而84xππ≤≤，所以54366xπππ≤-≤，所以4xπ=10分18.解：(1)设数列{}nb的公差为d，3322222731833.6a S q d q S q d d q a +=⎧⎧+==⎧⎪⎪⇒⇒⎨⎨⎨==+=⎪⎩⎩⎪⎩ 13n na -∴=，3nb n = 6分 (2)由题意得：()332n n n S +=， ()9921113()22311n n c S n n n n ⎛⎫==⋅=- ⎪ ⎪++⎝⎭1111133[(1)()()]22311n n T n n n =-+-++-=++ 12分19.解：(Ⅰ)由125x -+<得5125x -<-+<713x ∴-<-<，得不等式的解集为{}24x x -<< 5分(Ⅱ)因为任意R ∈1x ，都有R ∈2x ，使得12()()f x g x =成立， 所以{|()}{|()}y y f x y y g x =⊆=， 7分 又()223|(2)(23)||3|f x x a x x a x a =-++≥--+=+，()|1|22g x x =-+≥，所以|3|2a +≥，解得1a ≥-或5a ≤-，所以实数a 的取值范围为1a ≥-或5a ≤- 12分 20.解：(1)由抽样调查阅读莫言作品在50篇以上的频率为100795050101513121811=++++++，据此估计该校学生阅读莫言作品超过50篇的概率约为=P 10079 5分 (2)根据列联表数据得()323.1010.1455550502520253010022<≈⨯⨯⨯⨯-⨯⨯=K ，所以没有75%的把握认为对莫言作品的非常了解与性别有关. 12分 21.解：(1)∵c ＝1，21a ＋294b ＝1，a 2＝b 2＋c 2，∴a ＝2，b∴椭圆C 的方程为24x ＋23y ＝1. 5分(2)假设存在符合条件的点M(x 0，y 0)，设直线l 的方程为x ＝my －1， 由2213412x my x y =-⎧⎨+=⎩，消去x 得：(3m 2＋4)y 2－6my －9＝0，由条件知Δ>0，设A(x 1，y 1)，B(x 2，y 2)，则y 1＋y 2＝2634m m +，∴AB 的中点为(－2434m +，2334m m +)， ∵四边形AMBF 2为平行四边形，∴AB 的中点与MF 2的中点重合， 即0202142343234x m y m m +⎧=-⎪⎪+⎨⎪=⎪+⎩，∴M(－2231234m m ++，2634m m +)， 把点M 的坐标代入椭圆C 的方程得：27m 4－24m 2－80＝0，解得m 2＝209，∴存在符合条件的直线l ，其方程为：y＝±10(x ＋1)． 12分 22.解：(Ⅰ)0x >，2'4224()22x x f x x x x+-=+-=，得到()f x 的增区间为(1,)+∞；'()0f x <，得到()f x 的减区间为(0，1)， 所以()f x 的最小值为min ()(1)3f x f ==。

长春市十一高中2019-2020学年度高二下学期期中考试数 学 试 题 （文）一、选择题（每题5分，共60分）1．设复数z 的共轭复数z 满足(1＋i )z ＝2，其中i 为虚数单位，则z 等于（ ）A .i +1B .i -1C .i 22+D . i 22-2．观察下列各式：1=+b a ，322=+b a ，433=+b a ，744=+b a ，1155=+b a ， 1866=+b a …，则=+88b a （ ）A .28B .47C .76D .1233．在极坐标系中，圆θρcos 2-=的圆心的极坐标为（ ）A .⎪⎭⎫⎝⎛2,1π B .⎪⎭⎫⎝⎛-2,1π C .()0,1D .()π.14．有以下四种变换方式：①②③ ; ④ ;其中能将sinx y =的图像变换成函数 ） A .①和③B .①和④C .②和④D .②和③5．已知α∈,2ππ⎛⎫⎪⎝⎭，sin α＝35，则tan 2α＝（ ）A .247B .2425C .－2425D .－2476．在△ABC 中，角C B A ,,的对边分别为c b a ,,，若)())((c b b c a c a +=-+，则A ∠=A .090B .060C .0120D .01507．已知双曲线12222=-by ax )0,0(>>b a 的一个焦点与抛物线2410y x =的焦点重合，且双曲线的离心率等于310，则该双曲线的方程为（ ） A .1922=-y xB .1922=-y xC .122=-y xD .19922=-y x8．已知直线⊥l 平面α，直线m ⊂平面β，给出下列命题,其中正确的是（ ） ①m l ⊥⇒βα// ②m l //⇒⊥βα ③βα⊥⇒m l //④βα//⇒⊥m lA .②④B .②③④C .①③D .①②③9．已知12,F F 为椭圆192522=+y x 的两个焦点，过1F 的直线交椭圆于两点，8AB =， 则22AF BF +=（ ）A . 20B . 18C .12D .1010．设等比数列{}n a 中,前n 项和为n S ,已知3S =8,6S =7,则987a a a ++等于（ ） A .18 B .-错误!未找到引用源。

吉林省长春市市第十一中学2020-2021学年高二数学文模拟试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 函数的图像大致是（）A. B. C. D.参考答案：D2. 设数集，如果把叫做集的“长度”。

那么集合的长度是（）A、 B、C、 D、参考答案：A3. 分别在区间和内任取一个实数，依次记为m和n，则m＞n的概率为( )A．B．C．D．参考答案：A考点：几何概型．专题：计算题．分析：本题考查的知识点是几何概型的意义，关键是要找出满足条件m＞n的图形面积，及在区间和内的点对应的面积，再代入几何概型计算公式求解．解答：解：如图，则在区间和内任取一个实数，依次记为m和n，则（m，n）表示的图形面积为3×5=15其中满足m＞n，即在直线m=n右侧的点表示的图形面积为：，故m＞n的概率P=，故选A．点评：几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．解决的步骤均为：求出满足条件A的基本事件对应的“几何度量”N（A），再求出总的基本事件对应的“几何度量”N，最后根据P=N（A）/N求解．4. 在5张扑克牌中有3张“红心”和2张“方块”，如果不放回地依次抽取2张牌，则在第一次抽到“红心”的条件下，第二次抽到“红心”的概率为A. B. C. D.参考答案：D【分析】因为是不放回抽样，故在第一次抽到“红心”时，剩下的4张扑克中有2张“红心”和2张“方块”，根据随机事件的概率计算公式，即可计算第二次抽到“红心”的概率。

【详解】因为是不放回抽样，故在第一次抽到“红心”的条件下，剩下的4张扑克中有2张“红心”和2张“方块”，第二次抽取时，所有的基本事件有4个，符合“抽到红心”的基本事件有2个，则在第一次抽到“红心”的条件下，第二次抽到“红心”的概率为;故答案选D【点睛】本题给出无放回抽样模型，着重考查抽样方法的理解和随机事件的概率等知识，属于基础题。

长春市十一高中2015-2016学年度高二下学期期中考试数学试题（理科〉本试卷分笫I卷（选择题）和笫II卷（非选择题）两部分，满分150分，考试时间120分钟.第I卷（选择题，共60分）一、选择题：本大题共12小题，每小题5分，共60分•在每小题给岀的四个选项中，只有一项是符合题目要求的.1.若复数—羽一題（才是虚数单位），则z的虚部为（）C. -22.某工厂生产3C三种不同型号的产品，产品数量之比为2=3=5，现用分层抽样的方法抽取容量为刃的样本，样本中/型号产品有M件，则样本容量1■为（）A.« B ™ C.« D «3.用反证法证明命题“三角形三个内角至少有一个不大于余尸”时，应假设（）C.三个内角至多有一个大于®*尸D.三个内角至多有两个大于砂A.三个内角都大于砂B.三个内角都不大于砂4.某程序框图如右图所示，该程序执行后输出的L等于（）A. 7B. 15C. 31D. 63X=15.已知6. 12名同学合影，站成前排4人后排8人，现摄影师要从后排8人屮抽2人调整到前排，若其他人的相对顺序不变，则不同调整方法的总数是（）A. 168B. 560C. 840D. 16807. 在区间内随机取两个实数工，*,则满足的概率是（）112 3 A. 3B. 4 c. 3D. 58. 已知紅」为等差数列，为正项等比数列，公比若%=仏，则（） A. 5=4B. 2*C.D. 25或眄=毎9. 假设关于某设备的使用年限兀和所支出的维修费用卩（万元），有如下的统计资料：h2P3P4.er5 •-6，7「8。

10・，由资料可知*对兀呈线性相关关系，且线性回归方程为，=还"，请估计使用年限为20 年时，维修费用约为（）A MlB. 2Mc MD M310.边长为出的等边3匕中，Q 为边"的中点，若P 为线段6的中点，则的值为（）A. 11B.C.讣D. 一诂A.B. 53C."53D. i11.已知数列耳的前11项和为耳且满足B. 0则鸟m 二和为（）A MB 55c aD.«第II 卷（非选择题，共90分）二、填空题:本大题共4小题，每小题5分，共20分.13.已知数集▲二仇忌行｝,则建立从集合/到集合A 的不同函数的个 数为 .（胡.14•若二项式U 刃 的展开式的常数项为240,则正实数灯=■15.下列说法中：JT只需把函数》=金皿的图彖向右平移E 个单位长度.其中正确说法的序号是 _____________16.已知定义在厲上的函数加满足：/®=1,加Vg,则关于X 的不等式血也占的解集为 ___________________ •三、解答题：本大题共6小题，共70分•解答应写出文字说明、证明过程或演算步骤.17.（本小题满分10分）已知直线』过定点航5,且与圆b «-廊■久相交于 U 两点.JT（I ）若直线』的倾斜角为求线段"中点JT 的坐标；（II ）当的面积最大时，求直线［的方程.18.（本小题满分12分）在一次数学测试中，某班40名学生的成绩频率分布直方图如右图所示（学生成绩都在冋呵 之间）.（I ）求频率分布直方图中■的值，并估算该班数学成绩的平均值;①终边落在P 轴上的角的集合是{"I②函数图象的一个除）③函数在其定义域内是增函数；④为了得到函数对称中心是的图彖,（II ）若规定成绩达到90分及以上为优秀，从该班40名学生中任选2人，求至少有一人成绩为优秀的概率.19. （本小题满分12分）已知数列专的前$项和为$■，对任意的“时，点在二次函数的图象上. （I ）求通项公式11叫（II ）设"一工・，且"0,求数列餡的前現项和并.20. （本小题满分12分）求£«C 的面积. 21. （本小题满分12分）已知椭関孑忖-3"®的-个顶点皿0,离心率为1 ,过左焦点禹的直线J 交 椭圆于3两点，右焦点为耳. （I ） 求椭圆的标准方程；（II ） 若冋^8•皿I 成等差数列，求直线』的方程. 22. （本小题满分12分）已知函数I "其中■是自然对数的底数.（I ）若用在4刈上是单调增函数，求•的取值范围；（II ）当0」时，求整数科勺所有值，使方程心-丹4在肛亠1】上有解.(II)已知3C 的内角"・C 对应的边分别为若C 知函数的周期为兀.时，求函数 的值域;长春市十一高中2015-2016学年度高二下学期期中考试数学《理科）参考答案三、解答题（第17小题10分，第18. 19. 20. 21. 22小题各12分，共70分）17.解：（I ）过点P （l,0）且倾斜角为兰的直线/的方程为y = x-l.与圆相交，由儿何4意义知，CM 丄/,所以CM 所在直线方程为j = -x + 2 + V2 •解方程组y = x-tl 得点M 的坐标为 y = -x + 2 +丁2,（II ）当直线/有斜离时，设方程为y = k （x-l ）.当AABC 的面积最大时，CA 丄CB,所以圆心C （2,Q ）到直线y =心-1）的距离为1,一、选择题（每小 题5分，共60分）（5分）15.②④16. （-oo,0）13. 6414. 22k-41-kJ/+1 当直线/无斜离时，即直线所以=1,解得k=—4（8分）所以直线/方程为寿-（兀―1）和x = l.（10 分）18. W ：（ I ）由题意得，（2a + 2a + 3a + 66z + 7d ）xl0 = l,解得a = 0.005. （3 分）平均成绩约为 55x —+ 65x —+ 75x —+ 85x —+ 95x —= 76.520 20 20 20 20 2（II ） 90分及以上人数为40x — = 4人.20（6分）（8分）C 2 5 设“至少有一人成绩为优秀”为事件A,则P （A ） = 1-一寻=—Qo 2619.解：（I ）因为点（诃）在二次函数/（x ） = %2的图象上,所以S fl = n 2, （1分）（12 分）当 n>2 时，有 S,-=S — 1）2,所以色二 S“—S”_ 严卅一仪_］）2 = 2〃 —1,（3 分）71 71 ,入 71 “ 7龙 1 , • s 兀、八,所以石5力+石所以■2~Sin(2x + _6)~-<A + -< —,所以 A + - = —,所以 A =—. 6 6 6 6 6 3由余弦定理/ =b 2 +c 2 -2bccosA ,即 \ 6 = b 2 +c 2+bc ,所以 16 = (Z? + c)2 -be , 因为b + c = 5,所以bc = 9 ,所以S M8C = —/?csinA = —x9xsin —= —V3 (12 分) 321.解：（I ）因为A （O,1）为椭圆的一个顶点，所以b = l,又离心率为―，即£ =2a 2b = \所以解方程组\-=— 得a = Ji,b = \,c = \,所以椭圆方程为—+ /=1.（4分）a 2 2a 1=h 2+c 2（9分）又 di = S] = 1,而 Q] = 2x1 —1 = 1, a n =2n-l 成立，数列｛%｝的通项公式为：a n =2n-l.（4分） （5分）(II)由(1)7；=丄+ A + 2 + - +丝二① "2 2223 T所以訊专+尹歹352/?-3 2n-l+ ••• + - + 一 22” c”+i一 一 1 丁 1 』1 1 11 ）①-②，訐飞+片尹+尹尹+…+討 1 2〃一12”-1) 2 1所以 7；=3-2n + 3（12 分）] V320.解：(I ) /(兀)= cos? 0r + V5sinMcosM = —(l + cos2mv) + ^sin2M 2 21+-•（3分）因为"m>。

第Ⅰ卷（共 60分）一、选择题：本题共12小题，每小题5分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.1．若12z i =+，23()z ai a =+∈R ，12z z +的和所对应的点在实轴上，则a 为（ ）A ．3B ．2C ．1D ．1-2．已知角α的终边在直线y =上，则sin 2α=（ ）A ．2B ．C ．D ．12±3．观察下列各式：52252-2===…．若=n m -=（ ） A ．43B ．57C ．73D ．914．心脏每跳动一次，就完成一次收缩和舒张.心脏跳动时，血压在增大或缩小，并呈周期性变化，血压的最大值和最小值分别称为收缩压和舒张压.某人的血压满足函数()11025sin(150)p t t π=+，其中()p t 为血压(单位：mmHg )，t 为时间(单位：min )，则相邻的收缩压和舒张压的时间间隔是（ ） A ．1150B ．1110C ．170D ．1755．α､β是两个不重合的平面，在下列条件下，可判定//αβ的是（ ） A ．α､β都平行于直线l ､mB ．α内有三个不共线的点到β的距离相等C ．l ､m 是α内的两条直线且l β//，//m βD ．l ､m 是两条异面直线且//l α，//m α，l β//，//m β长春市十一高中2020-2021学年度高二下学期第二学程考试 数 学 试 题6．对两个变量x ，y 进行回归分析，得到组样本数据()11,x y ，()22,x y ，，(),n n x y ，则下列说法不正确的是（ ）A ．由样本数据得到的回归直线方程ˆˆˆy bx a =+必经过样本中心点(),x yB ．相关指数2R 越大，残差的平方和越小，其模型的拟合效果越好C ．若线性回归方程为ˆ0.610yx =+，当解释变量x 每增加1个单位时，预报变量y 平均增加0.6个单位D ．变量x ，y 相关性越强，相关系数r 越接近17．已知双曲线两条渐近线方程为y x =±，并且经过点，则其标准方程为（ ）A ．22144x y -=B ．22144-=y xC ．221332x y -= D ．221152y x -= 8．已知sin 33πα⎛⎫+= ⎪⎝⎭，则cos 23πα⎛⎫-= ⎪⎝⎭（ ） ABC ．13D ．13-9．若函数()ln mf x x m x x=+-在区间[]35，上不是单调函数，则m 的取值范围是（ ） A ．92546⎛⎫ ⎪⎝⎭，B ．()8+∞， C ．256⎡⎫+∞⎪⎢⎣⎭， D ．984⎡⎫⎪⎢⎣⎭，10．中国折叠扇有着深厚的文化底蕴.如图（2），在半圆O 中作出两个扇形OAB 和OCD ，用扇环形ABDC （图中阴影部分）制作折叠扇的扇面.记扇环形ABDC 的面积为1S ，扇形OAB 的面积为2S ，当1S 与2S时，扇面的形状较为美观，则此时弧CD 与弧AB 的长度之比为（ ）A 51+ B 51- C ．35 D 5211．已知()1,0A x ，()2,0B x 两点是函数()2sin()1(0,(0,))f x x ωϕωϕπ=++>∈与x 轴的两个交点，且满足12min3x x π-=,现将函数()f x 的图像向左平移6π个单位，得到的新函数图像关于y 轴对称，则ϕ的可能取值为（ ） A ．6π B ．3πC ．23π D ．56π 12．已知函数()f x 的定义域为,22ππ⎛⎫- ⎪⎝⎭，其导函数满足()cos ()sin 0f x x f x x '+<，则关于x 3()2cos 6x f x π⎛⎫<⎪⎝⎭的解集为（ ） A ．,32ππ⎛⎫ ⎪⎝⎭ B ．,62ππ⎛⎫⎪⎝⎭ C ．,63ππ⎛⎫-- ⎪⎝⎭ D ．,26ππ⎛⎫-- ⎪⎝⎭第Ⅱ卷（共 90分）二、填空题：本题共4小题,每小题5分,共20分. 13．已知tan 2θ=-，则2sin sin cos θθθ-=________．14．已知函数()(1)x f x x e =-，则()f x 在点(1,0)处的切线方程为___________. 15．设a ，b ，c 分别为ABC ∆内角A ，B ，C 的对边.233a b c-=222a cb ac+-的取值范围为______________．16．天文学家卡西尼在研究土星及其卫星的运行规律时发现：平面内到两个定点的距离之积为常数的点的轨迹是卡西尼卵形线（Cassini Oval ）．在平面直角坐标系中，设定点为1(,0)F c -，2(,0)F c ，点O 为坐标原点，动点(,)P x y 满足212PF PF a ⋅=（0a ≥且为常数），化简得曲线222224:4E x y c x c a ++=+．下列四个命题中，正确命题的序号是_____________．①曲线E 既是中心对称又是轴对称图形； ②当a c =时，||PO 的最大值为2a ； ③12PF PF +的最小值为2a ； ④12F PF △面积不大于212a ． 三、解答题：本题共6小题,第17题10分，其余各题每题12分，共70分. 17．已知函数()2sin cos 23sin cos 44f x x x x x ππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭ （1）求函数()f x 的对称轴方程； （2）将函数()f x 的图象向右平移3π个单位长度，得到函数()g x 的图象，当0,2x π⎡⎫∈⎪⎢⎣⎭，求()g x 的值域．18．如图，在以A 、B 、C 、D 、E 为顶点的五面体中，AD ⊥平面ABC ，//AD BE ，22AC =，244AB BE AD ===.ABC 的面积4S =且BAC ∠为锐角.（1）求证：AC ⊥平面BCE ； （2）求三棱锥B DCE -的体积V .19．已知ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，()3cos cos 2A CB -+=，设(),m b c =，(),n a b =且//m n ．（1）求角B 的大小；（2）延长BC 至D ，使5BD =，若ACD △的面积S =AD 的长．20．2021年，某省将实施新高考，2018年秋季入学的高一学生是新高考首批考生，新高考不再分文理科，采用33+模式，其中语文、数学、外语三科为必考科目，满分各150分，另外，考生还要依据想考取的高校及专业的要求，结合自己的兴趣爱好等因素，在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试（6选3），每科目满分100分.为了应对新高考，某高中从高一年级1000名学生（其中男生550人，女生450人）中，采用分层抽样的方法从中抽取n 名学生进行调查.（1）已知抽取的n 名学生中含女生45人，求n 的值及抽取到的男生人数；（2）学校计划在高一上学期开设选修中的“物理”和“历史”两个科目，为了了解学生对这两个科目的选课情况，对在（1）的条件下抽取到的n 名学生进行问卷调查（假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目），下面表格是根据调查结果得到的22⨯列联表，请将下面的列联表补充完整，并判断是否有95%的把握认为选择科目与性别有关？说明你的理由；（3）在抽取到的45名女生中，在（2）的条件下，按选择的科目进行分层抽样，抽出6名女生，了解女生对“历史”的选课意向情况，在这6名女生中再抽取3人，求这3人中选择“历史”的人数为2人的概率. 参考数据：（参考公式：()()()()()22n ad bc K a b c d a c b d -=++++，其中n a b c d =+++）21．已知椭圆C 的中心在原点，焦点在x 轴上，椭圆长轴两个端点间的距离与两个焦点之间的距离的差为1). （1）求椭圆C 的方程；（2）过点(1,0)作直线l 交C 于P ､Q 两点，试问：在x 轴上是否存在一个定点M ，使MP MQ ⋅为定值？若存在，求出这个定点M 的坐标；若不存在，请说明理由.22.已知函数.ln )1ln()(a x ae x f x ++-=（1）若)(x f 在0=x 处取得极值，求a 的值及函数)(x f 的单调区间； （2）若1)(≥x f ，求a 的取值范围.长春市十一高中2020-2021学年度高二下学期第二学程考试数学文科参考答案一、选择题二、填空题 13.6514.e e 0x y15.()()0,216.①②④三、解答题17．【答案】（1）对称轴方程为x 212k ππ=+，k ∈Z ．（2）[ 【详解】（1）∵函数f （x ）＝2sin x cos x （x 4π+）cos （x 4π+）＝sin2x （2x 2π+）＝sin2x x ＝2sin （2x 3π+），∴令2x 3π+=k π2π+，求得x 212k ππ=+，k ∈Z ，故函数f （x ）的对称轴方程为x 212k ππ=+，k ∈Z ． ---------------5分 （2）()=f 2sin 22sin 23333g x x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫-=-+=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦令22[,)333t x πππ=-∈-则[2s n i t ∈，故()g x 的值域为[ ---------------10分18．【详解】（1）证明：由1sin 2ABCSAB AC BAC =⋅⋅∠=14sin 42BAC ⨯⨯∠=，解得sin 2BAC ∠=，又BAC ∠为锐角，所以π4BAC ∠=.在ABC 中，由余弦定理可得，2222cos BC AB AC AB AC BAC =+-⋅⋅∠2242482=+-⨯⨯=，即BC =所以ABC 为等腰三角形，且π4CBA CAB ∠=∠=，故π2ACB ∠=，即AC CB ⊥.//,EB DA DA ⊥平面ABC ，BE ∴⊥平面ABC ，而AC ⊂平面ABC ，AC BE ∴⊥，又AC CB ⊥，BEBC B =，BE ⊂平面BCE ，CB ⊂平面BCE ，AC ∴⊥平面BCE . ---------------6分（2）由//AD BE ，利用等体积法，可得B DCE V -D ECB A BCE E ACB V V V ---===， 因为BE⊥平面ABC ，2BE =，4ABCS=，所以E ACB V -184233=⨯⨯=， 故三棱锥B DCE -的体积为83. ---------------12分19．【详解】（1）由()3cos cos 2A C B -+=可知()()3cos cos 2A C A C --+=， 即3cos cos sin sin cos cos sin sin 2A C A C A C A C +-+=， 可得3sin sin 4A C =． 由//m n 可得20b ac -=，由正弦定理可知23sin sin sin 4B AC ==，因为()0,πB ∈，所以sin B =，因此π3B =或2π3．分别代入()3cos cos 2A CB -+=，可知当2π3B =时，()cos 2A C -=，不成立．因此π3B =． ---------------6分（2）由π3B =可知()cos 1A C -=，即A C =， 因此ABC 为等边三角形，即a b c ==，()()112πsin 5sin 5223ACD S AC CD ACD b a a a =⋅∠=-=-=△ 整理可得()54a a -=，即254a a -=-， 由余弦定理可知，在ABD △中，22222π2cos255255213AD AB BD AB BD c c a a =+-⋅⋅=+-=+-=，因此AD ---------------12分20【详解】解：（1）由题意，根据分层抽样的方法，可得451000450n =，解得100n =， 所以男生人数为：100550551000⨯=人.100n =，男生人数为：55人； ---------------2分 （2）由（1）中得知；男生人数为55人，选择“历史”的有10人，因此选择“物理”的有551045-=人；男生人数为45人，选择“物理”的有30人，因此选择“历史”的有453015-=人，所以22⨯列联表为：22100(45153010) 3.030 3.84175254555K ⨯⨯-⨯==<⨯⨯⨯.所以没有95%的把握认为选择科目与性别有关. ---------------4分 （3）选择物理与选择历史的女生人数的比为2：1，所以按分层抽样有4人选择物理，设为a ，b ，c ，d ，2人选择历史，设为A ，B ，..从中选取3人，共有20种选法，可表示为abc ，abd ，acd ，bcd ，abA ，abB ，acA ，acB ，adA ，adB ，bcA ，bcB ，bdA ，bdB ，cdA ，cdB ，aAB ，bAB ，cAB ，dAB.其中有2人选择历史的有aAB ，bAB ，cAB ，dAB 4种， 故这3人中有2人选择历史的概率为41.205p == ---------------12分 21.【答案】（1）2212x y +=；（2）存在，定点5,04M ⎛⎫ ⎪⎝⎭.【详解】（1）由题意得：221)2a c c e a ⎧-=⎪⎨==⎪⎩，解得1a c ⎧=⎪⎨=⎪⎩222211b a c =-=-=， 所以椭圆C 的方程为：2212x y +=. ---------------4分（2）当直线l 不与x 轴重合时，可设直线l 的方程为：1x ky =+，1122(,),(,)P x y Q x y ，联立直线与曲线方程22221x y x ky ⎧+=⎨=+⎩，整理得：()222210k y ky ++-=，则222(2)4(2)(1)880k k k ∆=-+-=+>，1221222212k y y k y y k ⎧+=-⎪⎪+⎨⎪⋅=-⎪+⎩，假设存在定点(,0)M m ，使得MP MQ ⋅为定值，则()()()()11221212,,MP MQ x m y x m y x m x m y y ⋅=-⋅-=--+()()1211ky m ky m =+-+-()()2212121(1)(1)k y y k m y y m =++-++-()2222212(1)(1)22k k m m k k +-=--+-++222(23)1(1)2m k m k --=+-+ ()222(23)2(54)(1)2m k m m k -++-=+-+ =2222545423(1)2+2+2m m m m m k k ---+-+=-+. 当且仅当540m -=，即54m =时，716MP MQ ⋅=-(为定值)，这时5,04M ⎛⎫ ⎪⎝⎭， 当直线l 与x 轴重合时，此时(P ，Q ，(),0MP m =-，(2,0)MQ m =， 22MP MQ m ⋅=-， 当54m =时，716MP MQ ⋅=-(为定值)，满足题意. 所以存在定点5,04M ⎛⎫ ⎪⎝⎭使得对于经过(1,0)点的任意一条直线l 均有716MP MQ ⋅=-(恒为定值). ---------------12分22.【答案】（1）2212x y +=；（2）存在，定点5,04M ⎛⎫ ⎪⎝⎭. 【详解】(1)分），），增区间为（的减区间为（解得解得令时，当时，当，分）上单调递增，在（令得由8----------.00,1-)(,01,0)(,0,0)(,0)(0,0)(010)0(41-)(0)2()(,1)1()(,11)1()(.1,0)0(,11)(,ln )1ln()(''''''∞+∴<<-<>>>><<<-∴=---------------∞+∴>+=∴-+=+-+=∴=∴=--=++-=x f x x f x x f x g x x g x g x g x e x g x e x g x x e x f a f x ae x f a x ae x f x x x x x（2)[)分，的取值范围是综上，满足题意时，当，满足题意故）知时，由（当不合题意时，当12.1.11)1ln(ln )1ln()(1.1)(,1)0()(11.,1ln )0(10min ---------------∞+=-+≥+->++-=>≥===<+=<<a x x x e a x ae x f a x f f x f a a a f a x x。

吉林省长春市第一中学2020-2021学年高二下学期期中考试数学（理）试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．已知i 为虚数单位，复数11i -的虚部是（ ）. A ．12B ．12- C ．1i 2D ．1i 2-2成立，只需证（ ）A ．22<B ．22<C ．22<D ．22(< 3．已知随机变量ξ服从正态分布()22,N σ，若(3)0.84ξ<=P ，则(1)P ξ≤=（ ）A ．0.16B ．0.32C ．0.68D ．0.844．如图是函数()y f x =的导函数()f x '的图象，则下面判断正确的是（ ）A ．在区间()2,1-上()f x 是增函数B ．在区间()1,3上()f x 是减函数C ．在区间()4,5上()f x 是增函数D ．在区间()3,5上()f x 是增函数5．设~(,)B n p ξ，12E ξ=，4D ξ=，则,n p 的值分别为 （ ） A ．18，23B ．36,13C ．36，23D ．18，136．一车间为规定工时定额，需要确定加工零件所花费的时间，为此进行了4次试验，测得的数据如下根据上表可得回归方程9.49.1y x =+，则实数a 的值为（ ） A ．37.3B ．38C ．39D ．39.57．函数3223125y x x x =--+在[]2,1-上的最大值、最小值分别是（ ） A ．12,15-B ．1,8-C ．5,16-D ．12,8-8．利用数学归纳法证明不等式()11112321nf n ++++<-（2n ≥，n *∈N ）的过程中，由n k =变到1n k =+时，左边增加了（ ） A ．1项 B ．k 项 C ．12k -项D ．2k 项9．甲、乙二人进行围棋比赛，采取“三局两胜制”，已知甲每局取胜的概率为23，则甲获胜的概率为 ( )．A ．22213221333C ⎛⎫⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭B ．22232233C ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭C ．22112221333C ⎛⎫⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭D ．21112221333C ⎛⎫⎛⎫⎛⎫+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭10．已知函数()f x 为偶函数，且0x ≥时，1()sin 2f x x x =+，则关于x 的不等式()(21)f x f x >-的解集为（ ）A ．{|13}x x <<B ．{|1}<x xC ．1{|3x x <或1}x >D ．1{|1}3x x << 11．已知()()()()()()*1232,f x x x x x n n n N =++++≥∈，其导函数是()f x '，若()()10n f a f '-=，则50a =（ ）A ．150!B ．150C ．50D ．50!12．已知可导函数()()f x x R ∈满足()()f x f x '>，则当0a >时，()f a 和(0)a e f 的大小关系为（ ） A ．()(0)a f a e f > B ．()(0)a f a e f <C ．()(0)a f a e f =D ．()(0)a f a e f ≤二、填空题13．一个物体的位移s （米）与时间t （秒）的关系为2210s t t =+-，则该物体在3秒末的瞬时速度是______米/秒 14．曲线313y x =在1x =处切线的倾斜角为______． 15．设1()cos 0x f x x x ≤≤=<⎪⎩，，则12()f x dx π-=⎰________.16．下列各命题中，正确的是______． （1）若()f x 是连续的奇函数，则()0aaf x dx -=⎰（2）若()f x 是连续的偶函数，则()()02aaaf x dx f x dx -=⎰⎰（3）若()f x 在[],a b 上连续且恒为正，则()0baf x dx >⎰（4）若()f x 在[],a b 上连续且()0baf x dx >⎰，则()f x 在[],a b 上恒为正．三、解答题17．为了解某班学生喜爱打篮球是否与性别有关，对本班45人进行了问卷调查得到了如下的列联表：已知在全部45人中随机抽取1人，是男同学的概率为59（1）请将上面的列联表补充完整；（2）是否有99.9%的把握认为喜爱打篮球与性别有关，请说明理由．附参考公式：22()()()()()n ad bc K n a b c d a b c d a c b d -==+++++++，18．已知曲线2()2f x ax =+在1x =处的切线与230x y -+=平行． （1）求()f x 的解析式（2）求由曲线()f x 与3,0,2y x x x ===所围成的平面图形的面积． 19．已知函数()322f x x ax =++，2x =是()f x 的一个极值点，求：（1）实数a 的值；（2）()f x 在区间[]1,3-上的最大值和最小值．20．从某小组的5名女生和4名男生中任选3人去参加一项公益活动. (1)求所选3人中恰有一名男生的概率(2)求所选3人中男生人数ξ的分布列及数学期望 21．已知函数()31(),3f x x ax b a b R =++∈在2x =处取得极小值43-．（1）求函数()f x 的单调增区间；（2）若3211033x ax b m m ++≤++对[4,3]x ∈-恒成立，求实数m 的取值范围． 22．已知函数()()()3221132,32f x x x a a x b a b R =---+-∈.（Ⅰ）若函数()f x 在区间()1,+∞上是单调函数，求a 的取值范围； （Ⅱ）若函数()f x 在区间()1,1-上不是单调函数，求a 的取值范围．参考答案1．A 【解析】11i 11i 1i (1)(1)22i i +==+--+， 则其虚部为12， 本题选择A 选项.2．C 【解析】分析：不等式两边同时平方要求两边都是正数，再结合分析法即可.因为不等式两边为负数，故变形为证明：22< 即可，故选C.点睛：本题是易错题，证明不等式的左右两边大小关系，在选择两边同时平方时要注意不等号两边是否同时为正数. 3．A 【分析】根据正态分布的对称性进行求解即可. 【详解】由(3)0.84(3)10.840.16P P ξξ<=⇒≥=-=， 因为正态分布()22,N σ的对称轴为：2x =，所以(1)(3)0.16P P ξξ≤=≥=. 故选：A 【点睛】本题考查了正态分布对称性的应用，考查了数学运算能力，属于基础题. 4．C 【分析】利用导数与函数单调性的关系即可求解.由导函数()f x '的图象知在区间()4,5上，()0f x '>， 所以函数()f x 在()4,5上单调递增． 故选：C ． 【点睛】本题考查了由导数的图像研究函数的单调性，需掌握导数与函数单调性的关系，属于基础题. 5．A 【分析】由ξ～B （n ，p ），E ξ＝12，D ξ＝4，知np ＝12，np （1﹣p ）＝4，由此能求出n 和p ． 【详解】∵E ξ＝12，D ξ＝4， ∴np ＝12，np （1﹣p ）＝4， ∴n ＝18，p 23=． 故选A ． 【点睛】本题考查离散型随机变量的期望和方差，解题时要注意二项分布的性质和应用． 6．C 【分析】求出(),x y ，代入回归方程，即可得到实数a 的值． 【详解】根据题意可得：2345 3.54x +++==,26495412944a ay ++++==，根据回归方程过中心点(),x y 可得：1299.4 3.59.14a+=⨯+，解得：39a =； 故答案选C 【点睛】本题主要考查线性回归方程中参数的求法，熟练掌握回归方程过中心点(),x y 是关键，属于基础题． 7．D求得导函数，令'0y =即可求得极值点．再代入端点值即可求得最大值与最小值． 【详解】函数3223125y x x x =--+所以()()2'6612612y x x x x =--=+-，令'0y =解方程可得121,2x x =-=由表格可知，函数3223125y x x x =--+在[]2,1-上的最大值为12，最小值为8-所以选D 【点睛】本题考查利用导数求函数在某区间内的最大值与最小值，注意函数端点处对函数最值的影响，属于基础题． 8．D 【分析】依题意，当1n k =+时，不等式左边为11111111232122121k k k k ++++⋯++++⋯+-+-，与n k =时不等式的左边比较即可得到答案. 【详解】用数学归纳法证明等式()11112321nf n ++++<-（2n ≥，n *∈N ）的过程中， 假设n k =时不等式成立，左边11112321k =++++-， 则当1n k =+时，左边11111111232122121k k kk +=++++++++-+-，∴由n k =递推到1n k =+时不等式左边增加了：111122121k k k +++++-，共()121212k k k +--+=项.故选：D ． 【点睛】本题考查数学归纳法，考查分析、解决问题的能力，属于基础题.. 9．C 【分析】先确定事件“甲获胜”包含“甲三局赢两局”和“前两局甲赢”，再利用独立重复试验的概率公式和概率加法公式可求出所求事件的概率． 【详解】事件“甲获胜”包含“甲三局赢两局”和“前两局甲赢”，若甲三局赢两局，则第三局必须是甲赢，前面两局甲赢一局，所求概率为2121233C ⎛⎫⋅⋅ ⎪⎝⎭，若前两局都是甲赢，所求概率为223⎛⎫ ⎪⎝⎭，因此，甲获胜的概率为22112221333C ⎛⎫⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，故选C ． 【点睛】本题考查独立重复事件的概率，考查概率的加法公式，解题时要弄清楚事件所包含的基本情况，考查分类讨论思想，考查计算能力，属于中等题． 10．D 【详解】 由题得1()1cos 02f x x '=+>，所以函数()f x 在[0,)+∞单调递增，由于函数f(x)是偶函数，所以不等式()()21f x f x >-转化为()()21fx f x >-，所以2212144113x x x x x x >-∴>-+∴<<，故选D.11．B 【分析】求出()1f '-和()0f ，可得出n a 的表达式，进而可计算得出50a 的值. 【详解】()()()()()123f x x x x x n =++++，其中2n ≥且n *∈N ，()()()()()()()2313f x x x x n x x x n '∴=++++++++()()()121x x x n ++++-，()()11231f n '∴-=⨯⨯⨯⨯-，()()01231f n n =⨯⨯⨯⨯-⨯，则()()110n f a f n'-==， 因此，50150a =. 故选：B. 【点睛】本题考查导数值的计算，考查计算能力，属于中等题. 12．A 【分析】根据条件构造函数()()xf xg x e =，求导可知()g x 单调递增，比较(),(0)g a g 的大小，可得()f a 和(0)a e f 的大小关系.【详解】解：令()()x f x g x e =，则'''2()()()()()x x x xf x e f x e f x f xg x e e--==，因为()()f x f x '>，所以'()0g x >，所以()g x 在(),-∞+∞上单调递增；因为0a >，所以()(0)g a g >，即()(0)a f a f e e>，即()(0)af a e f >. 故选：A. 【点睛】本题考查构造函数法比较大小，考查利用导数求函数的单调性，属于基础题. 13．4 【分析】首先求出函数的导数，求出3t =时的导数值，利用导数的定义即可求解. 【详解】由题意，物体的位移s （米）与时间t （秒）的关系为2210s t t =+-， 则102s t '=-，当3t =时，10234s '=-⨯=，即3秒末的瞬时速度为4米/秒. 故答案为：4 【点睛】本题考查了导数的概念、基本初等函数的导数公式以及导数的运算法则，属于基础题. 14．4π 【分析】求出导函数，再求出1x =的导数值，利用导数的几何意义即可求解. 【详解】313y x =，21,1x y x y =''∴==， ∴切线的倾斜角α满足tan 1α=， 0απ≤<，4πα∴=．故答案为：4π 【点睛】本题考查了导数的几何意义、基本初等函数的导数公式，属于基础题. 15．14π+【解析】 【分析】由题意得，122()cos f x dx xdx ππ--=+⎰⎰，根据定积分的几何意义可知，可得1表示的是四分之一的圆的面积，再根据微积分基本定理，可求2cos xdx π-⎰，最后相加即可得到结果. 【详解】由题意得，122()cos f x dx xdx ππ--=+⎰⎰，根据定积分的几何意义可知，1表示的是在x 轴上方的半径为1的四分之一圆的面积，如图（阴影部分）：故14π=，又022cos sin |sin 0sin()12xdx x πππ--==--=⎰，所以10022()cos 14f x dx xdx πππ--=+=+⎰⎰.所以本题答案为14π+. 【点睛】本题考查微积分基本定理和定积分的几何意义，利用定积分准确表示封闭图形的面积并正确计算是解答的关键，属基础题. 16．（1）（2）（3） 【分析】若()f x 是连续的奇函数，根据奇函数的对称性及定积分的几何意义可判断（1）；若()f x 是连续的偶函数，根据偶函数的对称性及定积分的几何意义可判断（2）；若()f x 在[],a b 上连续且恒为正，根据其单调性即可判断出是否正确，进而判断（3）；对于（4），可举出反例即可否定． 【详解】 对于（1），()f x 是连续的奇函数，()()()()()00aaaaaaf x dx f x dx f x dx f x dx f x dx --=+=-+=∴⎰⎰⎰⎰⎰，故（1）正确； 对于（2），()f x 是连续的偶函数，()()()()002a a aaaf x dx f x dx f x dx f x dx --∴=+=⎰⎰⎰⎰，故（2）正确： 对于（3），()f x 在[],a b 上连续且恒正，()00bb aaf x dx dx >∴=⎰⎰，故（3）正确；对于（4），举反例24321114044x x dx --==->⎰， 而()3f x x =在区间[)1,0-上小于0，即函数()f x 在区间[]1,2-上不恒为正，故（4）不正确． 故答案为：（1）（2）（3） 【点睛】本题考查了根据函数的性质求定积分、定积分的概念，属于基础题. 17．（1）见解析（2）见解析 【分析】（1）根据题意，补充列联表即可；（2）根据表中数据，计算K 2，对照临界值得出结论； 【详解】（1）根据题意，男同学有545259⨯=人 补充列联表如下：（2）根据表中数据，计算()2245201555108913.6137.8792520202580K ⨯⨯-⨯==≈⨯⨯⨯＞， 故有99.9%的把握认为喜爱打篮球与性别有关 【点睛】本题考查了列联表与独立性检验的应用问题，考查计算能力，是基础题． 18．（1）()22f x x =+；（2）1【解析】 【分析】（1）求得()f x 的导数，由两直线平行的条件可得斜率相等，求得a ，进而得到所求解析式；（2）由图象可得()()1222012332S xx dx x x dx =+-+--⎰⎰，运用定积分公式，计算可得所求值． 【详解】（1）由题意得：()2f x ax '= 22a ∴=，解得：1a =()22f x x ∴=+（2）在平面直角坐标系中画出曲线图形如下图所示：则所求面积为：()()1222322301121331233222013223S x x dx x x dx x x x x x x ⎛⎫⎛⎫=+-+--=+-+-- ⎪ ⎪⎝⎭⎝⎭⎰⎰138312642132323⎛⎫=+-+-----= ⎪⎝⎭【点睛】本题考查导数的运用：求切线斜率；考查定积分的运用：求面积，考查直线方程的运用，属于基础题．19．（1）3a =-；（2）最大值是2，最小值是2-． 【分析】（1）根据(2)0f '=解得3a =-； （2）令()0f x '=，得10x =，22x =．列出当x 变化时()f x '，()f x 的变化情况表，根据表格可得答案. 【详解】（1）因为()232f x x ax '=+，()f x 在2x =处有极值， 所以()20f '=，即3440a ⨯+=，所以3a =-．经检验3a =-时，32()32f x x x =-+在2x =时取得极小值2-， 所以3a =-.（2）由（1）知3a =-，所以()3232f x x x =-+，()236f x x x '=-．令()0f x '=，得10x =，22x =．当x 变化时()f x '，()f x 的变化情况如下表：由上表可知()f x 在区间[]1,3-上的最大值是2，最小值是2-． 【点睛】本题考查了由函数的极值点求参数，考查了利用导数求函数的最值，属于基础题.20．（1）1021；（2）见解析. 【分析】（1）先求出所选3人中恰有一名男生的选法种数，然后利用古典概型的概率公式计算出所求事件的概率；（2）ξ的可能取值为0、1、2、3，然后利用超几何分布概率公式求出相应的概率，即可得出随机变量ξ的分布列，并计算出其数学期望. 【详解】（1）从某小组的5名女生和4名男生中任选3人，共有3984C =种，所选3人中恰有一名男生，有215440C C =种，故所选3人中恰有一名男生的概率为40108421=； （2）随机变量ξ的可能取值有0、1、2、3，()35395042C P C ξ===，()21543910121C C P C ξ===，()1254395214C C P C ξ===， ()34391321C P C ξ===.所以，随机变量ξ的分布列如下表所示：因此，随机变量ξ的数学期望为5105140123422114213E ξ=⨯+⨯+⨯+⨯=. 【点睛】本题考查古典概型概率公式的应用，考查离散型随机变量分布列及其数学期望，在列分布列时，要弄清随机变量所满足的分布列类型，结合相应公式求出事件的概率，进而得出概率分布列以及数学期望，考查计算能力，属于中等题.21．（1）增区间为(,2)-∞-，(2,)+∞；（2）2m ≥或3m ≤-【解析】 【分析】(1)首先求得函数的解析式，然后结合导函数的解析式即可确定函数的单调递增区间； (2)首先求得函数()f x 的最大值，然后由恒成立的条件得到关于m 的不等式，求解不等式可得实数m 的取值范围. 【详解】（1） ()2f x x a '=+，由()20f '=得4a =-，由4(2)3f =-得4b =，则21()443f x x x =-+， 令2()40f x x '=->得2x >或2x <-()f x ∴的增区间为(,2)-∞-，(2,)+∞；（2）由4284(4),(2),(2),(3)1333f f f f -=--==-=()f x 的最大值为328，要使3211033x ax b m m ++≤++对[4,3]x ∈-恒成立，只要2max 10()3f x m m ≤++就可以了，即2281033m m ≤++，解得2m ≥或3m ≤- 所以实数m 的取值范围是2m ≥或3m ≤-．【点睛】本题主要考查导数研究函数的单调性，由不等式恒成立求解参数的取值范围等知识，意在考查学生的转化能力和计算求解能力. 22．（Ⅰ）[]1,2；（Ⅱ）330,,322⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭. 【分析】（Ⅰ）由题意得出()0f x '≥对任意的()1,x ∈+∞恒成立，利用参变量分离法得出2232a a x x -+≤-，求得函数2yx x 在区间()1,+∞上的值域，可得出关于a 的不等式，即可解得实数a 的取值范围；（Ⅱ）根据题意知，函数()y f x =在区间()1,1-上有极值点，然后解方程()0f x '=，得出11x a =-，22x a =-，根据极值点的定义得出关于a 的不等式，即可解得实数a 的取值范围. 【详解】 （Ⅰ）()()322113232f x x x a a x b =---+-，()()2232f x x x a a ∴=---+'，要使题意成立，必须且只需()()22320f x x x a a '=---+≥在区间()1,+∞上成立．即2232a a x x -+≤-，()1,x ∈+∞， 当()1,x ∈+∞时，函数2yx x 单调递增，则20y x x =->.2320a a ∴-+≤，解得12a ≤≤；（Ⅱ）解方程()22320x x a a ---+=，得11x a =-，22x a =-，依题意，方程()22320x x a a ---+=在区间()1,1-有根．故有11112a a a -<-<⎧⎨-≠-⎩或12112a a a-<-<⎧⎨-≠-⎩，解得330,,322a ⎛⎫⎛⎫∈⋃ ⎪ ⎪⎝⎭⎝⎭.因此，实数a 的取值范围是330,,322⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭. 【点睛】本题考查利用函数在区间上的单调性求参数，考查化归与转化思想的应用，属于中等题.。

吉林省长春市十一高中2020-2021学年高二数学下学期第三学程考试试题理第Ⅰ卷（共 60分）一、选择题：本题共12小题，每小题5分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.1. 已知集合，，则（）A. B.C. D.2. 在复平面内，复数3-412ii+对应的点位于（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 已知命题，，命题，，则下列为真命题的是（）A. B. C. D.4．研究表明，我国研制的新冠灭活疫苗，人体接种这种疫苗需要接种两次，间隔2~4周，接种完第一剂以后，7天开始普遍产生抗体，接种完第二剂28天以后，中和抗体阳转率或者叫阳性率均达百分之百．也就是说，按照规范的免疫程序接种两剂我国研制的新冠灭活疫苗28天后，所有人都能产生足以抵抗新冠病毒的抗体，某研究所在500名志愿者身上进行了人体新冠灭活疫苗注射，接种完第一剂7天后发现这些志愿者均已经产生了稳定的免疫应答，这些志愿者的免疫反应蛋白M的数值X（单位：/mg L）近似服从正态分布()225,Nσ，且X在区间(10,40)内的人数占总人数的98%，则这500名志愿者中免疫反应蛋白M的数值不大于10mg/L的人数大约为（）A．5 B．10 C．50 D．1005．有红色、黄色小球各两个，蓝色小球一个，所有小球彼此不同，现将五球排成一行，颜色相同者不相邻，不同的排法共有（）种A．48 B．72 C．78 D．846．甲乙二人争夺一场围棋比赛的冠军，若比赛为“五局三胜”制，甲在每局比赛中获胜的概率均为23，且各局比赛结果相互独立，则在甲获胜得冠军的情况下，比赛进行了四局的概率为（ ）. A ．13B ．38C ．37D ．127．已知变量y 关于变量x 的回归方程为ln 0.24y b x =+，其一组数据如下表所示：若10e x =，则y 的值大约为（ ） A ．4.94 B ．5.74C ．6.81D ．8.048.已知平面向量a ，b 的夹角为3π，且对任意实数λ，a b a b λ-≥-恒成立，则:a b =（ ）A ．1:2B ．2:1C ．D9．某校高一年级研究性学习小组利用激光多普勒测速仪实地测量复兴号高铁在某时刻的速度，其工作原理是：激光器发出的光平均分成两束射出，在被测物体表面汇聚，探测器接收反射光，当被测物体横向速度为零时，反射光与探测光频率相同，当横向速度不为零时，反射光相对探测光会发生频移2sin p f νϕλ=，其中v 为测速仪测得被测物体的横向速度，λ为激光波长，ϕ为两束探测光线夹角的一半，如图，若激光测速仪安装在距离高铁1m 处，可近似计算sinϕ=≈0.02，发出的激光波长为1500nm （91nm 10m -=），某次检验中可测频移范围为99.50010⨯（1/h ）至910.00010⨯（1/h ），该高铁以运行速度（337.5km /h 至375km /h ）经过时，可测量的概率为（ ）A ．12B ．13C ．23D ．5610. 已知函数()f x 的导函数为()'f x ，e 为自然对数的底数，对x R ∀∈均有()()()'f x xf x xf x +>成立，且()22=f e ，则不等式()2x xf x e >的解集是A ．(),e -∞B ．(),e +∞C ．(),2-∞D ．11．已知n S 是数列{}n a 的前n 项和，若2021220210122021(12)x b b x b x b x -=++++，数列{}n a 的首项20211211122021,222n n n b b b a a S S ++=+++=⋅，则2021S =（ ） A ．12021-B ．12021C ．2021D ．2021-12．对于函数()y f x =，若存在区间[],a b ，当[],x a b ∈时，()f x 的值域为[],ka kb ，则称()y f x =为k 倍值函数．若()ln f x x x =+是k 倍值函数，则k 的取值范围为（ ） A ．10,e ⎛⎫ ⎪⎝⎭B ．1,e ⎛⎫+∞ ⎪⎝⎭C ．11,1e ⎛⎫+ ⎪⎝⎭D ．11,e ⎛⎫++∞⎪⎝⎭第Ⅱ卷（共90分）二、填空题：本题共4小题,每小题5分,共20分.13. 已知()f x 为奇函数，当0x <时，3()=2xf x ex e -+则曲线()y f x =在(1,(1))f 处切线方程是______. 14. 若3(2n x x的展开式中第四项为常数项，则n=_______.15. 我校5位同学报考了北京大学“强基计划”第I专业组，并顺利通过各项考核，已知5位同学将根据综合成绩和志愿顺序随机地进入教学类､物理学类､力学类这三个专业中的某一个专业，则这三个专业都有我校学生的概率是__________(结果用最简分数表示). 16．已知F1，F2分别为双曲线x2﹣＝1的左、右焦点，过F2且倾斜角为θ的直线与双曲线的右支交于A，B两点，记△AF1F2的内切圆O1的半径为r1，△BF1F2的内切圆O2的半径为r2，圆O1的面积为S1，圆O2的面积为S2，则______________①．θ的取值范围是（，）②．直线O1O2与x轴垂直③．若r1+r2＝2，则|AB|＝6 ④．S1+S2的取值范围是[2π，）三、解答题：本题共5小题,每题12分，共70分.17. 设三角形的内角､､所对的边长分别是､､，且222sin cos sin sin sin1B C A A C+=-+.（1）求的大小；（2）若不是钝角三角形，求2ac的取值范围.18.如图，在直三棱柱中，正方形边长为3，4BC=，，M是线段上一点，设．（1）若，证明：BD∥平面；（2）若二面角的余弦值为，求的值．19．国务院办公厅印发了《关于防止耕地“非粮化”稳定粮食生产的意见》，意见指出要切实稳定粮食生产，牢牢守住国家粮食安全的生命线.为了切实落实好稻谷､小麦､玉米三大谷物种植情况，某乡镇抽样调查了A 村庄部分耕地(包含永久农田和一般耕地)的使用情况，其中永久农田100亩，三大谷物的种植面积为90亩，棉､油､蔬菜等的种植面积为10亩；一般耕地50亩，三大谷物的种植面积为30亩，棉､油､蔬菜等的种植面积为20亩. （1）以频率代替概率，求A 村庄每亩耕地(包括永久农田和一般耕地)种植三大谷物的概率； （2）上级有关部门要恪促落实整个乡镇三大谷物的种植情况，现从本乡镇抽测5个村庄，每个村庄的三大谷物的种植情况符合要求的概率均为A 村庄每亩耕地(永久农田和一般耕地)种植三大谷物的概率.若抽测的村庄三大谷物的种植情况符合要求，则为本乡镇记1分，若不符合要求，记-1分.X 表示本乡镇的总积分，求X 的分布列及数学期望；（3）目前在农村的劳动力大部分是中老年人，调查中发现，80位中老年劳动力中有65人种植三大谷物，其余种植棉､油､蔬菜等农作物；20位青壮年劳动力中有15人种植需要技术和体力，短期收益大的棉､油､蔬菜等农作物，其余种植三大谷物.请完成下表，并判断是否有99.9%的把握认为种植作物的种类与劳动力的年龄层次有关？ 劳动力年龄层次种植情况 合计种植三大谷物 种植棉，油，蔬菜等 中老年劳动力 青壮年劳动力 合计附：()()()()()22n ad bc K a b c d a c b d -=++++，其中n a b c d =+++.()20P K k ≥ 0.100.050.0250.0100.0010k2.7063.841 5.024 6.635 10.82820. 已知抛物线：的焦点为，为坐标原点．过点的直线与抛物线交于，两点．（1）若直线与圆：相切，求直线的方程；（2）若直线与轴的交点为．且，，试探究：是否为定值？若为定值，求出该定值；若不为定值，试说明理由．21.已知函数()2222()ln ,()1ln (1)2,f x a x x ax g x a x a x x a R =-+=-+--∈. （1）当0a >时，求函数()f x 的单调区间；（2）若()()2f x g x ax ≤+恒成立，求实数a 的取值范围.22．在直角坐标系xOy 中，曲线C 1的参数方程为（t 为参数），以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 2的极坐标方程为ρsin 2θ＝4cos θ． （1）求曲线C 1和C 2的直角坐标方程； （2）已知点P （1，），曲线C 1与C 2相交于A ，B 两点，求||．23．已知函数()221f x x x =-++，x ∈R . （1）求函数()f x 的图象与直线6y =围成区域的面积；（2）若对于0m >，0n >，且4m n +=时，不等式()f x mn ≥恒成立，求实数x 的取值范围.数学（理）试卷答案一、选择题：本题共12小题，每小题5分.在每小题给出的四个选项中，只有一个选项 是符合题目要求的. 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C DCAABCBADAC二、填空题：本题共4小题,每小题5分,共20分. 13. 2y ex e =- 14. 【答案】5 15. 508116．②③④ 三、解答题：本题共5小题,每题12分，共70分. 17. 【答案】（1）3π；（2）[1,4]. 【详解】（1）因为222sin cos sin sin sin 1B C A A C +=-+ 所以222sin sin sin sin sin B A C A C =+- 由正弦定理，得所以又因为，所以；（2）因为，由，得：由正弦定理得当时，当时，所以.18.【答案】（1）证明见解析；（2）3 =4λ．【详解】（1）连接交于点N，连接，则M，N分别为和的中点，∴；∵BD⊄平面，平面；∴平面；（2）以C为原点，，，分别为x轴，y轴，z轴正方向建立空间直角坐标系，，，，设，其中；则，，，平面的法向量，平面的法向量；∴，．19． 【答案】（1）45；（2）分布列答案见解析，数学期望：3；（3）表格答案见解析，有99.9%的把握认为种植作物的种类与劳动力的年龄层次有关. 【详解】解：（1）设事件M 为“耕地(包括永久农田和一般耕地)种植三大谷物”， 则()90304100505P M +==+.所以A 村庄每亩耕地种植三大谷物的概率为4.5（2）由（1）知，每个村庄的三大谷物的种植情况符合要求的概率均为45由题意知,X 的所有可能取值为5,3,1,1,3,5---则()5415153125P X ⎛⎫=-=-= ⎪⎝⎭，()4154443155625P X C ⎛⎫=-=⨯-=⎪⎝⎭ ()232544321155625P X C ⎛⎫⎛⎫=-=⨯-=⎪ ⎪⎝⎭⎝⎭ ()3235441281155625P X C ⎛⎫⎛⎫==⨯-=⎪ ⎪⎝⎭⎝⎭()445442563155625P X C ⎛⎫⎛⎫==⨯-=⎪ ⎪⎝⎭⎝⎭()55541024553125P X C ⎛⎫===⎪⎝⎭则该乡镇的总积分X 的分布列为X-5 -3 -1 1 3 5P1312546253262512862525662510243125 ()()()()14325313125625625E X=-⨯+-⨯+-⨯+1282561024 1353 6256253125⨯+⨯+⨯=（3）劳动力年龄层次种植情况合计种植三大谷物种植棉､油､蔬菜等中老年劳动力65 15 80 青壮年劳动力 5 15 20 合计70 30 1002K的观测值2100(6515155)24.107.80207030k⨯⨯-⨯=≈⨯⨯⨯因为24.10710.828>所以有99.9%的把握认为种植作物的种类与劳动力的年龄层次有关.20. 【答案】（1）；（2），理由见解析；【分析】【详解】（1）由题意知：且圆半径为，圆心(0,0)O，即有在圆外，∴设直线为，则圆心到直线的距离，解之得：，即直线的方程为.（2）由过的直线与抛物线交于，两点，与轴的交点为，即斜率存在且，设直线为，有，联立直线方程与椭圆方程，有，可得，设，，即有，，，，， 由，，可得，， ∴，即可得为定值21.【答案】（1）增区间为(0,)a ，减区间为(,)a +∞；（2）[1,)+∞.【详解】（1）由题意，函数22()ln f x a x x ax =-+的定义域为(0,)+∞， 且2222(2)()()2a x ax a x a x a f x x a x x x -+++-=-+==-'，因为0a >，可得02aa -<<，令()0f x '>，即(2)()0x a x a +-<，解得0x a <<；令()0f x '>，即(2)()0x a x a +->，解得x a >，所以()f x 的增区间为(0,)a ，减区间为(,)a +∞.（2）由()()2f x g x ax ≤+恒成立，即()2()0g x ax f x +-≥恒成立，设2()()2()(2)ln ,(0)x g x ax f x ax a x x x ϕ=+-=+-->，只需函数min [()]0x ϕ≥， 由212(2)1(1)(21)()2(2)ax a x ax x x ax a x x x ϕ+---+=+--'==，①当0a ≤时，由于0x >，故()0x ϕ'<，此时()ϕx 在(0,)+∞上递减，因此min [()]x ϕ不存在，故min [()]0x ϕ≥不成立；②当0a >时，(1)(21)()ax x x x ϕ-+='，因为1102a -<<，令()0x ϕ'>，即(1)(21)0ax x -+>，解得1x a >；令()0x ϕ'<，即(1)(21)0ax x -+<，解得10x a <<，所以()x ϕ的减区间为10,a ⎛⎫ ⎪⎝⎭，増区间为1,a ⎛⎫+∞ ⎪⎝⎭，所以2min 111111[()](2)ln 1ln x a a a a a a a a ϕϕ⎛⎫⎛⎫⎛⎫==⋅+--=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 由min [()]0x ϕ≥，即111ln 0a a --≥，可得11ln 1a a ≤-， 令10t a=>，可得ln 1t t ≤-， 设()ln 1,0m t t t t =+->，可得1()10m t t'=+>，所以()m t 在(0,)+∞上为单调递增函数， 又由(1)0m =，所以01t <≤，即101a<≤，解得1a ≥， 综上所述，当1a ≥时，()()2f x g x ax ≤+恒成立，所以实数a 的取值范围是[1,)+∞.22．解：（1）曲线C 1的参数方程为（t 为参数），消去参数t 得：． 曲线C 2的极坐标方程为ρsin 2θ＝4cos θ，根据转换为直角坐标方程为y 2＝4x ．（2）曲线C 1的参数方程为（t 为参数），转换为标准式为（t 为参数），代入y 2＝4x ，得到：， 所以，．故．23．【答案】（1）6；（2）[)4,0,3⎛⎤-∞-+∞ ⎥⎝⎦.【解析】（1）由()3,14,123,2x x f x x x x x -≤-⎧⎪=+-<<⎨⎪≥⎩与6y =围成的区域是ABC ，如图所示，其中()2,6A -，()1,3B -，()2,6C ， 所以4AC =，B 到直线AC 的距离为3， 故所求面积为14362ABC S =⨯⨯=△.（2）因为0m >，0n >，且4m n +=， 所以22m n mn +⎛⎫≤ ⎪⎝⎭，即4mn ≤， 若不等式()f x mn ≥恒成立，则有()()max f x mn ≥，即()4f x ≥，解不等式2214x x -++≥，可得134x x ≤-⎧⎨-≥⎩或1244x x -<<⎧⎨+≥⎩或234x x ≥⎧⎨≥⎩， 解之得43x ≤-或0x ≥，所以实数x 的取值范围为[)4,0,3⎛⎤-∞-+∞ ⎥⎝⎦.附：什么样的考试心态最好大部分学生都不敢掉以轻心，因此会出现很多过度焦虑。

吉林省长春市北师大附属学校2020-2021学年高二数学下学期期中试题 文考试时间： 120分钟 满分： 150 分2021年5月10日一、选择题（本大题共12小题，每小题5分，共60分）1．已知命题P ：0x R ∃∈，032x x >，则P ⌝为 （ ） A ．0x R ∃∈，032x x ≤ B ．x R ∀∈，32>x x C ．0x R ∃∉，032x x ≤ D ．x R ∀∈，32≤x x2．计算1ii+= （ ）A ．1i --B ．1i -C ．1i -+D ．1i +3．已知x ，y 之间的一组数据：则y与x 的线性回归方程y bx a=+表示的直线必过点（ ）A ．（2，2）B ．（1.5，0）C ．（1，2）D ．（1.5，4）4．袋内有红球3个､白球2个，从中任取2个，则互斥而不对立的两个事件是 （ ）A ．事件A ：恰有1红球；事件B ：恰有2红球B ．事件A ：至少有1个红球；事件B ：至少有1个白球C ．事件A ：至少有1个红球；事件B ：全是红球D ．事件A ：至少有1个红球；事件B ：全是白球5．“1a =-”是“直线1x ay +=与1ax y +=平行”的 （ ）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件6．已知下列命题：①由独立性检验可知，有99%的把握认为物理成绩与数学成绩有关，若某人数学成绩优秀，则他有99%的可能物理成绩优秀；②在回归分析中，可用相关指数2R 的值判断模型的拟合效果，2R 越大，模型的拟合效果越好；③在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高；④若“p q ∧是假命题，p q∨是真命题，则命题p ，q 一真一假”．其中真命题的个数是 （ ）A ．4B ．3C ．2D ．17．在下面的表格中，每格填上一个数字后，使每一行成等差数列，每一列成等比数列，则a+b 的值是（ ） A ．1613 B ．1629 C ．1645 D ．85 8．如图是某学校抽取的学生体重的频率分布直方图，已知图中从左到右的前3个小组的频率满足：第一小组与第三小组的频率和是第二小组频率的2倍，第二小组的频数为15，则抽取的学生人数为 （ ）A ．30B ．45C ．60D ．120（ 第7题图） （第8题图）1221 1ab（第9题图）9．已知在边长为3的正方形ABCD 中，2AM MB =，则DM DB ⋅= （ ）A ．-17B ．-2C ．15D ．9 10．古希腊数学家欧几里德在公元前300年左右提出了欧几里 德算法，又叫辗转相除法．如右图，若输入m ，n 的值分别为 779，209，则输出的m = （ ）A ．19B ．20C ．21D ．2211．《周髀算经》中给出了：冬至、小寒、大寒、立春、雨水、 惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二节气的日 影长依次成等差数列的结论．已知某地立春与雨水两个节气的日影长分别为10.5尺和9.5尺，现在从该地日影长小于9尺的节 气中随机抽取2个节气进行日影长情况统计，则所选取这2个节 气中恰好有1个节气的日影长小于5尺的概率为 （ ）A ．37B ．47C ．1321D ．5712．如图，设椭圆1C ：22221x y a b +=（0a b >>）与双曲线2C ：22221x y m n-=（0m >，0n >）的公共焦点为1F ，2F ，将1C ，2C 的离心率分别记为1e ，2e ，点A 是1C ，2C 在第一象限的公共点，若点A 关于2C 的一条渐近线的对称点为1F ，则221222e e += （ ）A ．2B ．52C ．72D ．4r（ 第10题图）二、填空题（本大题共4小题，每小题5分，共20分）13．若复数221(2)z m m m i =-+--为纯虚数，则实数m 的值为________．14．已知一组数据4，2a ，3﹣a ，5，6的平均数为4，则a 的值是 ，这一组数据的方差是 ．15．如下图，九连环是我国从古至今广泛流传的一种益智游戏，它用九个圆环相连成串，以解开为胜．据明代杨慎《丹铅总录》记载：“两环互相贯为一，得其关捩，解之为二，又合面为一“．在某种玩法中，用a n 表示解下n （n ≤9，n ∈N *）个圆环所需移动的最少次数，若a 1＝1．且a n ＝1121,22,n n a n a n ---⎧⎨+⎩为偶数为奇数，则解下5个环所需的最少移动次数为 ．16．甲、乙两艘轮船都要在某个泊位停靠6小时，假定它们在一昼夜的时间段中随机地到达，则这两艘船中至少有一艘在停靠泊位时必须等待的概率是 ．三、解答题（本大题共6小题，共70分）17．（本小题10分）已知数列{}n a 是等比数列，公比q ＜1，前n 项和为S n ，若22a =，37S =． （1）求{}n a 的通项公式； （2）求证：S n ＜8．18．（本小题12分）已知ABC ∆内角A ，B ，C 所对的边分别为a ，b ，c ，22cos 2cos a B b A c +=． （1）求c 的值； （2）若3C π=，22a b +=ABC ∆的面积．19．（本小题12分）在直角坐标系xOy 中，直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧=+=t y t x 21232（t 为参数），以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为. 9)sin 9(cos 222=+θθρ（1）求直线l 的普通方程和曲线C 的直角坐标方程；（2）若直线l 与曲线C 交于M ，N 两点，设()2,0P ，求PM PN +的值．20．（本小题12分）如图，三棱柱ABC —A 1B 1C 1中， 底面ABC 为直角三角形，侧棱⊥1AA 底面ABC ，D 、E 分别是AB 、BB 1的中点，AA 1=AC =CB =2．（1）求证：1BC //平面1ACD ； （2）求三棱锥E —A 1DC 的体积．21．（本小题12分）某高校共有学生15000人，其中男生10500人，女生4500人，为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据（单位：小时）．（1）应收集多少位女生的样本数据？（2）根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图（如图所示），其中样本数据的分组区间为：[0,2]，（2,4]，（4,6]，（6,8]，（8,10]，（10,12]，试估计该校学生每周平均体育运动时间的平均数．（3）已知在样本数据中，有60位女生的每周平均体育运动时间超过4小时，请完成下面的列联表，并判断是否有95%的把握认为“该校学生的每周平均体育运动时间超过4小时与性别有关”．附：K2＝错误!．每周平均体育运动时间超过4小时 每周平均体育运动时间不超过4小时总计男女 60总计300P （K 2≥k 0） 0．10 0．050．010 0．005 k 02．7063．8416．6357．87922．（本小题12分）已知椭圆2222:1(0)x y C a b a b +=>>经过点13,)2P ，且离心率3e = （1）求椭圆C 的方程；（2）过椭圆右焦点F 做直线l 与椭圆交于A ，B 两点，点43(Q ，设直线AQ ，BQ 的斜率分别为21,k k ．证明：021=+k k ．北师大长春附属学校2020—2021学年度下学期高二年级期中考试 数学学科（文） 考试时间： 120分钟 满分： 150 分2021年5月10日一、选择题（本大题共12小题，每小题5分，共60分）1．已知命题P ：0x R ∃∈，032x x >，则P ⌝为 （ D ） A ．0x R ∃∈，032x x ≤ B ．x R ∀∈，32>x x C ．0x R ∃∉，032x x ≤ D ．x R ∀∈，32≤x x2．计算1ii+= （ B ） A ．1i -- B ．1i - C ．1i -+ D ．1i +3．已知x ，y 之间的一组数据：x0 1 2 3 y2356则y与x 的线性回归方程y bx a=+表示的直线必过点（ D ）A ．（2，2）B ．（1．5，0）C ．（1，2）D ．（1．5，4）4．袋内有红球3个､白球2个，从中任取2个，则互斥而不对立的两个事件是 （ A ）A ．事件A ：恰有1红球；事件B ：恰有2红球B ．事件A ：至少有1个红球；事件B ：至少有1个白球C ．事件A ：至少有1个红球；事件B ：全是红球D ．事件A ：至少有1个红球；事件B ：全是白球5．“1a =-”是“直线1x ay +=与1ax y +=平行”的 （ C ）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件6．已知下列命题：①由独立性检验可知，有99%的把握认为物理成绩与数学成绩有关，若某人数学成绩优秀，则他有99%的可能物理成绩优秀；②在回归分析中，可用相关指数2R 的值判断模型的拟合效果，2R 越大，模型的拟合效果越好；③在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高；④若“p q ∧是假命题，p q∨是真命题，则命题p ，q 一真一假”．其中真命题的个数是 （ B ）A ．4B ．3C ．2D ．17．在下面的表格中，每格填上一个数字后，使每一行成等差数列，每一列成等比数列，则a+b 的值是 （ A ）A ．1613 B ．1629 C ．1645 D ．85 8．如图是某学校抽取的学生体重的频率分布直方图，已知图中从左到右的前3个小组的频率满足：第一小组与第三小组的频率和是第二小组频率的2倍，第二小组的频数为15，则抽取的学生人数为 （ C ）A ．30B ．45C ．60D ．120（ 第7题图） （第8题图）1221 1ab（第9题图）9．已知在边长为3的正方形ABCD 中，2AM MB =，则DM DB ⋅= （ C ）A ．-17B ．-2C ．15D ．9 10．古希腊数学家欧几里德在公元前300年左右提出了欧几里 德算法，又叫辗转相除法．如右图，若输入m ，n 的值分别为 779，209，则输出的m = （ A ）A ．19B ．20C ．21D ．2211．《周髀算经》中给出了：冬至、小寒、大寒、立春、雨水、 惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二节气的日 影长依次成等差数列的结论．已知某地立春与雨水两个节气的日影长分别为10.5尺和9.5尺，现在从该地日影长小于9尺的节 气中随机抽取2个节气进行日影长情况统计，则所选取这2个节 气中恰好有1个节气的日影长小于5尺的概率为 （ B ）A ．37B ．47C ．1321D ．5712．如图，设椭圆1C ：22221x y a b +=（0a b >>）与双曲线2C ：22221x y m n-=（0m >，0n >）的公共焦点为1F ，2F ，将1C ，2C 的离心率分别记为1e ，2e ，点A 是1C ，2C 在第一象限的公共点，若点A 关于2C 的一条渐近线的对称点为1F ，则221222e e += （ D ） A ．2B ．52C ．72D ．4r（ 第10题图）二、填空题（本大题共4小题，每小题5分，共20分）13．若复数221(2)z m m m i =-+--为纯虚数，则实数m 的值为 1 ．14．已知一组数据4，2a ，3﹣a ，5，6的平均数为4，则a 的值是 2 ，这一组数据的方差是 514．15．如下图，九连环是我国从古至今广泛流传的一种益智游戏，它用九个圆环相连成串，以解开为胜．据明代杨慎《丹铅总录》记载：“两环互相贯为一，得其关捩，解之为二，又合面为一“．在某种玩法中，用a n 表示解下n （n ≤9，n ∈N *）个圆环所需移动的最少次数，若a 1＝1．且a n ＝1121,22,n n a n a n ---⎧⎨+⎩为偶数为奇数，则解下5个环所需的最少移动次数为 16 ．16．甲、乙两艘轮船都要在某个泊位停靠6小时，假定它们在一昼夜的时间段中随机地到达，则这两艘船中至少有一艘在停靠泊位时必须等待的概率是 167 ．三、解答题（本大题共6小题，共70分）17．（本小题10分）已知数列{}n a 是等比数列，公比q ＜1，前n 项和为S n ，若22a =，37S =． （1）求{}n a 的通项公式； （2）求证：S n ＜8．解：（1）由22a =，37S =得1211127a q a a q a q =⎧⎨++=⎩，解得1412a q =⎧⎪⎨=⎪⎩或112a q =⎧⎨=⎩ ， 1q <， 114,2a q， 1311422n n n a ；（2）由（1）可知，S n ＝1141(1)1281811212n n n n a q S q ⎛⎫- ⎪-⎛⎫⎝⎭===-< ⎪-⎝⎭- 18．（本小题12分）已知ABC ∆中，角A ，B ，C 所对的边分别为a ，b ，c ，22cos 2cos a B b A c +=． （1）求c 的值； （2）若3C π=，a b +=ABC ∆的面积．解：（1）因为ABC ∆中，22cos 2cos a B b A c +=，所以22222222222c bca cb b ac b c a a =-+⋅+-+⋅化简得：2,22==c c c （2）因为3C π=，由余弦定理得：22223cos 2=-+πab b a ，即43)(222=-+=-+abb a ab b a 把a b +=34=ab 所以ABC ∆的面积为33sin 21=C ab 。