认识不等式优质课一等奖

教案标题：不等式的性质教案概述：本教案旨在帮助学生掌握不等式的性质，包括不等式的基本概念、不等式的解集表示及其图示、不等式的性质及其运算法则等。

通过教学，使学生能够灵活运用不等式的性质解决实际问题，并以此为基础，进一步拓展应用数学领域的知识。

教学目标：1. 理解不等式的基本概念，并能够准确地表示不等式的解集；2. 掌握不等式在数轴上的图示方法，并能正确地解读不等式的图示；3. 知道不等式相等时的特殊情况，并能运用不等式的性质解决相关问题；4. 熟练运用不等式的运算法则，进行不等式的简化及合并。

教学内容：一、不等式的基本概念1. 不等式的定义及表示法；2. 不等式的解集表示；3. 解不等式的方法和步骤。

二、不等式的图示1. 数轴的表示方法；2. 不等式在数轴上的图示；3. 不等式图示的应用。

三、不等式的性质1. 不等式中的对称性与传递性；2. 不等式中的加法性质与乘法性质；3. 不等式中的相等性质及特殊情况。

四、不等式的运算法则1. 不等式的简化与合并；2. 不等式的乘法运算法则；3. 不等式的除法运算法则；4. 不等式的加减运算法则。

教学重点与难点：教学重点：1. 不等式的基本概念与解集表示；2. 不等式的图示方法及应用；3. 不等式的性质与运算法则。

教学难点：1. 不等式的图示解读与应用；2. 不等式的运算法则的灵活运用。

教学过程：Step 1：引入不等式的基本概念（15分钟）1. 通过举例，向学生介绍不等式的基本概念，并与等式进行对比；2. 引导学生体会不等式中的“大于”、“小于”关系，并结合实际生活中的例子进行讲解；3. 教师总结不等式的定义及表示法，并引导学生完成相关练习。

Step 2：讲解不等式的图示方法（20分钟）1. 通过图示方法，解释数轴的概念和表示方法；2. 教师以示例的方式，讲解不等式在数轴上的图示方法，并引导学生完成相关练习；3. 指导学生练习不等式的图示解读，并使学生能够在实际问题中灵活运用不等式的图示。

数学《不等式基本性质》教学设计一等奖1、数学《不等式基本性质》教学设计一等奖不等式的基本性质教学目的掌握不等式的基本性质，会用不等式的基本性质进行不等式的变形，数学教案－不等式基本性质。

教学过程老师:我们已经学习了平等和不平等。

现在，我们来看两组公式(老师在黑板上展示了两组公式)。

请观察，哪些是方程？什么是不平等？第一组：1+2=3; a+b=b+a; S =ab; 4+x =7.第二组：-7 < -5; 3+4 > 1+4; 2x ≤6, a+2 ≥0; 3≠4.生：第一组都是等式，第二组都是不等式。

老师:那么，什么是方程？什么是不平等？生：表示相等关系的式子叫做等式；表示不等式的式子叫做不等式。

师：在数学炽，我们用等号“=”来表示相等关系，用不等式号“〈”、“〉”或“≠”表示不等关系，其中“＞”和“＜”表示大小关系。

表示大小关系的不等式是我们中学教学所要研究的。

我们以前研究过这个方程。

你还记得等式的性质吗？生:方程有这样的性质，方程两边加，或减，或乘，或除(除数不为零)同一个数，结果还是方程。

师：很好！当我们开始研究不等式的时候，自然会联想到，是否有与等式相类似的性质，也就是说，如果在不等式的两边都加上，或都减去，或都乘以，或都除经（除数不为零）同一个数，结果将会如何呢？让我们先做一些试验练习，初中数学教案《数学教案－不等式基本性质》。

练习1 (回答)用小于号“<”或大于号“>”填空。

（1）7 ___ 4; （2）- 2____6; （3）- 3_____ -2；（4）- 4_____-6练习2(口头回答)从练习1的四个不等式出发，进行如下操作。

(1)两边加(或减)5。

结果如何呢？等号的方向变了吗？（2）两边都乘以（或都除以）5，结果怎样？不等号的方向改变了吗？（3）两边都乘以（或都除以）（-5），结果怎样？不等号的方向改变了吗？生：我们发现：在练习2中，第（1）、（2）题的结果是不等号的方向不变；在第（3）题中，结果是不等号的.方向改变了！老师:学生们观察得很仔细。

不等式性质教案引言：不等式是数学中的重要概念之一，它用于比较两个数的大小关系。

在数学教学中，教授不等式的性质对学生的数学素养提高具有重要意义。

本文将为您介绍一份关于不等式性质的教案。

一、教学目标：1.了解不等式的定义和基本操作；2.认识不等式性质及其在实际问题中的应用；3.提高学生解决不等式问题的能力和思维能力。

二、教学内容：1.不等式的定义和基本操作：a.了解不等号的意义及使用方法；b.掌握不等式中加减乘除的运算规则；c.掌握不等式中分数的运算规则。

2.不等式的性质：a.不等式的传递性：若a<b，b<c，则a<c；b.不等式两侧同时加（减）一个相同的数，不等式的关系不变；c.不等式两侧同时乘（除）一个正数，不等式的关系不变；d.不等式两侧同时乘（除）一个负数，并改变不等号的方向。

3.实际问题中的不等式应用：a.根据不等式描述实际情况，提高数学建模能力；b.通过实际问题训练学生解决复杂不等式的能力。

三、教学过程：1.概念讲解：a.引导学生了解不等式的基本概念和符号表示方法；b.通过示例和练习，让学生熟悉不等式的基本操作；c.讲解不等式的传递性和运算规则，引导学生理解不等式的性质。

2.知识点讲解：a.依次介绍不等式的传递性和运算规则，并通过具体例子进行说明；b.引导学生自己总结不等式的性质，并与他们进行讨论和解答疑惑。

3.练习和应用：a.提供一系列练习题，让学生运用所学知识解决不等式问题；b.引导学生通过实际情境应用不等式，培养他们的数学建模能力。

四、教学评价：1.课堂练习：a.针对不等式的定义和基本操作设置练习题目；b.通过课堂练习，检查学生掌握不等式的基本操作情况。

2.作业评价：a.布置书面作业，包含不等式性质的练习题；b.检查学生对不等式性质的理解情况和解题能力。

五、教学拓展：1.引导学生进一步探究和研究不等式的性质；2.扩展教学内容，讲解更复杂的不等式应用；3.引导学生用数学语言描述和解决实际生活中的问题。

初中数学不等式教案一、教学目标1. 理解不等式的概念和性质，能够正确读写不等式。

2. 掌握不等式的解集、解集的图示表示和表示方法。

3. 学会利用不等式解决实际问题。

4. 培养学生分析和解决问题的能力，提高逻辑思维能力。

二、教学重点1. 不等式的定义和基本性质。

2. 不等式的解集和表示方法。

三、教学难点1. 不等式的解集的图示表示。

2. 不等式解决实际问题的应用。

四、教学内容及进度1. 不等式的基本概念和性质1.1 不等关系的定义和表示方法。

1.2 不等式求解的基本步骤。

2. 不等式的解集和表示方法2.1 解不等式的过程和解集的概念。

2.2 解集的图示表示方法。

3. 利用不等式解决实际问题3.1 实际问题的转化和建模。

3.2 分析问题并给出解决步骤。

3.3 通过解不等式找出问题的解集。

五、教学方法1. 案例导入法：通过具体的问题引出不等式的概念和意义。

2. 归纳法：引导学生总结不等式的基本性质和解法。

3. 演练法：以多种类型的不等式进行练习，巩固学生的解题能力。

4. 活动合作法：组织学生进行小组合作，解决实际问题。

六、教学资源1. 教材：包括不等式的相关知识点和例题。

2. 板书：重点概念、公式、解题步骤等。

七、学情分析与教学策略不等式作为初中数学的重要内容之一，是学生接触到的第一个代数内容。

因此，学生对不等式的概念和性质掌握程度不高，存在一定的困难。

针对这一情况，教学中需注重引导学生形成概念，理解不等式的基本含义与解的概念，通过例题演练巩固基本解不等式的步骤。

在解决实际问题的应用中，教师可以结合学生的实际情况，如购物、旅行等，引导学生进行问题建模和解决。

八、教学步骤1. 导入通过一个简单的问题，引出不等式的概念和应用：“小明的体重是随着年龄的增长而逐渐增加的。

我们怎么表示小明的体重不超过60kg这个条件呢？”2. 概念讲解讲解不等式的基本概念和性质，如不等关系的定义、不等式的读写方法等。

3. 解不等式的基本步骤引导学生总结解不等式的基本步骤，包括去括号、合并同类项、移项、求解等。

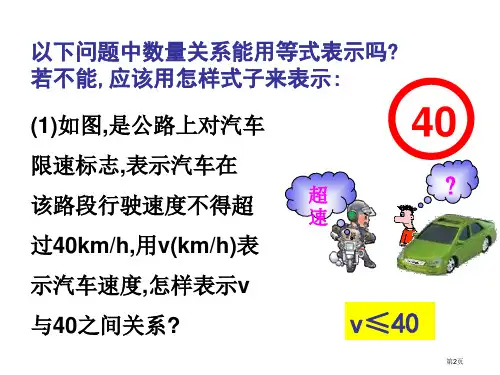
1 不等式及其基本性质》一等奖创新教学设计第7章一元一次不等式与不等式组7.1不等式及其基本性质【教学目标】知识与技能1.理解不等式的概念，能够识别不等式，会列不等式.2.掌握不等式的基本性质，能灵活运用不等式的基本性质进行不等式的变形.过程与方法了解不等式的概念，掌握不等式的基本性质，培养学生的观察、演绎能力，提高学生的归纳概括能力.情感态度有意识地引导学生积极参与到数学活动过程中，培养学生的观察、归纳能力，通过学习，体验成功的喜悦，激发学生学习数学的兴趣.【教学重点】不等式的基本性质.【教学难点】正确应用不等式的基本性质进行不等式变形.【教学过程】一、情境导入，初步认识在上课之前我请两位同学上来比比身高，除了身高，这两位同学还有哪些不等关系？观看交通动画，问同学们动画中有什么不等关系？二、思考探究，获取新知1.不等式.能用语言描述交通标志中数学符号所表示的意义吗？用正数v，m，a，h分别表示速度、重量、宽度和高度。

v≤40千米/小时m≤20吨a＜3米h＜4.5米类比于等式的概念，想一想什么是不等式？【归纳结论】用不等式（＞、≥、＜、≤或≠）表示不等关系的式子叫做不等式.辨一辨：下列式子1）-2＞0；2）3x-5＞0；3）x=1；4）x -x ；5）x≠-2；6）x+2＞x-1，其中是不等式的有____。

好消息1、一次性消费金额不低于60元的顾客可以凭收银条参加抽奖活动。

乘客须知2、在大人的带领下，不超过1.2米的儿童乘车可以免买车票。

网吧通告3、未满18周岁的青少年禁止入内！调查研究4、全班有多少同学骑电瓶车上学呢？至少达到多大年龄才可以骑呢？试一试：用不等式表示（1）a与b的和小于0；（2）x的5倍与1的差小于x的3倍；（3）x与y的积是正数；（4）m与n的和的平方是非负数；（5）a的相反数不大于2.2.不等式的性质.复习回顾：等式具有哪些性质？等式基本性质1：等式的两边都加上（或减去）同一个数或同一个整式，所得结果仍是等式。