MATLAB信号处理仿真实验教程

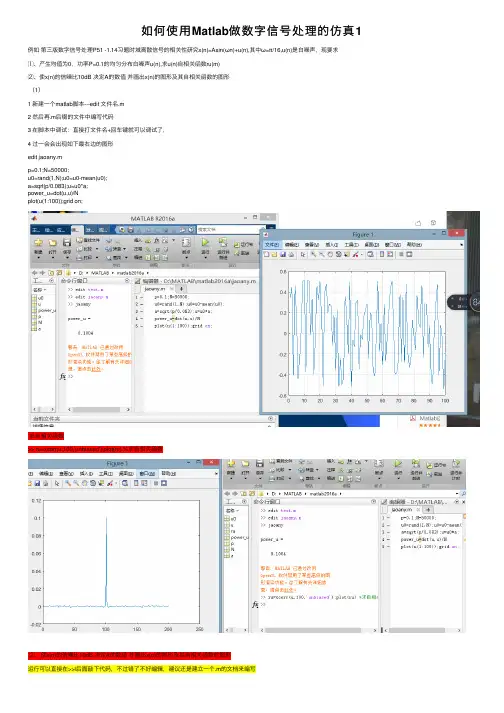
如何使⽤Matlab做数字信号处理的仿真1例如第三版数字信号处理P51 -1.14习题时域离散信号的相关性研究x(n)=Asin(ωn)+u(n),其中ω=π/16,u(n)是⽩噪声，现要求
⑴、产⽣均值为0，功率P=0.1的均匀分布⽩噪声u(n),求u(n)⾃相关函数ru(m)
⑵、使x(n)的信噪⽐10dB 决定A的数值 并画出x(n)的图形及其⾃相关函数的图形
（1）
1 新建⼀个matlab脚本---edit ⽂件名.m
2 然后再.m后缀的⽂件中编写代码
3 在脚本中调试：直接打⽂件名+回车键就可以调试了，
4 过⼀会会出现如下最右边的图形
edit jaoany.m
p=0.1;N=50000;
u0=rand(1,N);u0=u0-mean(u0);
a=sqrt(p/0.083);u=u0*a;
power_u=dot(u,u)/N
plot(u(1:100));grid on;
求⾃相关函数
>> ru=xcorr(u,100,'unbiased');plot(ru) %求⾃相关函数
⑵、使x(n)的信噪⽐10dB 决定A的数值 并画出x(n)的图形及其⾃相关函数的图形
运⾏可以直接在>>l后⾯敲下代码，不过错了不好编辑，建议还是建⽴⼀个.m的⽂档来编写
n=0:49999;
y=0.5*pi*sin(0.0625*pi*n);
x=y+u;
plot(x(1:100));grid on;
求⾃相关函数>> rx=xcorr(x,100,'unbiased');plot(rx)%求⾃相关函数。

实验1 连续时间信号和离散信号的实现实验内容与方法一、验证性试验1、生成直流信号f（t）=6MA TLAB程序代码：t = -10:0.01:10;a1 = 6;subplot(3,3,1)plot(t,a1,'b');title('直流信号');xlabel('时间(t)');ylabel('幅值(f)')2、生成正弦交流信号f（t）=sin（wt+φ）MA TLAB程序代码：t = 0:0.01:1;f = sym('sin(2*pi*t)');subplot(3,3,2)ezplot(f,[0,1]);title('正弦交流信号');xlabel('时间(t)');ylabel('幅值(f)')3、生成单位阶跃信号f（t）=ε（t）MA TLAB程序代码：t0=0;t1=-1;t2=3;dt=0.01;t=t1:dt:-t0;n=length(t);t3=-t0:dt:t2;n3=length(t3);u=zeros(1,n);u3=ones(1,n3);subplot(3,3,3)plot(t,u);hold on;plot(t3,u3);plot([-t0,-t0],[0,1]);hold off;axis([t1,t2,-0.2,1.5]);xlabel('时间(t)');ylabel('幅值(f)');title('单位阶跃信号')4、生成单位冲激信号f（t）=δ（t）MA TLAB程序代码：t0=0;t1=-1;t2=5;dt=0.1;t=t1:dt:t2;n=length(t);x=zeros(1,n);x(1,(t0-t1)/dt+1)=1/dt;subplot(3,3,4)stairs(t,x);axis([t1,t2,0,1/dt]);xlabel('时间(t)');ylabel('幅值(f)');title('单位冲激信号')5、生成周期方波信号MA TLAB程序代码：t=(0:0.0001:1);y=square(2*pi*15*t);subplot(3,3,5)plot(t,y);axis([0,1,-1.5,1.5]);xlabel('时间(t)');ylabel('幅值(f)');title('周期方波信号')6、生成三角波信号MA TLAB程序代码：t=(-3:0.0001:5);y=tripuls(t,4,0.5);subplot(3,3,6)plot(t,y);xlabel('时间(t)');ylabel('幅值(f)');title('三角波信号')7、生成正弦序列信号MA TLAB程序代码：k1=-20;k2=20;k=k1:k2;f=sin(k*pi/6);subplot(3,3,7)stem(k,f,'filled');xlabel('时间(t)');ylabel('幅值(f)');title('正弦序列')8、生成单位斜波序列信号MA TLAB程序代码：k1=-20;k2=20;k0=0;n=[k1:k2];if k0>=k2x=zeros(1,length(n));elseif (k0<k2)&(k0>k1)x=[zeros(1,k0-k1),[0:k2-k0]];elsex=(k1-k0)+[0:k2-k1];endsubplot(3,3,8)stem(n,x);xlabel('时间(t)');ylabel('幅值(f)');title('单位斜波序列')9、生成幅值调制序列信号MA TLAB程序代码：n=0:100;m=0.4;fH=0.1;fL=0.01;xH=sin(2*pi*fH*n);xL=sin(2*pi*fL*n);y=(1+m*xL).*xH;subplot(3,3,9)stem(n,y);grid;xlabel('时间(k)');ylabel('幅值f(k)');title('幅值调制序列')10、生成复指数信号y（t）=e^（-at+bjt）MA TLAB程序代码：t=0:0.01:3;a=-3;b=4;z=exp((a+i*b)*t);subplot(2,2,1);plot(t,real(z)),title('实部'):xlabel('时间(t)');ylabel('幅值(f)'); subplot(2,2,2);plot(t,imag(z)),title('虚部'):xlabel('时间(t)');ylabel('幅值'); subplot(2,2,3);plot(t,abs(z)),title('模'):xlabel('时间(t)');ylabel('幅值'); subplot(2,2,4);plot(t,real(z)),title('相角'):xlabel('时间(t)');ylabel('幅值')二、程序设计实验①a=3;x=-10:0.01:10;y=(1-2*abs(x))/a;subplot(3,3,1)plot(x,y,'b')axis([-12,12,-10,5]);xlabel('x');ylabel('y');title('(1-2*abs(x))/a')②t = 0:0.01:6*pi;f = sym('cos(3*t)+sin(2*t)');subplot(3,3,2)ezplot(f,[0,6*pi]);title('信号');xlabel('时间(t)');ylabel('幅值(f)')③t0=-5;t1=-10;t2=5;dt=0.01;t=t1:dt:t0;n=length(t);t3=t0:dt:t2;n3=length(t3);u=zeros(1,n);u3=ones(1,n3);subplot(3,3,3)plot(t,u);hold on;plot(t3,u3);plot([t0,t0],[0,1]);hold off;axis([t1,t2,-0.2,1.2]);xlabel('时间(t)');ylabel('幅值(f)');title('u(t+5)')④k1=-20;k2=20;k=k1:k2;f=cos(5*k)+sin(4*k);subplot(3,3,7)stem(k,f,'filled');xlabel('时间(k)');ylabel('幅值f(k)');title('信号4')⑤x=0:0.01:3;z=5*exp(-x);subplot(2,2,1);plot(x,real(z)),title('信号5'):xlabel('时间(x)');ylabel('幅值(f)')⑥k0=0;k1=-1;k2=10;dk=1;k=k1:dk:k2;n=length(k);x=zeros(1,n);x(1,(k0-k1)/dk+1)=1/dk;subplot(3,3,4)stairs(k+5,x);axis([k1,k2,0,1/dk]);xlabel('时间(k)');ylabel('幅值(f)');title('信号6')⑦t0=-5;t1=-6;t2=0;t=t1:t0-1;n=length(t);t3=t0:t2;n3=length(t3);u=zeros(1,n);u3=ones(1,n3);subplot(3,3,7)stem(t,u,'filled');hold on;stem(t3,u3,'filled');hold off;axis([t1,t2,-0.2,1.5]);xlabel('时间(t)');ylabel('幅值(f)');title('信号7');。

数字信号MATLAB仿真实验数字信号MATLAB仿真实验一．实验目的1.通过本次实验熟悉数字信号处理的方波和三角波的产生2.对FFT加强理解和直观地认识3.理解并掌握频谱分析和谐波分析4.对噪声对信号的影响认识二．实验内容5.自编程序得到一个方波信号（f=50Hz,幅值为1，1 ，各半个周期），对其一个周期分别采样256点和1024点，利用光盘所附的基于Matlab 语言所编FFT程序或自编FFT程序做谐波分析分析，并与理论分析结果对照（注意FFT计算频谱与谐波分析的区别）。

6.对三角波信号（可以由方波信号求导得到）重复作业一的各项要求。

7.对一、二信号叠加一个白噪声信号（均值为零，方差为0.2）所构成的随机信号用FFT进行频谱分析8.对以上结果进行讨论三．实验程序1.方波分析cclearT=0.02,l=0.5,hu=1,hd=-1; %T是周期，l为占空比，hu为上幅度，hd为下幅度t=[0:0.001:2]; %显示连续图形的采样点for i=1:length(t) %生成方波if rem(t(i),T)<t*l< p="">y(i)=hu;elsey(i)=hd;endendn=0:0.02/256:(0.02-0.02/256); %256采样点for i=1:length(n) %生成方波取256采样点值if rem(n(i),T)<t*l< p="">yn(i)=hu;elseyn(i)=hd;endendn2=0:0.02/1024:(0.02-0.02/1024);for i=1:length(n2) %生成方波取1024采样点值if rem(n2(i),T)<t*l< p="">yn2(i)=hu;elseyn2(i)=hd;endendfigure(1)subplot(3,1,1)stairs(t,y); %画方波xlabel('时间t'),ylabel('幅度y'),grid on; subplot(3,1,2); %画256采样图stem(n,yn,'.');xlabel('采样时间t'),ylabel('幅度y'),grid on; subplot(3,1,3); %画1024采样图stem(n2,yn2,'.');xlabel('采样时间t'),ylabel('幅度y'),grid on; ynfft=fft(yn); %256点FFTynfft2=fft(yn2); %1024点FFTmagyn=abs(ynfft); %256点幅度谱，对数幅度谱，相位谱lgmagyn=20*log10(abs(ynfft));argyn=angle(ynfft);magyn2=abs(ynfft2); %1024点幅度谱，对数幅度谱，相位谱lgmagyn2=20*log10(abs(ynfft2));argyn2=angle(ynfft2);nf=0:2*pi/256:(2*pi-2*pi/256); %计算FFT各点频率nf2=0:2*pi/1024:(2*pi-2*pi/1024);ind1=find(magyn); %取fft后的幅值非零频率分量magynxb=magyn(:,ind1) ;ind2=find(magyn2);magynxb2=magyn2(:,ind2);if ind1(1)~=1 %判断是否有直流分量，并求基波频率%调整各各次谐波的存储在相应位置bf1=gcd(ind1(1)-1,ind1(2)-1)*2*pi/256;elsebf1=gcd(ind1(2)-1,ind1(3)-1)*2*pi/256;magynxb=magyn(:,2:ind1) ;ind11=ind1(2:length(ind1))-1;endif ind2(1)~=1bf2=gcd(ind2(1)-1,ind2(2)-1)*2*pi/1024;elsebf2=gcd(ind2(2)-1,ind2(3)-1)*2*pi/256;magynxb2=magyn2(2:1024); %去掉直流分量ind2=ind2(2:length(ind2))-1endfigure(2) %画各谐波的幅度谱subplot(2,1,1)stem(ind1-1,magynxb,'.');xlabel('谐波频率'),ylabel('幅值'),grid on;subplot(2,1,2)stem(ind2-1,magynxb2,'.');xlabel('谐波频率'),ylabel('幅值'),grid on;learT=0.02,l=0.5,hu=1,hd=-1; %T是周期，l为占空比，hu为上幅度，hd为下幅度t=[0:0.001:2]; %显示连续图形的采样点for i=1:length(t) %生成方波if rem(t(i),T)<t*l< p="">y(i)=hu;elsey(i)=hd;endendn=0:0.02/256:(0.02-0.02/256); %256采样点for i=1:length(n) %生成方波取256采样点值if rem(n(i),T)<t*l< p="">yn(i)=hu;elseyn(i)=hd;endendn2=0:0.02/1024:(0.02-0.02/1024);for i=1:length(n2) %生成方波取1024采样点值if rem(n2(i),T)<t*l< p="">yn2(i)=hu;elseyn2(i)=hd;endendfigure(1)subplot(3,1,1)stairs(t,y); %画方波xlabel('时间t'),ylabel('幅度y'),grid on;subplot(3,1,2); %画256采样图stem(n,yn,'.');xlabel('采样时间t'),ylabel('幅度y'),grid on;subplot(3,1,3); %画1024采样图stem(n2,yn2,'.');xlabel('采样时间t'),ylabel('幅度y'),grid on;ynfft=fft(yn); %256点FFTynfft2=fft(yn2); %1024点FFTmagyn=abs(ynfft); %256点幅度谱，对数幅度谱，相位谱lgmagyn=20*log10(abs(ynfft));argyn=angle(ynfft);magyn2=abs(ynfft2); %1024点幅度谱，对数幅度谱，相位谱lgmagyn2=20*log10(abs(ynfft2));argyn2=angle(ynfft2);nf=0:2*pi/256:(2*pi-2*pi/256); %计算FFT各点频率nf2=0:2*pi/1024:(2*pi-2*pi/1024);ind1=find(magyn); %取fft后的幅值非零频率分量magynxb=magyn(:,ind1) ;ind2=find(magyn2);magynxb2=magyn2(:,ind2);if ind1(1)~=1 %判断是否有直流分量，并求基波频率bf1=gcd(ind1(1)-1,ind1(2)-1)*2*pi/256;else ind1bf1=gcd(ind1(2)-1,ind1(3)-1)*2*pi/256;magynxb=magyn(:,2:ind1) ;endif ind2(1)~=1bf2=gcd(ind2(1)-1,ind2(2)-1)*2*pi/1024; elsebf2=gcd(ind2(2)-1,ind2(3)-1)*2*pi/256; magynxb2=magyn2(2:1024); %去掉直流分量endfigure(2) %画各谐波的幅度谱subplot(2,1,1)stem(ind1,magynxb,'.');xlabel('频率'),ylabel('幅值'),grid on; subplot(2,1,2)stem(ind2,magynxb2,'.');xlabel('频率'),ylabel('幅值'),grid on;2.三角波分析clearT=0.02,l=0.5,hu=1,hd=-1; %T是周期，l为占空比，hu为上幅度，hd为下幅度t=[0:0.0001:2]; %显示连续图形的采样点for i=1:length(t) %生成三角波if rem(t(i),T)<t*l< p="">y(i)=-(hu-hd)/(T*l)*rem(t(i),T)+hu;elsey(i)=(hu-hd)/(T*(1-l))*(rem(t(i),T)-l*T)+hd;endendn=0:0.02/256:(0.02-0.02/256); %256采样点for i=1:length(n) %生成256点采样值if rem(n(i),T)<t*l< p="">yn(i)=-(hu-hd)/(T*l)*rem(n(i),T)+hu;elseyn(i)=(hu-hd)/(T*(1-l))*(rem(n(i),T)-l*T)+hd;endendn2=0:0.02/1024:(0.02-0.02/1024);for i=1:length(n2) %生成1024点采样值if rem(n2(i),T)<t*l< p="">yn2(i)=-(hu-hd)/(T*l)*rem(n2(i),T)+hu;elseyn2(i)=(hu-hd)/(T*(1-l))*(rem(n2(i),T)-l*T)+hd;endendfigure(1)subplot(3,1,1)plot(t,y); %画三角波xlabel('时间t'),ylabel('幅度y'),grid on;subplot(3,1,2); %画256采样图stem(n,yn,'.');xlabel('采样时间t'),ylabel('幅度y'),grid on;subplot(3,1,3); %画1024采样图stem(n2,yn2,'.');xlabel('采样时间t'),ylabel('幅度y'),grid on;ynfft=fft(yn); %256点FFTynfft2=fft(yn2); %1024点FFTmagyn=abs(ynfft); %256点幅度谱，对数幅度谱，相位谱lgmagyn=20*log10(abs(ynfft));argyn=angle(ynfft);magyn2=abs(ynfft2); %1024点幅度谱，对数幅度谱，相位谱lgmagyn2=20*log10(abs(ynfft2));argyn2=angle(ynfft2);nf=0:2*pi/256:(2*pi-2*pi/256); %计算FFT各点频率nf2=0:2*pi/1024:(2*pi-2*pi/1024);ind1=find(magyn); %取fft后的幅值非零频率分量magynxb=magyn(:,ind1) ;ind2=find(magyn2);magynxb2=magyn2(:,ind2);if ind1(1)~=1 %判断是否有直流分量，并求基波频率bf1=gcd(ind1(1)-1,ind1(2)-1)*2*pi/256;elsebf1=gcd(ind1(2)-1,ind1(3)-1)*2*pi/256;magynxb=magyn(2:length(magyn)) ;ind11=ind1(2:length(ind1));endif ind2(1)~=1bf2=gcd(ind2(1)-1,ind2(2)-1)*2*pi/1024;elsebf2=gcd(ind2(2)-1,ind2(3)-1)*2*pi/256;magynxb2=magyn2(2:length(magyn2)); %去掉直流分量ind22=ind2(2:length(ind2));endfigure(2) %画各谐波的幅度谱subplot(2,1,1)stem(ind11-1,magynxb,'.');xlabel('频率'),ylabel('幅值'),grid on;subplot(2,1,2)stem(ind22-1,magynxb2,'.');xlabel('频率'),ylabel('幅值'),grid on;叠加噪声分析3.叠加了噪声的程序TclearT=0.02,l=0.5,hu=1,hd=-1; %T是周期，l为占空比，hu为上幅度，hd为下幅度t=[0:0.0001:2]; %显示连续图形的采样点for i=1:length(t) %生成方波if rem(t(i),T)<t*l< p="">yrect(i)=hu;elseyrect(i)=hd;endendfor i=1:length(t) %生成三角波if rem(t(i),T)<t*l< p="">ytri(i)=-(hu-hd)/(T*l)*rem(t(i),T)+hu;elseytri(i)=(hu-hd)/(T*(1-l))*(rem(t(i),T)-l*T)+hd;endendnoise=sqrt(0.2)*randn(1,length(t));%noise=sqrt(12*0.2)*rand(1,length(t))y=yrect+noise;y2=ytri+noise;n=0:0.02/1024:(0.02-0.02/1024); %1024采样点n2=nfor i=1:length(n) %生成方波取1024采样点值if rem(n(i),T)<t*l< p="">yn(i)=hu;elseyn(i)=hd;endendfor i=1:length(n2) %生成1024点三角波采样值if rem(n2(i),T)<t*l< p="">yn2(i)=-(hu-hd)/(T*l)*rem(n2(i),T)+hu;elseyn2(i)=(hu-hd)/(T*(1-l))*(rem(n2(i),T)-l*T)+hd;endendn=[0:0.02/1024:0.02-0.02/1024];n2=n;noisen=sqrt(0.2)*randn(1,length(n));%noise=sqrt(12*0.2)*rand(1,length(n))yn=yn+noisen;yn2=yn2+noisen;figure(1)subplot(4,2,1)stairs(t,yrect)ylabel('方波图'),grid on;subplot(4,2,5)plot(t,y);ylabel('叠加了噪声的方波图'),grid on;subplot(4,2,7);stem(n,yn,'.')ylabel('叠加了噪声的方波图的抽样'),grid on;subplot(4,2,3)plot(t,noise)ylabel('正态分布噪声'),grid on;subplot(4,2,4)ylabel('噪声的分布检测'),grid on;hist(noise,50)subplot(4,2,2)stairs(t,ytri)ylabel('三角波图'),grid on;subplot(4,2,6)plot(t,y2)ylabel('叠加了噪声的三角波图'),grid on; subplot(4,2,8)ylabel('叠加了噪声的三角波图的抽样'),grid on; stem(n2,yn2,'.')ynfft=fft(yn);ynfft2=fft(yn2);magyn=abs(ynfft);lgmagyn=20*log10(abs(ynfft));argyn=angle(ynfft);magyn2=abs(ynfft2);lgmagyn2=20*log10(abs(ynfft2));argyn2=angle(ynfft2);figure(2)subplot(3,2,1)plot(n,magyn)ylabel('叠加了噪声的方波幅度响应'),grid on; subplot(3,2,3)plot(n,lgmagyn)ylabel('叠加了噪声的方波对数幅度响应'),grid on; subplot(3,2,5)plot(n,argyn)ylabel('叠加了噪声的方波相位响应'),grid on; subplot(3,2,2)plot(n2,magyn2)ylabel('叠加了噪声的三角波幅度响应'),grid on; subplot(3,2,4)plot(n2,lgmagyn2)ylabel('叠加了噪声的三角波对数幅度响应'),grid on; subplot(3,2,6)plot(n2,argyn2)ylabel('叠加了噪声的三角波相位响应'),grid on;实验结果分析四．实验结果及分析1.方波分析由于方波为半波对称，所以偶次谐波的幅值为零，只有奇次谐波存在，能量主要集中在低次谐波上，且fft变换后基波频率不一样，可见FFT所求的傅里叶变换周期不是完全有原信号决定的。

MATLAB信号处理仿真实验1. 引言信号处理是一种广泛应用于各个领域的技术，它涉及到对信号的获取、处理和分析。

MATLAB是一种强大的数学软件，提供了丰富的信号处理工具箱，可以用于信号处理的仿真实验。

本文将介绍如何使用MATLAB进行信号处理仿真实验，并提供详细的步骤和示例。

2. 实验目的本实验旨在通过MATLAB软件进行信号处理仿真，以加深对信号处理原理和算法的理解，并掌握使用MATLAB进行信号处理的基本方法和技巧。

3. 实验步骤3.1 生成信号首先，我们需要生成一个待处理的信号。

可以使用MATLAB提供的信号生成函数，如sine、square和sawtooth等。

以生成一个正弦信号为例，可以使用以下代码：```MATLABfs = 1000; % 采样频率t = 0:1/fs:1; % 时间向量f = 10; % 信号频率x = sin(2*pi*f*t); % 生成正弦信号```3.2 添加噪声为了更真实地摹拟实际信号处理场景，我们可以向生成的信号中添加噪声。

可以使用MATLAB提供的随机噪声生成函数，如randn和awgn等。

以向生成的信号中添加高斯白噪声为例，可以使用以下代码：```MATLABSNR = 10; % 信噪比y = awgn(x, SNR); % 向信号中添加高斯白噪声```3.3 进行滤波处理滤波是信号处理中常用的一种技术，用于去除信号中的噪声或者提取感兴趣的频率成份。

可以使用MATLAB提供的滤波函数，如fir1和butter等。

以设计并应用一个低通滤波器为例，可以使用以下代码：```MATLABorder = 10; % 滤波器阶数cutoff = 0.1; % 截止频率b = fir1(order, cutoff); % 设计低通滤波器filtered_y = filter(b, 1, y); % 应用滤波器```3.4 进行频谱分析频谱分析是信号处理中常用的一种技术，用于分析信号的频率成份。

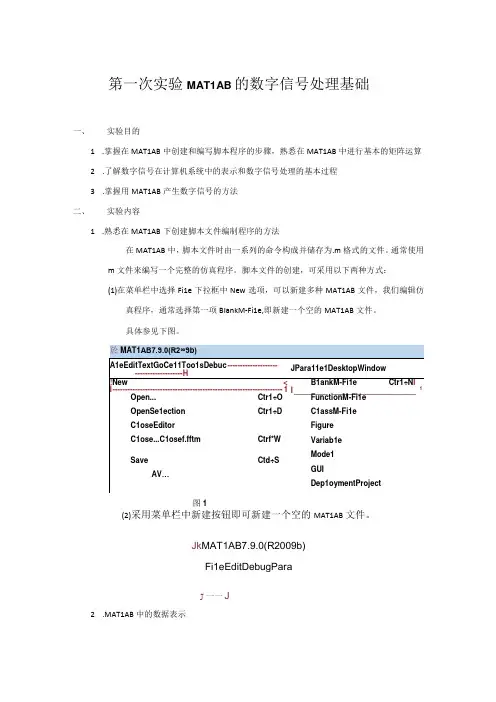
第一次实验MAT1AB的数字信号处理基础一、实验目的1.掌握在MAT1AB中创建和编写脚本程序的步骤，熟悉在MAT1AB中进行基本的矩阵运算2.了解数字信号在计算机系统中的表示和数字信号处理的基本过程3.掌握用MAT1AB产生数字信号的方法二、实验内容1.熟悉在MAT1AB下创建脚本文件编制程序的方法在MAT1AB中，脚本文件时由一系列的命令构成并储存为.m格式的文件。

通常使用m文件来编写一个完整的仿真程序。

脚本文件的创建，可采用以下两种方式：(1)在菜单栏中选择Fi1e下拉框中New选项，可以新建多种MAT1AB文件，我们编辑仿真程序，通常选择第一项BIankM-Fi1e,即新建一个空的MAT1AB文件。

具体参见下图。

图1(2)采用菜单栏中新建按钮即可新建一个空的MAT1AB文件。

Jk MAT1AB7.9.0(R2009b)Fi1eEditDebugParaJ一一J2.MAT1AB中的数据表示MAT1AB中的基本数据单元为数组矩阵，MAT1AB中的数学运算都是基于矩阵的。

掌握了矩阵运算，就掌握了MAT1AB编程的关键。

MAT1AB中使用到的变量无需事先声明其数据类型，大小等，MAT1AB会自动根据赋值情况进行解析。

比如，可用通过以下命令产生一个矩阵：3.常用序列的MAT1AB实现(1)单位抽样序列。

在MAT1AB中可以用以下函数来实现单位抽样序列function[x,n]=impseq(nθ,n1z n2)%产生x(n)=de1ta(n-n0);n1<=n0<=n2if((nθ<n1)∣(nθ>∩2)∣(n1>n2))error('参数必须满足n1<=nθ<=n2,)endn=[n1:n2];x=[zeros(1,(nO-n1))4∕Zθros(1z(n2-nO))];stem(x);图3(2)单位阶跃序列。

在MAT1AB中可用〃>=0来实现〃(〃一%)。

实验一 用于信号处理的MATLAB 基本操作一、[实验目的]1．学习和掌握MATLAB 最基本的矩阵运算与绘图工具2．复习离散时间的信号，离散时间重要类型的信号和它们的运算的实现 3．复习离散时间信号理论中一些重要的结果，在数字信号处理中很有用 二、[实验原理] 1．典型序列单位抽样序列1,0()0,0n n n δ=⎧=⎨≠⎩单位阶跃序列1,0()0,0n u n n ≥⎧=⎨<⎩实数指数序列n a n x =)(1 ，a =5，010n ≤≤ 复数指数序列()2(),2,1,010,a jw n x n e a w n +===≤≤表示出实部虚部，模和相位 正余弦序列30()sin()(),anT x n Ae nT u n -=Ω0444.128,02,502,T 0.001s ;050A a n ==Ω==≤≤ 随机序列：MATLAB 可用rand （1，N ）和randn （1，N ）来生成 周期序列：4()2,010,151515n x n n =≤≤对该序列以周期为延拓，画出[-，]的图形 2．序列的运算信号加：13()(),010x n x n n +≤≤， 信号乘：13()(),010x n x n n ⋅≤≤，插值与抽取：11121n(),010y (n)(2),y (n)()2x n n x n x ≤≤==已知，求移位：33343(),010y (n)(5),y (n)(5)x n n x n x n ≤≤=+=-已知，求 折叠：fliplr(x) 353(),010y (n)()x n n x n ≤≤=-已知，求取样和：sum(x(n1:n2)) 10363m 0(),010y (n)(m)x n n x =≤≤=∑已知，求信号能量：sum(abs(x).^2) 102373m 0(),010y (n)(m)x n n x =≤≤=∑已知，求信号功率：sum(abs(x).^2)/length(x)102283m 01(),010y (n)|(m)|11x n n x =≤≤=∑已知，求3．一些有用的结果软件实现 （1）本实验用到的一些matlab 函数stem(x,y)，plot(x,y):x 轴和y 轴均为线性刻度（linear scale ） Xlable(‘x ’),Ylable(‘y ’) Title(‘x ’)Axis([xmin ,xmax,ymin,ymax]):调整图轴的范围 Subplot(x,y ,z)：同时画出数个小图形在同一视窗中 Real(x):求复数x 的实数部分 Imag(x):求复数x 的虚数部分 Abs （x ）：求复数x 的模 Angle(x):求复数x 的相位Conv(x,y):求x 和y 的卷积，注意下标是从1开始 Fliplr(x):信号反折（2）Matlab 编程和调试技巧：因为Matlab 语言是一种解释性语言，所以有时matlab 程序的执行速度不是很理想。

3 信号处理仿真实验（教师）3.1 MATLAB信号处理基础实验一、实验目的1．掌握MATLAB常用信号处理波形；2．学习信号序列的各种操作；3．学习离散傅立叶变换的MATALB相关操作。

二、实验内容1．产生下列各种波形，并记录结果。

（1）单位抽样序列x=[1 zeros(1,n-1)]>> n=7;>> x=[1 zeros(1,n-1)]x =1 0 0 0 0 0 0（2）单位阶跃矩阵x=ones(1,N)>> N=6;>> x=ones(1,N)x =1 1 1 1 1 1（3）实指数序列n=0:N-1;x=a.^n;>> a=6;>> N=6;>> n=0:N-1;>> x=a.^nx =1 6 36 216 1296 7776（4）复指数序列n=0:N-1;x=ex((lu+j*w0)*n);>> N=6;lu=3;w0=40;n=0:N-1;x=exp((lu+j*w0)*n)x =1.0e+006 *0.0000 -0.0000 + 0.0000i -0.0000 - 0.0004i0.0066 + 0.0047i -0.1588 + 0.0357i 1.5926 - 2.8548i（5）随机序列rand(1,N);randn(1,N);>> N=6;>> rand(1,N)ans =0.4565 0.0185 0.8214 0.4447 0.6154 0.7919 >> randn(1,N)ans =1.1892 -0.0376 0.3273 0.1746 -0.1867 0.7258 （6）方波t=0:0.1*pi:6*pi;y=square(t);axis([0 7*pi -1.5 1.5]);plot(t,y);xlabel('时间');ylabel('幅值');（7）正弦波t=0:0.01*pi:2*pi;x=sin(2*pi*t);plot(t,x);xlabel('时间');ylabel('幅值');（8）锯齿波Fs=10000;t=0:1/Fs:1.5;x=sawtooth(2*pi*50*t);plot(t,x);axis([0 0.2 -1 1]);（9）基本非周期波形t=0:1/1000:2;x=chirp(t,0,1,150);specgram(x,256,1000,256,250);（10）sinc信号t=linspace(-5,5);x=sinc(t);plot(t,x);（11）pulstran信号t=0:1/50E3:10E-3;d=[0:1/1E3:10E-3;0.8.^(0:10)]';x=pulstran(t,d,'gauspuls',10E3,0.5);plot(t,x);（12）diric信号t=[-4*pi:0.1/pi:4*pi];x=diric(t,7);y=diric(t,8);subplot(1,2,1);title('n为奇数');plot(t,x);subplot(1,2,2);plot(t,y);title('n为偶数');2．有两信号分别为)2sin(11t x πω=，)2sin(222t x πω=，其中Hz501=ω，Hz1202=ω，编程实现此二信号的叠加，并计算它的抽样和、抽样积、信号能量和信号功率。

信号处理仿真及应用实验指导书实验一 电路的建模与仿真——MATLAB 程序设计一、实验目的：1、熟悉MATLAB 命令和编辑、运行、调试环境；2、编写M 文件，实现电路仿真。

二、实验原理与方法：仿真RLC 电路的响应，要求运用电路分析知识编写M 文件，计算电流，并绘制出图形。

二、实验内容及步骤：方法一：采用函数文件形式进行仿真（参考教材P18例子）1、如下图所示电路的初始能量为零，t=0时刻，将一个25mA 的直流源作用到电路上，其中电容C=0.1F ，电感L=1H ，电阻R=4Ω，画出图中电感L 支路上电流i L 的图形。

列写出关于电感L 支路上电流i L 的微分方程 2、根据建模分析 3、进行MA TLAB 仿真建立M 文件，运行求解微分方程 4、绘制电感支路电流图形方法二、采用MA TLAB 函数dsolve 进行仿真1、运用电路分析知识建立电路模型如上图所示电路的初始能量为零，t=0时刻，将一个25mA 的直流源作用到电路上，其中电容C=25nF ，电感L=25mH ，电阻R=400Ω（注意该参数与前面的参数不同）。

列写出关于电感L 支路上电流i L 的微分方程因为电路初始能量为0，而且电感上的电流不能突变，所以在开关打开瞬间电感上的电流),0(0)(==t t i L 电感上的电压),0(0)(==t t V L 又,/)(*)(dt i d L t V L L =所以：0)0(=+dtdi L （1）根据电路图及基尔霍夫电流定律可得：I i i i C R L =++ （2）其中，C R i i ,的表达式分别如下：RV i R =，dtdV Ci C = （3）在上式中，V 为电阻R 两端电压，同时也就是电容两端电压，又有如下式关系：dtdi LV L =22dti d LdtdV L = （4）将（3）式与（4）式依次代入（2）式，可得如下表达式：LCI LCi dtdi RC dti d L L L =++1222、进行MATLAB 仿真建立M 文件，运行求解微分方程 desolve ：求解微分方程符号的一般指令，其通用格式为： ('1,2,','1,2,r d s o l v e e q e q c o n d c o n d v=⋅⋅⋅⋅⋅⋅其中，eq1,eq2,…分别代表按序排列的不同微分方程，cond1、cond2分别代表微分方程式的初始条件，v 代表微分方程中的独立变量（其默认独立变量为t ）。

MATLAB仿真与信号处理实践指导第一章：MATLAB仿真基础MATLAB是一种功能强大的数学软件，广泛应用于科学与工程领域的仿真和信号处理任务。

本章将向读者介绍MATLAB的基本概念和使用方法，帮助读者快速入门。

1.1 MATLAB简介MATLAB是由MathWorks公司开发的一种高级技术计算语言和环境。

它集成了数值计算、可视化和编程功能，可用于进行数据分析、仿真、建模、图像处理等多种任务。

1.2 MATLAB界面MATLAB的主要界面由命令窗口、脚本编辑器和变量浏览器组成。

命令窗口可以直接输入MATLAB命令，脚本编辑器用于编写和运行MATLAB脚本，变量浏览器可以查看和管理当前工作空间中的变量。

1.3 基本数据类型MATLAB支持多种基本数据类型，如数值、字符和逻辑类型。

数值类型包括整数、浮点数和复数。

字符类型用于表示文本数据，逻辑类型用于表示真假值。

1.4 基本操作MATLAB提供了丰富的数学和矩阵操作函数，如加法、乘法、求逆、求特征值等。

同时，MATLAB还支持向量化操作，可一次对整个矩阵或向量进行计算，提高运算效率。

第二章：MATLAB仿真实践本章将介绍MATLAB在仿真领域的应用，包括利用MATLAB进行线性系统仿真、非线性系统仿真和电路仿真等方面的实践。

2.1 线性系统仿真MATLAB提供了强大的线性系统仿真工具，如系统传输函数建模、频域分析、时域响应等。

通过MATLAB，可以对各种线性系统进行仿真和分析，如低通滤波器、控制系统等。

2.2 非线性系统仿真与线性系统仿真相比，非线性系统仿真更加复杂。

MATLAB提供了多种工具箱，如Simulink和Simscape，用于建立和仿真非线性系统模型。

通过这些工具，可以更加准确地模拟和预测非线性系统的行为。

2.3 电路仿真MATLAB还提供了用于电路仿真的工具，如Circuit Design Toolbox和Simscape Electronics。

信号分析与处理MATLAB仿真实验报告2009.12.25院系：电气工程学院专业: 自动化班级：姓名：学号：实验7 离散时间序列的卷积实验目的：学会用MATLAB实现对离散时间序列的卷积,掌握利用h(n) 与输入x(n)卷积来求系统零状态响应的方法。

实验要求：使用MATLAB中求卷积函数的conv(),并对结果分析总结。

实验内容：LTI系统的单位脉冲响应为h(n)=(0.9)n ε(n),输入序列为x(n)=ε(n)- ε(n-10),求系统的输出y(n)。

程序function [y,ny]=conv_m(x,nx,h,nh);y=conv(x(5:45),h);ny=nh;y=y(1:41);subplot(3,1,1);stem(nx,x,'filled');axis([-4,40,0,1]);title('x[n]');subplot(3,1,2);stem(nh,h,'filled');axis([-4,40,0,1]);title('h[n]');subplot(3,1,3);stem(ny,y,'filled');axis([-4,40,0,8]);title('y[n]');实验结果：结果分析：改变参数以后的程序：function [y,ny]=conv_m(x,nx,h,nh);y=conv(x(5:45),h);ny=nh;y=y(1:41);subplot(3,1,1);stem(nx,x,'filled');axis([-4,40,0,1]);title('x[n]'); subplot(3,1,2);stem(nh,h,'filled');axis([-4,40,0,1]);title('h[n]'); subplot(3,1,3);stem(ny,y,'filled');axis([-4,40,0,2]);title('y[n]');输出结果：实验8 连续时间信号的卷积实验目的：学会用MATLAB实现对连续时间信号的卷积，掌握利用卷积的方法求系统零状态响应，并与离散系统比较。

信号处理仿真(MATLAB)实验指导书青岛大学自动化工程学院电子工程系2011年4月MATLAB 实验一一、实验目的：1. Be familiar with MATLAB Environment2. Be familiar with array and matrix二、实验内容：1. Be familiar with Matlab 6.5Startup Matlab 6.5, browse the major tools of the Matlab desktop⏹ The Command Windows⏹ The Command History Windows⏹ Launch Pad⏹ The Edit/Debug Window⏹ Figure Windows⏹ Workspace Browser and Array Editer⏹ Help Browser⏹ Current Directory BrowserPART I:下列选择练习，不需提交实验报告1． Give the answer of the following questions for the array1.10.02.13.560.01.16.62.83.412.10.10.30.41.31.45.10.01.10.0a r r a y -⎡⎤⎢⎥-⎢⎥=⎢⎥-⎢⎥-⎣⎦ 1）What is the size of array1?2）What is the value of array1(4,1)?3）What is the size and value of array1(:,1:2)?4） What is the size and value of array1([1 3], end)?2． Give the answer of the following commad1) a=1:2:5; 2) b=[a ’ a ’ a ’]; 3) c=b(1:2:3,1:2:3);4) d=a+b(2,:) 5) w=[zeros(1,3) ones(3,1)’ 3:5’]3． Give the answer of the sub-arrays1.10.02.13.560.01.16.62.83.412.10.10.30.41.31.45.10.01.10.0a r r a y -⎡⎤⎢⎥-⎢⎥=⎢⎥-⎢⎥-⎣⎦ 1) array1(3,:); 2) array1(:,3); 3) array1(1:2:3,[3 3 4]) 4) array1([1 1],:)4． Give the answer of the following operations22111,,,(2)12022a b c d e y e --⎡⎤⎡⎤⎡⎤====⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦ 1) a+b 2) a*d 3) a.*d 4) a*c5) a.*c 6)a\b 7) a.\b 8)a.^bEXERCISE II:TEXT BOOK (4TH EDITION) PAGE 17-18:1.1, 1.4, 1.7MATLAB实验二一、实验目的：1. Be familiar with array and matrix2. Be familiar with MATLAB operations and simple plot functionPART I:下列选择练习，不需提交实验报告1．Edit & Run the m-file% test step response functionwn=6; kosi=[0.1:0.1:1.0 2];figure(1); hold onfor kos=kosinum=wn^2; den=[1,2*kos*wn,wn.^2]; step(num,den)endhold off;2．Edit & Run the m-file% test plot functionx=0:pi/20:3*pi; y1=sin(x); y2=2*cos(2*x); plot(x,y1,'rv:',x,y2,'bo--');title('Plot the Line of y=sin(2x) and its derivative'); xlabel('X axis'); ylabel('Y axis');legend('f(x)','d/dx f(x)'); grid on;3．Edit & Run the m-file% test subplot and loglog functionx=0:0.1:10; y=x.^2-10.*x+26;subplot(2,2,1); plot(x,y); grid on;subplot(2,2,2); semilogx(x,y); grid on;subplot(2,2,3); semilogy(x,y); grid on;subplot(2,2,4); loglog(x,y); grid on;4．Edit & Run the m-file% test max and plot functionvolts=120; rs=50; rl=1:0.1:100;amps=volts./(rs+rl); pl=(amps.^2).*rl; [maxvol,index]=max(pl);plot(rl,pl,rl(index),pl(index),'rh'); grid on;PART II:下列选择练习，需提交实验报告EXERCISE II:TEXT BOOK (4TH EDITION) PAGE 69-73:2.9 , 2.11, 2.13, 2.14，2.17 , 2.18MATLAB 实验三一、实验目的：1. Learn to design branch statements program2. Be familiar with relational and logical operators3. Practice 2D plotting二、实验内容：PART I: (选择练习，不需提交实验报告)1. Hold command exercisex=-pi:pi/20:pi;y1=sin(x); y2=cos(x); plot(x,y1, 'b-'); hold on;plot(x,y2, 'k--'); hold off;legend ('sinx', 'cosx')2. Figure command exercisefigure(1);subplot(2,1,1);x=-pi:pi/20:pi; y=sin(x); plot(x,y); grid on;title('Subplot 1 Title');subplot(2,1,2);x=-pi:pi/20:pi; y=cos(x); plot(x,y); grid on;title('Subplot 2 Title');3． Polar Plots exerciseg=0.5;theta=0:pi/20:2*pi;gain=2*g*(1+cos(theta));polar(theta,gain,'r-');title('\fontsize{20} \bfGain versus angle \theta');4. Assume that a,b,c, and d are defined, and evaluate the following expression.a=20; b=-2; c=0; d=1;(1) a>b; (2) b>d; (3) a>b&c>d; (4) a==b; (5) a&b>c; 6) ~~b;a=2; b=[1 –2;-0 10]; c=[0 1;2 0]; d=[-2 1 2;0 1 0];(7) ~(a>b) (8) a>c&b>c (9) c<=da=2; b=3; c=10; d=0;(10) a*b^2>a*c (11) d|b>a (12) (d|b)>aa=20; b=-2; c=0; d=’Test’;(13) isinf(a/b) (14) isinf(a/c) (15) a>b&ischar(d) (16) isempty(c)5. Write a Matlab program to solve the function 1()ln1y x x =-, where x is a number <1.Use an if structure to verify that the value passed to the program is legal. If the value of x is legal, caculate y(x). If not ,write a suitable error message and quit.PART II: (需提交实验报告)1. Write out m. file and plot the figures with gridsAssume that the complex function f(t) is defined by the equationf(t)=(0.5-0.25i)t-1.0Plot the amplitude and phase of function for 0 4.t ≤≤2. Write the Matlab statements required to calculate y(t) from the equation22350()350t t y t t t -+≥⎧=⎨+<⎩for value of t between –9 and 9 in steps of 0.5. Use loops and branches to perform this calculation.EXERCISE II:TEXT BOOK (4TH EDITION) PAGE 121-124:3.1， 3.3 , 3.5, 3.6, 3.7, 3.11, 3.14一、实验目的：1. Learn to design loop statements program2. Be familiar with relational and logical operators3. Practice 2D plotting二、实验内容：PART I: (选择练习，不需提交实验报告)pare the 3 approaches follows (Loops and Vectorization)%A. Perform calculation by For Loop with pre-initialize arraytic;square=zeros(1,10000) %pre-initialize arrayfor ii=1:10000square(ii)=ii^2;square_root(ii)=ii^(1/2);cube_root(ii)=ii^(1/3);endtoc; t1=toc%B. Perform calculation by For Loop without pre-initialize arraytic;for ii=1:10000square(ii)=ii^2;square_root(ii)=ii^(1/2);cube_root(ii)=ii^(1/3);endtoc; t2=toc%C. Perform calculation with vectorstic;ii=1:10000square(ii)=ii.^2;square_root(ii)=ii.^(1/2);cube_root(ii)=ii.^(1/3);endtoc; t3=tocEXERCISE II:TEXT BOOK (4TH EDITION) PAGE 165-171: 4.7，4.16，4.18，4.19，4.20，4.27一、实验目的：1. Learn to write MATLAB functions2. Be familiar with complex data and character data3. Practice 2D plotting二、实验内容：1. Write three Matlab functions to calculate the hyperbolic sine, cosine, and tangent functions:s i n h (),c o s h (),t a n ()22x xx x x x x x e e e e e e h e e -----+-=+ then plot the shapes of hyperbolic sine, cosine, and tangent functions on one figure, 55x -≤≤.2. Write a program use the function 32()552f x x x x =-+- and plot the line, and search for the minimum and maximum in 200 steps over the range of 13x -≤≤, mark the minimum and maximum on the line figure.3. Write a function to calculate the distance between two points 11(,)x y and 22(,)x y , that the points should be given by ‘input ’ function.4. Write a function complex_to that accept a complex number var , and returns two output arguments containing the magnitude mag and angle theta of the complex number. The output angle should be in degrees.Write another function polar_to_complex that accepts two input arguments containing the magnitude mag and angle theta of the complex number in degrees, and returns the complex number var .4. Write a program that accepts a series of strings from a user with the input function, sorts the strings into ascending order, and prints them out.EXERCISE II:TEXT BOOK (4TH EDITION) PAGE 213-223： 5.10， 5.11， 5.19， 5.25， 5.26， 5.33一、实验目的：1. Learn to write MATLAB functions2. Be familiar with complex data and character data5. Practice 2D plotting二、实验内容：1. Write three Matlab functions to calculate the hyperbolic sine, cosine, andtangent functions:s i n h (),c o s h (),t a n ()22x xx x x x x x e e e e e e h e e -----+-=+ then plot the shapes of hyperbolic sine, cosine, and tangent functions on one figure, 55x -≤≤.2. Write a program use the function 32()552f x x x x =-+- and plot the line,and search for the minimum and maximum in 200 steps over the range of 13x -≤≤, mark the minimum and maximum on the line figure.3. Write a function to calculate the distance between two points 11(,)x y and 22(,)x y , that the pointsshould be given by ‘input ’ function.4. Write a function complex_to that accept a complex number var , and returns two output arguments containing the magnitude mag and angle theta of the complex number. The output angle should be in degrees.Write another function polar_to_complex that accepts two input arguments containing the magnitude mag and angle theta of the complex number in degrees, and returns the complex number var .5. Write a program that accepts a series of strings from a user with the input function, sorts the strings into ascending order, and prints them out.EXERCISE II:TEXT BOOK (4TH EDITION) PAGE 265-267:6.2， 6.10， 6.11一、实验目的：1. Practice 2D plotting and 3D plotting2. Learn to use fplot function3. Be familiar with cell arrays and structure arrays二、实验内容：1. Give the 3D plot figure of 0.30.1()sin(3),()cos()t t x t e t y t e t --== use plot3 function, 020x ≤≤, and grid on, linewidth is 3.0.2. Plot the function sin x y e x -=, 02x ≤≤, step 0.1. Create the following plot types: (a) stem plot; (b) stair plot; (c) bar plot; (d) compass plot.3. Plot the function ()f x = over the range 0.110.0x ≤≤ using function fplot, and grid on.4. Create a cell arrays:5. Create a structure arrays and to calculate the mean billing of three patients:一、实验目的：Be familiar with Input/Output functions二、实验内容：1. Write a m-file. The m-file creates an array containing 150⨯random values, sorts the array into ascending order, opens a user-specified file for writing only, then writes the array to disk in 32-bit floating-point format , and close the file. It then opens the file and read the data back into 510⨯array.2. Edit a file as data4_4.txt that contains 44⨯square matrix, then import the array use uiimport function, and calculate the inverse of the square matrix .3.Write a program to read a set of integers from an input data file, and locate the largest andsmallest values within the data file. Print out the largest and smallest values, together with the lines on which they were found in one figure.一、实验目的：1.Be familiar with sound file2. Learn about create sound and use speaker.3. Making Music with MATLAB二、实验内容：Before we actually start making music, let's revise a few AC waveform basics. Consider the sine wave shown in the figure below:The sine wave shown here can be described mathematically as:v = A sin 2 π f twhere A is the Amplitude (varying units), f is the frequency (Hertz) and t is the time (seconds).T is known as the time period (seconds) and T=1/fBased on the equation,when t=0; v = A sin 2 π f(0) = 0when t=T/4; v = A sin 2 π f (T/4) = A sin 2 π f(1/4f) = A sin ( π/2) = A;when t=T/2; v = A sin 2 π f (T/2) = A sin 2 π f(1/2f) = A sin ( π) = 0;and so on.Sound waves are created when a waveform as shown here is used to vibrate molecules in a material mediumat audio frequencies (300 Hz <= f <= 3 kHz).If you wish to create a waveform such as the one shown in the figure, you would need to evaluate the function, v = A sin 2 π f t, at discrete times, t (shown as the time instants of the red dots), typically at equal time intervals. These time intervals must be "sufficiently" small (how small is small? Remember the Nyquist criterion?..........) to obtain a "smooth" waveform.This time interval is called the "Sampling Interval" and the process of breaking up a continuous waveform by specifying it only at discrete points in time is called sampling. (you should already know much of this stuff from the previous Clinic on Data Acquisition Basics).The sampling interval, shown here is T s; corresponding to that there exists a "Sampling Frequency", fs = 1/T s.As an example, the MATLAB code to create a sine wave of amplitude A = 1, at audio frequency of 466.16Hz (corresponds to A# in the Equal Tempered Chromatic Scale) would be:>> v = sin(2*pi*466.16*[0:0.000125:1.0]);The vector, v, now contains samples of the sine wave, starting at t=0 s, to t=1.0 s, in samples spaced 0.000125 s apart (the sampling interval T s). This corresponds to a sampling frequency of 8 KHz, which is standard for voice grade audio channel.Now, you can either plot this sine wave; or you can hear it!!!To plot, simply do>> plot(v);To hear v, you need to convert the data contained in v to some standard audio format that can be played using a Sound Card and Speakers on your PC. One such standard audio format is called the "wav" format. Matlab provides a function called wavwrite to convert a vector into wav format and save it on disk. Do >> help wavwrite for more details. Now, to create a wav file, do>> wavwrite(v, 'asharp.wav'); (you can give any file name between the ' ' s)Now, you can "play" this wav file called asharp.wav using any multimedia player. For example, you could use the Sound Recorder program. Start this by pointing to Start - Programs - Accessories - Multimedia - Sound Recorder. Open the wav file using the File Menu and press Play. If you have installed a sound card and a pair of speakers on your PC, you should be able to hear a short note.Now that you can make a single note, you can put notes together and make music!!!Let's look at the following piece of music:A A E E F# F# E ED D C#C# B B A AE E D D C# C# B B (repeat once)(repeat first two lines once)The American Standard Pitch for each of this notes is:A: 440.00 HzB: 493.88 HzC#: 554.37 HzD: 587.33 HzE: 659.26 HzF#: 739.99 HzAssuming each note lasts for 0.5 seconds, the MA TLAB m-file for creating a wav file for this piece of music would be:clear;a=sin(2*pi*440*(0:0.000125:0.5));b=sin(2*pi*493.88*(0:0.000125:0.5));cs=sin(2*pi*554.37*(0:0.000125:0.5));d=sin(2*pi*587.33*(0:0.000125:0.5));e=sin(2*pi*659.26*(0:0.000125:0.5));fs=sin(2*pi*739.99*(0:0.000125:0.5));line1=[a,a,e,e,fs,fs,e,e,];line2=[d,d,cs,cs,b,b,a,a,];line3=[e,e,d,d,cs,cs,b,b];song=[line1,line2,line3,line3,line1,line2];wavwrite(song,'song.wav');HINT: Before you code the entire song, just code the first line, create a wav file, play it and make sure everything works.MATLAB实验十-十六。

第二部分上机实验实验一连续时间信号的时域分析一、实验目的：1、熟悉表示连续时间信号的MATLAB函数；2、掌握用MATLAB描绘二维图像的方法。

3、掌握用MATLAB对连续信号进行基本的运算和时域变换的方法。

二、实验原理：（一）连续时间信号的时域表示信号是消息的载体，是消息的一种表现形式。

信号可以是多种多样的，通常表现为随时间变化的某些物理量，一般用x(t)或x(n)来表示。

信号按照自变量的取值是否连续可分为连续时间信号和离散时间信号。

连续时间信号是指自变量的取值范围是连续的，且对于一切自变量的取值，除了有若干不连续点以外，信号都有确定的值与之对应。

严格来说，MATLAB并不能处理连续信号，而是用等时间间隔点的样值来近似地表示连续信号。

当取样时间间隔足够小时，这些离散的样值就能较好地近似连续信号。

在MATLAB中通常用向量来表示连续时间信号，向量需要与时间变量相对应。

对于连续时间信号x(t)，可用x、t两个行向量来表示。

其中向量t是形如t = t1:p:t2的MATLAB命令定义的时间范围向量，t1为信号起始时间，t2为终止时间，p为时间间隔。

向量x为连续信号x(t)在向量t所定义的时间点上的样值。

如产生连续信号t ttSa tx)sin( )()(==可用如下命令实现：t =-10:1.5:10;x=sin(t)./ t;在命令窗口（Command Window）中可得到程序执行的结果即x、t的具体值。

注意：在MATLAB程序调试过程中，有时程序执行不出结果或虽然出结果但存在一些问题，MATLAB 都会在Command窗口中给出错误说明，掌握利用Command窗口中的说明检查程序的方法。

用上述向量对连续信号进行表示后，就可以用plot命令绘制信号的时域波形。

命令如下：plot(t,x)title(‘x(t)=Sa(t)’)xlabel(‘t’)axis([-10,10,-0.2,1.2])绘制的信号波形如图一所示，当把t改为：t =-10:0.5:10;则可得到图二。

数字信号处理的Matlab仿真（一）、连续信号及其MATLAB实现1、单位冲击信号例1.1：t=1/A=50时，单位脉冲序列的MA TLAB实现程序如下：clear all;t1=-0.5:0.001:0;A=50;A1=1/A;n1=length(t1);u1=zeros(1,n1);t2=0:0.001:A1;t0=0;u2=A*stepfun(t2,t0);t3=A1:0.001:1;n3=length(t3);u3=zeros(1,n3);t=[t1 t2 t3];u=[u1 u2 u3];plot(t,u)axis([-0.5 1 0 A+2])2、任意函数例1.2：用MA TLAB画出如下表达式的脉冲序列clear all;t=-2:1:3;N=length(t);x=zeros(1,N);x(1)=0.4;x(2)=0.8x(3)=1.2;x(4)=1.5;x(5)=1.0;x(6)=0.7;stem(t,x);axis([-2.2 3.2 0 1.7])3、单位阶跃函数例1.3：用MA TLAB实现单位阶跃函数clear all;t=-0.5:0.001:1;t0=0;u=stepfun(t,t0);plot(t,u)axis([-0.5 1 -0.2 1.2])4、斜坡函数例1.4：用MA TLAB实现g(t)=3(t-1) clear all;t=0:0.01:3;B=3;t0=1;u=stepfun(t,t0);n=length(t);for i=1:nu(i)=B*u(i)*(t(i)-t0);endplot(t,u)axis([-0.2 3.1 -0.2 6.2])5、实指数函数例1.5：用MA TLAB实现clear all;t=0:0.001:3;A=3;a=0.5;u=A*exp(a*t);plot(t,u)axis([-0.2 3.1 -0.2 14])6、正弦函数例1.6：用MA TLAB实现正弦函数f(t)=3cos(10πt+1) clear all;t=-0.5:0.001:1;A=3;f=5;fai=1;u=A*sin(2*pi*f*t+fai);plot(t,u)axis([-0.5 1 -3.2 3.2])（二）、离散信号及其MA TLAB实现1、单位冲激序列例2.1：用MA TLAB产生64点的单位冲激序列clear all;N=64;x=zeros(1,N);x(1)=1;xn=0:N-1;stem(xn,x)axis([-1 65 0 1.1])2、任意序列例2.2：用MA TLAB画出如下表达式的脉冲序列clear all;N=8;x=zeros(1,N);x(1)=8.0;x(2)=3.4x(3)=1.8;x(4)=5.6;x(5)=2.9;x(6)=0.7;xn=0:N-1;stem(xn,x)axis([-1 8 0 8.2])3、单位阶跃序列例2.3：用MA TLAB实现单位阶跃函数clear all;N=32;x=ones(1,N);xn=0:N-1;stem(xn,x)axis([-1 32 0 1.1])4、斜坡序列例2.4：用MA TLAB实现g(n)=3(n-4)点数为32的斜坡序列clear all;N=32;k=4B=3;t0=1;x=[zeros(1,k) ones(1,N-k)];for i=1:Nx(i)=B*x(i)*(i-k);endxn=0:N-1;stem(xn,x)axis([-1 32 0 90])5、正弦序列例2.5：用MA TLAB实现幅度A=3，频率f=100，初始相位Φ=1.2，点数为32的正弦信号clear all;N=32;A=3;f=100;fai=1.2;xn=0:N-1;x=A*sin(2*pi*f*(xn/N)+fai);stem(xn,x)axis([-1 32 -3.2 3.2])6、实指数序列例2.6：用MA TLAB实现，点数为32的实指数序列clear all;N=32;A=3;a=0.7;xn=0:N-1;x=A*a.^xn;stem(xn,x)7、复指数序列例2.7：用MA TLAB实现幅度A=3，a=0.7，角频率ω=314，点数为32的实指数序列clear all;N=32;A=3;a=0.7;w=314;xn=0:N-1;x=A*exp((a+j*w)*xn);stem(xn,x)8、随机序列利用MATLAB产生两种随机信号：rand(1,N)在区间上产生N点均匀分布的随机序列randn(1,N)产生均值为0，方差为1的高斯随机序列，即白噪声序列例2.8：用MA TLAB产生点数为32的均匀分布的随机序列与高斯随机序列clear all;N=32;x_rand=rand(1,N);x_randn=randn(1,N);xn=0:N-1;figure(1);stem(xn,x_rand)figure(2);stem(xn,x_randn)（三）、离散信号的基本运算1、信号的延迟给定离散信号x(n)，若信号y(n)定义为：y(n)=x(n-k)，那么y(n)是信号x(n)在时间轴上右移k个抽样周期得到的新序列。

实验一一、实验要求：IIR 数字滤波器的设计和实现DTMF 信号的编码: 把你的联系电话号码 DTMF 编码生成为一个 .wav 文件。

技术指标：根据 ITU Q.23 建议，DTMF 信号的技术指标是：传送/接收率为每秒 10 个号码，或每个号码 100ms。

每个号码传送过程中，信号存在时间至少 45ms，且不多于 55ms，100ms 的其余时间是静音。

在每个频率点上允许有不超过±1.5% 的频率误差。

任何超过给定频率±3.5% 的信号，均被认为是无效的，拒绝接收。

二、实验代码d=input('please enter number: ','s'); % 输入电话号码sum=length(d);total_x=[];sum_x=[];sum_x=[sum_x,zeros(1,800)];for a=1:sum %循环sum次symbol=abs(d(a)); % 求输入的ASCII码tm=[49,50,51,65;52,53,54,66;55,56,57,67;42,48,35,68]; % DTMF表中键的% 16个ASCII码for p=1:4;for q=1:4;if tm(p,q)==abs(d(a)); break,end % 检测码相符的列号qendif tm(p,q)==abs(d(a)); break,end % 检测码相符的行号p endf1=[697,770,852,941]; % 行频率向量f2=[1209,1336,1477,1633]; % 列频率向量n=1:400;x=sin(2*pi*n*f1(p)/8000) + sin(2*pi*n*f2(q)/8000); % 构成双频信号x=[x,zeros(1,400)]; %加长序列，增加静音sum_x=sum_x+x;total_x=[total_x x]; %将所有编码连接起来endsound(total_x); % 播放声音t=total_x/2;wavwrite(t,'我的手机号码'); %生成声音文件plot(total_x);title('DTMF信号时域波形');% 接收检测端的程序k1 = [18 20 22 24 31 34 38 42]; % 要求的DFT样本序号%k2 = [35 39 43 47 61 67 74 82]; % 要求的DFT样本序号kx=k1+1;%ky=k2+1;N=205;SK=[];out=[];for a=1:summ=800*(a-1);X=goertzel(total_x(m+1:m+N),kx); % 用Goertzel算法val = abs(X);SK=[SK;val];limit = 80; % 判决门限for s=5:8;if SK(a,s) > limit, break, end % 查找列号endfor r=1:4;if SK(a,r) > limit, break, end % 查找行号endend三、实验结果生成声音文件“我的手机号码”。

用MatLab仿真通信原理系列实验一、引言通信原理是现代通信领域的基础理论，通过对通信原理的研究和仿真实验可以更好地理解通信系统的工作原理和性能特点。

MatLab作为一种强大的数学计算软件，被广泛应用于通信原理的仿真实验中。

本文将以MatLab为工具，介绍通信原理系列实验的仿真步骤和结果。

二、实验一：调制与解调1. 实验目的通过MatLab仿真，了解调制与解调的基本原理，并观察不同调制方式下的信号特征。

2. 实验步骤（1）生成基带信号：使用MatLab生成一个基带信号，可以是正弦波、方波或任意复杂的波形。

（2）调制：选择一种调制方式，如调幅（AM）、调频（FM）或相移键控（PSK），将基带信号调制到载波上。

（3）观察调制后的信号：绘制调制后的信号波形和频谱图，观察信号的频谱特性。

（4）解调：对调制后的信号进行解调，还原出原始的基带信号。

（5）观察解调后的信号：绘制解调后的信号波形和频谱图，与原始基带信号进行对比。

3. 实验结果通过MatLab仿真，可以得到不同调制方式下的信号波形和频谱图，观察到调制后信号的频谱特性和解调后信号的还原效果。

可以进一步分析不同调制方式的优缺点，为通信系统设计提供参考。

三、实验二：信道编码与解码1. 实验目的通过MatLab仿真，了解信道编码和解码的基本原理，并观察不同编码方式下的误码率性能。

2. 实验步骤（1）选择一种信道编码方式，如卷积码、纠错码等。

（2）生成随机比特序列：使用MatLab生成一组随机的比特序列作为输入。

（3）编码：将输入比特序列进行编码，生成编码后的比特序列。

（4）引入信道：模拟信道传输过程，引入噪声和干扰。

（5）解码：对接收到的信号进行解码，还原出原始的比特序列。

（6）计算误码率：比较解码后的比特序列与原始比特序列的差异，计算误码率。

3. 实验结果通过MatLab仿真，可以得到不同编码方式下的误码率曲线，观察不同信道编码方式对信号传输性能的影响。

《信号与系统》MATLAB仿真实验讲义（第二版）肖尚辉编写宜宾学院电信系电子信息教研室《信号与系统》课程2004年3月 宜宾使用对象：电子专业02级3/4班（本科）实验一 产生信号波形的仿真实验一、实验目的：熟悉MATLAB软件的使用，并学会信号的表示和以及用MATLAB来产生信号并实现信号的可视化。

二、实验时数：3学时+3学时（即两次实验内容）三、实验内容：信号按照自变量的取值是否连续可分为连续时间信号和离散时间信号。

对信号进行时域分析，首先需要将信号随时间变化的规律用二维曲线表示出来。

对于简单信号可以通过手工绘制其波形，但对于复杂的信号，手工绘制信号波形显得十分困难，且难以绘制精确的曲线。

在MATLAB中通常用三种方法来产生并表示信号，即（1）用MATLAB软件的funtool符合计算方法（图示化函数计算器）来产生并表示信号；（2）用MATLAB软件的信号处理工具箱（Signal Processing Toolbox）来产生并表示信号；（3）用MATLAB软件的仿真工具箱Simulink中的信号源模块。

（一） 用MATLAB软件的funtool符合计算方法（图示化函数计算器）来产生并表示信号在MATLAB环境下输入指令funtool，则回产生三个视窗。

即figure No.1：可轮流激活，显示figure No.3的计算结果。

figure No.2：可轮流激活，显示figure No.3的计算结果。

figure No.3：函数运算器，其功能有：f，g可输入函数表达式；x是自变量，在缺省时在[－2pi，2pi]的范围内；自由参数是a；在分别输入完毕后，按下面四排的任一运算操作键，则可在figure No.1或figure No.2产生相应的波形。

学生实验内容：产生以下信号波形3sin(x)、5exp(-x)、sin(x)/x、1－2abs(x)/a、sqrt(a*x)（二） 用MATLAB软件的信号处理工具箱（Signal Processing Toolbox）来产生并表示信号一种是用向量来表示信号，另一种则是用符合运算的方法来表示信号。

matlab数字信号处理仿真第一实验室：基础实验篇第Ⅰ部分基本训练题目第Ⅱ部分简介各题目的原理、程序、效果第Ⅲ部分基研训练程序软件压缩文件第Ⅰ部分基本训练题目1-1-1 序列的图示方法 DSP11011-1-2 连续信号及采样信号的图示方法 DSP 11021-1-3单位冲激序列函数impseq单位冲激序列图示 DSP 11031-1-4 单位阶跃序列函数stepseq单位阶跃序列图示 DSP11041-1-5 矩形序列)(n R N 及图示 DSP11051-1-6 实指数序列)(n a n ε及图示 DSP11061-1-7 正弦序列)sin(n *ω及图示 DSP11071-1-8 复指数序列n jm e *+)(σ及图示 DSP11081-1-9 周期序列)()(N n x n x +=及图示 DSP 11091-1-10 常用5种连续信号及图示 DSP11101-1-11 离散序列的运算 DSP11111-1-12 输入序列)(n x 与系统冲激响应)(n h 的卷积),(h x conv DSP11121-1-13 非零起点时两信号的卷积),(h x convm DSP11131-2-1 指数序列)(8.0)(n n x n ε=的离散时间傅立叶变换DSP 12011-2-2 矩形序列)(n R N 的离散时间傅立叶变换 DSP12021-2-3 离散时间傅立叶变换的性质 DSP12031-2-4 正弦序列输入，输出为正弦序列，幅度相位因)(ωj e H 变化DSP1204 1-2-5 模拟信号t a e t x 1000)(-=付氏变换与采样信号的离散时间傅立叶变换DSP 12051-3-1 N 点离散傅立叶变换 dft(xn,N)1-3-2 N 点离散傅立叶反变换 idft(xn,N)1-3-3 DFT 与)(n x 的Z 变换关系 DSP13031-3-4 DFT 与)(n x 的离散时间傅立叶变换的关系 DSP 13041-3-5 有限长序列添零填充，得高密度DFT ，离散时间付氏频谱不变DSP1305 1-3-6 采样点增多的高分辨率DFT ，采样点数少仅添零的高密度DFT DSP1306 1-3-7 DFT 的圆周移位函数cirshftt 1-3-8 DFT 圆周移位实例 DSP13081-3-9 圆周卷积 DSP13091-3-10 复共轭序列的DFT DSP13101-3-11 DFT 的共轭对称性 DSP 13111-3-12 补零填充实现线性卷积 DSP13121-3-13 重迭保留法实现线性卷积 DSP13131-3-14 重迭保留实现函数 ovrlpsav1-3-15 DET 对连续信号作近似谱分析：滤高频，避免混迭频谱；截高时；变有限长序列，避免泄漏频谱 DSP13151-3-16 采样点为100，进行200点DFT ，对)(t e t ε-进行谱分析DSP 1316 1-3-17 实序列的奇偶分解及DFT 的虚实分量 DSP1317 1-3-18 实序列的奇偶分解函数 DSP13181-3-19 用FFT 分析信号频率成分 DSP13191-3-20 用FFT 分析语言信号的频谱 DSP13201-3-21 DCT 变换 DSP13211-3-22 用DCT 变换进行语言压缩 DSP13221-3-23 线性调频Z 变换 DSP13231-3-24 利用CZT 计算滤波器100—150HZ 频率特性的细节DSP13242-1-1 直接型实现系统函数H （Z ）的IIR 数字滤波器 DSP 2101 2-1-2 级联型实现系统H （Z ）的IIR 数字滤波器 DSP21022-1-3 级联型实现H （Z ）的IIR 数字滤波器 DSP21032-1-4 直接型实现H （Z ）的IIR 数字滤波器 DSP21042-1-5 并联型实现H （Z ）的IIR 数字滤波器 DSP 21052-1-6 并联型 DSP 21062-1-7 直接型 DSP21072-1-8 最终的级联，并联 DSP21082-1-9 直接型?级联型 dir2cas(b,a)2-1-10 级联型→直接型 cas2par(b0,B,A)2-1-11 直接型→并联型 dir2par2-1-12 并联型→直接型 par2dire2-1-13 并联型→级联型 casfilter2-1-14 级联型→并联型 parfilter2-2-1 FIR 直接型滤波器 DSP 22012-2-2 FIR 级联型滤波器 DSP22022-2-3 FIR 的频率取样形式结构 DSP 22032-2-4 （原例11）由频率样本{2,1,0315,......5,415.00)(====k k k k H求频率采样形式，及单位冲激响应)(n h DSP22042-2-5 窄带滤波器中的频率采取滤波器是由直接型转换为频率采样型 dir2fs(n)3-1-1 偶对称奇序列的⒈型FIR 滤波器的振幅响应 hr_type13-1-2 偶对称奇序列的)(ωH 及零极点分布 DSP31023-1-3 偶对称偶序列的Ⅱ型FIR 滤波器的振幅响应 hr_type23-1-4 偶对称偶序列的)(ωH 及零极点分布 DSP31043-1-5 奇对称奇序列的Ⅲ型FIR 滤波器的振幅响应 hr_type33-1-6 奇对称奇序列的)(ωH 及零极点分布 DSP31063-1-7 奇对称偶序列的Ⅳ型FIR 滤波器的振幅响应 hr_type43-1-8 奇对称偶序列的)(ωH 及零极点分布 DSP31083-1-9 线性相位FIR 滤波器的零点位置有4种可能 DSP31093-1-10 常用加窗函数 DSP32103-1-11 对信号用加窗函数的DFT 分析频谱 DSP32113-2-1 计算理想低通滤波器的)(n h a DSP32013-2-2 计算FIR 滤波器的绝对和相对的幅度响应 DSP32023-2-3 提取大于50dB 衰减的汉明窗FIR 低通滤波器 DSP3203 3-2-4 理想高通，偶对称因果序列，N 为奇的窗函数，滤波器的单位冲激响应)(n h d DSP32043-2-5 汉宁窗，44dB 最小阻带衰减，过度带N π2.6 DSP3205 3-2-6 理想高通，奇对称因果序列，N 为偶的窗函数，滤波器的单位冲激响应)(n h d DSP32063-2-7 汉宁窗，44dB 最小阻带衰减，过度带N π2.6 DSP3207 3-2-8 理想高通，偶对称因果序列，N 为奇的窗函数，滤波器的单位冲激响应)(n h d DSP32083-2-9 设计一个数字FIR 带通滤波器 DSP32093-2-10 理想带通数字滤波器的频率响应)(e H jw d DSP3210 3-2-11 设计一个具有2π相移的数字FIR 带通滤波器 DSP3211 3-2-12 理想带阻，偶对称因果序列，N 为奇的窗函数，滤波器的单位冲激响应)(n h d ideal-be()3-2-13 设计一个数字FIR带阻滤波器DSP32133-3-1 采样点ω=0处的频率采样法DSP33013-3-2 在过渡带上加两个T1和T2 DSP33023-3-3 设计2型FIR低通滤波器 DSP33033-3-4 设计1型FIR高通滤波器 DSP33043-3-5 设计4型FIR高通滤波器 DSP33053-3-6 设计2型FIR带通滤波器 DSP33063-3-7 设计1型FIR带阻滤波器 DSP33073-3-8 设计1型FIR低通滤波器 DSP33083-3-9 设计1型FIR高通滤波器 DSP33093-3-10 设计4型FIR高通滤波器 DSP33103-3-11 设计3型FIR带通滤波器 DSP33113-4-1 用频率响应采样法1设计具有线性相位 DSP34013-4-2 用窗函数法设计具有线性相位 DSP34023-4-3 用频率采样法1设计低通滤波器对其进行除噪 DSP3403 4-1-1 在MATLAB中用afd_butt(Omegap,Omegar,Ap,Ar)函数来设计巴特沃斯模拟低通滤波器 DSP41014-1-2 若设计非归一化（Ωc≠1）巴特沃斯模拟低通滤波器原型DSP4102 4-1-3 freqs_m(b,a,Omega_max)函数 DSP4103 4-1-4 sdir2cas函数 DSP41044-1-5 设计一个巴特沃斯模拟滤波器 DSP41054-2-1 用来实现N阶、通带波动为δ的归一化切比学夫1型模拟低通滤波器DSP42014-2-2 根据技术指标设计切比学夫1型模拟滤波器 DSP42024-2-3 设计一个低通切比学夫1型滤波器 DSP42034-2-4 设计归一化切比学夫2型模拟滤波器 DSP42044-2-5 根据给定指标设计切比学夫2型模拟滤波器 DSP42054-2-6 设计一个切比学夫2型低通滤波器 DSP42064-3-1 用imp_invr函数实现脉冲响应不变法DSP 43014-3-2 设计一个巴特沃斯模拟滤波器 DSP43024-3-3 设计低通数字滤波器 DSP43034-3-4 设计低通数字滤波器 DSP43044-4-1 双线性变换法设计低通数字滤波器 DSP44014-4-2 切比雪夫滤波器原型用双线性变换法设计低通数字滤波器DSP44024-5-14-5-24-5-34-5-4 分别设计一个巴特沃斯滤波器和切比雪夫高通滤波器DSP45044-5-5 分别设计一个巴特沃斯滤波器和切比雪夫高通滤波器DSP45054-5-6 设计一个巴特沃斯带通滤波器 DSP45064-5-7 设计一个切比雪夫带通滤波器 DSP45074-5-8 设计一个滤波器 DSP45084-5-9 设计一个滤波器 DSP45094-5-10 设计一个滤波器 DSP45104-6-1 zampping DSP46014-6-2用zmapping函数实现例11中的高通滤波器 DSP4602 4-6-3切比雪夫1型高通数字滤波器，上述过程由chebhpf函数实现 DSP4603 4-6-4用数字频域变换法，设计一个切比雪夫1型高通数字滤波器 DSP46044-6-5 用双线性变换法设计低通滤波器 DSP46054-6-6 用脉冲响应不变法设计的低通滤波器对其除噪 DSP4606 4-6-7 模拟信号DSP46075-1-1下采样DSP 51015-1-2 例题DSP51025-1-3上采样DSP51035-1-4 程序DSP51045-1-5 采样率的非整数倍转换DSP51055-1-6 程序DSP51065-1-7 例题DSP51075-1-8 用傅立叶变换对信号进行消噪声处理DSP51085-1-9 信号特定频率的提取DSP51095-1-10例题DSP51105-1-11信号特定频率区间的抑制DSP5111第Ⅱ部分简介各题目的原理、程序、效果1-1-1 序列的图示方法DSP1101原理：数字信号处理中，所有信号都是离散时间信号——序列。

MATALB信号处理实习报告一、实习目的“数字信号处理”是电子信息工程专业的主干课程，其理论性较强，学生通过理论课的系统学习后，应通过MATLAB语言对其所涉及的算法进行仿真，这不仅能帮助学生理解其抽象的物理概念，工程概念和复杂算法，加强感性认识，而且能激发学生更进一步地在该领域的学习和探索热情。

二、实习任务及功能概述1. FT与DFT关系的MATLAB仿真任务要求：（1）任设一个长度为N的实序列；（2）编写MATLAB代码，实现该序列的傅立叶变换和离散傅立叶变换；（3）调试运行代码，得到仿真图形；（4）通过仿真图形观察二者的关系，并得出结论。

% x is original sequency,N is transforming point% X is FT result of x,XK is DFT result of xfunction [X,Xk]=mydft(x,N)w=2*pi*(0:127)/128;X=x*exp(-j*[1:length(x)]'*w) % x 的傅立叶变换FTsubplot(211)plot(w,abs(X))k=0:N-1;XK=x*exp(-j*[1:length(x)]'*(2*pi*k)/N) % x的离散傅立叶变换DFTsubplot(212)stem(k,abs(XK))end>> x=[1 0 1 0 0 1 0 1];>> N=32;>> mydft(x,N)由图可得DFT 是有限长序列傅里叶变换的有限点离散采样。

2. DFT 的快速算法FFT 的仿真任务要求：（1）在熟悉FFT 算法原理的基础上，对所给的时域信号进行分析；（2）对信号做时域分析时要注意混叠现象的发生；（3）对混合信号)2sin()2sin()2sin()(321t f ft t f t f πππ++=做快速傅立叶变换FFT 运算，其中1f 、2f 、3f 自设，变换点数根据所设的情况自定；（4）对变换结果做分析。