2017春沪教版数学五下48《表面积的变化》同步练习2
- 格式:doc
- 大小:14.00 KB
- 文档页数:2
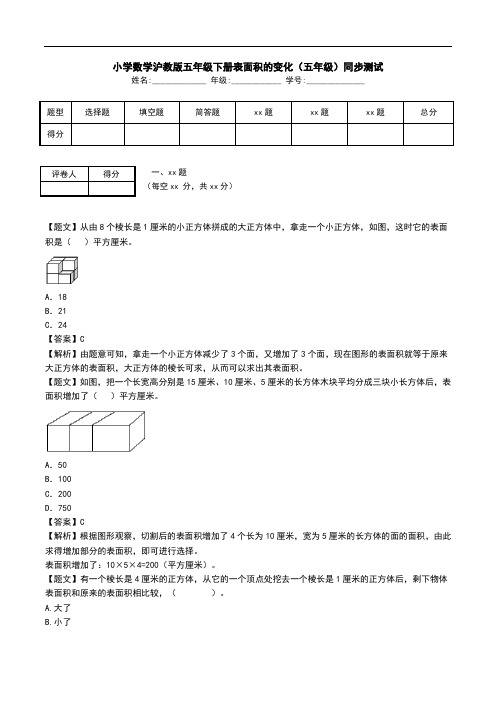
小学数学沪教版五年级下册表面积的变化(五年级)同步测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题(每空xx 分,共xx分)【题文】从由8个棱长是1厘米的小正方体拼成的大正方体中,拿走一个小正方体,如图,这时它的表面积是()平方厘米。
A.18B.21C.24【答案】C【解析】由题意可知,拿走一个小正方体减少了3个面,又增加了3个面,现在图形的表面积就等于原来大正方体的表面积,大正方体的棱长可求,从而可以求出其表面积。
【题文】如图,把一个长宽高分别是15厘米、10厘米、5厘米的长方体木块平均分成三块小长方体后,表面积增加了()平方厘米。
A.50B.100C.200D.750【答案】C【解析】根据图形观察,切割后的表面积增加了4个长为10厘米,宽为5厘米的长方体的面的面积,由此求得增加部分的表面积,即可进行选择。
表面积增加了:10×5×4=200(平方厘米)。
【题文】有一个棱长是4厘米的正方体,从它的一个顶点处挖去一个棱长是1厘米的正方体后,剩下物体表面积和原来的表面积相比较,()。
A.大了B.小了评卷人得分C.不变D.无法确定【答案】C【解析】根据观察可得:挖去小正方体后,减少三个面,同时又增加三个面,其实剩下的图形的表面积与原正方体的面表积是相等的。
【题文】如图是一个长3厘米,宽与高都是2厘米的长方体,在它的上面挖掉一个棱长为1厘米的小正方体,这时它的表面积是()平方厘米。
A.32B.34C.不能计算【答案】B【解析】由图意可知:在它的上面挖掉一个棱长为1厘米的小正方体,则增加了小正方体的2个面的面积,于是利用正方体的表面积加上小正方体的2个面的面积,问题即可得解。
3×2×4+2×2×2+(2÷2l【答案】D【解析】由题意得:减少部分是这个正方体的两个面的面积,由此解答出正确的结果,即可得出正确答案。





表面积的变化(练习3-4)教学内容:练习3、4。
教学目标:知识与技能:利用表面积等有关知识,探索多个相同长方体叠放后表面积变化的规律。
通过动手动脑,培养学生合理归纳、分析的能力,进一步促进空间观念的形成。
过程和方法:在操作、观察、分析等活动中,综合运用了相关知识,解决物体表面积变化的问题。
情感态度价值观:学生在活动中体会合作的乐趣,感悟数学与生活的密切联系。
学生能运用知识解释生活中的一些现象,将数学知识应用到日常生活中去。
教学重点:利用表面积等有关知识,探索多个相同长方体叠放后表面积变化的规律。
教学难点:在操作、观察、分析等活动中,综合运用了相关知识,解决物体表面积变化的问题。
课前准备:多媒体课件。
教学过程:一、创设情景,导入新知。
(练习3)1.今天,小胖的妈妈休息,她到农工商超市去买2盒巧克力,回家后交给小胖,让他包装好以后送给表妹。
2.妈妈提出问题:将2盒巧克力包成一包,可能有几种不同的包装方法?哪种方法包装纸最省?【设计意图:通过妈妈让小胖包装巧克力的的事情,给学生设疑,激发学生学习兴趣。
】二、学生探究1.学生讨论有几种不同的包装方法?上(下)面重叠;前(后)面重叠;左(右)面重叠一共有三种不同的包装方法?2.讨论得出:包装后表面积最小的那种方法最节省包装纸?3.计算表面积方法一的表面积=3×2×2+3×2×2+2×2×2=32dm2方法二的表面积=2×1×2+6×2×2+6×1×2=40dm2方法三的表面积=3×1×2+4×1×2+4×3×2=38dm232dm2<38dm2<40dm2方法一最节省包装纸。
4.们还有其他更好的办法吗?小组讨论:最大的面合一起,表面积就最小【设计意图:以学生为主体,提供给他们自主探索规律的问题。
课题:表面积的变化热身练习(1)将2个棱长为1厘米的小正方体,拼成一个长方体,拼成后的长方体的表面积比原来2个单独的小正方体的表面积减少了 2 个正方形的面积;(2)将5个棱长为1厘米的小正方体,拼成一个长方体,拼成后的长方体的表面积比原来5个单独的小正方体的表面积减少了8个正方形的面积;(3)将棱长为2厘米的3个小正方体拼成一个长方体,拼成后的长方体表面积比原来3个小正方体的表面积之和减少了16 平方厘米;知识精要(1)多个小正方体拼成长方体表面积的变化★把长方体或正方体切成两个或几个长方体(正方体),每切一下会增加2个切面的面积。
反之,把几个长方体或正方体拼成一个长方体,每拼一下会减少2个面的面积。
以此类推得到,增加(或减少)的表面积与切(或拼)的次数n有关,为n×2个拼切面的面积★如何使包装最小几个相同长方体包装在一起,要想使包装纸最节约,就要使最大的面叠加在一起,只有这样,露在外面的面即包装后的表面积最小,包装最节约精解名题【例1】把5个完全一样的正方体拼成一个长方体,长方体的表面积是198平方厘米,求原来一个正方体的表面积?解:54平方厘米【例2】一个长方体长5厘米、宽2厘米、高4厘米,把这个长方体截成大小相等的两个小长方体,两个小长方体的表面积之和比原来这个长方体的表面积增加多少平方厘米?解:3种情况:2×5×2 2×5×4 2×2×4【例3】将3盒长20厘米,宽15厘米,高5厘米的巧克力装成一包,怎样包才能节约包装纸?(接口处不计)需要多少平方厘米的包装纸?解:垒成一个长20厘米,宽15厘米,高5×3=15厘米的大长方体直接运用表面积公式计算包装纸的面积:2×(20×15+20×15+15×15)(2)长、宽、高的变化所引起表面积的变化★若长方体或正方体的高增加(或减少),那么表面积增加(或减少)的大小=长和宽所形成的底面的周长×高增加的数量。
表面积的变化练习题
班级姓名学号
一、填空:
1、5个棱长1cm的正方体小方块排成一行后,它的表面积就是( )。
2、把两个棱长都就是3dm的正方体拼成一个长方体,这个长方体的表面积比原来
减少( )。
3、把一个长10cm、宽6cm、高9cm 的长方体木块,锯成两个小长方体,表面
积最多增加( )cm2,最少增加( )cm2。
4、一种正方体的棱长3cm,用4个这样的正方体拼成一个大长方体,大长方体
的表面积可能就是()cm2,也可能就是( ) cm2。
5、每立方分米的铁重7、8千克,6立方分米的铁重()千克;390千克的
铁,体积就是( )立方米。
6、把15个体积都就是1立方厘米的小正方体木块拼成一个长方体,可以有( )
种不同的拼法,它的表面积分别就是( ),体积就是()。
二、应用:
1、抽屉长6分米、宽4分米、高2分米,做这样的10个抽屉,至少需要木板
多少平方米?
2、一个教室长8m,宽6m,高4、5m,要粉刷教室四周与顶棚,除去门窗面积22
平方米,如果每平方米用涂料0、2千克,一共需要多少千克涂料?
3、一块长45厘米、宽32厘米的长方形铁皮,在它的四个角上剪去边长10厘
米的正方形,然后焊接成一个无盖的长方体铁皮盒。
求这个盒子的最大容积就是多少立方厘米?
4、把一根6分米长的长方体木料,垂直于长平均锯成3段,表面积增加了
3、6平方分米.这根木料的体积就是多少立方分米?
5、一个长10米的水落管,管道口就是长15厘米、宽8厘米的长方形,做这个水落管至少要用铁皮多少平方米?
6、有一块长方体木料长5米,宽2分米、厚1分米,已知这块木料重72千克。
(1)1立方米这种木料重多少千克?
(2)工地上需要36立方米这种木料,这些木料重多少千克?
(3)一辆卡车一共装了7、2吨这种木料,这些木料的体积就是多少立方米? 7、做一个无盖的长方体铁皮油桶,长3分米,宽4分米,高5分米,做这个
铁桶至少要铁皮多少平方分米?如果每升油重0、82千克,装满油桶可以放多少千克油?
8、一个长方体长16dm、高6dm,如果沿着水平方向把它横切成两个小长方体,
那么表面积增加160dm2。
求原长方体的体积。
三、解方程.
2、5×40-5x=25 8(1、5x+2)÷4=10
9(2x-1、8)=8、1 9、5x-1=7、1x+5
0、9(12+x)=16、2 0、4(2-3x)=2x
四、递等式计算:
(0、02+28、16÷32)×0、1 2、6×0、26—0、26+0、84×2、6
0、25×(0、4+0、8)×1、25 3、2÷[(2-0、84÷0、7)×0、2]
五、列综合算式或方程解.
(1)5比一个数的4、6倍多2、7,求这个数。
(2)0、96与2、44的与被5个6、8的与除,商就是多少?。