2015高三数学一轮复习053双曲线

高三数学第一轮复习：双曲线的定义、性质及标准方程【本讲主要内容】双曲线的定义、性质及标准方程双曲线的定义及相关概念、双曲线的标准方程、双曲线的几何性质【知识掌握】【知识点精析】1. 双曲线的定义：（1）第一定义：平面内与两定点F1、F2的距离之差的绝对值是常数（小于|F1F2|）的点的轨迹叫做双曲线，这两个定点叫做双曲线的焦点，两焦点的距离叫做焦距。

（2）第二定义：平面内到一个定点F的距离与到一条定直线l的距离的比等于常数（e>1）的点的轨迹叫做双曲线，定点F为焦点，定直线l称为准线，常数e称为离心率。

说明：（1）若2a等于2c，则动点的轨迹是射线（即F1F2、F2F1的延长线）；（2）若2a大于2c，则动点轨迹不存在。

2. 双曲线的标准方程、图形及几何性质：标准方程)0b,0a(1byax2222>>=-中心在原点，焦点在x轴上yaxba b2222100-=>>(,)中心在原点，焦点在y轴上图形几何性质X围x a≤-或x a≥y a≤-或y a≥对称性关于x轴、y轴、原点对称（原点为中心）顶点()()1200A a A a-，、，()()1200A a A a-，、，轴实轴长122A A a=，虚轴长122B B b=离心率ecae=>()1准线2212:,:a al x l xc c=-=2212:,:a al y l yc c=-=实轴、虚轴长相等的双曲线称为等轴双曲线，焦点在x 轴上，标准方程为()2220x y a a -=≠；焦点在y 轴上，标准方程为()2220y x a a -=≠。

其渐近线方程为y＝±x 。

等轴双曲线的离心率为e =4. 基础三角形：如图所示，△AOB 中，,,,tan b OA a AB b OB c AOB a===∠=。

5. 共渐近线的双曲线系方程：与双曲线x a y b22221-=（a>0，b>0）有相同渐近线的双曲线系可设为()22220x y a b λλ-=≠，若λ>0，则双曲线的焦点在x 轴上；若λ<0，则双曲线的焦点在y 轴上。

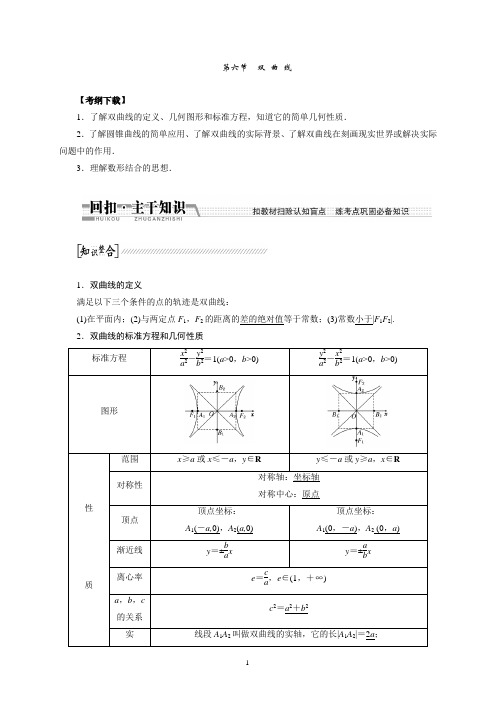
第六节双曲线【考纲下载】1．了解双曲线的定义、几何图形和标准方程，知道它的简单几何性质．2．了解圆锥曲线的简单应用、了解双曲线的实际背景、了解双曲线在刻画现实世界或解决实际问题中的作用．3．理解数形结合的思想．1．双曲线的定义满足以下三个条件的点的轨迹是双曲线：(1)在平面内；(2)与两定点F1，F2的距离的差的绝对值等于常数；(3)常数小于|F1F2|.2．双曲线的标准方程和几何性质1．与两定点F 1，F 2的距离之差的绝对值大于、等于或小于常数2a 的动点的轨迹各是什么？ 提示：当2a <|F1F 2|且2a ≠0时，轨迹是双曲线；若2a ＝|F 1F 2|，则轨迹是以F 1，F 2为端点的两条射线；若2a >|F 1F 2|，则轨迹不存在．2．双曲线的离心率的大小与双曲线“开口”大小有怎样的关系？ 提示：离心率越大，双曲线的“开口”越大．1．双曲线2x 2－y 2＝8的实轴长是( ) A ．2 B ．2 2 C ．4 D ．4 2 解析：选C 由题意知，a ＝2，故实轴长为2a ＝4.2．双曲线方程为x 2－2y 2＝1，则它的左焦点的坐标为( ) A.⎝⎛⎭⎫－22，0 B.⎝⎛⎭⎫－52，0 C.⎝⎛⎭⎫－62，0 D ．(－3，0) 解析：选C 双曲线方程x 2－2y 2＝1可化为x 2－y 212＝1，所以a 2＝1，b 2＝12，c 2＝a 2＋b 2＝32，c＝62.因此，左焦点坐标为⎝⎛⎭⎫－62，0. 3．设P 是双曲线x 216－y 220＝1上一点，F 1，F 2分别是双曲线左右两个焦点，若|PF 1|＝9，则|PF 2|等于( )A ．1B ．17C ．1或17D ．以上答案均不对解析：选B 由题意知|PF 1|＝9<a ＋c ＝10，所以P 点在双曲线的左支，则有|PF 2|－|PF 1|＝2a ＝8，故|PF 2|＝|PF 1|＋8＝17.4．双曲线方程：x 2|k |－2＋y 25－k ＝1，那么k 的取值范围是( )A ．(5，＋∞)B ．(2,5)C ．(－2,2)D ．(－2,2)或(5，＋∞)解析：选D 由题意知，(|k |－2)(5－k )<0，解得－2<k <2或k >5.5．已知双曲线x 29－y 2a ＝1的右焦点的坐标为(13，0)，则该双曲线的渐近线方程为____________________．解析：依题意知(13)2＝9＋a ，所以a ＝4，故双曲线方程为x 29－y 24＝1，则渐近线方程为x 3±y2＝0.即2x ±3y ＝0.答案：2x ＋3y ＝0或2x －3y ＝0数学思想(十)方程思想在求解离心率(范围)中的应用[典例] 已知点F 是双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的左焦点，点E 是该双曲线的右顶点，过点F且垂直于x 轴的直线与双曲线交于A ，B 两点，△ABE 是锐角三角形，则该双曲线的离心率e 的取值范围是( )A ．(1，＋∞)B ．(1,2)C ．(1,1＋2)D ．(2,1＋2)[解题指导] 根据△ABE 的特征，得出边的关系，列出关于a ，c 的不等式求解即可．[解析] 由AB ⊥x 轴，可知△ABE 为等腰三角形，又△ABE 是锐角三角形，所以∠AEB 为锐角，即∠AEF <45°，于是|AF |<|EF |，b 2a <a ＋c ，于是c 2－a 2<a 2＋ac ，即e 2－e －2<0，解得－1<e <2.又双曲线的离心率e >1，从而1<e <2.[答案] B[题后悟道] 离心率是圆锥曲线的重要几何性质，求解椭圆或者双曲线的离心率的关键是建立一个关于a ，b ，c 的方程(不等式)，通过这个方程(不等式)和b 与a ，c 的关系消掉b后，建立a ，c 之间的方程(不等式)，只要能通过这个方程求出ca 即可，不一定具体求出a ，c 的数值．(2014·郑州模拟)已知点F 、A 分别为双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的左焦点、右顶点，点B (0，b )满足FB ·AB ＝0，则双曲线的离心率为( )A. 2B.3C.1＋32D.1＋52解析：选D 依题意得F (－c,0)，A (a,0)，又B (0，b )，则FB ＝(c ，b )，AB ＝(－a ，b )．由FB ·AB ＝0，得b 2＝ac ，所以c 2－a 2＝ac ，c 2－a 2ac ＝1，即e －1e ＝1，e 2－e －1＝0，解得e ＝1±52.又e >1，所以e ＝1＋52，即双曲线的离心率等于1＋52.。

第六节双曲线[考情展望] 1.考查双曲线的定义及标准方程.2.考查双曲线的几何性质(以渐近线的离心率为主).3.多以客观题形式考查，属中低档题目．一、双曲线定义平面内动点P与两个定点F1、F2(|F1F2|＝2c＞0)的距离之差的绝对值为常数2a(2a＜2c) ，则点P的轨迹叫做双曲线．集合P＝{M|||MF1|－|MF2||＝2a}，|F1F2|＝2c，其中a、c为常数且a＞0，c ＞0.(1)当2a＜|F1F2|时，P点的轨迹是双曲线；(2)当2a＝|F1F2|时，P点的轨迹是两条射线；(3)当2a＞|F1F2|时，P点不存在．二、双曲线的标准方程和几何性质巧设双曲线方程(1)与双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)有共同渐近线的方程可表示为x 2a 2－y 2b 2＝t (t ≠0)．(2)过已知两个点的双曲线方程可设为x 2m ＋y 2n ＝1(mn ＜0)．1．双曲线方程为x 2－2y 2＝1，则它的右焦点坐标为( )A.⎝ ⎛⎭⎪⎫22，0B.⎝ ⎛⎭⎪⎫52，0 C.⎝ ⎛⎭⎪⎫62，0 D ．(3，0)【解析】 双曲线的方程可化为x 2－y 212＝1，∴a 2＝1，b 2＝12，c 2＝a 2＋b 2＝32， ∴c ＝62，∴右焦点为⎝ ⎛⎭⎪⎫62，0.【答案】 C2．设双曲线x 2a 2－y 29＝1(a ＞0)的渐近线方程为3x ±2y ＝0，则a 的值为( ) A ．4 B ．3 C ．2 D ．1【解析】 渐近线方程可化为y ＝±32x .∵双曲线的焦点在x 轴上， ∴9a 2＝⎝ ⎛⎭⎪⎫±322，解得a ＝±2.由题意知a ＞0，∴a ＝2. 【答案】 C3．设P 是双曲线x 216－y 220＝1上一点，F 1，F 2分别是双曲线左右两个焦点，若|PF 1|＝9，则|PF 2|等于( )A ．1B ．17C ．1或17D ．以上答案均不对【解析】 由双曲线定义||PF 1|－|PF 2||＝8， 又|PF 1|＝9，∴|PF 2|＝1或17，但应注意双曲线的右顶点到右焦点距离最小为 c －a ＝6－4＝2＞1， ∴|PF 2|＝17. 【答案】 B4．已知双曲线C ：x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的离心率e ＝2，且它的一个顶点到较近焦点的距离为1，则双曲线C 的方程为________．【解析】 依题意c －a ＝1，① 又e ＝ca ＝2，即c ＝2a ② 由①②联立，得a ＝1，c ＝2.∴b 2＝c 2－a 2＝3，故双曲线C 为x 2－y 23＝1.【答案】 x 2－y 23＝15．(2013·北京高考)若双曲线x 2a 2－y 2b 2＝1的离心率为3，则其渐近线方程为( )A ．y ＝±2xB ．y ＝±2xC ．y ＝±12xD ．y ＝±22x【解析】 ∵e ＝3，∴ca ＝3，即a 2＋b 2a 2＝3，∴b 2＝2a 2，∴双曲线方程为x 2a 2－y22a 2＝1，∴渐近线方程为y ＝±2x . 【答案】 B6．(2013·陕西高考)双曲线x 216－y 2m ＝1的离心率为54，则m 等于________．【解析】x216－y2m＝1中，a＝4，b＝m，∴c＝16＋m.而e＝54，∴16＋m4＝54，∴m＝9.【答案】9考向一[151]双曲线的定义及应用(1)(2012·大纲全国卷)已知F1、F2为双曲线C：x2－y2＝2的左、右焦点，点P在C上，|PF1|＝2|PF2|，则cos∠F1PF2＝()A.14 B.35 C.34 D.45(2)已知定点A(0,7)，B(0，－7)，C(12,2)；以点C为一个焦点作过A、B的椭圆，求另一个焦点F的轨迹方程．【思路点拨】(1)由双曲线定义，求△PF1F2的边长，根据余弦定理可解．(2)探求|F A|与|FB|间的关系，借助双曲线定义求轨迹方程．【尝试解答】(1)由x2－y2＝2，知a＝b＝2，c＝2.由双曲线定义，|PF1|－|PF2|＝2a＝22，又|PF1|＝2|PF2|，∴|PF1|＝42，|PF2|＝22，在△PF1F2中，|F1F2|＝2c＝4，由余弦定理cos∠F1PF2＝|PF1|2＋|PF2|2－|F1F2|22|PF1|·|PF2|＝34，选C.【答案】 C(2)设F(x，y)为轨迹上的任意一点，依题意，得|F A|＋|CA|＝|FB|＋|CB|＝2a(a表示椭圆的长半轴长)．∴|F A|－|FB|＝|CB|－|CA|＝122＋92－122＋(－5)2＝2，∴|F A|－|FB|＝2＜14.由双曲线的定义知，F点在以A、B为焦点，2为实轴长的双曲线的下支上，∴点F 的轨迹方程是y 2－x 248＝1(y ≤－1)．规律方法1 1.(1)抓住“焦点三角形PF 1F 2”中的数量关系是求解第(1)题的关键.(2)第(2)小题中，点F 的轨迹是双曲线的下支，一定分清是差的绝对值为常数，还是差为常数.2.利用双曲线定义求方程，要注意三点：(1)距离之差的绝对值，(2)2a ＜|F 1F 2|，(3)焦点所在坐标轴的位置.对点训练 已知动圆M 与圆C 1：(x ＋4)2＋y 2＝2外切，与圆C 2：(x －4)2＋y 2＝2内切，求动圆圆心M 的轨迹方程．【解】 设动圆M 的半径为r ， 则由已知|MC 1|＝r ＋2，|MC 2|＝r －2， ∴|MC 1|－|MC 2|＝22， 又C 1(－4,0)，C 2(4,0)， ∴|C 1C 2|＝8， ∴22＜|C 1C 2|.根据双曲线定义知，点M 的轨迹是以C 1(－4,0)、C 2(4,0)为焦点的双曲线的右支．又a ＝2，c ＝4， ∴b 2＝c 2－a 2＝14，∴点M 的轨迹方程是x 22－y 214＝1(x ≥2)．考向二 [152] 双曲线的标准方程(1)已知双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)和椭圆x 216＋y 29＝1有相同的焦点，且双曲线的离心率是椭圆离心率的两倍，则双曲线的方程为________．(2)已知椭圆D ：x 250＋y 225＝1与圆M ：x 2＋(y －5)2＝9，双曲线G 与椭圆D 有相同焦点，它的两条渐近线恰好与圆M 相切，求双曲线G 的方程．【思路点拨】 (1)由已知椭圆的焦点和离心率得a ，b 满足的方程．从而可求出双曲线的方程．(2)先由椭圆方程可得双曲线G 的焦距，再设出双曲线G 的渐近线方程，利用已知条件求解．【尝试解答】(1)由x216＋y29＝1，知c＝16－9＝7，∴焦点F1(－7，0)，F2(7，0)，且离心率e′＝7 4.又双曲线x2a2－y2b2＝1与椭圆x216＋y29＝1有相同的焦点．∴a2＋b2＝(7)2＝7，∵双曲线的离心率e＝ca＝7 a，∴7a＝274，则a＝2.从而b2＝c2－a2＝7－22＝3.故所求的双曲线的方程为x24－y23＝1.【答案】x24－y23＝1(2)椭圆D的两个焦点为F1(－5,0)，F2(5,0)，因而双曲线中心在原点，焦点在x轴上，且c＝5.设双曲线G的方程为x2a2－y2b2＝1(a＞0，b＞0)，∴渐近线方程为bx±ay＝0且a2＋b2＝25.又圆心M(0,5)到两条渐近线的距离为r＝3，∴|5a|b2＋a2＝3，得a＝3，b＝4.∴双曲线G的方程为x29－y216＝1.规律方法2求双曲线的标准方程关注点：(1)确定双曲线的标准方程也需要一个“定位”条件，两个“定量”条件，“定位”是指确定焦点在哪条坐标轴上，“定量”是指确定a，b的值，常用待定系数法.(2)利用待定系数法求双曲线的标准方程时应注意选择恰当的方程形式，以避免讨论.①若双曲线的焦点不能确定时，可设其方程为Ax2＋By2＝1(AB＜0).②若已知渐近线方程为mx ＋ny ＝0，则双曲线方程可设为m 2x 2－n 2y 2＝λ(λ≠0).对点训练 与双曲线x 29－y 216＝1有共同的渐近线，且过点(－3，23)，求双曲线的标准方程．【解】 法一 设双曲线的方程为x 2a 2－y 2b 2＝1(a ＞0，b ＞0)， 由题意，得⎩⎪⎨⎪⎧b a ＝43，(－3)2a 2－(23)2b 2＝1，解得a 2＝94，b 2＝4，所以双曲线的方程为x 294－y 24＝1.法二 设所求双曲线方程为x 29－y 216＝λ(λ≠0)， 将点(－3,23)代入得λ＝14. 所以双曲线方程为x 29－y 216＝14， 即x 294－y 24＝1. 考向三 [153] 双曲线的几何性质(1)已知中心在原点，焦点在y 轴上的双曲线的离心率为5，则它的渐近线方程为( )A ．y ＝±2xB ．y ＝±52x C ．y ＝±12xD ．y ＝±6x(2)双曲线C ：x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的右顶点为A ，x 轴上有一点Q (2a,0)，若C 上存在一点P ，使AP →·PQ→＝0，求此双曲线离心率的取值范围．【思路点拨】 (1)焦点在y 轴上的渐近线方程为y ＝±ab x ，由双曲线的离心率可确定ab 的值．(2)先设p (x ，y )，由AP →·PQ →＝0得到的方程与x 2a 2－y 2b 2＝1联立，消去y 后，再利用双曲线的几何性质x ≥a ，可得到关于a 、b 的一个不等关系式，进一步求得离心率的取值范围．【尝试解答】 (1)设双曲线的方程为y 2a 2－x 2b 2＝1(a ＞0，b ＞0)，∵e ＝ca ＝5，c ＝a 2＋b 2，∴a 2＋b 2a 2＝1＋⎝ ⎛⎭⎪⎫b a 2＝5，∴b a ＝2，∴双曲线的渐近线方程为y ＝±a b x ＝±12x ，故选C.【答案】 C(2)设P 点坐标为(x ，y )， 则由AP →·PQ →＝0，得AP ⊥PQ ， ∴P 点在以AQ 为直径的圆上， ∴⎝ ⎛⎭⎪⎫x －3a 22＋y 2＝⎝ ⎛⎭⎪⎫a 22.① 又P 点在双曲线上，得x 2a 2－y 2b 2＝1.② 由①，②消去y ，得(a 2＋b 2)x 2－3a 3x ＋2a 4－a 2b 2＝0， 即[(a 2＋b 2)x －(2a 3－ab 2)](x －a )＝0.当x ＝a 时，P 与A 重合，不符合题意，舍去． 当x ＝2a 3－ab 2a 2＋b 2时，满足题意的P 点存在，需x ＝2a 3－ab 2a 2＋b 2＞a ，化简得a 2＞2b 2， 即3a 2＞2c 2，c a ＜62.又e ＞1，∴离心率e ＝c a ∈⎝⎛⎭⎪⎫1，62.规律方法3求双曲线的离心率(取值范围)的策略,求双曲线离心率是一个热点问题.若求离心率的值，需根据条件转化为关于a，b，c的方程求解，若求离心率的取值范围，需转化为关于a，b，c的不等式求解，正确把握c2＝a2＋b2的应用及e＞1是求解的关键.对点训练(2013·湖南高考)设F1，F2是双曲线C：x2a2－y2b2＝1(a>0，b>0)的两个焦点．若在C上存在一点P，使PF1⊥PF2，且∠PF1F2＝30°，则C的离心率为________．【解析】设点P在双曲线右支上．∵PF1⊥PF2，|F1F2|＝2c，且∠PF1F2＝30°，∴|PF2|＝c，|PF1|＝3c.又点P在双曲线右支上，∴|PF1|－|PF2|＝(3－1)c＝2a.∴e＝ca＝23－1＝3＋1.【答案】3＋1思想方法之十九分类讨论思想在判断直线与双曲线交点问题中的妙用研究直线与圆锥曲线位置关系的问题，通常转化为研究方程组的解的问题，利用直线方程与圆锥曲线方程所组成的方程组消去一个变量后，将交点问题(包括公共点个数、与交点坐标有关的问题)转化为一元二次方程根的问题，结合根与系数的关系及判别式解决问题，当一元二次方程中含有参数时，通常需要进行分类讨论，注意不要忽视了二次项系数的讨论．————[1个示范例]————[1个对点练]————已知双曲线C：2x2－y2＝2与点P(1,2)求过P(1,2)点的直线l的斜率取值范围，使l与C分别有一个交点，两个交点，没有交点．【解】 (1)当直线l 的斜率不存在时，l 的方程为x ＝1，与曲线C 有一个交点，当l 的斜率存在时，设直线l 的方程为y －2＝k (x －1)，代入C 的方程，并整理得(2－k 2)x 2＋2(k 2－2k )x －k 2＋4k －6＝0.(*)(ⅰ)当2－k 2＝0，即k ＝±2时，方程(*)有一个根，l 与C 有一个交点 (ⅱ)当2－k 2≠0，即k ≠±2时，Δ＝[2(k 2－2k )]2－4(2－k 2)(－k 2＋4k －6)＝16(3－2k )①当Δ＝0，即3－2k ＝0，k ＝32时，方程(*)有一个实根，l 与C 有一个交点． ②当Δ＞0，即k ＜32，又k ≠±2，故当k ＜－2或－2＜k ＜2或2＜k ＜32时，方程(*)有两不等实根，l 与C 有两个交点．③当Δ＜0，即k ＞32时，方程(*)无解，l 与C 无交点．综上知：当k ＝±2，或k ＝32，或k 不存在时，l 与C 只有一个交点； 当2＜k ＜32，或－2＜k ＜2，或k ＜－2时，l 与C 有两个交点； 当k ＞32时，l 与C 没有交点．过点⎝ ⎛⎭⎪⎫2，12能作几条与双曲线x 24－y 2＝1有一个公共点的直线．【解】 (1)当斜率不存在时，直线方程为x ＝2，显然符合题意． (2)当斜率存在时，设斜率为k ， 则直线方程为y －12＝k (x －2)， 联立x 24－y 2＝1得(1－4k 2)x 2＋(16k 2－4k )x －(16k 2－8k ＋5)＝0， ①当1－4k 2≠0时，令Δ＝0，解得k ＝58，一条．②当1－4k2＝0时，此时直线与渐近线平行，符合题意，两条．故共4条．。

解析几何—双曲线一、学习目标知识与技能：了解圆锥曲线的实际背景，感受圆锥曲线在解决实际问题时的应用。

过程与方法：掌握双曲线的定义、标准方程及简单的几何性质。

情感态度价值观：理解数形结合的思想，了解椭圆的简单应用。

二、学习重难点重点：双曲线的定义的灵活应用、利用标准方程研究几何性质，尤其是离心率求值问题。

难点：双曲线的综合问题三、考纲解读：掌握双曲线的定义、标准方程,能够根据条件利用待定系数法求双曲线方程. 四、知识链接1.共渐近线的双曲线系方程：与双曲线x 2a 2－y 2b 2＝1有相同渐近线的双曲线系方程可设为x 2a 2－y 2b 2＝λ(λ≠0)，若λ>0，则双曲线的焦点在 轴上；若λ<0，则双曲线的焦点在 轴上．2.双曲线的形状与e 的关系：∵双曲线渐近线的斜率k ＝ba ＝c 2－a 2a＝c 2a2－1＝e 2－1，∴e 越大，则渐近线的斜率的绝对值就越大，这时双曲线的形状就从扁狭逐渐变得开阔．故双曲线的离心率越大，它的开口就越宽阔．3. 双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的渐近线方程为 ，而双曲线y 2a 2－x 2b 2＝1(a >0，b >0)的渐近线方程为 应注意其区别与联系．4．平行于双曲线的渐近线的直线与双曲线有且仅有 个交点． 五、基础检测A1．已知()()3,0,3,0,6M N PM PN --=，则动点P 的轨迹是（ ） A ．一条射线B ．双曲线右支C ．双曲线D ．双曲线左支【答案】A 因为6PM PN MN -==，故动点P 的轨迹是一条射线：0,3y x =≥A2．若12,F F 分别是双曲线2211620x y-=的左、右焦点,P 为双曲线C 上一点,且19PF =,则2PF 的长为( )A ．1B ．17或1C ．17D ．12【答案】C 因为194610PF a c =<+=+=,所以P 必在双曲线左支上, :212248PF PF a -==⨯=,又19PF =,所以298PF -=,解得:217PF =,A3．若00(,)P x y 是双曲线22124x y -=左支上一点，则0x 的取值范围是_____【答案】(,-∞六、学习过程B1．已知双曲线()2222:10,0x y C a b a b -=>>的左、右焦点分别为1F 、2F ，O 为坐标原点，P 是双曲线上在第一象限内的点，直线PO 、2PF 分别交双曲线C 左、右支于另一点M 、N ，122PF PF =，且260MF N ∠=，则双曲线C 的离心率为（ ）A B CD 【答案】B122PF PF =，122PF PF a -=，14PF a ∴=，22PF a =.连接1MF 、2MF ，根据双曲线的对称性可得12MF PF 为平行四边形，260MF N ∠=o Q ，1260F PF ∴∠=，由余弦定理可得2224164242cos60c a a a a =+-⋅⋅⋅o ，c ∴=，ce a∴== B2．已知△ABP 的顶点A 、B 分别为双曲线的左右焦点，顶点P 在双曲线C 上，则sin sin sin A BP-的值等于（ ）AB C ．54D ．45【答案】D 由题意得双曲线22:1169x y C -=得4a =, 3b =,根据双曲线的定义得:28PB PA a -==‖,又210AB c ===, 从而由正弦定理,得sin sin 4sin 5PB PA A B P AB --==‖，B4．双曲线C 与双曲线2212y x -=有共同的渐近线，且过点．（1）求双曲线C 的方程；（2）若直线:1l y kx =+与双曲线C 左支交于,A B 两点，求k 的取值范围；【答案】（1）2212y x -=；（2） （1）因为双曲线C 与双曲线2212y x -=有共同的渐近线，所以设双曲线C 的方程为222y x λ-=，把点代入C中，即(22λ-=，解得λ1=-，所以双曲线C 的方程为2212y x -=.（2）联立22112y kx y x =+⎧⎪⎨-=⎪⎩，消去y 得：()222230k x kx ---=，①因为直线与双曲线左支有两个交点,A B ，设()()1122,,,A x y B x y ，且120,0x x <<，解不等式()2221221222041220202302k k k k x x k x x k ⎧-≠⎪+->⎪⎪⎨+=<⎪-⎪-⎪=>-⎩，解得：k k k ⎧<<⎪⎪≠⎨⎪>⎪⎩k <<B5．已知双曲线两个焦点分别是())12,F F，点)P在双曲线上.（1）求双曲线的标准方程;（2）过双曲线的右焦点2F 且倾斜角为60︒的直线与双曲线交于,A B 两点，求1F AB ∆的周长.【答案】（1）221x y -=；（2）12 （1）()22,0F，)P2P F x∴⊥轴 221b PF a∴==且c =又222c a b =+，即220a a +-=，解得：1a = 21b ∴=∴双曲线的标准方程为：221x y -=（2）由（1）知，双曲线渐近线为y x =，倾斜角为45 直线AB 过2F 且倾斜角为60 ,A B ∴均在双曲线的右支上122BF BF ∴-=，122AF AF -= 112244AF BF AF BF AB ∴+=++=+设直线AB方程为：y x =代入双曲线方程得：2270x -+=4AB ∴== 1F AB ∴∆的周长为：114212AF BF AB AB ++=+=七、达标检测A1．设1k >，则关于,x y 的方程()22211k x y k -+=-所表示的曲线是（ ）A ．长轴在y 轴上的椭圆B ．长轴在x 轴上的椭圆C ．实轴在y 轴上的双曲线D ．实轴在x 轴上的双曲线【答案】C ∵k ＞1，∴1+k >0，k 2-1＞0，方程()22211k x y k -+=-，即222111y x k k -=-+，表示实轴在y 轴上的双曲线，A2．已知双曲线的渐近线为2y x =±，实轴长为4，则该双曲线的方程为（ ） A ．22142x y -=B ．22142x y -=或22148y x -=C ．22148y x -=D ．22142x y -=或22148y x -=【答案】D双曲线的渐近线方程为2y x =±，实轴长为4，24a ∴=，则2a =，∴当双曲线的焦点在x 轴上时，设双曲线方程为22214x y b -=，0b >，此时2b =b =∴双曲线方程为22142x y -=，当双曲线的焦点在y 轴上时，设双曲线方程为22214y x b-=，0b >，此时22b =，解得b =22148x y -=． B3．已知双曲线22:1(04)4x y C m m m-=<<-的渐近线与圆22(2)3x y -+=相切，则m =（ ）A ．1B C ．2D ．3【答案】A 双曲线22:1(04)4x y C m m m-=<<-的渐近线方程为y =将y =0= 由双曲线的渐近线0±=与圆22(2)3x y -+==解得1m = C4．设分别为双曲线的左、右焦点，双曲线上存在一点使得则该双曲线的离心率为( ) A ．B ．C ．D ．3【答案】B 因为是双曲线上一点，所以，又所以，，所以又因为，所以有，，即解得：（舍去），或；所以，所以B5．设双曲的一个焦点为F ，虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近线垂直，那么此双曲线的离心率为( )A B C ．12D ．12【答案】D设该双曲线方程为2222100x ya ba b-=（＞，＞），可得它的渐近线方程为by xa=±，焦点为F（c，0），点B（0，b）是虚轴的一个端点，∴直线FB的斜率为FBb bkc c-==--，∵直线FB与直线by xa=互相垂直，1b bc a∴-⨯=-,2b ac∴=,22222b c a c a ac=-∴-=，,210e e∴--=,e∴=,。