新北师版初中数学八年级下册3.2第2课时旋转作图过关习题和解析答案

旋转的基本作图一、选择题1、将如图绕某点逆时针旋转90°后，得到的图形是（）A．B．C．D．2、如下左图所示的图案是由六个全等的菱形拼成的，它也可以看作是以一个图案为“基本图案”，通过旋转得到的．以下图案中，不能作为“基本图案”的一个是（）A．B．C．D．3、在图中，将左边方格纸中的图形绕O点顺时针旋转90°得到的图形是（）A．B．C．D．二、解答题4、已知：如图，四边形ABCD及一点P．求作：四边形A′B′C′D′，使得它是由四边形ABCD绕P点顺时针旋转90°得到的．（不写作法保留作图痕迹）5、我们学习过：在平面内，将一个图形绕一个定点沿着某个方向转动一个角度，这样的图形运动叫做旋转，这个定点称为旋转中心，旋转的角度称为旋转角．如图，△ABC经过旋转得到△DEF．试用直尺和圆规作出旋转中心（保留作图痕迹，不写作法）．6、（1）图1，平移方格纸中的图形，使点A平移到点A′处，画出移后的图形．（2）在图2方格纸中画出三角形绕O点逆时针旋转90°后的图形．7、实验操作（1）如图1，在平面直角坐标系xOy中，△ABC的顶点的横、纵坐标都是整数，若将△ABC以点P（1，-1）为旋转中心，按顺时针方向旋转90°得到△DEF，请在坐标系中画出点P及△DEF；（2）如图2，在菱形网格图（最小的菱形的边长为1，且有一个内角为60°）中有一个等边△ABC，它的顶点A，B，C都落在格点上，若将△ABC以点P为旋转中心，按顺时针方向旋转60°得到△A′B′C′，请在菱形网格图中画出△A′B′C′．其中，点A旋转到点A′所经过的路线长为 __________ ．8、如图，△ABC中，∠C=90°，将△ABC绕点A旋转得到△AB1C1，点C的对应点C1恰好落在AB边上．（1）作图：作出△AB1C1（保留作图痕迹，不要求写作法）；（2）已知AC=5，BC=12，求BB1的长．9、如图，已知边长为a的正方形ABCD．求作该正方形绕点A逆时针旋转30°后的正方形AB1C1D1．（说明：请用无刻度的直尺和圆规作图，并保留作图痕迹）10、如图1，正方形ABCD是一个6×6网格电子屏的示意图，其中每个小正方形的边长为1．位于AD中点处的光点P按图2的程序移动．（1）请在图1中画出光点P经过的路径；（2）求光点P经过的路径总长（结果保留π）．11、画△ABC绕O点顺时针方向旋转90°后得到△A′B′C′．12、如图，在10×10的小正方形网格中，△ABC的顶点A、B、C在网格点上，P1、P2、P3、P4是其中一个小正方形的四个格点，将△ABC绕A点逆时针旋转90°，再向下平移2个单位，得到△A′B′C′；将△ABC按一定的规律顺次旋转，第一次将△ABC绕点P1逆时针旋转90°得到△A1B1C1；第二次将△A1B1C1绕点P2逆时针旋转90°得到△A2B2C2；第三次将△A2B2C2绕点P3逆时针旋转90°得到△A3B3C3，依次按旋转中心为P1、P2、P3、P4、P1、P2…旋转下去．（1）在网格中画出△A′B′C′和△A2B2C2；（2）△ABC至少旋转第__________次后所得的三角形刚好与△A′B′C′重合．13、如图所示，左边方格纸中每个正方形的边长均为a，右边方格纸中每个正方形的边长均为b，将左边方格纸中的图形顺时针旋转90°，并按b：a的比例画在右边方格纸中．14、请按下面要求画图（1）请在图1中画出一个直角梯形MNPQ，使它与梯形ANMB构成一个等腰梯形；（2）在图2中，将直角梯形ABMN绕点M按逆时针旋转180°，画出旋转后的图形．15、分析图①、②、④中阴影部分的分布规律，按此规律在图③中画出其中的阴影部分．旋转的基本作图的答案和解析一、选择题1、答案：C试题分析：抓住几个关键图形逆时针旋转90°后的位置，结合选项进行判断即可．试题解析：绕某点逆时针旋转90°后，得到的图形是．故选C．2、答案：B试题分析：认真观察旋转得到的图案，找到旋转中心，即可判断．试题解析：A、顺时针，连续旋转60度，三次即可得到．B、不能作为“基本图案”．C、旋转180度，即可得到．D、旋转60度即可．故选B．3、答案：B试题分析：根据旋转的性质，找出图中三角形的关键处（旋转中心）按顺时针方向旋转90°后的形状即可选择答案．试题解析：根据旋转的性质可知，绕O点顺时针旋转90°得到的图形是．故选B．二、解答题4、答案：试题分析：利用旋转的性质分别得出对应点位置进而得出答案．试题解析：如图所示：四边形A′B′C′D′即为所求．5、答案：试题分析：根据旋转的性质，连接对应点AD、BE，再分别作AD、BE的垂直平分线，相交于点O，则点O即为旋转中心．试题解析：如图所示，点O即为△ABC旋转到△DEF的旋转中心．6、答案：试题分析：（1）利用网格特点和平移的性质画图；（2）利用网格特点和旋转的性质画图．试题解析：（1）如图1：（2）如图2：7、答案：试题分析：（1）先做出P点，然后找出点A、B、C绕点P顺时针旋转90°的位置，然后顺次连接即可；（2）找出点A、B、C绕点P顺时针旋转60°的位置，顺次连接A'B'、B'C'、C'A'，然后根据弧长公式求出点A旋转到点A′所经过的路线长．试题解析：（1）（2）所作图形如下：；点A的运动路线==π．故答案为：π．8、答案：试题分析：（1）以点A为圆心，以AC为半径画弧，与AB相交于点C1，再以点A为圆心，以AB为半径画弧，以C1为圆心，以CB为半径画弧，两弧相交于点B1，然后顺次连接即可；（2）利用勾股定理列式求出AB，再求出BC1，再利用勾股定理列式计算即可得解．试题解析：（1）△AB1C1如图所示；（2）由勾股定理得，AB==13，BC1=13-5=8，B1C1=12，所以，BB1==4．9、答案：试题分析：①以点A为圆心，AD长为半径作圆，再以点D为圆心，DA长为半径作弧，与圆的交点为E，连接AE，DE，△ADE就是一个等边三角形．∠EAD=60°；②作∠EAD的角平分线，得到一个30°的角，角平分线与圆的交点为D1；③连接AC，以AC为一边根据②中30度的角作∠CAC1=30°，以点A为圆心，AC长为半径画弧与角的另一边交点为C1；④以AB为一边，作∠BAB1等于已知角30度，与圆的交点为B1．试题解析：所作图形如下：10、答案：试题分析：（1）按图2中的程序旋转一一找到对应点，第一次是绕点A顺时针旋转90°，得到对应点，再绕点B顺时针旋转90°，得到对应点．再绕点C顺时针旋转90°，得到对应点，再绕点D顺时针旋转90°，得到对应点即可．（2）从中可以看出它的路线长是4段弧长，根据弧长公式计算即可．（1）如图；（2）∵，∴点P经过的路径总长为6π．11、答案：试题分析：根据旋转的性质，将A，B，C绕O点顺时针旋转90°，由此即可画出旋转后的图形．试题解析：如图所示：12、答案：试题分析：（1）根据旋转和平移的概念在网格中画出△A′B′C′和△A2B2C2；（2）根据△ABC的旋转规律，把△ABC进行旋转，得到三角形刚好与△A′B′C′重合的旋转次数．试题解析：（1）如图：（2）把点A按照△ABC的旋转规律进行旋转，可以发现旋转第5次后所得的三角形刚好与A′重合，故答案为：5．13、答案：试题分析：将左边方格纸中的图形顺时针旋转90°，并按b：a的比例画在右边方格纸中．因为方格的比例就是b：a，所以只要顺时针旋转90°，在格点上的还让它在格点上，得到的图形就是所求的图形．试题解析：14、答案：试题分析：（1）画出一个直角梯形MNPQ，使它与梯形ANMB构成一个等腰梯形；根据等腰梯形的性质，即可作出图形；（2）将直角梯形ABMN绕点M按逆时针旋转180°，根据旋转的性质，即可作出旋转后的图形．试题解析：（1）如图1：（2）如图2：15、答案：试题分析：由①到②是旋转了90°，由②到④是旋转了180度，即通过两次旋转90度得到，据此即可判断．试题解析：如图。

找出旋转图形的旋转方向、旋转中心、旋转角一、选择题1、如图，将三角尺ABC（其中∠ABC=60°，∠C=90°）绕B点按顺时针方向转动一个角度到A1BC1的位置，使得点A，B，C1在同一条直线上，那么这个角度等于( )A .120°B .90°C .60°D .30°2、如图，在平面直角坐标系xOy中，△A′B′C′由△ABC绕点P旋转得到，则点P 的坐标为（）A．（0，1）B．（1，-1）C．（0，-1）D．（1，0）3、在如图4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△，则其旋转中心可能是( )A .点AB .点BC .点CD .点D4、如图，将△ABC绕点P顺时针旋转90°得到△A′B′C′，则点P的坐标是( )A .（1，1）B .（1，2）C .（1，3）D .（1，4）5、在如图4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M1N1P1，则其旋转中心可能是（）A．点A B．点B C．点C D．点D6、如图，点A、B、C、D都在方格纸的格点上，若△AOB绕点O按逆时针方向旋转到△COD的位置，则旋转的角度为（）A．30°B．45°C．90°D．135°7、如图，在6×4方格纸中，格点三角形甲经过旋转后得到格点三角形乙，则其旋转中心是（）A．点M B．格点N C．格点P D．格点Q8、如图，点A、B、C、D、O都在方格纸的格点上，若△COD是由△AOB绕点O 按逆时针方向旋转而得，则旋转的角度为( )A .30°B .45°C .90°D .135°二、填空题9、如图，在▱ABCD中，∠A=70°，将▱ABCD绕顶点B顺时针旋转到▱A1BC1D1，当C1D1首次经过顶点C时，旋转角∠ABA1= __________ ．10、分别以正方形的各边为直径向其内部作半圆得到的图形如图所示．将该图形绕其中心旋转一个合适的角度后会与原图形重合，则这个旋转角的最小度数是__________度．11、如图所示，两个全等的正方形ABCD与CDEF，旋转正方形ABCD能和正方形CDEF重合，则可以作为旋转中心的点有__________个．三、解答题12、在△ABC中，∠B+∠ACB=30°，AB=4，△ABC逆时针旋转一定角度后与△ADE重合，且点C恰好成为AD中点，如图（1）指出旋转中心，并求出旋转角的度数．（2）求出∠BAE的度数和AE的长．13、如图，在△BDE中，∠BDE=90°，BD=4，点D的坐标是（5，0），∠BDO=15°，将△BDE旋转到△ABC的位置，点C在BD上，则旋转中心的坐标为 __________ ．14、如图1，有一组平行线l1∥l2∥l3∥l4，正方形ABCD的四个顶点分别在l1，l2，l3，l4上，EG过点D且垂直l1于点E，分别交l2，l4于点F，G，EF=DG=1，DF=2．（1）AE= __________ ，正方形ABCD的边长= __________ ；（2）如图2，将∠AEG绕点A顺时针旋转得到∠AE′D′，旋转角为α（0°＜α＜90°），点D′在直线l3上，以AD′为边在E′D′左侧作菱形AB′C′D′，使B′，C′分别在直线l2，l4上．①写出∠B′AD′与α的数量关系并给出证明；②若α=30°，求菱形AB′C′D′的边长．15、如图，已知：BC与CD重合，∠ABC=∠CDE=90°，△ABC≌△CDE，并且△CDE可由△ABC逆时针旋转而得到．请你利用尺规作出旋转中心O（保留作图痕迹，不写作法，注意最后用墨水笔加黑），并直接写出旋转角度是 __________ ．16、如图是两个等边三角形拼成的四边形．（1）这个图形是不是旋转对称图形？是不是中心对称图形？若是，指出对称中心．（2）若△ACD旋转后能与△ABC重合，那么图形所在平面上可以作为旋转中心的点共有几个？请一一指出．17、如图1，△ABC为边长为6的等边三角形，点D为AB边上的点，且AD=2BD；过D作DE∥BC交AC边于E；AH⊥BC于H，AH交于DE于点O．（1）求梯形BDEC的面积；（2）将图1中的△ADE以每秒1个单位长度的速度沿直线AH从上往下平移，直到点A与点H重合为止，设运动时间为t秒，△ADE与四边形BDEC重叠部分的面积为S，请求出S与t的函数关系，并写出相应的t的取值范围；（3）将图1中的△ADE沿直线DE向下翻折得△A′DE，连接CO：将△A′DE绕点O旋转，设直线A′O与直线BC相交于点P．问：是否存在这样的时刻，使得△CPO为等腰三角形？若存在，直接写出△A′DE绕点O旋转的方向（顺时针或逆时针）以及对应的旋转角度α的大小（0°＜α＜180°）；若不存在，请说明理由．找出旋转图形的旋转方向、旋转中心、旋转角的答案和解析一、选择题1、答案：A试题分析：利用旋转的性质计算．解：∵∠ABC=60°，∴旋转角∠CB=180°-60°=120°．∴这个旋转角度等于120°．故选：A．2、答案：B试题分析：根据网格结构，找出对应点连线的垂直平分线的交点即为旋转中心．试题解析：由图形可知，对应点的连线CC′、AA′的垂直平分线的交点是点（1，-1），根据旋转变换的性质，点（1，-1）即为旋转中心．故旋转中心坐标是P（1，-1）．故选B．3、答案：B试题分析：连接、、，分别作、、的垂直平分线，看看三线都过哪个点，那个点就是旋转中心．解：∵△MNP绕某点旋转一定的角度，得到△，∴连接、、，作的垂直平分线过B、D、C，作的垂直平分线过B、A，作的垂直平分线过B，∴三条线段的垂直平分线正好都过B，即旋转中心是B．故选：B．4、答案：B试题分析：先根据旋转的性质得到点A的对应点为点A′，点B的对应点为点B′，再根据旋转的性质得到旋转中心在线段AA′的垂直平分线，也在线段BB′的垂直平分线，即两垂直平分线的交点为旋转中心。

八年级数学下册第三章图形的平移与旋转3.2.2 图形的旋转课后作业（新版）北师大版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（八年级数学下册第三章图形的平移与旋转3.2.2 图形的旋转课后作业（新版）北师大版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为八年级数学下册第三章图形的平移与旋转3.2.2 图形的旋转课后作业（新版）北师大版的全部内容。

3.2.2图形的旋转课后作业1。

已知如图1所示的四张牌,若将其中一张牌旋转180º后得到图2，则旋转的牌是（）2。

已知点A的坐标为（a，b）,O为坐标原点,连结OA，将线段O A绕点O按逆时针方向旋转90°得OA₁,则点A₁的坐标为（）。

A．()-， D．()b a-，b aa b， C．()-， B．()a b-3. 如图所示，五角星的顶点是一个正五边形的五个顶点．这个五角星可以由一个基本图形(图中的阴影部分）绕中心O至少经过____________次旋转而得到，每一次旋转_______度．4.如图，将△ABC绕点A顺时针旋转60°得到△A ED,若线段AB=5，求出BE的长是多少？参考答案1.A,2.C，3. 4，724.解：∵将△ABC绕点A顺时针旋转60°得到△AED，∴∠BAE=60°，AB=AE，∴△BAE是等边三角形，∴BE=5．。

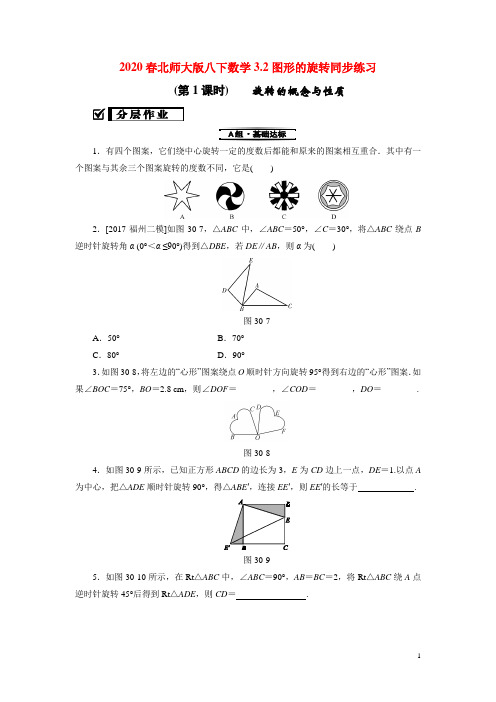
2020春北师大版八下数学3.2图形的旋转同步练习(第1课时)旋转的概念与性质1．有四个图案，它们绕中心旋转一定的度数后都能和原来的图案相互重合．其中有一个图案与其余三个图案旋转的度数不同，它是()2．[2017·福州二模]如图30-7，△ABC中，∠ABC＝50°，∠C＝30°，将△ABC绕点B 逆时针旋转角α (0°＜α≤90°)得到△DBE，若DE∥AB，则α为()图30-7A．50°B．70°C．80°D．90°3．如图30-8，将左边的“心形”图案绕点O顺时针方向旋转95°得到右边的“心形”图案．如果∠BOC＝75°，BO＝2.8 cm，则∠DOF＝________，∠COD＝________，DO＝________.图30-84．如图30-9所示，已知正方形ABCD的边长为3，E为CD边上一点，DE＝1.以点A 为中心，把△ADE顺时针旋转90°，得△ABE′，连接EE′，则EE′的长等于.图30-95．如图30-10所示，在Rt△ABC中，∠ABC＝90°，AB＝BC＝2，将Rt△ABC绕A点逆时针旋转45°后得到Rt△ADE，则CD＝.图30-106．如图30-11，△ABC的三个顶点都在方格纸的格点上，其中点A的坐标是(－1,0)，现将△ABC绕点A顺时针旋转90°，则旋转后点C的坐标是________．图30-117．时钟的时针在不停地旋转，从上午6时到上午9时，时针旋转的旋转角是多少度？从上午9时到上午10时呢？8．如图30-12所示，将两个斜边长相等的三角形纸片按图①放置，其中∠ACB＝∠CED ＝90°，∠A＝45°，∠D＝30°，把△DCE绕点C顺时针旋转15°得到△D1CE1，如图②，连接D1B，则∠E1D1B的度数为()图30-12A．10°B．20°C．7.5°D．15°9．如图30-13，在平面直角坐标系xOy中，点A的坐标为(－2,0)，等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD.(1)△AOC沿x轴向右平移得到△OBD，则平移的距离是个单位长度，△AOC与△BOD关于直线对称，则对称轴是_______，△AOC绕原点O顺时针旋转得到△DOB，则旋转角可以是________度；(2)连接AD，交OC于点E，求∠AEO的度数．图30-13参考答案1．B 2.C 3.75°20° 2.8 cm4．25 5.22－2 6.(2,1)7．90°30°8.D9.(1)2y轴120(2)90°(第2课时)旋转作图1．如图31-6，将△ABC绕点P顺时针旋转得到△A′B′C′，则点P的坐标是()A. (1,1)B．(1,2)C．(1,3) D．(1,4)图31-62．如图31-7，在平面直角坐标系中，点B，C，E在y轴上，Rt△ABC经过变换得到Rt△ODE，若点C的坐标为(0,1)，AC＝2，则这种变换可以是()图31-7A．△ABC绕点C顺时针旋转90°，再向下平移3B．△ABC绕点C顺时针旋转90°，再向下平移1C．△ABC绕点C逆时针旋转90°，再向下平移1D．△ABC绕点C逆时针旋转90°，再向下平移33．[2017·建邺区一模]如图31-8，点A、B、C、D都在方格纸的格点上，若△AOB绕点O按逆时针旋转到△COD的位置，则旋转角为________.图31-84．在如图31-9所示的方格纸中，每个小方格都是边长为1个单位长度的正方形，△ABC 的三个顶点都在格点(每个小方格的顶点叫格点)上．画出△ABC绕点O逆时针旋转90°后的△A′B′C′.图31-95．如图31-10，方格纸中每个小正方形的边长都是1个单位长度，Rt△ABC的三个顶点分别为A(－2,2)，B(0,5)，C(0,2)．(1)将△ABC以点C为旋转中心旋转180°，得到△A1B1C，请画出△A1B1C的图形；(2)平移△ABC，使点A的对应点A2坐标为(－2，－6)，请画出平移后对应的△A2B2C2的图形；(3)若将△A1B1C绕某一点旋转可得到△A2B2C2，请直接写出旋转中心的坐标．图31-106．[2017·福建]如图31-11，网格纸上正方形小格的边长为1.图中线段AB和点P绕着同一个点做相同的旋转，分别得到线段A′B′和点P′，则点P′所在的单位正方形区域是()图31-11A．1区B．2区C．3区D．4区7．如图31-12，在Rt△ABC中，∠ABC＝90°，点D在BC的延长线上，且BD＝AB.过点B作BE⊥AC，与BD的垂线DE交于点E.(1)求证：△ABC≌△BDE；(2)△BDE可由△ABC旋转得到，利用尺规作出旋转中心O(保留作图痕迹，不写作法)．图31-12参考答案【分层作业】1．B 2.A 3.90° 4.略5．(1)略(2)略(3)(0，－2) 6.D7.略(第3课时)坐标系中的平移作图1．[2017·邵阳]如图29-5，三架飞机P，Q，R保持编队飞行，某时刻在坐标系中的坐标分别为(－1,1)，(－3，1)，(－1，－1).30秒后，飞机P飞到P′(4,3)位置，则飞机Q，R的位置Q′，R′分别为()图29-5A．Q′(2,3)，R′(4,1) B．Q′(2,3)，R′(2,1)C．Q′(2,2)，R′(4,1) D．Q′(3,3)，R′(3,1)2．如图29-6，点A，B的坐标分别为(1,0)，(0,2)．若将线段AB平移到A1B1，点A1，B1的坐标分别为(2，a)，(b,3)，则a＋b＝________.图29-63．如图29-7，在平面直角坐标系中，点B的坐标为(4,2)，过点B作BA⊥x轴于点A，连接OB.(1)将△OAB平移得到△O′A′B′，点A，B，O的对应点分别是A′，B′，O′，且点B′的坐标为(2，－1)，在平面直角坐标系中画出平移后的△O′A′B′；(2)若连接AA′，OO′，求四边形OO′A′A的面积．图29-74．如图29-8所示，△ABC中，任意一点P(a，b)经平移后的对应点是P1(a－2，b＋3)．将△ABC作同样的平移得到△A1B1C1，求点A1，B1，C1的坐标．图29-85．如图29-9，A，B两点的坐标分别为A(2，2)，B(5，0)．(1)求△OAB的面积；(2)若将△OAB向左平移2个单位长度得△O′A′B′，求△O′A′B′三个顶点的坐标．图29-9参考答案【分层作业】1．A 2.2 3.(1)略(2)124．A1(－1,4)B1(－3,2)C1(2,1)5．(1)5(2)O′(－2，0)A′(0,2)B′(5－2，0)。

3.2图形的旋转一、选择题1．平面图形的旋转一般情况下改变图形的（）A.位置B.大小C.形状D.性质2.．9点钟时，钟表的时针和分针之间的夹角是（）A.30°B.45°C.60°D.90°3．将平行四边形ABCD旋转到平行四边形A′B′C′D′的位置，下列结论错误的是（）A.AB=A′B′B.AB∥A′B′C.∠A=∠A′D.△ABC≌△A′B′C′4．如图3-52所示，请仔细观察A，B，C，D四个图案，其中与E图案完全相同的是( )5．如图3-53所示，把菱形ABOC（四条边都相等）绕点O顺时针旋转得到菱形DFOE，则下列角中，不是旋转角的为（）A. ∠BOFB. ∠AODC. ∠COED. ∠AOF6．如图3-54所示，把△ABC绕点C顺时针旋转90°得到△DEC，若∠A＝25°，则∠CED等于（）A.55°B．65°C．45°D．75°7．如图3-55所示，该图案是经过( )A．平移得到的B．旋转或轴对称得到的C．轴对称得到的D．旋转得到的二、填空题8．钟表上的指针随时间的变化而移动，这可以看作是数学上的_______. 9．菱形ABCD 绕点O 沿逆时针方向旋转到四边形D C B A '''',则四边形D C B A ''''是__________.10．△ABC 绕一点旋转到△A ′B ′C ′，则△ABC 和△A ′B ′C ′的关系是_______.11．钟表的时针经过20分钟，旋转了_______度.12．图形的旋转只改变图形的_______，而不改变图形的_______.13．如图3-56所示，△ABC 与△A ′B ′C ，是全等三角形，那么△A ′B ′C ，可以看做是由△ABC 以O 为旋转中心，旋转 度形成的．14．等边三角形至少要旋转 度才能与自身重合．15．如图3-57所示，钟表的指针AOBC 绕中心O 沿顺时针方向旋转60°得到四边形DOEF ，那么四边形DOEF 绕中心O 沿顺时针方向旋转 度才能得到四边形AOBC . 三、探索·创新16．下图中的两个正方形的边长相等，请你指出可以通过绕点O 旋转而相互得到的图形并说明旋转的角度.17.在四边形ABCD 中,∠ADE=∠B=900,DE ⊥AB,垂足为E,且DE=EB=5,请用旋转图形的方法求四边形ABCD 的面积.18．如图3-58所示，分析下列图形中阴影部分的分布规律，按此规律在图(3)中画出其中的阴影部分．19．如图3-59所示，边长为4的正方形ABCD 绕点D 逆时针旋转30°后能与四边形A ′B ′C ′D ′重合． (1)旋转中心是哪一点?(2)四边形A ′B ′C ′D ′，是怎样的图形?面积是多少? (3)求∠C ′DC 和∠CDA ′的度数； (4)连接AA ′，求∠DAA ′的度数．20．如图3-60所示，△ABC 外侧有正方形ABDE 与正方形ACFG ，请你设计一个方案，将△ABC 旋转一个角度，使得△AEG 与由△ABC 旋转得到的三角形的一边重合，另一边在同一条直线上．21．如图3-61所示，画出△ABC 绕点O 逆时针旋转60°后得到的△DEF ，使A，┌ ┌DCA E BB，C的对应点分别为D，E，F．答案1. A （旋转的性质）2. D3. B4．C5．D6．B7．B8. 旋转9. 菱形10. 全等11. 10 （时针每小时旋转30度）12. 位置形状和大小13．18014．12015．300[提示：都按顺时针方向旋转，由四边形AOBC到DOEF的旋转角度为60°，则由四边形DOEF到AOBC的旋转角度为360-60°＝300°.]16. △OAE和△OBF，△OEB和△OFC，△OAB和△OBC，旋转的角度为90°17. 25（使三角形ADE绕点D旋转，使得旋转后边AD与边DC重合，通过割补则原图形变换为一个正方形，求出正方形的面积即可。

3.2图形的旋转同步习题一．选择题1．下列图形中，不是旋转对称图形的是（）A．正三角形B．等腰梯形C．正五边形D．正六边形2．下列各图中，能通过一个三角形绕一点旋转一次得到另一三角形的图形是（）A．B．C．D．3．把如图的五角星绕着它的中心旋转一定角度后与自身重合，则这个旋转角度可能是（）A．36°B．72°C．90°D．108°4．如图，把△OAB绕点O逆时针旋转80°，得到△OCD，则下列结论错误的是（）A．BD＝OB B．AB＝CD C．∠AOC＝∠BOD D．∠A＝∠C5．如图，在△ABC中，∠B＝50°，将△ABC绕点A按逆时针方向旋转得到△AB′C′．若点B′恰好落在BC边上，则∠CB′C′的度数为（）A．50°B．60°C．80°D．100°6．如图，将△ABC绕点C顺时针旋转得到△DEC，使点A的对应点D恰好落在边AB上，点B 的对应点为E，连接BE，下列四个结论：①AC＝AD；②AB⊥EB；③BC＝EC；④∠A＝∠EBC；其中一定正确的是（）A．①②B．②③C．③④D．②③④7．如图，在△ABC中，AB＝AC＝10，BC＝16，点D是边BC上一点（点D不与点B，点C重合），将AC绕点A顺时针旋转至AC1，AC1交BC于点H，且AD平分∠CAC1，若DC1∥AB，则点B到线段AD的距离为（）A．2B．C．4D．38．如图，将△ABC绕A点逆时针旋转60°得到△ADE，连接CD，若∠CDE＝90°，则∠BCD 的度数是（）A．110°B．120°C．130°D．150°9．如图，Rt△ABC中，∠BAC＝30°，∠C＝90°，将△ABC绕点A旋转，使得点C的对应点C′落在AB上，则∠BB′C′的度数为（）A．12°B．15°C．25°D．30°10．如图，在Rt△ABC中，∠ABC＝90°，AB＝2，BC＝4，点D是BC上的一点，BD＝1，点P是AC上的一个动点，连接DP，将线段DP绕点D顺时针旋转90°得到线段BQ，连接BQ，则线段BQ长的最小值是（）A．1B．2C．D．二．填空题11．如图，在△ABC中，∠BAC＝105°，将△ABC绕点A逆时针旋转得到△AB′C′．若点B 恰好落在BC边上，且AB′＝CB′，则∠C′的度数为°．12．如图，Rt△ABC和Rt△DCE中，∠ACB＝∠DCE＝90°，∠A＝30°，∠E＝45°．B，C，E三点共线，Rt△ABC不动，将△DCE绕点C逆时针旋转α（0°＜α＜360°），当DE∥BC 时，α＝．13．如图，等边△ABC，边长为4，动点D从点B出发，沿射线BC方向移动，以AD为边在右侧作等边△ADE，取AC中点F，连接EF，当EF的值最小时，BD＝．14．如图，在Rt△ABC中，∠ACB＝90°，将△ABC绕顶点C逆时针旋转得到△A′B′C，M 是BC的中点，P是A′B′的中点，连接PM，若BC＝2，∠BAC＝30°，则线段PM的最大值是．15．如图，在Rt△ABC中，∠C＝90°，∠A＝30°，点P在AC边上，以点P为中心，将△ABC 顺时针旋转90°，得到△DEF，DE交边AC于G，当P为中点时，AG：DG的值为．三．解答题16．如图，D是△ABC的边BC延长线上一点，连接AD，把△ACD绕点A顺时针旋转60°恰好得到△ABE，其中D，E是对应点，若∠CAD＝18°，求∠EAC的度数．17．如图，P是等边△ABC内的一点，且P A＝5，PB＝4，PC＝3，将△APB绕点B逆时针旋转，得到△CQB．（1）求点P与点Q之间的距离；（2）求∠BPC的度数；（3）求△ABC的面积．18．如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C（﹣1，3）．分别画出下列图形．（1）若△ABC经过平移后得到△A1B1C1，已知点C1的坐标为（4，0）；（2）若△ABC和△A2B2C2关于原点O成中心对称图形；（3）将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3．参考答案一．选择题1．解：A、正三角形旋转120°，可以与原图形重合，是旋转对称图形，不合题意；B、等腰梯形，不是旋转对称图形，符合题意；C、正五边形旋转72°，可以与原图形重合，是旋转对称图形，不合题意；D、正六边形旋转60°，可以与原图形重合，是旋转对称图形，不合题意；故选：B．2．解：根据旋转的定义，A，B，C中的三角形绕一点旋转一次不能得到另一三角形，不符合题意，选项D符合题意．故选：D．3．解：五角星可以被中心发出的射线分成5个全等的部分，因而旋转的角度是360°÷5＝72°，故选：B．4．解：∵△OAB绕点O逆时针旋转80°得到△OCD，∴∠A＝∠C，∠AOC＝∠BOD，AB＝CD，OB＝OD，∵∠BOD≠90°，∴BD≠OB．故选：A．5．解：∵将△ABC绕点A按逆时针方向旋转得到△A′B′C′，∴AB＝AB′，∠C′B′A＝∠B，∴∠AB′B＝∠B，∵∠B＝50°，∴∠C′B′A＝∠AB′B＝50°，∴∠CB′C′＝180°﹣∠C′B′A﹣∠AB′B＝80°，故选：C．6．解：∵将△ABC绕点C顺时针旋转得到△DEC，∴AC＝CD，BC＝CE，AB＝DE，故①错误，③正确；∴∠ACD＝∠BCE，∴∠A＝∠ADC＝，∠CBE＝，∴∠A＝∠EBC，故④正确；∵∠A+∠ABC不一定等于90°，∴∠ABC+∠CBE不一定等于90°，故②错误．故选：C．7．解：如图，过点B作BF⊥AD于F，过点A作AE⊥BC于E，∵AB＝AC＝10，BC＝16，AE⊥BC，∴CE＝BE＝8，∠C＝∠ABC，∴AE＝＝＝6，∵将AC绕点A顺时针旋转至AC1，∴AC＝AC1，∵AD平分∠CAC1，∴∠CAD＝∠C1AD，在△ACD和△AC1D中，，∴△ACD≌△AC1D（SAS），∴∠C＝∠C1，∵DC1∥AB，∴∠C1＝∠HAB，∵∠ADB＝∠C+∠CAD，∠DAB＝∠DAC1+∠HAB，∴∠DAB＝∠ADB，∴AB＝DB＝10，∴DE＝BD﹣BE＝2，∴AD＝＝＝2，∵S△ABD＝×BD×AE＝×AD×BF，∴10×6＝2×BF，∴BF＝3，故选：D．8．解：∵将△ABC绕点A逆时针旋转60°得到△ADE，∴∠CAE＝60°，∠E＝∠ACB，∴∠CAE+∠CDE＝360°﹣（∠ACD+∠E），∵∠BCD＝360°﹣∠ACB﹣∠ACD＝360°﹣（∠ACD+∠E），∴∠BCD＝∠CDE+∠CAE＝60°+90°＝150°，故选：D．9．解：由旋转的性质可知，∠B′AB＝∠BAC＝30°，AB＝AB′，∴∠ABB′＝∠AB′B＝（180°﹣30°）＝75°，∵∠BCB＝90°，∴∠BB′C＝90°﹣75°＝15°，故选：B．10．解：过点D作DT⊥BC交AC于点T，在DC上取一点G，使得DG＝DT，连接TG，GQ，过点B作BR⊥QG于R．∵∠TDC＝∠PDQ＝90°，∴∠PDT＝∠GDQ，在△PDT和△QDG中，，∴△PDT≌△QDG（SAS），∴∠DTP＝∠DGQ，∴点Q在射线GQ上运动，∠DGQ是定值，∵∠TDC＝∠B＝90°，∴DT∥AB，∴＝，∠DTC＝∠A，∴＝，∠DGQ＝∠A，∴DT＝DG＝，∵∠ABC＝90°，AB＝2，BC＝4，∴AC＝＝＝2，∴sin∠DGR＝sin∠A，∴＝，∴＝，∴BR＝，根据垂线段最短可知，当BQ与BR重合时，BQ的值最小，最小值为．故选：D．二．填空题11．解：∵∠BAC＝105°，∴∠B+∠C＝75°，∵AB′＝CB′，∴∠C＝∠CAB'，∴∠AB'B＝∠C+∠CAB'＝2∠C，∵将△ABC绕点A逆时针旋转得到△AB′C′，∴AB＝AB'，∴∠B＝∠AB'B＝2∠C，∴∠C＝25°，故答案为：25．12．解：如图1，当DE位于BC的上方，∵DE∥BC，∴∠D＝∠BCD，∵∠E＝45°，∠DCE＝90°，∴∠D＝90°﹣∠E＝45°，∴∠BCD＝45°，∴α＝∠ACD＝45°，如图2，当DE位于BC的下方，∵DE∥BC，∴∠E＝∠BCE＝45°，∴α＝∠ACB+∠BCE+∠ECD＝90°+45°+90°＝225°，∴当DE∥BC时，α＝45°或225°．故答案为：45°或225°．13．解：如图，连接CE，∵点F是AC的中点，∴AF＝CF＝2，∵△ABC和△ADE是等边三角形，∴AB＝AC，AD＝AE，∠BAC＝∠DAE＝60°，∴∠BAD＝∠CAE，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），∴CE＝BD，∠ABD＝∠ACE＝60°，∴点E在∠ACB的外角的角平分线上运动，∴当EF⊥CE时，EF有最小值，∴∠CFE＝30°，∴CE＝CF＝1，∴BD＝1，故答案为1．14．解：如图连接PC．在Rt△ABC中，∵∠A＝30°，BC＝2，∴AB＝4，根据旋转不变性可知，A′B′＝AB＝4，∴A′P＝PB′，∴PC＝A′B′＝2，∵CM＝BM＝1，又∵PM≤PC+CM，即PM≤3，∴PM的最大值为3（此时P、C、M共线）．故答案为：3．15．解：设BC＝x，在Rt△ABC中，∠A＝30°，∴AB＝2x，AC＝x，∵点P是AC中点，∴PC＝P A＝x，由旋转得，DP＝DF＝AC＝x，DG＝DE＝AB＝x，根据勾股定理得，PG＝＝＝x，∴AG＝AP﹣PG＝x﹣x，∴＝＝．故答案为．三．解答题16．解：∵把△ACD绕点A顺时针旋转60°恰好得到△ABE，∴∠DAE＝60°，∴∠EAC＝∠EAD﹣∠CAD＝42°．17．解：（1）连接PQ，如图1，∵△ABC是等边三角形，∴∠ABC＝60°，BA＝BC，∵△QCB是△P AB绕点B逆时针旋转得到的，∴△QCB≌△P AB，∴BP＝BQ，∠PBQ＝∠ABC＝60°，CQ＝AP＝5，∵BP＝BQ＝4，∠PBQ＝60°，∴△PBQ是等边三角形，∴PQ＝PB＝4；（2）∵QC＝5，PC＝3，PQ＝4，而32+42＝52，∴PC2+PQ2＝CQ2，∴△PCQ是直角三角形，且∠QPC＝90°，∵△PBQ是等边三角形，∴∠BPQ＝60°，∴∠BPC＝∠BPQ+∠QPC＝60°+90°＝150°；（3）如图2，过点C作CH⊥BP，交BP的延长线于H，∵∠BPC＝150°，∴∠CPH＝30°，∴CH＝PC＝，PH＝HC＝，∴BH＝4+，∴BC2＝BH2+CH2＝+（4+）2＝25+12，∵S△ABC＝BC2，∴S△ABC＝（25+12）＝+9．18．解：（1）如图，△A1B1C1即为所求作．（2）如图，△A2B2C2即为所求作．（3）如图，△A3B3C3即为所求作．。

《图形的旋转》习题一、选择题1．下列图形中，绕某个点旋转90°能与自身重合的有( )①正方形；②长方形；③等边三角形；④线段；⑤角；⑥平行四边形．A.1个B.2个C.3个D.4个2．五角星可以看成由一个四边形旋转若干次而生成的，则每次旋转的度数可以是( )A.36°B.60°C.72°D.90°3．下面的图形(1)-(4)，绕着一个点旋转120°后，能与原来的位置重合的是( )A.（1），（4）B.（1），（3）C.（1），（2）D.（3），（4）4．在平面上有一个角是60°的菱形绕它的中心旋转，使它与原来的菱形重合，那么旋转的角度至少是( )A.90°B.180°C.270°D.360°5．数学课上，老师让同学们观察如图所示的图形，问：它绕着圆心O旋转多少度后和它自身重合？甲同学说：45°；乙同学说：60°；丙同学说：90°；丁同学说：135°．以上四位同学的回答中，错误的是( )A.甲B.乙C.丙D.丁6．下面四个图案中，是旋转对称图形的是( )A. B. C. D.7．如图所示的图形中，是旋转对称图形的有( )A.1个B.2个C.3个D.4个二、填空题8．请写出一个既是轴对称图形又是旋转对称图形的图形_____．9．将等边三角形绕其对称中心O旋转后，恰好能与原来的等边三角形重合，那么旋转的角度至少是_____．10．如图所示的五角星_____旋转对称图形．(填“是”或“不是”)．11．给出下列图形：①线段、②平行四边形、③圆、④矩形、⑤等腰梯形，其中，旋转对称图形有_____(只填序号)．三、解答题12．如下图是由三个叶片组成的，绕点O旋转120°后可以和自身重合，若每个叶片的面积为5cm2，∠AOB=120°，则图中阴影部分的面积之和为多少cm2．13．如图，已知AD=AE，AB=AC．(1)求证：∠B=∠C；(2)若∠A=50°，问△ADC经过怎样的变换能与△AEB重合？14．如图，△ABC和△BED是等边三角形，则图中三角形ABE绕B点旋转多少度能够与三角形重合．15．如图，已知△ABC和△AEF中，∠B=∠E，AB=AE，BC=EF，∠EAB=25°，∠F=57°；(1)请说明∠EAB=∠FAC的理由；(2)△ABC可以经过图形的变换得到△AEF，请你描述这个变换；(3)求∠AMB的度数．参考答案一、选择题1．答案：A解析：【解答】①正方形旋转的最小的能与自身重合的度数是90度，正确；②长方形旋转的最小的能与自身重合的度数是180度，错误；③等边三角形旋转的最小的能与自身重合的度数是120度，错误；④线段旋转的最小的能与自身重合的度数是180度，错误；⑤角旋转的最小的能与自身重合的度数是360度，错误；⑥平行四边形旋转的最小的能与自身重合的度数是180度，错误．故选A．【分析】根据旋转对称图形的旋转角的概念作答．2．答案：C解析：【解答】根据旋转的性质可知，每次旋转的度数可以是360°÷5=72°或72°的倍数．故选C【分析】分清基本图形，判断旋转中心，旋转次数，旋转一周为360°．3．答案：C解析：【解答】①旋转120°后，图形可以与原来的位置重合，故正确；②旋转120°后，图形可以与原来的位置重合，故正确；③五角星中心角是72°，120不是72的倍数，图形无法与原来的位置重合，故错误；④旋转90°后，图形无法与原来的位置重合，故错误．故选C．【分析】根据旋转的性质，对题中图形进行分析，判定正确选项．4．答案：B解析：【解答】因为菱形是中心对称图形也是旋转对称图形，要使它与原来的菱形重合，那么旋转的角度至少是180°．故选B．【分析】根据中心对称图形、旋转对称图形的性质．5．答案：B解析：【解答】圆被平分成八部分，旋转45°的整数倍，就可以与自身重合，因而甲，丙，丁都正确；错误的是乙．故选B【分析】根据圆周角的度数．6．答案：D解析：【解答】A、B、C不是旋转对称图形；D、是旋转对称图形．故选D．【分析】根据旋转的定义．7．答案：C解析：【解答】旋转对称图形的有①、②、③．故选C【分析】图形①可抽象出正六边形，图形②可抽象出正五边形，图形③可抽象出正六边形，而④中为等腰三角形，然后根据旋转对称图形的定义进行判断．二、填空题8．答案：圆（答案不唯一）解析：【解答】根据旋转对称图形和轴对称图形的定义：旋转对称图形：把一个图形绕着一个定点旋转一个角度后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角．（0度＜旋转角＜360度）．如果一个图形沿着一条直线对折后两部分完全重合，叫轴对称图形．可以得出圆、正方形等都符合答案．【分析】根据旋转对称图形和轴对称图形的定义找出符合图形，得出答案．9．答案：120°解析：【解答】该图形被经过中心的射线平分成三部分，因而每部分被分成的圆心角是120°，那么它至少要旋转120°．故答案为：120．【分析】正三角形被经过中心的射线平分成三部分，因而每部分被分成的圆心角是120°，因而旋转120度的整数倍，就可以与自身重合．10．答案：是．解析：【解答】因为五角星的五个顶点到其中心的距离相等，将圆周角5等分，故五角星是旋转对称图形．【分析】五角星的五个顶点到其中心的距离相等，将周角平分为5份，可判断是旋转图形．11．答案：①②③④解析：【解答】①线段，旋转中心为线段中点，旋转角为180°，是旋转对称图形；②平行四边形，旋转中心为对角线的交点，旋转角为180°，是旋转对称图形；③圆，旋转中心为圆心，旋转角任意，是旋转对称图形；④矩形，旋转中心为对角线交点，旋转角为180°，是旋转对称图形；⑤等腰梯形，是轴对称图形，不能旋转对称．故旋转对称图形有①②③④．【分析】根据每个图形的特点，寻找旋转中心，旋转角，逐一判断．三、解答题12．答案：5cm2解析：【解答】每个叶片的面积为5c m2，因而图形的面积是15cm2，图形中阴影部分的面积是图形的面积的三分之一，因而图中阴影部分的面积之和为5cm2．【分析】根据旋转的性质和图形的特点解答．13．答案：见解答过程．解析：【解答】（1）证明：在△AE B与△ADC中，AB=AC，∠A=∠A，AE=AD；∴△AEB≌△ADC，∴∠B=∠C．（2）解：先将△ADC绕点A逆时针旋转50°，再将△ADC沿直线AE对折，即可得△ADC与△AEB重合．或先将△ADC绕点A顺时针旋转50°，再将△ADC沿直线AB对折，即可得△ADC与△AEB重合．【分析】（1）要证明∠B=∠C，可以证明它们所在的三角形全等，即证明△ABE≌△ACD；已知两边和它们的夹角对应相等，由SAS即可判定两三角形全等．（2）因为△ADC≌△AED，公共点A，对应线段CD与BE相交，所以要通过旋转，翻折两次完成．14．答案：60度．解析：【解答】已知△ABC和△BED是等边三角形，∠ABC=∠EBD=60°⇒∠EBC=60°，又因为AB=BC，EB=BD，∠ABE=∠CBD=120°，所以△ABE≌△CBD．故△ABE绕B点旋转60度能够与△CBD重合．【分析】根据旋转对称图形的定义以及全等三角形的判定作答．15．答案：见解答过程．解析：【解答】（1）∵∠B=∠E，AB=AE，BC=EF，∴△ABC≌△AEF，∴∠C=∠F，∠BAC=∠EAF，∴∠BAC-∠PAF=∠EAF-∠PAF，∴∠BAE=∠CAF=25°；（2）通过观察可知△ABC绕点A顺时针旋转25°，可以得到△AEF；（3）由（1）知∠C=∠F=57°，∠BAE=∠CAF=25°，∴∠AMB=∠C+∠CAF=57°+25°=82°．【分析】（1）先利用已知条件∠B=∠E，AB=AE，BC=EF，利用SAS可证△ABC≌△AEF，那么就有∠C=∠F，∠BAC=∠EAF，那么∠BAC-∠PAF=∠EAF-∠PAF，即有∠BAE=∠CAF=25°；（2）通过观察可知△ABC绕点A顺时针旋转25°，可以得到△AEF；（3）由（1）知∠C=∠F=57°，∠BAE=∠CAF=25°，而∠AMB是△ACM的外角，根据三角形外角的性质可求∠AMB．。

2图形的旋转第1课时旋转的认识知识点1旋转的有关概念1．下面生活中的实例，不是旋转的是（）A．传送带传送货物B．螺旋桨的运动C．风车风轮的运动D．自行车车轮的运动2．如图，点A，B，C，D，O都在方格纸的格点上，若△COD是由△AOB绕点O按顺时针方向旋转而得到的，则旋转的角度为．第2题图第3题图3．如图，△ABC是等边三角形，点D是BC边上的中点，△ABD经过旋转后到达△ACE 的位置，那么：（1）旋转中心是点；（2）点B，D的对应点分别是点；（3）线段AB，BD，DA的对应线段分别是；（4）∠B的对应角是；（5）旋转的角度为．知识点2旋转的性质4．如图，△ABC绕点A逆时针旋转30°至△ADE，AB＝5 cm，BC＝8 cm，∠BAC ＝130°，则AD＝＝cm，DE＝＝cm，∠EAC＝∠＝，∠DAC＝．5．如图，△ABC以点C为旋转中心，旋转后得到△EDC.已知AB＝1.5，BC＝4，AC ＝5，则DE的长为（）A．1.5 B．3 C．4 D．5第5题图第6题图6．（2019·湘潭）如图，将△OAB绕点O逆时针旋转70°到△OCD的位置．若∠AOB ＝40°，则∠AOD＝（）A．45°B．40°C．35°D．30°7．（2020·天津）如图，在△ABC中，∠ACB＝90°，将△ABC绕点C顺时针旋转得到△DEC，使点B的对应点E恰好落在边AC上，点A的对应点为D，延长DE交AB于点F，则下列结论一定正确的是（）A．AC＝DEB．BC＝EFC．∠AEF＝∠DD．AB⊥DF知识点3确定旋转中心8．如图，在平面直角坐标系中，△ABC的顶点都在正方形网格线的格点上，将△ABC 绕点P按逆时针方向旋转90°，得到△A′B′C′，则点P的坐标为（）A．（0，0）B．（0，1）C．（－1，1）D．（1，1）9．（2020·赤峰）下列图形绕某一点旋转一定角度都能与原图形重合，其中旋转角度最小的是（）A．等边三角形B．平行四边形C．正八边形D．圆及其一条弦10．（2020·齐齐哈尔）有两个直角三角形纸板，一个含45°角，另一个含30°角，如图1所示叠放，先将含30°角的纸板固定不动，再将含45°角的纸板绕顶点A顺时针旋转，使BC∥DE，如图2所示，则旋转角∠BAD的度数为（）A．15°B．30°C．45°D．60°11．（2019·内江）如图，在△ABC中，AB＝2，BC＝3.6，∠B＝60°，将△ABC绕点A顺时针旋转得到△ADE，当点B的对应点D恰好落在BC边上时，则CD的长为（）A．1.6 B．1.8 C．2 D．2.6第11题图变式图【变式】如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C.连接AA′，若∠1＝27°，则∠B的度数是（）A．84°B．72°C．63°D．54°12．（2020·聊城）如图，在Rt△ABC中，AB＝2，∠C＝30°，将Rt△ABC绕点A旋转得到Rt△AB′C′，使点B的对应点B′落在AC上，在B′C′上取点D，使B′D＝2，那么点D到BC的距离等于（）A．2（33＋1）B.33＋1C.3－1D.3＋113．（2019·苏州）如图，在△ABC中，点E在BC边上，AE＝AB，将线段AC绕A点旋转到AF的位置，使得∠CAF＝∠BAE，连接EF，EF与AC交于点G.（1）求证：EF＝BC；（2）若∠ABC＝65°，∠ACB＝28°，求∠FGC的度数．14．（2019·河南）如图，在△OAB中，顶点O（0，0），A（－3，4），B（3，4），将△OAB与正方形ABCD组成的图形绕点O顺时针旋转，每次旋转90°，则第70次旋转结束时，点D的坐标为（）A．（10，3）B．（－3，10）C．（10，－3）D．（3，－10）错误!第2课时旋转作图知识点旋转作图1．将△AOB绕点O旋转180°得到△DOE，则下列作图正确的是（）2．如图，在4×4的正方形网格中，△MNP绕某点旋转一定角度得到△M1N1P1，则其旋转中心是．第2题图第3题图3．如图，它可以看作“◇”通过连续平移3次得到，也可以看作“◇”绕中心旋转3次，每次旋转度得到．4．如图，在正方形网格中，以点A为旋转中心，将△ABC按逆时针方向旋转90°，画出旋转后的△AB1C1.5．（教材P78做一做变式）如图，△ABC 绕点O 旋转后，顶点A 的对应点为A′，试确定旋转后的三角形．易错点 旋转方向不确定导致漏解6．在平面直角坐标系xOy 中，已知点A （3，4），将OA 绕坐标原点O 旋转90°到OA′，则点A′的坐标是 ．7．同学们曾玩过万花筒，它是由三块等宽等长的玻璃片围成的．如图看到的是万花筒的一个图案，图中所有小三角形均是全等的等边三角形，其中的平行四边形AEFG 可以看成是将平行四边形ABCD 以A 为中心（ ）A ．顺时针旋转60°得到B ．顺时针旋转120°得到C ．逆时针旋转60°得到D ．逆时针旋转120°得到8．如图，已知Rt △ABC 和三角形外一点P ，按要求完成图形． （1）将△ABC 绕顶点C 顺时针方向旋转90°，得△A ′B ′C ′； （2ABC 绕点P 逆时针方向旋转60°，得△A ″B ″C ″.ABC·P9．（2020·江西改编）如图，在正方形网格中，△ABC的顶点在格点上．请仅用无刻度直尺作△ABC绕点A顺时针旋转一定角度后，顶点仍在格点上的△AB′C′.参考答案：第1课时旋转的认识知识点1旋转的有关概念1．下面生活中的实例，不是旋转的是（A）A．传送带传送货物B．螺旋桨的运动C．风车风轮的运动D．自行车车轮的运动2．如图，点A，B，C，D，O都在方格纸的格点上，若△COD是由△AOB绕点O按顺时针方向旋转而得到的，则旋转的角度为90°．第2题图第3题图3．如图，△ABC是等边三角形，点D是BC边上的中点，△ABD经过旋转后到达△ACE 的位置，那么：（1）旋转中心是点A；（2）点B，D的对应点分别是点C，E；（3）线段AB，BD，DA的对应线段分别是线段AC，CE，EA；（4）∠B的对应角是∠ACE；（5）旋转的角度为60°．知识点2旋转的性质4．如图，△ABC绕点A逆时针旋转30°至△ADE，AB＝5 cm，BC＝8 cm，∠BAC ＝130°，则AD＝AB＝5cm，DE＝BC＝8cm，∠EAC＝∠BAD＝30°，∠DAC＝100°．5．如图，△ABC以点C为旋转中心，旋转后得到△EDC.已知AB＝1.5，BC＝4，AC ＝5，则DE的长为（A）A．1.5 B．3 C．4 D．5第5题图第6题图6．（2019·湘潭）如图，将△OAB绕点O逆时针旋转70°到△OCD的位置．若∠AOB ＝40°，则∠AOD＝（D）A．45°B．40°C．35°D．30°7．（2020·天津）如图，在△ABC中，∠ACB＝90°，将△ABC绕点C顺时针旋转得到△DEC，使点B的对应点E恰好落在边AC上，点A的对应点为D，延长DE交AB于点F，则下列结论一定正确的是（D）A．AC＝DEB．BC＝EFC．∠AEF＝∠DD．AB⊥DF知识点3确定旋转中心8．如图，在平面直角坐标系中，△ABC的顶点都在正方形网格线的格点上，将△ABC 绕点P按逆时针方向旋转90°，得到△A′B′C′，则点P的坐标为（C）A．（0，0）B．（0，1）C．（－1，1）D．（1，1）9．（2020·赤峰）下列图形绕某一点旋转一定角度都能与原图形重合，其中旋转角度最小的是（C）A．等边三角形B．平行四边形C．正八边形D．圆及其一条弦10．（2020·齐齐哈尔）有两个直角三角形纸板，一个含45°角，另一个含30°角，如图1所示叠放，先将含30°角的纸板固定不动，再将含45°角的纸板绕顶点A顺时针旋转，使BC∥DE，如图2所示，则旋转角∠BAD的度数为（B）A．15°B．30°C．45°D．60°11．（2019·内江）如图，在△ABC中，AB＝2，BC＝3.6，∠B＝60°，将△ABC绕点A顺时针旋转得到△ADE，当点B的对应点D恰好落在BC边上时，则CD的长为（A）A．1.6 B．1.8 C．2 D．2.6第11题图变式图【变式】如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C.连接AA′，若∠1＝27°，则∠B的度数是（B）A．84°B．72°C．63°D．54°12．（2020·聊城）如图，在Rt△ABC中，AB＝2，∠C＝30°，将Rt△ABC绕点A旋转得到Rt△AB′C′，使点B的对应点B′落在AC上，在B′C′上取点D，使B′D＝2，那么点D到BC的距离等于（D）A．2（33＋1）B.33＋1C.3－1D.3＋113．（2019·苏州）如图，在△ABC中，点E在BC边上，AE＝AB，将线段AC绕A点旋转到AF的位置，使得∠CAF＝∠BAE，连接EF，EF与AC交于点G.（1）求证：EF＝BC；（2）若∠ABC ＝65°，∠ACB ＝28°，求∠FGC 的度数．解：（1）证明：∵∠CAF ＝∠BAE ， ∴∠BAC ＝∠EAF.∵线段AC 绕A 点旋转到AF 的位置，∴AC ＝AF.在△ABC 和△AEF 中，⎩⎨⎧AB ＝AE ，∠BAC ＝∠EAF ，AC ＝AF ，∴△ABC ≌△AEF （SAS ）． ∴EF ＝BC.（2）∵AB ＝AE ，∠ABC ＝65°， ∴∠BAE ＝180°－65°×2＝50°. ∴∠FAG ＝∠BAE ＝50°.∵△ABC ≌△AEF ，∴∠F ＝∠C ＝28°. ∴∠FGC ＝∠FAG ＋∠F ＝50°＋28°＝78°.14．（2019·河南）如图，在△OAB 中，顶点O （0，0），A （－3，4），B （3，4），将△OAB 与正方形ABCD 组成的图形绕点O 顺时针旋转，每次旋转90°，则第70次旋转结束时，点D 的坐标为（D ）A ．（10，3）B ．（－3，10）C ．（10，－3）D ．（3，－10）错误!模型展示条件：OA绕原点O逆时针旋转90°至OA′.结论：△AOB≌△A′OB′.条件：AB绕点A顺时针旋转90°至AB′.结论：△ABD≌△B′AC.第2课时旋转作图知识点旋转作图1．将△AOB绕点O旋转180°得到△DOE，则下列作图正确的是（C）2．如图，在4×4的正方形网格中，△MNP绕某点旋转一定角度得到△M1N1P1，则其旋转中心是点B．第2题图第3题图3．如图，它可以看作“◇”通过连续平移3次得到，也可以看作“◇”绕中心旋转3次，每次旋转90度得到．4．如图，在正方形网格中，以点A为旋转中心，将△ABC按逆时针方向旋转90°，画出旋转后的△AB1C1.解：如图所示．5．（教材P78做一做变式）如图，△ABC绕点O旋转后，顶点A的对应点为A′，试确定旋转后的三角形．解：如图所示．易错点旋转方向不确定导致漏解6．在平面直角坐标系xOy中，已知点A（3，4），将OA绕坐标原点O旋转90°到OA′，则点A′的坐标是（－4，3）或（4，－3）．02中档题7．同学们曾玩过万花筒，它是由三块等宽等长的玻璃片围成的．如图看到的是万花筒的一个图案，图中所有小三角形均是全等的等边三角形，其中的平行四边形AEFG可以看成是将平行四边形ABCD以A为中心（D）A．顺时针旋转60°得到B．顺时针旋转120°得到C．逆时针旋转60°得到D．逆时针旋转120°得到8．如图，已知Rt△ABC和三角形外一点P，按要求完成图形．（1）将△ABC绕顶点C顺时针方向旋转90°，得△A′B′C′；（2）将△ABC绕点P逆时针方向旋转60°，得△A″B″C″.解：（1）△A′B′C′如图所示．（2）△A″B″C″如图所示．9．（2020·江西改编）如图，在正方形网格中，△ABC的顶点在格点上．请仅用无刻度直尺作△ABC绕点A顺时针旋转一定角度后，顶点仍在格点上的△AB′C′.解：（1）如图，△A′B′C′即为所求．（2）如图，△AB′C′即为所求．。

3.2.2图形的旋转
课后作业
1.已知如图1所示的四张牌，若将其中一张牌旋转180º
后得到图2，则旋转的牌是（ ）
2. 已知点A 的坐标为（a ，b ），O 为坐标原点，连结OA ，将线段O A 绕点O 按逆时针方向旋转90°得OA ₁，则点A ₁的坐标为（ ）.
A ．()a b -，
B ．()a b -，
C ．()b a -，
D ．()b a -，
3. 如图所示，五角星的顶点是一个正五边形的五个顶点．这个五角星可以由一个基本图形（图中的阴影部分）绕中心O 至少经过____________次旋转而得到， 每一次旋转_______度．
4. 如图，将△ABC 绕点A 顺时针旋转60°得到△A ED ，若线段AB=5，求出BE 的长是多少？
参考答案
1.A，
2.C，
3. 4,72
4.解：∵将△ABC绕点A顺时针旋转60°得到△AED，∴∠BAE=60°，AB=AE，
∴△BAE是等边三角形，
∴BE=5．。