山东省淄博实验中学2017-2018学年高三上学期第一次(10月)诊断考试数学(文)试题 Word版含答案

4•已知l<x<10, a = lgx\A = lg(lgx),c = (lgx)2 > 那么有()A・c>a>b B. c>b>a C・a>c> b D. a>b>c5.平面向量a必满足a・（a + &） = 3‘ c ；=2, I;=1,则向量7与&夹角的余弦值为（）1 A — B. -1C・主 D.匣22 2 2［人t fl*6•函数/心殆蹄讪呻〉到的函数为奇函数，则函数/(x)的图象(值为( )看作同一对“友好点对”).已知函数f(x)=log. x(x > 0)-宀4g 。

)’则此函数的“友好点对"9. A. 4B. 3^3C. 2^3D. 2设心)是定义在R 上的奇函数，夬2)=0, 当x>0时，有旳(3一您<0恒成立,则不等式X 2x 2fix)>0的解集是()A. (一2,0)U(2, +8) C. (一8, -2)U(2, +8)D. (一8, — 2)U(0,2)10.若直角坐标平面内的两点P 、Q 满足条件：①P 、Q 都在函数y = /(x)的图彖上；②P 、QB. (-2,0)U(0,2) 关于原点对称，则称点对［P,Q 〕是函数y = /(x)的一对“友好点对”(注：点对［P0与QP ］A.关于点 1 o ］对称 12'丿B.关于直线* =兰对称12C. 关于点 对称在AABC 中，a.b.c 分别为内角A.B.C所对的边，若a= V3,J7.国数/(x) = sin(ex + 0)e>0,岡申的最小正周期是〃，若其图線向右平移二个单.位后得 n2II.已^/(x)»sin^x-cosm.t •和R).儿/(x)的仃何▲对称他“抽"的横坐标邙不MFIXffl(2^.3^),则a,的观flUIM ()12・定乂在*上的伽数/⑴満足①⑴.②/(x + 2)« f(x). %x€|OJ|f | /W = log 3(.V ?-x + l),则Ffitt^./(x)-logj|x|的■点个敷是()4A ・ 2B. 4C. 5D. 6_ 第II 卷(非选择题共90分)二、填空题(本大题共4小题，每小题5分，共20分)13. ______________________________________________________ 己知厶=(3,~4), 5 = (2,0,向在厶方向上的投影为-3, WJr= ____________________________ . 14. 已知Z\ABC 的周长为72+1,面积为-sinC,且sin J + sin B = x/2 sin C,丸角C 的6值为 ________ ・ 】5.已知函数/⑴』八2,xG,且/(切=_3,则/(6-a)= ________________ .・ log 2(x + l),x>l16. 若函数/(x) = gf+a,+加+c 有极值点Xpxjx, <x 2), /(xj =召，则关于工的方程［/⑴『十2”⑴+ “ 0的不同实数根的个数是 _______________ .三、解答题(本大題共6小题，共70分.解答应写出文字说明、证明过程或演算步赚)17. ( 10分)设“:实数X 满足：处+ 3/<0 (°>0),(i\w -'q ：实数x 满足:“二］，，m e(1,2)⑴若axL 且“人彳为仏求实数X 的取(ft 范鳳(•!)(/是"的充分不必婴条件，求实数a 的取他范H4.18. (本小题满分12分)在锐角MBC 中,内角A, B, C 的对边分别为a, b. c, 且 2asinB=>/3 b.伸川时何I 2017" 10 /)(I)求角 A 的大小；(11)^ a 4, b«c X ■求AAIU 1 的|h|枳.・D3 一 49 一821 . q : x ：： 12■■ p q 为真1 3得 x ，即实数x 的取值范围为2 4则A 是B 的真子集得+冷，即a 的取值范围为_3418.解：解：（1）v^ ABC 中，」 -■,•••根据正弦定理，得―二, •••锐角△ ABC 中，sinB >0, •等式两边约去sinB,得sinA=-2 ••• A 是锐角△ ABC 的内角，• A=;371（2）v a=4, A=,•由余弦定理 a 2=b 2+c 2- 2bccosA,得 16=b 2+c 2- 2bccos , ■-1化简得 b 2+c 2 - bc=16, ••• b+c=8,平方得 b 2+c 2+2bc=64, •••两式相减，得 3bc=48,可得bc=16. 因此，A ABC 的面积5=皿皿=X 16X sJ =4 ■.理科参考答案、DACCB ABCDB AD 、13. 21 14. 4 -15.33~216. 3三、17.解：I p : a::x ：： 3a a 0 ,II q 是p 的充分不必要条件，记 A::x 3a,a 0 '1 37 <^7 4 4 ' 12 e x V 1r1 3"—<x <-2 4：『今或」a<23a 1（9分）3a _1•••（ 5 分）19. 解：1 f x = 3sin — cos - — cos X 1' * 2 2 2.3 . 1 cos x A . 3 . 1 1 sin x1sin x cos x —2 2 2 2 2.(IT V 1=sin x ------- i + -\、 6丿 25x2二 F x 一訂 6二—I 11( 八1 113)f (x )=—，即si x — -1 十一=得sin X --- 110< 6丿2 10 < 6丿 5 Tt 兀 JI 31 / 4幣0兰x 兰一, ■ 一一兰 X — 一兰—, 二 X-一 1 = 2 6 6 3 6丿 5 ( JI ji、\ (JI ' J 3 (1 sinx =sin x — - +— =sin x — - ——+ cos X - 一 I 6 61 62 1 62 6X -6 = 6：，即x 八时，f x min "3 .34 1 3、3 4-6 2 6 2 10 20.解：I •/ f (x^» 是奇函数，二f(x)，f(-x)=O 恒成立… x 2+bx+1 2 a b x a =0恒成立， a=0,b = 0 f(x)=£，x +1 f'(x)二 2(1 x)(1 x) (x 2 1)2 由 f '(x) 0 ,得-1 v x v 1 ；由 f '(x) ：：0 ,得 x > 1 或 x v -1 故函数f （x ）的增区间为 -1,1 , f （x ）的减区间为（」-,-1）和（1,；）II T 2m — 1 > f （x ）有解，••• 2m — 1 > f （x ）min 即可 当 x 0时，f x 0;当x = 0^, f 0 = 0;当x ：0时，f x ：： 0由I 知f x 在-:：，-1上为减函数，在-1,0上为增函数（2分）（3分）（4分）（6分）一（7 分） •• （ 8 分） • （ 10 分） • （ 12 分） （1分）• （ 3 分）..（4 分）• （ 5 分）•• （ 6分）（7分） • （ 8 分） • ( 10 分) (12 分)21.解：I 令 v t =100-5t=0，解得 t=4秒或t = -5秒 舍 •••( 2 分)/ 3(t +1 ) 3从发现前方事故到车辆完全停止行驶距离为 s(n)因为f (x )的图象与x 轴交于两个不同的点 AgQ ),B (x 2,0 )所以方程2 In x _x 2 +ax =0的两个根为x 1, x 2，则咅- = 0，两式相减得0n x 2 - x 2 + ax 2 = 0s =0.9 空空 + 43600正一 5t dt3 t 1 3=30+^In t 1 -5t 24=30+10| n5-5II 设高速上油费总额为y ，速度v 满足60岂v 乞120，则I v 40= 4 S』250 v S -5-S wv 40yw . v(250v当且仅当 丄 =4! , v =100时取等号250 v 一(10 分)由v =100222 (12 分)解：(I)由 f (x) 2x a ，得切线的斜率 k = f(2)=a-3=-1, a=2,,故xf(x) =21 nx-X 2 2x ,由 f x _ 2x m 得 m ^2ln x —x 2•••不等式f x -2x m 在［1, e ］上有解，所以m 兰(21 nx 「x 2)max e令 g(x) =21 n x-x 2 则 g(x )=2_2x 」(x 1)(x1)x••• x ・［一，e ］，故 g (x) =0 时，x=1 •当-:::x ：：：1 时，g (x) .0 ； 当 1 ：：：x ：：：e 时，g ：：：g(x)在 X =1处取得最大值g(1) - -1,所以m 乞-12 In 为一In X 2----------------------------------------- ?X i — X2又 f X = 2In x _x 2 ax, f x -2X a ，贝卩 v丿XX i X 2 = .2 X i X 24_XiX 2a 二亠 _2InX i 」nX2X i+x 2X i- X 2下证 4 捲+x 2X i 2(InXi —lnx 2)“( *),即证明 2化一Xi)f 冬 7山冬X 2X i X 2X20 ：：X i ：：X 2,. 0 ::: t ::: i,即证明 u t ■■=. 22 +i亠I nt ：：； 0在0 ::: t ::; i 上恒成立因为 (t+i) t i：2t (t i)2二启又—，所以u t 0所以，u t 在0,i 上是增函数，则 u t ::: u i = 0 ,从而知2 X2 一“ . |门-^ :::故亠一込土乞0，即 X-I X 2论 一 X 2宁0成立。

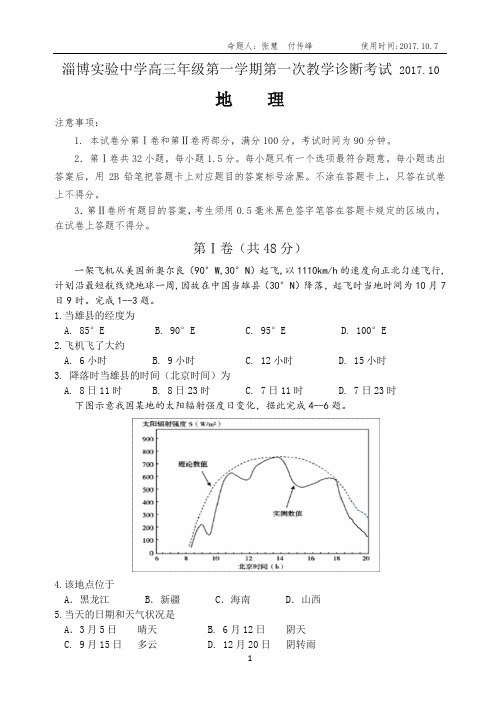
淄博实验中学高三年级第一学期第一次教学诊断考试2017.10地理注意事项：1. 本试卷分第Ⅰ卷和第Ⅱ卷两部分，满分100分，考试时间为90分钟。

2．第Ⅰ卷共32小题，每小题1.5分。

每小题只有一个选项最符合题意。

每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

不涂在答题卡上，只答在试卷上不得分。

3．第Ⅱ卷所有题目的答案，考生须用0.5毫米黑色签字笔答在答题卡规定的区域内，在试卷上答题不得分。

第Ⅰ卷（共48分）一架飞机从美国新奥尔良（90°W,30°N）起飞,以1110km/h的速度向正北匀速飞行,计划沿最短航线绕地球一周,因故在中国当雄县（30°N）降落，起飞时当地时间为10月7日9时。

完成1--3题。

1.当雄县的经度为A. 85°EB. 90°EC. 95°ED. 100°E2.飞机飞了大约A. 6小时B. 9小时C. 12小时D. 15小时3. 降落时当雄县的时间（北京时间）为A. 8日11时B. 8日23时C. 7日11时D. 7日23时下图示意我国某地的太阳辐射强度日变化，据此完成4--6题。

4.该地点位于A．黑龙江B．新疆C．海南D．山西5.当天的日期和天气状况是A．3月5日晴天 B. 6月12日阴天C. 9月15日多云D. 12月20日阴转雨6.当地日落时刻的太阳辐射强度，理论与实测数值均大于日出，最有可能的影响因素是A．纬度 B.气温 C.海拔 D.地形读“某地等高线地形图”，完成7--8题。

7. 根据上图信息，下列判断正确的是A．a河的总体流向为自东向西 B．a河的落差比b河大，水流更急C．P点到山顶的相对高度可能为300m D．陡崖顶部的海拔高度可能为450m8.该地计划修建一条连接a、b两河的运河，在c、d两方案中最终选择了d方案，原因是A．d方案的距离较短，工程量较小 B．地势西高东低，有利于河水自流C．经过河谷地势较低，有天然河道 D．沿等高线修建，水流平缓利于航行我国东南沿海某地拟修建一座水位60米的水库。

山东省实验中学20l5级高三第一次诊断性考试数学试题(理科)2017．09说明：本试卷满分l50分，分为第I 卷(选择题)和第II 卷(非选择题)两部分，第I 卷为第l 页至第3页，第II 卷为第3页至第5页．试题答案请用2B 铅笔或0.5mm 签字笔填涂到答题卡规定位置上，书写在试题上的答案无效．考试时间120分钟．第I 卷 (共60分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．)1．已知集合{}{}234005A x x x B x x A B =--<=≤≤⋃=，，则 A ．[)0,4B ．[]0,4C ．[]15-，D ．(]15-，2．已知1213,3z i z i =+=+，其中i 是虚数单位，则12z z 的虚部为 A ．1-B.45C ．i -D ．45i3.在602,6ABC ABC AB BC BC ∆∠===o中，，，在上任取一点D ，使ABD ∆为钝角三角形的概率为 A.16B.13C.12D.234．在等比数列{}n a 中，13282,81n n a a a a -+=⋅=，且前n 项和121n S =，则此数列的项数n 等于 A ．4B ．5C ．6D ．75．(421x x ⎛⎫+- ⎪⎝⎭的展开式中x 的系数是A. 1-B. 3C. 3-D. 16．将长方体截去一个四棱锥得到的几何体如右图所示，则该几何体的侧视图为的展开式中x 的系数是A. 16163π-B. 32163π-C. 1683π-D. 3283π-7．设偶函数()[)0f x +∞在，上单调递增，则使得()()21f x f x >-成立的x 的取值范围是 A ．1,13⎛⎫ ⎪⎝⎭ B ．()1,1,3⎛⎫-∞⋃+∞ ⎪⎝⎭ C. 11,33⎛⎫- ⎪⎝⎭ D. 11,,33⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭8．下图是一个算法流程图，则输出的x 的值是A ．37B ．42C ．59D ．659．已知曲线12:2cos ,:3sin 2cos2C y x C y x x ==-，则下面结论正确的是 A ．把1C 各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移23π个单位长度，得到曲线C 2B ．把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移至3π个单位长度，得到曲线C 2C ．把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移23π个单位长度，得到曲线C 2D ．把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移3π个单位长度，得到曲线C 210．过抛物线24y x =的焦点F 的直线交抛物线于A ，B 两点，若3=AF BF =，则 A ．52B ．2C ．32 D ．1211．已知函数()42xxf x m =⋅-，若存在非零实数0x ，使得()()00f x f x -=成立，则实数m 的取值范围是 A ．1,2⎡⎫+∞⎪⎢⎣⎭B ．10,2⎛⎫ ⎪⎝⎭C. ()0,2D. [)2,+∞12.一个二元码是由0和1组成的数字串()12,n x x x n N *⋅⋅⋅∈，其中()1,2,3k x k n ⋅⋅⋅=称为第k 位码元.二元码是通信中常用的码，但在通信过程中有时会发生码元错误（即码元由0变为1，或者由1变为0.已知某种二元码127x x x ⋅⋅⋅的码元满足如下校验方程组：4567236713570,0,0,x x x x x x x x x x x x ⊕⊕⊕=⎧⎪⊕⊕⊕=⎨⎪⊕⊕⊕=⎩其中运算定义为000,01,101,110⊕=⊕⊕=⊕=.现已知一个这种二元码在通信过程中仅在第k 位发生码元错误后变成了1101101，那么利用上述校验方程组可判定k 等于 A.3B.4C.5D.6第II 卷(非选择题，共90分)二、填空题(本题共4小题，每小题5分，共20分．)13．已知向量()()1,1,2,a b y a b a b y ==+=⋅=r r r r r r，若，则___________l4．已知,x y 满足,4,22.y x x y z x y x y k ≥⎧⎪+≤=+⎨⎪-≥⎩若有最大值8，则实数k 的值为___________.l5．在三棱锥P ABC -中，26,4,PA PB PC AC AB AC AB =====⊥且，则该三棱锥外接球的表面积为________16．已知抛物线24y x =的准线与双曲线()22221,0x y a b a b-=>交于A 、B 两点，点F 为抛物线的焦点，若FAB ∆为直角三角形，则双曲线离心率的取值范围是__________．三、解答题(共70分．解答应写出文字说明、证明过程或演算步骤．第17—21题为必考题每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．)17．(12分)在ABC ∆中，角A ，B ，C 的对边分别为,,,2sin 3sin .a b c b c B A ==，且 (1)求cos B 的值；(2)若2a ABC =∆，求的面积． 18．(12分)在三棱柱111ABC A B C -，侧面11ABB A 为矩形，112,22,AB AA D AA ==是中点，BD 与1AB 交于点O ，且OC ⊥平面11ABB A .（1）证明：平面1AB C ⊥平面BCD ；（2）若1,OC OA AB C =∆的重心为G ，求直线GD 与平面ABC 所成角的正弦值.19．(12分)某公司每个工作日由位于市区的总公司向位于郊区的分公司开一个来回的班车（每年按200个工作日计算），现有两种使用班车的方案，方案一是购买一辆大巴，需花费90万元，报废期为10年，车辆平均每年的各种费用合计5万元，司机年工资6万元，司机每天请假的概率为0.1（每年请假时间不超过15天不扣工资，超过15天每天100元），若司机请假则需从公交公司雇佣司机，每天支付300元工资.方案二是租用公交公司的车辆（含司机），根据调研每年12个月的车辆需求指数如直方图所示，其中当某月车辆需求指数在()()212,1,2,3,4,51010n n n -⎛⎤=⎥⎝⎦时，月租金为10.2n +万元. （1）若购买大巴，设司机每年请假天数为x ，求公司因司机请假而增加的花费y （元）及使用班车年平均花费ζ（万元）的数学期望E ζ.（2）试用调研数据，给出公司使用班车的建议，使得年平均花费最少.20．(12分)已知椭圆()2222:10x y E a b a b +=>>的左，右焦点分别为12F F ，离心率12e =，过点2F 的直线交椭圆于A ，B 两点，且1ABF ∆的周长为8． （1）求椭圆E 的标准方程；（2）过原点的直线与交椭圆E 于M ，N 两点，且满足AB//MN ，求证2MN AB为定值，并求出该定值．21．(12分)已知函数()ln 1f x x kx =-+.（1）函数函数()f x 在点()()2,2f 处的切线与210x y -+=平行，求k 的值； （2）若()0f x ≤恒成立，试确定实数k 的取值范围；（3）证明：()111,2n n nn en N n n --*+⎛⎫<∈≥ ⎪⎝⎭．(二)选考题：共10分．请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分． 22．[选修4-4，坐标系与参数方程】(10分)已知曲线1C 的极坐标方程为6cos ρθ=，曲线2C 的极坐标方程为()4R πθρ=∈，曲线12C C 、相交于点A ；B ．(1)将曲线12C C 、的极坐标方程化为直角坐标方程； (2)求弦AB 的长．23．【选修4—5：不等式选讲】(10分) 已知函数()21f x x a x =-+-． (1)当1a =时，解不等式()2f x ≥； (2)求证：()12f x a ≥-．山东省实验中学2015级高三第一次诊断性考试数学试题(理科) 2017．09一、选择题 DBABBD ACDCBC 二、填空题 13．3 14．4-15．36π 16．,+∞)三、解答题17.解：⑴因为2sin B A =，所以2b =．…………………………………2分所以a =3分所以222cos 22a c b B ac b +-===…………………………………6分 ⑵因为2a =，所以b c ==8分又因为cos 3B =，所以sin 3B =．…………………………………………………10分 所以2363221sin 21=⨯⨯⨯==∆B ac S ABC ………………………………………12分 18. 解：⑴11A ABB Θ为矩形，2=AB ，221=AA ，D 是1AA 的中点，ο90=∠∴BAD ，ο901=∠ABB ，221=BB ，2211==AA AD 22tan ==∠∴AB AD ABD ，22tan 11==∠BB AB B AB B AB ABD 1∠=∠∴…………………………………………………………2分2111π=∠+∠=∠+∠∴BAB ABD BAB B AB2π=∠∴AOB ，即BD AB ⊥1……………………………………4分⊥CO Θ平面11A ABB ，⊂1AB 平面11A ABB CO AB ⊥∴1又O CO BD =I ，⊥∴1AB 平面BCD ⊂1AB Θ平面C AB 1∴平面C AB 1⊥平面BCD ………………………6分⑵如图，以O 为坐标原点，OC OB OD ,,1所在直线为zy x ,,轴建立空间直角坐标系。

高三年级第一学期第一次教学诊断考试试题数 学（人文）第I 卷（共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的。

1.设集合{}11M x x =-<，{}2N x x =<，则M N = （ ）A.()1,1-B. ()1,2-C. ()0,2D. ()1,2 2．命题“存在一个无理数，它的平方是有理数”的否定是（ ）A ．任意一个有理数，它的平方是有理数B ．任意一个无理数，它的平方不是有理数C ．存在一个有理数，它的平方是有理数D ．存在一个无理数，它的平方不是有理数 3．“sin cos αα=”是“cos20α=”的（ ）A 充分不必要条件B 必要不充分条件C 充分必要条件D 既不充分也不必要 4．已知函数f （x ）=3x﹣（13）x，则f （x ）（ ） A ．是偶函数，且在R 上是增函数 B ．是奇函数，且在R 上是增函数 C ．是偶函数，且在R 上是减函数 D ．是奇函数，且在R 上是减函数5.已知命题p ：,x ∃∈R 210x x -+≥;命题q ：若22a b <,则a <b .下列命题为真命题的是（ ） A ．p q ∧ B.p q ∧⌝ C.p q ⌝∧ D.p q ⌝∧⌝6．设函数()f x 在R 上可导，其导函数()f x '，且函数()f x 在2x =-处取得极小值，则函数()y xf x '=的图象可能是（ ）.7.为了得到函数y=sin )3(π+x 的图象，只需把函数y=sin x 的图象上所有的点（ ）A.向左平行移动3π个单位长度 B. 向右平行移动3π个单位长度 C.向上平行移动3π个单位长度 D. 向下平行移动3π个单位长度8．在ABC ∆中，AB=3，AC=2，BC=10，则AB AC ⋅= ( ) A ．23-B ．32- C ．32 D ．239． 若，则( )A ．B ．C ．D ．10.某公司为激励创新，计划逐年加大研发奖金投入。

淄博实验中学高三年级第一学期第一次诊断考试试题英语第I卷第一部分听力（共两节，满分30分）第一节（共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从每题所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1.What do we know about the woman?A. She often plays chess.B. She is poor in playing chess.C. She hates playing chess.2.What does the man mean?A. The woman has got a lot of shoes.B. He will buy the woman a pair of shoes.C. The woman’s shoes match her new dress well.3.What can we learn from the conversation?A. The woman is a firefighter.B. The speakers had a barbecue.C. The man is too lazy to tidy up.4.What are the speakers mainly talking about?A. Where Tom’s family moved.B. What Tom’s new school is like.C. Why Tom went to a new school.5.What will the weather be like?A. Hot.B. Warm.C. Cool.第二节（共15小题；每小题1.5分，满分22.5分）请听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

淄博实验中学高三年级第一学期笫一次教学诊断考试2017.10生物本试处分为遶掙泾柯非遶强1!两邮分，共44小满分100分.考试.用时90分伸.注意事项：1.#卷前・考生务必将自己的姓名、考试号、班级、座号填涂柱答风卡上.2.作#选择题时，选出毎小题#案后，请用2B铅笔在答M卡上对应风目选项的答峯估農点涂黑，如需改动，用棣皮擦干净后，再选涂其他答案。

3.非选择忌必须用黑色字址的钢笔或签字笔作答，备案必须写在答題卡各题目指定区城内相应位置上；如果需要改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔或除改液. 不按以上要求作答无效。

4.考生必须保证答题卡的整洁。

考试结束后，请将答题卡交回。

一、选择題：每小题只有一个选项是符合题目要求的，共40小题，每小题1.5分，共60分.1.下列说法正确的是（）A.在孟德尔两对相对性状的杂交实验中，R的表现型与亲本中黄色圆粒作为母本还是父本无关B.性状分离是子代同时表现出显性性状和隐性性状的现象C.受精卵中的遗传物质一半来自父方，一半来自母方D.在豌豆杂交实验中，应在豌豆开花时进行去雄和授粉，实现亲本的杂.交2.孟德尔通过杂交实验发现了一些有规律的遗传现象，通过对这些现象的研兜提出了遗传的两大基本规律。

下列哪项不是这些有规律遗传现象所具有的因素（）A.R体细胞中各基因遗传信息表达的机会相等B.片自交后代各种基因型发育成活的机会相等C.各基因在F,体细胞中出现的机会相等D.每种类型雌配子与毎种类型雄配子相遇的机会相等3.假说一演绎法定现代科学研兜中常用的方法，包括“观察实验现線、提出问题、作出假设、演绎推理、验证假设、得出结论”并个廉本环节・利用该方法，孟德尔发现了遗传規t札下列关于孟徨尔研几过程的分析正确的肚（）A.为了验证做出的敷设丛否正确，孟黴设计并完成了正、尺交实验B.孟律尔所作他设的核心内容圧“生物体能产生数除相第的雌规配子”C.孟建尔发观的遗传规律町以生物所YiIIIX-性状的遗传现您D.提出何理肘沁在腕总纯介亲本杂交和叫1'1交血付实的的廉础上4.己知牛的有角与无角为1对相对性状・山用染色体匕的般ttMW A *j a控制・在自由放养多年的一牛群中，两墓因预率相审•毎头即牛一次只生产1头小牛・以下关于性状遗传的10. 下列涉及自由组合定徉理解的农述・IE 确的地（）A. AaBb 个体产生配子的过程一定遵術门山纽介皿EB. X 染色体上的展因与常染色体上的雄闪能『1山组合C. X*Y 个体产生两种配子的过榨体现了门由俎介定律D. 同源染色体上的非尊付星因能发生门由俎合11. 下图足某生物体细胞有丝分裂的不同分裂时期的图像，对图像的描述正确的是（ ） A. 该生物可能是低等植物B. 甲、乙、丙三细胞内染色体、染色单体与DNA 分子数比例都为1 ：2：2C. 甲细胞进行中心体复•制，发出星射线，形成了纺锤体D. 甲、乙、丙三细胞分别处于有丝分裂的前期、后期和中期12. 显微镜F 观察一个正在正常分裂的人类细胞，发现该细胞不均等缢裂，且染色体已经分 ）C.没有Y 染色体D.没有同源染色体 相关叙述不准确的是（） 则四分体Q J_QB. 若该图表示基因表达的过程，则d 主要发生在细胞质中C. 若该图表示酵母菌有氧呼吸的第一、二阶段，则e 过程发生在线粒体D. 若a 、b 、c 表示三种物质，d 、e 表示酶，则如果控制酶d 的基因不表达，控制酶e 的 基因仍可表达14. 人类男性经减数分裂产生的精子中，染色体数可表示为22+X 或22+Y,下列就这23条 染色体源自双亲的说法正确的是（）A. 常染色体来自母方，X 染色体来自父方B. 常染色体来自母方，Y 染色体来自父方C. 常染色体慶机来自母方或父方，X 染色体来自父方D. 常染色体随机来自母方或父方，Y 染色体来自父方15. 星因型为AaXF 的果现在产生轿子的过程中，某一初级精母细胞产生了一个基因型为Aaf 的轿子，則相关描述正确的足（）A. 该粉阳细胞产生的将子-半正常，一半异常B. 片与X*、Y 与Y 的分离发生在减数第一次分裂后期C. 该果規产生的星因型为AaX 、的榊子与卵细胞结合的概宰圧1/2D. —个精原细胞可能产生AX'、aXl AY 、且丫四种粕片成了两组.关2命&人：徐红杰.泮玉竹16. 下列关于生物体内華因、DNA 与染色体的说法■正确的雄（ ）A. 细胞桟圣因与染色体在械数分裂过P 』中的行为圧平行的B. 生物体内的基因都分布在细胞枝染色体的DNA 上C. 基因只有在染色体上才能指导蛋白质合成D. 人类基因组计划测定的是23条染色体上屣因的碱廉序列 17. 人的X 染色体和Y 染色体大小、形态不完全相同，但存在猶同源区（H ）和IE 同源区（I 、 01）,如图所示.下列有关叙述中错误的是（）A. 若某病是由位于非同源区段III 上的致病基因控制的，则患者均 为男性B. 若X 、Y 染色体上存在一对等位基因，则该对等位基因位于同源区（II ）上C. 若某病是由位于非同源区段I 上的显性基因控制的，则男性患者的儿子一定患病D. 若某病是由位于非同源区段I 上的隐性基因控制的，则息病女性的儿子一定是患者18. 牵牛花的颜色可随液泡中的酸碱度不同而发生变化，如液泡为碱性时显蓝色，中性时显 紫色，酸性时显红色，生理机制如下，则下列说法中不正确的是A. 图示相关物质中共有5种碱基，8种核昔酸B. 基因R 的化学本质是DNA 分子上有遗传效应的片段C. 图中a 、b 的过程是同时进行的，也能够发生在原核 细胞中D. 蛋白R 是一种载体蛋白19. 真核细胞内RNA 的酶促合成过程如图所示。

参考答案CACBB DABDB AD11.【解析】由题知有解，令，，故函数在递减，在递增，所以，解得. 12．【解析】()()()'23'2f x xf x f x x x ⎡⎤-=⎢⎥⎣⎦，时()()'220,f x f x x x ⎡⎤>∴⎢⎥⎣⎦在上递增，又是锐角， ,,sin sin ,0cos sin 222A B B A B A A B πππ⎛⎫∴+>>->-<< ⎪⎝⎭， ()()22cos sin cos sin f A f B A B ∴<， ()()22cos sin sin cos f A B f B A ∴<，故选D.13. 0，14． 15.1725016． 【解析】令，得，则()11e *1e e e x x x x f x ==++， ()()111e 1e e ex x x x f x f x ---=++=++=，即函数为偶函数，即（1）正确； ()21x xxxe f x e ee --=='-，当时，，当时，，即在处取得极小值3，即（2）正确；的单调增区间为，即（3）（4）错误；故填. 17．【答案】．解析：由已知得， {|1}B x m x m =-≤≤．∵是的必要不充分条件， ∴．则有．∴，故的取值范围为． 18．【答案】(1);(2).解析：（1）函数可化为()3,2,{21,21,3,1,x f x x x x -≤-=+-<<≥当时，，不合题意；当时， ()2110f x x x =+>⇒>，即；当时，，即.综上，不等式的解集为.（2）关于的不等式有解等价于()()max412f x m +≥-，由（1）可知，（也可由()()()21213f x x x x x =+--≤+--=，得），即，解得.19．【答案】(1)；（2）.解：(1) 222sin sin sin sin sin A C B A C +=-,,2221cos 222a cb ac B ac ac +-∴==-=-, , .(2) 在中,由正弦定理:,得1sin 1sin 4BD B BAD AD ∠===, 217cos cos212sin 12168BAC BAD BAD ∴∠=∠=-∠=-⋅=,sin BAC ∴∠===.20．[解] (1)因为3(a n ＋2＋a n )－10a n ＋1＝0，所以3(a n q 2＋a n )－10a n q ＝0，即3q 2－10q ＋3＝0. 因为公比q>1，所以q ＝3.又首项a 1＝3， 所以数列{a n }的通项公式为a n ＝3n .(2)因为⎩⎨⎧⎭⎬⎫b n ＋13a n 是首项为1，公差为2的等差数列，所以b n ＋13a n ＝1＋2(n －1)．即数列{b n }的通项公式为b n ＝2n －1－3n －1， 前n 项和S n ＝－(1＋3＋32＋…＋3n －1)＋[1＋3＋…＋(2n －1)]＝－12(3n －1)＋n 2.21．【答案】(1);(2).（1）由题意可得： ()()()πf x ωx φcos ωx φ2sin ωx φ6⎛⎫=+-+=+- ⎪⎝⎭， 因为相邻量对称轴间的距离为，所以，， 因为函数为奇函数，所以，，， 因为，所以，函数∵∴要使单调减，需满足， 所以函数的减区间为； （2）由题意可得：∵，∴∴π1sin 4x 3⎛⎫-≤-≤ ⎪⎝⎭，∴ 即函数的值域为. 22．【答案】（1）的单调递增区间为，递减区间为；（2）. 解析：（1）的定义域为，时， 令()001f x x >⇒<<'，∴在上单调递增； 令，∴在上单调递减综上，的单调递增区间为，递减区间为.（2）()()2ln 1ln 11x x a x x f x x x ---=++， 令()()()2ln 11g x x x a x x =--≥，，令()()ln 12h x g x x ax ==+-'，则（1）若，在上为增函数， ()()1120g x g a ≥=-'>' ∴在上为增函数，，即. 从而，不符合题意. （2）若，当时，，在上单调递增，()()1120g x g a >=-'>'，同Ⅰ），所以不符合题意 （3）当时，在上恒成立.∴在递减， ()()1120g x g a ≤=-'≤'. 从而在上递减，∴，即. 结上所述，的取值范围是.。

山东省实验中学2017-2018学年高三上学期第一次诊断测试文科数学试题一、选择题（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1、已知i 为虚数单位，若复数z 满足()20152016z i i ⋅-=+，则z 为（ ）A ．20152016i + B ．20152016i - C ．20162015i -+ D ．20162015i -- 2、已知全集{}U 1,2,3,4,5=，集合{}1,2,3A =，{}2,4B =，则()U A B ð为（ ） A ．{}1,2,4 B ．{}2,3,4 C ．{}2,4,5 D ．{}2,3,4,53、函数()f x =的定义域为（ ）A ．[)(]2,00,2-B ．()(]1,00,2-C ．[]2,2-D ．(]1,2- 4、在某次测量中得到的A 样本数据如下：582，584，584，586，586，586，588，588，588，588．若B 样本数据恰好是A 样本数据都加20后所得数据，则A ，B 两样本的下列数字特征对应相同的是（ ）A ．众数B ．平均数C ．中位数D ．标准差5、设:p 函数2sin 2y x π⎛⎫=+ ⎪⎝⎭是奇函数；:q 函数cos y x =的图象关于直线2x π=对称．则下列判断正确的是（ ）A ．p 为真B ．q ⌝为假C ．p q ∧为假D ．p q ∨为真6、若实数x ，y 满足1000x y x y x -+≥⎧⎪+≥⎨⎪≤⎩，则目标函数2z x y =+的取值范围是（ ）A ．[]0,2B ．[]0,1C ．[]1,2D ．[]2,1- 7、执行如图所示的程序框图，则输出的S 值为（ ） A ．4 B ．6 C ．8 D ．168、设函数()1ln 3f x x x =-（0x >），则函数()f x （）A ．在区间()0,1，()1,+∞内均有零点B ．在区间()0,1，()1,+∞内均有零点C ．在区间()0,1内有零点，在区间()1,+∞内无零点D ．在区间()0,1内无零点，在区间()1,+∞内有零点 9、函数cos 622x xxy -=-的图象大致为（ ）A ．B ．C ．D ．10、若()f x 是定义在R 上的函数，对任意的实数x ，都有()()44f x f x +≤+，且()()22f x f x +≥+，若()34f =，则()2015f 的值是（ ）A ．2014 B ．2015 C ．2016 D ．2017二、填空题（本大题共5小题，每小题5分，共25分．） 11、如图，正方体1111CD C D AB -A B 的棱长为1，E 为线段1C B 上的一点，则三棱锥1D D A -E 的体积为 ． 12、已知数列{}n a 的前n 项和21n S n n =++，则89101112a a a a a ++++= ．13、()()sin f x x ωϕ=A +（A ，ω，ϕ为常数，0A >，0ω>，0ϕπ<<）的图象如图所示，则3f π⎛⎫⎪⎝⎭的值为 ．14、已知m 、n 为正实数，向量(),1a m =，()1,1b n =-，若//a b ，则12m n+的最小值为 ．15、已知双曲线1C :22221x y a b-=（0a >，0b >）的离心率为2，若抛物线2C :22x py =（0p >）的焦点到双曲线1C 的渐近线的距离为2，则p = ． 三、解答题（本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．） 16、（本小题满分12分）在C ∆AB 中，a ，b ，c 分别是角A ，B ，C 的对边，且cosC cos 2cos b c a +B =B ．()I 求角B 的大小；()II 若函数()()()2sin 2sin 22cos 1f x x x x =+B +-B +-，R x ∈． ()1求函数()f x 的最小正周期； ()2求函数()f x 在区间,44ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值．17、（本小题满分12分）山东省济南市为了共享优质教育资源，实现名师交流，甲、乙两校各有3名教师报名交流，其中甲校2男1女，乙校1男2女．()I 若从甲校和乙校报名的教师中各任选1名，写出所有可能的结果，并求选出的2名教师性别相同的概率；()II 若从报名的6名教师中任选2名，写出所有可能的结果，并求选出的2名教师来自同一学校的概率．18、（本小题满分12分）如图，在四棱锥CD P -AB 中，D P ⊥平面CD AB ，D DC C 1P ==B =，2BA =，//DC AB ，CD 90∠B =，点E 、F 、G 分别是线段AB 、C P 、D E 的中点．()I 求证：FG//平面PAB ；()II 求证：DF ⊥平面C PB ．19、（本小题满分12分）已知n S 为等差数列{}n a 的前n 项和，2716a a +=，10100S =．()I 求数列{}n a 的通项公式； ()II 若数列{}n b 满足：122n a n n b a -=⋅，求数列{}n b 的前n 项和n T ．20、（本小题满分13分）如图，椭圆:M 22221x y a b+=（0a b >>）的离心率为12，直线x a =±和y b =±所围成的矩形CD AB 的面积为．()I 求椭圆M 的标准方程；()II 若P 为椭圆M 上任意一点，O 为坐标原点，Q 为线段OP的中点，求点Q 的轨迹方程；()III 已知()1,0N ，若过点N 的直线l 交点Q 的轨迹于E ，F两点，且1812F 75-≤NE⋅N ≤-，求直线l 的斜率的取值范围．21、（本小题满分14分）已知函数()21ln 22f x ax x =--，R a ∈． ()I 当1a =时，求曲线()y f x =在点()()1,1f 处的切线的斜率；()II 讨论函数()f x 的单调性；()III 若函数()f x 有两个零点，求实数a 的取值范围．山东省实验中学2016届高三上学期第一次诊断测试文科数学试题参考答案一、选择题：1-10 DCBDC ACDDC 二、填空题：11.1612.100 13.1 14． 3+ 15.8 三、解答题16.解：(Ⅰ) cos cos 2cos b C c B a B +=，由射影定理，得2cos a a B =1cos .23B B π∴=∴=……………4分或边化角,由cos cos 2cos b C c B a B +=,变为B A B C C B cos sin 2cos sin cos sin =+,即B A A cos sin 2sin = 1cos .23B B π∴=∴=(Ⅱ)由(Ⅰ)知3B π=，所以2()=sin (2+)+sin(2)+2cos 133f x x x x ππ--=sin 2cos cos 2sin sin 2cos cos 2sin cos 23333x x x x x ππππ++-+sin 2cos 2)4x x x π=+=+……………7分（1）()f x 的最小正周期22T ππ==.……………8分（2）3[,],2[,],2[,]4422444x x x πππππππ∈-∴∈-+∈-，sin(2)[42x π+∈-所以，())[4f x x π=+∈-……………10分故max min ()() 1.f x f x ==-……………12分17.(I) 从甲校和乙校报名的教师中各任选1名，所有可能的结果为(甲男1,乙男)、(甲男2, 乙男)、(甲男1, 乙女1)、(甲男1, 乙女2)、(甲男2, 乙女1)、(甲男2, 乙女2)、(甲女, 乙女1)、(甲女, 乙女2) 、(甲女, 乙男)，共9种；…………………4分选出的2名教师性别相同的结果有(甲男1,乙男)、(甲男2, 乙男)、(甲女1, 乙女1)、(甲女1, 乙女2)，共4种，所以选出的2名教师性别相同的概率为49. ……………………6分 （II ）从报名的6名教师中任选2名，所有可能的结果为(甲男1,乙男)、(甲男2, 乙男)、(甲男1, 乙女1)、(甲男1, 乙女2)、(甲男2, 乙女1)、(甲男2, 乙女2)、(甲女, 乙女1)、(甲女, 乙女2) 、(甲女, 乙男) 、(甲男1, 甲男2)、(甲男1, 甲女)、(甲男2, 甲女)、(乙男, 乙女1)、(乙男, 乙女2)、(乙女1, 乙女2)，共15种；………………………10分选出的2名教师来自同一学校的所有可能的结果为(甲男1, 甲男2)、(甲男1, 甲女)、(甲男2, 甲女)、(乙男, 乙女1)、(乙男, 乙女2)、(乙女1, 乙女2)，共6种，所以选出的2名教师来自同一学校的概率为62155=. ………………………12分 18.（I ）因为DC=1，BA=2，AB ∥DC ， E 是线段AB 的中点， 所以AE ∥DC ，且AE=DC ，所以四边形AECD 为平行四边形。

淄博实验中学高三年级第一学期第一次教学诊断考试 2017.10化学参考答案1.B2.A3.C4.B5.D6.A7.A8.B9.C 10.C 11.A 12.D 13.D 14.B 15.C 16.D 17. （共13分，除标注外其他每空均为2分）（1）+6 重结晶（1分）（2）MoO3、SO2 3.5N A（3）b（4）MoO3+Na2CO3=Na2MoO4+CO2↑（5）2Al + MoO3 Mo + Al2O318.（共16分，除标注外其他每空均为2分）I、（1）Fe3+(1分) 取少量X溶液放在试管中，加入几滴KSCN溶液，溶液不变红色说明无Fe3+（其它合理答案也可）。

(1分)（2）①3Fe2++4H++NO3-＝3Fe3++NO↑+2H2O ②AlO2－+CO2+2H2O＝Al(OH)3↓+HCO3－（3）Fe3+＞0．07mol （或Cl－＜0．07mol）II、(1) 生成的硫覆盖在Cu2S表面，阻碍浸取；Cu2S+2CuC12=4CuC1+S （2）CuSO4·H2O 19. （共13分，除标注外其他每空均为2分）（1）NaNO2+NH4Cl N2↑+NaCl+2H2O （2）A、D、C、E（3）F 排除装置中的空气，保证反应在无水无氧环境下进行（4）B装置可以吸收水，但不能阻止空气中的氧气，不能保证反应在无氧环境下进行（5）蒸馏（1 分）（6）取少量合金样品于试管中，滴加过量NaOH溶液，振荡，静置后取上层清液，再逐滴滴入稀盐酸至过量，若有沉淀产生且最终沉淀不完全溶解，则证明样品中Si（合理答案均可给分）20. （共10分,每空2分）（1）NH 4++OH﹣═NH3•H2O；空气可以将生成的氨气带走，使NH3•H2O NH3+ H2O化学平衡向正反应方向移动，利于除氨（2）3ClO﹣+2NH4+=N2↑+3Cl﹣+2H++3H2O （3）①1:2 ② 0.1 mol·Lˉ1。

山东省淄博市2018届高三数学上学期第一次教学诊断考试试题理（扫描版）理科参考答案一、DACCB ABCDB AD二 、13.214 14. 3π 15. 32- 16. 3 三、17.解：()I ()03:><<a a x a p ，41=a 时 ，4341:<<x p …（1分）121:<<x q …（2分）q p ∧ 为真 p ∴真且q 真 …（3分）⎪⎪⎩⎪⎪⎨⎧<<<<1214341x x ，得4321<<x ，即实数x 的取值范围为⎭⎬⎫⎩⎨⎧<<4321x x …（5分） ()II q 是p 的充分不必要条件，记⎭⎬⎫⎩⎨⎧<<=121x x A ，{}0,3><<=a a x a x B则A 是B 的真子集 …（7分）1231a a ⎧≤⎪⎨⎪>⎩或⎪⎩⎪⎨⎧≥<1321a a …（9分） 得2131≤≤a ，即a 的取值范围为1132⎡⎤⎢⎥⎣⎦，…（10分） 18.解：解：（1）∵△ABC 中，， ∴根据正弦定理，得，∵锐角△ABC 中，sinB ＞0， ∴等式两边约去sinB ，得sinA= ∵A 是锐角△ABC 的内角，∴A=；（2）∵a=4，A=，∴由余弦定理a 2=b 2+c 2﹣2bccosA ，得16=b 2+c 2﹣2bccos ，化简得b 2+c 2﹣bc=16，∵b+c=8，平方得b 2+c 2+2bc=64， ∴两式相减，得3bc=48，可得bc=16． 因此，△ABC 的面积S=bcsinA=×16×sin=4．19.解：()I ()12cos 2cos 2sin 32+-=x x x x f21cos 21sin 2312cos 1sin 23+-=++-=x x x x …（2分） 216sin +⎪⎭⎫ ⎝⎛-=πx …（3分） ⎥⎦⎤⎢⎣⎡∈ππ,2x πππ6563≤-≤∴x …（4分）ππ656=-∴x ，即π=x 时， ()1min =x f …（6分） ()II ()1011=x f ，即1011216sin =+⎪⎭⎫ ⎝⎛-πx ，得536sin =⎪⎭⎫ ⎝⎛-πx …（7分）20π≤≤x ， 366πππ≤-≤-∴x ，546cos =⎪⎭⎫⎝⎛-∴πx …（8分）1sin sin sin cos 66662x x x x ππππ⎛⎫⎛⎫⎛⎫=-+=-+-⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭…（10分）341552=+⨯= …（12分） 20.解：()I ∵22()()1x a f x x bx -=++是奇函数,∴()()0f x f x +-=恒成立…（1分） ()20a b x a ∴++=恒成立，0,0a b ∴== …（3分） 22()1xf x x ∴=+， 222(1)(1)'()(1)x x f x x -+=+ …（4分） 由'()0f x >,得-1＜x ＜1；由'()0f x <,得x ＞1或x ＜-1 …（5分） 故函数()f x 的增区间为()1,1-，()f x 的减区间为(,1)(1,)-∞-+∞和…（6分） ()II ∵2m —1＞()f x 有解，∴2m —1＞min ()f x 即可 …（7分） 当()()()0,0;0,00;00x f x x f x f x >>==<<时当时当时， …（8分） 由()I 知()f x 在(),1-∞-上为减函数，在()1,0-上为增函数()()min 11f x f ∴=-=- …（10分）∴2m —1＞1-，∴m ＞0 …（12分）21.解：()I 令()()1005=0313v t t t =-+，解得()45t t ==-秒或秒舍 …（2分）从发现前方事故到车辆完全停止行驶距离为ss =3120100.93600⨯⨯+()401005313t dt t ⎛⎫-⎪+⎝⎭⎰ …（4分） =30+()2401005ln 136t t ⎡⎤+-⎢⎥⎣⎦=30+1005ln 51636-⨯=70()米 …（6分） ()II 设高速上油费总额为y ，速度v 满足60120v ≤≤，则 …（7分）S y w v=⨯=40250v S v ⎛⎫+ ⎪⎝⎭≥=45S …（9分）当且仅当40250vv=，100v =时取等号 …（10分）由[]10060120v=∈，，即100/v km h =时，高速上油费最少 …（12分）22（12分）解：（Ⅰ）由，得切线的斜率(2)31,2,k f a a '==-=-∴=，故2()2ln 2f x x x x =-+，由()2f x x m ≥+得22ln m x x ≤-∵不等式()2f x x m ≥+在1[e]e,上有解，所以2max (2ln )m x x ≤-令2()2ln g x x x =-，故()0g x '=时，1x =．当()0g x '>；当1e x <<时，()0g x '<．故()g x 在1x =处取得最大值(1)1g =-， 所以1m ≤-（Ⅱ）因为()f x 的图象与x 轴交于两个不同的点()()12,0,,0A x B x 所以方程22ln 0x xax -+=的两个根为12,x x ，则211122222ln 02ln 0x x ax x x ax ⎧-+=⎪⎨-+=⎪⎩，两式相减得()()1212122ln ln x x a x x x x -=+--，又()()222ln ,2f x x x ax f x x a x'=-+=-+，则()()1212121212122ln ln 442x x x x f x x a x x x x x x -+⎛⎫'=-++=-⎪++-⎝⎭ 下证()1212122ln ln 40x x x x x x --<+-（*），即证明()211112222ln 0,x x x x t x x x x -+<=+ 120,01,x x t <<∴<<即证明()()21ln 01t u t t t -=+<+在01t <<上恒成立 因为()()()()222221211114(1)(1)(1)t t t u t t t t t t t -+---'=+=-=+++又01t <<，所以()0u t '> 所以，()u t 在()0,1上是增函数，则()()10u t u <=，从而知()2111222ln 0x x xx x x -+<+故()1212122ln ln 40x x x x x x --<+-，即1202x x f +⎛⎫'< ⎪⎝⎭成立。