光波导色散曲线
- 格式:docx
- 大小:137.14 KB
- 文档页数:3

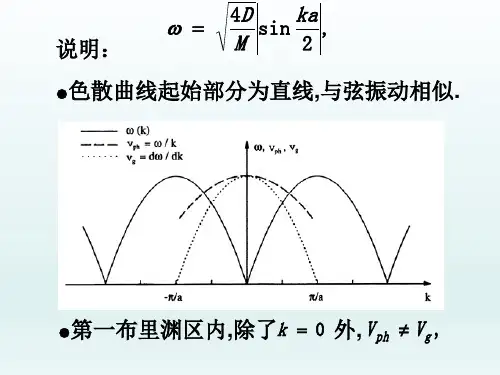


光纤典型衰耗曲线
光纤的衰耗曲线描述了光信号随着传输距离而减弱的过程。
一般而言,光纤的衰耗主要包括两个主要成分:色散(Dispersion)和损耗(Attenuation)。
色散:色散是由于不同波长的光在光纤中传播速度不同而引起的。
它导致信号的波形发生扭曲。
有两种主要的色散:色散分为色散对波长的依赖性,即色散对光波长的敏感程度。
典型的色散曲线包括色散的两个主要类型:色散曲线和零色散波长。
损耗:损耗是光信号逐渐减弱的过程。
它可以分为吸收损耗、散射损耗和弯曲损耗等。
通常,损耗与传输波长有关,不同波长的光在光纤中会有不同的衰减情况。
典型的光纤损耗曲线是一个呈指数下降的曲线,以dB/km为单位。
在通信光纤中,损耗通常在0.2 dB/km到0.5 dB/km的范围内。
不同类型的光纤(如单模光纤和多模光纤)以及不同的制造工艺都会导致略微不同的损耗曲线。
需要注意的是,具体的衰耗曲线还取决于光纤的波长、纤芯直径、材料质量等多个因素。
因此,具体的数据可能需要查阅相关厂商提供的光纤规格表或参考文献。
1。

光波导理论与技术第一次作业题目:非对称平板波导设计*名:**学号:************指导老师:***完成日期:2014 年03 月10 日一、题目根据以下的平板光波导折射率数据:(1)作出不同波导芯层厚度h (015h m μ<<)对应的TE 模式与TM 模式的色散图;(2)给出满足单模与双模传输的波导厚度范围; (3)确定包层所需的最小厚度a 与b 的值。
二、步骤依题意知,平板波导参数为:537.11=TE n ,510.12=TE n ,444.13=TE n ;530.11=TM n ,5095.12=TM n ,444.13=TM n 。
其中321n n n 、、分别代表芯心、上包层、下包层相对于nm 1550=λ光波的折射率。
在实际应用中,平板波导的有效折射率N 必须12n N n <<才能起到导光的作用。
经过推导,非对称平板波导的色散方程为:2212322212222210arctan arctan Nn n N N n n N m N n h k --+--+=-π (TE 模) 221232232122122222212210arctan arctan N n n N n n N n n N n n m N n h k --+--+=-π (TM 模)非对称平板波导光波模式截止时对应的芯层厚度为:(TE 模)22210222123222221arctan nn k n n n n n n m h c ---+=π2221022213222arctan nn k n n n n m h c ---+=π (TM 模)非对称平板波导上下包层的最小透射深度为:222101nn k a -=(上包层)232101nn k b -= (下包层)其中a 、b 取TE 、TM 中按上述公式计算出来的结果中的最大值。
由以上分析建立脚本m 文件PlanarWaveguide.m 与函数m 文件DispersionFun.m 及MinDepthFun.m 如下:PlanarWaveguide.m 脚本文件:close all ; clear all ; clc;NTE = linspace(1.510,1.537,1000); NTM = linspace(1.5095,1.530,1000); for m = 0:3[hTE,hTM] = DispersionFun(NTE,NTM,m); plot(hTE,NTE,'r',hTM,NTM,'b'); hold on ; end ;axis([0,15,1.5090,1.538]); xlabel('h/μm'); ylabel('N');title('非对称平板波导色散曲线'); legend('TE','TM',4); grid on;gtext('m=0');gtext('m=1');gtext('m=2');gtext('m=3'); zoom on ; clc;NTE = 1.510; NTM = 1.5095;[hTEc0,hTMc0] = DispersionFun(NTE,NTM,0) [hTEc1,hTMc1] = DispersionFun(NTE,NTM,1) [hTEc2,hTMc2] = DispersionFun(NTE,NTM,2)[aMin,bMin] = MinDepthFun()DispersionFun.m函数文件:function [hTE,hTM] = DispersionFun(NTE,NTM,m)lambda = 1.55e-6;k0 = 2*pi/lambda;n1TE = 1.537;n2TE = 1.510;n3TE = 1.444;n1TM = 1.530;n2TM = 1.5095;n3TM = 1.444;hTE = 1e6*((m*pi+atan(sqrt((NTE.^2-n2TE^2)./(n1TE^2-NTE.^2)))...+atan(sqrt((NTE.^2-n3TE^2)./(n1TE^2-NTE.^2))))./(k0*sqrt(n1TE^2-N TE.^2)));hTM = 1e6*((m*pi+atan(sqrt((n1TM^2*(NTM.^2-n2TM^2))./(n2TM^2*(n1TM^2-NT M.^2))))...+atan(sqrt((n1TM^2*(NTM.^2-n3TM^2))./(n3TM^2*(n1TM^2-NTM.^2))))). /(k0*sqrt(n1TM^2-NTM.^2)));MinDepthFun.m函数文件:function [aMin,bMin] = MinDepthFun()lambda = 1.55e-6;k0 = 2*pi/lambda;n1TE = 1.537;n2TE = 1.510;n3TE = 1.444;n1TM = 1.530;n2TM = 1.5095;n3TM = 1.444;aMinTE = 1e6/(k0*sqrt((n1TE^2-n2TE^2)));aMinTM = 1e6/(k0*sqrt((n1TM^2-n2TM^2)));if(aMinTE >= aMinTM)aMin = aMinTE;elseaMin = aMinTM;end;bMinTE = 1e6/(k0*sqrt((n1TE^2-n3TE^2)));bMinTM = 1e6/(k0*sqrt((n1TM^2-n3TM^2)));if(bMinTE >= bMinTM)bMin = bMinTE;elsebMin = bMinTM;end;三、运行结果及分析实验结果共画出0~3阶TE、TM模的非对称平板波导的色散曲线,如图1所示:510151.511.5151.521.5251.531.535h/μmN平板波导色散曲线图1 非对称平板波导色散曲线同时在命令窗口得到如下运行结果: hTEc0 = 0.8555 hTMc0 = 1.0664 hTEc1 = 3.5575 hTMc1 = 4.1711 hTEc2 = 6.2595 hTMc2 = 7.2758 aMin = 0.9883 bMin = 0.4878 运行结果表示:(1)0TE 的芯层厚度范围为: 3.55758555.0<<h m ;(2)0TM 的芯层厚度范围为: 4.17111.0664<<h m μ; (3)1TE 的芯层厚度范围为: 6.25955575.3<<h m μ; (4)1TM 的芯层厚度范围为:7.27581711.4<<h m μ; (5)上包层的最小厚度为0.9883m μ; (6)下包层的最小厚度为0.4878m μ。


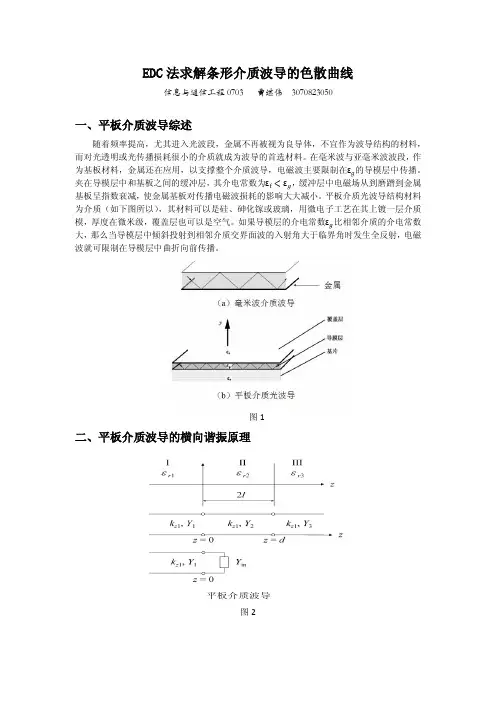


§2.2 介质光波导中的色散一、)(~λωβ或关系由特征方程可以看出,当给定波导参数和工作波长时,模阶数m 越大则θ1越小,因而传输常数β越小。
在所有导模中,最低阶模TE 0、TM 0的β值最大。
对于给定的模式,β值是随角频率ω(或工作波长λ)而变化的,即)(sin 01ωβθβm m m k n ==。
ω越小,k 0越小,θm 越小,因而β也越小。
所以,特征方程实际给出了β与ω(或λ)的关系,因此,称为色散方程。
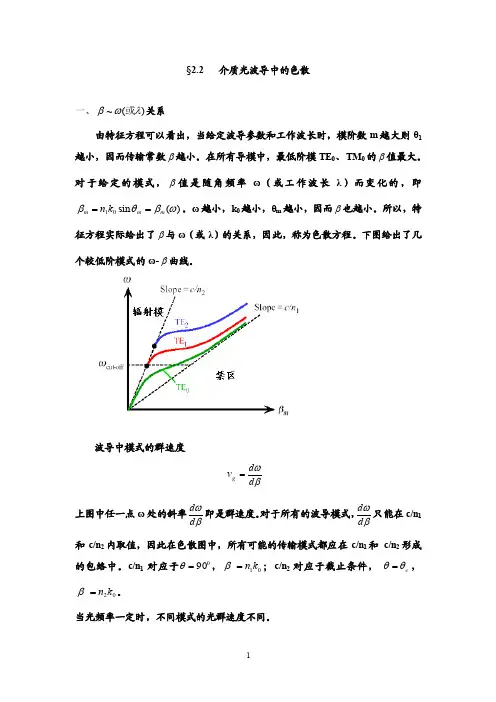
下图给出了几个较低阶模式的ω-β曲线。
波导中模式的群速度βωd d v g = 上图中任一点ω处的斜率βωd d 即是群速度。
对于所有的波导模式,βωd d 只能在c/n 1和c/n 2内取值,因此在色散图中,所有可能的传输模式都应在c/n 1和 c/n 2形成的包络中。
c/n 1对应于090=θ,01k n =β;c/n 2对应于截止条件, c θθ=,02k n =β。
当光频率一定时,不同模式的光群速度不同。
当模式一定时,不同光频率的光群速度不同。
二、模式色散(intermodal dispersion )当波导中能够传输多个模式时,低阶模与高阶模的群速度不同。
最低阶模的群速度最小,接近于c/n 1,最高阶模的群速度最大。
这是因为高阶模渗透到包层中的能量较多,而包层的折射率小,因此传输快。
此现象称为模式色散(或模间色散)。
长距离传输时,将导致输出端的信号脉冲展宽。
脉冲展宽的大小取决于各个模式在波导中传输的时间差τ∆。
设传输距离为L ,模式色散量定义为g m a n g v L v L-∆m i n =τv gmin 是最慢模式的群速度,v gman 是最快模式的群速度。
估算:由上图,v gmin ≈ c/n 1,v gmax 不超过c/n 2,近似得传输单位长度的色散量 cn n L 21-≈∆τ n 1= 1.48, n 2= 1.46,km ns m s L /67/107.611=⨯≈∆-τ。
有效折射率法求矩形波导色散曲线(附M a t l a b程序)光波导理论与技术第二次作业题目:条形波导设计*名:**学号: ************指导老师:***完成日期: 2014 年 03 月 19 日一、题目根据条形光波导折射率数据,条形波导结构如图1所示,分别针对宽高比d a :为1:1与1:2两种情形,设计:(1)满足单模与双模传输的波导尺寸范围;(需要给出色散曲线)(2)针对两种情况,选取你认为最佳的波导尺寸,计算对应的模折射率。
(计算时假设上、下包层均很厚)图1 条形波导横截面示意图二、步骤依题意知,条形波导参数为:5370.11=TE n ,5100.12=TE n ,444.13=TE n ;5360.11=TM n ,5095.12=TM n ,444.13=TM n 。
其中321n n n 、、分别代表芯心、上包层、下包层相对于nm 1550=λ光波的折射率。
本设计采用有效折射率法作条形波导的归一化色散曲线,条形波导的横截面区域分割情况如图2所示:图2 条形波导横截面分割图对于xmn E 模式,x E 满足如下波动方程:[]0),(22202222=-+∂∂+∂∂eff x x n y x n k yE x E 由于导波模式在x 与y 方向上是非相干的,采用分离变量法后再引入)(220x N k 得到如下两个独立的波动方程:0)()](),([)(222022=-+∂∂y Y x N y x n k yy Y 0)(])([)(222022=-+∂∂x X n x N k xx X eff 可以将条形波导等效成y 方向和x 方向受限的平板波导,先求y 方向受限平板波导的TE 模式,求得x N 后将其作为x 方向受限的平板波导的芯层折射率并求其TM 模式,得到的有效折射率eff n 就是整个条形波导的有效折射率。
y 方向受限平板波导的TE 模式的色散方程为:2212422212222210arctan arctan xx x x xN n n N N n n N n N n d k --+--+=-π (...2,1,0=n ) 其中1n 、2n 、4n 都是TE 模式的有效折射率从而x 方向受限平板波导的TM 模式的色散方程为:⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎭⎫ ⎝⎛--+=-2225225222232232220arctan arctan effx eff xeffx eff xeffx n N n n n N n N n n n N m n N a k π(...2,1,0=m )其中3n 、5n 都是TM 模式的有效折射率。
《光纤通信》大作业阶跃光纤模式色散曲线计算光纤材料色散计算光纤光栅特性分析指导老师:专业:姓名:学号:一、阶跃光纤模式色散曲线计算1.原理分析模式色散是指多模式传输时同一波长分量的各种传导模式的相位常数不同,群速度不同,引起到达终端的脉冲展宽的现象。
对光纤中光的传播理论的研究,可以有多种方法,比如射线法,标量近似分析法等,但为了更广泛地描述光纤波导中光的传播,更详细地研究光纤的传输特性,就必须运用波动光学理论对光纤进行分析。
要对光在光纤中的传播特性有详细的理解,必须依靠麦克斯韦方程,结合问题中的边界条件,求解电磁矢量场.求解的方法一般是:1、先求出亥姆霍兹方程组以及电磁场纵向分量Ez 和Hz 的具体形式。
2、2、把Ez 和Hz 有具体形式代入麦克斯韦方程以求取其他电磁场横向分量θE 、Er 、θH 、Hr 。
3、3、利用界面上电磁场θE 和θH 切向连续条件,求取模式本征方程。
对于时谐场光波,在均匀、无源介质中,同样满足矢量的亥姆霍兹方程(式1-1,1-2)022=+∇E k E (1-1)022=+∇H k H (1-2)对于在圆柱形光纤中传播的电磁波.电场和磁场具有如下形式的函数关系(式1-3,1-4):)(),(),(t z j e r E y x E ωβθ-= (1-3))(),(),(t z j e r H y x H ωβθ-=(1-4)代入,得到亥姆霍兹方程(式1-5,1-6)。
02202=+∇z z E n k E (1-5)02202=+∇z z H n k H (1-6) 经过推导,可以得到关于r 的贝塞尔方程或修正的贝塞尔方程(式1-7)。
(1-7) 最后可解得电场和磁场的纵向分量Ez 和Hz 。
⎪⎪⎩⎪⎪⎨⎧>≤=);()()();()()(a r e r a W K W K A a r e r a U J U J A E im m m im m m z θθ0)(])[()()(2222120222=--+∂∂+∂∂r R m r n k r r R r r r R r β光纤中传播模式及传输特性都是由它自身的本征方程确定的。
BPM波导matlab,⽤Matlab画平板波导⾊散图详解.doc根据以下的平板光波导在波长为1550 nm时的折射率数据,(1)作出不同波导芯厚度h(0(2)给出满⾜单模与双模传输的波导厚度范围;(3)确定包层所需的最⼩厚度a与b的值。
解答:(1)⾊散图如下:由图可得出该波导结构在1550nm波长处⼏点规律 :1、当波导芯厚度和模式相同时,TM模的等效折射率⼤于TE模的等效折射率;2、当波导芯厚度相同时,⾼阶模的等效折射率都⽐低阶的⼤很多;3、当模式⼀定时,TE模和TM模的等效折射率都随芯层厚度增⼤⽽增⼤,最后趋于稳定。
(2)某个模式(即导模)能在波导结构稳定传输,就意着它在芯层传输的 等效折射率⼤于周围介质层的折射率,否者不能在芯层稳定传输。
单模传输,那么只能允许基模传输,所以由⾊散图可知芯层厚度h应该⼤于1.0241μm,但由允许⼀阶模传输,那么芯层厚度h应该⼩于3.8554μm,所以该波导单模传输的芯层厚度范围为:1.0241μm < h < 3.8554μm。
同理可分析出双模传输的芯层厚度范围为:3.8554μm < h < 6.4458μm。
(3)由公式,,,可得, 。
单模传输时,N取临界最⼤值1.528。
则通过matlab计算可得a > 1 / p = 1.0853μm;b > 1 / q = 0.4949μm。
双模传输时,N取临界最⼤值1.5328。
则通过matlab计算可得a > 1 / p = 0.9577μm;b > 1 / q = 0.4809μm。
(4)波长放⼤⼗倍的分析由上图可知,忽略⾊散时,波长放⼤⼗倍后,为了是光波在波导中稳定传输,所需的最⼩芯层厚度变⼤了很多。
% clear all% clc;% % 画平板光波导波导层厚度h关于有效折射率N的⾊散图% syms y x% n3 = 1.4444;% lambda = 15.5;% k = 2 * pi / lambda;% figure;% for m = 0:3 %做0到3阶模的循环% %画TE模的⾊散图% n1 = 1.5350;% n2 = 1.5105;% h = ezplot(m*pi + atan(sqrt((y^2*k^2 - n2^2*k^2)/( n1^2*k^2 - y^2*k^2 ))) + atan(sqrt((y^2*k^2 - n3^2*k^2)/( n1^2*k^2 -y^2*k^2 ))) - sqrt(n1^2*k^2 - y^2*k^2 )*x,[0,45,1.44,1.54]);% set(h,'color','r','linewidth',1.2);% hold on;% %画TM模的⾊散图% n1 = 1.5365;% n2 = 1.5110;% h = ezplot(m*pi + atan((n1^2/n2^2)*sqrt((y^2*k^2 - n2^2*k^2)/( n1^2*k^2 - y^2*k^2 ))) +atan((n1^2/n3^2)*sqrt((y^2*k^2 - n3^2*k^2)/( n1^2*k^2 - y^2*k^2 ))) - sqrt(n1^2*k^2 - y^2*k^2 )*x,[0,45,1.44,1.54]);% set(h,'color','g','linewidth',1.2);% hold on;% end% %画N = 1.5105,以便判断TE模的最⼩波导厚度% y = 1.5105;% x = 0:0.1:45;% plot(x,y,'-');% hold off;%clear allclc;n3 = 1.4444;lambda = 1.55;k = 2 * pi / lambda;for m = 0:3n1 = 1.5350;n2 = 1.5105;N_TE = 1.5:0.0000001:1.5365;h_TE = (m*pi.*ones + atan(sqrt((N_TE.^2 - n2^2)./(n1^2 - N_TE.^2))) + atan(sqrt((N_TE.^2 - n3^2)./(n1^2 - N_TE.^2))))./...(sqrt(n1^2*k^2 - N_TE.^2*k^2) );n1 = 1.5365;n2 = 1.5110;N_TM = 1.5:0.0000001:1.5365;h_TM = (m*pi.*one。
什么是光的色散曲线?
当光通过透明介质时,它的速度会发生改变。
速度改变引起的相位差使得光波前面的部分先接触到新介质而弯曲,这个现象称为偏折(refraction)。
当光从空气等低折射率介质进入玻璃、水等高折射率介质时,其波长会缩短,频率不变。
这是因为介质折射率越大,传播速度就越慢,从而导致波长缩短。
色散曲线表示的是不同波长的光在物质中传播时,它们所对应的折射率的关系。
通常,以光的波长作为自变量,以相应的折射率作为因变量,在一张平面直角坐标系上画出曲线。
在空气中,由于折射率为1,所以色散曲线与波长轴重合。
而在其他介质中,色散曲线的形状与材料的性质有关。
例如,具有正常色散的材料,如玻璃、水等,其曲线呈现向上凸起的形状。
这是因为随着波长的增加,折射率也随之增加,但增加的速度逐渐减缓。
而具有反常色散的材料,则是相反的情况,其曲线呈现向下凸起的形状。
在这种材料中,随着波长的增加,折射率增加的速度会逐渐加快。
最著名的例子就是光在三棱镜中的折射。
当白光通过三棱镜时,由于不同颜色的光在玻璃中传播速度和折射率不同,所以它们在经过玻璃时被不同程度地弯曲,因此出现了七彩分光的现象。
总之,色散曲线是描述光在不同介质中传播时波长与折射率之间关系的一种图形。
每个介质都有自己的色散曲线,可以用来研究光的物理特性,例如光的色彩、它们如何被分离或合并等。
设计工作1
(1) T E 模式和TM 模式的色散方程用有效折射率分别表示为:
0k m π=++----------(TE )
0k m π=++-------(TM ) 我们取m=0,1,2,3分别求出有效折射率N 与波导芯厚度h 的关系。
用Matlab 实现,程序如下:
%不同波导芯厚度h 对应的TE 模式也TM 模式色散图程序 k0=2*pi/1.55;
for m=0:1:3
n1=1.537; %TE 模式下的折射率分布 n2=1.444;
n3=1.51;
N1=1.510:0.0001:1.537; %TE 模式下有效折射率的范围 %TE 模式下波导芯厚度
h_te=(m*pi.*ones()+atan(((N1.^2-n2.^2)./(n1.^2-N1.^2)).^0.5)+atan(((N
1.^2-n3.^2)./(n1.^2-N1.^2)).^0.5))./(k0.*(n1.^2-N1.^2).^0.5);
n1=1.530; %TM 模式下的折射率分布 n2=1.444;
n3=1.5095;
N2=1.5095:0.0001:1.530; %TM 模式下有效折射率的范围
%TM模式下波导芯厚度
h_tm=(m*pi.*ones()+atan((((N2.^2-n2.^2)./(n1.^2-N2.^2)).^0.5).*n1.^2. /n2.^2)+atan((((N2.^2-n3.^2)./(n1.^2-N2.^2)).^0.5).*n1.^2./n3.^2))./(k0. *(n1.^2-N2.^2).^0.5);
title('色散图')
plot(h_te,N1,'-b',h_tm,N2,'-r')
axis([0,15,1.509,1.537])
legend('TE','TM','Location','Northwest')
xlabel('h(um)','fontsize',10)
ylabel('N','fontsize',10)
hold on
grid on
grid minor
end
色散图为:
(2)当波导厚度薄到仅基模能传播的时候,该波导称为单模波导。
由图可知,在TE模式下,单模传输的厚度范围为1~3um。
满足双模传输的厚度范围为3~7um。
在TM模式下,满足单模传输的厚度范围为1~4um,满足双模传输的厚度范围为4~7.5um。
(3)不会做。