下载文档原格式
脉冲传递函数g(z)脉冲传递函数g(z)是一种常见的信号处理工具，它可以用于描述一种线性系统对输入脉冲信号的响应。
在工程研究中，脉冲传递函数g(z)在控制工程、通信系统、网络处理等领域中得到了广泛应用。
下面我们将从定义、性质、应用等方面来详述脉冲传递函数g(z)。
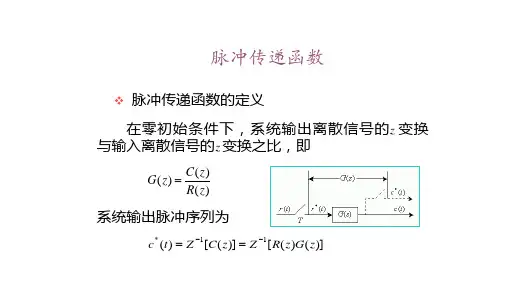
一、定义脉冲传递函数g(z)是指在离散时间下，单位脉冲信号经过线性系统后所得到的系统响应的比例函数。
数学上，脉冲传递函数可以表示为：g(z) = Y(z)/X(z)其中，Y(z)表示输出信号的Z变换，X(z)表示输入信号的Z变换。
二、性质1. 线性性：脉冲传递函数g(z)具有线性性质，即当输入信号是信号1、信号2的线性组合时，输出信号也是对应的线性组合。
2. 时不变性：当输入信号延迟m个时间单位时，输出信号也会延迟相同的m个时间单位。
3. 卷积性质：当有两个系统的脉冲传递函数分别为g1(z)和g2(z)时，它们的卷积g(z) = g1(z) g2(z)三、应用脉冲传递函数g(z)在工程实践中有很多应用，如下面几个方面：1. 控制工程：在控制系统设计中，脉冲传递函数g(z)用于描述控制器、传感器等系统的特性，以达到控制系统的设计目标。
2. 通信系统：在数字通信系统中，脉冲传递函数g(z)是一个能够描述信道传输特性的关键参数，可以用于设计调制解调器、信道均衡器等模拟信号处理器件。
3. 网络处理：在计算机网络处理中，脉冲传递函数g(z)可以描述网络传输的延迟、带宽等重要参数，以提高网络传输的可靠性和效率。
总之，脉冲传递函数g(z)是一种非常重要的信号处理工具，它在信号处理和系统控制领域中被广泛应用。
我们需要深入学习和掌握脉冲传递函数的特性和应用，以提高自己的技能和工程实践水平。
第八章 脉冲传递函数及性能分析分析线性定常线性离散系统时，脉冲传递函数也是一个很重要的概念，线性定常线性离散系统的动态特性可以由脉冲传递函数来描述。
通过脉冲传递函数，可以对线性定常线性离散系统的性能进行分析。
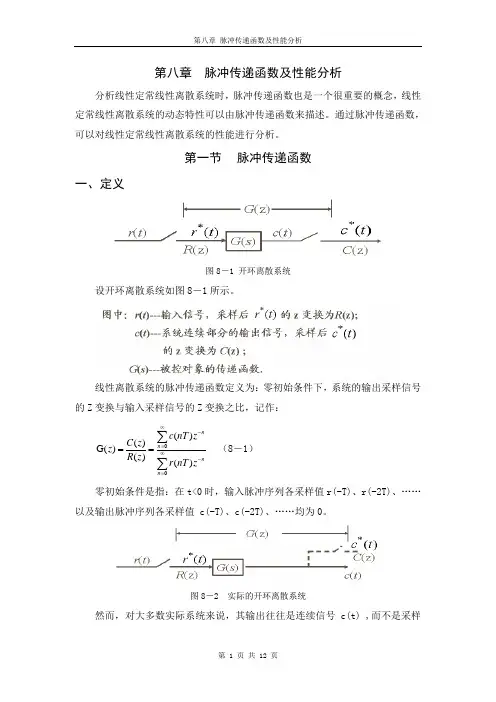
第一节 脉冲传递函数一、定义图8－1 开环离散系统设开环离散系统如图8－1所示。
线性离散系统的脉冲传递函数定义为：零初始条件下，系统的输出采样信号的Z 变换与输入采样信号的Z 变换之比，记作：()()G ()()()nn nn c nT zC z z R z r nT z∞-=∞-===∑∑ （8－1）零初始条件是指：在t<0时，输入脉冲序列各采样值r(-T)、r(-2T)、……以及输出脉冲序列各采样值 c(-T)、c(-2T)、……均为0。
图8－2 实际的开环离散系统然而，对大多数实际系统来说，其输出往往是连续信号 c(t) ,而不是采样信号*()c t，如图8－2所示。
此时，可以在系统输出端虚设一个理想采样开关，如图8－2中虚线所示。
它与输入采样开关同步工作，并具有相同的采样周期。
如果系统的实际输出c(t)比较平滑，且采样频率较高，则可由*()c t近似描述c(t)。
必须指出，虚设的采样开关是不存在的，它只是表明了脉冲传递函数所能描述的，只是输出连续函数在采样时刻上的离散值*()c t。
二、脉冲传递函数的求法1、由差分方程求（1）令初始条件为零，对差分方程两边作为z变换（查z变换表及用z变换定理）；（2）据脉冲传递函数的定义G(z)=C(z)／R(z)，求出脉冲传递函数G(z)。
2、由系统方块图求脉冲传递函数同样可以用方块图表示。
求取脉冲传递函数时，可以利用方块图变换来实现。
但是，在离散系统的方块图中，除了信号线、函数方块、引出点和比较点，还增加了采样开关。
连续系统的方块图分析法，不能照搬到离散系统。
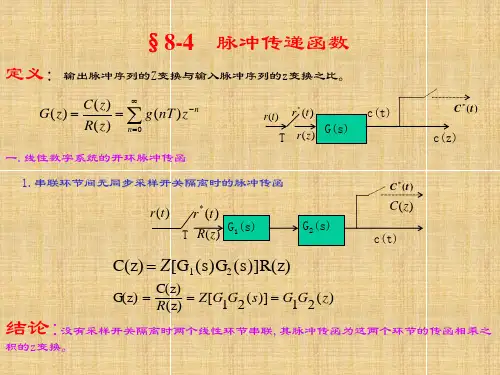
第二节开环系统脉冲传递函数一、串联环节1、离散环节串联——串联环节之间有采样开关等效的脉冲传递函数等于各环节脉冲传递函数之乘积，即G(z)=Z[G1(s)]*Z[G2(s)]=G1(z)G2(z) 图8－3 离散环节串联2、连续环节串联——串联环节之间无采样开关等效的脉冲传递函数等于各环节传递函数乘积之z变换，即G(z)=Z[G1(s)G2(s)]= G1G2(z)。
第八章 脉冲传递函数及性能分析分析线性定常线性离散系统时，脉冲传递函数也是一个很重要的概念，线性定常线性离散系统的动态特性可以由脉冲传递函数来描述。
通过脉冲传递函数，可以对线性定常线性离散系统的性能进行分析。
第一节 脉冲传递函数一、定义图8－1 开环离散系统设开环离散系统如图8－1所示。
线性离散系统的脉冲传递函数定义为：零初始条件下，系统的输出采样信号的Z 变换与输入采样信号的Z 变换之比，记作：()()G ()()()nn nn c nT zC z z R z r nT z∞-=∞-===∑∑ （8－1）零初始条件是指：在t<0时，输入脉冲序列各采样值r(-T)、r(-2T)、……以及输出脉冲序列各采样值 c(-T)、c(-2T)、……均为0。
图8－2 实际的开环离散系统然而，对大多数实际系统来说，其输出往往是连续信号 c(t) ,而不是采样信号*()c t，如图8－2所示。
此时，可以在系统输出端虚设一个理想采样开关，如图8－2中虚线所示。
它与输入采样开关同步工作，并具有相同的采样周期。
如果系统的实际输出c(t)比较平滑，且采样频率较高，则可由*()c t近似描述c(t)。
必须指出，虚设的采样开关是不存在的，它只是表明了脉冲传递函数所能描述的，只是输出连续函数在采样时刻上的离散值*()c t。
二、脉冲传递函数的求法1、由差分方程求（1）令初始条件为零，对差分方程两边作为z变换（查z变换表及用z变换定理）；（2）据脉冲传递函数的定义G(z)=C(z)／R(z)，求出脉冲传递函数G(z)。
2、由系统方块图求脉冲传递函数同样可以用方块图表示。
求取脉冲传递函数时，可以利用方块图变换来实现。
但是，在离散系统的方块图中，除了信号线、函数方块、引出点和比较点，还增加了采样开关。
连续系统的方块图分析法，不能照搬到离散系统。
第二节开环系统脉冲传递函数一、串联环节1、离散环节串联——串联环节之间有采样开关等效的脉冲传递函数等于各环节脉冲传递函数之乘积，即G(z)=Z[G1(s)]*Z[G2(s)]=G1(z)G2(z) 图8－3 离散环节串联2、连续环节串联——串联环节之间无采样开关等效的脉冲传递函数等于各环节传递函数乘积之z变换，即G(z)=Z[G1(s)G2(s)]= G1G2(z)。
图8－4 连续环节串联3、G 1(z)G 2(z)≠G 1G 2(z)图8－5 不同结构的环节串联示例在图8－5中，bs s G as s G +=+=1)(,1)(21。
（1）对于a 图来说, 其脉冲传递函数为))(()]([)]([0221bT aT bT aT e z ez zez z ez z s G Z s G Z ------=-⋅-=（2）对于b 图来说, 其脉冲传递函数为⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛+-+⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡++=b s a s a b Z b s a s Z s G s G Z 111))((1)]()([21))()(()(10bT aT bT aT bT aT e z ez a b eez e z z e z z a b ----------=⎪⎭⎫⎝⎛----=4、有零阶保持器时图8－6 有零阶保持器的串联环节1()()(1)()p G C z G z z Z R z s -⎡⎤==-⎢⎥⎣⎦——包含保持器的广义被控对象的脉冲传递函数5、开环助记法从输入信号开始，依次写出各传递函数相应的代号字母（不带s ），当遇到采样开关时，填上(z)。
二、并联环节图8－7 并联环节并联环节的脉冲传递函数，等于各环节脉冲传递函数之和，即G(z)=Z[G 1(s)]+Z[G 2(s)]=G 1(z)+G 2(z)第三节 闭环系统脉冲传递函数在离散系统中，由于采样开关所在位置的不同，可以有多种结构形式，求出的脉冲传递函数也多种多样。
一、反馈通道和前向通道间没有采样开关()()()1()G z R z C z GH z =+图8－8（a ） 闭环系统之一二、反馈通道和前向通道间有采样开关()()()1()()G z R z C z G z H z =+图8－8（b ） 闭环系统之二三、助记法,,(),,()()1,,,(),s z C z z =+前向通道上从输入信号开始依次写出各传递函数相应的代号字母不带当遇到采样开关时填上从离反馈点最近的采样开关之后依次将各传递函数相应的代号字母写出遇到采样开关时填上循环一周即可【例】图8－8（c ） 闭环系统之三1212()()()1()z G G C z R z H z G G =+式中 G 1G 2(z)=Z[G 1(s)G 2(s)]，G 1G 2H(z)=Z[G 1(s)G 2(s)H(s)]【例】图8－8（d ） 闭环系统之四12345345123412()()()()1()()()()RG G z G z G G z C z G z G G H z H H z H G G z =+注：式子中没有单独的R(z)时，得不出脉冲传递函数。
四、其它结构的方块图图8－9 系统方块图及其表达式第四节 线性定常离散系统稳定性判别一、 S 平面到Z 平面的映射图8－10 S 平面、Z 平面、W 平面映射关系图由z 变换的定义Tsz e=，s 域中的任意点s j σω=+，映射到 z 域则为()j TTj Tz eeeσωσω+== （8－2）于是s 域到z 域的基本映射关系为,Tz ez T σω=∠=。
（1） S 平面的虚轴映射在Z 平面上就是单位圆；（2） S 左半平面的点，0σ<，故||1z <，映射在Z 平面的单位圆内； （3） S 右半平面的点，0σ>，故||1z >，映射在Z 平面的单位圆外内；二、线性定常离散系统稳定充要条件因此，线性定常离散系统稳定的充要条件为：闭环脉冲传递函数的全部极点，应位于z 平面上以原点为圆心的单位圆内。
——全部极点的模小于1反之，若闭环脉冲传递函数有位于单位圆外的极点，则闭环系统不稳定。
若有位于单位圆上的极点，则系统处于临界稳定。
通过对闭环脉冲传递函数极点的分析，当然可以判定系统是否稳定。
但是，若系统阶次较高，求根就很困难。
可以借助劳斯判据，来判断线性定常离散系统的稳定性。
劳斯判据不需要求解特征方程，就可以判定全部特征根是否都位于复平面的左半平面。
三、W 变换为了使用劳斯判据，引入W 变换11,11w z z w w z ++==--或 （8－3）W 变换把Z 平面变换到W 平面。
W 平面和Z 平面又有什么关系呢？令222222()12(1)(1)z x jy x y y w jx yx y=++-=+-+-+所以，当222||1z x y =+>时，w 的实部为正，即（1） Z 平面上单位圆外的部分，映射到W 平面的右半平面； （2） Z 平面上单位圆内的部分，映射到W 平面的左半平面； （3） Z 平面上的单位圆，映射到W 平面的虚轴。
四、劳斯判据劳斯判据为表格形式，称为劳斯表。
如表8－1所示。
按照劳斯稳定判据，线性系统稳定的充要条件是：劳斯表中第一列各值严格为正。
如果劳斯表第一列中出现小于零的数值，系统就不稳定。
且第一列各系数符号的改变次数，代表特征根方程的正实部根的数目。
用劳斯判据判定系统稳定性的步骤：1、求出闭环系统的脉冲传递函数；2、写出特征根方程；3、根据式（8－3）作W 变换、化简成w 的表达式；4、列出劳斯表，求取各行系数；5、判断第一列是否都是正数。
第八章 脉冲传递函数及性能分析第 9 页 共 12 页表8－1 劳斯表nwn a2-n a 4-n a6-n a (1)n w-1n a -3-n a5n a -7-n a (2)n w-12311n n n n n a a a a b a -----=15412-----=n n n n n a a a a a b3b 4b……3n w-121311b b a a b c n n ---=151321n n c b a b b a ---=3c4c……wa说明：（1） 阶次从高到低排列，第一、二行的系数由特征方程得到，且两列间隔一阶次。
（2） 根据上面相邻两行的系数，计算下一行的系数； （3） 分母是相邻第二行的第一个系数；（4） 分子的第一项，是（相邻第二行的第一个系数）×（相邻下一列的、相邻第一行的系数）；注：从上到下（一、二） （5） 分子的第二项，是（相邻第一行的第一个系数）×（相邻下一列的、相邻第二行的系数）。
第八章 脉冲传递函数及性能分析【例】设离散系统的闭环特征方程为3245117119390z z z ---=，试判断此系统的稳定性。
解：首先进行11w z w +=-变换，得3211145()117()119()390111w w w w w w +++---=---经过化简得32402210w w w +++=列劳斯表如下3210402211801w w w w-由于第一列不全是正数，所以系统不稳定。
【例】设闭环离散系统如图8－11所示，其中采样周期T=0.1s 。
试求系统稳定时，K的取值范围。
图8－11 闭环离散系统解：先求出G(s)的z 变换20.632() 1.3680.368K z G z z z =-+因为该系统的闭环传递函数()()1()G z z G z Φ=+，故其特征方程21()(0.632 1.368)0.3680G z z K z +=+-+=令11w z w +=-得211()(0.632 1.368)()0.368011w w K w w +++-+=--经过化简得20.632 1.264(2.7360.632)0K w w K ++-=列出劳斯表200.632 2.7360.6321.26402.7360.632w KK w w K --系统稳定的充要条件，是劳斯表的第一列系数全为正，即0.63202.7360.6320K K >⎧⎨->⎩解得0 4.33K <<第五节 离散系统极点分布与动态响应的关系系统稳定是系统能够正常工作的前提。
但对于稳定的系统，还需要有较好的动态性能，一般要求系统跟踪输入变化的速度要快、跟踪精度要高。
闭环脉冲传递函数的极点在单位圆内的分布，对离散系统的动态性能具有重要的影响。
图8－12 Z 平面上极点分布与脉冲响应的关系图由图8－12可以看出，若极点位于单位圆外或单位圆上，输出序列是发散的或等幅的，系统不稳定。
极点位于单位圆内时，尽管系统是稳定的，但系统的动态性能并不一样：（1）当极点位于负实轴上时，虽然输出序列是收敛的，但它是正负交替的衰减振荡过程；——将导致机械系统强烈地振动（2）当极点是共轭复数极点时，输出是振荡衰减的；（3）极点在单位圆内的正实轴上时，这时系统的输出为指数衰减，且不出现振荡；而且极点越靠近原点，收敛越快。
