当前位置：文档之家 › MSA-GRR数据自动生成工具演示教学

MSA-GRR数据自动生成工具演示教学

  • 格式：xls
  • 大小：64.00 KB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

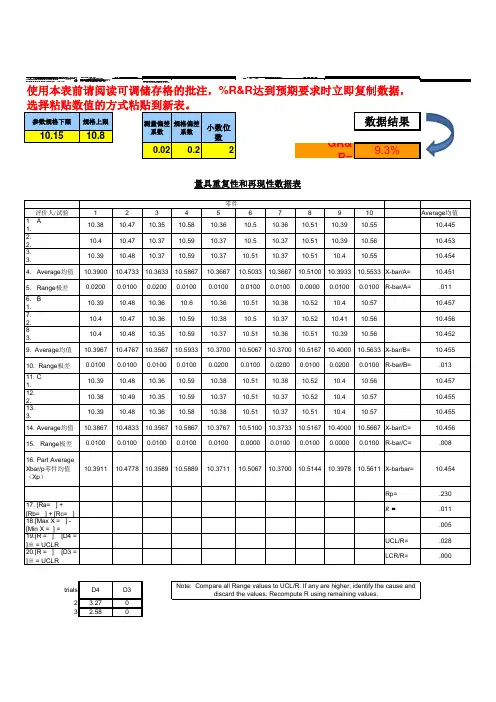
MSA-GRR数据自动生成工具(已经解密)

MSA-GRR数据自动生成工具(已经解密)


使用本表前请阅读可调储存格的批注，%R&R达到预期要求时立即复制数据， 选择粘贴数值的方式粘贴到新表。 参数规格下限 规格上限 数据结果 测量偏差 规格偏差 小数位
10.15 10.8
10.475 0.13 系数 系数
数
0.02
0.2
2
GR&R=
11.7%
量具重复性和再现性数据表
零件 评价人/试验 1 2. 3. 4. Average均值 5. Range极差 6. B 7. 8 9. Average均值 10. Range极差 11. C 12. 13. 14. Average均值 15. Range极差 16. Part Average Xbar/p零件均值 （Xp） A 1 1. 10.53 2. 10.53 3. 10.54 10.5333 0.0100 1. 10.53 2. 10.55 3. 10.55 10.5433 0.0200 1. 10.54 2. 10.55 3. 10.53 10.5400 0.0200 2 10.55 10.56 10.57 3 10.37 10.38 10.38 4 10.42 10.42 10.42 5 10.45 10.45 10.46 10.4533 0.0100 10.47 10.47 10.45 10.4633 0.0200 10.45 10.45 10.46 10.4533 0.0100 6 10.51 10.53 10.52 7 10.39 10.39 10.39 8 10.44 10.44 10.45 9 10.43 10.43 10.45 10 10.56 10.57 10.57 Average均值 10.465 10.470 10.475 10.470 .011 10.476 10.477 10.475 10.476 .012 10.474 10.476 10.473 10.474 .010
《GRR知识简介》PPT课件

《GRR知识简介》PPT课件


与其他质量管理工具的关系
03
GRR与SPC、FMEA等工具相互补充，共同构建完善的质量管理
体系。
如何将GRR融入质量管理体系
明确GRR应用范围和目的
根据产品特性和生产过程需求，确定GRR的 应用范围和目的。
实施GRR评估
按照计划进行GRR评估，记录评估结果并进 行分析。
制定GRR实施计划
包括测量设备选择、操作人员培训、测量程 序制定等。
GRR的应用范围和重要性。
通过案例分析和经验分享，提高 操作人员对GRR操作技巧和注意
事项的认识和掌握程度。
04
GRR在质量管理体系中的地位 和作用
质量管理体系简介及核心思想
质量管理体系定义
为实现质量管理目标而建立的组 织结构、职责、程序、过程和资
源。
核心思想
以客户为中心，全员参与，持续改 进，基于事实的决策方法。
机械制造
应用GRR分析工艺过程中 的变异来源，优化生产流 程，提高生产效率和产品 合格率。
服务业中GRR应用实例
金融务
运用GRR评估信用风险模 型的稳定性和预测能力， 提高风险管理的准确性和 效率。
物流服务
通过GRR分析运输过程中 的变异因素，优化配送路 线和计划，提高物流效率 和客户满意度。
教育培训
02
1. 选择合适的样本和测量人员 。
03
2. 进行多次重复测量，记录数 据。
04
3. 使用统计软件对数据进行处
理和分析。
05
4. 根据分析结果计算GRR值。
06
判定标准及意义
判定标准：通常将GRR值与公差范围进 行比较，判断测量系统是否可接受。
若GRR值大于公差范围的30%，则测量 系统不可接受，需重新设计或选择其他 测量方法。
MSA-GRR 全自动数据生成

MSA-GRR 全自动数据生成

MSA（MeasurementSystemAnalysis）使用数理统计和图表的方法对测量系统的分
R&R是指量具（gage）的重复性（Repeatability）和再现性（reproducibility)。

R&R数值 > 30% 表示该量具系统不能接受，须予以改进。

R&R=开根号(EV平方+ AV平方)
EV（Equipment Variation）是重复性－设备变差
AV（Appraiser Variation）是再现性－评价人变差
当R&R的值大于30%的时候，表面设备变差和评价人变差超过了标准允许的范围，量具的重复性
对测量系统的分辨率和误差进行分析，以评估测量系统的分辨率和误差对于被测量的参数来说是否合适，并确定测量roducibility)。

准允许的范围，量具的重复性和再现性结果不可接受，必须改进！
数来说是否合适，并确定测量系统误差的主要成分。

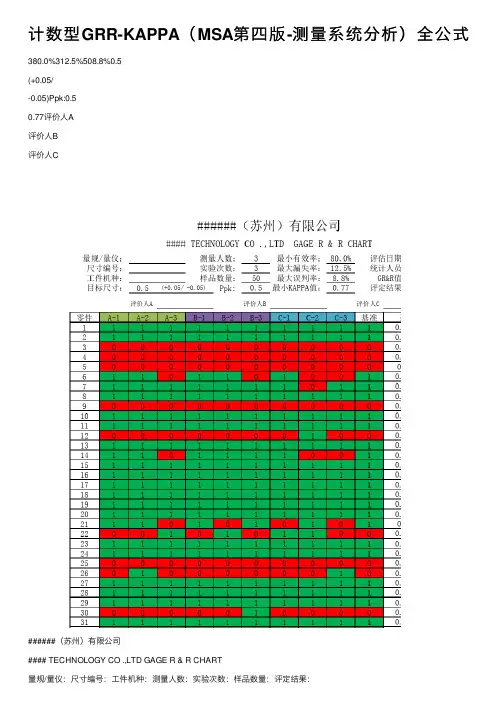
计数型GRR-KAPPA（MSA第四版-测量系统分析）全公式

计数型GRR-KAPPA（MSA第四版-测量系统分析）全公式

计数型GRR-KAPPA（MSA第四版-测量系统分析）全公式380.0%312.5%508.8%0.5
(+0.05/
-0.05)Ppk:0.5
0.77评价⼈A
评价⼈B
评价⼈C
######（苏州）有限公司
#### TECHNOLOGY CO .,LTD GAGE R & R CHART
量规/量仪：尺⼨编号：⼯件机种：测量⼈数：实验次数：样品数量：评定结果：
评估⽇期：统计⼈员：GR&R值：24%
最⼩有效率：最⼤漏失率：最⼤误判率：最⼩KAPPA值：⽬标尺⼨：
变差来源
总检查数
相配数
错误的拒收
错误的接受
不相配
95%UCI
计算所得结果
95%LCI
总检查数
⼀致的数量
95%UCI
计算所得结果
95%LCI
样本：
补充：
kappa⼤于0.75表⽰有很好的⼀致
对于产品控制的情况下，当测量结果与决定准则是确定“符合或不
符合某特性的规范”（如：100%检验或抽样），样品（或标准）必须被选择，但不需要包括整个过程范围。

测量系统的评估是以特性公差为基础（如对公差的%GRR）。

在过程研究情况下，当测量结果与决定准则是确定“过程稳定性、
⽅向以及是否符合⾃然的过程变差”（如：SPC、过程控制、能⼒及过程改进），在整个作业过程范围的样本可获得性变得⾮常重要。

当评估⼀测量系统对过程控制的适⽤性时（如对过程变差
的%GRR），推荐采⽤过程变差的独⽴估计法（过程能⼒研究）。

如果Ppk⼤于1，则将测量系统与过程进⾏⽐较
如果Ppk⼩于1，则将测量系统与公差进⾏⽐较。

MINITAB之GRR学习课件

MINITAB之GRR学习课件

9.79 100.00
Number of Distinct Categories = 0
Gage R&R for Vibrator Fre
Distinct Categories
根據AIAG的建議﹐當此數值小于2時﹐代表測 試系統無法控制制程品質﹔而當此數值為2 時﹐代表測試系統可以識別Low 和 high 兩種 狀態﹔當此數值為3時﹐代表測試系統可以識 別Low/Middle/high 三種狀態﹔當此數值為4 以上時﹐代表測試系統有足夠的能力控制制程 品質
190 180 170 160 150 140 130 120 110
Oper
Response By DUT
1
2
3
4
190 180 170 160 150 140 130 120 110
0
Xbar Chart by DUT
1
2
3
4
MULCCeLaL=n=1=1415640.8.71.4
Average
試工位(DUT)當作是一個操作員﹐本例中涉及4個DUT﹐即 DUT1﹐DUT2﹐DUT3﹐DUT4
MINITAB 應用實例 -GRR
2.3 用同樣的方法在Measurement data 中輸入Vibrator Frequency, 即分析的對象
* Measurement data 為測試結果
MINITAB 應用實例 -GRR
tolerance;Historical sigma等。詳細設定及其含義請參考Minitab 手冊或相關統計學知識﹐本例中使用其默認之參數設定。在Title一 欄中可以輸入一個名稱如“GRR of Vibrator Frequency”,此標題會 出現在GRR圖表中
msa grr标准

msa grr标准

msa grr标准MSA GRR标准是度量系统分析（MSA）的工具之一，用于评估测量系统的能力和稳定性。

此标准适用于逐次检测测量数据（例如，测量某物件的长度时，可以多次测量并记录结果）。

以下是针对MSA GRR标准的中文解释。

一、测量系统能力测量系统能力是指测量系统提供正确性和精确性的能力。

若测量系统的能力不足，则所获得的数据可能无法准确反映实际情况。

测量系统的能力评估可通过分析系统的偏倚、线性性和稳定性来完成。

1. 偏倚测量系统的偏倚是指系统得出的平均值与实际值偏离程度的大小。

在MSA GRR标准中，可以通过测量平均向和偏差（分析的是每个测量结果和整体平均值之间的偏离程度）来评估系统的偏倚。

2. 线性性测量系统的线性性是指系统在整个测量范围内是否能保持恒定的量程。

这可以通过分析线性回归来评估。

3. 稳定性测量系统的稳定性是指系统在同一时间内多次测量同一物件时，得出的结果的变化程度大小。

在MSA GRR标准中，稳定性评估可通过分析方差成分来完成。

二、GRR分析GRR（Gage Repeatability and Reproducibility）分析是MSA GRR标准中用于评估测量系统稳定性的一种方法。

GRR分析包括确定系统误差和操作员误差。

1. 系统误差系统误差指由于测量系统本身导致的误差。

在GRR分析中，可以通过测量重复度（重复检测同一物件，检测者亦相同），来评估系统误差。

2. 操作员误差三、数据分析在完成GRR分析后，需要对测量数据进行统计分析。

以下是MSA GRR标准中常用的数据分析方法：1. Cp和Cpk指标：可用于衡量测量系统的能力是否足够，以满足产品或过程的规格要求。

2. 误差图：可以帮助用户直观地评估测量系统的稳定性和误差。

3. 方差分析（ANOVA）：可用于确定系统误差和操作员误差及其交互作用的大小。

综上所述，MSA GRR标准是一种用于评估测量系统能力和稳定性的方法。

通过对系统偏差、线性性和稳定性进行评估，以及GRR分析和数据分析，可以获得全面的测量系统能力信息。

GRR(重复性和再现性)简单介绍

GRR(重复性和再现性)简单介绍

MSA中GRR（重复性和再现性）简单介绍在日常生产中，我们经常根据获得的过程加工部件的测量数据去分析过程的状态、过程的能力和监控过程的变化；那么，怎么确保分析的结果是正确的呢？我们必须从两方面来保证，一是确保测量数据的准确性/质量，使用测量系统分析（MSA）方法对获得测量数据的测量系统进行评估；二是确保使用了合适的数据分析方法，如使用SPC工具、试验设计、方差分析、回归分析等。

测量系统的误差由稳定条件下运行的测量系统多次测量数据的统计特性：偏倚和方差来表征。

偏倚指测量数据相对于标准值的位置，包括测量系统的偏倚（Bias）、线性（Linearity）和稳定性（Stability）；而方差指测量数据的分散程度，也称为测量系统的R&R，包括测量系统的重复性（Repeatability）和再现性（Reproducibility）。

01 引言一般来说，测量系统的分辨率应为获得测量参数的过程变差的十分之一。

测量系统的偏倚和线性由量具校准来确定。

测量系统的稳定性可由重复测量相同部件的同一质量特性的均值极差控制图来监控。

测量系统的重复性和再现性由Gage R&R研究来确定。

分析用的数据必须来自具有合适分辨率和测量系统误差的测量系统，否则，不管我们采用什么样的分析方法，最终都可能导致错误的分析结果。

在QS9000中，对测量系统的质量保证作出了相应的要求，要求企业有相关的程序来对测量系统的有效性进行验证。

02测量系统是用来对被测特性定量测量或定性评价的仪器或量具、标准、操作、方法、夹具、软件、人员、环境和假设的集合；用来获得测量结果的整个过程。

03表标准构成测量系统的主体元素之测量仪器必须经过校准至可追溯的标准国家标准←第一级标准(连接国家标准和私人公司、科研机构等)←第二级标准(从第一级标准传递到第二级标准)←工作标准(从第二级标准传递到工作标准)←量具04 术语4.1 分辨率：最小读数单位、测量分辨率、刻度限度或探测度。

MSA指标%P T与 %GRR知识梳理

MSA指标%P T与 %GRR知识梳理

MSA指标%P/T与%GRR知识梳理一．前言：任何一个制造系统皆处于随机波动过程中，透过量测所获得之数据，无形中隐含许多的变异，使得高质量产品的现代工业充满对量测数据产生质疑。

量测系统分析即是将量测资料或是一些衍生出的统计量与过程的管制界线进行分析比较，藉以评价整个量测系统过程是否可接受或应进行改善。

此篇主要以量测系统评价中之量测能力指标，以两种不同的表达方式进行探讨，因此对量测系统之变异并不个别予以研究(假设为已知)。

二．量测系统：探讨量测数据的质量，必须先对量测系统进行整体性了解：1．系统中有哪些过程？2．每一阶段过程应进行那些步骤？3．每一步骤是否有那些变异发生？4．最后对系统作出决定？三．量测数据的质量：量测数据的质量决定于稳定条件下进行操作的量测系统中所得的统计特性，一般量测所得资料皆为观测变异值，此值受到制造过程之变异及量测系统中变异所影响。

制造过程变异则分别受到零件变异、短期过程变异及长期过程变异所牵引，而量测变异亦同时由零件变异、量具产生之变异及评价者产生之变异所影响。

量测系统的变异而言，我们把焦点着重在由评价者产生之变异(Reproducibility)与量具本身之重复性(Repeatability)对整个量测变异贡献度之程度。

四．量测系统之统计特性：1.量测系统均须在统计管制下而其所产生之变异应根源于共同原因，而非特殊原因。

2.量测系统之变异须相对小于生产制程之变异。

3.量测系统之变异须相对小于规格界限。

4.量测系统之最小刻度须相对小于制程变异或规格界限之较小者。

五．量测系统的变异种类：1. 位置变异：◎准确度(Accuracy)◎偏倚(Bias)◎稳定性(Stability)◎线性(Linearity)2. 宽度变异：◎精密度(Precision)◎重复性(Repeatability)◎再现性(Reproducibility)◎GRR (Gage Repeatability & Reproducibility)3. 量测系统变异：◎量测系统能力(Capability)◎量测系统性能(Performance)六．量测系统评价：1. 量测能力指标%P/T精密度(Precision)对公差(Tolerance)之比例。

MSAGRR计算方法详细算法

MSAGRR计算方法详细算法

MSAGRR计算方法详细算法MSA（Measurement Systems Analysis）GR&R（Gauge Repeatability and Reproducibility）是一种衡量测量系统准确性和可再现性的方法。

它主要用于评估测试设备（例如测量工具，仪器等）和测试员之间的差异，以确定测量系统的可靠性和稳定性。

下面将详细介绍MSA GR&R的计算方法。

1. 推导总变异（Total Variation）：首先，收集所需测量数据。

这些数据通常由多名测试员对同一物品进行多次测量而得到。

然后计算每次测量结果的平均值，并计算所有平均值的总平均值。

然后计算每个测量结果与总平均值之间的差异，并将这些差异平方相加得到总变异。

2. 推导工件变异（Part Variation）：对测量数据中的每个测量值，计算其与其所属工件的平均值之间的差异，并将这些差异平方求和得到工件变异。

3. 推导重复性变异（Repeatability Variation）：对于每个测试员进行的多次测量，计算其测量结果与其自身平均值之间的差异，并将这些差异平方求和得到重复性变异。

4. 推导再现性变异（Reproducibility Variation）：对于每个工件，计算不同测试员进行的测量结果之间的差异，并将这些差异平方求和得到再现性变异。

5. 计算GR&R可靠性指标：首先计算测量系统误差的平均值，即重复性变异和再现性变异之和。

然后计算测量系统误差与总变异的比值，得到可再现性（Reproducibility）指标。

最后，计算测量系统误差与工件变异的比值，得到重复性（Repeatability）指标。

6.评估和改进：通过对可再现性和重复性指标的分析，评估测量系统的可靠性和稳定性。

如果得到较高的指标值，则说明测量系统的误差较小，系统较为可靠。

如果得到较低的指标值，则需要对测量系统进行改进或调整以提高其准确性和稳定性。

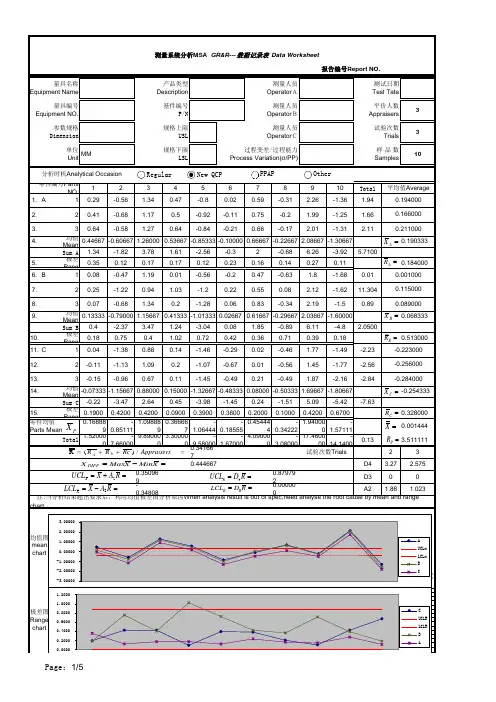
GR&R自动生成Excel表格(MSA第四版)

GR&R自动生成Excel表格(MSA第四版)


0.59 0.75 0.66
均值Mean 0.44667 -0.60667 1.26000 0.53667 -0.85333 -0.10000 0.66667 -0.22667 2.08667 -1.30667 Sum A 极差Range 1 2 3 1.34 0.35 0.08 0.25 0.07 -1.82 0.12 -0.47 -1.22 -0.68 3.78 0.17 1.19 0.94 1.34 1.61 0.17 0.01 1.03 0.2 -2.56 0.12 -0.56 -1.2 -1.28 -0.3 0.23 -0.2 0.22 0.06 2 0.16 0.47 0.55 0.83 -0.68 0.14 -0.63 0.08 -0.34 6.26 0.27 1.8 2.12 2.19 -3.92 0.11 -1.68 -1.62 -1.5 0.01 11.304 0.89 5.7100
X^2/nkr 0.0001878 SUMSQ(sum(men-part))/r
ndc
1.104596 1.146135 17.61% 20.04% 26.68% 96.38%
UCLx
基于公差base on parts spec
基于零件变差base on parts variation
基于过程变差base on process v ariation
X C = -0.254333
RC = 0.328000
零件均值 Parts Mean
XP
0.168889 -0.851111 1.098889 0.366667 -1.064444 -0.185556 0.454444 -0.342222 1.940000 -1.571111
-7.660000 9.890000
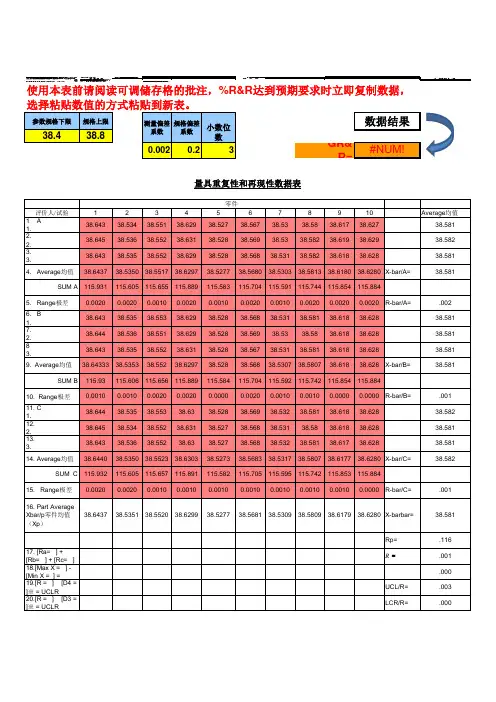
MSA-GRR数据自动生成工具

MSA-GRR数据自动生成工具


9
10
38.623 38.631
Average均值 38.607
2.
2. 38.64 38.617 38.566 38.603 38.582 38.535 38.658 38.622 38.625 38.632
38.608
3.
3. 38.64 38.616 38.568 38.601 38.581 38.536 38.657 38.621 38.623 38.632
38.608
7.
2.38.639 38.618 38.567 38.602 38.582 38.536 38.658 38.621 38.624 38.631
38.608
8
3. 38.64 38.618 38.567 38.602 38.581 38.535 38.656 38.622 38.623 38.631
9. Average均值 38.63967 38.6173 38.567 38.6017 38.58167 38.5353 38.657 38.6217 38.624 38.6317 X-bar/B=
使用本表前请阅读可调储存格的批注，%R&R达到预期要求时立即复制数据， 日完零测总DPCTR结S开GRGoeaih&ug期成件试偏果始rtsaaRianAeftdurgo人编特差总研接量li:Npalfleir证Ttincpom号性概究cs受具oater.实aeeoSlc和s前量&nerdvcu人irtf欲s名e，具NeomBftdpnarai获称ym必ctccmgB:et取eaMa须doye=12345678123rg:re:更y考sea:尽 零 使 确 测 相GWoPTpAaMRC>详stpr3ah虑aseo1aeo可 件 用 保 量 关h<uep0scran0>ga细cet1ru的r%ccsds->see能 必 的 测 应 的ain03rneou的iu>setid-mn重%0Rsiplnp从 须 仪 量 以 材rs>ntg:et%情tu&osr-ght要svarmuh工 被 器 适 说 随 料si.Rand况rmests因eatrc艺 确 必 当 明 机 上ehibiV在 RYNLbnetaM，erohe素oltae证ng&o流 认 须 的 书 顺 ，elusSeb>测if可nrstoeimRold>ieA实sds程 具 尺 可 序 应unp.ga量er/>查fahes.r(Ttobrn人o1(>%中 备 寸 用 进 该miae系oxertpus看difeo-plnf选 对 性 行 尽eulReBei统rdelmrseMrrsi7偏 √ 对 基 检&Mcpea2d取 工 和 量inetbdnt中6uornrapiS.RneamoAEpig.差 于 于 测sst， 艺 便 采cmraA5Rayco.b全att.emraiiV参sae-测 量 系nletrtho并 变 于 用bnet查satu部mn-.sneasfegm=Sl考量 具 统rt且 量 评 可sdgvr看earr的meaehissueeaomn手系 的 需tec要 审 获1potco如)neau变uidc/atuendM册a1统 应 要niate能 者 取idoiil下nshorssc量d0dlrpeynsctea用 改,mucf的代 阅 的tm可,可tsrobhsna可ehrinel8mreya、 进edb分ye表 读 最apo以接ets0vm参molarcistdeat花 。ne.e0辨该 接am.es接e5受20orea看.nbu-melat.0r费 尽en率t零 近h14受aecr输o3siv2Mocete%setran和 可%t件 的dnTms入eeSnceiegl.rydadc修 能uteA的 数itou数rsceabamd.u参fpoit理 的pllri整 据msdepel据sboer.t考reomaiem等 找r个aem的lnbradinc-手n因 到lpSts工taedi指hhemeruye.册oea素 问dus艺r导epvueAt.npobe的 题nc过MGd.1rrVGmeatoeti/a重 ，Sa量l程n.1caroe=g量nsAe0Dgn要 并bw部 具的eutcsoeteo具ref..sNf性 予oe门 名 类各pfitMNocoda号fyattebi考 以h.fo称 型特nDpaemb日rtead.kneaaey虑 纠:性epet:ie期tnrn:epepx， 正ce（al:apievdcc而 。re0每e.atehmc%srts选ty天ioeaaRen>>dnrn择P随ef&,>>tufcVo接>>ic机Raot=rso>>lst=受抽ltelteoon与取cftitdie否rg1JeeRda到W卡 计n&)g.t02e尺 量iRf2个y,1=302t零h0.1e.件0%%，直至0收.0集2%到足够的零件）CH检E查CK 选择粘贴数值的方式粘贴到新表。

MSA量测表GRR


B5 MSA的Q&A(Ⅰ)
Q1:MSA 已有軟件操作，而且運用的得心應手，我們為什麽還要去學習它的基本原理？ A1:我們並不贊成去學它的基本原理，因為那相當深奧而且費時極長，但是我們強調
必須建立正確的觀念，因為，許多熟悉軟件操作的品管人卻完全沒有正確的 MSA 觀念。 Q2:請問，哪些方面觀念不正確請舉出來，我也是其中一員，我覺得我觀念很清楚？ A2:例如，什麽是再生性什麽是再現性，都搞不清楚。 Q3:這有什麽不清楚，再現性 Repeatability，再生性是 Reproduce，這二個英文我 可以慢慢背出，沒什麽了不起？ A3:這不是背英文的問題，而是要知道再現性與再生性的意義何在，再現性是儀器造 成的誤差變異，再生性是人為造成的誤差變異，這二種變異的觀念必須清楚。 Q4:好，我承認觀念沒有很清楚，那知道了這二種變異性，我又有哪些觀念不清楚？ A4:因為你不知道二種變異造成的總變異是什麽，總變異包括人為誤差變異與儀器誤 差變異的結合變異（不能稱總和變異）。它是用勾股定律可簡易定義出來。
二、VGRR=VAV+VEV
1、% GRR=TV/(USL－LSL)×100%=？ 2、TV AV EV 3、USL－LSL=T=Tolerance=公差
A6 量測系統的判定
1、%GRR＜10%：可接受 2、10%＜%GRR＜30%：有條件接受，依其重要
性由工程部決定 3、%GRR＞30%：不可接受，必須修理、停用或
（ ）
2 1
2 2
12
意義六：計算出的 TV 總變異數的大小沒有任何絕對意義，它只
有一種相對意義存在，必須要和公差的大小來比較，所
謂公差即是「容忍度」（Tolerance）
意義七：當二者比較後，如果超過公差變異數的 10%，則這些數 據即不可使用不能接受（Un-Acceptance）

APQP PAP MSA测量系统分析自动表格 GRR 可编辑版本

372371.41012345678910Total 1.A 1#####################71.70371.682#####################71.70371.682717.00182.2#####################71.698971.6821#####################71.698971.6821716.9913.3#####################71.702971.6834#####################71.702971.6834716.99584.均值Mean 71.7240371.6859071.7040771.7016071.6825071.7240371.6859071.7040771.7016071.6825071.699620Sum A 215.1721215.0577215.1122215.1048215.0475215.1721215.0577215.1122215.1048215.04752150.98865. 极差Rang0.00170.00060.00290.00410.00140.00170.00060.00290.00410.00140.0021406.B 171.723371.689171.704671.703371.68371.723371.689171.704671.703371.683717.00667.271.725671.688571.704371.7034#######71.725671.688571.704371.7034#######11.3048.3#######71.691771.704671.703971.6829#######71.691771.704671.703971.6829717.01649.均值Mean 71.7246771.6897771.7045071.7035371.6834771.7246771.6897771.7045071.7035371.6834771.701187Sum B 215.174215.0693215.1135215.1106215.0504215.174215.0693215.1135215.1106215.05042151.035610. 极差Rang0.00320.00030.00060.00160.00230.00320.00030.00060.00160.00152211.C 1#######71.690171.701871.704471.6824#######71.690171.701871.704471.6824717.008812.2#######71.689671.701971.704571.6834#######71.689671.701971.704571.6834717.006213.371.724771.690471.702571.70471.684271.724771.690471.702571.70471.6842717.011614.均值Mean71.7247071.6900371.7020771.7043071.6833371.7247071.6900371.7020771.7043071.6833371.700887Sum C 215.1741215.0701215.1062215.1129215.05215.1741215.0701215.1062215.1129215.052151.026615. 极差Rang0.00200.00080.00070.00050.00180.00200.00080.00070.00050.00180.00116071.72446771.68856771.70354471.70314471.68310071.72446771.68856771.70354471.70314471.6831071.700564645.520200645.197100645.331900645.328300645.147900645.520200645.197100645.331900645.328300645.1479006453.05080.0413670.00160723D4 3.27 2.57571.7022090.004139D30071.698920.000000A2 1.88 1.02312345678910UCLx 71.702271.702271.702271.702271.702271.702271.702271.702271.702271.7022LCLx 71.698971.698971.698971.698971.698971.698971.698971.698971.698971.6989UCL R0.00410.00410.00410.00410.00410.00410.00410.00410.00410.0041LCLR0.00000.00000.00000.00000.00000.00000.00000.00000.00000.0000公差：6σpp变差PV PV 0.013014PV TVTV#DIV/0!TV基于公差base%#DIV/0!基于零件变差%#DIV/0!基于过程变差%#DIV/0!基于过程能力%#DIV/0!公式A Formula ndc 14.77027381公式B FormulaX^2/nkr 462687.3847462687.3847462687.403462687.4035462687.4035Source DF SS MS F P Source DF SS MS F P Parts 90.018640.00207524.016570.0000090.018640.002071166.10.0000020.000040.00002 5.247340.0160220.000040.0000211.6770.00003180.000070.00000 3.519300.00013600.000070.00000780.000140.00000Total 890.01882890.01882Source VarComp Stdev %Contributi %TV %Tolerance Source VarComp Stdev %Contribut %TV %Tolerance0.000000.00162 1.13%10.63% 1.62%0.000000.00155 1.04%10.18% 1.55%0.000000.001060.48% 6.95% 1.06%0.000000.001330.76%8.74% 1.33%0.000000.001230.65%8.04% 1.23%0.000000.000800.27% 5.22%0.80%0.000000.000750.24% 4.91%0.75%0.000000.000800.27% 5.22%0.80%0.000000.000970.41% 6.37%0.97%0.000230.0151698.87%99.43%15.16%0.000230.0151798.96%99.48%15.17%测试日期Test Tate 量具编号Equipment NO.基件编号P/N 测量人员Operator ＢB平价人数Appraisers 测量系统分析MSA GR&R---数据记录表 Data Worksheet报告编号Report NO.量具名称Equipment Name 产品类型Description 测量人员Operator ＡA试验次数Trials 单位UnitMM 规格下限LSL过程变差/过程能力Process Variation(σ/PP)样 品 数Samples参数规格Dimension规格上限USL 测量人员Operator ＣC71.69958071.70066071.70126071.70164071.70088071.700620分析时机Analytical Occasion零件编号PartsNO.平均值Average 71.70018071.699100sumSQ(sum(men))/nr SUMSQ(sum(1-10part))/kr 71.701160零件均值Parts Mean Total试验次数Trials 0.001567Part - To - Part Part - To - Part 注:当分析结果超出要求后，利用均值极差图分析原因When analysis result is out of spec,need analyse the root cause by mean and range chart 。

MSA GRR测量系统分析 核心讲解(迎11.11 前50名免费)

江西省南昌市2015-2016学年度第一学期期末试卷（江西师大附中使用）高三理科数学分析一、整体解读试卷紧扣教材和考试说明，从考生熟悉的基础知识入手，多角度、多层次地考查了学生的数学理性思维能力及对数学本质的理解能力，立足基础，先易后难，难易适中，强调应用，不偏不怪，达到了“考基础、考能力、考素质”的目标。

试卷所涉及的知识内容都在考试大纲的范围内，几乎覆盖了高中所学知识的全部重要内容，体现了“重点知识重点考查”的原则。

1．回归教材，注重基础试卷遵循了考查基础知识为主体的原则，尤其是考试说明中的大部分知识点均有涉及，其中应用题与抗战胜利70周年为背景，把爱国主义教育渗透到试题当中，使学生感受到了数学的育才价值，所有这些题目的设计都回归教材和中学教学实际，操作性强。

2．适当设置题目难度与区分度选择题第12题和填空题第16题以及解答题的第21题，都是综合性问题，难度较大，学生不仅要有较强的分析问题和解决问题的能力，以及扎实深厚的数学基本功，而且还要掌握必须的数学思想与方法，否则在有限的时间内，很难完成。

3．布局合理，考查全面，着重数学方法和数学思想的考察在选择题，填空题，解答题和三选一问题中，试卷均对高中数学中的重点内容进行了反复考查。

包括函数，三角函数，数列、立体几何、概率统计、解析几何、导数等几大版块问题。

这些问题都是以知识为载体，立意于能力，让数学思想方法和数学思维方式贯穿于整个试题的解答过程之中。

二、亮点试题分析1．【试卷原题】11.已知,,A B C 是单位圆上互不相同的三点，且满足AB AC →→=，则AB AC →→⋅的最小值为（ ）A ．14-B ．12-C ．34-D ．1-【考查方向】本题主要考查了平面向量的线性运算及向量的数量积等知识，是向量与三角的典型综合题。

解法较多，属于较难题，得分率较低。

【易错点】1．不能正确用OA ，OB ，OC 表示其它向量。

2．找不出OB 与OA 的夹角和OB 与OC 的夹角的倍数关系。

MSA计量型测量系统分析GRR表格(全公式自动生成未加密)

331012345678910Total 1.A 10.29-0.56 1.340.47-0.80.020.59-0.31 2.26-1.36 1.942.20.41-0.681.170.5-0.92-0.110.75-0.21.99-1.251.663.30.64-0.58 1.270.64-0.84-0.210.66-0.17 2.01-1.31 2.114.均值Mean0.44667-0.60667 1.260000.53667-0.85333-0.100000.66667-0.22667 2.08667-1.306670.190333Sum A 1.34-1.82 3.78 1.61-2.56-0.32-0.68 6.26-3.92 5.71005. 极差Rang0.350.120.170.170.120.230.160.140.270.110.1840006.B 10.08-0.47 1.190.01-0.56-0.20.47-0.63 1.8-1.680.017.20.25-1.220.941.03-1.20.220.550.082.12-1.6211.3048.30.07-0.68 1.340.2-1.280.060.83-0.34 2.19-1.50.899.均值Mean0.13333-0.79000 1.156670.41333-1.013330.026670.61667-0.29667 2.03667-1.600000.068333Sum B0.4-2.37 3.47 1.24-3.040.08 1.85-0.89 6.11-4.8 2.050010. 极差Rang0.180.750.4 1.020.720.420.360.710.390.180.51300011.C 10.04-1.380.880.14-1.46-0.290.02-0.46 1.77-1.49-2.2312.2-0.11-1.131.090.2-1.07-0.670.01-0.56 1.45-1.77-2.5613.3-0.15-0.960.670.11-1.45-0.490.21-0.491.87-2.16-2.8414.均值Mean-0.07333-1.156670.880000.15000-1.32667-0.483330.08000-0.50333 1.69667-1.80667-0.254333Sum C -0.22-3.47 2.640.45-3.98-1.450.24-1.515.09-5.42-7.6315. 极差Rang0.19000.42000.42000.09000.39000.38000.20000.10000.42000.67000.3280000.168889-0.851111.0988890.366667-1.06444-0.185550.454444-0.34222 1.940000-1.571110.0014441.520000-7.660009.890000 3.300000-9.58000-1.67000 4.090000-3.0800017.460000-14.14000.13 3.5111110.34166723D4 3.27 2.5750.3509690.879792D300-0.348080.00000A2 1.88 1.02312345678910UCLx0.35100.35100.35100.35100.35100.35100.35100.35100.35100.3510LCLx-0.3481-0.3481-0.3481-0.3481-0.3481-0.3481-0.3481-0.3481-0.3481-0.3481UCL R 0.87980.87980.87980.87980.87980.87980.87980.87980.87980.8798LCL R0.00000.00000.00000.00000.00000.00000.00000.00000.00000.0000公差：6σpp变差PV PV 1.104596PV TVTV#DIV/0!TV基于公差base%#DIV/0!基于零件变差%#DIV/0!基于过程变差%#DIV/0!基于过程能力%#DIV/0!公式A Formulandc 5.0936924公式B FormulaX^2/nkr 0.0001878 3.167450088.362122291.88836694.647300Source DF SS MS F P Source DF SS MS F PParts 988.361939.81799492.291420.00000988.361939.81799245.610.000002 3.16726 1.5836379.406050.000002 3.16726 1.5836339.6170.00000180.358980.019940.433720.9741160 2.758930.0459878 3.117920.03997Total 8994.647118994.64711Source VarComp Stdev %Contribu %TV %Toleranc Source VarComp Stdev %Contribut %TV%Tolerance 0.098110.313228.27%28.75%#DIV/0!0.091430.302377.76%27.86%#DIV/0!0.045980.21443 3.87%19.68%#DIV/0!0.039970.19993 3.39%18.42%#DIV/0!0.052120.22830 4.39%20.96%#DIV/0!0.051460.22684 4.37%20.90%#DIV/0!0.052120.22830 4.39%20.96%#DIV/0!0.051460.22684 4.37%20.90%#DIV/0!0.000000.000000.00%0.00%#DIV/0!1.08867 1.0433991.73%95.78%#DIV/0! 1.08645 1.0423392.24%96.04%#DIV/0!Reproducibility Reproducibility Operator Operator Operators*Part 极差图Range chartSUMSQ(sum(men-part))/r sumSQ(all)n=part k=men ANOVA Table With Operator*Part Interaction ANOVA Table Without Operator*Part InteractionParts Operators Gauge R&R With Operator*Part Interaction Gauge R&R Without Operator*Part InteractionTotal Gauge R&R Total Gauge R&R Repeatability Repeatability Operators Operators*Part Repeatability Repeatability Total Part - To - Part Part - To - Part 注:当分析结果超出要求后，利用均值极差图分析原因When analysis result is out of spec,need analyse the root cause by mean and range chart 。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

零特规NMRNdRPT=eoVaueoeeE件性范ftrmptp=aaanteeresu编：lV:tboAaauelVedtatt号raaruternhirbbcoamev和ieaiftgabllieito名ttaliiryynluoRnittaine称-&yvEAPlseRK-VV：===1 R确0R-.b0pa认00S3rx2.b03qQ4Ka：0RS3Rr37402qtRxT(84..3(=R(6E0R820tV0.&8.(^0.(58R52X0699)^-720b+48a+8(rAPDVV0I^F.^20F2)1)Ax2Xp6K-bp72ar)ar^bi2sa-eT(rrE=Krs23iaV2l^s2/(n量r1)30)具P)..857K1a名 号 类2345678938900r1t4607：s52816 计 x-0B0量.5743.aK432047531r30376431724596 T%o%Tl.nAor=E====tVVa%=l%=R=P&V04R.=0=制05 Num日 完be期 成r ： 人o(fRP9EA：2020pt&9Vr..Vai.418052Ra9r//6908tlTRN/7sT%%oV%/oV=opl.l=)of ((VTVTooaallrreeiiaarreettiioonnnncc1ee))03)) .1<<90<<6<<8<<
.012 13.835 13.836 13.834 13.835
15. Range极差 0.0100 0.0100 0.0100 0.0200 0.0200 0.0100 0.0200 0.0100 0.0100 0.0200 R-bar/C=
.014
16. Part Average Xbar/p零件均值 （Xp）
日完零测总DPCTR结S开GRGoeaih&ug期成件试偏果始rtsaaRianAeftdurgo人编特差总研接量l:iNalpfl证ierTtincpom号性概究受cs具oater实.aeeolc和s量前&nerdvc人irtfs名具e，oBtdpnri称y必ctcB:eedy=12345678123: 尽 零 使 确 测 相GWoPTpAaMRC>pr3has1eoaeo<可 件 用 保 量 关hep0sr0>angac1etur%-sds>ese能 必 的 测 应a0n3rui>useti-mn%0sil从 须 仪 量 以 材>srntg%eu-gsrms.t V在 RYN证ae&o>测rsR>i实a量>/Tt人>i系ol 7偏 √ 对 基 检Mcp6oreaAoE.差 于 测s-测 量 系lobe查u.fem=量 具 统res
9. Average均值
0.0100 0.0100 0.0100 0.0100 0.0200 0.0100 0.0200 0.0100 0.0100 0.0100 R-bar/A=
13.44 13.68 14.28 14.23 13.35 14.32 13.43 14.18 13.9 13.58
13.43
13.4267 13.6833 14.2633 14.2233 13.3500 14.3133 13.4300 14.1667 13.8933 13.5667 X-bar/A=
Average均值 13.826 13.835 13.834 13.832
5. Range极差
6. B 1. 7. 2. 8 3.
选择粘贴数值的方式粘贴到新表。
参数规格下限
12.32
规格上限
15.68
14
测量偏差 规格偏差 小数位
系数
系数
数
0.672 0.02 0.2
2
数据结果
GR& R=
2.6%
CH检E查CK
量具重复性和再现性数据表
评价人/试验 1A 1. 2. 2. 3. 3.
4. Average均值
1 13.42
2 13.68
800.205.1.589%%
AG.VGGa量.a=ga量Dgg部 具ee具eN门 名 类ptN号yat.称 型Dpmo日ea.e::期t:e: 0% R>>P&>>V>>R=>>= JR卡 计W&0尺 量R21=3020.6.0%% 0.20%
使用本表前请阅读可调储存格的批注，%R&R达到预期要求时立即复制数据，
.012 13.839 13.838 13.834 13.837
10. Range极差
11. C 1. 12. 2. 13. 3.
14. Average均值
0.0100 0.0200 0.0200 0.0100 0.0000 0.0100 0.0200 0.0100 0.0000 0.0200 R-bar/B= 13.43 13.68 14.27 14.22 13.34 14.33 13.44 14.18 13.89 13.57 13.43 13.69 14.26 14.24 13.36 14.32 13.43 14.17 13.9 13.56 13.42 13.69 14.27 14.22 13.35 14.32 13.42 14.17 13.9 13.58 13.4267 13.6867 14.2667 14.2267 13.3500 14.3233 13.4300 14.1733 13.8967 13.5700 X-bar/C=
13.4300 13.6867 14.2678 14.2256
13.3500
14.3178 13.4300 14.1722 13.8967 13.5689 X-barbar=
13.835
17. [Ra= ] +
[Rb= ] + [Rc= ] 18.[Max X = ] -
[Min X = ] = 19.[R = ] × [D4 = ]※ = UCLR 20.[R = ] × [D3 = ]※ = UCLR
RБайду номын сангаас=
.968
R=
.013
.005
UCL/R=
.033
LCR/R=
.000
trials D4
D3
2 3.27
0
3 2.58
0
Note: Compare all Range values to UCL/R. If any are higher, identify the cause and discard the values. Recompute R using remaining values.
3 14.26
4 14.22
零件
5
6
13.34 14.31
7 13.42
8 14.16
9 13.89
10 13.56
13.43 13.69 14.27 14.22 13.36 14.31 13.44 14.17 13.89 13.57
13.43 13.68 14.26 14.23 13.35 14.32 13.43 14.17 13.9 13.57
13.7 14.28 14.23
13.35
14.32 13.44 14.17 13.9 13.56
13.44 13.69 14.26 14.22 13.35 14.31 13.42 14.18 13.9 13.57
13.4367 13.6900 14.2733 14.2267 13.3500 14.3167 13.4300 14.1767 13.9000 13.5700 X-bar/B=