结构构件上的荷载及支座反力计算

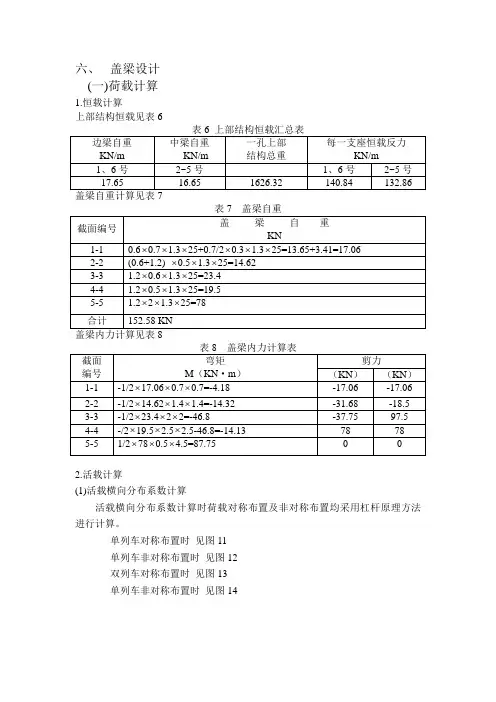
六、盖梁设计(一)荷载计算1.恒载计算上部结构恒载见表62.活载计算(1)活载横向分布系数计算活载横向分布系数计算时荷载对称布置及非对称布置均采用杠杆原理方法进行计算。

单列车对称布置时见图11单列车非对称布置时见图12双列车对称布置时见图13单列车非对称布置时见图141 2 300.12210.8750.437 2ηηη===⨯=1 2 310.560.27821(0.4340.315)0.375 210.6480.3242ηηη=⨯==⨯+==⨯=图110.8750.8750.566图120.6840.434 0.31512310.2860.143210.7010.350210.950.4752ηηη=⨯==⨯==⨯=12310.5560.27821(0.4340.315)0.37521(0.6480.355)0.5022ηηη=⨯==⨯+==⨯+=(2)按顺桥向活载移动情况，求支座活荷载反力的最大值 布载长度L 取15.96m a. 单孔荷载（见图15）0.556 0.7011 0.951 0.4340.3150.648 0.355图14 图130.286b.单列车时支座反力R 2=140×(1+0.913)+120×(0.474+0.386)×30×0.199=236.99KN 两列车时支座反力2×R 2=2×236.99=473.96 KN b.双孔荷载（见图16）单列车时支座反力R 1=140×(0.562+0.65)=169.68 KN R 2=120×(1+0.913)+30×0.725=251.31KN R=R 1 +R 2=169.68+251.31=420.99KN 双列车时支座反力2×（R 1 + R 2）=2×420.99=841.98KN (3)载横向分布后各梁支点反力计算见表9表9 主梁支点反力计算120 140 30140 120 图150.913 0.474 0.3860.199120 140 30140120 0.650.913 1.00 0.7250.562R 2图16(4)各梁恒载、活载反力组合各梁恒载、活载反力组合计算见表10，表中均取主梁最大值。

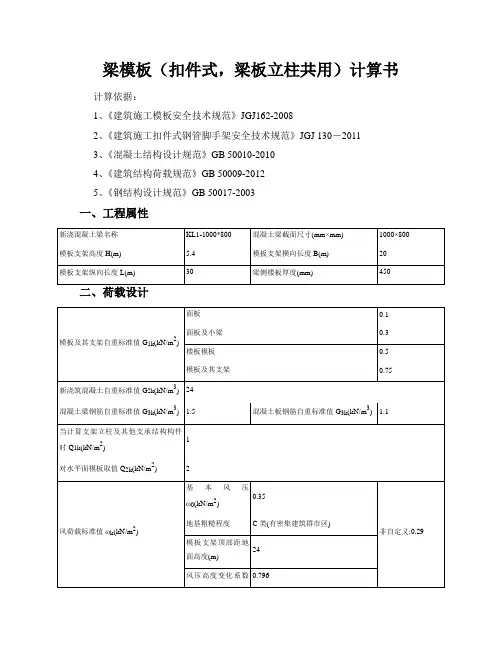
梁模板（扣件式，梁板立柱共用）计算书计算依据：1、《建筑施工模板安全技术规范》JGJ162-20082、《建筑施工扣件式钢管脚手架安全技术规范》JGJ 130－20113、《混凝土结构设计规范》GB 50010-20104、《建筑结构荷载规范》GB 50009-20125、《钢结构设计规范》GB 50017-2003一、工程属性二、荷载设计平面图立面图四、面板验算面板类型覆面木胶合板面板厚度t(mm) 15面板抗弯强度设计值[f](N/mm2) 15 面板抗剪强度设计值[τ](N/mm2) 1.5面板弹性模量E(N/mm2) 5400W＝bh2/6=1000×15×15/6＝37500mm3，I＝bh3/12=1000×15×15×15/12＝281250mm4q1＝0.9×max[1.2(G1k+(G2k+G3k)×h)+1.4Q2k，1.35(G1k+(G2k+G3k)×h)+1.4ψc Q2k]×b=0.9×max[1.2×(0.1+(24+1.5)×0.8)+1.4×2，1.35×(0.1+(24+1.5)×0.8)+1.4×0.7×2]×1＝26.671kN/mq1静＝0.9×1.35×[G1k+(G2k+G3k)×h]×b＝0.9×1.35×[0.1+(24+1.5)×0.8]×1＝24.908kN/mq1活＝0.9×1.4×0.7×Q2k×b＝0.9×1.4×0.7×2×1＝1.764kN/mq2＝[1×(G1k+(G2k+G3k)×h)]×b＝[1×(0.1+(24+1.5)×0.8)]×1＝20.5kN/m计算简图如下：1、强度验算M max＝0.107q1静L2+0.121q1活L2＝0.107×24.908×0.1432+0.121×1.764×0.1432＝0.059kN·mσ＝M max/W＝0.059×106/37500＝1.567N/mm2≤[f]＝15N/mm2满足要求！2、挠度验算νmax＝0.632q2L4/(100EI)=0.632×20.5×142.8574/(100×5400×281250)＝0.036mm≤[ν]＝L/250＝142.857/250＝0.571mm满足要求！3、支座反力计算设计值(承载能力极限状态)R1=R5=0.393q1静L+0.446q1活L=0.393×24.908×0.143+0.446×1.764×0.143＝1.511kNR2=R4=1.143q1静L+1.223q1活L=1.143×24.908×0.143+1.223×1.764×0.143＝4.375kNR3=0.928q1静L+1.142q1活L=0.928×24.908×0.143+1.142×1.764×0.143＝3.59kN 标准值(正常使用极限状态)R1'=R5'=0.393q2L=0.393×20.5×0.143＝1.151kNR2'=R4'=1.143q2L=1.143×20.5×0.143＝3.347kNR3'=0.928q2L=0.928×20.5×0.143＝2.718kN五、小梁验算梁底面板传递给左边小梁线荷载：q1左＝R1/b=1.511/1＝1.511kN/m梁底面板传递给中间小梁最大线荷载：q1中＝Max[R2,R3,R4]/b=Max[4.375,3.59,4.375]/1=4.375kN/m梁底面板传递给右边小梁线荷载：q1右＝R5/b=1.511/1＝1.511kN/m小梁自重：q2＝0.9×1.35×(0.3-0.1)×1/7 =0.035kN/m梁左侧模板传递给左边小梁荷载q3左＝0.9×1.35×0.5×(0.8-0.45)=0.213kN/m梁右侧模板传递给右边小梁荷载q3右＝0.9×1.35×0.5×(0.8-0.45)=0.213kN/m梁左侧楼板传递给左边小梁荷载q4左＝0.9×Max[1.2×(0.5+(24+1.1)×0.45)+1.4×2，1.35×(0.5+(24+1.1)×0.45)+1.4×0.7×2]×(0.8-1/2)/2×1=2.414kN/m梁右侧楼板传递给右边小梁荷载q4右＝0.9×Max[1.2×(0.5+(24+1.1)×0.45)+1.4×2，1.35×(0.5+(24+1.1)×0.45)+1.4×0.7×2]×((1.6-0.8)-1/2)/2×1=2.414kN/m左侧小梁荷载q左＝q1左+q2+q3左+q4左=1.511+0.035+0.213+2.414=4.172kN/m中间小梁荷载q中= q1中+ q2=4.375+0.035=4.41kN/m右侧小梁荷载q右＝q1右+q2+q3右+q4右=1.511+0.035+0.213+2.414=4.172kN/m小梁最大荷载q=Max[q左,q中,q右]=Max[4.172,4.41,4.172]=4.41kN/m正常使用极限状态：梁底面板传递给左边小梁线荷载：q1左'＝R1'/b=1.151/1＝1.151kN/m梁底面板传递给中间小梁最大线荷载：q1中'＝Max[R2',R3',R4']/b=Max[3.347,2.718,3.347]/1=3.347kN/m梁底面板传递给右边小梁线荷载：q1右'＝R5'/b=1.151/1＝1.151kN/m小梁自重：q2'＝1×(0.3-0.1)×1/7 =0.029kN/m梁左侧模板传递给左边小梁荷载q3左'＝1×0.5×(0.8-0.45)=0.175kN/m梁右侧模板传递给右边小梁荷载q3右'＝1×0.5×(0.8-0.45)=0.175kN/m梁左侧楼板传递给左边小梁荷载q4左'＝[1×(0.5+(24+1.1)×0.45)]×(0.8-1/2)/2×1=1.769kN/m梁右侧楼板传递给右边小梁荷载q4右'＝[1×(0.5+(24+1.1)×0.45)]×((1.6-0.8)-1/2)/2×1=1.769kN/m左侧小梁荷载q左'＝q1左'+q2'+q3左'+q4左'=1.151+0.029+0.175+1.769=3.124kN/m 中间小梁荷载q中'= q1中'+ q2'=3.347+0.029=3.376kN/m右侧小梁荷载q右'＝q1右'+q2'+q3右'+q4右' =1.151+0.029+0.175+1.769=3.124kN/m 小梁最大荷载q'=Max[q左',q中',q右']=Max[3.124,3.376,3.124]=3.376kN/m为简化计算，按三等跨连续梁和悬臂梁分别计算，如下图：1、抗弯验算M max＝max[0.1ql12，0.5ql22]＝max[0.1×4.41×0.3782，0.5×4.41×0.32]＝0.198kN·m σ=M max/W=0.198×106/23625=8.4N/mm2≤[f]=11.44N/mm2满足要求！2、抗剪验算V max＝max[0.6ql1，ql2]＝max[0.6×4.41×0.378，4.41×0.3]＝1.323kNτmax=3V max/(2bh0)=3×1.323×1000/(2×70×45)＝0.63N/mm2≤[τ]=1.232N/mm2满足要求！3、挠度验算ν1＝0.677q'l14/(100EI)＝0.677×3.376×3784/(100×7040×53.156×104)＝0.125mm≤[ν]＝l1/250＝378/250＝1.512mmν2＝q'l24/(8EI)＝3.376×3004/(8×7040×53.156×104)＝0.913mm≤[ν]＝2l2/250＝2×300/250＝2.4mm满足要求！4、支座反力计算承载能力极限状态R max=[1.1qL1,0.4qL1+qL2]=max[1.1×4.41×0.378,0.4×4.41×0.378+4.41×0.3]=1.99kN 同理可得：梁底支撑小梁所受最大支座反力依次为R1=1.882kN,R2=1.99kN,R3=1.636kN,R4=1.636kN,R5=1.636kN,R6=1.636kN,R7=1.99kN ,R8=1.882kN正常使用极限状态R max'=[1.1q'L1,0.4q'L1+q'L2]=max[1.1×3.376×0.378,0.4×3.376×0.378+3.376×0.3]=1.523 kN同理可得：梁底支撑小梁所受最大支座反力依次为R1'=1.41kN,R2'=1.523kN,R3'=1.239kN,R4'=1.239kN,R5'=1.239kN,R6'=1.239kN,R7'=1.523kN,R8'=1.41kN六、主梁验算主梁类型钢管主梁截面类型(mm) Φ48×3.5主梁计算截面类型(mm) Φ48×2.8主梁抗弯强度设计值[f](N/mm2) 205主梁抗剪强度设计值[τ](N/mm2) 125 主梁截面抵抗矩W(cm3) 4.25主梁弹性模量E(N/mm2) 206000 主梁截面惯性矩I(cm4) 10.191、抗弯验算主梁弯矩图(kN·m)σ=M max/W=0.325×106/4250=76.359N/mm2≤[f]=205N/mm2满足要求！2、抗剪验算主梁剪力图(kN)V max＝3.541kNτmax=2V max/A=2×3.541×1000/398＝17.796N/mm2≤[τ]=125N/mm2满足要求！3、挠度验算主梁变形图(mm)νmax＝0.185mm≤[ν]＝L/250＝600/250＝2.4mm满足要求！4、支座反力计算承载能力极限状态支座反力依次为R1=0.331kN，R2=6.813kN，R3=6.813kN，R4=0.331kN 正常使用极限状态支座反力依次为R1'=0.247kN，R2'=5.164kN，R3'=5.164kN，R4'=0.247kN 七、2号主梁验算主梁类型钢管主梁截面类型(mm) Φ48×3.5主梁计算截面类型(mm) Φ48×2.8主梁抗弯强度设计值[f](N/mm2) 205主梁抗剪强度设计值[τ](N/mm2) 125 主梁截面抵抗矩W(cm3) 4.25主梁弹性模量E(N/mm2) 206000 主梁截面惯性矩I(cm4) 10.19主梁计算方式三等跨连续梁可调托座内主梁根数 2主梁受力不均匀系数0.6主梁自重忽略不计，主梁2根合并，其主梁受力不均匀系数=0.6P＝max[R2，R3]×0.6=Max[6.813，6.813]×0.6=4.088kN，P'＝max[R2'，R3']×0.6＝Max[5.164，5.164]×0.6=3.099kN1、抗弯验算2号主梁弯矩图(kN·m)σ=M max/W=0.541×106/4250=127.262N/mm2≤[f]=205N/mm2满足要求！2、抗剪验算2号主梁剪力图(kN)V max＝2.657kNτmax=2V max/A=2×2.657×1000/398＝13.353N/mm2≤[τ]=125N/mm2满足要求！3、挠度验算2号主梁变形图(mm)νmax＝0.737mm≤[ν]＝L/250＝756/250＝3.024mm满足要求！4、支座反力计算极限承载能力状态支座反力依次为R1=5.519kN，R2=8.789kN，R3=8.789kN，R4=5.519kN立柱所受主梁支座反力依次为P2=8.789/0.6=14.649kN，P3=8.789/0.6=14.649kN八、纵向水平钢管验算钢管截面类型(mm) Φ48×3.5钢管计算截面类型(mm) Φ48×2.8钢管截面面积A(mm2) 398 钢管截面回转半径i(mm) 16钢管弹性模量E(N/mm2) 206000 钢管截面惯性矩I(cm4) 10.19 钢管截面抵抗矩W(cm3) 4.25 钢管抗弯强度设计值[f](N/mm2) 205 钢管抗剪强度设计值[τ](N/mm2) 125P＝max[R1，R4]=0.331kN，P'＝max[R1'，R4']＝0.247kN计算简图如下：1、抗弯验算纵向水平钢管弯矩图(kN·m)σ＝M max/W＝0.044×106/4250＝10.304N/mm2≤[f]＝205N/mm2满足要求！2、抗剪验算纵向水平钢管剪力图(kN)V max＝0.215kNτmax＝2V max/A=2×0.215×1000/398＝1.081N/mm2≤[τ]＝125N/mm2满足要求！3、挠度验算纵向水平钢管变形图(mm)νmax＝0.059mm≤[ν]＝L/250＝756/250＝3.024mm满足要求！4、支座反力计算支座反力依次为R1=0.447kN，R2=0.712kN，R3=0.712kN，R4=0.447kN同理可得：两侧立柱所受支座反力依次为R1=0.712kN，R4=0.712kN九、可调托座验算荷载传递至立柱方式可调托座2 可调托座承载力容许值[N](kN) 30 扣件抗滑移折减系数k c 11、扣件抗滑移验算两侧立柱最大受力N＝max[R1,R4]＝max[0.712,0.712]＝0.712kN≤1×8=8kN单扣件在扭矩达到40～65N·m且无质量缺陷的情况下，单扣件能满足要求！2、可调托座验算可调托座最大受力N＝max[P2，P3]＝14.649kN≤[N]=30kN满足要求！十、立柱验算l0=h=1800mmλ=l0/i=1800/16=112.5≤[λ]=150长细比满足要求！查表得，φ＝0.5022、风荷载计算M w＝0.9×φc×1.4×ωk×l a×h2/10＝0.9×0.9×1.4×0.29×0.756×1.82/10＝0.081kN·m3、稳定性计算根据《建筑施工模板安全技术规范》JGJ162-2008，荷载设计值q1有所不同：1)面板验算q1＝0.9×[1.2×(0.1+(24+1.5)×0.8)+1.4×0.9×2]×1＝24.408kN/m2)小梁验算q1＝max{1.388+0.9×1.2×[(0.3-0.1)×1/7+0.5×(0.8-0.45)]+0.9×[1.2×(0.5+(24+1.1)×0.45)+1.4×0.9×1]×max[0.8-1/2，(1.6-0.8)-1/2]/2×1，4.011+0.9×1.2×(0.3-0.1)×1/7}=4.042kN/m 同上四～八计算过程，可得：R1＝0.604kN，P2＝13.367kN，P3＝13.367kN，R4＝0.604kN立柱最大受力N w＝max[R1+N边1，P2，P3，R4+N边2]+0.9×1.2×0.15×(5.4-0.8)+M w/l b ＝max[0.604+0.9×[1.2×(0.5+(24+1.1)×0.45)+1.4×0.9×1]×(0.756+0.8-1/2)/2×0.756，13.367，13.367，0.604+0.9×[1.2×(0.5+(24+1.1)×0.45)+1.4×0.9×1]×(0.756+1.6-0.8-1/2)/2×0.756]+0.745+ 0.081/1.6＝14.162kNf＝N/(φA)+M w/W＝14162.276/(0.502×398)+0.081×106/4250＝89.943N/mm2≤[f]＝205N/mm2满足要求！十一、高宽比验算根据《建筑施工扣件式钢管脚手架安全技术规范》JGJ130-2011 第6.9.7：支架高宽比不应大于3H/B=5.4/20=0.27＜3满足要求，不需要进行抗倾覆验算！十二、立柱地基基础计算f ak 140kPa满足要求！。

建筑力学常见问题解答3 静定结构內力计算1.为保证结构物正常工作，结构应满足哪些要求？答：为保证结构物正常工作，结构应满足以下要求（1）强度要求：构件在外力作用下不会发生破坏，即构件抵抗破坏能力的要求，称为强度要求。

（2）刚度要求：构件在外力作用下所产生的变形不应超过一定的范围，即构件抵抗变形能力的要求，称为刚度要求。

（3）稳定性要求：构件在外力作用下，其原有平衡状态不能丧失，即构件抵抗丧失稳定能力的要求，称为稳定性要求。

只有满足上述各项要求，才能保证构件安全正常的工作，达到建筑结构安全使用的目的。

2.什么是变形体？变形体分为哪两类？答：各种物体受力后都会产生或大或小的变形，称为变形体。

根据变形的性质，变形可分为弹性变形和塑性变形。

所谓弹性变形，是指变形体在外力去掉后，能恢复到原来形状和尺寸的变形。

当外力去掉后，变形不能完全消失而留有残余，则消失的变形是弹性变形，残余的变形称为塑性变形或残余变形。

3.在建筑力学范围内，我们所研究的物体，一般都作哪些假设？答：在建筑力学范围内，对所研究的变形体作出如下的基本假设：（1）均匀连续假设：即认为整个物体内部是连续不断地充满着均匀的物质，且在各点处材料的性质完全相同。

（2）各向同性假设：即认为制成物体的材料沿着各个方向都具有相同的力学性质。

（3）弹性假设：即当作用于物体上的外力不超过某一限度时，将物体看成是完全弹性体。

总之，在建筑力学的范围内，我们研究的材料是均匀连续的，各向同性的弹性体，且杆件的变形是很小的。

4.什么是杆件？什么是等直杆？答：所谓杆件，是指长度远大于其他两个方向尺寸的变形体。

如房屋中的梁、柱、屋架中的各根杆等等。

杆件的形状和尺寸可由杆的横截面和轴线两个主要几何元素来描述。

横截面是指与杆长方向垂直的截面，而轴线是各横截面中心的连线。

横截面与杆轴线是互相垂直的。

轴线为直线、横截面相同的杆称为等直杆。

建筑力学主要研究等直杆。

图3-15.杆件变形的基本形式有哪几种？答：杆件变形的基本形式有下列四种：（1）轴向拉伸或压缩(图3-2a、b)：在作用线与杆轴线重合的外力作用下，杆件将产生长度的改变(伸长或缩短)。

三等跨连续梁支座反力计算
在工程建设中，连续梁是常用的结构形式，它由多个跨度组成，在跨度过大时常常采用三等跨连续梁的结构形式。

在梁体支撑方面，支座是连接梁体和支撑结构的重要构件之一，支座的反力计算是保证梁体正常工作的重要环节。

下面将从三等跨连续梁支座反力计算的步骤来进行一一阐述。

一、梁体受力分析
首先，需要进行梁体受力分析，计算每个跨度的受力情况，在这个过程中需要考虑梁的自重、荷载、风荷载等等多种外因素对梁的影响。

二、支座位移计算
通过第一步的梁体受力分析之后，可以对支座进行位移计算，在计算之前，需要对三等跨连续梁的结构形式进行了解，通常情况下，三等跨连续梁的中间跨度大梁会采用两端跨度小梁的支座设置方法，中间跨度小梁采用三个支座分别设置。

计算时需要考虑不同跨度的支座位移及其所产生的影响。

三、计算支座反力
通过前两部分的计算，即可开始计算支座反力。

在计算支座反力的过程中需要考虑梁体自身重量、梁体受到的荷载、支座的长板、短板分别所承受的压力、支座位移对支座反力的影响、梁体弯矩对支座反力的影响等等因素。

四、检查计算结果
完成支座反力计算之后，需要对结果进行检查，包括检查计算结果是否合理、是否满足规范要求等等，以确保计算结果的准确性和合理性。

综上所述，三等跨连续梁支座反力计算是建设工程中十分关键的环节，需要认真细致的进行。

只有在正确计算的基础上，才能够确保梁体和支撑结构正常工作，同时也能够为工程建设提供更好的保障。

第一章1-1什么是结构：房屋、桥梁、隧道、大坝等用以担负预定任务、支撑荷载的建筑物。

结构力学的研究对象主要是杆系结构，其主要任务是:1、研究结构在荷载等因素作用下的内里和位移的计算。

2、研究结构的稳定计算，以及在动力荷载作用下的动力反应。

3、研究结构的组成规则和合理形式等问题。

1-2什么是荷载：作用在结构上的主动力。

按作用时间分：恒载和活载按作用位置分：固定荷载和移动荷载按产生的动力效应大小：静力荷载和动力荷载静力荷载：是指大小、方向和位置不随时间变化或者变化很缓慢的荷载，它不致结构产生显著的加速度，因而可以略去惯性力的影响。

动力荷载：是指随时间迅速变化的荷载，它将引起结构振动，使结构产生不容忽视的加速度，因而必须考虑惯性力的影响。

1-4什么是结构的计算简图：对实际结构加以简化，表现其主要特点，略去次要因素，用一个简化的图形来代替实际结构，这个图形就是结构的计算简图。

如何结构的计算简图：1杆件的简化：常以其轴线代表。

2支座和结点简化：3荷载的简化：常简化为集中荷载及线分布荷载。

4体系的简化：将空间结构转化为平面结构。

1-5支座：把结构和基础联系起来的装置。

1）活动铰支座2）固定铰支座3）固定支座4）滑动支座结点：结构中杆件相互连接处。

刚结点、铰结点、组合结点。

1-6按照几何特征分：杆系结构、薄壁结构、实体结构杆系结构受力特性：梁：是一种受弯构件，轴线通常为直线，当荷载垂直于梁轴线时，横截面上的内力只有弯矩和剪力，没有轴力。

拱：拱的轴线为曲线且在竖向荷载作用下会产生水平反力（推力），这使得拱比跨度、荷载相同的梁的弯矩及剪力都要小，而有较大的轴向压力。

刚架：由直杆组成并具有刚结点，各杆均为受弯杆，内力通常是弯矩、剪力、轴力都有桁架：由直杆组成，但所有结点均为铰结点，当只受到作用于结点的集中荷载时各杆只产生轴力组合结构：由桁架和梁或者桁架和钢架组合在一起的结构有些只受轴力，另一些同时还承受着弯矩和剪力悬索结构：主要承重构件为悬挂于塔、柱上的缆索，只受轴向拉力。

2 常用结构计算2-1 荷载与结构静力计算表2-1-1 荷载1．结构上的荷载结构上的荷载分为下列三类：（1）永久荷载如结构自重、土压力、预应力等。

（2）可变荷载如楼面活荷载、屋面活荷载和积灰荷载、吊车荷载、风荷载、雪活载等。

（3）偶然荷载如爆炸力、撞击力等。

建筑结构设计时，对不同荷载应采用不同的代表值。

对永久荷载应采用标准值作为代表值。

对可变荷载应根据设计要求，采用标准值、组合值、频遇值或准永久值作为代表值。

对偶然荷载应按建筑结构使用的特点确定其代表值。

2．荷载组合建筑结构设计应根据使用过程中在结构上可能同时出现的荷载，按承载能力极限状态和正常使用极限状态分别进行荷载（效应）组合，并应取各自的最不利的效应组合进行设计。

对于承载能力极限状态，应按荷载效应的基本组合或偶然组合进行荷载（效应）组合。

γ0S≤R （2-1）式中γ0——结构重要性系数；S——荷载效应组合的设计值；R——结构构件抗力的设计值。

对于基本组合，荷载效应组合的设计值S应从下列组合值中取最不利值确定：（1）由可变荷载效应控制的组合（2-2）式中γG——永久荷载的分项系数；γQi——第i个可变荷载的分项系数，其中Y Q1为可变荷载Q1的分项系数；S GK——按永久荷载标准值G K计算的荷载效应值；S QiK——按可变荷载标准值Q ik计算的荷载效应值，其中S Q1K为诸可变荷载效应中起控制作用者；ψci——可变荷载Q i的组合值系数；n——参与组合的可变荷载数。

（2）由永久荷载效应控制的组合（2-3）（3）基本组合的荷载分项系数1）永久荷载的分项系数当其效应对结构不利时：对由可变荷载效应控制的组合，应取1.2；对由永久荷载效应控制的组合，应取1.35；当其效应对结构有利时：一般情况下应取1.0；对结构的倾覆、滑移或漂浮验算，应取0.9。

2）可变荷载的分项系数一般情况下应取1.4；对标准值大于4kN/m2的工业房屋楼面结构活荷载应取1.3。

第4章结构构件上的荷载及支座反力计算第4章主要是研究结构构件上所受到的荷载以及支座反力的计算。

结构构件上的荷载通常由外部荷载和内部荷载两部分组成。

外部荷载是指结构构件受到的来自外界的荷载作用，例如自重、活荷载、风荷载、地震作用等。

内部荷载是指结构构件内部的荷载，例如弯矩、剪力、轴力等。

在计算结构构件上的荷载时，通常采用静力学的原理，根据平衡条件和变形条件进行计算。

其中，平衡条件是指结构构件上受力的总和必须为零，即ΣF=0，ΣM=0；变形条件是指结构构件上的变形必须满足一定的条件，例如梁的弯曲变形必须满足梁的曲率方程。

在计算支座反力时，一般可以采用静力平衡的原理进行计算。

静力平衡的原理是指在结构构件的静力平衡状态下，结构构件上的受力总和必须为零。

在计算支座反力时，可以通过荷载和受力的平衡条件，根据结构构件的几何特性和荷载分布进行计算。

支座反力的计算是结构设计中的重要内容，其准确性对于结构的稳定性和安全性至关重要。

支座反力的计算需要考虑结构的几何形状、荷载分布、材料特性等因素，并且需要根据结构的使用要求和安全标准进行计算。

常用的计算方法包括力平衡法、变形平衡法、弹性平衡法等。

支座反力的计算是结构设计中的一项基本工作，它为结构的合理设计和安全使用提供重要依据。

合理的支座反力计算可以保证结构的稳定性和安全性，并且对于结构的经济性和可行性也有一定的影响。

总之，第4章是研究结构构件上的荷载及支座反力计算的重要内容。

荷载计算是结构设计的基础工作，而支座反力的计算对于结构的稳定性和安全性具有重要意义。

只有通过合理的计算方法和准确的计算结果，才能够保证结构的合理设计，从而满足设计要求和安全标准。

支座反力总结引言在工程力学中，支座反力是指一个结构或构件在支撑点上受到的力的总和。

支座反力是结构分析的重要结果之一，对于工程设计、施工以及安全评估具有重要意义。

本文将总结支座反力的概念、计算方法以及常见应用。

支座反力的定义与分类支座反力是指一个结构在支撑点上受到的力的总和。

根据支撑点的类型和结构的约束条件，支座反力可以分为以下几类：1.钉子支座：在一个固定支座中，结构可以绕任意一个轴旋转，但在该轴向上不能发生横移动。

钉子支座在水平方向上提供反力，但不提供弯矩。

2.滑动支座：滑动支座在水平和垂直方向上都可以提供反力，但不提供弯矩。

滑动支座可以滑动，但不可以转动。

3.旋转支座：旋转支座可以提供反力和弯矩。

它可以绕一个轴旋转，但在该轴向上不能发生横移动。

4.固定支座：固定支座可以提供反力、弯矩和剪力。

它既不能滑动，也不能转动。

支座反力的计算方法支座反力的计算方法根据结构的类型和支座的约束条件而有所不同。

下面将介绍一些常见的计算方法。

钉子支座的反力计算钉子支座只能提供水平方向上的反力，不提供弯矩。

计算方法如下：1.在水平方向上的总受力为零。

即水平方向上的反力之和等于零。

2.根据结构的平衡条件，可以计算出每个支座上的反力。

滑动支座的反力计算滑动支座在水平和垂直方向上都可以提供反力，但不提供弯矩。

计算方法如下：1.在水平和垂直方向上的总受力为零。

即水平和垂直方向上的反力之和等于零。

2.根据结构的平衡条件，可以计算出每个支座上的反力。

旋转支座的反力计算旋转支座可以提供反力和弯矩。

计算方法如下：1.在垂直方向上的总受力为零。

即垂直方向上的反力之和等于零。

2.在水平方向上的总弯矩为零。

即所有支座上的弯矩之和等于零。

3.根据结构的平衡条件和弹性力学原理，可以计算出每个支座上的反力和弯矩。

固定支座的反力计算固定支座可以提供反力、弯矩和剪力。

计算方法如下：1.在垂直方向上的总受力为零。

即垂直方向上的反力之和等于零。

2.在水平方向上的总弯矩为零。