第十二章 压杆稳定(习题解答)

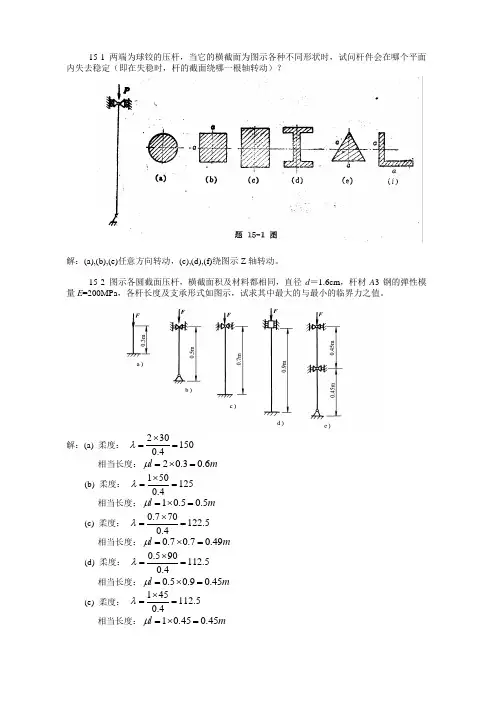
15-1 两端为球铰的压杆，当它的横截面为图示各种不同形状时，试问杆件会在哪个平面内失去稳定（即在失稳时，杆的截面绕哪一根轴转动）？解：(a),(b),(e)任意方向转动，(c),(d),(f)绕图示Z 轴转动。

15-2 图示各圆截面压杆，横截面积及材料都相同，直径d ＝1.6cm ，杆材A 3钢的弹性模量E =200MPa ，各杆长度及支承形式如图示，试求其中最大的与最小的临界力之值。

解：(a) 柔度： 2301500.4λ⨯== 相当长度：20.30.6l m μ=⨯=(b) 柔度： 1501250.4λ⨯== 相当长度：10.50.5l m μ=⨯=(c) 柔度： 0.770122.50.4λ⨯== 相当长度：0.70.70.49l m μ=⨯=(d) 柔度： 0.590112.50.4λ⨯== 相当长度：0.50.90.45l m μ=⨯=(e) 柔度： 145112.50.4λ⨯== 相当长度：10.450.45l m μ=⨯=由E=200Gpa 及各柔度值看出：各压杆的临界力可用欧拉公式计算。

即：()22cr EIF l πμ=各压杆的EJ 均相同，故相当长度最大的压杆(a)临界力最小，压杆(d)与(e)的临界力最大，分别为：()2948222320010 1.610640.617.6410cr EFF l N πππμ-⨯⨯⨯⨯⨯===⨯()2948222320010 1.610640.4531.3010cr EIF l Nπππμ-⨯⨯⨯⨯⨯===⨯15-3 某种钢材P σ=230MPa ，s σ=274MPa ，E =200GPa ，直线公式λσ22.1338-=cr ，试计算该材料压杆的P λ及S λ值，并绘制1500≤≤λ范围内的临界应力总图。

解：92.633827452.5p s s a λπσλ===--===15-4 6120型柴油机挺杆为45钢制成的空心圆截面杆，其外径和内径分别为，12mm 和10mm ，杆长为383mm ，两端为铰支座，材料的E ＝210GPa ，P σ=288MPa ，试求此挺杆的临界力cr F 。

工程力学（静力学与材料力学）习题第12章 失效分析与设计准则12－ 1 对于建立材料在一般应力状态下的失效判据与设计准则，试选择如下合适的论述。

（A ）逐一进行试验，确定极限应力；（B ）无需进行试验，只需关于失效原因的假说；（C ）需要进行某些试验，无需关于失效原因的假说； （D ）假设失效的共同原因，根据简单试验结果。

正确答案是 。

12－2 对于图示的应力状态（y x σσ>）若为脆性材料，试分析失效可能发生在：（A ）平行于x 轴的平面； （B ）平行于z 轴的平面；（C ）平行于Oyz 坐标面的平面； （D ）平行于Oxy 坐标面的平面。

正确答案是 。

12－3 对于图示的应力状态，若x y σσ=，且为韧性材料，试根据最大切应力准则，失效可能发生在：（A ）平行于y 轴、其法线与x 轴的夹角为45°的平面，或平行于x 轴、其法线与y 轴的夹角为45°的平面内；（B ）仅为平行于y 轴、法线与z 轴的夹角为45°的平面； （C ）仅为平行于z 轴、其法线与x 轴的夹角为45°的平面； （D ）仅为平行于x 轴、其法线与y 轴的夹角为45°的平面。

正确答案是 。

12－4 铸铁处于图示应力状态下，试分析最容易失效的是：（A ）仅图c ；（B ）图a 和图b ； （C ）图a 、b 和图c ； （D ）图a 、b 、c 和图d 。

正确答案是 。

12－5低碳钢处于图示应力状态下，若根据最大切应力准则，试分析最容易失效的是： （A ）仅图d ； （B ）仅图c ； （C ）图c 和图d ； （D ）图a 、b 和图d 。

正确答案是 。

12－6 韧性材料所处应力状态如图所示，根据最大切应力准则，试分析二者同时失效的条件是： （A ）τσ>，3/2στ=； （B ）τσ<，3/4στ=； （C ）τσ=；（D ）τσ>，3/2τσ=。

1、 中心受压细长直杆丧失承载能力的原因为（ ）。

（A ） 横截面上的应力达到材料的比例极限；（B ） 横截面上的应力达到材料的屈服极限；（C ） 横截面上的应力达到材料的强度极限；（D ） 压杆丧失直线平衡状态的稳定性2、一细长压杆当轴向压力F =F cr 时发生失稳而处于微弯平衡状态。

此时若解除压力F ，则压杆的微弯变形（ ）。

A 、完全消失；B 、有所缓和；C 、保持不变；D 、继续增大。

3、压杆失稳将在（ ）的纵向平面内发生。

A 、长度系数μ最大；B 、截面惯性半径i 最小；C 、柔度λ最大；D 、柔度λ最小。

4、欧拉公式的适用条件是（ ）。

()A λ≤()B λ≥()C λ≥()D λ5、两根细长压杆a 、b 的长度，横截面面积、约束状态及材料均相同，若其横截面形状分别为正方形和圆形，则两压杆的临界压力F acr 和F bcr 的关系为（ ）。

A 、F acr <F bcr ；B 、F acr =F bcr ；C 、F acr >F bcr ；D 、不可确定。

6、在稳定性计算中，有可能发生两种情况：一是用细长杆的公式计算中长杆的临界压力；一是用中长杆的公式计算细长杆的临界压力。

其后果是（ ）。

A 、前者的结果偏于安全，后者偏于不安全；B 、二者的结果都偏于安全；C 、前者的结果偏于不安全，后者偏于安全；D 、二者的结果都偏于不安全。

7、由低碳钢制成的细长压杆，经过冷作硬化后，其（ ）。

A 、稳定性提高，强度不变；B 、稳定性不变，强度提高；C 、稳定性和强度都提高；D 、稳定性和强度都不变。

8、一正方形截面细长压杆，因实际需要在n-n 横截面处钻一横向小孔如图所示。

（1）在计算压杆的临界力时，所用的惯性矩为（ ）；4()12b A 44()1264b d B π- 43()1212b bd C - 43()1212b b d D - （2）在对杆进行强度计算时，横截面面积应取（ ）。

压杆稳定性计算公式例题在工程结构设计中，压杆是一种常见的结构元素，用于承受压力和稳定结构。

在设计过程中，需要对压杆的稳定性进行计算，以确保结构的安全性和稳定性。

本文将介绍压杆稳定性计算的基本原理和公式，并通过一个例题进行详细说明。

压杆稳定性计算的基本原理。

压杆稳定性是指压杆在受压力作用下不会发生侧向屈曲或失稳的能力。

在进行压杆稳定性计算时，需要考虑压杆的材料、截面形状、长度、支座条件等因素，以确定其稳定性。

一般来说，压杆的稳定性可以通过欧拉公式或约束条件来计算。

欧拉公式是描述压杆稳定性的经典公式，其表达式为：Pcr = (π^2 E I) / (K L)^2。

其中，Pcr表示压杆的临界压力，E表示弹性模量，I表示截面惯性矩，K表示约束系数，L表示压杆的有效长度。

这个公式是基于理想的弹性理论，适用于较长的细杆，但在实际工程中，压杆的稳定性计算可能还需要考虑其他因素。

除了欧拉公式外，压杆稳定性计算还需要考虑约束条件。

约束条件是指压杆在受力时的支座和边界条件，对压杆的稳定性有重要影响。

在实际工程中，约束条件可以通过有限元分析等方法来确定，以获得更精确的稳定性计算结果。

压杆稳定性计算的例题分析。

下面我们通过一个例题来说明压杆稳定性计算的具体步骤和方法。

假设有一根长度为2m的钢质压杆，截面形状为矩形，截面尺寸为100mm ×50mm，弹性模量为2.1 × 10^5 N/mm^2。

现在需要计算在这根压杆上施加的最大压力，使得其不会发生侧向屈曲或失稳。

首先，我们需要计算压杆的有效长度。

对于简支压杆，其有效长度可以通过以下公式计算：Le = K L。

其中，K为约束系数，对于简支压杆，K取1。

所以，这根压杆的有效长度为2m。

接下来，我们可以使用欧拉公式来计算压杆的临界压力。

根据欧拉公式，可以得到：Pcr = (π^2 E I) / L^2。

其中，E为弹性模量，I为截面惯性矩。

根据矩形截面的惯性矩公式，可以计算得到I = (1/12) b h^3 = (1/12) 100mm (50mm)^3 = 5208333.33mm^4。

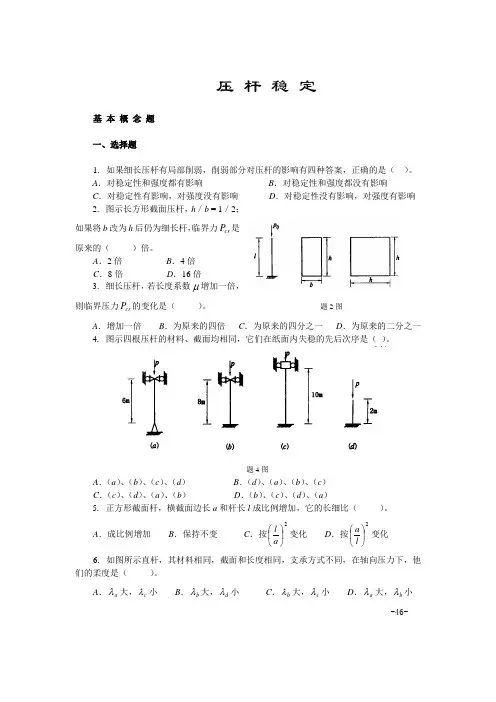
压 杆 稳 定基 本 概 念 题一、选择题1. 如果细长压杆有局部削弱，削弱部分对压杆的影响有四种答案，正确的是（ ）。

A ．对稳定性和强度都有影响 B ．对稳定性和强度都没有影响C ．对稳定性有影响，对强度没有影响D ．对稳定性没有影响，对强度有影响 2. 图示长方形截面压杆，h ／b = 1／2；如果将b 改为h 后仍为细长杆，临界力cr P 是原来的（ ）倍。

A ．2倍B ．4倍C ．8倍D ．16倍 3. 细长压杆，若长度系数μ增加一倍，则临界压力cr P 的变化是（ ）。

题2图A ．增加一倍B ．为原来的四倍C ．为原来的四分之一D ．为原来的二分之一4. 图示四根压杆的材料、截面均相同，它们在纸面内失稳的先后次序是（ ）。

题4图A ．（a ）、（b ）、（c ）、（d ）B ．（d ）、（a ）、（b ）、（c ）C ．（c ）、（d ）、（a ）、（b ）D ．（b ）、（c ）、（d ）、（a ）5. 正方形截面杆，横截面边长a 和杆长l 成比例增加，它的长细比（ ）。

A ．成比例增加B ．保持不变C ．按2⎪⎭⎫ ⎝⎛a l 变化D ．按2⎪⎭⎫⎝⎛l a 变化6. 如图所示直杆，其材料相同，截面和长度相同，支承方式不同，在轴向压力下，他们的柔度是（ ）。

A ．a λ大，c λ小B ．b λ大，d λ小C ．b λ大，c λ小D ．a λ大，b λ小 -46-7. 若压杆在两个方向上的约束情况不同，且y μ＞z μ。

那么该压杆的合理截面应满足的条件是（ ）。

A ．z y I I =B ．y I ＜z IC ．y I ＞z ID ．y z λλ=题6图8. 两压杆为管状薄壁容器式的细长杆，管两端封闭，且为铰支承。

(a )杆无内压，(b ) 杆有内压，其它条件相同。

则两杆临界应力的关系是（ ）。

A ．()()b cr a cr σσ=B ．()a cr σ＞()b cr σC ．()a cr σ＜()b cr σD ．无法比较9. 两根细长杆，直径、约束均相同，但材料不同，且212E E =，则两杆临界应力的关系是（ ）。

压杆的稳定一、是非题（正确在括号内打（√）、错误打（×））1、 压杆的临界压力（或临界应力）与作用载荷大小有关。

（ ）2、 两根材料、长度、截面面积和约束条件都相同的压杆，其临界压力也一定相同。

（ ）3、 压杆的临界应力值与材料的弹性模量成正比。

（ ）4、 细长压杆，若其长度系数增加一倍，cr P 增加到原来的4倍。

（ ）5、 一端固定，一端自由的压杆，长1.5m ，压杆外径mm 76=D ，内径mm 64=d 。

材料的弹性模量GPa 200=E ，压杆材料的p λ值为100，则杆的临界应力MPa 135≈cr σ。

（ ）6、 上题压杆的临界力为kN 178=cr P 。

（ ）二、单项选择题：1．细长压杆，若其长度系数增加一倍，则（ ）。

A ．cr P 增加一倍；B ．cr P 增加到原来的4倍；C ．cr P 为原来的二分之一倍；D ．cr P 增为原来的四分之一倍 。

2．下列结论中哪些是正确的？答（ ）。

（1） 若压杆中的实际应力不大于该压杆的临界应力，则杆件不会失稳；（2） 受压杆件的破坏均由失稳引起；（3） 压杆临界应力的大小可以反映压杆稳定性的好坏；（4） 若压杆中的实际应力大于22λπσE cr =，则压杆必定破坏。

A ．（1），（2）； B ．（2），（4）； C ．（1），（3）； D ．（2），（3）。

三、填空题：1．决定压杆柔度的因素是 。

2．若两根细长压杆的惯性半径AI i =相等，当 相同时，它们的柔度相等。

3．若两根细长压杆的柔度相等，当 相同时，它们的临界应力相等。

4．两端铰支的圆截面压杆，若100=P λ，则压杆的长度与横截面直径之比dL 在 时，才能应用欧拉公式。

5．大柔度压杆和中柔度压杆一般是因 而失效，小柔度压杆是因而失效。

6．（a ）、（b ）两根都是大柔度杆，材料、杆长和横截面形状大小都相同，杆端约束不同。

其中（a ）为两端铰支，（b ）为一端固定，一端自由。

12-4 图示边长为a 的正方形铰接结构，各杆的E 、I 、A 均相同，且为细长杆。

试求达到临界状态时相应的力P 等于多少？若力改为相反方向，其值又应为多少？N BB CN B AB CC D解：（1）各杆的临界力222..222cr BD cr EI EI P P aaππ===外（2）求各杆的轴力与P 的关系。

由对称性可知，外围的四个杆轴力相同，AB BC CD DA N NN N ===。

研究C 、B 结点，设各杆都是受拉的二力杆，则与结点相联系的杆施与背离结点指向杆内的拉力，C 、B 结点受力如图所示。

第一种情况：C:)02450CB CB X P N cos N =→--=→=-∑ 压杆B:()02450BD BC BD BC Y N N cos N P =→--=→==∑拉杆 令2,.2=C B cr C B cr EI N P P P aaπ=-==↔外第二种情况： )C B P N =拉杆 ()-BD BC N P ==压杆22.22-==22BD BC cr BD EI EI N P P P aaππ===↔12-6 图示矩形截面松木柱，其两端约束情况为：在纸平面内失稳时，可视为两端固定；在出平面内失稳时，可视为上端自由下端固定。

试求该木柱的临界力.解：（1）计算柔度：①当压杆在在平面内xoz 内失稳，y 为中性轴。

0.57101.04xz xz yl i μλ⋅⨯===②当压杆在出平面内xoy 内失稳，z 为中性轴。

27242.490.200xy xy zli μλ⋅⨯===③λ越大，压杆越容易失稳，故此压杆将在在平面内先失稳。

m ax(.)242.49xz xy λλλ==（2）松木75242.49P λ=<，故采用欧拉公式计算P cr 222112(0.110)(0.1200.200)40.28242.49cr cr E P A Aπσλπ=⋅=⋅⨯⨯=⨯⨯=N kN12-7铰接结构ABC 由具有相同截面和材料的细长杆组成。

压 杆 稳 定典型习题解析1 图示№20a 工字钢，在温度20℃时安装，这时杆不受力，试问：当温度升高多少度时，工字钢将丧失稳定？钢的线膨胀系数α=12.5×10-61/℃。

解题分析：计算λ时，取i 的最小值。

此题是一度静不定问题，利用变形协调方程求解。

解：1、求柔度λ，查表№20a 工字钢 。

cm 12.2n i m =i №20a题1图p 2142m1012.2m 65.0λµλ>=××==−i lc 2、求失稳时的温度杆为细长杆，临界应力公式为22cr )(πλσE =当温度上升∆T 时，杆内的应力 T E ∆T ⋅⋅=ασ 若温度上升∆T 时，杆开始失稳，则有T cr σσ=或 T E E∆⋅⋅=αλ22)(π 于是C 2.39142C 1/105.12ππ∆26222D D=××⋅⋅==−E T ααλ安装时的温度为20℃，故失稳时的温度为°=∆+°=2.5920T T2 图示结构中，AB 及AC 均为圆截面杆，直径d = 80 mm ，材料为Q235钢，求此结构的临界载荷F cr 。

解题分析：分别计算各杆可承担的临界载荷，取小值。

解：1、计算在F 力作用下各杆的轴力F F F 2160cos N1==D ，1N 2F F = F F F 2360sin N2==D ，2N 2N 15.132F F F ==F N2题2图2、计算各杆的柔度1734/mm 08cos30mm 40001ll 1=××==D i l µλ1004/mm 0830sin mm 40001222=××==D i l µλ两杆均为大柔度杆3、分别计算各杆的临界轴力，确定结构的临界载荷kN 7.330N 107.330)30cos m 41(64m)1080(πPa 10200π)(π324392212N1=×=××××××==−D l EI F µkN 4.6612N1cr1==F FkN 990N 10990)30sin m 41(64m)1080(πPa 10200π)(π324392222N2=×=××××××==−D l EI F µ kN 113915.12N 2cr ==F F该结构的临界载荷取两者中较小者，即 F cr =661.4 kN3 图示结构中，分布载荷q = 20 kN /m 。

压杆稳定习题1、对于不同柔度的塑性材料压杆，其最大临界应力将不超过材料的 。

2、图示边长为mm a 10032⨯=的正方形截面大柔度杆，承受轴向压力kN F 24π=，弹性模量GPa E 100=。

则该杆的工作安全系数为 。

A 、4=w n B 、3=w nC 、2=w n D 、1=w n3、两端铰支圆截面细长压杆，在某一截面上开有一小孔。

关于这一小孔对杆承载能力的影响，以下论述中正确的是___。

Ａ、对强度和稳定承载能力都有较大削弱 Ｂ、对强度和稳定承载能力都不会削弱Ｃ、对强度无削弱，对稳定承载能力有较大削弱 Ｄ、对强度有较大削弱，对稳定承载能力削弱极微4. 理想均匀直杆与轴向压力P ＝Pcr 时处于直线平衡状态。

当其受到一微小横向干扰力后发生微小弯曲变形，若此时解除干扰力，则压杆( ) A 弯曲变形消失，恢复直线形状 B 弯曲变形减小，不能恢复直线形状 C 微弯变形状态不变 D 弯曲变形继续增大5. 两根细长压杆的长度、横截面面积、约束状态及材料均相同，若a 、b 杆的横截面形状分别为正方形和圆形，则二压杆的临界压力Pa 和Pb 的关系为( ) A Pa ＜Pb B Pa ＞Pb C Pa ＝Pb D 不可确定6.细长杆承受轴向压力P 的作用，其临界压力与( )无关A 杆的材质B 杆的长度C 杆承受压力的大小D 杆的横截面形状和尺寸7. 压杆的柔度集中地反映了压杆的( )对临界应力的影响A 长度、约束条件、截面形状和尺寸B 材料、长度和约束条件C 材料、约束条件、截面形状和尺寸D 材料、长度、截面尺寸和形状8. 在材料相同的条件下，随着柔度的增大( )A 细长杆的临界应力是减小的，中长杆不变B 中长杆的临界应力是减小的，细长杆不变C 细长杆和中长杆的临界应力均是减小的D 细长杆和中长杆的临界应力均不是减小的9. 两根材料和柔度都相同的压杆，( )A 临界应力一定相等，临界压力不一定相等B 临界应力不一定相等，临界压力一定相等C 临界应力和临界压力一定相等D 临界应力和临界压力不一定相等10. 在下列有关压杆临界应力σcr的结论中，( )是正确的A 细长杆的σcr值与杆的材料无关B 中长杆的σcr值与杆的柔度无关C 中长杆的σcr值与杆的材料无关D 粗短杆的σcr值与杆的柔度无关11. 在横截面面积等其他条件均相同的条件下，压杆采用图( )所示截面形状，其稳定性最好.A. AB. BC. CD. D二、计算题10.1图示为支撑情况不同的圆截面细长杆,各杆直径和材料相同,哪个杆的临界力最大。

压杆稳定1. 图示结构，AB 为刚性杆，其它杆均为直径10 mm d =的细长圆杆，弹性模量200 GPa E =, 屈服极限s 360 MPa σ=，试求此结构的破坏载荷F 值。

解：12.37 m, sin 26H α⎛⎫== ⎪⎝⎭,0.169()Cy Dy F F F =-=↓,N1N4N2N30.507F F F F F ==-=-=由杆1，4，N11s 0.507F F A σ==，s 155.8 kN 0.507AF σ==由杆2，3，2N2cr 2π0.673 kN EIF F l ===, cr 2 1.33 kN 0.507F F ==结构破坏载荷 1.33 kN F =2. 图示桁架由5根圆截面杆组成。

已知各杆直径均为30 mm d =， 1 m l =。

各杆的弹性模量均为200 GPa E =，p 100λ=，061λ=，直线经验公式系数304 MPa a =， 1.12 MPa b =，许用应力[]160 MPa σ=，并规定稳定安全因数st []3n =，试求此结构的许可载荷[]F 。

解：由平衡条件可知杆1，2，3，4受压，其轴力为N1N2N3N4N F F F F F ===== 杆5受拉，其轴力为N5F F = 按杆5的强度条件：N5[], []113 kN F F A Aσσ≤≤= 按杆1，2，3，4的稳定条件 p 133λλ=> 由欧拉公式 cr 78.48 kN F =crst N[]F n F ≥ 37.1 kN F ≤ ， []37.1 kN F =3. 钢杆和铜杆截面、长度均相同，都是细长杆。

将两杆的两端分别用铰链并联，如图，此时两杆都不受力。

试计算当温度升高多少度时，将会导致结构失稳？已知杆长 2 m l =，横截面积220 cm A =，惯性矩440 cm z I =；钢的弹性模量s 200 GPa E =，铜的弹性模量c 100 GPa E =，钢的线膨胀系数6s 12.510α-=⨯℃-1，铜的线膨系数6c 16.510α-=⨯℃-1。

例1：已知AB 为A 3钢，杆l AB =80cm, n st =2，1001＝λ572＝λ，试校核AB 杆。

解：杆件工作时的压力：分析CBD 的受力，根据平衡方程可得 P AB =159kN 临界压力：8044801＝＝＝⨯i lμλ 21λλλ≥≥ 用经验公式确定临界应力：MPa b a cr 4.2148012.1304=⨯-=－＝λσ P cr =σcr A=270kN269.1159270=≤===st cr n P P n 所有AB 杆不安全。

思考? 若校核整个结构，解题的思路？若由AB 杆确定整个结构的许用外载荷，思路？例2：杆AB 、AC ：d=80cm, A 3钢， 1001＝λ 572＝λ，n st =5，E=210GPa ，求[P]。

解：P AB =0.5P P AC =0.866P173408.030cos 41＝＝⨯=il AB AB μλ用欧拉公式确定临界压力：()kN l EIP AB crAB 34822==μπ55.0348≥==PP P n ABcrABP ≤139.2kN100408.030sin 41＝＝⨯=il ACAC μλ用欧拉公式确定临界压力： ()kN l EIP AC crAC 8.104122==μπ5866.08.1041≥==PP P n ACcrAC P ≤240.6kN[P]=139.2kN例3：已知压杆为球铰，A 3钢，l=2.4m ，压杆由两根等边角钢铆成，A=2×28.9cm 2，铆钉孔直径为23mm ，P ＝800kN n st =1.48 ，[σ]=160MPa ，试校核压杆是否安全。

解： 1稳定校核：66.624.21 min＝＝zi i l⨯=μλ M P a b a cr 8.23366.6212.1304=⨯-=－＝λσstcr n PAn >==69.1σ稳定计算时用毛面积。

2强度校核：角钢在铆钉孔处截面削弱：A 0=2×28.9×10-4－2×0.023×0.012=5.28×10-3m 2[]σσ<==MPa A P 1530强度计算用净面积。