2021年全国普通高等学校招生统一考试文科数学试卷 全国甲卷(含答案)(word 试卷版)

高考精品文档高考全国甲卷文科数学·2021年考试真题与答案解析同卷地区贵州省、四川省、云南省西藏自治区、广西自治区高考全国甲卷：《文科数学》2021年考试真题与答案解析一、选择题本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设集合M={1，3，5，7，9}.N={x|2x>7}，则M∩N=（）A.{7，9}B.{5，7，9)C.{3，5，7，9}D.{1，3，5，7，9}答案：B2.为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如下频率分布直方图，根据此频率分布直方图，下面结论中不正确的是（）A.该地农户家庭年收入低于4.5万元的农户比率估计为6%B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%C.估计该地农户家庭年收入的平均值不超过6.5万元D.估计该地有一半以上的农户，其家庭年收入介于4.5万元至8.5万元之间答案：C3．已知(1-i)2z=3+2i ，则z=（ ）A.-1-i B.-1+i C.-+i D.--i 答案：B4．下列函数中是增函数的为（ ）A.f(x)=-xB.f(x)=C.f(x)=x 2D.f(x)=3x 答案：D5．点(3，0)到双曲线=1的一条渐近线的距离为（ ）A.23232323x⎪⎭⎫⎝⎛3291622y x -59B.C.D.答案：A6.青少年视力是社会普遍关注的问题，视力情况可借助视力表测量。

通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L 和小数记录法的数据V 满足L =5+lg V 。

已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据约为（ ）(1010≈1.259)A.1.5B.1.2C.0.8D.0.6答案：C7.在一个正方体中，过顶点A 的三条棱的中点分别为E ，F ，G ，该正方体截去三棱锥A-EFG 后，所得多面体的三视图中，正视图如右图所示，则相应的侧视图是A 、585654B.C.D.答案：A8.在∆ABC中，已知B=120°, AC=19, AB=2, 则BC=（）A.1B.2C.5D.3答案：D9.记S n为等比数列{a n}的前n项和。

2021年普通高等学校招生全国统一考试数学试题(甲卷·文科)压轴题解读11．若α∈(0，π2)，tan2α＝cos α2−sinα，则tanα＝( ) A ．√1515B ．√55 C ．√53D ．√153【命题意图】考查三角恒等变换，考查数学运算，逻辑推理能力。

【答案】A【解析】由题意得222sin cos cos ,sin 2sin 1cos αααααα=--整理得222sin cos cos ,cos sin 2sin ααααα=-- 即22sin 1,12sin 2sin ααα=--解得1sin 4α=，则cos 4α=所以tan 15α=选A 。

【解题方法】重视三角函数的“三变”：“三变”是指“变角、变名、变式”.(1)变角：对角的分拆要尽可能化成同角、特殊角；(2)变名：尽可能减少函数名称；(3)变式：对式子变形一般要尽可能有理化、整式化、降低次数等.12．设f (x )是定义域为R 的奇函数，且f (1＋x )＝f －x )．若f (−13)＝13，则f (53)＝( )A ．−53B ．−13C ．13D ．53【命题意图】本题主要考查了利用函数的奇偶性求解函数值，解题的关键是进行合理的转化，考查了学生的抽象思维及逻辑思维能力． 【答案】C【解析】由(1)()f x f x +=-，得(1)()f x f x +=-，则(2)(1)()f x f x f x +=-+=，所以函数()f x 的周期为2，则5111()(2)()3333f f f =-=-=。

故选C 。

【规律总结】根据函数的周期性和奇偶性求给定区间上的函数值或解析式时，应根据周期性或奇偶性，由待求区间转化到已知区间.16．已知F 1，F 2为椭圆C ：x 216＋y 24＝1两个焦点，P ，Q 为C 上关于坐标原点对称的两点，且|PQ|＝|F 1F 2|，则四边形PF 1QF 2的面积为______．【命题意图】本题主要考查椭圆的性质，椭圆的定义，考查方程思想与运算求解能力，属于中档题． 【答案】C【解析】因为P ，Q 为C 上关于坐标原点对称的两点，且12||||PQ F F =，所以四边形12PF QF 为矩形， 设1||PF m =，2||PF n =，由椭圆的定义可得12||||||||28PF PF m n a +=+==，所以22264m mn n ++=， 因为2222221212||||||44()48PF PF F F c a b +===-=，即2248m n +=，所以8mn =， 所以四边形12PF QF 的面积为12||||8PF PF mn ==．16.解法1：设(,),P x y 由||OP =得2212,x y += ① 又221164x y +=，②①②联立解得||y =所以四边形12PFQF 的面积为1212||||8.2F F y ⨯⋅== 解法2：由题意知，四边形12PFQF 为矩形，由椭圆定义得12||||28,PFPF a +== 即212(||||)64,PF PF +=所以221212||||2||||64,PF PF PF PF ++⋅=又2221212||||||48,PF PF F F +==所以12||||8,PFPF ⋅=即四边形12PFQF 的面积为8. 答案：820．设函数f(x)＝a 2x 2＋ax −3lnx ＋1，其中a >0． (1)讨论f (x )的单调性；(2)若y ＝f (x )的图像与x 轴没有公共点，求a 的取值范围．【命题意图】考查利用导数研究函数的单调性，函数的零点，考查数学抽象，逻辑推理，数学运算的能力 【解析】（1）因为f(x)＝a 2x 2＋ax −3ln x ＋1，所以定义域为()0,+∞，所以222323(23)(1)'()2a x ax ax ax f x a x a x x x +-+-=+-==，因为0,0a x >>，所以230ax x +>，令1'()0101,f x ax ax x a>⇒->⇒>⇒> 令1'()0101,f x ax ax x a <⇒-<⇒<⇒<因为0x >，所以10x a <<，所以()f x 在10,a ⎛⎫⎪⎝⎭上单调递增，在1,a ⎛⎫+∞ ⎪⎝⎭上单调递减. （2）由（1）知()f x 在10,a ⎛⎫ ⎪⎝⎭上单调递增，在1,a ⎛⎫+∞ ⎪⎝⎭上单调递减. 而1133ln f a a ⎛⎫⎛⎫=-⎪ ⎪⎝⎭⎝⎭，当0x →时，()f x →+∞，当x →+∞时，()f x →+∞， 所以要使()y f x =的图象与x 轴没有公共点，则1111111033ln 033ln 1ln 1ln ln 1f a a a a a a a e ⎛⎫>⇒->⇒>⇒>⇒>-⇒>-⇒> ⎪⎝⎭所以a 的取值范围为1,e ⎛⎫+∞ ⎪⎝⎭.21．抛物线C 的顶点为坐标原点O ，焦点在x 轴上，直线:1l x =交C 于P ，Q 两点，且OP OQ ⊥．已知点(2,0)M ，且M 与l 相切． （1）求C ，M 的方程；（2）设1A ，2A ，3A 是C 上的三个点，直线12A A ，13A A 均与M 相切．判断直线23A A 与M 的位置关系，并说明理由． 【命题意图】本题主要考查抛物线方程的求解，圆的方程的求解，分类讨论的数学思想，直线与圆的位置关系，同构、对称思想的应用等知识，属于中等题．【解析】（1）因为1x =与抛物线有两个不同的交点，故可设抛物线C 的方程为：22(0)y px p =>，令1x =，则y =，根据抛物线的对称性，不妨设P 在x 轴上方，Q 在X 轴下方，故(1(1P Q ，因为OP OQ ⊥，故1102p =⇒=， 抛物线C 的方程为：2y x =，因为M 与l 相切，故其半径为1，故22:(2)1M x y -+=． （2）设11(A x ，1)y ，22(A x ，2)y ，33(A x ，3)y ．当1A ，2A ，3A 中有一个为坐标原点，另外两个点的横坐标的值均为3时，满足条件， 且此时直线23A A 与M 也相切，当123x x x ≠≠时，可知，直线12A A 的方程为1212?()0x y y y y y ++=，1=，即22212121(?1)23?0y y y y y ++=， 同理，由对称性可得，22213131(?1)23?0y y y y y ++=， 所以2y ，3y 是方程222111(?1)23?0y t y t y ++= 的两根， 依题意有，直线23A A 的方程为2323?()0x y y y y y ++=．，令M 到直线23A A 的距离为d ，则有22122223122123213?(2)(2)?11?21()1()?1y y y y d y y y y ++===+++，此时，直线23A A 与M 也相切． 综上，直线23A A 与M 相切．压轴题模拟1．（2021·湖南长沙市·雅礼中学高三月考）已知(0,)2πα∈，cos 2cos 2αα=-tan 2α=( ) AB．-CD．【答案】B【解析】cos 2cos 2αα=-，2cos 22cos1αα=-， 24cos 20αα∴+-=，解得cos α=cos α=舍去)， 又(0,)2πα∈，sin α∴=tan α∴= 22tan tan 21tan ααα==-故选：B . 2．（2020·梅河口市第五中学高三模拟）已知cos2cos(),sin 04πααπαα⎛⎫=-+≠ ⎪⎝⎭，则tan 3πα⎛⎫+ ⎪⎝⎭的值为（ ） A．2--B．2C．2D．2【答案】A【解析】22cos2cossin sin cos cos sin (cos )44ππαααααα⎫=-=-⋅-⎪⎭，所以22cos sin (cos sin )cos ααααα-=-，所以(cos sin )sin 0ααα-=． 又sin 0α≠，所以cos sin αα=，所以tan 1α=，因此tantan 3tan 231tan tan 3παπαπα+⎛⎫+==-- ⎪⎝⎭-A 3．（2021·宁夏银川市·高三模拟）已知()y f x =为R 上的奇函数，()1y f x =+为偶函数，若当[]0,1x ∈，()()2log a f x x =+，则()2021f =（ ）A ．2-B ．1-C ．1D ．2【答案】C 【解析】()f x 为R 上的奇函数，且当[]0,1x ∈时，()()2log a f x x =+∴()00f =，即2log 0a =， 1a，∴当[]0,1x ∈时，()()2log 1f x x =+，()1f x +为偶函数，()()11f x f x ∴+=-+， ()()2f x f x ∴+=-，又()f x 为R 上的奇函数，()()f x f x ∴-=-，()()2f x f x ∴+=-，()()()42f x f x f x ∴+=-+=，∴()f x 是周期为4的周期函数，∴()()()()22021450511log 111f f f =⨯+==+=，故选：C.4．（2021·天津市耀华中学高三模拟）已知函数()1y f x =+是定义在R 上的偶函数，且()f x 在(),1-∞上单调递减，()20f =，则()()10+<f x f x 的解集为（ ）A ．()()2,10,1--⋃B ．()()1,01,2-C ．()1,2-D ．()2,1-【答案】B【解析】因为函数()1y f x =+是偶函数，所以()f x 的图象关于直线1x =对称． 由()f x 在(),1-∞上单调递减，得()f x 在()1,+∞上单调递增，且()()020f f ==， 所以当0x <或2x >时，()0f x >，当02x <<时，()0f x <． 函数()f x 的图象如图所示，()()10+<f x f x 等价于()()0,10f x f x ⎧>⎪⎨+<⎪⎩或()()0,10,f x f x ⎧<⎪⎨+>⎪⎩ 即02012x x x ⎧⎨<+<⎩或或02,1012x x x <<⎧⎨++⎩或 解得10x -<<或12x <<，故选：B ．5．（2021·湖北襄阳五中高三模拟）已知A 、F 分别是椭圆C ：22221x y a b+=()0a b >>的下顶点和左焦点，过A 且倾斜角为60︒的直线l 分别交x 轴和椭圆C 于M ，N 两点，且N 点的纵坐标为35b ，若FMN 的周长为6，则FAN 的面积为_____.【解析】如图所示，由题意得，()0,A b -，(),0F c -，直线MN 的方程为y b =-， 把35y b =代入椭圆方程解得45x a =，∴4355N a b ⎛⎫ ⎪⎝⎭，，∴N 在直线MN 上，∴3455b a b =-，解得2b a =.又222a b c =+，∴222)b c =+，解得b =，令y b =-=0，则M ⎫⎪⎭，即(),0M c ，∴M 为椭圆的右焦点，∴2FM c =， 由椭圆的定义可知，2NF NM a +=， ∴FMN 的周长为6，∴226a c +=，∴2b a =，∴2a c =，∴1,2,===c a b∴()138255FANSFM b b c b ⎡⎤=⋅⋅--=⋅=⎢⎥⎣⎦.6．（2021·河北石家庄二中高三模拟）我设1F ，2F 是椭圆C ：2214x y +=的两个焦点，过1F ，2F 分别作直线1l ，2l ，且12l l //，若1l 与椭圆C 交于A ，B 两点，2l 与椭圆C 交于C ，D 两点（点A ，D 在x 轴上方），则四边形ABCD 面积的最大值为__________． 【答案】4【解析】当两平行直线没有斜率时，此时2221||1,122OABb AB Sa ===∴=⨯=当两平行直线有斜率时，设直线AB 的方程为(y k x =即0kx y -=，联立椭圆方程2214x y +=，消去y 得2222(14)1240k x x k +++-=，由弦长公式得2224(1)||1414kABk k+==++，又原点到直线AB的距离为d=所以222114(1)=||221414OABkS d ABk k+⨯=⨯=++所以4242222421212()12(14)1681OABk k k kSk k k++=⨯=+++，设2(0)k t t=>，所以2222121212(41)(21)(),()1681(1681)t t t tf t f tt t t t+-+-'=∴=++++，当12t<<时，()0f t'>，此时函数()f t单调递增，当12t>时，()0f t'<，此时函数()f t单调递减，所以max1()()12f t f==，所以OABS的最大值为1，因为1>，所以OABS∆的最大值为1，因为四边形ABCD的面积为||2AB d⨯，所以四边形ABCD的面积为4OABS,所以此时四边形ABCD的面积的最大值为4.7．（2021·河南郑州外国语学校）已知函数()2ln,0x m xf x mx-=＞.（1）当()'10f=时，讨论()f x的单调性；（2）若曲线()y f x=与直线y m=有交点，求证：m1≥.【解析】（1）因为()2ln lnx m x m xf x xx x-==-，所以()222ln ln'1,0mx m x x m x mxf x xx x⋅-+-=-=＞，则()221ln1'1011m mf m+-==⇒=，所以()22ln1',0x xf x xx+-=＞，令()2ln1,0g x x x x=+-＞，显然，()g x 在()0,∞+上单调递增， 又()10g =，所以当01x ＜＜时，()'0f x ＜，函数()f x 在()0,1上单调递减， 当1x ＞时，()'0f x ＞，函数()f x 在()1,+∞上单调递增； （2）证明：令()()h x f x m =-，当0m ＞时，曲线()y f x =与直线y m =有交点即函数()h x 在()0,∞+有零点， 由()0h x =得，21ln x xm x +=， 令()2ln ,0,x xF x x x +=＞ 所以直线1y m=与()F x 图像 有交点 则()()24112ln 'x x x x x F x x ⎛⎫+-+ ⎪⎝⎭= 32ln 1,0x x x x--+=＞， 令()2ln 1x x x ϕ=--+，显然()x ϕ在()0,∞+上单调递减，且()10ϕ=， 所以()F x 在()0,1上单调递增，在()1,+∞在上单调递减， 故()F x 在1x =处取最大值为()11F =，当0x →时，()F x →-∞，当x →+∞时，()0F x →， 要使直线1y m=与()F x 图像 有交点， 只需11m≤， 又因为0m ＞，所以m 1≥.8．（2021·安徽高三其他模拟）已知函数()()32413f x x a x ax =-++-. （1）若()f x 在()2,+∞上有极值，求a 的取值范围；（2）求证：当1a 2-<<时，过点()0,1P -只有一条直线与()f x 的图象相切. 【解析】（1）由题意得：()()()()2421212f x x a x a x x a '=-++-=---，由()0f x '=得：112x =，22a x =，()f x 在()2,+∞上有极值，22a∴>，解得：4a >，a ∴的取值范围为()4,+∞.（2）设过点()0,1P -的直线与()f x 的图象切于点()324,13t t a t at ⎛⎫-++- ⎪⎝⎭， 则切线斜率()()()32241134210t a t at k f t t a t a t -++-+==-++-'=-，整理可得：()3281103t a t -++=，若过点()0,1P -只有一条直线与()f x 的图象相切，则关于t 的方程()3281103t a t -++=有且仅有1个实根，设()()328113g t t a t =-++，则()()2821g t t a t '=-+， 由()0g t '=得：10t =，2104a t +=>， ∴当()1,0,4a t +⎛⎫∈-∞+∞ ⎪⎝⎭时，()0g t '>；当10,4a t +⎛⎫∈ ⎪⎝⎭时，()0g t '<；()g t ∴在(),0-∞，1,4a ∞+⎛⎫+ ⎪⎝⎭上单调递增，在10,4a +⎛⎫⎪⎝⎭上单调递减， ()01g =，()()333118111114341648a a a g a +++⎛⎫⎛⎫=⋅-+=-++ ⎪ ⎪⎝⎭⎝⎭， 12a -<<，013a ∴<+<，()3111048a ∴-++>，即104a g +⎛⎫> ⎪⎝⎭，∴当0t >时，()0g t >，()()885110333g a a -=--+=--<-<，又()g t 在(),0-∞上单调递增，()0g t ∴=在(),0-∞上有唯一的实数根()01,0t ∈-，即当1a 2-<<时，过点()0,1P -只有一条直线与()f x 的图象相切.9．（2021·浙江高三模拟）已知动直线l ：()210mx y m m R --+=∈恒过定点M ，且点M 在抛物线1C ：()220x py p =>上.（1）求点M 到抛物线1C 的准线的距离；（2）将曲线1C 沿y 轴向上平移1个单位长度得到曲线2C ，若点()00,P x y 在曲线2C 上，且在曲线1C 上存在A ，B ，C 三点，使得四边形PABC 为平行四边形，求平行四边形PABC 的面积S 的最小值.【解析】（1）将210mx y m --+=整理为()()210m x y ---=，由20,10,x y -=⎧⎨-=⎩得2,1,x y =⎧⎨=⎩，故()2,1M .将()2,1代入()220x py p =>，得2p =，所以抛物线1C 的方程为24x y =.所以抛物线1C 的准线方程为1y =-，所以点M 到抛物线1C 的准线的距离为2. （2）由（1）知，抛物线1C 的方程为214y x =，将曲线1C 沿y 轴向上平移1个单位长度得到曲线2C ，其方程为2114y x =+. 点()00,P x y 在曲线2C ：2114y x =+上，故20044x y -=-∴. 连接AC ，当直线AC 的斜率不存在时，AC x ⊥轴，与抛物线1C 只有一个交点，不符合题意，故舍去. 当直线AC 的斜率存在时，设直线AC 的方程为y kx b =+，()11,Ax y ，()22,C x y ，联立，得2,4,y kx b x y =+⎧⎨=⎩得2440x kx b --=，216160k b =+>△，则124x x k +=，124x x b =-，故线段AC 的中点()22,2D k k b +. 若四边形PABC 为平行四边形，则B ，P 关于点D 对称，所以()2004,42B k x k b y -+-.又点B 在抛物线1C 上，故()()22004442k x k b y -=+-，即()2000148kx b x y +=+ ∴. 点P 到直线AC的距离d =，124AC x x =-==，所以1122PAC S AC d =⋅⋅=⨯=△00kx b y +-，结合∴∴得，2004PACS x y =-△===012k x =时，PACS 取得最小值2. 因为2PACS S=，所以S10．（2021·山西高三二模（文））已知P 为抛物线C ：()220y px p =>上一动点，F 为C 的焦点，定点()3,1Q 在C 的内部，若PQ PF +的最小值为4. （1）求C 的方程；（2）不经过原点的直线l 与C 交于A ，B 两点(其中点A 在x 轴上方)，若以线段AB 为直径的圆经过点F ，且圆心在11直线1y =-上.证明：直线l 与C 在点A 处的切线垂直.【解析】（1）过点P 作C 的准线的垂线，垂足为N ，连接NQ ， 由抛物线的定义知PN PF =，则PQ PF PQ PN NQ +=+≥， 当N ，P ，Q 三点共线时，NQ 取得最小值， ∴342p +=，解得2p =，故抛物线C 的方程为24y x =. （2）证明：设直线l ：()0x my n n =+≠，且直线l 与抛物线C 交于()11,A x y ，()22,B x y ，则由24x my n y x=+⎧⎨=⎩，化简得2440y my n --=，且216160m n ∆=+>，即20m n +>， ∴121244y y m y y n+=⎧⎨⋅=-⎩，则可得21221242x x m n x x n ⎧+=+⎨⋅=⎩， ∴以AB 为直径的圆的圆心坐标为()22,2m n m +，∴圆心在直线1y =-上，∴21m =-，12m =-， 又∴以线段AB 为直径的圆经过点()1,0F ，∴0FA FB ⋅=，∴()()1212110x x y y --+=，∴()12121210x x x x y y -+++=，即()2242140n m n n -++-=，化简得260n n -=，可得0n =(舍去)或6n =， ∴直线l 的方程为162x y =-+，即2120x y +-=，且直线l 的斜率为12k =-， 由21624x y y x⎧=-+⎪⎨⎪=⎩得()4,4A ， ∴当0y >时，抛物线24y x =在x轴上方曲线的方程为y =∴'y =24y x =在()4,4A 处的切线的斜率为41'|2x k y ===切； ∴11(2)12k k ⋅=-⨯=-切，∴直线l 与抛物线C 在点A 处的切线垂直.。

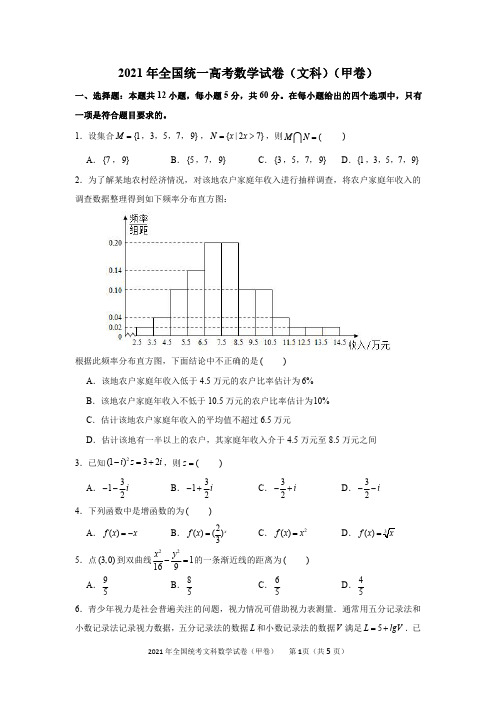
2021年全国统一高考数学试卷（文科）（甲卷）一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设集合{1M =，3，5，7，9}，{|27}N x x =>，则(M N = )A ．{7，9}B ．{5，7，9}C ．{3，5，7，9}D ．{1，3，5，7，9}2．为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如下频率分布直方图：根据此频率分布直方图，下面结论中不正确的是()A ．该地农户家庭年收入低于4.5万元的农户比率估计为6%B ．该地农户家庭年收入不低于10.5万元的农户比率估计为10%C ．估计该地农户家庭年收入的平均值不超过6.5万元D ．估计该地有一半以上的农户，其家庭年收入介于4.5万元至8.5万元之间3．已知2(1)32i z i -=+，则(z =)A ．312i--B ．312i-+C ．32i-+D ．32i--4．下列函数中是增函数的为()A ．()f x x=-B ．2()()3xf x =C ．2()f x x =D ．()f x =5．点(3,0)到双曲线221169x y -=的一条渐近线的距离为()A ．95B ．85C ．65D ．456．青少年视力是社会普遍关注的问题，视力情况可借助视力表测量．通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L 和小数记录法的数据V 满足5L lgV =+．已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据约为(10)(10 1.259)≈A ．1.5B ．1.2C ．0.8D ．0.67．在一个正方体中，过顶点A 的三条棱的中点分别为E ，F ，G ．该正方体截去三棱锥A EFG -后，所得多面体的三视图中，正视图如图所示，则相应的侧视图是()A ．B ．C ．D ．8．在ABC ∆中，已知120B =︒，19AC =，2AB =，则(BC =)A ．1B 2C 5D ．39．记n S 为等比数列{}n a 的前n 项和．若24S =，46S =，则6(S =)A ．7B ．8C ．9D ．1010．将3个1和2个0随机排成一行，则2个0不相邻的概率为()A ．0.3B ．0.5C ．0.6D ．0.811．若(0,)2πα∈，cos tan 22sin ααα=-，则tan (α=)A ．1515B ．55C ．53D ．15312．设()f x 是定义域为R 的奇函数，且(1)()f x f x +=-．若11(33f -=，则5()(3f =)A ．53-B ．13-C ．13D ．53二、填空题：本题共4小题，每小题5分，共20分。

2021年普通⾼等学校招⽣全国统⼀考试（甲卷）⽂科数学一､选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 设集合{}{}1,3,5,7,9,27M N x x ==>，则M N =I （）A.{}7,9 B.{}5,7,9 C.{}3,5,7,9 D.{}1,3,5,7,92. 为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如下频率分布直方图：根据此频率分布直方图，下面结论中不正确的是（）A.该地农户家庭年收入低于4.5万元的农户比率估计为6%B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%C.估计该地农户家庭年收入的平均值不超过6.5万元D.估计该地有一半以上的农户，其家庭年收入介于4.5万元至8.5万元之间3. 已知2(1)32i z i -=+，则z =（）A.312i --B.312i -+ C.32i -+ D.32i --4.下列函数中是增函数的为（）A.()f x x=- B.()23xf x æö=ç÷èøC.()2f x x= D.()f x =5. 点()3,0到双曲线221169x y -=的一条渐近线的距离为（）A.95B.85C.65D.456.青少年视力是社会普遍关注的问题，视力情况可借助视力表测量．通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L 和小数记录表的数据V 的满足5lg L V =+．已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据为（）（ 1.259»）A.1.5B.1.2C.0.8D.0.67. 在一个正方体中，过顶点A 的三条棱的中点分别为E ，F ，G ．该正方体截去三棱锥A EFG -后，所得多面体的三视图中，正视图如图所示，则相应的侧视图是（）A. B. C. D.8.在ABC V 中，已知120B =°，AC =，2AB =，则BC =（）A.1B.C.D.39.记n S 为等比数列{}n a 的前n 项和.若24S =，46S =，则6S =（）A. 7B. 8C. 9D. 1010.将3个1和2个0随机排成一行，则2个0不相邻的概率为（）A. 0.3B. 0.5C. 0.6D. 0.811.若cos 0,,tan 222sin p a a a a æöÎ=ç÷-èø，则tan a =（）A.15B.5C.3D.312. 设()f x 是定义域为R 的奇函数，且()()1f x f x +=-.若1133f æö-=ç÷èø，则53f æö=ç÷èø（）A.53-B.13-C.13D.53二､填空题：本题共4小题，每小题5分，共20分.13.若向量,a b r r满足3,5,1a a b a b =-=×=r r r r r ，则b =r _________.14. 已知一个圆锥的底面半径为6，其体积为30p 则该圆锥的侧面积为________.15. 已知函数()()2cos f x x w j =+的部分图像如图所示，则2f p æö=ç÷èø_______________.16.已知12,F F 为椭圆C ：221164x y+=的两个焦点，P ，Q 为C 上关于坐标原点对称的两点，且12PQ F F =，则四边形12PFQF 的面积为________．三､解答题：共70分.解答应写出交字说明､证明过程程或演算步骤，第17~21题为必考题，每个试题考生都必须作答.第22､23题为选考题，考生根据要求作答.(一)必考题：共60分.17. 甲、乙两台机床生产同种产品，产品按质量分为一级品和二级品，为了比较两台机床产品的质量，分别用两台机床各生产了200件产品，产品的质量情况统计如下表：一级品二级品合计甲机床15050200乙机床12080200合计270130400（1）甲机床、乙机床生产的产品中一级品的频率分别是多少?（2）能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异?附：22()()()()()n ad bc K a b c d a c b d -=++++()2P K k ³0.0500.0100.001k3.8416.63510.82818.记n S 为数列{}n a 的前n 项和，已知210,3n a a a >=，且数列是等差数列，证明：{}na 是等差数列.19. 已知直三棱柱111ABC A B C -中，侧面11AA B B 为正方形，2AB BC ==，E ，F 分别为AC 和1CC 的中点，11BF A B ^.（1）求三棱锥F EBC -的体积；（2）已知D 为棱11A B 上的点，证明：BF DE ^.20.设函数22()3ln 1f x a x ax x =+-+，其中0a >.（1）讨论()f x 的单调性；（2）若()y f x =的图象与x 轴没有公共点，求a 的取值范围.21.抛物线C 的顶点为坐标原点O ．焦点在x 轴上，直线l ：1x =交C 于P ，Q 两点，且OP OQ ^．已知点()2,0M ，且M e 与l 相切．（1）求C ，M e 的方程；（2）设123,,A A A 是C 上的三个点，直线12A A ，13A A 均与M e 相切．判断直线23A A 与M e 的位置关系，并说明理由．(二)选考题：共10分.请考生在第22､23题中任选一题作答.如果多做，则按所做的第一题计分.[选修4-4：坐标系与参数方程]22.在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为r q =．（1）将C 的极坐标方程化为直角坐标方程；（2）设点A 的直角坐标为()1,0，M 为C 上的动点，点P 满足AP =u u u ru u u r，写出Р的轨迹1C 的参数方程，并判断C 与1C 是否有公共点．[选修4-5：不等式选讲]23.已知函数()2,()2321f x x g x x x =-=+--．（1）画出()y f x =和()y g x =的图像；（2）若()()f x a g x +³，求a 的取值范围．答案及解析一､选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 设集合{}{}1,3,5,7,9,27M N x x ==>，则M N =I （）A.{}7,9 B.{}5,7,9 C.{}3,5,7,9 D.{}1,3,5,7,9【答案】B 【解析】【分析】求出集合N 后可求M N Ç.【详解】7,2N æö=+¥ç÷èø，故{}5,7,9M N Ç=，故选：B.2. 为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如下频率分布直方图：根据此频率分布直方图，下面结论中不正确的是（）A.该地农户家庭年收入低于4.5万元的农户比率估计为6%B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%C.估计该地农户家庭年收入的平均值不超过6.5万元D.估计该地有一半以上的农户，其家庭年收入介于4.5万元至8.5万元之间【答案】C 【解析】【分析】根据直方图的意义直接计算相应范围内的频率，即可判定ABD,以各组的中间值作为代表乘以相应的频率，然后求和即得到样本的平均数的估计值，也就是总体平均值的估计值，计算后即可判定C.【详解】因为频率直方图中的组距为1，所以各组的直方图的高度等于频率.样本频率直方图中的频率即可作为总体的相应比率的估计值.该地农户家庭年收入低于4.5万元的农户的比率估计值为0.020.040.066%+==,故A 正确；该地农户家庭年收入不低于10.5万元的农户比率估计值为0.040.0230.1010%+´==,故B 正确；该地农户家庭年收入介于4.5万元至8.5万元之间的比例估计值为0.100.140.2020.6464%50%++´==>,故D 正确；该地农户家庭年收入的平均值的估计值为30.0240.0450.1060.1470.2080.2090.10100.10110.04120.02130.02140.027.68´+´+´+´+´+´+´+´+´+´+´+´=(万元)，超过6.5万元，故C 错误.综上，给出结论中不正确的是C.故选：C.【点睛】本题考查利用样本频率直方图估计总体频率和平均值，属基础题，样本的频率可作为总体的频率的估计值，样本的平均值的估计值是各组的中间值乘以其相应频率然后求和所得值，可以作为总体的平均值的估计值.注意各组的频率等于´频率组距组距.3. 已知2(1)32i z i -=+，则z =（）A.312i --B.312i -+C.32i -+ D.32i --【答案】B 【解析】【分析】由已知得322iz i+=-，根据复数除法运算法则，即可求解.【详解】2(1)232i z iz i -=-=+，32(32)23312222i i i i z i i i i ++×-+====-+--×.故选：B.4.下列函数中是增函数的为（）A.()f x x =-B.()23xf x æö=ç÷èøC.()2f x x= D.()f x =【答案】D 【解析】【分析】根据基本初等函数的性质逐项判断后可得正确的选项.【详解】对于A ，()f x x =-为R 上的减函数，不合题意，舍.对于B ，()23xf x æö=ç÷èø为R 上的减函数，不合题意，舍.对于C ，()2f x x =在(),0-¥为减函数，不合题意，舍.对于D ，()f x =为R 上的增函数，符合题意，故选：D.5. 点()3,0到双曲线221169x y -=的一条渐近线的距离为（）A.95B.85C.65 D.45【答案】A 【解析】【分析】首先确定渐近线方程，然后利用点到直线距离公式求得点到一条渐近线的距离即可.【详解】由题意可知，双曲线的渐近线方程为：220169x y -=，即340±=x y ，结合对称性，不妨考虑点()3,0到直线340x y +=的距离：d =故选：A.6. 青少年视力是社会普遍关注的问题，视力情况可借助视力表测量．通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L 和小数记录表的数据V 的满足5lg L V =+．已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据为（）（ 1.259»）A. 1.5 B. 1.2C. 0.8D. 0.6【答案】C 【解析】【分析】根据,L V 关系，当 4.9L =时，求出lg V ，再用指数表示V ，即可求解.【详解】由5lg L V =+，当 4.9L =时，lg 0.1V =-，则10.11010100.8V --===».故选：C .7.在一个正方体中，过顶点A 的三条棱的中点分别为E ，F ，G ．该正方体截去三棱锥A EFG -后，所得多面体的三视图中，正视图如图所示，则相应的侧视图是（）A. B. C. D.【答案】D 【解析】【分析】根据题意及题目所给的正视图还原出几何体的直观图，结合直观图进行判断.【详解】由题意及正视图可得几何体的直观图，如图所示，所以其侧视图为故选：D8. 在ABC V 中，已知120B =°，AC =，2AB =，则BC =（）A.1B.C.3【答案】D 【解析】【分析】利用余弦定理得到关于BC 长度的方程，解方程即可求得边长.【详解】设,,AB c AC b BC a ===，结合余弦定理：2222cos b a c ac B =+-可得：21942cos120a a =+-´´o ，即：22150a a +-=，解得：3a =（5a =-舍去），故3BC =.故选：D.【点睛】利用余弦定理及其推论解三角形的类型：(1)已知三角形的三条边求三个角；(2)已知三角形的两边及其夹角求第三边及两角；(3)已知三角形的两边与其中一边的对角，解三角形．9. 记n S 为等比数列{}n a 的前n 项和.若24S =，46S =，则6S =（）A.7 B.8 C.9 D.10【答案】A 【解析】【分析】根据题目条件可得2S ，42S S -，64S S -成等比数列，从而求出641S S -=，进一步求出答案.【详解】∵n S 为等比数列{}n a 的前n 项和，∴2S ，42S S -，64S S -成等比数列∴24S =，42642S S -=-=∴641S S -=，∴641167S S =+=+=.故选：A.10. 将3个1和2个0随机排成一行，则2个0不相邻的概率为（）A. 0.3B. 0.5C. 0.6D. 0.8【答案】C 【解析】【分析】利用古典概型的概率公式可求概率.【详解】解：将3个1和2个0随机排成一行，可以是：00111,01011,01101,01110,10011,10101,10110,11001,11010,11100，共10种排法，其中2个0不相邻的排列方法为：01011,01101,01110,10101,10110,11010，共6种方法，故2个0不相邻的概率为6=0.610，故选：C.11.若cos 0,,tan 222sin p a a a a æöÎ=ç÷-èø，则tan a =（）A.15B.5C.3D.3【答案】A 【解析】【分析】由二倍角公式可得2sin 22sin cos tan 2cos 212sin a a a a a a ==-，再结合已知可求得1sin 4a =，利用同角三角函数的基本关系即可求解.【详解】cos tan 22sin aa a=-Q 2sin 22sin cos cos tan 2cos 212sin 2sin a a a aa a a a\===--，0,2p a æöÎç÷èøQ ，cos 0a \¹，22sin 112sin 2sin a a a \=--，解得1sin 4a =，cos 4a \==，sin tan cos 15a a a \==.故选：A.【点睛】关键点睛：本题考查三角函数的化简问题，解题的关键是利用二倍角公式化简求出sin a .12.设()f x 是定义域为R 的奇函数，且()()1f x f x +=-.若1133f æö-=ç÷èø，则53f æö=ç÷èø（）A.53-B.13-C.13D.53【答案】C 【解析】【分析】由题意利用函数的奇偶性和函数的递推关系即可求得53f æöç÷èø的值.【详解】由题意可得：522213333f f f f æöæöæöæö=+=-=-ç÷ç÷ç÷ç÷èøèøèøèø，而21111133333f f f f æöæöæöæö=-==--=-ç÷ç÷ç÷ç÷èøèøèøèø，故5133f æö=ç÷èø.故选：C.【点睛】关键点点睛：本题主要考查了函数的奇偶性和函数的递推关系式，灵活利用所给的条件进行转化是解决本题的关键.二､填空题：本题共4小题，每小题5分，共20分.13.若向量,a b r r满足3,5,1a a b a b =-=×=r r r r r ，则b =r _________.【答案】【解析】【分析】根据题目条件，利用a b -r r模的平方可以得出答案【详解】∵5a b -=r r∴222229225a b a b a b b -=+-×=+-=r r r r r r r∴b =r.故答案为：14.已知一个圆锥的底面半径为6，其体积为30p 则该圆锥的侧面积为________.【答案】39p 【解析】【分析】利用体积公式求出圆锥的高，进一步求出母线长，最终利用侧面积公式求出答案.【详解】∵216303V h p p =×=∴52h =∴132l ===∴136392S rl p p p ==´´=侧.故答案为：39p .15.已知函数()()2cos f x x w j =+的部分图像如图所示，则2f p æö=ç÷èø_______________.【答案】【解析】【分析】首先确定函数的解析式，然后求解2f p æöç÷èø的值即可.【详解】由题意可得：31332,,241234T T Tp p p pp w =-=\===，当1312x p =时，()131322,2126x k k k Z p w j j p j p p +=´+=\=-Î，令1k =可得：6pj =-，据此有：()52cos 2,2cos 22cos62266f x x f p p p p p æöæöæö=-=´-==ç÷ç÷ç÷èøèøèø.故答案为：.【点睛】已知f (x )＝Acos (ωx ＋φ)(A ＞0，ω＞0)的部分图象求其解析式时，A 比较容易看图得出，困难的是求待定系数ω和φ，常用如下两种方法：(1)由ω＝2Tp即可求出ω；确定φ时，若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标x 0，则令ωx 0＋φ＝0(或ωx 0＋φ＝π)，即可求出φ.(2)代入点的坐标，利用一些已知点(最高点、最低点或“零点”)坐标代入解析式，再结合图形解出ω和φ，若对A ，ω的符号或对φ的范围有要求，则可用诱导公式变换使其符合要求.16.已知12,F F 为椭圆C ：221164x y+=的两个焦点，P ，Q 为C 上关于坐标原点对称的两点，且12PQ F F =，则四边形12PFQF 的面积为________．【答案】8【解析】【分析】根据已知可得12PF PF ^，设12||,||PF m PF n ==，利用勾股定理结合8m n +=，求出mn ，四边形12PFQF 面积等于mn ，即可求解.【详解】因为,P Q 为C 上关于坐标原点对称的两点，且12||||PQ F F =，所以四边形12PFQF 为矩形，设12||,||PF m PF n ==，则228,48m n m n +=+=，所以22264()2482m n m mn n mn =+=++=+，8mn =，即四边形12PFQF 面积等于8.故答案为：8.三､解答题：共70分.解答应写出交字说明､证明过程程或演算步骤，第17~21题为必考题，每个试题考生都必须作答.第22､23题为选考题，考生根据要求作答.(一)必考题：共60分.17.甲、乙两台机床生产同种产品，产品按质量分为一级品和二级品，为了比较两台机床产品的质量，分别用两台机床各生产了200件产品，产品的质量情况统计如下表：一级品二级品 合计甲机床15050200乙机床12080200合计270130400（1）甲机床、乙机床生产的产品中一级品的频率分别是多少?（2）能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异?附：22()()()()()n ad bc K a b c d a c b d -=++++()2P K k ³0.0500.0100.001k 3.841 6.63510.828【答案】（1）75%；60%；（2）能.【解析】【分析】根据给出公式计算即可【详解】（1）甲机床生产的产品中的一级品的频率为15075%200=,乙机床生产的产品中的一级品的频率为12060%200=.（2）()22400150801205040010 6.63527013020020039K ´-´==>>´´´,故能有99%的把握认为甲机床的产品与乙机床的产品质量有差异.18.记n S 为数列{}n a 的前n 项和，已知210,3n a a a >=，且数列是等差数列，证明：{}na 是等差数列.【答案】证明见解析.【解析】【分析】先根据的公差d ，进一步写出的通项，从而求出{}na 的通项公式，最终得证.【详解】∵数列是等差数列，设公差为d =-==(n =+-=，()n *ÎN ∴12n S a n =，()n *ÎN ∴当2n ³时，()221111112n n n a S S a n a n a n a -=-=--=-当1n =时，11121=a a a ´-，满足112n a a n a =-，∴{}n a 的通项公式为112n a a n a =-，()n *ÎN ∴()()111111221=2n n a a a n a a n a a --=----éùëû∴{}n a 是等差数列.【点睛】在利用1n n n a S S -=-求通项公式时一定要讨论1n =的特殊情况.19. 已知直三棱柱111ABC A B C -中，侧面11AA B B 为正方形，2AB BC ==，E ，F 分别为AC 和1CC 的中点，11BF A B ^.（1）求三棱锥F EBC -的体积；（2）已知D 为棱11A B 上的点，证明：BF DE ^.【答案】(1)13；(2)证明见解析.【解析】【分析】(1)首先求得AC 的长度，然后利用体积公式可得三棱锥的体积；(2)将所给的几何体进行补形，从而把线线垂直的问题转化为证明线面垂直，然后再由线面垂直可得题中的结论.【详解】(1)如图所示，连结AF ，由题意可得：BF ===，由于AB ⊥BB 1，BC ⊥AB ，1BB BC B =I ，故AB ^平面11BCC B ，而BF Ì平面11BCC B ，故AB BF ^，从而有3AF ===，从而AC ===，则222,AB BC AC AB BC +=\^，ABC V 为等腰直角三角形，111221222BCE ABC S s æö==´´´=ç÷èø△△，11111333F EBC BCE V S CF -=´´=´´=△.(2)由(1)的结论可将几何体补形为一个棱长为2的正方体1111ABCM A B C M -，如图所示，取棱,AM BC 的中点,H G ，连结11,,A H HG GB ，正方形11BCC B 中，,G F 为中点，则1BF B G ^，又111111,BF A B A B B G B ^=I ，故BF ^平面11A B GH ，而DE Ì平面11A B GH ，从而BF ^DE .【点睛】求三棱锥的体积时要注意三棱锥的每个面都可以作为底面，例如三棱锥的三条侧棱两两垂直，我们就选择其中的一个侧面作为底面，另一条侧棱作为高来求体积．对于空间中垂直关系（线线、线面、面面）的证明经常进行等价转化.20. 设函数22()3ln 1f x a x ax x =+-+，其中0a >.（1）讨论()f x 的单调性；（2）若()y f x =的图象与x 轴没有公共点，求a 的取值范围.【答案】（1）()f x 的减区间为10,a æöç÷èø，增区间为1,+a æö¥ç÷èø；（2）1a e >.【解析】【分析】（1）求出函数的导数，讨论其符号后可得函数的单调性.（2）根据()10f >及（1）的单调性性可得()min 0f x >，从而可求a 的取值范围.【详解】（1）函数的定义域为()0,¥+，又()23(1)()ax ax f x x+-¢=，因为0,0a x >>，故230ax +>，当10x a <<时，()0f x ¢<；当1x a>时，()0f x ¢>；所以()f x 的减区间为10,a æöç÷èø，增区间为1,+a æö¥ç÷èø.（2）因为()2110f a a =++>且()y f x =的图与x 轴没有公共点，所以()y f x =的图象在x 轴的上方，由（1）中函数的单调性可得()min 1133ln 33ln f x f a a a æö==-=+ç÷èø，故33ln 0a +>即1a e>.【点睛】方法点睛：不等式的恒成立问题，往往可转化为函数的最值的符号来讨论，也可以参变分离后转化不含参数的函数的最值问题，转化中注意等价转化.21. 抛物线C 的顶点为坐标原点O ．焦点在x 轴上，直线l ：1x =交C 于P ，Q 两点，且OP OQ ^．已知点()2,0M ，且M e 与l 相切．（1）求C ，M e 的方程；（2）设123,,A A A 是C 上的三个点，直线12A A ，13A A 均与M e 相切．判断直线23A A 与M e 的位置关系，并说明理由．【答案】（1）抛物线2:C y x =，M e 方程为22(2)1x y -+=；（2）相切，理由见解析【解析】【分析】（1）根据已知抛物线与1x =相交，可得出抛物线开口向右，设出标准方程，再利用对称性设出,P Q 坐标，由OP OQ ^，即可求出p ；由圆M 与直线1x =相切，求出半径，即可得出结论；（2）先考虑12A A 斜率不存在，根据对称性，即可得出结论；若121323,,A A A A A A 斜率存在，由123,,A A A 三点在抛物线上，将直线121223,,A A A A A A 斜率分别用纵坐标表示，再由1212,A A A A 与圆M 相切，得出2323,y y y y +×与1y 的关系，最后求出M 点到直线23A A 的距离，即可得出结论.【详解】（1）依题意设抛物线200:2(0),(1,),(1,)C y px p P y Q y =>-，20,1120,21OP OQ OP OQ y p p ^\×=-=-=\=uu u r uu u r Q ，所以抛物线C 的方程为2y x =，(0,2),M M e 与1x =相切，所以半径为1，所以M e 的方程为22(2)1x y -+=；（2）设111222333(),(,),(,)A x y A x y A x y 若12A A 斜率不存在，则12A A 方程为1x =或3x =，若12A A 方程为1x =，根据对称性不妨设1(1,1)A ，则过1A 与圆M 相切的另一条直线方程为1y =，此时该直线与抛物线只有一个交点，即不存在3A ，不合题意；若12A A 方程为3x =，根据对称性不妨设12(3,A A则过1A 与圆M 相切的直线13A A为(3)3y x -=-，又1313313131,03A A y y k y x x y y -====\=-+，330,(0,0)x A =，此时直线1323,A A A A 关于x 轴对称，所以直线23A A 与圆M 相切；若直线121323,,A A A A A A 斜率均存在，则121323121323111,,A A A A A A k k k y y y y y y ===+++，所以直线12A A 方程为()11121y y x x y y -=-+，整理得1212()0x y y y y y -++=，同理直线13A A 的方程为1313()0x y y y y y -++=，直线23A A 的方程为2323()0x y y y y y -++=，12A A Q 与圆M相切，1=整理得22212121(1)230y y y y y -++-=，13A A 与圆M 相切，同理22213131(1)230y y y y y -++-=所以23,y y 为方程222111(1)230y y y y y -++-=的两根，2112323221123,11y y y y y y y y -+=-×=--，M 到直线23A A的距离为：2123|2|y -+=221==，所以直线23A A 与圆M 相切；综上若直线1213,A A A A 与圆M 相切，则直线23A A 与圆M 相切.【点睛】关键点点睛：（1）过抛物线上的两点直线斜率只需用其纵坐标（或横坐标）表示，将问题转化为只与纵坐标（或横坐标）有关；（2）要充分利用1213,A A A A 的对称性，抽象出2323,y y y y +×与1y 关系，把23,y y 的关系转化为用1y 表示.(二)选考题：共10分.请考生在第22､23题中任选一题作答.如果多做，则按所做的第一题计分.[选修4-4：坐标系与参数方程]22.在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为r q =．（1）将C 的极坐标方程化为直角坐标方程；（2）设点A 的直角坐标为()1,0，M 为C 上的动点，点P 满足AP =u u u ru u u r，写出Р的轨迹1C 的参数方程，并判断C 与1C 是否有公共点．【答案】（1）(222x y -+=；（2）P 的轨迹1C 的参数方程为32cos 2sin x y qqì=-+ïí=ïî（q 为参数），C 与1C 没有公共点.【解析】【分析】（1）将曲线C 的极坐标方程化为2cos r q =，将cos ,sin x y r q r q ==代入可得；（2）设(),P x y ，设)Mq q +，根据向量关系即可求得P 的轨迹1C 的参数方程，求出两圆圆心距，和半径之差比较可得.【详解】（1）由曲线C 的极坐标方程r q =可得2cos r q =，将cos ,sin x y r q r q ==代入可得22x y +=，即(222x y -+=，即曲线C 的直角坐标方程为(222x y +=；（2）设(),P x y ，设)Mq qQAP =u u u r u u u r，())()1,22cos x y q q q q \-=+-=+，则122cos 2sin x y q q ì-=+ïí=ïî，即32cos 2sin x y q q ì=+ïí=ïî，故P 的轨迹1C 的参数方程为32cos 2sin x y qqì=+ïí=ïî（q 为参数）Q曲线C 的圆心为)，曲线1C 的圆心为()3-，半径为2，则圆心距为3-，32-<-Q ，\两圆内含，故曲线C 与1C 没有公共点.【点睛】关键点睛：本题考查参数方程的求解，解题的关键是设出M 的参数坐标，利用向量关系求解.[选修4-5：不等式选讲]23.已知函数()2,()2321f x x g x x x =-=+--．（1）画出()y f x =和()y g x =的图像；（2）若()()f x a g x +³，求a 的取值范围．【答案】（1）图像见解析；（2）112a ³【解析】【分析】（1）分段去绝对值即可画出图像；（2）根据函数图像数形结和可得需将()y f x =向左平移可满足同角，求得()y f x a =+过1,42A æöç÷èø时a 的值可求.【详解】（1）可得2,2()22,2x x f x x x x -<ì=-=í-³î，画出图像如下：34,231()232142,2214,2x g x x x x x x ì-<-ïïï=+--=+-£<íïï³ïî，画出函数图像如下：（2）()|2|f x a x a +=+-，如图，在同一个坐标系里画出()(),f x g x 图像，()y f x a =+是()y f x =平移了a 个单位得到，则要使()()f x a g x +³，需将()y f x =向左平移，即0a >，当()y f x a =+过1,42A æöç÷èø时，1|2|42a +-=，解得112a =或52-（舍去），则数形结合可得需至少将()y f x =向左平移112个单位，112a \³.【点睛】关键点睛：本题考查绝对值不等式的恒成立问题，解题的关键是根据函数图像数形结合求解.。

2021年全国统一高考数学(文科)试卷(甲卷)(附答案详解)2021年全国统一高考数学（文科）试卷（甲卷）一、单选题（本大题共12小题，共60.0分）1.设集合M={1,3，5，7}，M={M|2M>7}，则M∩M=()A。

{7,9}B。

{5,7，9}C。

{3,5，7，9}D。

{1,3，5，7，9}2.为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如下频率分布直方图：根据此频率分布直方图，下面结论中不正确的是()A。

该地农户家庭年收入低于4.5万元的农户比率估计为6%B。

该地农户家庭年收入不低于10.5万元的农户比率估计为10%C。

估计该地农户家庭年收入的平均值不超过6.5万元D。

估计该地有一半以上的农户，其家庭年收入介于4.5万元至8.5万元之间3.已知(1−M)2M=3+2M，则M=()A。

−1−2M/3B。

−1+2M/3C。

−2+M/3D。

−2−M/34.下列函数中是增函数的为()A。

M(M)=−MB。

M(M)=(3M)/M^2C。

M(M)=M^2−16/9M^2D。

M(M)=3√M5.点(3,0)到双曲线M^2/9−M^2/4=1的一条渐近线的距离为() A。

5/6B。

5/8C。

5/4D。

5/26.青少年视力是社会普遍关注的问题，视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L和小数记录法的数据V满足M=5+MMM.已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据约为()A。

1.5B。

1.2C。

0.8D。

0.67.在一个正方体中，过顶点A的三条棱的中点分别为F，M.该正方体截去三棱锥M−MMM后，为E，所得多面体的三视图中，正视图如图所示，则相应的侧视图是()A.B.C.D.8.在△MMM中，已知M=120°，MM=√19，则MM=()A。

1B。

√2C。

√5D。

39.记MM为等比数列{MM}的前n项和.若M2=4，M4=6，则M6=()A。

D.shouIdn'八年级上册一阶段测试卷一选择填空(15分)()16. you go to the party if you are ill. A. canB. mustC. shou I d)17. Taki ng a wa I k every day may he I p you keep i n. A. healthy B. heaI th C. heaIthiIy D. unheaI thy)18. I have a toothache. I shouId see a. A. doctor B. dent i st C. teacher D. fr i end)!9. WouId you Iike to go for a waIk with us?, but I'm busy. A. No, I can' t B. Yes, I wi I I C. I' d I ove to D. I like )20. You hard Iy know him , ?A. are youB. aren't youC. do youD. don't you)21.——do you surfthe Internet ?--- Once a week.A. HowB. How o I dC. How oftenD. How many )22.Tom just f i n i shed h i s Ietter to hi sfr i end.A. writingB. to wr i teC. wroteD, wr i te)23. The IittIe baby has two __________A. toothB. toothsC. toothesD.teeth )24. She canboth French and English .A. sayB. tel IC. talkspeak)25. It' s easy for Yao M i ng _________ basketbaI I.A. to p I ayB. playingC. p I ayD. p I ays)26. I have to te I I you.A. anyth i ng exc i t i ngB. exc i t i ng someth i ngC. exciting anythingD. something exciting)27. -I'm going to Tibet next Monday.A. I know .B. That sounds exciting .C. I 1m sorry to hear that . D. Thank you . )28.My motheri s 38 years o1d short cur 1y hair,and she ______ good-1ook i ng.A. with, isB. has, isC. with, hasD. i s,)29. --Can you p 1 ay ____ gu i tar?一Yes, and1 can p1 ay _____ footba11, too.A. the, theB. /, theC. the, /D. a, the)30. A1 though he i s very o1d, _________ h e works very hard. A. and Bbut C. / D. so 二.完形填空(10分)One day, a sma I I boy was walking 31 a street i n London. H i s name was Tom.It was a cold winter day in 1900. 32 he couId not have breakfast or Iunch . He didn't have any money. His father died (死了) when he was young. His mother was often ill, so shecouId not 33 Tom and his brother Mike. Both of them had to work to he I p the i r mother . He was sma I I but h i s dream (梦想)was very 34 .His wi sh was to be a famous actor. He worked very hard to s ing and dance 35 . One day , a man came to him and asked, “ 36 in my f iIm ? ” "Cer tainly, " he answered. And he did h i s 37 i n it . Many peop I e sa i d , “We have never seen such an 38 film. " Th i rty years 59 , th i s boy was among 40 famous peop I e i n the wor I d . He made manyi nterest i ng films , and 1ots of peop1e admi red （敬仰）him。

2021年普通高等学校招生全国统一考试数学试卷（文科）（全国甲卷）一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

（共12题；共60分）1.设集合，则（）A. B.C. D.2.为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如下频率分布直方图：根据此频率分布直方图，下面结论中不正确的是（）A.该地农户家庭年收入低于4.5万元的农户比率估计为6%B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%C.估计该地农户家庭年收入的平均值不超过6.5万元D.估计该地有一半以上的农户，其家庭年收入介于4.5万元至8.5万元之间3.已知，则z＝（）A.－1－iB.－1＋iC.－＋iD.－－i4.下列函数中是增函数的为（）A. B. C. D.5.点到双曲线的一条渐近线的距离为（）A. B. C. D.6.青少年视力是社会普遍关注的问题，视力情况可借助视力表测量，通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L和小数记数法的数据V满足L＝5＋lgV。

已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据约为（）（≈1.259）A.1.5B.1.2C.0.8D.0.67.在一个正方体中，过顶点A的三条棱的中点分别为E，F，G.该正方体截去三棱锥A－EFG后，所得多面体的三视图中，正视图如下图所示，则相应的侧视图是（）A. B.C. D.8.在中，已知，则（）A.1B.C.D.39.记为等比数列的前项和．若，则（）A.7B.8C.9D.1010.将3个1和2个0随机排成一行，则2个0不相邻的概率为（）A.0.3B.0.5C.0.6D.0.811.若，，则（）A. B. C. D.12.设f（x）是定义域为R的奇函数，且f（1＋x）＝f（－x）．若（）A. B. C. D.二、填空题：本题共4小题，每小题5分，共20分。

2021年普通高等学校招生全国统一考试（全国甲卷）文科数学一、选择题1.设集合{1,3,5,7,9}M =，{|27}N x x =>，则M N ⋂=（）A.{7,9}B.{5,7,9}C.{3,5,7,9}D.{1,3,5,7,9}答案：B 解析：依题意可知{| 3.5}N x x =>，所以{5,7,9}M N ⋂=.2.为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如下频率分布直方图：根据此频率分布直方图，下面结论不正确的是（）A.该地农户家庭年收入低于4.5万元的农户比率估计为6%B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%C.估计该地农户家庭年收入的平均值不超过6.5万元D.估计该地有一半以上的农户，其家庭年收入介于4.5万元至8.5万元之间答案：C 解析：A.低于4.5万元的比率估计为0.0210.0410.066%⨯+⨯==，正确.B.不低于10.5万元的比率估计为(0.040.023)10.110%+⨯⨯==，正确.C.平均值为(30.0240.0450.160.1470.280.290.1100.1⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+110.04120.02130.02140.02)17.68⨯+⨯+⨯+⨯⨯=万元，不正确.D.4.5万到8.5万的比率为0.110.1410.210.210.64⨯+⨯+⨯+⨯=，正确.3.已知2(1)32i z i -=+，则z =（）A.312i --B.312i-+C.32i-+D.32i--答案：B 解析：232322331(1)222i i i z i i ++-+====-+--.4.下列函数中是增函数的是（）A.()f x x =-B.2()(3xf x =C.2()f x x =D.()f x =答案：D 解析：∵()f x x =-，2()(3xf x =，在R 上单调递减，2()f x x =在(,0)-∞上单调递减，故A，B，C 错误；()f x =在R 上单调递增，故D 正确.5.点(3,0)到双曲线221169x y -=的一条渐近线的距离为（）A.95B.85C.65D.45答案：A 解析：双曲线221169x y -=的渐近线为34y x =±，则点(3,0)到双曲线221169x y -=的一条渐近线的95=.6.青少年视力是社会普遍关注的问题，视力情况可借助视力表测量，通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L 和小数记录法的数据V 满足5lg L V =+.已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据约为（ 1.259≈）（）A.1.5B.1.2C.0.8D.0.6答案：C 解析：代入5lg L V =+，知lg 4.950.1V =-=-，故0.1100.8V -==≈.7.在一个正方体中，过顶点A 的三条棱的中点分别为E ，F ，G ，该正方体截去三棱锥A EFG -后，所得多面体的三视图中，正视图如图所示，则相应的侧视图是（）A.B.C.D.答案：D解析：由题可得直观图，如下图.故选D.8.在ABC ∆中，已知120B =︒，19AC =2AB =，则BC =（）A.125D.3答案：D解析：由余弦定理可得22222cos 2150AC AB BC AB BC ABC BC BC =+-⋅∠⇒+-=，解得3BC =.9.记n S 为等比数列{}n a 的前n 项和.若24S =，46S =，则6S =（）A.7B.8C.9D.10答案：A 解析：由等比数列的性质可知：24264,,S S S S S --成等比数列，即64,2,6S -成等比数列，所以661S -=，即67S =，故选A.10.将3个1和2个0随机排成一行，则2个0不相邻的概率为（）A.0.3B.0.5C.0.6D.0.8答案：C解析：求出所有的排列数，先将3个1排成一排，有4个空位，当每个空位排一个0，即从4个空位中选2个，有6种排法，此时2个0不相邻；当两个0相邻时，即从4个空位中选出一个来排两个0，有4种选法，从而总的排法数有10个，再根据古典概型概率公式可得概率60.610=，故选C.11.若(0,2πα∈，cos tan 22sin ααα=-，则tan α=（） A.1515B.5 C.53 D.153答案：A解析：cos tan 22sin ααα=-.2222tan 2sin cos cos tan 21tan cos sin 2sin ααααααααα===---∴222sin (2sin )cossin αααα-=-∴22224sin 2sin cos sin 12sin ααααα-=-=-∴1sin 4α=.又∵(0,2πα∈.如图，tan 15α==.12.设()f x 是定义域为R 的奇函数，且(1)()f x f x +=-.若11(33f -=，则5(3f =（）A.53-B.13-C.13D.53答案：C解析：∵()f x 是定义在R 上的奇函数，(1)()()f x f x f x +=-=-∴(1)()f x f x +=-，∴(2)(1)()f x f x f x +=-+=∴()f x 周期为2的周期函数.∴5511((2)(3333f f f =-=-=.二、填空题13.若向量,a b 满足||3a = ，||5a b -= ，1a b ⋅= ，则||b =.答案：解析：||5a b -= ，∴22225a ab b -+= ，∴22||2||25a ab b -+= ，∴292||25b -+= ，∴2||18b = ，∴||b =.14.已知一个圆锥的底面半径为6，其体积为30π，则该圆锥的侧面积为.答案：39π解析：圆锥底面半径6r =，体积21303V r h ππ==，则圆锥的高52h =，则母线长132l =，则圆锥的侧面积12392S rl ππ=⨯=.15.已知函数()2cos()f x x ωϕ=+的部分图像如图所示，则(2f π=.答案：解析：由图可知31332241234T T πππππωω=-=⇒==⇒=，由131313()22cos()2212666f ππππϕϕπϕ=⇒+=⇒+=⇒=-，所以(2cos(2226f πππ=⨯-=.16.已知1F ，2F 为椭圆22:1164x y C +=的两个焦点，P ，Q 为C 上关于坐标原点对称的两点，且12||||PQ F F =，则四边形12PFQF 的面积为.答案：解析：答案：8解析：如图，由12||||PQ F F =及椭圆对称性可知，四边形12PF QF 为矩形.设1||PF m =，2||PF n =，则222128||48m n m n F F +=⎧⎪⎨+==⎪⎩①②，22-①②得216mn =.所以，四边形12PF QF 面积为8mn =.三、解答题17.甲、乙两台机床生产同种产品，产品按质量分为一级品和二级品，为了比较两台机床产品的质量，分別用两台机床各生产了200件产品，产品的质量情况统计如下表：（1）甲机床、乙机床生产的产品中一级品的频率分别是多少？（2）能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异？附：22()()()()()n ad bcKa b c d a c b d-=++++，答案：见解析解析：（1）由表格数据得：甲机床生产的产品中一级品的频率为1503= 2004；乙机床生产的产品中一级品的频率为1203 2005=；（2）由题意222()400(1508012050)()()()()20020027030n ad bcka b c d a c b d-⨯⨯-⨯==++++⨯⨯⨯10.256 6.635≈>.所以有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异.18.记n S 为数列{}n a 的前n 项和，已知0n a >，213a a =，且数列是等差数列，证明：{}n a 是等差数列.答案：见解析解析：∵为等差数列，设公差为d .∴d =d =.d ==(1)n d nd =-=.∴22n S n d =，∴222221(1)(21)n n n a S S n d n d n d -=-=--=-(2)n ≥，即222n a d n d =⋅-(2)n ≥，又211a S d ==同样满足通项公式，所以{}n a 是等差数列.19．已知直三棱柱 th − 1t 1h 1中，侧面 1t 1t 为正方形．t ＝th ＝2， ， 分别为 h 和hh 1的中点，t ⊥ 1t 1．(1)求三棱锥F －EBC 的体积；(2)已知 为棱 1t 1上的点，证明：t ⊥ ．答案：见解析；解析；（1）11BF A B ⊥，则2229BF AB AF BF AB ⊥⇒=+=.又22228AF FC AC AC =+⇒=则AB BC ⊥.AC =1111122122323F EBC F ABC V V --==⨯⨯⨯⨯⨯=.（2）连1A E ，取BC 中点M 连1B M ，EM ，由EM 为AC ，BC 的中点，则//EM AB ，又11//AB A B ，11//A B EM ，则11A B ME 共面，故DE ⊂面11A B ME .又在侧面11BCC B 中1FCB MBB ∆≅∆，则1BF MB ⊥又1111111111111,BF A B MB A B B BF A B ME MB A B A B ME ⊥⎫⎪=⇒⊥⎬⎪⊂⎭ 面面，则BF DE ⊥.20.设函数2()3ln 1f x a x ax x 2=+-+，其中0a >.（1）讨论()f x 的单调性；（2）若()y f x =的图象与x 轴没有公共点，求a 的取值范围.答案：见解析解析：（1）222323(23)(1)()2a x ax ax ax f x a x a x x x +-+-'=+-==∵0a >，0x >，∴230ax +>，∴当1(0,)x a ∈时()0f x '<函数单调递减，当1(,)x a ∈+∞时，()0f x '>，函数单调递增.∴()f x 在1(0,)a 上递减，在1(,)a +∞上递增，（2）当0x →时()0f x >，结合函数单调性可知若()f x 与x 无交点时min ()0f x >即221111()3ln 10f a a a a a a=⨯+⨯-+>.化简可得1ln 1a <即11e a a e <⇒<.所以参数a 的取值范围为1(,)e+∞21.抛物线C 的顶点为坐标原点O ，焦点在x 轴上，直线:1l x =交C 于P ，Q 两点，且OP OQ ⊥，已知点(2,0)M ，且M 与l 相切.（1）求C ，M 的方程；（2）设1A ，2A ，3A 是C 上的三个点，直线12A A ，13A A 均与M 相切，判断直线23A A 与M 的位置关系，并说明理由.答案：见解析解析：（1）2:C y x =，22:(2)1M x y -+=.（2）设21(,)A a a ，22(,)A b b ，23(,)A c c .1221:()()0A A l y a x a x a b y ab a b -=-⇒-++=+，所以1d r =⇒=①.1321:()()0A B l y a x a x a c y ac a c -=-⇒-++=，所以所以b ，c 是方程2221(1)230a x ax a =⇒-+-+=的两根.又23:()0A A l x b c y bc -++=，所以2223|2|11a a d -+=.所以d r =，即直线23A A 与M 相切.22.在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρθ=.（1）将C 的极坐标方程化为直角坐标方程；（2）设点A 的直角坐标为(1,0)，M 为C 上的动点，点P 满足AP = ，写出P 的轨迹1C 的参数方程，并判断C 与1C 是否有公共点.答案：见解析解析：（（2）设(,)P x y ，00(,)M x y ，由22222(1,)(1,0)(1,)22222AP OM AP OA x y x y =⇒=+=-+=-+ .又M 在C 上，所以2222221))2(3)422x y x y -++=⇒++=.则1C 为(30)为圆心，半径为2的圆，所以112C C r r <-所以，两圆为内含关系，所以，圆C 与圆1C 无公共点.23.已知函数()|2|f x x =-，()|23||21|g x x x =+--.（1）画出()y f x =和()y g x =的图象；（2）若()()f x a g x +≥，求a 的取值范围.答案：见解析；解析：（1）2,2()2,2x x f x x x -≥⎧=⎨-<⎩；34,231()42,2214,2x g x x x x ⎧-≤-⎪⎪⎪=+-<<⎨⎪⎪≥⎪⎩（2）当0a ≤时，恒不满足，此时(2)0(2)4f a a g a -+=<-=；当0a >时，()()f x a g x +≥恒成立，必有11311()()||42222f a g a a +≥⇔-≥⇒≥.当112a ≥时，3(,)2x ∈-∞时，()0g x ≤，()0f x ≥，所以()()f x g x ≥.31[,]22x ∈-时，()42g x x =+，()2f x x a =+-，令()()()34F x f x g x x a =-=-+-，所以111()()022F x F a ≥=-≥.1(,)2x ∈+∞时，()2f x x a =+-，()4g x =.()()()6F x f x g x x a =-=+-。

试卷主标题姓名：__________ 班级：__________考号：__________一、未分类（共23题）1、设集合 M={1 , 3,5,7,9}. N={x|2x >7} ，则M∩N=A.{7,9}B.{5,7,9)C.{3,5,7,9}D.{1,3,5,7,9}2、为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如下频率分布直方图 :根据此频率分布直方图，下面结论中不正确的是A. 该地农户家庭年收入低于 4.5 万元的农户比率估计为6%B. 该地农户家庭年收入不低于10.5 万元的农户比率估计为10%C. 估计该地农户家庭年收入的平均值不超过 6.5 万元D. 估计该地有一半以上的农户，其家庭年收入介于 4.5 万元至8.5 万元之间3、已知 (1-i) 2 z =3+2i ，则z =A. -1- iB. -1+ iC. - +iD. - -i4、下列函数中是增函数的为A.f(x)= - xB.f(x)=C.f(x)= x 2D.f(x)=5、点 (3,0) 到双曲线=1 的一条渐近线的距离为A. B. C. D.6、青少年视力是社会普遍关注的问题，视力情况可借助视力表测量。

通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L 和小数记录法的数据V 满足 L=5+lgV 。

已知某同学视力的五分记录法的数据为 4.9 ，则其视力的小数记录法的数据约为A. 1.5B. 1.2C. 0.8D. 0.67、在一个正方体中，过顶点A 的三条棱的中点分别为E, F, G ，该正方体截去三棱锥A-EFG 后，所得多面体的三视图中，正视图如右图所示，则相应的侧视图是A. B.C. D.8、在∆ABC 中，已知则A. 1B.C.D. 39、记为等比数列的前n 项和。

若，则A. 7B. 8C. 9D. 1010、将 3 个 1 和 2 个0 随机排成一行，则 2 个0 不相邻的概率为A. 0.3B. 0.5C. 0.6D. 0.811、若∈ (0, ), = , 则=A. B. C. D.12、设 f(x) 是定义域为R 的奇函数，且f(1+x)=f(-x). 若f(- )= , 则f( )=A.-B.-C.D.13、若向量 a,b 满足 |a| =3, |a-b| =5,a·b=1, 则 |b| =________.14、已知一个圆锥的底面半径为 6 ，其体积为30π ，则该圆锥的侧面积为________.15、已知函数 f(x)=2 的部分图像如图所示，则 f( )=____________.16、已知 F1 ,F2为椭圆 C: 的两个焦点， P ，Q 为 C 上关于坐标原点对称的两点，且 |PQ| = |F1 F2| ，则四边形 P F1Q F2的面积为 _________.17、甲、乙两台机床生产同种产品产品按质量分为一级品和二级品，为了比较两台机床产品的质量，分别用两台机床各生产了 200 件产品产品的质量情况统计如下表:一级品二级品合计甲机床150 50 200乙机床120 80 200合计270 130 400(1) 甲机床、乙机床生产的产品中一级品的频率分别是多少?(2) 能否有99% 的把握为机品质量与乙机床的产品质量有差异?附 : ,0.0100.00118、 记 S n , 为数列 {a n } 的前 n 项和，已知 a n ,>0 ， a 3 =3a 1 , ，且数列 { } 是等差数列，证明 : {a n } 是等差数列 .19、 已知直 三棱柱 ABC- A 1 B 1 C 1 中 , 侧面 ,A A 1 B 1 B 为正方形 ,AB=BC=2,E,F 分别为 AC 和 C C 1 的中点， BF ⊥ A 1 B 1 ，(1) 求三棱锥 F-EBC 的体积 :(2) 已知 D 为棱 A 1 B 1 上的点，证明 : BF ⊥ DE. 20、 设函数 f (x)= a 2 x 2 +ax-3lhx+1 ，其中 a>0 。