2019年江苏省高三上学期期末数学试题分类：数列、存在性问题

江苏 13 大 2019年高三上学期年终数学试题分类汇编-- 数学概括法与二项式定理数学概括法与二项式定理1、〔常州市2018 届高三期末〕空间内有n 个平面，设这n个平面最多将空间分红a n个部分.〔1〕求a1, a2 , a3 , a4；〔2〕写出a n对于n的表达式并用数学概括法证明 .解：〔 1〕a12, a24, a38,a415；〔2〕1 (n3. 证明以下：a n5n6)6当n 1 时明显建立，设n k(k1,k N) 时结论建立，即a k 1( k35k，66)那么当n k 1 时，再添上第k 1 个平面，由于它和前k 个平面都订交，所以可得k条互不平行且不共点的交线，且此中任 3 条直线不共点，这k 条交线可以把第k 1 个平面划最多分红1 [( k1)2(k1)2)]个部分，每个部分把它所在的2原有空间地区区分红两个地区.所以，空间地区的总数增添了1[( k1)2(k1)2)]个，2ak 1a k 121 )13k (12k[ (1 )(1 ) 2 ) [ (k 1 ) k ( 2 k) ] 5 k 6 )2621[( k 1)3，5( k1)6)]6即当n k1时，结论也建立 .综上，对n N，a n 135n6). (n62、〔南京市、 城市 2018 届高三期末〕f ( x) (2x) n , 此中 nN * 、(1) 假 睁开式中含 x 3 的系数 14, 求 n 的 ；(2) 当 x3 , 求 ： f ( x) 必可表示成ss 1( s N * ) 的形式 .r， 故 x 3 的 系 数 C n 6 2n 6解 :(1)因T r 1C 8r 28 r x 2 , 因 此 r614，解得n7⋯⋯⋯ 5 分(2)由二式 定理可知, (23)nC 02n3 0 C12n 1 3 1C22n 23 2C n 2n3 ,nn nn(2 3) n x 3yx 2 3y 2，而假 有 (23) na b ， a, b N ，那么 (2 3) nab , a,b N ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 7 分∵ ( a b ) ( ab) (23)n(23) n 1 ，∴令 a s, s N ，那么必有 bs 1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9 分∴ (23) n 必可表示成ss 1 的形式，此中 sN ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 10 分注：用数学 法 明的， 明正确的也 相 的分数、3、〔南通市 2018 届高三期末〕 a n 1(n N ) 、数列 { a } 足： a 12a2,a n 1 1na *〔 1〕假a1 ，求数列 {n }的通 公式；a n N ， a 是 4 的倍数、〔 2〕假 a3 ， 明：*n解： (1) 当 a1，a 14,a n 1( 1)a n11、令b n a n1，那么b 15,b n1(1) n 、b因b 15 奇数， b n 也是奇数且只好1 ，所以，5, n 1, 即a n4, n 1, ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分b n1, n2,0,n 2.(2) 当 a 3 ，a 1 4, a n 13an11、⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分下边利用数学 法来 明：n是 4 的倍数、a当 n k (kN * ) ，命 建立，那么存在t N* ，使得 a k 4t ，a k 13ak1134t 1127 (41)4( t 1)1 27 (4 m1) 1 4(27m7) ，此中，4( t 1)C 14 4 t 5( 1) rr4 4 t 4 r4 t 3，4m 44( t 1)C4( t 1)C4( t 1)4m Z，当 n k 1 ，命 建立、10 分由数学 法原理知命 nN * 建立、⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4、〔徐州、淮安、宿迁市 2018 届高三期末〕数列{a n }足1 21na n 1(n N *且a 1 3.a n 12a n),2（1） 算a 2 , a 3 , a 4 的 ，由此猜想数列{a n } 的通 公式，并 出 明；（2）求 ：当 n2，a n n4n n .明：⑴a 2 4 ，a 35，a 46 ，猜想：ann + 2(n N *) 、⋯⋯⋯⋯⋯⋯⋯⋯2 分①当 n1 ， a 1 3 ， 建立；②假 当 n k (k ≥ 1,k N *) ， 建立，即a k k + 2，那么当 nk +1，1 2 1 1 21，a k 1a kka k1= (k + 2)k (k +2)+1= k+3=( k+1)+2222 2即当 n k + 1 ， 也建立，由①②得，数列{ a n } 的通 公式 a n n + 2(n N *)、5分⑵原不等式等价于2 ) n≥ 4 、(1+n明： 然，当n 2 ，等号建立；当 n2 ，2 n1 222 2n 2n1 222 232 3(1)C n C nn C n ( )C n ( )≥ C nC nC n ( )C n ( )nnn nnn> C nC 1n 2C n 2 (2)25 24 ，nnn上所述，当n ≥ 2 ， a n n ≥ 4n n 、⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10 分5、〔无 市 2018届高三期末〕函数f 〔x 〕 = 1 x 2+1nx 、2〔Ⅰ〕求函数 f 〔 x 〕在区 [1 ， e] 上的最大 、最小 ；〔Ⅱ〕g 〔 x 〕 =f 〔 x 〕，求 ： [ g( x)]ng (x n ) 2n 2(n N ) 、6、〔 州市2018 届高三期末〕数列{ a n } 是等差数列，且 a 1, a 2 ,a 3 是(11 m 睁开式的前x)2三 的系数 .〔Ⅰ〕求1 x)m 睁开式的中 ；(12〔Ⅱ〕当 n2 ， 比1 1 1 1 与1的大小.a nan 1an 2a n 23解：〔 Ⅰ〕1 x) m( 1 x) C( 1x)2依 意，，，(1 1 C 1 2 a 1 1 a1m am( m 1)2 m2 m 22238由2a 2 a 1 a 3 可得 m1〔舍去〕，或 m8 ⋯⋯⋯⋯⋯⋯⋯ 2 分所以睁开式的中 是第五 ：(1x)4；⋯⋯⋯⋯⋯⋯⋯ 4 分(11 x)mT C 4 35 x 425 8 28〔Ⅱ〕由〔Ⅰ〕知，a n 3n 2,当 n2 ，111 1 1 1 1 11169 1a nan 1a n2a n 2a 2 a 3 a 447 10 1403当 n3 ，1 1111 111a nan 1an 2a n 2a 3 a 4a 5a 911111111 ( 111) (11 1 ) 7 10 13 16 19 22 257 1013161922 25 1 ( 111) (1 1 1 ) 1 3 3 1 3 1 1 8 16 16 16 323232 8 1632 8 16163猜 ：当 n2 ， 11 111 ⋯⋯⋯⋯⋯⋯⋯ 6 分a nan 1an 2a n 23以下用数学 法加以 明：① n 3 ， 建立，② 当 nk ，1111 1 ，a kak 1ak 2a k 23那么 n k1 ，11 1 1a (k1)a (k1) 1a ( k 1) 2a(k1)21 1111111 1 ()(a k 2 2a(k 1) 2)a kak 1)a(k 1) 1a(k 1) 2a k 2a k 2 1a k1 (1111 ) 1(2k 1)123 a k 21 a k 22a(k 1)2a k3 3(k 1) 2 3k 21 (2k 1)(3k 2) [3( k 1)2 2] 13k 2 7k 3 3 [3(k 1)2 2][3 k 2]3 [3( k 1)2 2][3 k 2]由 k 3 可知，3k27k3 0即1111 1a ( k 1)a ( k 1) 1 a ( k 1) 2a(k 1)23合①②可得，当n 2 ， 1 1 11⋯⋯⋯⋯⋯⋯⋯ 10 分1a na n 1a n 2a n 237、〔 江市 2018 届高三期末〕函数f ( x)ln(2x)ax 在区 (0,1) 上是增函数 .〔 1〕求 数 a 的取 范 ；〔 2〕假 数列 a n 足a 1 (0,1)，a n 1ln(2 a n )a n，n Ｎ *， 明 0 a na n 1 1、解：〔 1〕 函数 f ( x)ln(2 x)ax 在区 (0,1) 上是增函数 .f x1 a 在区(0,1)上恒建立 ,⋯⋯2分2 xa1 , 又 g x1 在区 (0,1) 上是增函数2 x2 x1.⋯⋯3分a g 11即 数 a 的取 范 a〔2〕先用数学 法 明 0 a n 1. 当n 1 ， a 1 (0,1) 建立 , ⋯⋯ 4 分假 n k ，0 a k 1建立, ⋯⋯5 分当n k 1 ，由〔 1〕知 a 1 ，函数 f x ln 2 x x 在区 (0,1) 上是增函数a k 1 f a kln 2 a k a k 0 ln 2 f 0 f a k f 1 1, ⋯⋯ 7 分 即 0 a k 1 1建立 , 当 n N , 0 a n 1建立. ⋯⋯8 分下a na n 1 . 0a n 1, a n 1 a n ln 2 a nln1 0.⋯⋯ 9分a n a n 1 .上0 a na n 1 1.⋯⋯10分。

江苏省苏北三市2019届高三上学期期末考试数学试题(满分160分，考试时间120分钟)2019.1参考公式：样本数据x 1，x 2，…，x n 的方差一、 填空题：本大题共14小题，每小题5分，共70分.1. 已知集合A ＝{0，1，2，3}，B ＝{x |0<x ≤2}，则A ∩B ＝ Ｗ.2. 已知复数z ＝(2－i)2(i 是虚数单位)，则z 的模为 Ｗ.3. 已知一组样本数据5，4，x ，3，6的平均数为5，则该组数据的方差为 Ｗ.4. 运行如图所示的伪代码，则输出的结果S 为 Ｗ. I ←1While I <8 I ←I ＋2 S ←2I ＋3 End While Print S (第4题)5. 若从2，3，6三个数中任取一个数记为a ，再从剩余的两个数中任取一个数记为b ，则“a b是整数”的概率为 Ｗ.6. 若抛物线y 2＝2px (p >0)的焦点与双曲线x 2－y 23＝1的右焦点重合，则实数p 的值为Ｗ.7. 在等差数列{a n }中，若a 5＝12，8a 6＋2a 4＝a 2，则{a n }的前6项和 S 6的值为 Ｗ.8. 已知正四棱锥的底面边长为23，高为1，则该正四棱锥的侧面积为 Ｗ. 9. 已知a ，b ∈R ，函数f (x )＝(x －2)(ax ＋b )为偶函数，且在(0，＋∞)上是减函数，则关于x 的不等式f (2－x )>0的解集为 Ｗ.10. 已知a >0，b >0，且a ＋3b ＝1b －1a，则b 的最大值为 Ｗ.11. 将函数f (x )＝sin 2x 的图象向右平移π6个单位长度得到函数g (x )的图象，则以函数f (x )与g (x )的图象的相邻三个交点为顶点的三角形的面积为 Ｗ.12. 在△ABC 中，AB ＝2，AC ＝3，∠BAC ＝60°，P 为△ABC 所在平面内一点，满足CP →＝32PB →＋2PA →，则CP →·AB →的值为 Ｗ.13. 在平面直角坐标系xOy 中，已知圆C 1：x 2＋y 2＋2mx －(4m ＋6)y －4＝0(m ∈R )与以C 2(－2，3)为圆心的圆相交于A (x 1，y 1)，B (x 2，y 2)两点，且满足x 21－x 22＝y 22－y 21，则实数m 的值为 Ｗ.14. 已知x >0，y >0，z >0，且x ＋3y ＋z ＝6，则x 3＋y 2＋3z 的最小值为 Ｗ.二、 解答题：本大题共6小题，共90分. 解答时应写出必要的文字说明、证明过程或演算步骤.15. (本小题满分14分)在△ABC 中，sin A ＝23，A ∈(π2，π).(1) 求sin 2A 的值；(2) 若sin B ＝13，求cos C 的值.16. (本小题满分14分)如图，在直三棱柱ABCA 1B 1C 1中，D ，E ，F 分别是B 1C 1，AB ，AA 1的中点. (1) 求证：EF ∥平面A 1BD ；(2) 若A 1B 1＝A 1C 1，求证：平面A 1BD ⊥平面BB 1C 1C .如图，某公园内有两条道路AB ，AP ，现计划在AP 上选择一点C ，新建道路BC ，并把△ABC 所在的区域改造成绿化区域.已知∠BAC ＝π6，AB ＝2 km.(1) 若绿化区域△ABC 的面积为1 km 2，求道路BC 的长度；(2) 若绿化区域△ABC 改造成本为10万元/km 2，新建道路BC 成本为10万元/km.设∠ABC ＝θ(0<θ≤2π3)，当θ为何值时，该计划所需总费用最小？如图，在平面直角坐标系xOy 中，已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为22，且右焦点到右准线l 的距离为1.过x 轴上一点M (m ，0)(m 为常数，且m ∈(0，2))的直线与椭圆C 交于A ，B 两点，与l 交于点P ，D 是弦AB 的中点，直线OD 与l 交于点Q .(1) 求椭圆C 的标准方程；(2) 试判断以PQ 为直径的圆是否经过定点？若是，求出定点坐标；若不是，请说明理由.已知函数f(x)＝(x－a)ln x(a∈R).(1) 若a＝1，求曲线y＝f(x)在点(1，f(1))处的切线的方程；(2) 若对于任意的正数x，f(x)≥0恒成立，求实数a的值；(3) 若函数f(x)存在两个极值点，求实数a的取值范围.已知数列{a n}满足对任意的n∈N*，都有a n(q n a n－1)＋2q n a n a n＋1＝a n＋1(1－q n a n＋1)，且a n＋1＋a n≠0，其中a1＝2，q≠0.记T n＝a1＋qa2＋q2a3＋…＋q n－1a n.(1) 若q＝1，求T2 019的值；(2) 设数列{b n}满足b n＝(1＋q)T n－q n a n.①求数列{b n}的通项公式；②若数列{c n}满足c1＝1，且当n≥2时，c n＝2b n－1－1，是否存在正整数k，t，使c1，c k －c1，c t－c k成等比数列？若存在，求出所有k，t的值；若不存在，请说明理由.2019届高三模拟考试试卷数学附加题(满分40分，考试时间30分钟)21. 【选做题】 在A ，B ，C 三小题中只能选做2题，每小题10分，共20分.若多做，则按作答的前两题计分.解答时应写出必要的文字说明、证明过程或演算步骤.A. (选修42：矩阵与变换)已知矩阵A ＝⎣⎢⎡⎦⎥⎤0123，B ＝⎣⎢⎡⎦⎥⎤2018，求A －1B .B. (选修44：坐标系与参数方程)在极坐标系中，曲线C ：ρ＝2cos θ.以极点为坐标原点，极轴为x 轴非负半轴建立平面直角坐标系xOy ，设过点A (3，0)的直线l 与曲线C 有且只有一个公共点，求直线l 的斜率.C. (选修45：不等式选讲) 已知函数f (x )＝|x －1|.(1) 解不等式f (x －1)＋f (x ＋3)≥6；(2) 若|a |<1，|b |<1，且a ≠0，求证：f (ab )>|a |f (b a).【必做题】 第22，23题，每小题10分，共20分.解答时应写出必要的文字说明、证明过程或演算步骤.22. 如图， 在三棱锥DABC 中，DA ⊥平面ABC ，∠CAB ＝90°，且AC ＝AD ＝1，AB ＝2，E 为BD 的中点.(1) 求异面直线AE 与BC 所成角的余弦值； (2) 求二面角ACEB 的余弦值.23. 已知数列{a n }满足a 1＝13，a n ＋1＝－2a 2n ＋2a n ，n ∈N *.(1) 用数学归纳法证明：a n ∈(0，12)；(2) 令b n ＝12－a n ，求证：2019届高三模拟考试试卷(五)(苏北三市)数学参考答案及评分标准1. {1，2}2. 53. 24. 215. 136. 47. 152 8. 83 9. (0，4) 10.13 11. 3π2 12. －1 13. －6 14. 37415. 解：(1) 由sin A ＝23，A ∈(π2，π)，则cos A ＝－1－sin 2A ＝－1－（23）2＝－53，(2分) 所以sin 2A ＝2sin A cos A ＝2×23×(－53)＝－459.(6分)(2) 由A ∈(π2，π)，则B 为锐角.又sin B ＝13，所以cos B ＝1－sin 2B ＝1－（13）2＝223，(8分)所以cos C ＝－cos (A ＋B )＝－(cos A cos B －sin A sin B )(12分) ＝－(－53×223－23×13)＝210＋29.(14分) 16. 证明：(1) 因为E ，F 分别是AB ，AA 1的中点，所以EF ∥A 1B .(3分)因为EF ⊄平面A 1BD ，A 1B ⊂平面A 1BD ， 所以EF ∥平面A 1BD .(6分)(2) 在直三棱柱ABCA 1B 1C 1中，BB 1⊥平面A 1B 1C 1. 因为A 1D ⊂平面A 1B 1C 1，所以BB 1⊥A 1D . (8分) 因为A 1B 1＝A 1C 1，且D 是B 1C 1的中点， 所以A 1D ⊥B 1C 1.(10分)因为BB 1∩B 1C 1＝B 1，B 1C 1，BB 1⊂平面BB 1C 1C ， 所以A 1D ⊥平面BB 1C 1C .(12分) 因为A 1D ⊂平面A 1BD ，所以平面A 1BD ⊥平面BB 1C 1C . (14分)17. 解：(1) 在△ABC 中，已知∠BAC ＝π6，AB ＝2 km ，所以△ABC 的面积S ＝12×AB ×AC ×sin π6＝1，解得AC ＝2.(2分)在△ABC 中，由余弦定理得BC 2＝AB 2＋AC 2－2×AB ×AC ×cos π6＝22＋22－2×2×2×cos π6＝8－43，(4分)所以BC ＝8－43＝6－2(km).(5分)(2) 由∠ABC ＝θ，则∠ACB ＝π－(θ＋π6)， 0<θ≤2π3.在△ABC 中，∠BAC ＝π6，AB ＝2 km ，由正弦定理得AC sin B ＝BC sin A ＝ABsin C ，所以BC ＝1sin （θ＋π6），AC ＝2sin θsin （θ＋π6）.(7分)记该计划所需费用为F (θ)， 则F (θ)＝12×2sin θsin （θ＋π6）×2×12×10＋1sin （θ＋π6）×10＝10（sin θ＋1）sin （θ＋π6）(0<θ≤2π3).(10分)令f (θ)＝sin θ＋132sin θ＋12cos θ，则f ′(θ)＝sin （θ－π3）＋12（32sin θ＋12cos θ）2.(11分)由f ′(θ)＝0，得θ＝π6.所以当θ∈(0，π6)时，f ′(θ)<0，f (θ)单调递减；当θ∈(π6，2π3)时，f ′(θ)>0，f (θ)单调递增.(12分)所以当θ＝π6时，该计划所需费用最小.答：当θ＝π6时，该计划所需总费用最小.(14分)18. 解：(1) 设椭圆的右焦点为(c ，0)，由题意，得⎩⎪⎨⎪⎧c a ＝22，a 2c－c ＝1，解得⎩⎨⎧a ＝2，c ＝1，所以a 2＝2，b 2＝1，所以椭圆C 的标准方程为x 22＋y 2＝1.(4分)(2) 由题意，当直线AB 的斜率不存在或为零时显然不符合题意. 设AB 的斜率为k ，则直线AB 的方程为y ＝k (x －m ). 又准线方程为x ＝2，所以点P 的坐标为P (2，k (2－m )).(6分)由⎩⎪⎨⎪⎧y ＝k （x －m ），x 2＋2y 2＝2，得x 2＋2k 2(x －m )2＝2， 即(1＋2k 2)x 2－4k 2mx ＋2k 2m 2－2＝0，所以x D ＝12·4k 2m 2k 2＋1＝2k 2m 2k 2＋1，y D ＝k (2k 2m 2k 2＋1－m )＝－km2k 2＋1，(8分)所以k OD ＝－12k ，从而直线OD 的方程为y ＝－12kx ，所以点Q 的坐标为Q (2，－1k)，(10分)所以以PQ 为直径的圆的方程为(x －2)2＋[y －k (2－m )](y ＋1k)＝0，即x 2－4x ＋2＋m ＋y 2－[k (2－m )－1k]y ＝0.(14分)因为该式对∀k ≠0恒成立，所以⎩⎪⎨⎪⎧y ＝0，x 2－4x ＋2＋m ＋y 2＝0，解得⎩⎨⎧x ＝2±2－m ，y ＝0.所以以PQ 为直径的圆经过定点(2±2－m ，0).(16分)19. 解：(1) 因为f (x )＝(x －a )ln x (a ∈R )，所以当a ＝1时，f (x )＝(x －1)ln x ， 则f ′(x )＝ln x ＋1－1x.(1分)当x ＝1时，f (1)＝0，f ′(1)＝0，所以曲线f (x )在点(1，f (1))处的切线的方程为y ＝0.(3分) (2) 因为对于任意的正数x ，f (x )≥0恒成立，所以当ln x ＝0，即x ＝1时，f (x )＝0，a ∈R ；(5分)当ln x >0，即x >1时，x ≥a 恒成立，所以a ≤1； (6分) 当ln x <0，即x <1时，x ≤a 恒成立，所以a ≥1.综上可知，对于任意的正数x ，f (x )≥0恒成立，a ＝1. (7分) (3) 因为函数f (x )存在两个极值点，所以f ′(x )＝ln x －a x＋1存在两个不相等的零点.设g (x )＝ln x －a x＋1，则g ′(x )＝1x ＋a x2＝x ＋ax2.(8分)当a ≥0时，g ′(x )>0，所以g (x )单调递增，至多一个零点.(9分) 当a <0时，x ∈(0，－a )时，g ′(x )<0，g (x )单调递减， x ∈(－a ，＋∞)时，g ′(x )>0，g (x )单调递增，所以x ＝－a 时，g (x )min ＝g (－a )＝ln(－a )＋2. (11分)因为g (x )存在两个不相等的零点，所以ln(－a )＋2<0，解得－e －2<a <0. 因为－e －2<a <0，所以－1a>e 2>－a .因为g (－1a )＝ln(－1a)＋a 2＋1>0，所以g (x )在(－a ，＋∞)上存在一个零点.(13分)因为－e －2<a <0，所以a 2<－a .又g (a 2)＝ln a 2－1a ＋1＝2ln(－a )＋1－a ＋1，设t ＝－a ，则y ＝2ln t ＋1t ＋1(0<t <1e2).因为y ′＝2t －1t 2<0，所以y ＝2ln t ＋1t ＋1(0<t <1e 2)单调递减.又函数图象是连续的， 所以y >2ln 1e 2＋e 2＋1＝e 2－3>0，所以g (a 2)＝ln a 2－1a＋1>0，所以在(0，－a )上存在一个零点.综上可知，－e－2<a<0.(16分)20. 解：(1) 当q＝1时，由a n(q n a n－1)＋2q n a n a n＋1＝a n＋1(1－q n a n＋1)，得(a n＋1＋a n)2＝a n＋1＋a n.又a n＋1＋a n≠0，所以a n＋1＋a n＝1.(2分)又a1＝2，所以T2 019＝a1＋(a2＋a3)＋(a4＋a5)＋…＋(a2 018＋a2 019)＝1 011.(4分)(2) ①由a n(q n a n－1)＋2q n a n a n＋1＝a n＋1(1－q n a n＋1)，得q n(a n＋1＋a n)2＝a n＋1＋a n.又a n＋1＋a n≠0，所以a n＋1＋a n＝1q n.(6分)因为T n＝a1＋qa2＋q2a3＋…＋q n－1a n，所以qT n＝qa1＋q2a2＋q3a3＋…＋q n a n，所以(1＋q)T n＝a1＋q(a1＋a2)＋q2(a2＋a3)＋q3(a3＋a4)＋…＋q n－1(a n－1＋a n)＋q n a n，b n＝(1＋q)T n－q n a n＝a1＋1＋1＋…＋1＋q n a n－q n a n＝a1＋n－1＝n＋1，所以b n＝n＋1.(10分)②由题意，得c n＝2b n－1－1＝2n－1，n≥2.因为c1，c k－c1，c t－c k成等比数列，所以(c k－c1)2＝c1(c t－c k)，即(2k－2)2＝2t－2k， (12分)所以2t＝(2k)2－3·2k＋4，即2t－2＝(2k－1)2－3·2k－2＋1 (*).由于c k－c1≠0，所以k≠1，即k≥2.当k＝2时，2t＝8，得t＝3.(14分)当k≥3时，由(*)得(2k－1)2－3·2k－2＋1为奇数，所以t－2＝0，即t＝2，代入(*)得22k－2－3·2k－2＝0，即2k＝3，此时k无正整数解. 综上，k＝2，t＝3.(16分)2019届高三模拟考试试卷(五)(苏北三市)数学附加题参考答案及评分标准21. A. 解：由题意得A －1＝⎣⎢⎢⎡⎦⎥⎥⎤－3212 10，(5分) 所以A －1B ＝⎣⎢⎢⎡⎦⎥⎥⎤－3212 10⎣⎢⎡⎦⎥⎤2018＝⎣⎢⎢⎡⎦⎥⎥⎤－524 20.(10分) B. 解：曲线C ：ρ＝2cos θ的直角坐标方程为(x －1)2＋y 2＝1.(4分)设过点A (3， 0)的直线l 的直角坐标方程为x ＝my ＋3， 因为直线l 与曲线C 有且只有一个公共点，所以|1－3|1＋m 2＝1，解得m ＝± 3.(8分) 从而直线l 的斜率为±33.(10分) C. (1) 解：不等式的解集是(－∞，－3]∪[3，＋∞).(4分)(2) 证明：要证f (ab )>|a |f (b a)，只要证|ab －1|>|b －a |，只需证(ab －1)2>(b －a )2. 而(ab －1)2－(b －a )2＝a 2b 2－a 2－b 2＋1＝(a 2－1)(b 2－1)>0， 从而原不等式成立. (10分)22. 解：因为DA ⊥平面ABC ，∠CAB ＝90°，所以以A 为坐标原点，建立如图所示的空间直角坐标系Axyz .因为AC ＝AD ＝1，AB ＝2，所以A (0，0，0)，C (1，0，0)，B (0，2，0)，D (0，0，1).因为点E 为线段BD 的中点，所以E (0，1，12).(1) AE →＝(0，1，12)，BC →＝(1，－2，0)，所以cos 〈AE →，BC →〉＝AE →·BC →|AE →||BC →|＝－254×5＝－45，所以异面直线AE 与BC 所成角的余弦值为45.(5分)(2) 设平面ACE 的法向量为n 1＝(x ，y ，z )，因为AC →＝(1，0，0)，AE →＝(0，1，12)，所以n 1·AC →＝0，n 1·AE →＝0，即x ＝0且y ＋12z ＝0，取y ＝1，得x ＝0，z ＝－2，所以n 1＝(0，1，－2)是平面ACE 的一个法向量.设平面BCE 的法向量为n 2＝(x ，y ，z )，因为BC →＝(1，－2，0)，BE →＝(0，－1，12)，所以n 2·BC →＝0，n 2·BE →＝0，即x －2y ＝0且－y ＋12z ＝0，取y ＝1，得x ＝2，z ＝2，所以n 2＝(2，1，2)是平面BCE 的一个法向量.所以cos 〈n 1，n 2〉＝n 1·n 2|n 1||n 2|＝－35×9＝－55. (8分)所以二面角ACEB 的余弦值为－55. (10分) 23. 证明：(1) 当n ＝1时，a 1＝13∈(0，12)，结论显然成立；假设当n ＝k (k ≥1，k ∈N *)时，a k ∈(0，12)，则当n ＝k ＋1时，a k ＋1＝－2a 2k ＋2a k ＝－2(a k －12)2＋12∈(0，12).综上，a n ∈(0，12).(4分)(2) 由(1)知，a n ∈(0，12)，所以b n ＝12－a n ∈(0，12).因为a n ＋1＝－2a 2n ＋2a n ，所以12－a n ＋1＝12－(－2a 2n ＋2a n )＝2a 2n －2a n ＋12＝2(a n －12)2，即b n ＋1＝2b 2n .于是log 2b n ＋1＝2log 2b n ＋1，所以(log 2b n ＋1＋1)＝2(log 2b n ＋1)，故{log 2b n ＋1}构成以2为公比的等比数列，其首项为log 2b 1＋1＝log 216＋1＝log 213.于是log 2b n ＋1＝(log 213)·2n －1，从而log 2(2b n )＝(log 213)·2n －1＝log 2(13)2n －1，所以2b n ＝(13)2n －1，即b n ＝（13）2n －12，于是1b n ＝2·32n －1.(8分)因为当i ＝1，2时，2i －1＝i ， 当i ≥3时，2i －1＝(1＋1)i －1＝C 0i －1＋C 1i －1＋…＋C i －1i －1>C 0i －1＋C 1i －1＝i ， 所以对∀i ∈N *，有2i －1≥i ，所以32i －1≥3i ，所以1b i＝2·32i －1≥2·3i，从而＝1b 1＋1b 2＋…＋1b n ≥2(31＋32＋ (3))＝2×3（1－3n）1－3＝3n ＋1－3.(10分)。

宿迁市2018~2019学年度第一学期市直高三期末测试数 学参考公式：锥体的体积公式 13V Sh =，其中S 是锥体的底面面积，h 是高． 一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位．．．．．．置上．．． 1． 已知集合{|10,}A x x x =+>∈R ，{|230,}B x x x =-<∈R ，则A B =I ▲ ． 2． 已知复数z 满足()12i 3i z +=-（其中i 为虚数单位），则||z 的值为 ▲ ． 3． 交通部门对某路段公路上行驶的汽车速度实施监控，从速度不小于50km/h 的汽车中抽取200辆汽车进行测速分析，得到如图所示的时速的频率分布直方图，则时速 不低于80km/h 的汽车有 ▲ 辆．4． 如图是一个算法的伪代码，运行后输出S 的值为 ▲ ．5．春节将至，三个小朋友每人自制1张贺卡，然后将3张贺卡装在一盒子中，再由三人注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求1．本试卷共4页，均为非选择题（第1题～第20题，共20题）。

本卷满分为160分，考试时间为120分钟。

考试结束后，请将答题卡交回。

2．答题前，请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。

3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。

4．作答试题，必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效。

依次任意抽取1张，则三人都没抽到自己制作的贺卡的概率为 ▲ ．6. 设圆锥的轴截面是一个边长为2cm 的正三角形，则该圆锥的体积为 ▲ cm 3．7. 已知双曲线2222:1(0,0)x y C a b a b-=>>的离心率为2，右焦点与抛物线216y x =的焦点重合，则双曲线C 的顶点到渐近线的距离为 ▲ .8. 已知数列{}n a 前n 项和为n S ，121n n a a +-=，11a =，则9S 的值为 ▲ ． 9． 已知正实数,a b 满足22a b +=，则1+43a bab+的最小值为 ▲ ． 10. 已知点(1,0),(1,0)A B -，若圆22(1)(2)1x a y a -++--=上存在点M 满足3MA MB ⋅=u u u r u u u r,则实数a 的取值范围是 ▲ .11. 对于函数()y f x =，如果()f x 是偶函数，且其图象上的任意一点都在平面区域,y x y x⎧⎨-⎩≥≥内，则称该函数为“V 型函数”.下列函数：①1y x x =+；②1||y x x =-； ③||e x y =； ④ππ|tan |((,))22y x x =∈-.其中是“V 型函数”的是 ▲ .（将符合条件 的函数序号都填在横线上）.12. 如图所示，矩形ABCD 的边AB =4，AD =2，以点C 为圆心，CB 为半径的圆与CD 交于点E ，若点P 是圆弧»EB(含端点B 、E )上 的一点，则PA PB ⋅u u u r u u u r的取值范围是 ▲ .13.已知函数()(cos sin ))f x x x x x =⋅+-∈R ，设点111222(,),(,),P x y P x y …， (,)n n n P x y ，…都在函数()y f x =图象上，且满足1π6x =，*1π()4n n x x n +-=∈N ， 则122019y y y +++L 的值为 ▲ .14. 已知函数1,12,()12(),2,2x x f x f x x -<⎧⎪=⎨⎪⎩≤≥ 如果函数()()(3)g x f x k x =--恰有2个不同的零 点，那么实数k 的取值范围是 ▲ .二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答．．．．．．．．．．，解答时应写出文字说明、证明过程或计算步骤． 15. （本小题满分14分）已知三角形ABC 的面积是S，AB AC ⋅u u u r u u u r ．(第12题)（1）求sin A 的值；（2）若23BC =，当三角形ABC 的周长取得最大值时，求三角形ABC 的面积S ．16．（本小题满分14分）在四棱锥S ABCD -中，SA ABCD ⊥面，底面ABCD 是菱形． （1）求证：SAC SBD ⊥面面；（2）若点M 是棱AD 的中点，点N 在棱SA 上，且12AN NS =，求证：SC BMN 面∥．17．（本小题满分14分）如图所示，桌面上方有一盏电灯A ，A 到桌面的距离AO 可以变化，桌面上有一点B 到点O 的距离为a （a 为常数），设ABO θ∠=，灯A 对B 点的照度J 与sin θ成正比、与AB 长的平方成反比，且比例系数为正常数k .（1）求灯A 对B 点的照度J 关于θ的函数关系式；（2）问电灯A 与点O 多远时，可使得灯A 对B 点的照度J 最大？18．（本小题满分16分）如图所示，椭圆2222:1(0)x yM a ba b+=>>的离心率为2，右准线方程为4x=，过点(0,4)P作关于y轴对称的两条直线12,l l，且1l与椭圆交于不同两点,A B，2l与椭圆交于不同两点,D C.（1）求椭圆M的方程；（2）证明：直线AC与直线BD交于点(0,1)Q；（3）求线段AC长的取值范围.19．（本小题满分16分）已知数列{}n a各项均为正数，n S是数列{}n a的前n项的和，对任意的*n∈N都有2232n n nS a a=+-.数列{}n b各项都是正整数，11b=，24b=，且数列12b ba,a,3nb ba,,a⋅⋅⋅是等比数列．（1）证明：数列{}n a是等差数列；（2）求数列{}n b的通项公式n b；（3）求满足124nnSb<+的最小正整数n．20．（本小题满分16分）已知函数()ln xf x x=，()(,)g x kx b k b =+∈R . （1）求函数()y f x =的定义域和单调区间；（2）当2e =4b 且1x >时，若直线()y g x =与函数()y f x =的图象相切，求k 的值；（3）当=b k -时，若存在2e,e x ⎡⎤∈⎣⎦，使得1()()2f xg x +≤，求k 的取值范围.数学Ⅱ(附加题)本卷共4小题，每小题10分，共计40分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤． 21．（本小题满分10分）已知矩阵121⎡⎤=⎢⎥⎣⎦a M 的一个特征值为3λ=，其对应的一个特征向量为11α⎡⎤=⎢⎥⎣⎦u r ， 求直线1l ：210x y ++=在矩阵M 对应的变换作用下得到的曲线2l 的方程.22. （本小题满分10分）在平面直角坐标系xOy 中，椭圆C 的参数方程为3cos ,()sin ,x y t ααα⎧=⎪⎨=⎪⎩为参数．在极坐标系(与直角坐标系xOy 取相同的长度单位，且以原点O 为极点，以x 轴正半轴为极轴)中，直线l 的方程为πsin()24ρθ-=．(1)求直线l 的直角坐标方程和椭圆C 的普通方程； (2)若直线l 与椭圆C 有公共点，求t 的取值范围．23．（本小题满分10分）如图，在直三棱柱111ABC A B C -中，1AC BC AC BC ⊥==，，12BB =，点D 在棱1BB 上，且11C D AB ⊥． （1）求线段1B D 的长；（2）求二面角11D A C C --的余弦值．24．（本小题满分10分）已知12012()(1)nnn f x ax a a x a x a x =+=+++⋅⋅⋅+，若对于任意*n ∈N ，都有02()3nn i i a ==∑．（1）求实数a 的值；（2）若[]2220122()n n f x b b x b x b x =+++⋅⋅⋅+，求232123211113333nnb b b b +++⋅⋅⋅+的值．高三数学参考答案及评分标准一、填空题：本大题共14小题，每小题5分，共计70分．1．3(1,)2-； 2； 3．20； 4．13； 5.13;； 8. 1013 9．252； 10. [2,1]-；11. ③④； 12. [8-； 13. 14. 168(1,0)[,)2913-U .二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答．．．．．．．．．．，解答时应写出文字说明、证明过程或计算步骤．15解：（1）由2AB AC S ⋅=u u u r u u u r 得1cos sin 2AB AC A AB AC A ⋅⋅=⋅⋅，所以cos A A =. ………… …………………………2分在三角形ABC 中()0A ,π∈得tan A =4分所以3A π∠=,sin A =……………………………7分 （2）在三角形ABC 中，2222cos a b c bc A =+-，所以()21222cos3b c bc bc π=+--，即()2212332b c b c bc +⎛⎫+-=≤ ⎪⎝⎭，…………………………10分当且仅当b c =时取等号，所以b c +≤所以周长的最大值为b c ==所以面积1sin 2S AB AC A =⋅⋅=……………………………14分 解法二：在三角形ABC 中sin sin sin AB AC BCC B A==得4sin sin 3ABAC CC π===⎛⎫+ ⎪⎝⎭所以周长4sin 4sin 3l BC AB CA C C π⎛⎫=++=++ ⎪⎝⎭6C π⎛⎫=+ ⎪⎝⎭……………………………10分由203C ,π⎛⎫∈ ⎪⎝⎭得，当3C π=时，周长l取得最大值为此时AC AB ==所以面积1sin 2S AB AC A =⋅⋅=……………………………14分16解：（1）因为SA ABCD ⊥面，BD ABCD ⊂面，所以SA BD ⊥， ………………………………2分 又因为底面ABCD 是菱形，得AC BD ⊥， 由SA ，AC 都在面SAC 内，且SA AC A ⋂=， 所以BD SAC ⊥面，………………………………5分 由BD SAC ⊂面，得SAC SBD ⊥面面；…………7分 （2）由底面ABCD 是菱形，得AD BC ∥所以12AE AM AM EC BC AD ===………………9分 又因为12AN NS =，所以12AE AN EC NS == ，所以NE SC ∥…，………………………11分 因为NE BMN ,SC BMN ⊂⊄面面，所以SC BMN 面∥.………………………………14分A BCD SMN (第16题)17解：（1）因为2sin ()J kk AB θ=为正常数，………………3分 又0<<π()cos 2θθ=a AB ， 所以2222sin cos =sin 1-sin 2k J k a a θθπθθθ⋅=⋅（）（0<<），…………6分（2）令sin ,t t θ=∈则（0,1），232=1--1k J t t t t t a⋅因为（）=（0<<）， 由2=1-30J t '=得-33t =（舍），………………………0t J '∈>所以,,则J 单调递增； 10t J '∈<所以）,,则J 单调递减，…………………12分 t J所以当取得最大值，此时sin θθ== sin =tan cos OA OB aθθθ=所以时，J 取得最大值， 答：当电灯A 与点O 时，可使得灯A 对B 点的照度最大. ……14分18解：（1）由224c e a a c⎧==⎪⎪⎨⎪=⎪⎩ 得2a c ==，2224b a c ∴=-=，所以椭圆M 的方程22184x y +=.………………………………………………4分 （2）设直线14l y kx =+：，11221122(,),(,),(,),(,)A x y B x y D x y C x y --则，联立221844x y y kx ⎧+=⎪⎨⎪=+⎩，消y 得221+2)16240k x kx ++=（， 1212221624,1+21+2k x x x x k k -∴+=⋅=， …………………………………6分 又212111,BQ DQ y y k k x x --==-，212121211133BQ DQ y y kx kx k k x x x x --++∴-=-=+- 212122483()122+=2+2202412kx x k k k k k x x k -++==-=+，………8分=BQ DQ k k ∴，故点,,B D Q 三点共线，即直线BD 经过点(0,1)Q同理可得直线AC 经过点(0,1)Q ，所以直线AC 与直线BD 交于点(0,1)Q . …………………………10分（3）由（2）可知22222212121212()()()()AC x x y y x x k x x =++-=++-222121212()(+)4x x k x x x x ⎡⎤=++-⋅⎣⎦2222222222161624+41+21+21+2k k k k k k ⎡⎤⋅⋅=-⨯⎢⎥⎣⎦（）（） 42424+10164+4+1k k k k ⋅=⨯24261161+4+4+1k k k ⎡⎤-=⨯⎢⎥⎣⎦…………………………12分 令22161,6t t k k ==+-则 又由222=16424(12)0k k ∆-⨯⨯+>得23,2k >所以8t > 221616+114+4+166tAC t t ∴=++⎛⎫⎪⎝⎭29161++8+16t t t ⎡⎤=⎢⎥⎣⎦9161+16++8t t ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦……………………………………14分21616++810t t t '⎛⎫=-> ⎪⎝⎭Q 在8+t ∈∞（，）上恒成立 16++8t t∴在8+t ∈∞（，）上单调递增 16++818t t ∴>， 910162++8t t ∴<<，9311+162++8t t∴<< 21624AC ∴<<4AC ∴<<…………………………………………………16分19解：（1）当1n =时，2111232a a a =+-，即211320a a --=，()()113210a a +-=，由10a >得11a =； …………………………………………………1分当2n ≥时，由2232n n n S a a =+-得2111232n n n S a a ---=+-， 所以两式相减得2211233n n n n n a a a a a --=+--，所以()()1113n n n n n n a a a a a a ----+=+， …………………………3分 由0n a >知10n n a a -+> 所以113n n a a --=所以数列{}n a 是首项11a =，公差13d =的等差数列. …………………5分 (2)由（1）得()11211333n a n n =+-=+，由121412b b a a ,a a ,====所以数列{}n b a 是首项为1，公比为2的等比数列 所以12n n b a -=， …………………………………………………7分又1233n b n a b =+， 所以112233n n b n a b -=+=，即1322n n b -=⨯-.…………………………10分（3）由()()121526n n n a a S n n +==+， 所以22155623292n n nn n nS n n b -++==+⨯⨯，……………………………………12分 设()25292n nn S n n f n b +==+⨯，则()()()()22122215117612692152102592n nn n f n n n n n n f n n n n n ++++++++⎛⎫⨯===+ ⎪+++⎝⎭⨯，令()()11f n f n +>得222761360210n n ,n n n n ++>+-<+即， 由*n N ∈得1n =，所以()()()()()1234f f f f f n <>>>⋅⋅⋅>>⋅⋅⋅，………………14分 又因为()11611121834S f b ===>+， ()2214712236184S f b ===>+， ()332411327234S f b ===>+， ()44361421444S f b ===+， ()5550251522881444S f b ===<+， 所以当5n ≥时，()14f n <， 所以满足124n n S b <+的最小正整数n 为5. …………………………16分 20解（1）由ln 00x x ≠⎧⎨>⎩得()y f x =的定义域()()0,11+x ∈∞U ，，2ln 1()=ln x f x x-'∴ ，………………………………………………2分 由2ln 1()=0ln x f x x-'>得()+x e ∈∞，， 由2ln 1()=0ln x f x x-'<得()()0,11,x e ∈U ， 所以()y f x =的单调增区间为()+x e ∈∞，，单调减区间为()0,1x ∈和()1,e ；………………………………………4分（2）设24e y kx =+与()y f x =相切于点0000,1ln x x x x ⎛⎫> ⎪⎝⎭（）， 0020ln 1()=ln x k f x x -'∴=，且2000ln 4=0x e x k x --，2000200ln 4ln 1=0ln x e x x x x --∴-，化简得2200ln =4e x x ，………………………6分001,ln x x >∴Q令()ln 1)h x x x =>，1()h x x '∴==， 由()0h x '>得()2x e ∈1,，由()0h x '<得()2+x e ∈∞，，()y h x ∴=在()2x e ∈1,单调递增，在()2+x e ∈∞，单调递减，………8分2()=()=0y h x h e ∴=极大值，0ln x ∴方程01+)x ∈∞（，上有唯一解20=x e ， 2222ln 11()=ln 4e kf e e -'∴==.………………………………………10分（3）令2()()()ln x x f x g x kx k e x e x ϕ=-=-+≤≤（），依题意知min 1()2x ϕ≤， 22ln 1111()=ln ln 24x x k k x x ϕ-⎛⎫'∴-=--+- ⎪⎝⎭的值域为1,4k k ⎡⎤--⎢⎥⎣⎦，………12分①当0k -≥，即0k ≤时，()0x ϕ'∴≥，2()x e e ϕ⎡⎤∴⎣⎦在，单调递增，min 1()=()(1)2x e e k e ϕϕ∴=--≤， 解得12(1)e k e -≥-，不合题意，②当104k -≤，即14k ≥时，()0x ϕ'∴≤， 2()x e e ϕ⎡⎤∴⎣⎦在，单调递减，222min 1()=()(1)22e x e k e ϕϕ∴=--≤，解得12k ≥，满足题意，………………………………………14分 ③当104k <<时，存在唯一()20,x e e ∈满足0()=0x ϕ'， ()0x e x ∴∈,时，()0x ϕ'<；()20x x e ∈,时，()0x ϕ'>，()x ϕ∴在()0x e x ∈,单调递减，在()20x x e ∈,单调递增，0min 0001()=()(1)ln 2x x x k x x ϕϕ∴=--≤， 解得0000011111))(1)ln 2(1)222x x k x x x ≥->-=--(( ，这与104k <<矛盾，不合题意， 综上所述，k 的取值范围为12k ≥.………………………………………16分数学Ⅱ(附加题)参考答案与评分标准21解：由M αλα=u r u r得12113111a ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦， 所以2a =，1221M ⎡⎤=⎢⎥⎣⎦， ……………………………2分 设()111P x ,y 是直线1C 上任意一点，在矩阵M 对应的变换作用下得到点()222P x ,y ，且2P 在曲线2C 上，由12121221x x y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦得21121122x x y y x y =+⎧⎨=+⎩，…………………………4分所以12212212332133x x y y x y ⎧=-+⎪⎪⎨⎪=-⎪⎩， …………………………6分代入曲线1C 的方程得210x +=，所以曲线2C 的方程10x +=. ……………………………10分 22解:(1)2sin 4πρθ⎛⎫-= ⎪⎝⎭20y x --=，…………………2分由()sin x y t ααα⎧=⎪⎨=⋅⎪⎩为参数，得(22213x y t t+=≠. ……………………………………5分(2)由2222013y x x y t--=⎧⎪⎨+=⎪⎩消去y 得()3223121230t x x t +++-=.因为直线l 与椭圆C 有公共点,所以()()22212431230t t ∆=-+-≥,即420t t -≥．……………7分 所以t 的取值范围是11t t ≥≤-或，所以t的取值范围是((1][1+),-∞-∞U U U .………10分23解：在直三棱柱111ABC A B C -中，由AC BC ⊥，则以{}11111C A ,C B ,C C u u u u r u u u u r u u u u r为基底构建如图所示的空间直角坐标系，则()()()()()11102010000012002A ,,,B ,,,C ,,,B ,,,C ,,,所以()1112AB ,,=--u u u r, 设1B M t =，则()101C D ,,t =u u u u r,（1）由11DC AB ⊥得110C D A B ⋅=u u u u r u u u r ,所以11202t t -=⇒=, 所以1B M =12．……………………………………………3分 A 1 D1(第23题)A（2）由111B C AC C ⊥面，取11AC C 面的一个法向量为()11010C B ,,=u u u u r, 设1ACD 面的一个法向量()n x,y,z =r, 由（1）知()111111022A D ,,,AC ,,,⎛⎫=-=- ⎪⎝⎭u u u u r u u u r 又因为1100n A D n A C ⎧⋅=⎪⎨⋅=⎪⎩r u u u u r r u u u r ,所以10220x y z x z ⎧-++=⎪⎨⎪-+=⎩，取2z =， 则34y ,x ==,…………………6分所以()432n ,,=r,所以111n C C cos n,C C |n||C C |⋅<>==r u u u u rr u u u u r r u u u u r ．所以二面角111D AC B --的余弦值为29．…………………………10分24解（1）由012(1)(1)=nn f a a a a a =+=+++⋅⋅⋅+04()3nnii a ==∑, 所以13a =-,………………………………………………………………2分（2）[]2220122()nn f x b b x b x b x =+++⋅⋅⋅+2211=(1)=(1)33n n x x ⎡⎤--⎢⎥⎣⎦,所以21=3k kk nb C （-）， 令23(1)k k kk n b C =-，1,2,3,2k n =⋅⋅⋅，首先考虑1 C k 2n ＋1＋1 C k ＋12n ＋1＝k !(2n +1－k )!(2n ＋1)!＋(k ＋1)!(2n －k )!(2n ＋1)!＝k !(2n －k )!(2n ＋1－k ＋k ＋1)(2n ＋1)!＝k !(2n －k )!(2n ＋2)(2n ＋1)!＝2n ＋2(2n ＋1) C k 2n，则1C k 2n ＝2n ＋12n ＋2(1 C k 2n ＋1＋1C k ＋12n ＋1)， 因此1 C k 2n －1 C k ＋12n ＝2n ＋12n ＋2(1 C k 2n ＋1－1 C k ＋22n ＋1)． ………………………………6分故232123*********n nb b b b +++⋅⋅⋅+ 123222222(1)k k n n n n n n C C C C C =-+-+⋅⋅⋅+-+⋅⋅⋅+＝- 2n ＋12n ＋2(1 C 12n ＋1－1 C 32n ＋1＋1 C 32n ＋1－1 C 52n ＋1＋…＋1 C 2n －12n ＋1－1 C 2n ＋12n ＋1)＝- 2n ＋12n ＋2(1 C 12n ＋1－1 C 2n ＋12n ＋1)＝2n ＋12n ＋2(12n ＋1－1)＝nn ＋1． ………………………………………………………………………10分。

江苏各市2019届高三上学期期末数学试卷【导数类题】汇编及解析
江苏各市2019届高三上学期期末数学试卷
【导数类题】汇编
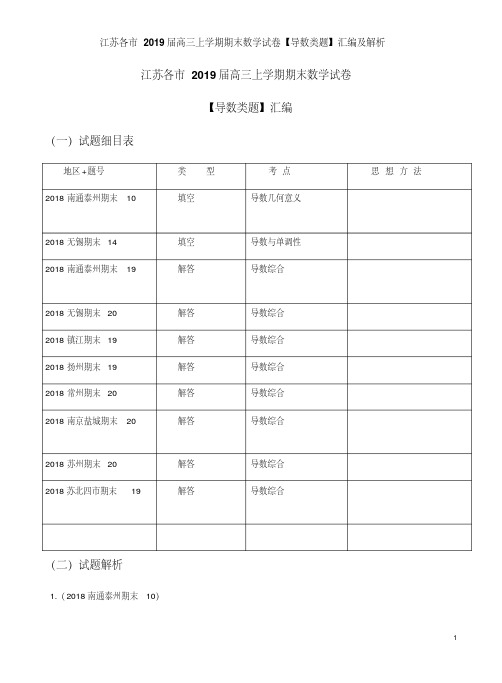
（一）试题细目表
地区+题号类型考点思想方法2018·南通泰州期末·10 填空导数几何意义
2018·无锡期末·14 填空导数与单调性
2018·南通泰州期末·19 解答导数综合
2018·无锡期末·20 解答导数综合
2018·镇江期末·19 解答导数综合
2018·扬州期末·19 解答导数综合
2018·常州期末·20 解答导数综合
2018·南京盐城期末·20 解答导数综合
2018·苏州期末·20 解答导数综合
2018苏北四市期末·19解答导数综合
（二）试题解析
1.（2018·南通泰州期末·10）
1。

江苏省常州市2019届高三上学期期末考试数学试题+Word版含答案编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（江苏省常州市2019届高三上学期期末考试数学试题+Word版含答案）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为江苏省常州市2019届高三上学期期末考试数学试题+Word版含答案的全部内容。

江苏省常州市2019届高三上学期期末考试数 学参考公式：样本数据12,,n x x x 的方差2211()ni i s x x n==-∑，其中11ni i x x n==∑。

柱体的体积V Sh =,其中S 为柱体的底面积，h 为高．一、 填空题:本大题共14小题，每小题5分，共70分. 1。

已知集合{0,1},{1,1}A B ==-，则A B =________.2.已知复数z 满足(1)1z i i +=-（i 是虚数单位）,则复数z =________。

3. 已知5位裁判给某运动员打出的分数为9.1,9.3,,9.2,9.4x ，且这5个分数的平均数为9.3，则实数x =________.4. 一个算法的伪代码如右图所示，执行此算法，若输出的y 值为1，则输入的实数x 的值为________.5。

函数y =________.6. 某校开设5门不同的选修课程，其中3门理科类和2门文科类,某同学从中选修2门课程，则该同学恰好选中1文1理的概率为________。

7。

已知双曲线2222:1(0,0)x y C a b a b-=>>的离心率为2，直线20x y ++=经过双C 的焦点，则双曲线C 的渐近线方程为________.8. 已知圆锥SO ，过SO 的中点P 作平行于圆锥底面的截面,以截面为上底面作圆柱PO ，圆柱的下底面落在圆锥的底面上（如图)，则圆柱PO 的体积与圆锥SO 的体积的比值为________.9. 已知正数,x y 满足1y x x+=，则1x x y+的最小值为________.OP（第8题）(第4题)10. 若直线0kx y k --=与曲线e x y =（e 是自然对数的底数)相切，则实数 k =________。

江苏13大2019年高三上学期年末数学试题分类汇编--数列数 列【一】填空题 1、〔常州市2018届高三期末〕数列{}n a 满足143a =，()*11226n n an N a +-=∈+，那么11ni ia =∑= ▲ 、答案：2324n n ⋅--2、〔连云港市2018届高三期末〕正项等比数列{a n }中，311a a =16，那么22212log log a a +=▲ .答案：43、〔南京市、盐城市2018届高三期末〕在等差数列{}n a 中, 假设9753=++a a a , 那么其前9项和9S 的值为 ▲答案：27 4、〔南通市2018届高三期末〕假设S n 为等差数列{a n }的前n 项和，S 9=－36，S 13=－104， 那么a 5与a 7的等比中项为 ▲ 、 答案：±、 5、〔徐州、淮安、宿迁市2018届高三期末〕等比数列}{n a 的前n 项和为n S ，假设62,256382-==S a a a a ，那么1a 的值是 ▲ .答案：－26、〔扬州市2018届高三期末〕数列{}n a 满足111,1(1)n n n aa a a +>-=-，()n N +∈，且122012111a a a +++=2，那么201314a a -的最小值为 ▲ 、答案：27- 7、〔镇江市2018届高三期末〕在等比数列{}n a 中，n S 为其前n 项和，5423a S =+，6523a S =+，那么此数列的公比q 为 ▲ 、答案：3;8、〔镇江市2018届高三期末〕 观看以下等式： 31×2×12＝1－122， 31×2×12＋42×3×122＝1－13×22， 31×2×12＋42×3×122＋53×4×123＝1－14×23，…，由以上等式推测到一个一般的结论：关于n ∈N *，31×2×12＋42×3×122＋…＋n ＋2n n ＋1×12n＝ ▲ 、 答案：()nn 2111⋅+-【二】解答题1、〔常州市2018届高三期末〕 数列{}n a 是等差数列，12315a a a ++=，数列{}n b 是等比数列，12327b b b =、〔1〕假设1243,a b a b ==、求数列{}n a 和{}nb 的通项公式；〔2〕假设112233,,a b a b a b +++是正整数且成等比数列，求3a 的最大值、 答案：解：〔1〕由题得225,3ab ==，因此123a b ==，从而等差数列{}na 的公差2d =，因此21n a n =+，从而349b a ==，因此13n n b -=、 ……………………3分 〔2〕设等差数列{}n a 的公差为d ，等比数列{}n b 的公比为q ，那么15a d =-，13b q =，35a d =+，33b q =.因为112233,,a b a b a b +++成等比数列，因此2113322()()()64a b a b a b +⋅+=+=、 设1133a b ma b n+=⎧⎨+=⎩，*,m n N ∈，64mn =，那么3553d mq d q n ⎧-+=⎪⎨⎪++=⎩，整理得，2()5()800d m n d m n +-++-=.解得d =〔舍去负根〕.35a d =+，∴要使得3a 最大，即需要d 最大，即n m -及2(10)m n +-取最大值.*,m n N ∈，64mn =，∴当且仅当64n =且1m =时，n m -及2(10)m n +-取最大值.从而最大的d =，因此，最大的3a =………16分 2、〔连云港市2018届高三期末〕数列{a n }中，a 2＝a (a 为非零常数)，其前n 项和S n 满足：S n ＝n (a n －a 1)2(n ∈N*).(1)求数列{a n }的通项公式； (2)假设a ＝2，且21114mn a S -=，求m 、n 的值；(3)是否存在实数a 、b ，使得对任意正整数p ，数列{a n }中满足na b p +≤的最大项恰为第3p －2项?假设存在，分别求出a 与b 的取值范围；假设不存在，请说明理由、 (1)证明:由，得a 1=S 1=1⋅(a 1－a 1)2=0，∴S n =na n2， ………………………2分 那么有S n +1=(n +1)a n +12， ∴2(S n +1－S n )=(n +1)a n +1－na n ，即(n －1)a n +1=na n n ∈N*， ∴na n +2=(n +1)a n +1，两式相减得，2a n +1=a n +2+a n n ∈N*， ……………………………4分 即a n +1－a n +1=a n +1－a n n ∈N*， 故数列{a n }是等差数列.又a 1=0，a 2=a ，∴a n =(n －1)a . ………………………………6分 (2)假设a =2，那么a n =2(n －1)，∴S n =n (n -1). 由21114m n a S -=，得n 2-n +11=(m -1)2，即4(m -1)2－(2n -1)2=43，∴(2m +2n -3)(2m －2n -1)=43. ………………………………8分 ∵43是质数， 2m +2n -3>2m －2n -1， 2m +2n -3>0，∴⎩⎨⎧2m －2n －1=12m +2n －3=43，解得m =12，n =11. ………………………………10分(III)由a n +b ≤p ，得a (n －1)+b ≤p .假设a <0，那么n ≥p －ba +1，不合题意，舍去; ……………………………11分 假设a >0，那么n ≤p －ba +1.∵不等式a n +b ≤p 成立的最大正整数解为3p －2，∴3p －2≤p －ba +1<3p －1， ………………………………13分即2a －b <(3a －1)p ≤3a －b ，对任意正整数p 都成立.∴3a －1=0，解得a =13， ………………………………15分如今，23－b <0≤1－b ，解得23<b ≤1.故存在实数a 、b 满足条件， a 与b 的取值范围是a =13，23<b ≤1. ………16分 3、〔南京市、盐城市2018届高三期末〕假设数列{}n a 是首项为612t -, 公差为6的等差数列；数列{}n b 的前n 项和为3n nS t =-.(1)求数列{}n a 和{}n b 的通项公式；(2)假设数列{}n b 是等比数列, 试证明: 关于任意的(,1)n n N n ∈≥, 均存在正整数n c , 使得1n n c b a +=, 并求数列{}n c 的前n 项和n T ；(3)设数列{}n d 满足n n n d a b =⋅, 且{}n d 中不存在如此的项k d , 使得“1k k d d -<与1k k d d +<”同时成立〔其中2≥k , *∈N k 〕, 试求实数的取值范围、答案：解: (1)因为{}n a 是等差数列,因此(612)6(1)612n a t n n t =-+-=-…………2分 而数列{}n b 的前n项和为3n n S t =-,因此当2n ≥时,11(31)(31)23n n n n b --=---=⨯,又113b S t ==-,因此13,123,2n n t n b n --=⎧=⎨⨯≥⎩……………………4分 (2)证明:因为{}n b 是等比数列,因此113232t --=⨯=,即1t =,因此612n a n =- ………………5分对任意的(,1)n n N n ∈≥,由于11123636(32)12n n n n b --+=⨯=⨯=⨯+-,数列{}n c 的前n 项和13112321322n n n T n n -=+=⨯+--…………………9分(3)易得6(3)(12),14(2)3,2n nt t n d n t n --=⎧=⎨-≥⎩, 由于当2n ≥时,114(12)34(2)3n n n nd d n t n t ++-=+---38[(2)]32n n t =--⨯,因此①假设3222t -<,即74t <,那么1n n d d +>,因此当2n ≥时,{}n d 是递增数列,故由题意得12d d ≤,即6(3)(12)36(22)t t t --≤-,74t ≤≤<,………13分②假设32232t ≤-<,即7944t ≤<,那么当3n ≥时,{}n d 是递增数列,, 故由题意得23d d =,即234(22)34(23)3t t -=-,解得74t =…………………14分③假设321(,3)2m t m m N m ≤-<+∈≥,即35(,3)2424m m t m N m +≤<+∈≥,那么当2n m ≤≤时,{}n d 是递减数列,当1n m ≥+时,{}n d 是递增数列, 那么由题意,得1m m d d +=,即14(2)34(21)3m m t m t m +-=--,解得234m t +=…………15分综上所述,t ≤≤234m t +=(,2)m N m ∈≥……16分4、〔南通市2018届高三期末〕数列{a n }中，a 2=1，前n 项和为S n ，且1()2n n n a a S -=、〔1〕求a 1；〔2〕证明数列{a n }为等差数列，并写出其通项公式； 〔3〕设1lg 3n n na b +=，试问是否存在正整数p ，q (其中1<p <q )，使b 1，b p ，b q 成等比数列？假设存在，求出所有满足条件的数组(p ，q )；假设不存在，说明理由、解：(1)令n =1，那么a 1=S 1=111()2a a -=0、………………………………………3分(2)由1()2n n n a a S -=，即2nn na S =，① 得11(1)2n n n a S +++=、 ② ②－①，得1(1)n nn a na +-=、 ③因此，21(1)n n nan a ++=+、④③+④，得212n n n nana na +++=，即212n n n a a a +++=、…………………………7分 又a 1=0，a 2=1，a 2－a 1=1，因此，数列{a n }是以0为首项，1为公差的等差数列、因此，a n =n －1、………………………………………………………………9分(3)假设存在正整数数组(p ，q )，使b 1，b p ，b q 成等比数列，那么lg b 1，lg b p ，lg b q 成等差数列，因此，21333p qp q =+、……………………………………………………11分 因此，213()33q p p q =-(☆)、易知(p ，q )=(2，3)为方程(☆)的一组解、………………………………………13分 当p ≥3，且p ∈N *时，112(1)224333p p p p p p +++--=<0，故数列{23pp }(p ≥3)为递减数列，因此2133p p-≤323133⨯-<0，因此如今方程(☆)无正整数解、 综上，存在唯一正整数数对(p ，q )=(2，3)，使b 1，b p ，b q 成等比数列、…………16分注在得到③式后，两边相除并利用累乘法，得通项公式并由此说明其为等差数列的，亦相应评分、但在做除法过程中未对n ≥2的情形予以说明的，扣1分、5、〔徐州、淮安、宿迁市2018届高三期末〕,0,0<>b a 且,0≠+b a 令,,11b b a a ==且对任意正整数k ，当0≥+kk b a 时，;43,412111k k k k k b b b a a =-=++当0<+kk b a 时，.43,214111k k k k k a a b a b =+-=++ （1） 求数列}{nn b a +的通项公式；（2） 假设对任意的正整数n ，0<+n n b a 恒成立，问是否存在b a ,使得}{nb 为等比数列？假设存在，求出b a ,满足的条件；假设不存在，说明理由； （3） 假设对任意的正整数,0,<+nn b a n 且,43122+=n nb b 求数列}{nb 的通项公式. ⑴当0n na b +≥时，11124n n n a a b +=-且134n nb b +=，因此111131()2442n n n n n n n a b a b b a b +++=-+=+，……………………………………2分 又当0n na b +<时，11142n n n b a b +=-+且134n na a +=，113111()4422n n n n n n n a b a a b a b +++=-+=+，…………………………………………4分 因此，数列{}nn b a +是以b a +为首项，12为公比的等比数列， 因此，nn ba +11()2n ab -⎛⎫=+ ⎪⎝⎭、………………………………………………………5分⑵因为0n na b +<，因此n n a a 431=+，因此134n n a a -⎛⎫= ⎪⎝⎭， 11()2n n n b a b a -⎛⎫=+- ⎪⎝⎭1113()24n n a b a --⎛⎫⎛⎫=+- ⎪⎪⎝⎭⎝⎭，…………………………………8分假设存在a ，b ，使得{}nb能构成等比数列，那么1b b =，224b a b-=，34516b a b -=， 故2245()()416b a b a b --=，化简得0=+b a ，与题中0a b +≠矛盾， 故不存在a ，b 使得{}n b 为等比数列、……………………………………………10分⑶因为0n na b <+且12243+=n nb b ，因此121222141--+-=n n n b a b 因此1243+n b 21212121211113142444n n n n n a b a b b -----=-+=-+- 因此2121212131()()44n n n n b b a b +----=-+，……………………………………………12分 由⑴知，2221211()2n n n a b a b ---⎛⎫+=+ ⎪⎝⎭，因此222121132n n n a b b b -+-+⎛⎫-=- ⎪⎝⎭)()(321213112----+-+=n n n b b b b b b246241111132222n a b b -⎡⎤+⎛⎫⎛⎫⎛⎫⎛⎫=-+++++⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦11114()141139414n n a b a b b b --⎡⎤⎛⎫-⎢⎥⎪⎡⎤++⎛⎫⎝⎭⎢⎥=-=--⎢⎥ ⎪⎢⎥⎝⎭⎢⎥⎣⎦-⎢⎥⎣⎦，…………………………………13分22133()114434n n n a b b b b +⎡⎤+⎛⎫==--⎢⎥⎪⎝⎭⎢⎥⎣⎦，………………………………………………14分因此，1224()11,943()1-1,434n n na b b n b a b b n -⎧⎡⎤+⎛⎫⎪⎢⎥-- ⎪⎪⎢⎥⎝⎭⎪⎣⎦=⎨⎡⎤⎪+⎛⎫⎢⎥⎪- ⎪⎢⎥⎝⎭⎪⎣⎦⎩．为奇数时,为偶数时…………………………………16分 6、〔苏州市2018届高三期末〕设数列{}n a 的前n 项和为n S ，满足21n n a S An Bn +=++〔0A ≠〕、〔1〕假设132a =，294a =，求证数列{}n a n -是等比数列，并求数列{}n a 的通项公式； 〔2〕数列{}n a 是等差数列，求1B A-的值、7、〔泰州市2018届高三期末〕数列16n a n =-,(1)15nn b n =--,其中*n N ∈ (1)求满足1n a+=n b 的所有正整数n 的集合〔2〕n ≠16,求数列n nb a 的最大值和最小值〔3〕记数列{}n n a b 的前n 项和为n S ，求所有满足22m nS S =〔m<n 〕的有序整数对(m,n)(1)a n +1=｜b n ｜，n －15=｜n －15｜，当n ≥15时,a n +1=｜b n ｜恒成立，当n <15时,n －15=－(n －15)，n =15n 的集合{n ｜n ≥15,n ∈N *}……………………………………….…………….…………….4分 (2)nn a b =1615)1(---n n n(i)当n>16时，n 取偶数n n a b =1615--n n =1+161-n当n=18时〔nn a b 〕max =23无最小值n 取奇数时nn a b =-1-161-n n=17时〔nn a b 〕min =-2无最大值……………………………………………………………8分(ii)当n<16时，nn a b =16)15()1(---n n n当n 为偶数时nn a b =16)15(---n n =-1-161-n n=14时〔nn a b 〕max =-21〔n n a b 〕min =-1413 当n 奇数n n a b =1615--n n =1+161-n ，n=1，〔nn a b 〕max =1-151=1514，n =15，〔nn a b 〕min =0………………………………………………11分综上，nn a b 最大值为23〔n =18〕最小值-2〔n =17〕 (12)分(3)n ≤15时，b n =(-1)n-1(n-15)，a 2k -1b 2k -1+a 2k b 2k =2(16-2k )≥0，n >15时，b n =(-1)n (n -15)，a 2k -1b 2k -1+a 2k b 2k =2(2k -16)>0，其中a 15b 15+a 16b 16=0∴S 16=S 14m =7，n =8…………………………………………………………….16分8、〔无锡市2018届高三期末〕数列{a n }中，a 1=2，n ∈N +，a n >0，数列{a n }的前n 项和S n ，且满足1122n n n a S S ++=-。

十、应用题（一）试题细目表1.（南通泰州期末·18）如图，某小区中央广场由两部分组成，一部分是边长为80cm 的正方形ABCD ，另一部分是以AD 为直径的半圆，其圆心为O .规划修建的3条直道AD ，PB ，PC 将广场分割为6个区域：Ⅰ、Ⅲ、Ⅴ为绿化区域（图中阴影部分），Ⅱ、Ⅳ、Ⅵ为休闲区域，其中点P 在半圆弧上，AD 分别与PB ，PC 相交于点E ，F .（道路宽度忽略不计）【答案】【解】以AD 所在直线为x 轴，以线段AD 的中垂线为y 轴建立平面直角坐标系. （1）直线PB 的方程为2y x =，半圆O 的方程为22240x y +=(0)y ≥，由2222,40(0),y x x y y =⎧⎨+=≥⎩得y =所以，点P 到AD 的距离为.（2）①由题意，得(40cos ,40sin )P θθ. 直线PB 的方程为sin 280(40)cos 1y x θθ++=++，令0y =，得80cos 8040sin 2E x θθ+=-+80cos 40sin sin 2θθθ-=+.直线PC 的方程为sin 280(40)cos 1y x θθ-+=--，令0y =，得80cos 8040sin 2F x θθ-=++80cos 40sin sin 2θθθ+=+.所以，EF 的长度为()F E f x x θ=-80sin sin 2θθ=+，0,2πθ⎛⎫∈ ⎪⎝⎭.②区域Ⅳ、Ⅵ的面积之和为1180sin 80802sin 2S θθ⎛⎫=⨯-⨯ ⎪+⎝⎭6400sin 2θ=+， 区域Ⅱ的面积为2140sin 2S EF θ=⨯⨯180sin 40sin 2sin 2θθθ⎛⎫=⨯⨯ ⎪+⎝⎭21600sin sin 2θθ=+， 所以2121600sin 6400sin 2S S θθ++=+(0)2πθ<<. 设sin 2t θ+=，则23t <<，2121600(2)6400t S S t-++=. 81600(4)t t=+-4)≥1)=.当且仅当t =，即sin 2θ=时“”成立.所以，休闲区域Ⅱ、Ⅳ、Ⅵ的面积12S S +的最小值为21)m .答：当sin 2θ=时，绿化区域Ⅰ、Ⅲ、Ⅴ的面积之和最大.2.（无锡期末·17）如图，点C 为某沿海城市的高速公路出入口，直线BD 为海岸线，3CAB π∠=，AB BD ⊥，BC是以A 为圆心，半径为1km 的圆弧型小路.该市拟修建一条从C 通往海岸的观光专线CP PQ -，其中P 为BC 上异于,B C 的一点，PQ 与AB 平行，设PAB θ∠=.（1）证明：观光专线CP PQ -的总长度随θ的增大而减小；（2）已知新建道路PQ 的单位成本是翻新道路CP 的单位成本的2倍.当θ取何值时，观光专线CP PQ -的修建总成本最低？请说明理由.【答案】解：（1）由题意，3CAP πθ∠=-，所以3CP πθ=-，又cos 1cos PQ AB AP θθ=-=-， 所以观光专线的总长度()1cos 3f πθθθ=-+-cos 13πθθ=--++，03πθ<<，因为当03πθ<<时，'()1sin 0f θθ=-+<，所以()f θ在(0,)3π上单调递减，即观光专线CP PQ -的总长度随θ的增大而减小. （2）设翻新道路的单位成本为(0)a a >， 则总成本()(22cos )3g a πθθθ=-+-(2cos 2)3a πθθ=--++，03πθ<<，'()(12sin )g a θθ=-+，令'()0g θ=，得1sin 2θ=，因为03πθ<<，所以6πθ=， 当06πθ<<时，'()0g θ<，当63ππθ<<时，'()0g θ>.所以，当6πθ=时，()g θ最小.答：当6πθ=时，观光专线CP PQ -的修建总成本最低.3.（镇江期末·17）如图，准备在墙上钉一个支架，支架由两直杆AC 与BD 焊接而成，焊接点D 把杆AC 分成 AD , CD 两段，其中两固定点A ，B 间距离为1米，AB 与杆 AC 的夹角为60︒，杆AC 长为1米，若制作 AD 段的成本为 a 元/米，制作 CD 段的成本是2a 元/米，制作杆BD 成本是4a 元/米.设∠ADB = α，则制作整个支架的总成本记为 S 元.（1）求S 关于α的函数表达式，并求出α的取值范围； （2）问AD 段多长时，S 最小？【答案】在△ABD 中,由正弦定理得12sin sin sin()33BD ADππαα==-，所以12BD AD ==，则11)2[1)]422S a a α=++-++3)2a =，由题意得2(,)33ππα∈（201cos 4α=所以当1cos 4α=时，S 最小，此时15sin ,42sin 210AD ααα+==+=答：（1）S 关于α的函数表达式为3()2sin 2S a αα=+，且2(,)33ππα∈；（2）当510AD +=时S 最小. 4.（扬州期末·17）如图，射线OA 和OB 均为笔直的公路，扇形OPQ 区域（含边界）是一蔬菜种植园，其中P 、Q 分别在射线OA 和OB 上。

江苏省无锡市2019届高三上学期期末考试数学试卷及答案解析江苏省无锡市2019届高三上学期期末考试数学试题一、填空题：1.设集合A =｛x｜x＞0｝，B =｛x｜－2＜x＜1｝，则A∩B＝____．【答案】｛x｜0＜x＜1｝【解析】【分析】利用交集的定义直接求解即可.【详解】取集合A，B的公共部分，得：A∩B＝｛x｜0＜x＜1｝.故答案为：｛x｜0＜x＜1｝.【点睛】本题主要考查了交集的运算，属于基础题.2.设复数 z 满足 (1+ i)z = 1－3i（其中 i 是虚数单位），则 z 的实部为____．【答案】-1【解析】【分析】由复数的除法运算得z，从而可得解.【详解】z＝＝＝，所以，实部为－1故答案为：-1.【点睛】本题主要考查了复数的除法运算，属于基础题.3.有A，B，C 三所学校，学生人数的比例为3：4：5, 现用分层抽样的方法招募 n 名志愿者，若在 A 学校恰好选出 9 名志愿者，那么n =____．【答案】36【解析】【分析】利用分层抽样列方程求解即可.【详解】设A，B，C三所学校学生人数为：3x，4x，5x，则总人数为：12x，所以，，解得：n＝36.故答案为：36.【点睛】本题主要考查了分层抽样的应用，属于基础题.4.齐王与田忌赛马，田忌的上等马优于齐王的中等马，劣于齐王的上等马，田忌的中等马优于齐王的下等马，劣于齐王的中等马，田忌的下等马劣于齐王的下等马.现从双方的马匹中随机选一匹进行一场比赛，则田忌的马获胜的概率为__________．【答案】.【解析】分析：由题意结合古典概型计算公式即可求得题中的概率值.详解：由题意可知了，比赛可能的方法有种，其中田忌可获胜的比赛方法有三种：田忌的中等马对齐王的下等马，田忌的上等马对齐王的下等马，田忌的上等马对齐王的中等马，结合古典概型公式可得，田忌的马获胜的概率为.点睛：有关古典概型的概率问题，关键是正确求出基本事件总数和所求事件包含的基本事件数．(1)基本事件总数较少时，用列举法把所有基本事件一一列出时，要做到不重复、不遗漏，可借助“树状图”列举．(2)注意区分排列与组合，以及计数原理的正确使用.5.执行如图的伪代码，则输出 x 的值为____．【答案】25【解析】【分析】模拟程序语言的运行过程知该程序运行后的结果.【详解】第1步：x＝1，x＝1；第2步：x＝2，x＝4；第3步：x＝5，x＝25；退出循环结果为25.故答案为：25.【点睛】本题考查了程序语言的应用问题，是基础题．6.已知 x，y 满足约束条件，则z = x+y 的取值范围是____．【答案】［0,3］【解析】【分析】画出可行域，平移目标函数即可得范围.【详解】不等式组表示的平面区域如下图，当目标函数z = x+y 经过点O（0,0）时，取到最小值为：0经过点A（1,2）时，取到最大值：3，所以，z = x+y 的范围为［0,3］故答案为：［0,3］.【点睛】本题考查线性规划中利用可行域求目标函数的最值和范围，求目标函数范围的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值，从而得到范围.7.在四边形ABCD 中，已知，，，其中，是不共线的向量，则四边形ABCD 的形状是___【答案】梯形【解析】【分析】利用向量的加法运算得，从而得四边形ABCD是梯形.【详解】＝.所以，，即AD∥BC，且AD＝2BC所以，四边形ABCD是梯形.故答案为：梯形.【点睛】本题主要考查了向量的加法运算与向量的共线关系，属于基础题.8.以双曲线的右焦点为焦点的抛物线的标准方程是____．【答案】【解析】【分析】先求出双曲线的焦点坐标进而得抛物线的焦点坐标，即可得抛物线方程.【详解】双曲线中，c＝＝3，所以，右焦点为F（3,0），抛物线的焦点也为（3,0），所以，p＝6，抛物线的标准方程为：故答案为：.【点睛】本题主要考查了双曲线的焦点坐标及抛物线的焦点坐标的求解，属于基础题.9.已知一个圆锥的轴截面是等边三角形，侧面积为6，则该圆锥的体积等于____．【答案】【解析】【分析】分别求得底面积和高，利用圆锥的体积公式求解即可.【详解】设圆锥的底面半径为R，因为轴截面是等边三角形，所以母线长为2R，高为，侧面积S＝，解得：R＝，所以，圆锥的体积为：V＝＝3.故答案为：.【点睛】本题主要考查了圆锥的体积的计算，属于基础题.10.设公差不为零的等差数列｛｝满足a3＝7，且a1－1，a2－1，a4－1 成等比数列，则 a10等于____．【答案】21【解析】【分析】由a1－1，a2－1，a4－1 成等比数列，列方程可得公差d，从而得解.【详解】依题意，有：（a2－1）2＝（a1－1）（a4－1），即，即：，化为：＝0，因为公差不为0，所以，d＝2，＝7+14＝21故答案为：21.【点睛】本题主要考查了等差等比数列的基本量运算，属于基础题.11.已知θ是第四象限角，且cosθ＝，那么的值为____．【答案】【解析】【分析】由同角三角函数的基本关系得sinθ，利用两角和公式及二倍角公式化简求解即可.【详解】依题意，有：sinθ＝－，＝＝＝故答案为：.【点睛】本题主要考查了同角三角函数的基本关系及二倍角公式、两角和的正弦公式，属于基础题. 12.已知直线y＝a(x+2)(a > 0) 与函数 y ＝｜cosx｜的图像恰有四个公共点 A(x1，y1)，B(x2，y2)，C(x3，y3)，D(x4，y4), 其中 x1 < x2 < x3 < x4，则x4＋＝____．【答案】-2【解析】【分析】利用数形结合可得直线与余弦函数图象在处相切，且∈，利用相切得a＝，利用公共点得a ＝，从而得，进而得解.【详解】直线y＝a(x+2)过定点（－2,0），如下图所示，由图可知，直线与余弦函数图象在x4处相切，且∈，即a(x4+2)＝－cos，所以，a＝又，即直线的斜率为：a＝，因此a＝＝，即＋＝＋＝－－2＝－2.故答案为：－2.【点睛】本题主要考查了函数与方程的应用，着重考查了学生的数形结合能力，属于难题.13.已知点 P 在圆 M： (x-a)2 +(y－a+2)2＝1 上， A，B 为圆 C：x2+(y-4)2＝4 上两动点，且 AB ＝2, 则的最小值是____．【答案】【解析】【分析】取AB的中点D，＝，进而只需求｜PD｜最小即可，由C、D、P、M在一条直线上时即可得解.【详解】取AB的中点D，因为AB ＝2，R＝2，CD＝＝1，所以，＝.C（0,4），M（a，a－2）当C、D、P、M在一条直线上时，｜PD｜最小，此时，｜PD｜＝｜CM｜－｜CD｜－｜PM｜＝所以，＝≥19－12，当a＝3时取到最小值19－12.故答案为：.【点睛】本题主要考查了数量积的运算及与圆有关的最值问题，着重考查了数形结合的思想，属于中档题.14.在锐角三角形 ABC 中，已知 2sin2 A+ sin2B = 2sin2C，则的最小值为___．【答案】【解析】【分析】如图，作BD⊥AC于D，设AD＝x，CD＝y，BD＝h，由条件利用正弦定理及勾股定理可得x＝3y，再由几何关系表示正切值得＝＝，从而得解.【详解】由正弦定理，得：，如图，作BD⊥AC于D，设AD＝x，CD＝y，BD＝h，因为，所以，，化简，得：，解得：x＝3y，，，＝＝＝＝，当且仅当时取得最小值.故答案为：.【点睛】本题主要考查了三角形中的正弦定理及勾股定理，两角和的正切公式，利用基本不等式求最值，着重考查了数形结合的思想及转化与化归的能力，属于难题.二、解答题：15.在△ABC 中，设 a，b，c 分别是角 A，B，C 的对边，已知向量= (a，sinC－sinB)，= (b + c，sinA + sinB)，且(1) 求角 C 的大小(2) 若 c = 3, 求△ABC 的周长的取值范围.【答案】（1）；（2）.【解析】【分析】（1）利用正弦定理将正弦化为边，进而利用余弦定理，即可得解；（2）由正弦定理得，从而得△ABC 的周长为：a+ b＋c＝，结合的范围即可得解.【详解】（1）由，得：a（sinA + sinB）＝（b + c）（sinC－sinB）由正弦定理，得：a（a+ b）＝（b + c）（c－b）化为：a2＋b2－c2＝－ab，由余弦定理，得：cosC＝－，所以，C＝（2）因为C＝，所以，B＝－A，由B＞0，得：0＜A＜，由正弦定理，得：，△ABC 的周长为：a+ b＋c＝＝＝＝，由0＜A＜，得：，所以，周长C＝∈.【点睛】本题主要考查了正余弦定理的应用及三角函数的值域问题，属于中档题.16.在四棱锥 P - ABCD 中，锐角三角形 PAD 所在平面垂直于平面PAB，AB⊥AD，AB⊥BC。