ARMA模型的敏感性分析及稳健性研究 2007

ARMA相关模型及其应用一、本文概述随着科技的快速发展和数据分析技术的不断进步，时间序列分析在金融、经济、工程等领域的应用日益广泛。

其中，自回归移动平均模型（ARMA模型）作为一种重要的时间序列分析工具，其理论和实践价值备受关注。

本文旨在深入探讨ARMA模型的基本理论、性质及其在实际问题中的应用，旨在为读者提供一个全面而深入的理解和应用ARMA模型的参考。

本文将简要介绍ARMA模型的基本概念、发展历程及其在时间序列分析中的地位。

随后，重点阐述ARMA模型的数学原理、参数估计方法以及模型的检验与优化。

在此基础上，本文将通过具体案例，展示ARMA模型在金融市场分析、经济预测、工程信号处理等领域的实际应用，并探讨其在实际应用中的优势与局限性。

本文旨在为研究者、学者和实践者提供一个关于ARMA模型及其应用的全面指南，帮助他们更好地理解和应用这一重要的时间序列分析工具。

通过案例分析，本文旨在为相关领域的学者和实践者提供新的思路和方法，推动ARMA模型在实际问题中的更广泛应用。

二、ARMA模型基础ARMA模型，全称为自回归移动平均模型（AutoRegressive Moving Average Model），是时间序列分析中的一种重要模型。

它结合了自回归模型（AR，AutoRegressive）和移动平均模型（MA，Moving Average）的特点，能够更全面地描述时间序列数据的动态变化特性。

ARMA模型的基本形式为ARMA(p, q)，其中p是自回归项的阶数，q是移动平均项的阶数。

模型的一般表达式为：_t = \varphi_1 _{t-1} + \varphi_2 _{t-2} + \cdots +\varphi_p _{t-p} + \epsilon_t + \theta_1 \epsilon_{t-1} +\theta_2 \epsilon_{t-2} + \cdots + \theta_q \epsilon_{t-q}) 其中，(_t)是时刻t的观察值，(\varphi_i)是自回归系数，(\epsilon_t)是时刻t的白噪声项，(\theta_i)是移动平均系数。

arma模型原理
ARMA模型（AutoRegressive Moving Average Model）是一种时间序列分析模型，它结合了自回归模型（AR）和移动平均模型（MA）。

ARMA 模型的原理是，对于一个时间序列，在保持平稳性的前提下，通过自回归和移动平均两个方面来描述序列的特征。

具体来说，AR表示当前时间点的值与前面若干个时间点的值有关，而MA表示当前时间点的值与前面若干个时间点的噪声有关。

因此，ARMA模型可以很好地捕捉时间序列数据的趋势和周期性。

在实际应用中，ARMA模型通常用于预测未来的时间序列值和分析时间序列的特征。

在ARMA模型中，参数估计和模型检验是重要的步骤，需要一定的统计学知识和技能。

常用的估计方法包括最大似然估计和贝叶斯估计，而模型检验可以通过残差分析和模型诊断来进行。

总之，ARMA模型是一种经典的时间序列模型，它结合了自回归模型和移动平均模型，可以用于预测未来的时间序列值和分析时间序列的特征。

在实际应用中需要谨慎使用，需要考虑时间序列数据的特征和背景知识，以及参数估计和模型检验的可靠性。

产品需求量非平稳时序的ANN-ARMA预测模型
采峰;曾凤章
【期刊名称】《北京理工大学学报》
【年(卷),期】2007(27)3
【摘要】针对基于非平稳时序的产品需求量预测方法存在的问题,研究了人工神经网络(ANN)与自回归滑动平均(ARMA)模型的集成建模与预测方法.产品需求量的非平稳时序可分解为确定项和随机项两个部分,用人工神经网络模型拟合确定项,以表示非平稳的变化趋势;用自回归滑动平均模型拟合随机项,以表示平稳的随机成分.将两个模型的预测值之和作为产品需求量的优化预测值.仿真结果表明,集成模型的预测精度高于单一的人工神经网络模型.
【总页数】6页(P277-282)
【关键词】产品需求量;非平稳时间序列;人工神经网络;自回归滑动平均模型
【作者】采峰;曾凤章
【作者单位】北京理工大学管理与经济学院
【正文语种】中文
【中图分类】F272.1;TP183
【相关文献】
1.城市燃气负荷非平稳时序预测模型的研究 [J], 焦文玲;赵林波;秦裕琨
2.非平稳时序循环平稳趋势提取与机械故障诊断 [J], 杨龙兴;贾民平
3.产品需求量近期预测模型 [J], 黄渭澄
4.面向教学资源的均值惩罚随机森林非平稳时序预测方法 [J], 罗佩;袁景凌;陈旻骋;盛德明
5.非平稳时间序列预测模型在农产品供求量预测中的应用研究 [J], 曹聪梅;甘仞初因版权原因，仅展示原文概要，查看原文内容请购买。

罗兰C接收机天波识别技术研究周新力;刘华芹;孟庆萍;程永茂【摘要】使用现代谱估计技术进行罗兰C接收机的天波延迟估计,有效地解决了常规接收机基准点固定的问题.文章提出的方法,在不断变化的天波干扰环境下根据数据调节相应的采样点,在低信噪比条件下分离出了地波和天波的到达时刻,且具有较高的分辨率.本文对基于参数建模和特征值分解的算法进行了讨论,充分说明了现代谱估计技术能减少对准基准点的时间,可提高现有罗兰C接收机的性能.【期刊名称】《现代电子技术》【年(卷),期】2007(030)023【总页数】3页(P36-37,44)【关键词】频谱分析;天波延迟;特征值分解;参数建模【作者】周新力;刘华芹;孟庆萍;程永茂【作者单位】海军航空工程学院,山东,烟台,264001;海军航空工程学院,山东,烟台,264001;海军航空工程学院,山东,烟台,264001;海军航空工程学院,山东,烟台,264001【正文语种】中文【中图分类】TN9111 引言罗兰C接收机通过测量不同发射台发射的地波信号到达接收机的时间差(TimeDifference of Arrival，TDOA)进行定位。

时间差的测量使用脉冲相位技术，即以地波信号载波上某一个相位零点为基准点，接收设备产生多个采样脉冲，使采样脉冲分别对准主、副台信号的基准点，测量采样脉冲的时间间隔得到时差值。

但是罗兰C接收机接收到的地波信号会不可避免地受到天波以及噪声等的影响，从而使得对准基准点时会产生误差。

但是通常天波延时随着不同的时间不同的季节变化，为了消除天波干扰，传统的接收机选择天波干扰到达之前的过零点作为基准点，通常为载波第三周过零点，脉冲包络30 μs处，因为天波相对于地波的延迟最小为37.5 μs处。

实际应用中，由于接收机带宽有限，前置滤波器增加了脉冲的上升时间，常常因为30 μs处基准点的信号幅度过小而得不到足够的采样信噪比(SNR)，从而大大地降低了接收机的抗干扰能力[1]。

kk
cov[(zt zˆt ), (ztk zˆtk )] var(zt zˆt ) var(ztk zˆtk )
11
例3：建文件：1952到1996（年度），调入book12的y。 第一步：看图。y的时序图：
Y
6
5
4
3
2
1 55 60 65 70 75 80 85 90 95
12
（1）数据量不大时，如70或80数据，取M=[n/4]。 （2）数据量较大时，如300个数据，可取M=[n/10]。 （3）数据量很大时，如成千上万，可取M=根号n 此例有45个数据，最大滞后期取12即可。可得相关图如下：
该思想与计量经济学的另一重要概 念不谋而合，即蒙特卡洛模拟。
27
（2）AR (p) 序列的自相关和偏自相关：
●φk截尾性：AR(p)为p阶截尾。
偏相关截 尾
由AR(1)的稳定性知||<1，当k时，呈指数形衰减。
该现象叫拖尾或称AR(1)有无穷记忆（infinite memory）。
注意：<0时，呈振荡衰减状。
（三）ARMA模型及其改进
23
例如：AR(1)：yt c yt1 t
（1）
yt c （c yt2 t-1） t
=
c
c
y2 t2
t
t-1
=(1+ + 2 +
+
n
)c+
y n +1 t
n
-1
t
t-1+ 2t-2 +
+ nt-n
在|α|<1条件下，则有 lim n =0，则上式变为： n
3
4
5

3 模型的识别
模型的识别的本质是确定 ARIMA( p, d, q)(P, D,Q)s 中的 p, d, q 以及 P, D,Q 与 S 的取值。借助于自相关函数（Auto correlation Function, ACF）以及自相关分析 图和偏自相关函数（Partial Correlation Function, PACF）以及偏自相关分析图来 识别时序特性，并进一步确定 p 、 q 、 P 、 Q 。
模型
AR( p)
MA(q )
ARMA( p, q)
拖尾
拖尾
自相关函数
指数衰减和（或） 截尾
指数衰减和（或）
正弦衰减
正弦衰减
拖尾
拖尾
偏自相关函数
截尾（阶）
指数衰减和（或） 指数衰减和（或）
正弦衰减
正弦衰减
关于 p, q 的取值 当不包括时滞 k 12（或 4），24（或 8）， p 取落入随机区间之外的偏相关系
j 1
rk j
k 1 k 2,3,
偏自相关系数kk ，可看作自变量 k 的函数，即偏自相关函数， 1 kk 1。 它用以测量当剔除其他滞后期（ t 1, 2,3, , k 1）的干扰的条件下，Yt 与Ytk 之 间相关的程度。与自相关系数类似，同样可以采用偏自相关分析图来对模型进行
识别。
3. 勾选自相关、偏自相关，转换暂时不选（如果为非平稳序列，可勾选差分/ 自然对数转换，其中差分的阶数需要根据自相关图形来确定，通常为 0,1,2）
未进行差分处理，由图可知几乎一半的自相 关系数未进入置信区间，说明该序列非平稳，此时需要进行差分处理，即在重复 第 2 步时，差分选项选择 1 或 2。
4.4 建立 ARIMA 模型

一、自协方差函数
• 理论自协方差函数和自相关函数 对于ARMA系统来说，设序列的均值为零，则自协方差函数
k E Xt Xtk
自相关函数
k

k 0
• 样本自相关函数的计算
在拟合模型之前，我们所有的只是序列的一个有限
样本数据，无法求得理论自相关函数，只能求样本的自
= 1.1
-4.0E+10 X
-6.0E+10
25 50 75 100 125 150 175 200 225 250
X
= -1.1
24
20
20
16 15
12
10
8
5
4
0
0
-5
-10 -4
25 50 75 100 125 150-15175 200 225 250
=1
X -20
25 50 75 100 125 150 175 200 225 250
第四章 ARMA模型的特性
4.1 格林函数和平稳性
一、线性常系数差分方程及其解的一般形式 先回忆线性常系数微分方程及其解的结构：
y(t) a0 y(t) u(t)
可转化为 y(t 1) a0 y(t) u(t) 其中 a0 1 a0
将上述方程中的近似号改为等号，实数t改为自然数k，
MA(m)模型的可逆性条件为其特征方程
V m 1V m1 2V m2 ... m 0 的特征根Vk
满足 Vk 1
• ARMA(n,m)系统格林函数与逆函数的关系
在格林函数的表达式中，用 I j 代替 G，j 代替 ，
代替 ，即可得到相对应的逆函数。
第三节 自协方差函数

(1) G j是前j个时间单位以前进入系统的扰动at j对系统现在行 为(响应)影响的权数。
(2)
G
客观地刻画了系统动态响应衰减的快慢程度。
j
(3)
G
是系统动态的真实描述。系统的动态性就是蕴含在时间
j
序列中的数据依存关系。
(4) 格林函数所描述的动态性完全取决于系统参数.
17
三、根据格林函数形成系统响应(时间序列)
说明：常系数非齐次线性差分方程的特解的求法与微分方程类 似。
10
x(t 2) x(t 1) 2x(t) 12
例3-3 求下列线性差分方程的通解和特解 。
（1） x(t) 5x(t 1) 4x(t 2) 0
（2） x(t 2) x(t 1) 2x(t) 12，x(0) 0, x(1) 1
解：（1）特征方程：2 5 4 0，特征根： 1 4，2 1，
齐次方程的通解：
x(t) C1 (4)t C2 (1)t
11
x(t 2) x(t 1) 2x(t) 12
（2） x(t 2) x(t 1) 2x(t) 12，x(0) 0, x(1) 1
x(t) 2t 4 C2t


x(t) C1 C2t C3 cos( 2 t) C4 sin( 2 t)
13
二、AR(1)系统的格林函数
格林函数就是描述系统记忆扰动程度的函数。AR(1)模型为
X t 1 X t1 at
由于在动态条件下，
（3.4）
X t1 1 X t2 at1 X t 1 (1 X t2 at1 ) at 12 X t2 1at1 at X t2 1 X t3 at2

q
步截尾性；偏自相关函数
随着滞后期 k 的增加，呈现指数或者正弦波衰减，趋向于0， 这种特性称为偏自相关函数的拖尾性
1 时间序列分析模型【ARMA模型 】简介
（2）AR（ p ）序列的自相关与偏自相关函数 偏自相关函数
k , 1 k p kk kp 0,
是 p 步截尾的 ； 自协方差函数 k 满足 ( B) k 自相关函数 k 满足 ( B) k
作如下假设检验： M
H0 : pk , pk 0, k 1,, M
H1 : 存在某个 k ，使 kk
2 统计量 N pM k p 1
0 ，且
2
pk M p
( ) 表示自由度为 M 的 分布 的上侧 分位数点 2 2 M ( )，则认为 对于给定的显著性水平 0 ，若 2 p ）模型 ； 2 M ( ) ，可认为 样本不是来自AR（
0 0
它们呈指数或者正弦波衰减，具有拖尾性 （3）ARMA（ p, q ）序列的自相关与偏自相关函数均是拖尾的
1 时间序列分析模型【ARMA模型 】简介
2、模型的识别 自相关函数与偏自相关函数是识别ARMA模型的最 主要工具，B-J方法主要利用相关分析法确定模型的阶数. q q ）序列 若样本自协方差函数 k 在 步截尾，则判断 X t 是MA（ ， 若样本偏自相关函数 kk在 p 步截尾，则可判断 X t 是AR（ p ）序列 若 k ， kk 都不截尾，而仅是依负指数衰减，这时可初步认为 X t 是
若时间序列 X t 满足 1）对任意时间 t ，其均值恒为常数； 2）对任意时间 t和 s ，其自相关系数只与时间间隔 t s 有关，而与t 和 s 的起始点无关。 那么，这个时间序列就称为平稳时间序列 。

ARMA 模型（一）模型的引进AR ：011t t k t k t Y Y Y βββε--=++++ （注意：如果假设t Y 的均值为零，0β可以不写）如果序列在其均值附近波动：t 可用： 12...TT Y Y Y F Y T+++==来预测1T F +，1211 (1)T T Y Y Y F T +++++=+来预测2T F +，等等。

事实上，新的信息更能反映未来，远离现在的数据对未来的影响应该变小。

所以，按照这样一种想法，改用移动平均）。

121212111111 (11)()()TT T T T T T T T Y Y Y F Y T Y Y F Y T F Y Y F Y F T T+++++++++++==++===+-≈+- 那么，1T Y +是实际值，1T F +是上一期的预测值，所以11()T T Y F ++-是误差，即1T e +。

可见，下一期的预测值是用前一期的预测值的基础上，加上修正误差。

实际上它是跟踪数据的变化，这就是移动平均提供的一个非常好的思想！当然，也有问题，就是滞后，前后两期的误差是否一样是需要考虑的。

以此类推，继续将1T F +写成T 时刻的预测值和T 时刻的误差修正之和，如此递推下去，就可将t Y 用不同滞后期的误差项表示：即MA ：11t t t k t k Y e e e μαα--=++++ （一定平稳！）。

而ARMA 模型为：01111t t p t p t t q t q Y Y Y e e e βββαα----=+++++++对时间序列的分析的一种重要工具——自相关。

注意：移动平均可平滑数据，消除周期变动和不规则变动的影响，使长期趋势显示出来。

（二）方法性工具自相关系数只是序列逐项之间的一种简单相关，它和x 和y 之间的简单相关系数实际上是一样的。

1.自相关函数：k γ当序列t Y 完全随机时，它的自相关系数理论上为零，没有任何自相关，但是我们不可能穷尽这个总体，所以，我们只能用它的样本数据来算，当使用样本数据来算的时候可能不是零，比如说0.008、0.007或者负的0.008、0.007。

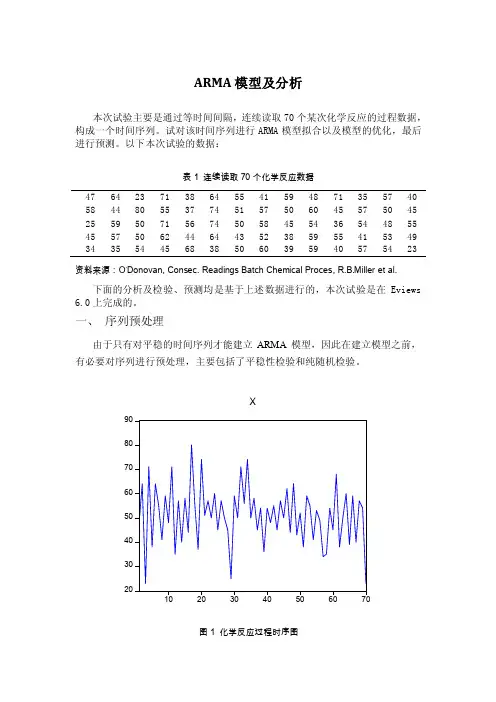
ARMA模型及分析本次试验主要是通过等时间间隔，连续读取70个某次化学反应的过程数据，构成一个时间序列。

试对该时间序列进行ARMA模型拟合以及模型的优化，最后进行预测。

以下本次试验的数据：表1 连续读取70个化学反应数据47 64 23 71 38 64 55 41 59 48 71 35 57 4058 44 80 55 37 74 51 57 50 60 45 57 50 4525 59 50 71 56 74 50 58 45 54 36 54 48 5545 57 50 62 44 64 43 52 38 59 55 41 53 4934 35 54 45 68 38 50 60 39 59 40 57 54 23 资料来源：O’Donovan, Consec. Readings Batch Chemical Proces, ler et al.下面的分析及检验、预测均是基于上述数据进行的，本次试验是在Eviews 6.0上完成的。

一、序列预处理由于只有对平稳的时间序列才能建立ARMA模型，因此在建立模型之前，有必要对序列进行预处理，主要包括了平稳性检验和纯随机检验。

图1 化学反应过程时序图序列时序图显示此化学反应过程无明显趋势或周期，波动稳定。

见图1。

图2 化学反应过程相关图和Q统计量从图2的序列的相关分析结果:1. 可以看出自相关系数始终在0周围波动，判定该序列为平稳时间序列2.看Q统计量的P值：该统计量的原假设为X的1期，2期……k期的自相关系数均等于0，备择假设为自相关系数中至少有一个不等于0，因此如图知，该P值在滞后2、3、4期是都为0,所以拒接原假设,即序列是非纯随机序列,即非白噪声序列(因为序列值之间彼此之间存在关联,所以说过去的行为对将来的发展有一定的影响,因此为非纯随机序列,即非白噪声序列)。

二、模型识别由于检验出时间序列是平稳的，且是非白噪声序列，因此可以建立模型，在建立模型之前需要识别模型阶数即确定阶数。

针对乳制品月产量数据的时间序列分析摘要：随着经济的发展，乳制品产业对国民健康水平的影响逐渐加大。

该文从乳制品行业月产量的角度出发，采用时间序列数据分析方法，对我国自1990年至2010年以来的乳制品行业月产量进行了建模分析，并在得到模型后对其进行了预测。

从分析结果来看，我国的乳制品产量在2004年发生突变，特定的月份也会对其产生影响，并且在不同的时间，影响会发生变化。

关键词：乳制品；月份特征；产量突变；产量预测；背景：纵观自1949年发展至今，整个行业可以分为四个发展阶段：1、缓慢发展阶段（1949~1977）：这段时期，我国乳产业受国家经济状况制约发展缓慢。

2、迅速扩张阶段（1978~1992）：由于开始实行多种所有制进行奶牛饲养与奶制品加工，原奶与乳品的产量、种类、质量都有明显的提高3、结构调整阶段（1993~1998）：1993年开始，乳品供给增长明显快于消费增长速度，产能出现比较严重的过剩，乳粉出现滞积，部分乳品企业发展艰难。

4、高速增长阶段（1999~至今）：1998年起，乳制品产业经过产品结构大力调整，经济效益明显提高，随着消费需求的迅速增长，乳制品产量也连年增长，乳产业已经从一个传统产业摇身一变成为一个朝阳产业。

从市场格局上看，乳制品企业可以分为4类：1、以伊利、蒙牛为代表的全国性企业；2、以光明、三鹿、维维等为代表的区域性企业；3、以北京三元、济南佳宝为代表的本省省会企业；4、以雀巢为代表的外资企业。

在行业中，企业之间的竞争非常激烈，特别地，在近十年中市场竞争引起了市场格局的极大改变。

本文将选取1993年1月起到2010年6月的月产量数据进行时间序列分析，尝试建立该时序的时间序列模型及其详细的建立过程，并对模型结果给出必要的经济意义解释。

建立模型过程：1、建模过程使用eviews软件，将1990年1月到2010年6月总计246个月度数据输入eviews中，Yt即是产量月度序列，现作出散点图如下：通过观察上图，认为不同时间下的Yt的数值差异过大，并且波动程度也差别过大，故先将序列作取对数处理，作出散点图如下：通过观察上图，认为该序列是一个典型的结构突变的过程，突变位置始于2003年12月。

ARMA模型AR模型是一种线性预测，即已知N个数据，可由模型推出第N点前面或后面的数据(设推出P点)，AR模型-模型简介所以其本质类似于插值，其目的都是为了增加有效数据，只是AR模型是由N点递推，而插值是由两点(或少数几点)去推导多点，所以AR模型要比插值方法效果更好。

ARMA模型(Auto-Regressive and Moving Average Model)是研究时间序列的重要方法，由自回归模型(简称AR模型)与滑动平均模型(简称MA 模型)为基础"混合"构成。

在市场研究中常用于长期追踪资料的研究，如：Panel研究中，用于消费行为模式变迁研究；在零售研究中，用于具有季节变动特征的销售量、市场规模的预测等。

ARMA模型的基本原理将预测指标随时间推移而形成的数据序列看作是一个随机序列，这组随机变量所具有的依存关系体现着原始数据在时间上的延续性。

一方面，影响因素的影响，另一方面，又有自身变动规律，假定影响因素为x1，x2，…，xk，由回归分析，其中Y是预测对象的观测值，e为误差。

作为预测对象Yt受到自身变化的影响，其规律可由下式体现，模型原理误差项在不同时期具有依存关系，由下式表示，模型原理图由此，获得ARMA模型表达式模型原理图模型原理总图模型预测模型-常见预测模型预测是对未来作出的估计和推断，为了达到这一目的，往往要对现实世界(或称研究对象)进行模仿或抽象，这一过程称之为建模；用建模手段获得现实世界(对象)的一种表示和体现就称为模型。

一切客观存在的事物及其运动形态我们统称为现实；现实和未来是不一样的，但是通过对于现实的研究可以预见未来，这就是预测。

从信息运动的角度看，现实之中包含着未来，孕育着未来。

因此，一个"好"的模型不仅能表达现实而且应该能准确的反映现实的发展规律。

时至今日，预测模型已多达一百余种，常用的也有二三十种。

任何预测模型都有它自身的优缺点；至今，还没有一种既有极高的预测精度，又适用于任何现实问题(研究对象)的预测模型。

可编辑课件PPT
7
自回归移动平均模型(ARMA)
如果时间序列Yt是它的当期和前期的随机误差 项以及前期值的线性函数，即可表示为：
Y t 1 Y t 1 2 Y t 2 . .p Y t . p u t 1 u t 1 q u t q
则称该序列为（p,q）阶自回归移动平均模型。 记为ARMA（p,q）
两者结合的模型（ARMA）
习惯上用AR(p)、MA(q)或ARMA(p,q)来 表示对应的滞后时期。
可编辑课件PPT
5
AR(p)模型
AR(p)模型是回归模型的一种形式，其一般形 式为：
Y t1 Y t 1 2 Y t 2 . ..p Y t p u t
另一种表达方式是用差分形式：
Y t Y t 1 1 Y t 1 . .p . 1 Y t p 1 u t
可编辑课件PPT
16
ARIMA模型
考虑ARIMA(p,d,q)模型 一个ARIMA(p,d,q)模型代表一个I(d)变量
经过d次差分后所做的AR(p)和MA(q)模 型。
可编辑课件PPT
17
此课件下载可自行编辑修改，此课件供参考！ 部分内容来源于网络，如有侵权请与我联系删除！感谢你的观看！
时间序列模型在上世纪80年代中期后得 到快速发展。
可编辑课件PPT
2
本章主要内容
时间序列模型的特点 AR、MA和ARMA模型的形式 AR、MA和ARMA模型的识别 AR、MA和ARMA模型的估计
可编辑课件PPT
3
时间序列分析模型的特点
时间序列分析通常并不需要建立在经济理论 所体现的经济关系基础之上，而是“让数据 自己说话”。Yt可由其自身的滞后值以及随 机误差项来解释，因此时间序列分析模型又 称乏理论（a-theoretic)模型。

金融风险预测模型中的多元时间序列分析方法研究与改进随着金融市场的不断发展和变化，预测金融风险的能力变得越来越重要。

多元时间序列分析方法作为一种常用的预测工具，在金融风险预测中起着关键作用。

本文将探讨金融风险预测模型中的多元时间序列分析方法的研究和改进。

多元时间序列分析方法旨在通过对多个相关变量的观察和分析，预测未来的金融风险。

其基本假设是变量之间存在着统计相关性，在过去的观测值和当前的信息基础上，可以预测未来的风险变化。

常用的多元时间序列分析模型包括自回归移动平均模型（ARMA）、自回归条件异方差模型（ARCH）以及其扩展模型GARCH等。

然而，传统的多元时间序列分析方法也存在一些局限性。

首先，它们通常基于线性假设，难以捕捉到金融市场的非线性特征。

其次，这些模型假设数据之间的关系是稳定的，但金融市场经常受到外部因素的干扰，导致数据之间的关系可能是非稳定的。

此外，传统模型对异常观测值比较敏感，容易受到极端事件的影响。

为了克服这些局限性，研究人员提出了许多改进的方法。

一种常见的方法是引入非线性模型，如神经网络模型（NN）和支持向量机模型（SVM）。

这些模型能够更好地捕捉金融市场的非线性特征，提高预测准确性。

另外，许多研究致力于解决数据不稳定性问题，采用了协整分析、平滑转换自回归模型（STAR）和门限自回归模型（TAR）等方法来考虑非稳定性。

除此之外，还有一些方法通过引入异常值处理模型，改进了传统模型的鲁棒性。

近年来，基于人工智能和机器学习的方法在金融风险预测中得到了广泛应用。

例如，深度学习模型如长短期记忆网络（LSTM）和卷积神经网络（CNN）在金融风险预测中取得了较好的效果。

这些模型能够自动学习变量之间的复杂关系，并能够处理大规模数据和非线性关系。

此外，集成学习方法如随机森林和梯度提升树等也被应用于金融风险预测中，通过结合多个模型的预测结果，提高整体的预测准确性。

除了方法的改进，还有一些研究致力于构建更好的数据集来支持金融风险预测。

注3：【2】满足平稳条件时， AR过程等价于无穷阶的MA 过程，即
X t 1 v1B v2 B
2
j ut v j B ut j 0
1 时间序列分析模型【ARMA模型 】简介
3、自回归移动平均【ARMA】模型 【B-J方法建模】
自回归移动平均序列
ARMA序列，它的阶要由从低阶到高阶逐步增加，再通过检验来确定. 但实际数据处理中，得到的样本自协方差函数和样本偏自相关函数只是
k
而只能是在某步之后围绕零值上下波动，故对于 k 和 kk 的截尾性 只能借助于统计手段进行检验和判定。
和 kk 的估计，要使它们在某一步之后全部为0几乎是不可能的，
H0 : pk , pk 0, k 1,
2 统计量 N pM
H1 : 存在某个 k ，使 kk
k p 1
0 ，且
2
pkM p
( ) 表示自由度为 M 的 分布 的上侧 分位数点 2 2 M ( )，则认为 对于给定的显著性水平 0 ，若 2 2 p ，可认为 样本不是来自AR（ ）模型 ； M ( )
【2】
( B) X t ut
AR（
的根均在单位圆外，即
p ）过程平稳的条件是滞后多项式 ( B)
( B) 0 的根大于1
1 时间序列分析模型【ARMA模型 】简介
2、移动平均【MA】模型
移动平均序列 X t ： 如果时间序列 X t 是它的当期和前期的随机误差 项的线性函数，即可表示为
时间序列的季节性是指在某一固定的时间间隔上，序列 重复出现某种特性.比如地区降雨量、旅游收入和空调销售额 等时间序列都具有明显的季节变化. 一般地，月度资料的时间序列，其季节周期为12个月；

随机时间序列分析模型随机时间序列分析模型是一种经济学和统计学领域常用的工具，用于研究一系列随机变量随时间的变化规律。

该模型基于假设，认为时间序列的观察值是随机过程的实现，且该过程具有一定的平稳性质。

下面我将介绍一种常用的随机时间序列分析模型- 自回归移动平均模型（ARMA模型）。

ARMA模型结合了自回归模型（AR）和移动平均模型（MA）的特点，用于描述时间序列数据之间的相关性。

在ARMA模型中，当前时刻的观察值被认为是过去时刻的观察值和随机误差项的线性组合。

其数学表示如下：\(X_t = c + \sum_{i=1}^{p} \phi_i X_{t-i} + \sum_{j=1}^{q}\theta_j \epsilon_{t-j} + \epsilon_t\)其中，\(X_t\)表示第t个时刻的观察值，\(c\)是常数，\(p\)和\(q\)分别表示自回归和移动平均过程的阶数，\(\phi_i\)和\(\theta_j\)是相应的回归系数，\(\epsilon_t\)表示误差项。

ARMA模型的核心思想是利用过去观察值的线性组合来预测当前观察值，并通过误差项来考虑模型无法完全解释的随机波动。

通过估计回归系数和误差项的方差，可以得到ARMA模型的具体参数估计。

ARMA模型的一个重要应用是时间序列预测。

通过拟合ARMA模型并利用已有观察值，可以对未来的观察值进行推断和预测。

这对于很多实际问题，如经济数据预测、股市走势分析等，具有重要的意义。

需要注意的是，ARMA模型在应用中需要满足一些前提条件，如观察值之间的相关性、平稳性等。

此外，ARMA模型的参数估计和模型选择也需要一定的经验和技巧。

总结起来，ARMA模型是一种常用的随机时间序列分析模型，可以用于描述时间序列数据之间的相关性和预测未来观察值。

通过合适的参数估计和模型选择，ARMA模型可以在实践中具有一定的预测能力。

随机时间序列分析是经济学和统计学中的重要方法，用于研究一系列随机变量随时间的变化规律。