第6章 尺寸链原理与应用
- 格式:doc
- 大小:12.37 MB
- 文档页数:18



尺寸链原理及其应用一、引言尺寸链原理是指在一个系统中,各个组成部分的尺寸之间存在着特定的比例关系。
这种比例关系可以用来设计和优化系统,提高系统的效率和性能。
尺寸链原理被广泛应用于各种领域,如机械设计、电子电路设计、化学反应等。
二、尺寸链原理的基本概念在一个系统中,各个组成部分的尺寸之间存在着特定的比例关系,这种比例关系可以用数学公式来表示。
例如,在机械设计中,轴承内径和外径之间的比例关系可以表示为d1/d2=k,其中d1为内径,d2为外径,k为常数。
三、尺寸链原理的应用1. 机械设计中的应用在机械设计中,利用尺寸链原理可以优化机械结构,并提高机械性能。
例如,在齿轮传动系统中,齿轮模数和齿数之间存在着特定的比例关系,在设计时可以根据这种比例关系来确定齿轮模数和齿数的取值范围。
2. 电子电路设计中的应用在电子电路设计中,利用尺寸链原理可以优化电路结构,并提高电路性能。
例如,在滤波器的设计中,电容和电感之间存在着特定的比例关系,可以根据这种比例关系来确定电容和电感的取值范围,从而优化滤波器的性能。
3. 化学反应中的应用在化学反应中,利用尺寸链原理可以优化反应条件,并提高反应效率。
例如,在合成有机物的反应中,反应物的摩尔比和反应时间之间存在着特定的比例关系,可以根据这种比例关系来确定最佳的反应条件。
四、尺寸链原理的优点1. 提高系统效率利用尺寸链原理可以优化系统结构和参数,从而提高系统效率。
2. 提高系统稳定性尺寸链原理可以保证系统各个部分之间存在着协调一致的比例关系,从而提高系统稳定性。
3. 提高设计效率利用尺寸链原理可以快速确定系统各个部分的参数范围,从而提高设计效率。
五、尺寸链原理在实际工程中的案例1. 汽车发动机设计中的应用在汽车发动机设计中,利用尺寸链原理可以优化发动机结构和参数,从而提高发动机的性能和效率。
例如,在汽车发动机的气缸直径和行程之间存在着特定的比例关系,可以根据这种比例关系来确定最佳的气缸直径和行程。


尺寸链的原理与应用1. 尺寸链的概述尺寸链是一种用于管理和控制物体尺寸之间关系的技术。
通过建立一系列连接,使得物体的尺寸能够相互影响和传递,从而实现自动的尺寸调整和适应性布局。
尺寸链在图形设计、UI设计和前端开发等领域有着广泛的应用。
2. 尺寸链的基本原理尺寸链的基本原理是通过建立连接关系,将物体的尺寸属性进行传递和关联。
根据物体间的依赖关系,可以将尺寸链分为以下几种类型:2.1. 父子尺寸链父子尺寸链是指将父容器的尺寸属性与子元素的尺寸属性进行关联。
当父容器的尺寸发生变化时,子元素的尺寸也会相应地进行调整。
这种尺寸链常见于响应式布局中,用于实现自适应和弹性布局。
2.2. 兄弟尺寸链兄弟尺寸链是指将同级元素的尺寸属性进行关联。
当一个元素的尺寸发生变化时,其他相邻的元素也会受到影响,从而实现整体布局的自动调整。
兄弟尺寸链常见于平铺式布局和流式布局中。
2.3. 链式尺寸链链式尺寸链是指将多个元素的尺寸属性进行连接形成一个链条。
当链条中的某个元素的尺寸发生变化时,其后续的元素也会相应地进行调整。
这种尺寸链常见于导航栏、分页器等需要自动调整布局的场景。
3. 尺寸链的应用实例尺寸链在实际开发中有着广泛的应用,下面以几个常见的实例介绍其具体应用:3.1. 响应式布局在响应式布局中,尺寸链被广泛应用于实现自适应和弹性布局。
通过建立父子尺寸链,子元素的尺寸会根据父容器的尺寸自动进行调整,从而使得页面能够在不同大小的屏幕上呈现出合适的布局。
3.2. 平铺式布局平铺式布局中常使用兄弟尺寸链来实现项目的等分布局。
当一个元素的尺寸发生变化时,其他相邻的元素也会按比例进行调整,保持整体布局的一致性。
3.3. 导航栏导航栏通常使用链式尺寸链实现自动调整布局。
当导航项的尺寸发生变化时,后续的导航项会相应地进行调整,从而保持导航栏的整体布局美观。
4. 总结尺寸链是一种用于管理和控制物体尺寸关系的技术,通过建立连接关系,可以实现自动的尺寸调整和适应性布局。
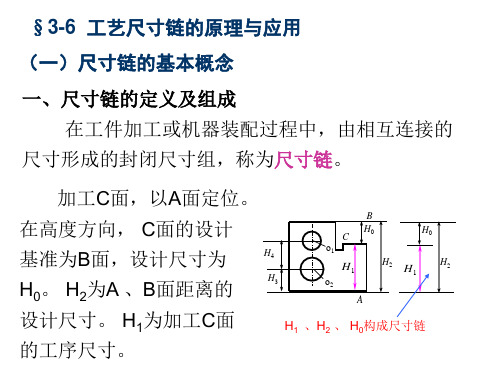
第6章 尺寸链原理与应用 6.1 尺寸链的基本概念(1) 尺寸链的定义及其特性(2)工艺尺寸链的组成 (3)尺寸链的分类(4) 工艺尺寸链的画法 6.1.1 尺寸链的定义及其特征在机器装配或零件加工过程中,由相互连接的尺寸形成的封闭尺寸组,称为工艺尺寸链,有时为了区分加工和装配工艺过程中的尺寸链,把加工过程中同一零件上的尺寸组成的尺寸链称为工艺尺寸链,把装配过程中由不同零件相关尺寸组成的尺寸链称为装配尺寸链。
如图6. 1所示零件,先按尺寸A2加工台阶,再按尺寸A1加工左右两侧端面,而0A 由1A 和2A 所确定,即012A A A =-。
那么,这些相互联系的尺寸1A 、2A 和0A 就构成了工艺尺寸链。
图6. 1零件加工和测量中的尺寸关系在图 6. 2所示的圆柱形零件的装配中,间隙0A 的大小由孔径1A 和轴颈2A 所决定,即012A A A =-。
这样,尺寸1A 、2A 和0A 也形成了一个装配尺寸链。
图图6. 2 零件装配中的尺寸关系通过以上的分析可以知道,工艺尺寸链具有以下主要特征:1)封闭性,即相互关联的尺寸必须按一定顺序排列成封闭的形式;2)关联性,指某个尺寸及精度的变化必将影响其他尺寸和精度变化,即它们的尺寸和精度互相联系,互相影响。
3)唯一性一个尺寸链只有一个封闭环,不能没有也不能出现两个或两个以上的封闭环。
A的位置。
同一个零件的加工顺序不同,不能增加或减少封闭环数,只能改变封闭环4)最少三环一个尺寸链最少有三个环,少于三环的尺寸链不存在。
6.1.3 尺寸链的分类1)按环的尺寸特征(1)长度尺寸链:全部尺寸均为长度尺寸的尺寸链,如图6. 1所示。
(2)角度尺寸链:全部尺寸均为角度尺寸的尺寸链,如图6. 3所示。
2)按环空间的位置关系(1)直线尺寸链:全部组成环平行于封闭环的尺寸链。
(2)平面尺寸链:全部组成环位于一个或几个平行平面内,但某些组成环不平行与封闭环的尺寸链,如图6. 4所示。
由直线尺寸和角度尺寸组成,且各尺寸均处于同一个或几个相互平行的平面内。
(3)空间尺寸链:全部尺寸位于几个不平行平面内的尺寸链。
空间尺寸链在空间机构运动分析和精度分析中,以及具有空间角度关系的零部件设计和加工中会遇到。
图6. 3 角度尺寸链图6. 4 平面尺寸链3)按尺寸链的应用(1) 工艺尺寸链:在加工工艺过程中,各工序的加工尺寸构成封闭的尺寸组合,或在某工序中工件、夹具、刀具、机床的有关尺寸形成了封闭的尺寸组合。
(2) 装配尺寸链:在机器或部件装配的过程中,零件或部件间有关尺寸构成了互相有联系的封闭尺寸组合,装配尺寸链有时可以和结构设计的尺寸链一致,但也可能因装配工艺不同而不同。
尺寸链还可以分为独立尺寸链和并联尺寸链基本尺寸链和派生尺寸链;标量尺寸链和矢量尺寸链等,详见GB/T 5847-2004《尺寸链计算方法》。
6.1.2 工艺尺寸链的组成工艺尺寸链中各尺寸简称环,根据各环在尺寸链中的作用,可分为封闭环和组成环两种。
1)环列入尺寸链中的每一个尺寸。
2)封闭环封闭环是尺寸链中在装配过程或加工过程间接得到(或最后形成)的一环。
封闭环常以下标“0”表示。
在如图6. 1所示的条件下,封闭环A是在所述加工或测量顺序条件下,最后形成的尺寸。
当加工或测量顺序改变,封闭环也随之改变。
在装配尺寸链中,封闭环很容易确定,如图6. 2所示,封闭环A就是零件专配后形成的间隙。
一个尺寸链中,封闭环既不可多,又不可缺,只能有一个。
3)组成环组成环是尺寸链中对封闭环有影响的所有环。
同一尺寸链中的组成环,一般以同一字母加下角标表示,如123...A A A、、。
组成环的尺寸是直接保证的,它又影响到封闭环的尺寸,根据组成环对封闭环的影响不同,组成环又可分为增环和减环。
4)增环尺寸链中的组成环,由于该环的变动引起封闭环同向变动。
即在其他组成环不变的条件下,此环增大时,封闭环随之增大。
在图6. 1和图6. 2中尺寸1A 为增环。
5)减环尺寸链中的组成环,由于该环的变动引起封闭环反向变动。
即在其它组成环不变的条件下,此环增大时,封闭环随之减小在图6. 1和图6. 2中尺寸2A 为减环。
6)补偿环尺寸链中预先选定的某一组成环,可以通过改变其大小或位置,使封闭环达到规定要求。
补偿环在装配尺寸链中经常用到。
如图6. 5所示2L 。
图6. 5 装配尺寸图6.1.4 工艺尺寸链的画法尺寸链图对于理解尺寸链的构成及尺寸链的计算有重要意义,其作法如图6. 6所示:1)首先根据工艺过程,找出间接保证的尺寸+0.34043.6 ,定出封闭环。
2)从封闭环开始,按照零件表面的联系,依次画出直接获得的尺寸+0.025020、+0.05019、1L ,作为组成环直至尺寸+0.3443.6的终端回到封闭环的起点,形成一个封闭图形。
3)确定组成环性质。
将封闭环尺寸箭头单方面画出,然后沿此方向,绕工艺尺寸链依次给各组成环画出箭头,凡是与封闭环箭头方向相同的就是减环,相反的就是增环。
在图6. 6中,尺寸+0.05019的方向与封闭环同向为减环,尺寸+0.025020、1L 的方向与封闭环反向为增环。
(a ) (b)图6. 6 画工艺尺寸链图需要注意的是:所建立的尺寸链,必须使组成环数最少,这样可以更容易满足封闭环的精度或者使各组成环的加工更容易,经济性更好。
6.2 尺寸链计算的基本公式6.2.1 尺寸链问题类型尺寸链的计算主要包括基本尺寸的计算、公差的计算和确定各环的偏差。
根据尺寸链的目的和计算顺序不同分为正计算、中间计算和反计算三类问题。
1)正计算(验算计算):已知所有组成环的基本尺寸及上、下偏差,求封闭环的基本尺寸及上、下偏差。
这种情况下,可直接利用尺寸链基本计算公式,一个方程一个未知数,即可求出封闭环的基本尺寸,最大极限尺寸或上偏差,最小极限尺寸或下偏差以及公差。
正计算用于校核图纸上的尺寸标注,或检验中间计算、反计算所得结果的正确性。
2)中间计算:已知封闭环和绝大部分组成环的基本尺寸及上、下偏差,求未知组成环的基本尺寸及上、下偏差。
同样在建立尺寸链后,利用尺寸链基本计算公式是不难求解的。
中间计算用于求解工艺尺寸链。
特别是用于加工过程中的尺寸换算。
3)反计算(设计计算):已知封闭环的基本尺寸及上、下偏差,求各组成环的基本尺寸及上、下偏差,反计算常在机器设计阶段使用。
反计算时,未知数的数目可能多于方程的个数,存在无数组解。
此时,需要人为设定一些限定条件,才能确定各组成环的公差和偏差。
尺寸链计算方法有极值法与概率法两种。
用极值法解尺寸链是从尺寸链各环均处于极值条件来求解封闭环尺寸与组成环尺寸之间关系的;用概率法解尺寸链则是运用概率伦理论来求解封闭环尺寸与组成环尺寸之间关系的。
6.2.2 尺寸链的极值解法从图中可以看出用极值法计算尺寸链的基本公式。
1)封闭环的基本尺寸封闭环的基本尺寸等于所有增环基本尺寸之和减去所有减环的基本尺寸之和,即1011mn z jz j m A A A -==+=-∑∑(6-1)0A —封闭环的基本尺寸z A —增环的基本尺寸 j A —减环的基本尺寸m —增环的环数 n —总环数2)封闭环的最大极限尺寸封闭环的最大极限尺寸风雨所有增环的最大极限尺寸之和减去减环的最小极限尺寸之和,即10max max max11mn z j z j m A A A -==+=-∑∑(6-2)0max A —封闭环的最大极限尺寸 max z A —增环的最大极限尺寸 max j A —环的最小极限尺寸3)封闭环的最小极限尺寸封闭环的最小极限尺寸等于所有增环的最小极限尺寸之和减去减环的最大极限尺寸之和,即10min min min 11mn z j z j m A A A -==+=-∑∑(6-3)0min A —封闭环的最小极限尺寸 min z A —增环的最小极限尺寸 min j A —减环的最大极限尺寸4)封闭环的上偏差封闭环的上偏差等于所有增环的上偏差之和减去所有减环的下偏差之和,即1011mn zjz j m ES ESEI-==+=-∑∑ (6-4)0ES —封闭环的上偏差 z ES —增环的上偏差 j EI —减环的下偏差5)封闭环的下偏差封闭环的下偏差等于所有增环的下偏差之和减去所有减环的上偏差之和,即1011mn zjz j m EI EIES-==+=-∑∑ (6-5)0EI —封闭环的上偏差 z EI —增环的下偏差 j ES —减环的上偏差6)封闭环的公差封闭环的公差等于所有组成环的公差之和,即101n j j T T -==∑(6-6)0T —封闭环的公差 j T —成环的公差由此可知,尺寸链的所有环中,封闭环的公差最大。
为了减小封闭环的公差应尽量减小尺寸链的环数,这就是在设计中应遵守的最短尺寸链原则用极值法求解尺寸链时,可以利用上述基本公式计算,也可以竖式法来计算。
竖式法计算的规则如下:在等号线以上将增环的基本尺寸和上下偏差自左至右依次排列;减环在排列时其基本尺寸前要加负号,上下偏差位置对调并变正负号。
将增减环的基本尺寸、上偏差、下偏差分别相加,其代数和列于等号线下,即为封闭环的基本尺寸和上下偏差。
[5]口诀:增环,上下偏差照抄;减环,上下偏差对调、反号。
[6]6.2.3 尺寸链的概率解法(数理统计法) 假设各组成环的实际尺寸符合正态分布。
1)将极限尺寸换算成平均尺寸max min2A A A ∆+=(6-7)式中max min A A A ∆、、—中间尺寸、最大极限尺寸和最小极限尺寸 2)将极限偏差换算成中间偏差ES+EI2∆=(6-8)式中ES EI ∆、、—中间偏差、上偏差和下偏差 3)封闭环的中间尺寸1011mn z j z j m L LL-∆∆∆==+=-∑∑ (6-9)式中0L ∆、0L ∆、j L ∆—封闭环、增环和减环的中间尺寸 4)封闭环的中间偏差1011mn z jz j m -==+∆=∆-∆∑∑ (6-10)式中0∆—封闭环、z ∆—增环和j ∆—减环的中间偏差 5)封闭环的公差0T =(6-11)6.2.4 尺寸链的解题步骤求解工艺尺寸链是确定工序尺寸的一个重要环节,尺寸链的计算步骤一般是:首先正确地画出尺寸链图;按照加工顺序确定封闭环、增环和减环;再进行尺寸链的计算;最后可以按封闭环公差等于各组成环公差之和的关系进行校核。
1)确定封闭环。
解工艺尺寸链时能否正确找出封闭环是求解关键。
工艺尺寸链的封闭环必须是在加工过程中最后间接形成的尺寸,即该尺寸是在获得若干直接得到的尺寸后而自然形成的尺寸。
2)查明全部组成环、画出尺寸链图。
确定封闭环后,由该封闭环尺寸循一个方向按照尺寸的相互联系依次找出全部组成环,并把它们与封闭环一起,按尺寸联系的相互顺序首尾相接,即得到尺寸链图。