教材知识梳理篇第七章圆第三节正多边形与圆有关的计算精练试题0207133【含解析】

正多边形和圆有关计算一、选择题1. 正三角形内切圆半径r 与外接圆半径R 之间的关系为（ ）A ．4R =5rB ．3R =4rC ．2R =3rD ．R =2r2. 用折纸的方法，可以直接剪出一个正五边形（如下图）.方法是：拿一张长方形纸对折，折痕为AB ，以AB 的中点O 为顶点将平角五等分，并沿五等分的线折叠，再沿CD 剪开，使展开后的图形为正五边形，则∠OCD 等于A ．108°B ．90°C ．72°D ．60°3. 一个正多边形的每个外角都是36°，这个正多边形是（ ） A ．正六边形B ．正八边形C ．正十边形D ．正十二边形4. 已知一个多边形的内角和是540°，则这个多边形是（ ） A ．四边形 B ．五边形 C ．六边形 D ．七边形5. 10．如图，小林从P 点向西直走12米后，向左转，转动的角度为α，再走12米，如此重复，小林共走了108米回到点P ，则α（ ） A ．30° B ．40° C ．80° D ．不存在6. 边长为a 的正六边形的内切圆的半径为（ ）A ．2aB ．aC ．2a D ．12a 7. 如图，⊙O 的内接多边形周长为3，⊙O 的外切多边形周长为3.4，则下列各数中与此圆的周长最接近的是（）A BC ．10D ．8. 将边长为3cm 的正三角形各边三等分，以这六个分点为顶点构成一个正六边形，则这个正六边形的面积为（ ）A.2cm 2 B.4cm 2 C.8cm 2D .2 9. 如图，两个正六边形的边长均为1，其中一个正六边形的一边恰在另一个正六边形的对角线上，则这个图形（阴影部分）外轮廓线的周长是A ．7B ．8C ．9D ．1010. 一个边长为2的正多边形的内角和是其外角和的2倍，则这个正多边形的半径是（ ） A ．2 B ． 3C ．1D ．1211. 如图，在⊙O 中，OA ＝AB ，OC ⊥AB ，则下列结论错误的是A ．弦AB 的长等于圆内接正六边形的边长B ．弦AC 的长等于圆内接正十二边形的边长P α αC ．AC BC =D ．∠BAC =30°二、填空题12. 若一个正多边形的内角和是其外角和的3倍，则这个多边形的边数是______．13. 如图是一个五角星图案，中间部分的五边形ABCDE 是一个正五边形，则图中∠ABC 的度数是14. 如图，正六边形内接于圆O ，圆O 的半径为10，则圆中阴影部分的面积为 ．15. 右图是对称中心为点O 的正六边形．如果用一个含30°角的直角三角板的角，借助点O （使角的顶点落在点O 处），把这个正六边形的面积n 等分，那么n 的所有可能的值是16. 点M 、N 分别是正八边形相邻的边AB 、BC 上的点，且AM ＝BN ，点O 是正八边形的中心，则∠MON ＝＿＿＿＿度．17. 若一个正n 边形的每个内角都等于120，则n = ．18. 如图，在半径为，圆心角等于45°的扇形AOB 内部作一个正方形CDEF ，使点C 在OA 上，点D E 、在OB 上，点F 在⌒AB 上，则阴影部分的面积为（结果保留π） ． 19. 如图，正六边形ABCDEF 的边长为2cm ，点P 为这个正六边形内部的一个动点，则点P 到这个正六边形各边的距离之和为__________cm ．三、解答题20. （1）如图1，图2，图3，在ABC △中，分别以AB AC ，为边，向ABC △外作正三角形，正四边形，正五边形，BE CD ，相交于点O ．①如图1，求证：ABE ADC △≌△； ②探究：如图1，BOC ∠= ； 如图2，BOC ∠= ； 如图3，BOC ∠= ．O ACM NE DDA（2）如图4，已知：AB AD ，是以AB 为边向ABC △外所作正n 边形的一组邻边；AC AE ，是以AC 为边向ABC △外所作正n 边形的一组邻边．BE CD ，的延长相交于点O ． ①猜想：如图4，BOC ∠= （用含n 的式子表示）； ②根据图4证明你的猜想．21. 问题背景某课外学习小组在一次学习研讨中，得到了如下两个命题：①如图1，在正三角形ABC 中，M N ，分别是AC AB ，上的点，BM 与CN 相交于点O ，若60BON =∠，则BM CN =；②如图2，在正方形ABCD 中，M N ，分别是CD AD ，上的点，BM 与CN 相交于点O ，若90BON =∠，则BM CN =．然后运用类比的思想提出了如下命题：③如图3，在正五边形ABCDE 中，M N ，分别是CD DE ，上的点，BM 与CN 相交于点O ，若108BON =∠，则BM CN =． 任务要求（1）请你从①，②，③三个命题中选择一个．．．．进行证明； （说明：选①做对的得4分，选②做对的得3分，选③做对的得5分） （2）请你继续完成下面的探索： ①如图4，在正(3)n n ≥边形ABCDEF中，M N ，分别是CD DE ，上的点，BM 与CN 相交于点O ，问当BON ∠等于多少度时，结论BM CN =成立？（不要求证明）②如图5，在正五边形ABCDE 中，M N ，分别是DE AE ，上的点，BM 与CN 相交于点O ，若108BON =∠时，请问结论BM CN =是否还成立？若成立，请给予证明；若不成立，请说明理由．（1）我选 ． 证明：22. 图1是“口子窖”酒的一个由铁皮制成的包装底盒，它是一个无盖的六棱柱形状的盒子（如图2），侧面是矩形或正方形．经测量，底面六边形有三条边的长是9cm ，有三条边的长是3cm ，每个内角都是120，该六棱柱的高为3cm ．现沿它的侧棱剪开展平，得到如图3的平面展形图．图5图1图2A图3图4ABCDE O MNF（1）制作这种底盒时，可以按图4中虚线裁剪出如图3的模片．现有一块长为17.5cm 、宽为16.5cm 的长方形铁皮，请问能否按图4的裁剪方法制作这样的无盖底盒？并请你说明理由；（2）如果用一块正三角形铁皮按图5中虚线裁剪出如图3的模片，那么这个正三角形的边长至少应为 cm ．（说明：以上裁剪均不计接缝处损耗．）图4 图523. 已知正n 边形的周长为60，边长为a ． （1）当3n =时，请直接写出a 的值；（2）把正n 边形的周长与边数同时增加7后，假设得到的仍是正多边形，它的边数为7n +，周长为67，边长为b ．有人分别取n 等于3，20，120，再求出相应的a 与b ，然后断言：“无论n 取任何大于2的正整数，a 与b 一定不相等．”你认为这种说法对吗？若不对，请求出不符合这一说法的n 的值．图1图2图39cm3cm3cm24. 等腰三角形是我们熟悉的图形之一，下面介绍一种等分等腰三角形面积的方法：在△ABC 中，AB AC ，把底边BC 分成m 等份，连接顶点A BC 和底边各等分点的线段，即可把这个三角形的面积m 等分．B C问题的提出：任意给定一个正n 边形，你能把它的面积m 等分吗？探究与发现：为了解决这个问题，我们先从简单问题入手：怎样从正三角形的中心（正多边形的各对称轴的交点，又称为正多边形的中心）引线段，才能将这个正三角形的面积m 等分？如果要把正三角形的面积四等分，我们可以先连接正三角形的中心和各顶点（如图①，这些线段将这个正三角形分成了三个全等的等腰三角形）；再把所得的每个等腰三角形的底边四等分，连接中心和各边等分点（如图②，这些线段把这个正三角形分成了12个面积相等的小三角形）；最后，依次把相邻的三个小三角形拼合在一起（如图③）．这样就能把正三角形的面积四等分．① ② ③实验与验证:仿照上述方法，利用刻度尺，在图④中画出一种将正三角形的面积五等分的示意简图．猜想与证明：怎样从正三角形的中心引线段，才能将这个正三角形的面积m 等分？叙述你的分法并说明理由． 答：拓展与延伸：怎样从正方形的中心引线段，才能将这个正方形的面积m 等分？（叙述分法即可，不需说明理由） ④A DB B B答：问题解决：怎样从正n边形的中心引线段，才能将这个正n边形的面积m等分？（叙述分法即可，不需说明理由）答：答案一、选择题1.D2. B3. C4. B5. B6. C7. C8. A9. B10. A11. DA456A二、填空题12. 813. 108°14. 100π-150 15. 2，3，4，6，12 16. 45 17. 6 18.5π382-19. 三、20. （1）①证法一：ABD △与ACE △均为等边三角形，AD AB ∴=，AC AE =2分且60BAD CAE ∠=∠=3分 BAD BAC CAE BAC ∴∠+∠=∠+∠， 即DAC BAE ∠=∠ 4分 ABE ADC ∴△≌△．5分证法二：ABD △与ACE △均为等边三角形， AD AB ∴=，AC AE = 2分 且60BAD CAE ∠=∠=3分 ADC ∴△可由ABE △绕着点A 按顺时针方向旋转60得到 4分 ABE ADC ∴△≌△． 5分②120，90，72． 8分（每空1分）（2）①360n10分②证法一：依题意，知BAD ∠和CAE ∠都是正n 边形的内角，AB AD =，AE AC =，(2)180n BAD CAEn-∴∠=∠=BAD DAE CAE DAE ∴∠-∠=∠-∠，即BAE DAC ∠=∠． 11分 ABE ADC ∴△≌△．12分 ABE ADC ∴∠=∠，180ADC ODA ∠+∠=，180ABO ODA ∴∠+∠= 13分360ABO ODA DAB BOC ∠+∠+∠+∠=，180BOC DAB ∴∠+∠=(2)180360180180n BOC DAB n n-∴∠=-∠=-= 14分 证法二：同上可证 ABE ADC △≌△．12分ABE ADC ∴∠=∠，如图，延长BA 交CO 于F ，180AFD ABE BOC ∠+∠+∠=， 180AFD ADC DAF ∠+∠+∠=13分360180BOC DAF BAD n∴∠=∠=-∠=14分证法三：同上可证 ABE ADC △≌△．12分ABE ADC ∴∠=∠．180()BOC ABE ABC ACB ACD ∠=-∠+∠+∠+∠180()BOC ADC ABC ACB ACD ∴∠=-∠+∠+∠+∠180ABC ACB BAC ∠+∠=-∠，180ADC ACD DAC ∠+∠=-∠ 180(360)BOC BAC DAC ∴∠=--∠-∠13分 即360180BOC BAD n∠=-∠=14分 证法四：同上可证 ABE ADC △≌△．12分AEB ACD ∴∠=∠．如图，连接CE ，BEC BOC OCE ∠=∠+∠ AEB AEC BOC ACD ACE ∴∠+∠=∠+∠-∠BOC AEC ACE ∴∠=∠+∠． 13分 即360180BOC CAE n∠=-∠=14分注意：此题还有其它证法，可相应评分．21. （1）选命题①．证明：在图1中，601260BON =∴+=，∠∠∠． 326013+=∴=，∠∠∠∠． 又60BC CA BCM CAN ===，∠∠，BCM CAN ∴△≌△． BM CN ∴=．选命题②．证明：在图2中，901290BON =∴+=，∠∠∠． 239013+=∴=，∠∠∠∠． 又90BC CD BCM CDN ===，∠∠，BCM CDN ∴△≌△． BM CN ∴=．选命题③．图1图2A证明：在图3中，10812108BON =∴+=，∠∠∠． 2318013+=∴=，∠∠∠∠． 又108BC CD BCM CDN ===，∠∠，BCM CDN ∴△≌△．BM CN ∴=．（2）①当(2)180n BON n-=∠时，结论BM CN =成立． ②BM CN =成立．证明：如图5，连结BD CE ，．在BCD △和CDE △中， 108BC CD BCD CDE CD DE ====，，∠∠，BCD CDE ∴△≌△．BD CE BDC CED DBC ECD ∴===，，∠∠∠∠．108CDE DEA ==∠∠，BDM CEN ∴=∠∠．108108OBC OCB OCB OCD MBC NCD +=+=∴=，，∠∠∠∠∠∠．又36DBC ECD ==∠∠，DBM ECN ∴=∠∠．BDM CEN BM CN ∴∴=．△≌△．22. （1）能．理由：由题设可知，图4中长方形的宽为616.5<．长方形的长为1217.5+<．故长为17.5cm ，宽为16.5cm 的长方形铁皮，能按图4的裁剪方法制作这样的无盖底盒．（2）15+．23. 解：（1）20a =3分图3图5 A B CD E O M N（2）此说法不正确4分 理由如下：尽管当3n =，20，120时，a b >或a b <，但可令a b =，得606077n n +=+， 即6067(*)7n n =+ 6分6042067n n ∴+-，解得60n -7分 经检验，60n =是方程(*)的根∴当60n =时，a b =，即不符合这一说法的n 的值为60． 8分24. （1）实验与验证：图（略）（2）猜想与证明：先连接正三角形的中心和各顶点，再把所得的每个等腰三角形的底边m 等分，连接中心和各等分点，依次把相邻的三个小三角形拼合在一起，即可把正三角形的面积m 等分．理由：正三角形被中心和各顶点连线分成三个全等的等腰三角形，所以这三个等腰三角形的底和高都相等；这个等腰三角形的底边被m 等分，所以所得到的每个小三角形的底和高都相等，即其面积都相等，因此，依次把相邻的三个小三角形拼合在一起合成的图形的面积也相等，即可把此正三角形的面积m 等分．（3）拓展与延伸：先连接正方形的中心和各顶点，再把所得的每个等腰三角形的底边m 等分，连接中心和各等分点，依次把相邻的四个小三角形拼合在一起，即可把正方形的面积m 等分．（4）问题解决：先连接正多边形的中心和各顶点，再把所得的每个等腰三角形的底边m 等分，连接中心和各等分点，依次把相邻的n 个小三角形拼合在一起，即可把正多边形的面积m 等分．。

24.3正多边形和圆知识梳理与同步练习人教版2024—2025学年九年级上册知识点1 正多边形的相关概念（1）正多边形：各边相等、各角也相等的多边形叫做正多边形。

（2）正多边形和圆：把一个圆n等分，依次联接各等分点所得的多边形是这个圆的内接正多边形，这个圆是这个正多边形的外接圆。

正多边形的外接圆的圆心叫做正多边形的中心。

（3）正多边形是对称图形。

当n为奇数时，是轴对称图形；当n为偶数时，既是轴对称图形，又是中心对称图形。

（4）与正多边形有关的概念：正多边形的中心：正多边形的外接圆的圆心；正多边形的半径：正多边形的外接圆的半径；正多边形的中心角：正多边形每一条边所对的外接圆的圆心角。

正n边形的每个中心角都等于360/n，正n边形的每个内角都等于【（n-2）×180】/n.正多边形的边心距：正多边形的中心到正多边形一条边的距离。

例题1.圆的半径扩大一倍，则它的相应的圆内接正n边形的边长与半径之比( )A.扩大了一倍B.扩大了两倍C.扩大了四倍D.没有变化例题2.正五边形共有__________条对称轴，正六边形共有__________条对称轴. 例题3.正n边形是对称图形，它的对称轴有条。

例题4.正n边形的每个内角是，每个中心角是。

例题5.如图，已知正六边形的外接圆半径为4，求这个正六边形的边长、周长、面积．知识点2 正多边形的计算1.正多边形的中心是这个正多边形的外接圆的圆心，也是内切圆的圆心；2.联接中心和正多边形的各顶点，所得线段都是外接圆的半径，相邻两条半径的夹角是中心角；3.在正n 变形中，分别经过各顶点的这些半径将这个正n 边形分成n 个全等的等腰三角形，每个等腰三角形的腰是正n 边形的半径，底边是正n 边形的边，顶角是正n 边形的中心角；底边上的高是正n 边形的内切圆的半径，它的长是正n 边形的边心距；注：正多边形半径R 和边长a 、边心距r 之间的数量关系式例题 6.司南是我国古代辨别方向用的一种仪器．其早在战国时期就已被发明，是现在所用指南针的始祖．如图，司南中心为一圆形，圆心为点O ，直径为20，根据八个方位将圆形八等分（图2中点A ～H ），过点E 作⊙O 的切线与AG 的延长线交于点M ，连接EG ．（1）相邻两个方位 间所夹的圆心角的度数为 ．（2）求AG 的长．（3）求ME 的长．2222⎪⎭⎫ ⎝⎛+=a r R例题7.如图，在正六边形ABCDEF中，P是BC的中点，点Q在CD上，且CQ ＝1，DQ＝3，求∠APQ的度数．例题8.正六边形ABCDEF的边长为4，求对角线AC的长和正六边形的面积．例题9.如图，正方形ABCD内接于⊙O，M为弧AD中点，连接BM，CM．（1）求证：BM＝CM；（2）连接OB、OM，求∠BOM的度数．课堂同步练习1.一个正方形、一个正五边形和一个正六边形组成了如图所示的图形，则∠ABF的度数为（）A．18°B．20°C．22°D．24°2．如图，点A，B，C，D，E，F是圆O上的六等分点，已知圆O的半径是2．则图中阴影部分的面积是（）A．B．C．D．3．刘徽在《九章算术注》中首创“割圆术”，利用圆的内接正多边形来确定圆周率，开创了中国数学发展史上圆周率研究的新纪元．某同学在学习“割圆术”的过程中，作了一个如图所示的圆内接正十二边形．若⊙O的半径为1，则这个圆内接正十二边形的面积为（）A．1B．3C．πD．2π4．如图，等边三角形ABC和正方形DEFG均内接于⊙O，若EF＝2，则BC的长为（）A．B．C．D．5．下列说法正确的是（）A．经过三个不同的点可以画一个圆B．平分弦的直径，平分这条弦所对的弧C．每条边都相等的圆内接多边形是正多边形D．如果两条弦相等，那么它们所对的圆周角也相等6．如图，正六边形螺帽的边长是a cm，这个扳手开口的距离是3cm，a的值是（）A．B．C．D．17．蜂巢结构精巧，其巢房横截面的形状均为正六边形．如图是部分巢房的横截面图，图中7个全等的正六边形不重叠且无缝隙，将其放在平面直角坐标系中，点P，Q，M均为正六边形的顶点．若点P，Q的坐标分别为，（0，﹣3），则点M的坐标为.8．如图，边长为1的正六边形ABCDEF内接于⊙O，则图中阴影部分的面积为.（结果保留π）9．如图，已知正方形ABCD内接于⊙O，点E在上，则∠BEC的度数为°．10．如图，A、B、C、D为一个正多边形的顶点，O为正多边形的中心，若∠ADB＝20°，则这个正多边形的边数为．11．如图，在⊙O中，AB＝AC，∠B＝70°，∠C度数是．12．在一个正多边形中，一个内角是与它相邻的一个外角的3倍．（1）求这个多边形的边数；（2）求这个多边形的每一个外角的度数．13．如图，正六边形ABCDEF的半径为5．（1）求对角线AC的长；（2）求这个正六边形的周长与面积．14．如图，正五边形ABCDE内接于⊙O，连结AC，BD交于点F．（1）求证：AB＝AF．（2）若⊙O的半径为10，求正五边形ABCDE的面积（结果精确到0.1，参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73）．15．如图，在正五边形ABCDE中，连结AC，AD，CE，CE交AD于点F．（1）求∠CAD的度数．（2）已知AB＝2，求DF的长．16．如图，正方形ABCD内接于⊙O，线段MN在对角线BD上运动，若⊙O的面积为2π，MN＝1，则（1）⊙O的直径长为；（2）△AMN周长的最小值是．。

《正多边形和圆》精编测试题及参考答案一、选择题1.已知圆的内接正三角形的边心距为1,则这个三角形的面积为( )A.2√3B.3√3C.4√2D.6√32.在半径为R的圆中,内接正方形与内接正六边形的边长之比为( )A.2:1B.√2:1C.√2:2D.√2:√33.如图,等边三角形ABC和正方形ADEF都内接于⊙O,则AD:AB的值是( )A.2√2:√3B.√2:√3C.√3:√2D.√3:2√2第3题第4题第5题第6题4.如图,正五边形ABCDE内接于⊙O,P为弧DE上的一点(点P不与点D重合),则∠CPD的度数为( )A.30°B.36°C.60°D.72°5.正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )A.√3B.2C.2√2D.2√36.如图,正五边形ABCDE内接于⊙O,连接OC,OD,则∠COD的度数是( )A.72°B.60°C.54°D.48°7.等边三角形的内切圆半径、外接圆半径和高的比为( )A.1:√2:√3B.1:2:√3C.1:√3:2D.1:2:38.一个正多边形的外接圆半径是其内切圆半径的√2倍,那么这个正多边形的边数是( )A.3B.4C.5D.无法确定9.下列圆的内接正多边形中,一条边所对的圆心角最大的是( )A.正三角形B.正方形C.正五边形D.正六边形10.若一个正多边形的一个内角是135°,则这个正多边形的中心角为( )A.20°B.45°C.60°D.90°11.圆内接正六边形的边长为2,则该圆内接正三角形的边长为( )A.4B.4√3C.2√2D.2√3 12.如图,⊙O 是正六边形ABCDEF 的外接圆,P 是弧EF 上一点,则∠BPD 的度数是( )A.30°B.60°C.55°D.75°第12题 第13题 第14题 第15题13.如图,两正方形彼此相邻且内接于半圆,小正方形的面积为16,半圆的半径为( )A.(4+√5)B.9C.4√5D.6√214.如图是以正八边形为背景图形设计成的剪纸作品,记正八边形 A 1B 1C 1D 1E 1F 1G 1H 1的面积为S 1,图中阴影部分面积S 2,则S 1:S 2的值为( )A.2√2B.1+ √22C.2-√2D.√24 15.如图,正方形ABCD 和正△AEF 都内接于⊙O,EF 与BC,CD 分别相交于点G,H,则EF:GH 的值是( )A.√62 B. √2 C. √3 D.2二、填空题16.如图,正五边形ABCDE 内接于⊙O,点P 为弧DE 上一点(点P 不与点D,点E 重合),连接PC 、PD,DG ⊥PC,垂足为G,则∠PDG 的度数是_____. 第16题 第14题 第18题 第19题17.如图,正六边形ABCDEF 内接于⊙O,点P 在弧AB 上,Q 是弧DE 的中点,则∠CPQ 的度数为_____.18.如图,正六边形ABCDEF的周长是24cm,连接这个六边形的各边中点G,H,K,L,M,N,则六边形GHKLMN的周长是_____.19.如图,正八边形ABCDEFGH内接于⊙O,若AC=4,则点O到AC距离为_____.20.如图,正六边形ABCDEF内接于⊙O,点P在弦AC上,若⊙O的半径为2,则阴影部分的面积是_____.三、解答题21.如图,正方形ABCD内接于⊙O,M为弧AD中点,连接BM,CM.(1)求证:BM=CM(2)连接OB,OM,求∠BOM的度数.22.如图,正六边形ABCDEF内接于⊙O,若⊙O的内接正△ACE的面积为48√3,求正六边形ABCDEF的周长.23.如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.(1)正方形ABCD与正六边形AEFCGH的边长之比为___;(2)连接BE,BE是否为⊙O的内接正n边形的一边?如果是,求出n的值;如果不是,请说明理由.24.如图,⊙O的半径为R,六边形ABCDEF是圆内接正六边形,四边形EFGH是正方形.(1)求∠OGF的度数;(2)求正六边形与正方形的面积比.25.(1)如图①, △ABC是⊙O的内接正三角形,P为弧BC上一动点,则PA,PB,PC的数量关系为______;(2)如图②,四边形ABCD是⊙O的内接正方形,P为弧BC上一动点,若∠APB=45°,(1)中PA,PB,PC之间的数量关系是否依然成立,若成立,请证明;若不成立,请说明理由.图1 图2参考答案一、选择题1-5 BBBBB 6-10 ADBAD 11-15 DBCBC二、填空题16. 54°17. 45°18. 12√3cm19. 220. 2√3三、解答题21(1)略(2)135°22.4823(1)√2：1(2)正十二边形的一边24(1)15°(2)3√3：225(1)PA+PB=PC(2)不成立。

第06讲 正多边形和圆1. 了解正多边形和圆的有关概念；2. 理解并掌握正多边形半径和边长、边心距、中心角之间的关系，会应用多边形和圆的有关知识画多边形．知识点1 圆内正多边形的计算（1）正三角形在⊙O 中△ABC 是正三角形，有关计算在Rt BOD ∆中进行：::2OD BD OB =；（2）正四边形同理，四边形的有关计算在Rt OAE ∆中进行，::OE AE OA =（3）正六边形同理，六边形的有关计算在Rt OAB ∆中进行，::2AB OB OA =. 知识点2 与正多边形有关的概念1、正多边形的中心正多边形的外接圆的圆心叫做这个正多边形的中心。

2、正多边形的半径正多边形的外接圆的半径叫做这个正多边形的半径。

3、正多边形的边心距正多边形的中心到正多边形一边的距离叫做这个正多边形的边心距。

4、中心角正多边形的每一边所对的外接圆的圆心角叫做这个正多边形的中心角。

知识点3正多边形的对称性1、正多边形的轴对称性正多边形都是轴对称图形。

一个正n边形共有n条对称轴，每条对称轴都通过正n边形的中心。

2、正多边形的中心对称性边数为偶数的正多边形是中心对称图形，它的对称中心是正多边形的中心。

3、正多边形的画法先用量角器或尺规等分圆，再做正多边形。

【题型1 正多边形与圆求角度】【典例1】（2023•青羊区校级模拟）如图，正六边形ABCDEF内接于⊙O，∠ADB的度数是（）A．20°B．30°C．45°D．60°【变式1-1】（2023•惠水县一模）如图，边长相等的正五边形、正六边形的一边重合，则∠1的度数为（）A．10°B．12°C．20°D．22°【变式1-2】（2022秋•曲周县期末）已知：如图，四边形ABCD是⊙O的内接正方形，点P是劣弧上不同于点C的任意一点，则∠BPC的度数等于（）A．45°B．60°C．35°D．55°【变式1-3】（2023•新市区校级一模）如图，⊙O与正五边形ABCDE的边AB、DE分别相切于点B、D，则劣弧所对的圆心角∠BOD的大小为（）A．150°B．144°C．135°D．120°【题型2正多边形与圆求线段长度】【典例2】（2023•龙港市二模）如图，要拧开一个边长为a的正六边形螺帽，则扳手张开的开口b至少为（）A．2a B．C．D．【变式2-1】（2023春•鼓楼区校级期中）如图，A、B、C、D为一个正多边形的顶点，若∠ADB＝15°，则该正多边形的边数为（）A．9B．10C．11D．12【变式2-2】（2022秋•烟台期末）如图，正六边形ABCDEF内接于⊙O，若⊙O 的周长等于6π，则正六边形的边长为（）A．B．3C．D．【变式2-3】（2023•苏州二模）如图，正六边形ABCDEF内接于⊙O，⊙O的半径为1，过O作OM垂直AB，交AB于点M，则OM的长为．【题型3正多边形与圆求半径】【典例3】（2022秋•巩义市期末）如图，已知⊙O的内接正方形ABCD的边长为1，则⊙O的半径为（）A．B．C．1D．【变式3-1】（2022秋•慈溪市期末）如图，正六边形ABCDEF内接于⊙O，正六边形的周长是12，则⊙O的半径是（）A．1B．C．2D．【变式3-2】（2023•宜春一模）若正方形的边长为8，则其外接圆的半径是．【题型4正多边形与圆求面积】【典例4】（2022秋•呈贡区期末）正六边形的边长为6cm，则该正六边形的内切圆面积为（）A．48πcm2B．36πcm2C．24πcm2D．27πcm2【变式4-1】（2023•大冶市一模）如图，有一个亭子，它的地基是边长为4m的正六边形，则地基的面积为（）A．4m2B．12m2C．24m2D．24m2【变式4-2】（2023•南山区二模）刘徽在《九章算术注》中首创“割圆术”，利用圆的内接正多边形来确定圆周率，开创了中国数学发展史上圆周率研究的新纪元．某同学在学习“割圆术”的过程中，作了一个如图所示的圆内接正八边形．若⊙O的半径为1，则这个圆内接正八边形的面积为（）A．πB．2πC．D．【变式4-3】（2023•济源一模）如图，正六边形ABCDEF，A（﹣2，0），D（2，0），点P从点A出发，沿A→B→C→D→E→F→A以每秒1个单位长度的速度运动，当运动到第2023秒时，△AOP的面积为（）A．B．C．D．1【题型5正多边形与圆求周长】【典例5】（2023•钦州一模）如图，若一个正六边形的对角线AB的长为10，则正六边形的周长（）A．5B．6C．30D．36【变式5-1】（2023春•余姚市期中）一个边长为1的正多边形的每个外角的度数是36°，则这个正多边形的周长是（）A．1B．10C．5D．【变式5-2】（2022秋•北辰区校级期末）边心距为3的正六边形的周长为（）A．18B．C．D．【变式5-3】（2022秋•河西区期末）六个带30°角的直角三角板拼成一个正六边形，直角三角板的最短边为10，求中间正六边形的周长．【题型6正多边形与直角坐标系综合】【典例6】（2023•西和县一模）在2022年北京冬奥会开幕式和闭幕式中，一片“雪花”的故事展现了“世界大同、天下一家”的主题，让世界观众感受到中国人的浪漫，如图，将“雪花”图案（边长为4的正六边形ABCDEF）放在平面直角坐标系中，“雪花”中心与原点重合，C，F在y轴上，则顶点B 的坐标为（）A．（4，2）B．（4，4）C．D．【变式6-1】（2023•洛龙区一模）在2022年北京冬奥会开幕式和闭幕式中，一片“雪花”的故事展现了“世界大同、天下一家”的主题，让世界观众感受了中国人的浪漫．如图，将“雪花”图案（边长为4的正六边形ABCDEF）放在平面直角坐标系中，若AB与x轴垂直，顶点A的坐标为（2，﹣3），则顶点C的坐标为（）A．）B．C．D．【变式6-2】（2022秋•绵阳期末）如图，在平面直角坐标系中，正六边形OABCDE 的边长是4，则它的内切圆圆心M的坐标是（）A．B．C．D．（2，4）1．（2023•临沂）将一个正六边形绕其中心旋转后仍与原图形重合，旋转角的大小不可能是（）A．60°B．90°C．180°D．360°2．（2023•内江）如图，正六边形ABCDEF内接于⊙O，点P在上，点Q是的中点，则∠CPQ的度数为（）A．30°B．45°C．36°D．60°3．（2023•安徽）如图，正五边形ABCDE内接于⊙O，连接OC，OD，则∠BAE ﹣∠COD＝（）A．60°B．54°C．48°D．36°4．（2023•自贡）第29届自贡国际恐龙灯会“辉煌新时代”主题灯组上有一幅不完整的正多边形图案，小华量得图中一边与对角线的夹角∠ACB＝15°，算出这个正多边形的边数是（）A．9B．10C．11D．12 5．（2022•绵阳）在2022年北京冬奥会开幕式和闭幕式中，一片“雪花”的故事展现了“世界大同、天下一家”的主题，让世界观众感受了中国人的浪漫．如图，将“雪花”图案（边长为4的正六边形ABCDEF）放在平面直角坐标系中，若AB与x轴垂直，顶点A的坐标为（2，﹣3），则顶点C的坐标为（）A．（2﹣2，3）B．（0，1+2）C．（2﹣，3）D．（2﹣2，2+）6．（2022•雅安）如图，已知⊙O的周长等于6π，则该圆内接正六边形ABCDEF 的边心距OG为（）A．3B．C．D．31．（2022秋•灵宝市期末）边长为4的正方形内接于⊙O，则⊙O的半径是（）A．B．2C．2D．4 2．（2023•梁溪区二模）如图所示，A、B、C、D是一个外角为40°的正多边形的顶点．若O为正多边形的中心，则∠OAD的度数为（）A．14°B．40°C．30°D．15°3．（2023春•汉寿县期末）若一个正多边形的一个内角的度数为144°，则这个正多边形的边数为（）A．7B．8C．9D．10 4．（2023•崆峒区校级三模）平凉市崆峒山塔群是研究院东地区砖石建筑艺术的宝贵实物资料，图①是位于崆峒山灵龟台西的灵秘塔，塔为石基砖砌身，呈六角六面四级阶状尖顶塔，图②是灵秘塔某层的平面示意图，若将其抽象为正六边形，则a的度数为（）A．45°B．50°C．60°D．72°5．（2023•玉林一模）如图，在由边长相同的7个正六边形组成的网格中，点A，B在格点上．再选择一个格点C，使△ABC是以AB为腰的等腰三角形，符合点C条件的格点个数是（）A．1B．2C．3D．4 6．（2023•夏津县一模）如图，用若干个全等的正五边形排成圆环状，图中所示的是其中3个正五边形的位置．要完成这一圆环排列，共需要正五边形的个数是（）A．7个B．8个C．9个D．10个7．（2023•咸宁模拟）如图，正五边形ABCDE内接于⊙O，其半径为1，作OF ⊥BC交⊙O于点F，则的长为（）A．πB．C．D．8．（2022•青岛）如图，正六边形ABCDEF内接于⊙O，点M在上，则∠CME 的度数为（）A．30°B．36°C．45°D．60°9．（2022秋•荔湾区校级期末）如图．点O是正五边形ABCDE的中心，⊙O 是正五边形的外接圆，∠ADE的度数为（）A．30°B．32°C．36°D．40°10．（2022•思明区校级二模）如图，正三角形PMN的顶点分别是正六边形ABCDEF三边的中点，则三角形PMN与六边形ABCDEF的面积之比（）A．1：2B．1：3C．2：3D．3：8 11．（2022•桐梓县模拟）如图，⊙O与正六边形OABCDE的边OA，OE分别交于点F，G，点M为劣弧FG的中点．若FM＝4．则点O到FM的距离是（）A．4B．C．D．12．（2023春•高邑县期末）定义：如果几个全等的正n边形依次有一边重合，排成一圈，中间可以围成一个正多边形，那么我们称作正n边形的环状连接．如图1，我们可以看作正八边形的环状连接，中间围成一个正方形．（1）若正六边形作环状连接，如图2，中间可以围成的正多边形的边数为；（2）若边长为a的正n边形作环状连接，中间围成的是等边三角形，则这个环状连接的外轮廓长为．（用含a的代数式表示）13．（2023•兴庆区校级一模）如图，在平面直角坐标系中，边长为2的正六边形ABCDEF的中心与原点O重合，AB∥x轴，交y轴于点P．将△OAP绕点O顺时针旋转，每次旋转90°，则第2023次旋转结束时，点A的坐标为．14．（2023•新城区校级二模）如图，已知⊙O的内接正六边形ABCDEF的边心距OM是，则正六边形的边长为．15．（2023•镇江一模）在九年级《数学实验手册》中，我们探究了最小覆盖圆与图形之间的关系．现有如图所示的等边三角形△ABC，边长为3，若分别以顶点A、B、C为圆心作三个等圆，这三个等圆能完全覆盖△ABC，则所作等圆的最小半径是．16．（2023•抚州一模）蜂巢的构造非常美丽、科学，如图是由7个形状、大小完全相同的正六边形组成的网络，正六边形的顶点称为格点，△ABC的顶点都在格点上．设定AB边如图所示，则△ABC是直角三角形的个数有．。

中考数学复习----《正多边形与圆》知识点总结与练习题（含答案）知识点总结1.正多边形与圆的关系把一个圆分成n（n是大于2的自然数）等份，依次连接各分点所得的多边形是这个圆的内接正多边形，这个圆叫做这个正多边形的外接圆。

2.正多边形的有关概念①中心：正多边形的外接圆的圆心叫做正多边形的中心。

②正多边形的半径：外接圆的半径叫做正多边形的半径。

③中心角：正多边形每一边所对的圆心角叫做正多边形的中心角。

④边心距：中心到正多边形的一边的距离叫做正多边形的边心距。

练习题1、（2022•长春）跳棋是一项传统的智力游戏．如图是一副跳棋棋盘的示意图，它可以看作是由全等的等边三角形ABC和等边三角形DEF组合而成，它们重叠部分的图形为正六边形．若AB＝27厘米，则这个正六边形的周长为厘米．【分析】根据对称性和周长公式进行解答即可．【解答】解：由图象的对称性可得，AM＝MN＝BN＝AB＝9（厘米），∴正六边形的周长为9×6＝54（厘米），故答案为：54．2、（2022•营口）如图，在正六边形ABCDEF中，连接AC，CF，则∠ACF＝度．【分析】设正六边形的边长为1，正六边形的每个内角为120°，在△ABC中，根据等腰三角形两底角相等得到∠BAC＝30°，从而∠CAF＝∠BAF﹣∠BAC＝120°﹣30°＝90°，过点B作BM⊥AC于点M，根据含30°的直角三角形的性质求出BM，根据勾股定理求出AM，进而得到AC的长，根据tan∠ACF＝＝＝即可得出∠ACF＝30°．【解答】解：设正六边形的边长为1，正六边形的每个内角＝（6﹣2）×180°÷6＝120°，∵AB＝BC，∠B＝120°，∴∠BAC＝∠BCA＝×（180°﹣120°）＝30°，∵∠BAF＝120°，∴∠CAF＝∠BAF﹣∠BAC＝120°﹣30°＝90°，如图，过点B作BM⊥AC于点M，则AM＝CM（等腰三角形三线合一），∵∠BMA＝90°，∠BAM＝30°，∴BM＝AB＝，∴AM＝＝＝，∴AC＝2AM＝，∵tan∠ACF＝＝＝，∴∠ACF＝30°，故答案为：30．3、（2022•呼和浩特）如图，从一个边长是a的正五边形纸片上剪出一个扇形，这个扇形的面积为（用含π的代数式表示）；如果将剪下来的扇形围成一个圆锥，圆锥的底面圆直径为．【分析】先求出正五边形的内角的度数，根据扇形面积的计算方法进行计算即可；扇形的弧长等于圆锥的底面周长，可求出底面直径．【解答】解：∵五边形ABCDE是正五边形，∴∠BCD＝＝108°，∴S扇形＝＝；又∵弧BD的长为＝，即圆锥底面周长为，∴圆锥底面直径为，故答案为：；．4、（2022•绥化）如图，正六边形ABCDEF和正五边形AHIJK内接于⊙O，且有公共顶点A，则∠BOH的度数为度．【分析】求出正六边形的中心角∠AOB和正五边形的中心角∠AOH，即可得出∠BOH的度数．【解答】解：如图，连接OA，正六边形的中心角为∠AOB＝360°÷6＝60°，正五边形的中心角为∠AOH＝360°÷5＝72°，∴∠BOH＝∠AOH﹣∠AOB＝72°﹣60°＝12°．故答案为：12．5、（2022•梧州）如图，四边形ABCD是⊙O的内接正四边形，分别以点A，O为圆心，取大1OA的定长为半径画弧，两弧相交于点M，N，作直线MN，交⊙O于点E，F．若OA 于2＝1，则BE⌒，AE，AB所围成的阴影部分面积为．【分析】连接OE、OB．由题意可知，∴△AOE为等边三角形，推出S阴影＝S扇形AOB﹣S弓形AOE﹣S△AOB＝S扇形AOB﹣（S扇形AOE﹣S△AOE）﹣S△AOB＝S扇形AOB﹣S扇形AOE+S△AOE ﹣S△AOB，即可求出答案．【解答】解：连接OE、OB，由题意可知，直线MN垂直平分线段OA，∴EA＝EO，∵OA＝OE，∴△AOE为等边三角形，∴∠AOE＝60°，∵四边形ABCD是⊙O的内接正四边形，∴∠AOB＝90°，∴∠BOE＝30°，∵S弓形AOE＝S扇形AOE﹣S△AOE，∴S阴影＝S扇形AOB﹣S弓形AOE﹣S△AOB＝S扇形AOB﹣（S扇形AOE﹣S△AOE）﹣S△AOB＝S扇形AOB﹣S扇形AOE+S△AOE﹣S△AOB＝S扇形BOE+S△AOE﹣S△AOB＝+﹣＝．故答案为：．6、（2022•宿迁）如图，在正六边形ABCDEF中，AB＝6，点M在边AF上，且AM＝2．若经过点M的直线l将正六边形面积平分，则直线l被正六边形所截的线段长是．【分析】设正六边形ABCDEF的中心为O，过点M、O作直线l交CD于点N，则直线l 将正六边形的面积平分，直线l被正六边形所截的线段长是MN，连接OF，过点M作MH ⊥OF于点H，连接OA，由正六边形的性质得出AF＝AB＝6，∠AFO＝∠AFE＝×＝60°，MO＝ON，进而得出△OAF是等边三角形，得出OA＝OF＝AF＝6，由AM＝2，得出MF＝4，由MH⊥OF，得出∠FMH＝30°，进而求出FH＝2，MH＝2，再求出OH＝4，利用勾股定理求出OM＝2，即可求出MN的长度，即可得出答案．【解答】解：如图，设正六边形ABCDEF的中心为O，过点M、O作直线l交CD于点N，则直线l将正六边形的面积平分，直线l被正六边形所截的线段长是MN，连接OF，过点M 作MH⊥OF于点H，连接OA，∵六边形ABCDEF是正六边形，AB＝6，中心为O，∴AF＝AB＝6，∠AFO＝∠AFE＝×＝60°，MO＝ON，∵OA＝OF，∴△OAF是等边三角形，∴OA＝OF＝AF＝6，∵AM＝2，∴MF＝AF﹣AM＝6﹣2＝4，∵MH⊥OF，∴∠FMH＝90°﹣60°＝30°，∴FH＝MF＝×4＝2，MH＝＝＝2，∴OH＝OF﹣FH＝6﹣2＝4，∴OM＝＝＝2，∴NO＝OM＝2，∴MN＝NO+OM＝2+2＝4，故答案为：4．。

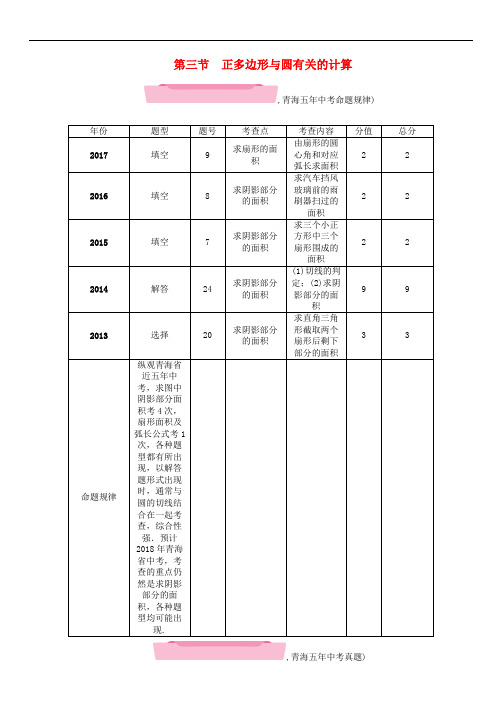
第三节正多边形与圆有关的计算,青海五年中考命题规律),青海五年中考真题)正多边形与圆1．(2015西宁中考)一元钱硬币的直径为24 mm ，则用它能完全覆盖住正六边形的边长最大不能超过( A )A ．12 mmB ．12 3 mmC ．6 mmD ．6 3 mm扇形与弧长之间的关系2．(2017青海中考)已知扇形的圆心角为240°，所对的弧长为16π3，则此扇形的面积是__32π3__．3．(2013西宁中考)如图，网格图中每个小正方形的边长为1，则AB ︵的长l ＝2π__．,(第3题图)),(第4题图))求阴影部分的面积4．(2013青海中考)如图，在直角△ABC 中，∠ACB ＝90°，AC ＝8 cm ，BC ＝6 cm ，分别以A ，B 为圆心，以AB 2的长为半径作圆，将直角△ABC 截去两个扇形，则剩余(阴影)部分的面积为( A )A .⎝ ⎛⎭⎪⎫24－254πcm 2 B .254π cm 2C .⎝⎛⎭⎪⎫24－58πcm 2 D .⎝⎛⎭⎪⎫24－256πcm 25．(2016青海中考)如图，AC 是汽车挡风玻璃前的雨刷器，如果AO ＝45 cm ，CO ＝5 cm ，当AC 绕点O 顺时针旋转90°时，则雨刷器AC 扫过的面积为__500π__cm 2.(结果保留π),(第5题图)) ,(第6题图))6．(2015青海中考)如图，三个小正方形的边长都为1，则图中阴影部分面积的和是__3π8__．(结果保留π)7．(2014青海中考)如图，BE 是⊙O 的直径，点A 在EB 的延长线上，弦PD⊥BE ，垂足为C ，连接OD ，∠AOD ＝∠APC.(1)求证：AP 是⊙O 的切线；(2)若⊙O 的半径是4，AP ＝43，求图中阴影部分的面积．解：(1)连接OP ，则OD ＝OP ，∴∠OPD ＝∠ODP.∵∠APC＝∠AOD，∴∠OPD ＋∠APC＝∠ODP＋∠AOD.又∵PD⊥BE，∴∠ODP ＋∠AOD＝90°，则∠OPD＋∠APC＝90°，即∠APO＝90°，∴A P 是⊙O 的切线；(2)在Rt △APO 中，∵AP ＝43，OP ＝4，∴AO ＝AP 2＋PO 2＝8，即PO ＝12AO ，∴∠A ＝30°，可知∠POA＝60°.又∵PD⊥BE，∴∠OPC ＝30°且PC ＝CD ，∠POD ＝120°，∴OC ＝12PO ＝2，则PC ＝PO 2－OC 2＝23.∴PD＝2PC ＝43，∴S 阴影＝S 扇形POD －S △OPD ＝120360·π·42－12×43×2＝163π－4 3.,中考考点清单)圆的弧长及扇形面积公式如果圆的半径是R ，弧所对的圆心角度数是n ，那么圆锥的侧面积与全面积正多边形与圆【方法点拨】1．牢记圆的有关计算公式，并灵活处理好公式之间的转换，当出现求不规则图形的面积时，注意利用割补法与等积变换转化为规则图形，再利用规则图形的公式求解．2．圆锥的侧面问题转化为平面问题，如最短路线问题．,中考重难点突破)弧长与扇形面积【例1】(昆明中考)如图，AB 是⊙O 的直径，∠BAC ＝90°，四边形EBOC 是平行四边形，EB 交⊙O 于点D ，连接CD 并延长交AB 的延长线于点F.(1)求证：CF 是⊙O 的切线；(2)若∠F＝30°，EB ＝4，求图中阴影部分的面积．(结果保留根号和π)【解析】(1)连接OD ，证出∠CDO＝90°即可；(2)阴影部分面积用2S △OAC 减去S 扇形OAD 即可．【答案】解：(1)连接OD ，∵四边形EBOC 是平行四边形，∴BE ＝OC ，BE ∥OC ，∴∠OBD ＝∠AOC，∠ODB ＝∠DOC.又∵OD＝OB ，∴∠OBD ＝∠ODB，∴∠DOC ＝∠AOC.在△DOC 和△AOC 中，DO ＝AO ，∠DOC ＝∠AOC，OC ＝OC ，∴△DOC ≌△AOC.∴∠CDO ＝∠CAO.∵∠CAO＝90°，∴OD ⊥CF.∵点D 在⊙O 上，OD 是半径，∴CF 是⊙O 的切线；(2)设OC 与⊙O 交于点G .∵∠F＝30°，EB ＝4.由(1)得OC ＝BE ＝4，∠FCA ＝60°，∠FOD ＝60°，∴∠FCO ＝∠OCA＝30°，∠DOC ＝∠AOC＝60°，∴OA ＝12OC ＝2.在Rt △OCA 中，∠CAO ＝90°，由勾股定理得：AC ＝OC 2－OA 2＝42－22＝23，∴S △OAC ＝12OA·AC＝23，∴S扇形OAD ＝120π×22360＝43π，∴S 阴影＝2S △OAC －S扇形OAD＝43－43π.1．(2017烟台中考)如图，▱ABCD 中，∠B ＝70°，BC ＝6，以AD 为直径的⊙O 交CD 于点E ，则DE ︵长为( B )A .13πB .23πC .76πD .43π(第1题图)(第2题图)2．(2017河南中考)如图，将半径为2，圆心角为120°的扇形OAB 绕点A 逆时针旋转60°，点O ，B 的对应点分别为O′，B ′，连接BB′，则图中阴影部分的面积为( C )A .2π3 B ．23－π3C ．23－2π3 D ．43－2π33．(2017济宁中考)如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝BC ＝1.将Rt △ABC 绕点逆时针旋转30°后得到Rt △ADE ，点B 经过的路径为BD ︵，则图中阴影部分的面积是( A )A .π6B .π3C .π2－12D .12(第3题图)(第4题图)4．(宁波中考)如图，半圆O 的直径AB ＝2，弦C D∥AB，∠COD ＝90°，则图中阴影部分的面积为__π4__．5．(咸宁中考)如图，在△ABC 中，∠C ＝90°，∠BAC 的平分线交BC 于点D ，点O 在AB 上，以点O 为圆心，OA 为半径的圆恰好经过点D ，分别交AC ，AB 于点E ，F.(1)试判断直线BC 与⊙O 的位置关系，并说明理由； (2)若BD ＝23，BF ＝2，求阴影部分的面积．(结果保留π)解：(1)直线BC 与⊙O 相切．理由如下：连接OD ，∵AD 平分∠BAC，∴∠CAD ＝∠OAD.又∠OAD＝∠ODA，∴∠CAD ＝∠ODA，∴OD ∥AC ，∴∠BDO ＝∠C＝90°，∴直线BC 与⊙O 相切；(2)设⊙O 的半径为r ，则OD ＝r ，OB ＝r ＋2，由(1)知∠BDO＝90°，∴OD 2＋BD 2＝OB 2，即r 2＋(23)2＝(r ＋2)2，解得r ＝2.∵tan ∠BOD ＝BD OD ＝232＝3，∴∠BOD ＝60°，∴S阴影＝S △OBD －S扇形ODF＝12×OD×B D －60360×πr 2＝23－23π.6．(2016青海中考模拟)如图，在正方形ABCD 中，AD ＝2，E 是AB 的中点，将△BEC 绕点B 逆时针旋转90°后，点E 落在CB 的延长线上点F 处，点C 落在点A 处，再将线段AF 绕点F 顺时针旋转90°得线段FG ，连接EF ，CG.(1)求证：EF∥CG；(2)求点C ，点A 在旋转过程中形成的AC ︵，AG ︵与线段CG 所围成的阴影部分的面积．解：(1)∵∠ECB＋∠BEC＝∠ECB＋∠AFB＝90°.又∵∠AFG＝∠AFB＋∠CFG＝90°，∴∠ECB ＝∠GFC，∴EC ∥FG ，又∵EC＝FA ＝FG ，∴四边形EFGC 是平行四边形，∴EF ∥CG ；(2)S 阴影＝S △FCG ＋S △ABF ＋S 扇形ABC －S 扇形AFG ＝12×(1＋2)×1＋12×2×1＋90360π×22－90360π×(22＋12)＝52－14π.圆锥的侧面积与全面积【例2】(2017绵阳中考)“赶陀螺”是一项深受人们喜爱的运动，如图所示是一个陀螺的立体结构图，已知底面圆的直径AB ＝8 cm ，圆柱体部分的高BC ＝6 cm ，圆锥体部分的高CD ＝3 cm ，则这个陀螺的表面积是( )A ．68π cm 2B ．74π cm 2C ．84π cm 2D ．100π cm 2【解析】先算圆柱的底面积，再算圆柱的侧面积和圆锥的侧面积，最后求其和即可． 【答案】C7．(莱芜中考)将半径为3 cm 的圆形纸片沿AB 折叠后，圆弧恰好能经过圆心O ，用图中阴影部分的扇形围成一个圆锥的侧面，则这个圆锥的高为( A )A ．2 2 cmB . 2 cmC .10 cmD .32cm8．(2017泰安中考)工人师傅用一张半径为24 cm ，圆心角为150°的扇形铁皮做成一个圆锥的侧面，则这个圆锥的高为119__cm __．正多边形与圆的有关计算【例3】(2017宜宾中考)如图，⊙O 的内接正五边形ABCDE 的对角线AD 与BE 相交于点G ，AE ＝2，则EG 的长是________．【解析】由正五边形性质可求∠AEB＝∠ABE＝∠EAG＝36°，∠BAG ＝∠AGB＝72°，AB ＝BG ＝AE ＝2，从而可得△AEG∽△BEA，列比例线段求解即可．【答案】5－19．(2017宁德中考)将边长为2的正六边形ABCDEF 绕中心O 顺时针旋转α°与原图形重合，当α最小时，点A 运动的路径长为__2π3__．。

(完整word)正多边形和圆练习题- 1 -ORQPDCBA正多边形和圆一、有关概念1．把圆分成n 等份，依次连接各分点所得的多边形是______________．2．正多边形都是______对称图形，正n 边形有_______条对称轴，每条对称轴都经过正n 边形的__________．3．若n 为偶数,正n 边形为_________对称图形，它的中心就是__________．4．正n 边形的内角和为_______________，每个内角的度数为________________．5．正n 边形有n 个相等的中心角,每个中心角的度数为____________，正n 边形有n 个相等的外角,每个外角的度数为____________ 有关计算1.圆内接正六边形一边所对的圆周角是（ ） (A ）30︒．（B ）60︒．（C ）150︒．（D)30︒或150︒． 2．要用圆形要板截出一个边长为3cm 的正方形桌面，则选用的圆形木板的直径至少应为_____________cm ． 例1．如图,已知正六边形的外接圆半径为4，求这个正六边形的中心角、边长、周长、面积．3。

已知正三角形、正方形、正六边形的半径都是R ，请你将各正多边形的边长、边心距、周长和面积值填在下表中．（用R 来表示）边长边心距周长面积正三角形正方形正六边形4.下列图形中既是中心对称图形，又是轴对称图形的是（ ） （A ）正三角形．（B ）正五边形． （C ）正六边形．（D ）正七边形．5.若一个正多边形的每个内角的度数是中心角的3倍，则正多边形的边数是( )（A ）4．（B ）6．(C)8．（D ）12．6．正多边形的一个内角等于它的一个外角的8倍，那么这个正多边形的边数是________。

7。

要用圆形铁片截出边长为4cm 的正方形铁片，则选用的圆形铁片的直径最小要____________cm ．8。

如图，有一个边长为1。

5cm 的正六边形，如果要剪一张圆形纸片完全盖住这个图形，那么这张圆形纸片的最小半径为___________cm ．9．已知两个正多边形的边数之比为2：1，而它们的(完整word)正多边形和圆练习题- 2 -O 图3-34DBAC 图3-35PND ME BAC内角和之比为8:3，求这两个正多边形的边数．弧长及扇形的面积弧长公式: 扇形面积公式： 一、填空题：1。

§ 2.6 正多边形与圆一、概念知识点1 正多边形及其有关概念★正多边形：________相等、________也相等的多边形叫做正多边形.注：边数3n 的多边形必须同时满足“各边相等”和“各角相等”这两个条件，才能判定它是正多边形.例1 下列说法正确的是（）A.正三角形不是正多边形B.平行四边形是正多边形C.正方形是正多边形D.各角相等的多边形是正多边形知识点2 正多边形的对称性（重点）1.正多边形都是________图形.一个正n边形共有_______条对称轴，每一条对称轴都经过正n边形的_________.2.一个正多边形，如果有偶数条边，那么它是________________图形，也是_________________图形；如果有奇数条边，那么是_______________图形.注：（1）如果一个正多边形是中心对称图形，那么它的中心就是对称中心；（2）正n边形的内角和等于________________，每一个内角都等于___________________，每一个外角都等于_________________.知识点3 正多边形的判定例2 如图，在正∆ABC中，E,F,G,H,L,K分别是各边的三等分点，试说明六边形EFGHLK是正六边形.二、经典题型题型1 根据正多边形的性质求角例1 如图，正方形ABCD是O的内接正方形，点P是弧CD上不同于点C的任意一点，则∠BPC等于___________.题型2 利用正多边形的性质求图形的面积例 2 如图，正六边形内接于O，O的半径为10，则图中阴影面积_________.典例精讲：1． 下列边长为a 的正多边形与边长为a 的正方形组合起来，不能镶嵌成平面( ) 、(1)正三角形 (2)正五边形 (3)正六边形 (4)正八边形A ．(1)(2)B ．(2)(4)C ．(1)(3)D ．(1)(4)2. 若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r 3，r 4，r 6，则r 3：r 4：r 6等于( )A ．1:2:3B ．3:2:1C ．1:2:3D ． 3:2:13． 已知正六边形ABCDEF 内接于⊙O ，图中阴影部分的面积为312，则⊙O的半径为______________________．（第4题） （第5题）4．如图，正方形ABCD 内接于⊙O ，点E 在AD 上，则∠BEC= ．5．将一块正六边形硬纸片（图1），做成一个底面仍为正六边形且高相等的无盖纸盒（侧面均垂直于底面，见图2），需在每一个顶点处剪去一个四边形，例如图中的四边形AGA /H ，那么∠GA /H 的大小是 度．OB CDA EF E D C A O6．从一个半径为10㎝的圆形纸片上裁出一个最大的正方形，则此正方形的边长为 ．7.如图，若正方形A 1B 1C 1D 1内接于正方形ABCD 的内接圆，则AB B A 11的值为（ ）A ．21 B ．22 C ．41D ．42。

24.3正多边形和圆知识点1正多边形与圆的关系1．如果一个四边形的外接圆与内切圆是同心圆，那么这个四边形一定是()A．矩形B．菱形C．正方形D．不能确定2．如图24－3－1所示，已知△ABC是⊙O的内接等腰三角形，顶角∠BAC＝36°，弦BD，CE分别平分∠ABC，∠ACB.求证：五边形AEBCD是正五边形．图24－3－1知识点2与正多边形有关的计算3．如果一个正多边形的中心角为72°，那么这个正多边形的边数是()A．4 B．5 C．6 D．74．若正方形的边长为6，则其内切圆半径的大小为()A．3 2 B．3 C．6 D．6 25．2016·南平若正六边形的半径为4，则它的边长等于()A．4 B．2 C．2 3 D．4 36．如图24－3－2所示，正六边形ABCDEF内接于⊙O，则∠ADB的度数是()图24－3－2A．60°B．45°C．30°D．22.5°7．正八边形的中心角等于________度．8．将一个边长为1的正八边形补成如图24－3－3所示的正方形，这个正方形的边长等于________．(结果保留根号)图24－3－39．2017·资阳边长相等的正五边形和正六边形如图24－3－4所示拼接在一起，则∠ABC ＝________°.图24－3－410．如图24－3－5，已知正五边形ABCDE，M是CD的中点，连接AC，BE，AM.求证：(1)AC＝BE；(2)AM⊥CD.图24－3－5知识点3与正多边形有关的作图11．已知⊙O和⊙O上的一点A，作⊙O的内接正方形和内接正六边形(点A为正方形和正六边形的顶点)．12．如图24－3－6所示，⊙O的内接多边形的周长为3，⊙O的外切多边形的周长为3.4，则下列各数中与此圆的周长最接近的是()图24－3－6A. 6B.8C.10D.1713．若AB是⊙O内接正五边形的一边，AC是⊙O内接正六边形的一边，则∠BAC等于()A．120°B．6°C．114°D．114°或6°14．若等腰直角三角形的外接圆半径的长为2，则其内切圆半径的长为()A. 2 B．2 2－2C．2－ 2 D.2－115．2017·达州以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是()A.22 B.32 C. 2 D. 316．2017·云南如图24－3－7，边长为4的正方形ABCD外切于⊙O，切点分别为E，F，G，H.则图中阴影部分的面积为________．图24－3－717．如图24－3－8，正六边形ABCDEF内接于⊙O，若⊙O的内接正三角形ACE的面积为48 3，试求正六边形的周长．图24－3－818．如图24－3－9①②③④，M，N分别是⊙O的内接正三角形ABC，正方形ABCD，正五边形ABCDE，…，正n边形ABCDEFG…的边AB，BC上的点，且BM＝CN，连接OM，ON.图24－3－9(1)求图①中∠MON的度数；(2)图②中，∠MON的度数是________，图③中∠MON的度数是________；(3)试探究∠MON的度数与正n边形的边数n的关系(直接写出答案)．教师详解详析1．C [解析] 只有正多边形的外接圆与内切圆才是同心圆，故这个四边形是正方形．故选C .2．证明：∵△ABC 是等腰三角形，且∠BAC ＝36°， ∴∠ABC ＝∠ACB ＝72°.又∵BD 平分∠ABC ，CE 平分∠ACB ， ∴∠ABD ＝∠CBD ＝∠BCE ＝∠ACE ＝36°， 即∠BAC ＝∠ABD ＝∠CBD ＝∠BCE ＝∠ACE ， ∴BC ︵＝AD ︵＝CD ︵＝BE ︵＝AE ︵，∴A ，E ，B ，C ，D 是⊙O 的五等分点， ∴五边形AEBCD 是正五边形．3．B [解析] 设这个正多边形为正n 边形，由题意可知72n ＝360，解得n ＝5.故选B . 4．B5．A [解析] 正六边形的中心角为360°÷6＝60°，那么外接圆的半径和正六边形的边组成一个等边三角形．因为正六边形的外接圆半径等于4，所以正六边形的边长等于4.6．C [解析] 连接OB ，则∠AOB ＝60°， ∴∠ADB ＝12∠AOB ＝30°.7．45 8．1＋ 2[解析] 如图，∵△BDE 是等腰直角三角形，BE ＝1，∴BD ＝22， ∴正方形的边长等于AB ＋2BD ＝1＋ 2.9．24 [解析] 正六边形的一个内角＝16×(6－2)×180°＝120°，正五边形的一个内角＝15×(5－2)×180°＝108°，∴∠BAC ＝360°－(120°＋108°)＝132°.∵两个正多边形的边长相等，即AB ＝AC ，∴∠ABC ＝12×(180°－132°)＝24°.10．证明：(1)由五边形ABCDE 是正五边形，得AB ＝AE ，∠ABC ＝∠BAE ，AB ＝BC ， ∴△ABC ≌△EAB ，∴AC ＝BE.(2)连接AD ，由五边形ABCDE 是正五边形，得AB ＝AE ，∠ABC ＝∠AED ，BC ＝ED ， ∴△ABC ≌△AED ， ∴AC ＝AD.又∵M 是CD 的中点， ∴AM ⊥CD. 11．解：如图所示．作法：①作直径AC ；②作直径BD ⊥AC ，依次连接AB ，BC ，CD ，DA ，则四边形ABCD 是⊙O 的内接正方形；③分别以点A ，C 为圆心，OA 的长为半径画弧，交⊙O 于点E ，H 和F ，G ，顺次连接AE ，EF ，FC ，CG ，GH ，HA ，则六边形AEFCGH 为⊙O 的内接正六边形．12．C [解析] 根据两点之间，线段最短可得圆的周长大于3而小于3.4，选项中只有C 满足要求．13．D [解析] 分两种情况考虑：(1)如图①所示，∵AB 是⊙O 内接正五边形的一边，∴∠AOB ＝360°5＝72°.∵AC 是⊙O 内接正六边形的一边，∴∠AOC ＝360°6＝60°，∴∠BOC ＝72°－60°＝12°，∴∠BAC ＝12∠BOC ＝6°.(2)如图②所示，∠AOB ＝72°，∠AOC ＝60°，∴∠OAB ＝54°，∠OAC ＝60°，∴∠BAC ＝60°＋54°＝114°.综上所述，可知选D .14．B [解析] ∵等腰直角三角形的外接圆半径为2，∴此直角三角形的斜边长为4，两条直角边的长均为2 2.如图，根据三角形内切圆的性质可得CD ＝CE ＝r ，AD ＝BE ＝AO ＝BO ＝2 2－r ，∴AB ＝AO ＋BO ＝4 2－2r ＝4，解得r ＝2 2－2.故选B .15．A [解析] 如图①，∵OC ＝2，∴OD ＝1；如图②，∵OB ＝2，∴OE ＝2； 如图③，∵OA ＝2，∴OD ＝3， 则该三角形的三边长分别为1，2， 3. ∵12＋(2)2＝(3)2， ∴该三角形是直角三角形，∴该三角形的面积是12×1×2＝22.故选A .16．2π＋4 [解析] 如图，连接HO ，并延长交BC 于点P ，连接EO ，并延长交CD 于点M.∵正方形ABCD 外切于⊙O ， ∴∠A ＝∠B ＝∠AHP ＝90°，∴四边形AHPB 为矩形，∴∠OPB ＝90°. 又∵∠OFB ＝90°，∴点P 与点F 重合， ∴HF 为⊙O 的直径， 同理：EG 为⊙O 的直径．由∠D ＝∠OGD ＝∠OHD ＝90°且OH ＝OG 知，四边形DGOH 为正方形． 同理：四边形OGCF 、四边形OFBE 、四边形OEAH 均为正方形， ∴DH ＝DG ＝GC ＝CF ＝2，∠HGO ＝∠FGO ＝45°， ∴∠HGF ＝90°，GH ＝GF ＝GC 2＋CF 2＝2 2， 则阴影部分面积＝12S ⊙O ＋S △HGF＝12·π·22＋12×2 2×2 2 ＝2π＋4. 故答案为2π＋4.17．解：如图，连接OA ，作OH ⊥AC 于点H ，则∠OAH ＝30°.在Rt △OAH 中，设OA ＝R ，则OH ＝12R ，由勾股定理可得AH ＝OA 2－OH 2＝R 2－（12R ）2＝123R. 而△ACE 的面积是△OAH 面积的6倍，即6×12×12 3R ×12R ＝48 3，解得R ＝8， 即正六边形的边长为8，所以正六边形的周长为48.18．解：(1)方法一：如图①，连接OB ，OC.图①∵正三角形ABC 内接于⊙O ，∴∠OBM ＝∠OCN ＝30°，∠BOC ＝120°.又∵BM ＝CN ，OB ＝OC ，∴△OBM ≌△OCN ，∴∠BOM ＝∠CON ，∴∠MON ＝∠BOC ＝120°.方法二：如图②，连接OA ，OB.图②∵正三角形ABC内接于⊙O，∴AB＝BC，∠OAM＝∠OBN＝30°，∠AOB＝120°. ∵BM＝CN，∴AM＝BN.又∵OA＝OB，∴△AOM≌△BON，∴∠AOM＝∠BON，∴∠MON＝∠AOB＝120°.(2)90°72°(3)∠MON＝360°n.。

第三节 正多边形与圆有关的计算1．(2017沈阳中考)正方形ABCDEF 内接于⊙O，正六边形的周长是12，则⊙O 的半径是( B )A . 3B ．2C ．2 2D ．2 3(第1题图)(第2题图)2．(2017湘潭中考)如图，在半径为4的⊙O 中，CD 是直径，AB 是弦，且CD⊥AB，垂足为点E ，∠AOB ＝90°，则阴影部分的面积是( D )A ．4π－4B ．2π－4C ．4πD ．2π3．(德州中考)如图，要制作一个圆锥形的烟囱帽，使底面圆的半径与母线长的比是4∶5，那么所需扇形铁皮的圆心角应为 ( A )A ．288°B ．144°C ．216°D ．120°,(第3题图)),(第4题图))4．(2017临沂中考)如图，AB 是⊙O 的直径，BT 是⊙O 的切线，若∠ATB＝45°，AB ＝2，则阴影部分的面积是( C )A ．2B .32－14π C ．1 D .12＋14π5．(2017济宁中考)如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝BC ＝1，将Rt △ABC 绕点A 逆时针旋转30°后得到Rt △ADE ，点B 经过的路径为BD ︵，则图中阴影部分的面积是( A )A .π6B .π3C .π2－12D .12,(第5题图)) ,(第6题图))6．(宁波中考)如图，半圆O 的直径AB ＝2，弦C D∥AB，∠COD ＝90°，则图中阴影部分的面积为__π4__．7．(邵阳中考)如图所示，在3×3的方格纸中，每个小方格都是边长为1的正方形，点O ，A ，B 均为格点，则扇形OAB 的面积大小是__5π4__．,(第7题图)) ,(第8题图))8．(德州中考)如图，半径为1的半圆形纸片，按如图方式折叠，使对折后半圆弧的中点M 与圆心O 重合，则图中阴影部分的面积是2－π6__． 9．(烟台中考)如图所示，C 为半圆内一点，O 为圆心，直径AB 长为2 cm ，∠BOC ＝60°，∠BCO ＝90°，将△BOC 绕圆心O 逆时针旋转至△B ′OC ′，点C′在OA 上，则边BC 扫过区域(图中阴影部分)的面积为__14π__ cm 2.(第9题图) (第10题图)10．(烟台中考)如图所示，将弧长为6π，圆心角为120°的圆形纸片AOB 围成圆锥形纸帽，使扇形的两条半径OA 与OB 重合(粘连部分忽略不计)，则圆锥形纸帽的高是．11．(2016石家庄二十八中二模)如图，边长为1的菱形ABCD 的两个顶点B ，C 恰好落在扇形AEF 的弧EF 上．若∠BAD＝120°，则弧BC 的长度等于__π3__．(结果保留π)12．(潍坊中考)如图，在Rt △ABC 中，∠A ＝30°，BC ＝23，以直角边AC 为直径作⊙O 交AB 于点D ，则图中阴影部分的面积是( A )A .1534－32πB .1532－32π C .734－π6 D .732－π6,(第12题图)) ,(第13题图))13．(遵义中考)如图，在圆心角为90°的扇形OAB 中，半径OA ＝2 cm ，C 为AB ︵的中点，D ，E 分别是OA ，OB 的中点，则图中阴影部分的面积为__⎝ ⎛⎭⎪⎫12π＋2－12__cm 2.14．(2016廊坊二模)如图，在⊙O 中，AB 是直径，点D 是⊙O 上一点，且∠BOD＝60°，过点D 作⊙O 的切线CD 交AB 的延长线于点C ，E 为AD ︵的中点，连接DE ，EB.(1)求证：四边形BCDE 是平行四边形；(2)已知图中阴影部分面积为6π，求⊙O 的半径r.解：(1)连接OE. 依题意得，AE ︵＝ED ︵＝BD ︵， ∴∠AOE ＝∠EOD＝∠DOB＝60°， ∴∠EBA ＝12∠EOA＝30°，∠DEB ＝12∠DOB＝30°，∴∠EBA ＝∠DEB， ∴DE ∥AB.∵AE ︵＝ED ︵＝BD ︵，∴OD⊥BE . 又CD 是⊙O 切线， ∴OD ⊥CD ，∴BE ∥CD ， ∴四边形BCDE 为平行四边形； (2)∵阴影部分面积为6π， ∴S 阴影＝S 扇形BOD ＝60·π·r2360＝6π，∴r 2＝36，∴r ＝6.15．(2017广东中考)如图，AB 是⊙O 的直径，AB ＝43，点E 为线段OB 上一点(不与O ，B 重合)，作CE⊥OB，交⊙O 于点C ，垂足为点E ，作直径CD ，过点C 的切线交DB 的延长线于点P ，AF ⊥PC 于点F ，连接CB.(1)求证：CB 是∠ECP 的平分线； (2)求证：CF ＝CE ；(3)当CF CP ＝34时，求劣弧BC ︵的长度(结果保留π)．解：(1)∵OC ＝OB ， ∴∠OCB ＝∠OBC.∵PF 是⊙O 的切线，CE ⊥AB ， ∴∠OCP ＝∠CEB＝90°， ∴∠PCB ＋∠OCB＝90°， ∠BCE ＋∠OBC＝90°， ∴∠BCE ＝∠BCP， ∴BC 是∠PCE 的平分线； (2)连接AC. ∵AB 是直径， ∴∠ACB ＝90°， ∴∠BCP ＋∠ACF＝90°，∠ACE ＋∠BCE＝90°.∵∠BCP ＝∠BCE， ∴∠ACF ＝∠ACE. ∵∠F ＝∠AEC＝90°， AC ＝AC ，∴△ACF ≌△ACE ，∴CF ＝CE ； (3)作BM⊥PF 于M ，则CE ＝CM ＝CF. 设CE ＝CM ＝CF ＝3a ，PC ＝4a ，PM ＝a. 易证△BMC∽△PMB，∴BM PM ＝CMBM .∵BM 2＝CM·PM＝3a 2，∴BM ＝3a ， ∴tan ∠BCM ＝BM CM ＝33，∴∠BCM ＝30°，∴∠OCB ＝∠OBC＝∠BOC＝60°， ∴BC ︵的长＝60π×23180＝233π.。