江苏省句容市九年级数学上册 4.3 等可能条件下的概率(二)学案苏科版

课题：4.3等可能性条件下的概率（二）目标确定的依据1．课程标准相关要求（1）在具体情境中进一步理解概率的意义，体会概率是描述不确定现象的数学模型；（2）能把等可能条件下的几何概型转化成古典概型，并进行简单的计算；（3）在具体情境中感受一类事件发生的概率（几何概型）的大小与面积的大小有关.2．教材分析课本通过学生熟悉的转盘，引导学生将等可能条件下的概率（几何概型）转化成等可能条件下的古典概型来研究.3．学情分析学生通过前两节课的学习，学生已学会表格、树状图方法列出所有可能出现的结果，并会求出一些事件的概率。

本节课的重点与难点是如何将无限可能的情况转化成有限可能的情况。

教学目标［B］1.95％以上学生能能把等可能条件下的几何概型转化成古典概型，并进行简单的计算；［B］2.90％以上学生在具体情境中感受一类事件发生的概率（几何概型）的大小与面积的大小有关.［C］3．85％以上学生能在具体情境中进一步理解概率的意义，体会概率是描述不确定现象的数学模型；体会转化的思想．教学重难点重点：几何概型的计算。

难点：无限等可能与有限等可能的转化．解决方案1：等分圆盘这个转盘被分成8个面积相等的扇形，并标上1、2、3……8，转动转盘，转盘的指针的位置在不断的改变.①动过程中指针所在的位置：所有可能结果有多少个？为什么？②每个结果出现的机会是均等的吗？③指针指向每一个扇形区域的概率分别是多少？解决方案2：等分并涂色等分转盘并涂色【设计意图】引导学生将无限的等可能转化成有限的等可能，感受几何概型的概率大小与面积大小有关。

自学提示二：2.取一根长度为30cm的绳子，拉直后在任意位置剪断，那么剪得两段的长度都不小于10cm的概率为多少？思考：①拉直后在任意位置剪断，有多少种剪法？②结果是等可能的吗？分析：记“剪得两段绳长都不小于10cm”为事件A.=发1事件A生的概率P(A)3把绳子三等分,于是当剪断位置处在中间一段上时,事件A发生. 由于中间一段的长度等于绳长的1/3.【设计意图】引导学生将无限的等可能转化成有限的等可能，感受几何概型的概率大小与线段的长度有关。

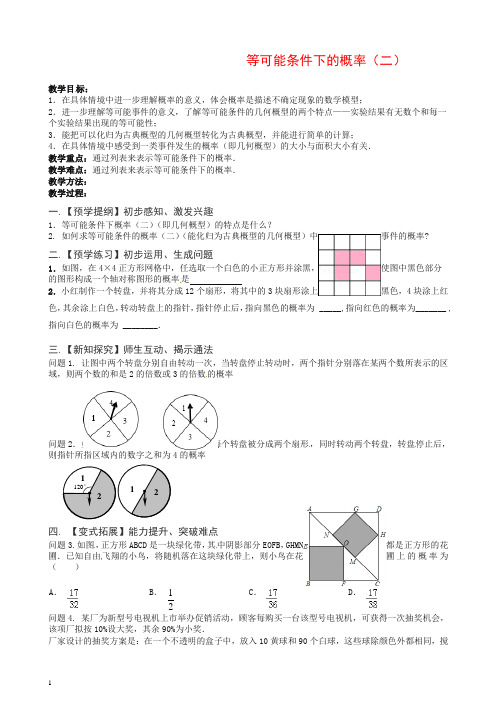
等可能条件下的概率（二） 教学目标：1．在具体情境中进一步理解概率的意义，体会概率是描述不确定现象的数学模型；2．进一步理解等可能事件的意义，了解等可能条件的几何概型的两个特点——实验结果有无数个和每一个实验结果出现的等可能性；3．能把可以化归为古典概型的几何概型转化为古典概型，并能进行简单的计算；4．在具体情境中感受到一类事件发生的概率（即几何概型）的大小与面积大小有关．教学重点：通过列表来表示等可能条件下的概率．教学难点：通过列表来表示等可能条件下的概率．教学方法：教学过程：一.【预学提纲】初步感知、激发兴趣1．等可能条件下概率（二）（即几何概型）的特点是什么？2. 如何求等可能条件的概率（二）（能化归为古典概型的几何概型）中事件的概率?二.【预学练习】初步运用、生成问题1．如图，在4×4正方形网格中，任选取一个白色的小正方形并涂黑，使图中黑色部分的图形构成一个轴对称图形的概率是2．小红制作一个转盘，并将其分成12个扇形，将其中的3块扇形涂上黑色，4块涂上红色，其余涂上白色，转动转盘上的指针，指针停止后，指向黑色的概率为 _____,指向红色的概率为_______ ,指向白色的概率为 ________．三.【新知探究】师生互动、揭示通法问题1. 让图中两个转盘分别自由转动一次，当转盘停止转动时，两个指针分别落在某两个数所表示的区域，则两个数的和是2的倍数或3的倍数的概率问题2．如图是两个可以自由转动的转盘，每个转盘被分成两个扇形，同时转动两个转盘，转盘停止后，的概率四. 【变式拓展】能力提升、突破难点问题3.如图，正方形ABCD 是一块绿化带，其中阴影部分EOFB ，GHMN都是正方形的花圃．已知自由飞翔的小鸟，将随机落在这块绿化带上，则小鸟在花圃上的概率为（ ）A ．B ． 12C ．D ．问题4. 某厂为新型号电视机上市举办促销活动，顾客每购买一台该型号电视机，可获得一次抽奖机会，该项厂拟按10%设大奖，其余90%为小奖．厂家设计的抽奖方案是：在一个不透明的盒子中，放入10黄球和90个白球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，摸到黄球的顾客获得大奖，摸到白球的顾客获得小奖．（1）厂家请教了一位数学老师，他设计的抽奖方案是：在一个不透明的盒子中，放入2黄球和3个白球，这些球除颜色外都相同，搅匀后从中任意摸出2个球，摸到的2个球都是黄球的顾客获得大奖，其余的顾客获得小奖．该抽奖方案符合厂家的设奖要求吗？请说明理由；（2）下图是一个可以自由转动的转盘，请你将转盘分为2个扇形区域，分别涂上黄、白两种颜色，并设计抽奖方案，使其符合厂家的设奖要求．（友情提醒：1．在用文字说明和扇形的圆心角的度数．2．结合转盘简述获奖方式，不需说明理由．）五.【回扣目标】学有所成、悟出方法1.可能条件的概率（二）的两个特点是什么?2.如何将等可能条件的概率（二）（能化归为古典概型的几何概型）转化为等可能条件下的概率（一）即古典概型?六.【当堂反馈】分层达标、收获成功1.已知地球表面陆地面积与海洋面积的比约为3:7.如果宇宙中飞来一块陨石落在地球上,则落在陆地上的概率是 .2.小明把如图所示的矩形纸板挂在墙上，玩飞镖游戏（每次飞镖均落在纸板上），则飞镖落在阴影区域的概率是．3．汶川大地震时，航空兵空投救灾物质到指定的区域（圆A）如图所示，若要使空投物质落在中心区域（圆B）的概率为12，则B⊙与A⊙的半径之比为( )A.4D. 24．甲、乙玩转盘游戏时，把质地相同的两个转盘A、B平均分成2份和3份，并在每一份内标有数字如图．游戏规则：甲、乙两人分别同时转动两个转盘各一次，当转盘停止后，指针所在区域的数字之和为偶数时甲获胜；数字之和为奇数时乙获胜．若指针落在分界线上，则需要重新转动转盘．（1）用画树状图或列表的方法，求甲获胜的概率；（2）这个游戏对甲、乙双方公平吗？请判断并说明理由．。

等可能条件下的概率（二）教学设计一、教学内容概述本节课为九年级上册，第4章等可能条件下的概率第3小节第2课时教学内容，本节课的主要任务是理解能转化为古典概型的几何概型概率的求法。

结合实际生活中的转盘模型及抽奖等生活实际，进一步理解概率在生活中的应用。

二、教学目标设计知识目标:1．在具体情境中进一步理解概率的意义，体会概率是描述不确定现象的数学模型．2．进一步理解等可能事件的意义，会解决能转化为古典概型的几何概型概率问题，会把事件分解成等可能的结果(基本事件)．能力目标:通过学生动手操作、实验、探索的过程，培养学生观察能力、动手能力、合作讨论的能力和转化思想解决问题的能力；情感目标:通过观察、实验、理解几何概型概率的求法，探索能转化为古典概型的几何概型概率的求解思想，掌握这类事件概率在实际生活的应用。

三、教学重难点设计1.教学重点：学会求一类事件的概率（能转化为古典概型的几何概型）的概率，理解概率的大小和面积大小有关，掌握这类问题在实际生活的应用,会用列举法(包括列表、画树状图)计算一些随机事件所含的可能结果(基本事件)数及事件发生的概率．2.教学难点：会将能转化为古典概型的几何概型概率转化成古典概型，理解这类事件概率的大小和面积大小有关，并利用概率公式并解决实际问题，并会灵活运用列举法(包括列表、画树状图)计算几何概型这类事件概率．四、学生学情分析学生在学习过程中，古典概型由于有八年级学习的基础和上节课学习的准备，易于理解，但要真正理解能转化为古典概型的几何概型的这一类问题中概率的大小与面积的大小有关，并能转化成古典概型利用概率公式解决实际问题，还有一定难度，让学生边学习边体会这些区别和变化。

五、教学策略设计说明本课题设计的基本理念是通过实验、观察、操作，主要采用的小组合作、讨论、研究和探索等策略，重点是探索和发现，几何概型概率求法和古典概型之间的关系，难点是理解几何概型问题中概率的大小和面积大小有关，并利用概率公式并解决实际问题，并由浅入深，逐渐深入研究本节课在实际问题的应用，采用探究、合作、交流、讨论法等教学方法。

(1) “几何概型”具有的特点：① ；② . (2)“几何概型”发生的概率大小与区域形状、位置无关，只与区域面积大小有关.活动二、某商场为了吸引顾客，开展有奖销售活动，设立了一个可以自由转动的转盘（如图），转盘等分为16份，其中红色1份、蓝色2份、黄色4份、白色9份.商场规定：顾客每购满1000元的商品，就可获得一次转动转盘的机会.转盘停止时，指针指向红、蓝、黄区域，顾客可分别获得1000元、200元、100元的礼品.某顾客购物1400元，他获得礼品的概率是多少？他分别获得1000元、200元、100元礼品的概率是多少？延伸：如果去掉转盘上的指针，改为向转动中的转盘投掷一枚飞镖，投到不同区域获得相应的礼品(假设飞镖击中转盘上的每一点是等可能的),刚才计算得到的一系列概率值会不会变化呢？数学理论：一般地，设试验结果落在某个区域S 中每一点的机会均等，用A 表示事件“试验结果落在S 中的一个小区域M 中”，那么事件A 发生的概率P(A)=的面积的面积S M活动三、如图,A 转盘的4个扇形的面积相等，B 转盘的6个扇形的面积相等.有人设计了如下游戏规则：甲、乙两人分别任意转动转盘A 、B 各1次，当转盘停止转动时，将指针所落扇形中的2个数字相乘，如果所得的积是偶数，那么甲获胜；如果所得的积是奇数，那么乙获胜. (1)你认为这样的规则公平吗？为什么？(2)如果不公平，请设计一个你认为公平的规则，并说明理由.学生练习：1.如图，转盘中6个扇形的面积都相等.任意转动转盘1次，当转盘停止转动时，例24 1 2 3 A1 23 4 56B求下列事件发生的概率.①P(指针指向6)= ；②P(指针指向偶数)= ；③P(指针指向小于4的数)= ；④P(指针指向不大于4的数)= ; ⑤P(指针指向大于0的数)= ; 2.如图，向正三角形区域投掷飞镖，假设飞镖击中图中每一个小三角形区域是等可能的，投掷飞镖1次，击中图中阴影部分的概率是 .3.小明向如图所示的正方形木板投掷1支飞镖，若飞镖击中图中每一个小正方形是等可能的，则击中阴影部分的概率是 .4.如图，A 、B 两个转盘分别被平均分成三个、四个扇形，分别转动A 盘、B 盘各一次．转动过程中，指针保持不动，如果指针恰好指在分割线上，则重转一次，直到指针指向一个数字所在的区域为止．请用列表或画树状图的方法，求两个转盘停止后指针所指区域内的数字之和小于6的概率．6 1 2 3 45 (1)(2) (3) 0 123 4 56AB。

等可能条件下的概率一、教学目标：1．在具体情境中进一步理解概率的意义，体会概率是描述不确定现象的数学模型；2．了解等可能条件的几何概型的两个特点——实验结果有无数个和每一个实验结果出现的等可能性；3．在具体情境中感受到一类事件发生的概率（即几何概型）的大小与面积大小有关．：二、教学重难点：1、会求等可能条件下的几何概型的概率．2、把等可能条件下，实验结果无限个的几何概型通过等积分割转化为古典概型三、学习与交流：某商场为了吸引顾客，开展有奖销售活动，设立了一个可以自由转动的转盘（如图12－4），转盘等分为16份，其中红色1份、蓝色2份、黄色4份、白色9份。

商场规定：顾客每购满1000元的商品，就可获得一次转动转盘的机会。

转盘停止时，指针指向红、蓝、黄区域，顾客可分别获得1000元、200元、100元的礼品。

某顾客购物1400元，他获得礼品的概率是多少？他分别获得1000元、200元、100元礼品的概率是多少？图１２－４说明：例题教学时学生要能说出每个事件可能出现的结果数m的值？该实验所有等可能出现的结果数n的值？然后再应用古典概率的公式P（A）= mn，就可以解决问题。

四.典型题例例题如图，正方形ABCD花坛中，AE=AH=2cm,EB=3cm,一只小鸟任意落下，落在阴影内的概率为（）（A）12（B）13（C）1225（D）1325五、达标检测1.如果小明将飞镖任意投中如图所示的正方形木板，那么飞镖落在阴影部分的概率是2.如图，一只飞虫在画有图案的纸上任意爬行，它刚好爬行在阴影部分上的概率是多少？3、小明与小华在玩一个掷飞镖游戏，如图甲是一个把两个同心圆平均分成8份的靶，当飞镖掷中阴影部分时，小明胜，否则小华胜（没有掷中靶或掷到边界线时重掷）．（1）不考虑其他因素，你认为这个游戏公平吗？说明理由．（2）请你在图乙中，设计一个不同于图甲的方案，使游戏双方公平．探索：小明和小刚想要利用如图的两个转盘玩游戏，请你帮助他们设计一个游戏，使游戏的规则对双方是公平的。

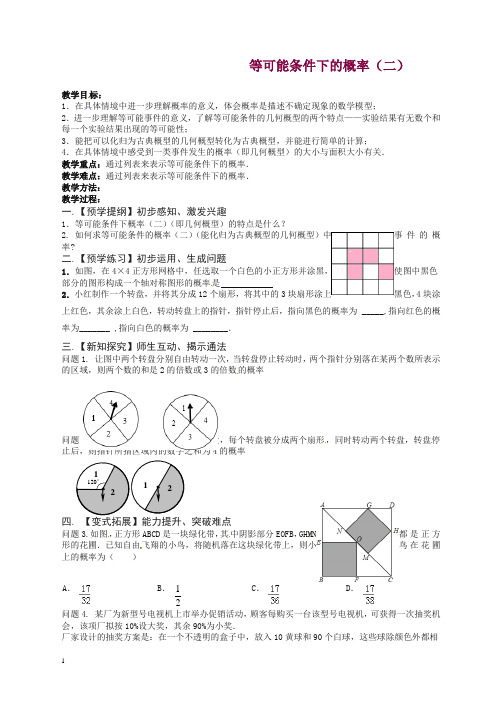
1 等可能条件下的概率（二） 教学目标：1．在具体情境中进一步理解概率的意义，体会概率是描述不确定现象的数学模型；2．进一步理解等可能事件的意义，了解等可能条件的几何概型的两个特点——实验结果有无数个和每一个实验结果出现的等可能性；3．能把可以化归为古典概型的几何概型转化为古典概型，并能进行简单的计算；4．在具体情境中感受到一类事件发生的概率（即几何概型）的大小与面积大小有关．教学重点：通过列表来表示等可能条件下的概率．教学难点：通过列表来表示等可能条件下的概率．教学方法：教学过程：一.【预学提纲】初步感知、激发兴趣1．等可能条件下概率（二）（即几何概型）的特点是什么？2. 如何求等可能条件的概率（二）（能化归为古典概型的几何概型）中事件的概率? 二.【预学练习】初步运用、生成问题1．如图，在4×4正方形网格中，任选取一个白色的小正方形并涂黑，使图中黑色部分的图形构成一个轴对称图形的概率是2．小红制作一个转盘，并将其分成12个扇形，将其中的3块扇形涂上黑色，4块涂上红色，其余涂上白色，转动转盘上的指针，指针停止后，指向黑色的概率为 _____,指向红色的概率为_______ ,指向白色的概率为 ________．三.【新知探究】师生互动、揭示通法问题1. 让图中两个转盘分别自由转动一次，当转盘停止转动时，两个指针分别落在某两个数所表示的区域，则两个数的和是2的倍数或3的倍数的概率问题2．如图是两个可以自由转动的转盘，每个转盘被分成两个扇形，同时转动两个转盘，转盘停4的概率问题3.如图，正方形ABCD 是一块绿化带，其中阴影部分EOFB ，GHMN 都是正方形的花圃．已知自由飞翔的小鸟，将随机落在这块绿化带上，则小鸟在花圃上的概率为（ ）A ．B ． 12C ．D ．问题4. 某厂为新型号电视机上市举办促销活动，顾客每购买一台该型号电视机，可获得一次抽奖机会，该项厂拟按10%设大奖，其余90%为小奖．厂家设计的抽奖方案是：在一个不透明的盒子中，放入10黄球和90个白球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，摸到黄球的顾客获得大奖，摸到白球的顾客获得小奖．（1）厂家请教了一位数学老师，他设计的抽奖方案是：在一个不透明的盒子中，放入2黄球和3个白球，这些球除颜色外都相同，搅匀后从中任意摸出2个球，摸到的2个球都是黄球的顾客获得大奖，其余的顾客获得小奖．该抽奖方案符合厂家的设奖要求吗？请说明理由；（2）下图是一个可以自由转动的转盘，请你将转盘分为2个扇形区域，分别涂上黄、白两种颜色，并设计抽奖方案，使其符合厂家的设奖要求．（友情提醒：1．在用文字说明和扇形的圆心角的度数．2．结合转盘简述获奖方式，不需说明理由．）五.【回扣目标】学有所成、悟出方法1.可能条件的概率（二）的两个特点是什么?2.如何将等可能条件的概率（二）（能化归为古典概型的几何概型）转化为等可能条件下的概率（一）即古典概型?六.【当堂反馈】分层达标、收获成功1.已知地球表面陆地面积与海洋面积的比约为3:7.如果宇宙中飞来一块陨石落在地球上,则落在陆地上的概率是 .2.小明把如图所示的矩形纸板挂在墙上，玩飞镖游戏（每次飞镖均落在纸板上），则飞镖落在阴影区域的概率是．3．汶川大地震时，航空兵空投救灾物质到指定的区域（圆A）如图所示，若要使空投物质落在中心区域（圆B）的概率为12，则B⊙与A⊙的半径之比为424．甲、乙玩转盘游戏时，把质地相同的两个转盘A、B平均分成2份和3份，并在每一份内标有数字如图．游戏规则：甲、乙两人分别同时转动两个转盘各一次，当转盘停止后，指针所在区域的数字之和为偶数时甲获胜；数字之和为奇数时乙获胜．若指针落在分界线上，则需要重新转动转盘．（1）用画树状图或列表的方法，求甲获胜的概率；（2）这个游戏对甲、乙双方公平吗？请判断并说明理由．2。

4.3等可能条件下的概率（二）一、教学目标知识目标：1.在具体情景中进一步了解概率的意义，体验概率是描述不确定现象的数学模型；2.借助具体情境，了解一类事件发生的概率，并能计算简单事件发生的概率.3.能设计符合要求的简单概率模型.能力目标：⑴体会事件发生的不确定性，建立初步的随机观念.⑵进一步体会“数学就在我们身边”，发展学生“用数学”的意识和能力.情感、态度与价值观：（1）通过分析随机事件的概率，初步认识概率与人类生活的密切联系，感受概率的应用价值，增强学生学数学，用数学的思想意识.（2）提高学生之间的合作交流能力和学习数学的兴趣.二、教学重点及难点重点：体会概率的意义，能计算另一类（几何概型）事件发生的概率.难点：体会概率的意义，能设计符合要求的简单概率模型.三、教材分析教材通过探究小猫停留在黑砖块上概率，让学生体验生活中的另一种概率模型――几何概率.所以，教学时应引导学生感悟以下两点：1．方砖除颜色不同外，其余完全相同，小猫在方砖上走动方式是随意的，停留在哪一块方砖上是随机的.2．几何概率的大小与面积有关，即“事件发生的概率等于此事件所有可能发生的结果所组成的图形面积除以所有可能发生的结果所组成的图形面积.四、教学设计(一)知识回顾1.摸到红球的概率？P（摸到红球）=（摸到红球可能出现的结果数）／（摸出一球所有可能出现的结果数）.2.三种事件发生的概率及表示？①必然事件发生的概率为1，记作P（必然事件）=1；②不可能事件发生的概率为0，记作P（不可能事件）=0；③若A为不确定事件，则0＜P（A）＜1(设计说明：由相关的旧知识展开课题，形成知识的“正迁移”，缩短了新、旧知识间的距离，使知识间的过渡自然、轻松、直观.)(二)创设情境，引入新课提出问题：下图是卧室和书房的示意图，图中每一块地砖除颜色外完全相同，小球分别在卧室和书房中滚来滚去.在哪个房间里，小球停留在黑砖上的概率大?(三)议一议，想一想1．议一议问题：假如小球在如图所示的地板上滚来滚去，并随意停留在某块方砖上，它最终停留在黑砖上的概率是多少? (图中每一块方砖除颜色外完全相同)方法一：如图所示的地板由16块方砖组成，这些方砖除颜色外完全相同，小猫停留在任何一块方砖上的概率都相等，因此，P(小猫停留在黑砖上的概率)＝4／16＝1／4.方法二：如图所示的地板由16块方砖组成，这些方砖除颜色外完全相同，其中黑砖的面积是总面积的1／4，因此，P(小猫停留在黑砖上的概率)＝1／4.2．想一想出示讨论题目：如图是一个可以自由转动的转盘，转动转盘，当转盘停止时，指针落在蓝色区域和红色区域的概率分别是多少？首先让学生独立思考、书写答案，然后小组交流，最后全班展示，教师总结.注意让学生重点讨论以下三种答案：方案一：指针不是落在蓝色区域就是落在红色区域，落在蓝色色区域和红色区域的概率相等，所以P（落在蓝色区域）=P（落在红色区域）= 12.方案二：先把红色区域等分成2份，这样转盘被分成3个扇形区域，其中1个是蓝色，2个是红色，所以P（落在蓝色区域）= 13，P（落在红色区域）=23.方案三：利用圆心角度数计算，所以P（落在蓝色区域）1201 3603=，P（落在红色区域）36012024023603603-== .结论：转盘应被等分成若干份.各种结果出现的可能性务必相同.例1：某商场制作了一个可以自由转动的转盘，转盘分为24个相同的扇形，其中红色扇形1个、蓝色扇形3个、黄色扇形5个、白色扇形15个（如图）.商场规定：顾客每购满1000元商品，可获得一次转动转盘的机会，当转盘停止转动时，指针落在红、蓝、黄区域，顾客可分别获得500元、100元、50元的礼品，某顾客购物1400元，他获得礼品的概率是多少？获得500元、100元、50元礼品的概率各是多少？解：该顾客购物1400元,可以获得一次转动转盘的机会.由于转盘被分成24个相同的扇形，当转盘停止转动时，指针落在24个扇形中的任何1个的可能性都相等，因此P（获得礼品）=13593 24248 ++==P（获得500元礼品）=1 24P（获得100元礼品）=31 248=P（获得50元礼品）=5 24即该顾客获得礼品的概率是38，获得500元、100元、50元礼品的概率分别是124、18、524.(四)数学生活化例2：世博会期间，某高级酒店为了吸引顾客，设立了一个可以自由转动的转盘，如图所示，并规定：顾客消费100元以上（不包括100元），就能获得一次转动转盘的机会，如果转盘停止后，指针正好对准九折、八折、七折、五折区域顾客就可以获得相应的打折优惠（转盘等分成16份，指针停在每个区域的机会相等）．若甲顾客消费150元，获得打折优惠的概率是多少？他获得九折、低于九折优惠的概率分别是多少？解：甲顾客消费150元，在100元以上，可以获得相应的打折优惠，根据概率公式得P（九折）==；P（五折、七折、八折）=．(设计说明：教学中首先让学生独立思考，然后进行交流，结果让学生上黑板板演，说明理由，并注意书写格式.发现错误，由学生自己解决，培养学生合作学习的意识.然后用多媒体进行展示，)(五)小结和同伴交流一下本节课你的收获与不足(设计说明：通过与同伴交流，学生互相补充进行小结，培养学生合作学习的意识与独立归纳总结的能力)(六)作业布置课本练习题。

4.3 等可能条件下的概率（二）教课目标【知识与能力】能把可以化归为古典概型的几何概型转变成古典概型，并能进行简单的计算.【过程与方法】进一步理解等可能事件的意义，认识等可能条件的几何概型的两个特色——实验结果有无数个和每一个实验结果出现的等可能性.【感情态度价值观】在详尽情境中进一步理解概率的意义，领悟概率是描述不确立现象的数学模型.教课重难点【教课要点】会求等可能条件下的几何概型的概率.【教课难点】把等可能条件下，实验结果无穷个的几何概型经过等积切割转变成古典概型.课前准备无教课过程创建情境情境1已知一个带指针的转盘，指针的地址固定，转动转盘后任其自由停止，假如在某个时辰观察指针的地址．[ 本源 ZXXK]问题 1（1）这时全部可能的结果有多少个？为何？（2）每个结果出现的机遇是均等的吗？情境 2现将转盘分成8 个面积相等的扇形，若每个扇形面积为单位1，转动转盘，转盘指针指向的地址在不停改变（指针指向两个扇形的交线时，看作指向右侧的扇形）．问题 2（1）当转盘停止时，指针指向每一个扇形地域的机遇均等吗？[ 本源 :（2）如何求指针指向每一个扇形地域的概率呢？情境 3现将转盘涂色，颜色为红、蓝、白三种颜色探究活动转盘都被分成 8 个面积相等的扇形，这些扇形除颜色外完整同样，指针指向任何一个扇形的可能性都相等．问题 3（1）转动转盘的试验全部等可能出现的结果数？（2）事件指针指向红色地域可能发生的结果数？（3）如何计算指针指向红色地域的概率？（4）你能计算出指针指向白色地域的概率吗？例题讲解 例某商场制作了一个可以自由转动的转盘（如图），转盘分为24个同样的扇形，此中红色扇形1 个、蓝色扇形 3 个、黄色扇形 5 个、白色扇形 15 个．商场规定：顾客每购满1000 元的商品，可获取一次转动转盘的机遇．当转盘停止转动时，指针指向红、蓝、黄地域，顾 客可分别获取 500 元、 100 元、 50 元的礼品．某顾客购物 1400 元，他获取礼品的概率是多少？获取 500 元、 100 元、 50 元礼品的概率各是多少？拓展延伸设计一个转盘， 任意转动转盘 1 次，当转盘停止转动时使得指针： （ 1）指向红色地域的概率为1，指向黄色地域的概率为1，指1 ； 24向蓝色地域的概率为41，指向黄色地域的概率为1，指（2）指向红色地域的概率为24向蓝色地域的概率为1．6课堂 小结你本节课的收获是什么？。

苏科版数学九年级上册4.3《等可能条件下的概率（二）》说课稿一. 教材分析《苏科版数学九年级上册》第4.3节《等可能条件下的概率（二）》是在学生已经掌握了等可能条件下的概率计算方法的基础上进行的一节内容。

本节内容主要介绍了利用树状图解决实际问题中的概率计算，进一步加深学生对等可能条件下概率计算方法的理解和应用。

通过本节课的学习，学生能够熟练运用树状图解决实际问题，提高解决概率问题的能力。

二. 学情分析九年级的学生已经学习过等可能条件下的概率计算方法，对概率的基本概念和计算方法有一定的了解。

但是，学生在解决实际问题时，往往不能将理论知识与实际问题相结合，对树状图在概率计算中的应用还不够熟练。

因此，在教学过程中，教师需要引导学生将理论知识与实际问题相结合，提高学生解决实际问题的能力。

三. 说教学目标1.知识与技能目标：学生能够理解树状图在等可能条件下的概率计算中的应用，掌握利用树状图解决实际问题的方法。

2.过程与方法目标：通过小组合作、讨论交流，培养学生解决实际问题的能力，提高学生的合作意识。

3.情感态度与价值观目标：培养学生对数学的兴趣，增强学生对概率问题的探究欲望，培养学生勇于面对挑战的精神。

四. 说教学重难点1.教学重点：学生能够熟练运用树状图解决实际问题，理解树状图在概率计算中的作用。

2.教学难点：如何引导学生将理论知识与实际问题相结合，提高学生解决实际问题的能力。

五. 说教学方法与手段1.教学方法：采用问题驱动法、小组合作法、讨论交流法，引导学生主动探究，提高学生解决问题的能力。

2.教学手段：利用多媒体课件、树状图、实际问题案例等，帮助学生形象地理解概率计算方法。

六. 说教学过程1.导入新课：通过回顾上节课的内容，引导学生复习等可能条件下的概率计算方法，为新课的学习做好铺垫。

2.探究新知：介绍树状图在概率计算中的应用，引导学生通过小组合作、讨论交流，探索如何利用树状图解决实际问题。

3.巩固新知：教师出示一系列实际问题，学生独立或小组合作利用树状图解决，巩固所学知识。

4.3 等可能条件下的概率（二）
．能把可以化归为古典概型的几何概型转化为古典概型，并能
．在具体情境中感受到一类事件发生的概率（即几何概型）的大小与面积大小有关．教学重点：会求等可能条件下的几何概型的概率．
个面积相等的扇形，若每个扇形面积为单位转动转盘，转盘指针指向的位置在不断改变（指针指向两个扇形
现将转盘涂色，颜色为红、蓝、白三种颜色．
个面积相等的扇形，这些扇形除颜色外完全相同，指
怎样计算指针指向红色区域的概率？
次，当转盘停止
1
课堂
3。