立体几何中球的内切和外接问题完美版PPT课件

格式：ppt
大小：1.69 MB
文档页数：46

下载文档原格式

高考数学一轮复习第六章专题六几何体的外接球与内切球问题课件

)
A.4 3π
B.8π
C.12π
D.20π
解析：在底面△ABC 中，由正弦定理得底面△ABC 外接圆的
半径为
r＝2sin B∠CBAC＝2sin2
3π＝ 4
2.
直三棱柱 ABC-A1B1C1 的外接球的半径 R＝ ( 2)2＋12＝ 3，
r2＋A2A12＝
则直三棱柱 ABC-A1B1C1 的外接球的体积为43πR3＝4 3π.
当
λ＝12时，cos〈E→B，E→G〉＝2
3
2 .
∴cos〈E→B，E→G〉的最大值为2
3
2 .
∵A→C＝(－1，1，0)，A→F＝(0，1，1)， ∴E→B·A→C＝E→B·A→F＝0. ∴EB⊥AC，EB⊥AF. ∵AC∩AF＝A，∴EB⊥平面 AFC. ∵E→B·E→G>0，∴cos〈E→B，E→G〉即为 EG 与平面 AFC 所成角
如图 6-7 所示，把四面体 S-ABC 补全为长方体 ABCD-SPMN，其中 SA，AB，BC 为长方体中首尾相连且两两相互垂直的三条棱，点 H 为 PM 中点.
图 6-7
∵GH∥AP，∴G，H 两点到平面 AEF 的距离相等.
设点 H 到平面 AEF 的距离为 d.
∵△APF 是边长为 2 2的等边三角形，
[例 1]已知一个圆锥底面半径为 1，母线长为 3，则该圆锥内
切球的表面积为( )
A.π
B.32π
C.2π
D.3π
解析：依题意，作出圆锥与球的轴截面，如图
6-1 所示.设球的半径为 r，易知轴截面三角形边 AB
上的高为 2 2，因为△SOD∽△SBE，所以SSOB＝OBED，
即2 32－r＝1r，解得 r＝ 22.所以圆锥内切球的表面

正方体内切球外接球棱切球图例演示ppt课件

正方体的内切球的半径是棱长的一半
经营者提供商品或者服务有欺诈行为的，应当按照消费者的要求增加赔偿其受到的损失，增加赔偿的金额为消费者购买商品的价款或接受服务的费用
正方体的棱切球
经营者提供商品或者服务有欺诈行为的，应当按照消费者的要求增加赔偿其受到的损失，增加赔偿的金额为消费者购买商品的价款或接受服务的费用
经营者提供商品或者服务有欺诈行为的，应当按照消费者的要求增加赔偿其受到的损失，增加赔偿的金额为消费者购买商品的价款或接受服务的费用
经营者提供商品或者服务有欺诈行为的，应当按照消费者的要求增加赔偿其受到的损失，增加赔偿的金额为消费者购买商品的价款或接受服务的费用
经营者提供商品或者服务有欺诈行为的，应当按照消费者的要求增加赔偿其受到的损失，增加赔偿的金额为消费者购买商品的价款或接受服务的费用
正方体的内切球
经营者提供商品或者服务有欺诈行为的，应当按照消费者的要求增加赔偿其受到的损失，增加赔偿的金额为消费者购买商品的价款或接受服务的费用
正方体的棱切球半径是面对角线长的一半
经营者提供商品或者服务有欺诈行为的，应当按照消费者的要求增加赔偿其受到的损失，增加赔偿的金额为消费者购买商品的价款或接受服务的费用
正方体的外接球
经营者提供商品或者服务有欺诈行为的，应当按照消费者的要求增加赔偿其受到的损失，增加赔偿的金额为消费者购买商品的价款或接受服务的费用
D A
D A11C BO Nhomakorabea1B1

高中数学难点突破：球的外切和内接问题 (共10张PPT)

解析：设正方体的棱长为a
∵球的外切正方体的棱长等于球直径：2R=a ∴ S甲 = 4πR22 = π
∵球内切于正方体的棱时
正方体的面对角线等于球的直径
2Rห้องสมุดไป่ตู้=
2a
∴ S乙
=
4πR
2 2
=
2π
球的内接正方体的体对角线等于球直径： 2R = 3a S丙 =4πR32 =3π
∴三球表面积之比为1:2:3
跟踪练习2
a
r1
=
a 2
a
r2 =
2a 2
a
r3 =
3a 2
a
2a
2a
• 画出正确的截面：(1)中截面； (2)对角面
• 找准数量关系
典型例题一
若正方体的棱长为a，求：正方体的外接球的体积 .
球的内接正方体的对角线等于球直径 .
D
C
A
A
B
O
D1
C1
对角面

A1
A1
B1
V2
=
4 3
π(
3a)3 = 2
3a3 π 2
解析：作轴截面如图所示，
CC = 6 , AC = 2 6 = 2 3
设球半径为R ,则：
R2 =OO2 +CC2
=( 6 )2 +( 3)2 = 9 ∴ R =3
∴ S球 =4πR2 =36π
V球
=
4 3
πR3
=36π
D’
C’
A’
B’
D
C
A
OB
A’
O’
C’
A
O
C
C 2RO= 3a

球的外接内切问题课件-高三数学二轮专题复习

(2)若长方体的同一顶点的三条棱长分别为a，b，c，
外接球的半径为Ra，2＋则b2＋2Rc2＝
.
一、直接法
A
C
O
A1
C1
1、求正方体的外接球的有关问题
例1、若棱长为3的正方体的顶点都在同一
球面上，则该球的表面积为 27 .
变式题：一个正方体的各顶点均在同一球的球面上，若该正方体的表面积为24，则该球的体
球与棱柱的组合体问题例1 甲球内切于正方体的各面，乙球内切于该正方体的各条棱，
丙球外接于该正方体，则三球表面面积之比为( )
A. 1:2:3 D
B. 1: 2: 3
C
C. 1:3 4:3 9
D. 1: 8: 27
A D1
A1
B
中截面
O
C1设棱长为1
球的外切正方体的棱长等于球直径。
B1
S甲 4 R12 =
1.正方体的内切球、棱切球、外接球
设正方体的棱长为a,则: 正方体的内切球、外接球、棱切球直径
径分别为:
1 2
a、 3 2
a、 2 2
a.
2.正四面体的内切球、棱切球、外接球设正四面体的棱长为a,则: 正四面体的内切球、棱切球、外接球
半径分别为: 6 a、 2 a、 6 a. 12 4 4
圆锥的内切球圆锥的外接球
课时小结:
解决与球有关的内切与外接问题的
关键是：
通过寻找恰当的过球心的截面, 把立体问题转化为平面问题, 通过解三角形求出球的半径R.
30
探究二：若正四面体的棱长为a，则
⑴正四面体的内切球直径＝ ⑵正四面体的外接球直径＝ ⑶与正四面体所有棱相切的球直＝
求棱长为a的正四面体外接球、内切球及棱切球

空间几何体的外接球,内切球课件,公开课

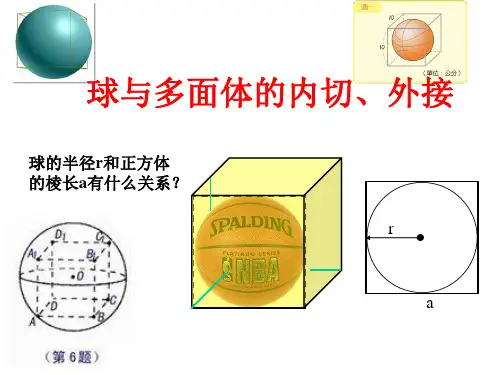
例 10 若棱长为 a 的正四面体的各个顶点都在半径为 R 的球面上,求球的表面积．
解2：补形法.
把正四面体放在正方体中，设正方体棱长为 x，
C
则
P
a＝
2x，由题意 2R＝
3x＝
3×
2a＝ 2
26a，
∴
S
球＝4π
R2＝3πa2. 2
O
•
A
B
LOGO
S
O
•
A
C
B
锥体模型侧面与底面垂直的几何体，外接球的球心在哪？
过PA,PD作轴截面，交BC边中点E, 连接OE，OF
∴PD=1,易知
， PE为斜高D,
由△POF∽△PED，得
r 1 r 3 23
，解得r=
1 3
3
3
S球=4πr2=
4 9
V球=
4 πr3=
3
4 81
A
轴截面法
作轴截面，球心在棱锥的高所在的直线上.
LOGO
P
O
C
D
E
B
P
rF
O
r
E D
探究新知 LOGO
的球心
16.已知三棱锥S ABC的所有顶点都在球O的球面上,
SC是球O的直径. 若平面SCA 平面SCB, SA AC ,
SB BC,三棱锥S ABC的体积为9, 则球O的表面积
为 36 . B
B
S
CS
OC
设OA r, 则 A
A
VA SBC
1 3
S△SBC
OA
1 3
1 2r r r 2
R2
r22
r12
(a)2 2

外接球、内切球模型总结专题课件-高三数学二轮复习备考课件

∴正三棱锥 − 的三条侧棱两两互相垂直
把三棱锥补形为正方体，则正方体外接球即为三棱锥的外接球
其直径为 =

=
1
2 + 2 + 2 + 2 + 2 + 2
2
=
1
2 + 2 + 2 =
2

1

2 + 2 + 2
半径为
6
2
4
球 = ×

找三条两两垂直的线段，直接用公式 2
即2 = 2 + 2 + 2 ，求出

2

= 2 + 2 + 2 ，

例1 （1）已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的
表面积是( C )
B. 20
A.16
C. 24
D. 32
= 2 ℎ = 16
则该四面体的外接球的表面积为( D )
A. 11
B. 7

1

C.
10

3
D.
40

3
在
��
2 = 2 + 2 − 2 ⋅ ⋅ cos120∘

=7
= 7
中
的外接球直径为
7 2 7

=
2 =
=
sin∠
3
3
2
∵ ⊥平面 ∴ ⊥ ∴ ∆是直角三角形
是这个球的外切多面体，这个球是这个多面体的内切球.

高三一轮复习专题《球的内切和外接问题》课件

C.
1变变:2式式则 :3题题：：在一已A个知正各B方顶中 BC 体点. 的都各在，顶一点个用均球在面同上解一的球正直的四球棱面柱角上高识，为三若4，该得体角正积方r为，体形 1的6，3表3则知面,这从积个为球2而 S的4，表O 则1面该积球为S的（体A2积为）AO 12 .
球外接于正方体
D A
D1 A1
C
对角面 A
B
O
设棱长为1
C1
A1
B1
C
2R 3
O
2
C1
球的内接正方体的对角线等于球直径。 S丙 4 R32 =3
二、构造法
1、构造正方体例4、若三棱锥的三条侧棱两两垂直，且侧棱长
均为 3 ，则其外接球的表面积是 9
变式题（浙江高考题）已知球O的面上四点A、B、C、D， D 平 A A，面 B A C B B ,D C A A B B C 3 则球O的体积等于
高为4，体积为16，则这个球的表面积为（ C ）【点评】由于正四面体本身的对称性可知，内切球和外接球的两个球心是重合的，为正四面体高的四等分点，即内切球的半径为 (h
A. 1 6 B. C. 2 4 D. 2 0 3 2 为正四面体的高)，且外接球的半径，从而可以通过截面图中建立棱长与半径之间的关系。
66x433,x2h,hx
1, 2 3．
∴正六棱柱的底面圆的半径 r 1，球心到底面的距离 .∴外接球的半径 Rr2d21, V 2球43 .
d
3 2
小结本题是运用公式 R2r2d2求球的半径的，该公式是求球
的半径的常用公式.
思考题：半径为R的球的外切圆柱(球与圆柱的侧面、两底面都相切)的表面积为________，体积为________．

球的外接、内切问题-2024届高三数学二轮专题复习课件

专题：与球有关的内切与外接问题
1
一、球体的体积与表面积
二、球与①多V面球体的43接、R切3
② S球面 4 R2
图3
图4
定义1：若一个多面体的各顶点都在一个球的球图面5 上，
则称这个多面体是这个球的内接多面体，
这个球是这个多面体的外接球。定义2：若一个多面体的各面都与一个球的球面相切，
则称这个多面体是这个球的外切多面体，
D A
D1
C 球内切于正方体的棱
B
中截面
O
.
C1
A1
B1
设棱长为1
正方形的对角线等于球的直径。 S乙 4 R22 =2
球外接于正方体
D A
D1 A1
C
B O
C1 B1
对角面 A
设棱长为1
A1
C
2R 3
O
2
C1
球的内接正方体的对角线等于球直径。 S丙 4 R32 =3
变题：
1. 已知长方体的长、宽、高分别是 3 、 5、1 ，求长方体的
A O
C
A B
B
O
D D
C
典型：正四面体ABCD的棱长为 a，求其内切球半径r与外接球半径R.
思考：若正四面体变成正三棱锥，方法是否有变化？
1、内切球球心到多面体各面的距离均相等，外接球球心到多面体各顶点的距离均相等 2、正多面体的内切球和外接球的球心重合 3、正棱锥的内切球和外接球球心都在高线上，但不重合 4、基本方法：构造三角形利用类似比和勾股定理 5、体积分割是求内切球半径的通用做法
球与棱柱的组合体问题例1 甲球内切于正方体的各面，乙球内切于该正方体的各条棱，
丙球外接于该正方体，则三球表面面积之比为( )

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

D A
D1 A1
C
B O
C1 B1
球的内接正方体的对角线等于球直径。
变式训练：已知正四面体内接于一个球，某人画出四个过球心的平面截球与正四面体所得的图形如下，
则（）D
①
②
③
④
• A．以下四个图形都是正确的
• C．只有④是正确的的
B．只有②④是正确的 D．只有①②是正确
解法2：
A B
O
D C 求正多面体外接球的半径
例4、正三棱锥的高为 1，底面边2 长6 为。求棱锥的全面积和它的内切球的表面积。
解法2：设球的半径为 r，则 VA- BCD =
A
VO-ABC + VO- ABD + VO-ACD + VO-BCD
1 3
2
V A BCD

3
4
2
6
1
O
D
1
3 r S全 3 2 2 3 r
SA=SB=SC=2，则该三棱锥的外接球的球心到平面 ABC 的距离为（）
S
A.
B.
C.1 D.
答案：D.
O
，即
.
C
A
M
B
7
若棱锥的顶点可构成共斜边的直角三角形，则共斜边的中点就是其外接球的球心。
例 9、已知三棱锥的四个顶点都在球的球面上，
且
，，
解：
且
，
，
因为
所以知
所以
所以可得图形为：
，
，
,
A B
O D
C
求正方体外接球的半径
4 直三棱柱的外接球的球心是上下底面三角形外心的连线的中点。
例 4、（2014）已知三棱柱若该棱柱的体积为
的侧棱垂直于底面，各顶点都在同一球面上，
．
，则此球的表面积等于_________．
解：由已知条件得： ∵
，∴ ，，∴ ，
设的外接圆的半径为，则
，∴ ，
例 2.（全国卷）一个四面体的所有棱长2 都为，
四个顶点在同一球面上，则此球的表面积为（）
A. 3
B4.
3 C3. 6
D.
2 破译规律-特别提醒
3 球与正四面体内切接问题
【例3】求棱长为a的正四面体内切球
的体积．
3 球与正四面体内切接问题
3 正四面体内切、外接结论球内接长方体的对角线是球的直径
OB OE2 BE2 9 1 13 42
V 4 R2 13 13
3
6
4 举一反三-突破提升
3.(2015 南昌二模）某几何体的三视图如图，该几何体的顶点都在球O 的球面上，球CO的表
面A.积2是 B.4（ C.）8 D.16
B
O1
E
r 6 2 S球 8 5 2 6
C 注意：①割补法，②
VV多多面面体
体 13
1
S全
3
S r内切全球

r内
切
球
变式训练：一个正方体内接于一个球，过球心作一截面，如图所示，则截面的可能图形是（）
①
②
③
④
• A ．①② Ｂ．②④ Ｃ．①②③ Ｄ．②③④
,求球的体积。
P
在
中斜边为在
中斜边为
B
取斜边的中点，在
中
在
中
所以在几何体中
，即为该四面体的外接球的球心
A
O
C
所以该外接球的体积为
03
破译规律-特别提
醒
2 例题剖析-针对讲解
04
举一反三-突破提
升
4 举一反三-突破提
1、（2015 海淀二模）升已知斜三棱柱的三视图如图所示，该斜三棱柱的体积为 ______.
1
剖析定义
一、由球心的定义确定球心
在空间，如果一个定点与一个简单多面体的所有顶点的距离都相等，那么这个定点就是该简单多面体的外接球球心。
1 一、定义法针对讲解
D
AO
C
图4 B
2 求正方体、长方体的外接球的有关问题
2 求正方体、长方体的外接球的有关问题
②出现正四面体外接球时利用构造法(补形法)，联系正方体。
4 举一反三-突破提升
2、（2015 郑州三模）正三角形ABC的2 边3 长
为，将它沿高AD翻折，使点B 与3 点C间的
距离为，此时四面体ABCD的BD 外DC接球3 的体
积为。
BC 3
ABC 等边三角形
BE 1 3 1 2 sin 60
AD 3 , BE 1 3 2 2 sin 60
A．
B.
C. 4
D.
5 正棱锥的外接球的球心是在其高上
例 6.一个正四棱锥的底面边长为 2，侧棱长为，五个顶点都在同一个球面上，
则此球的表面积为 9 .
P
设外接球半径为 R，在△OO1A 中有
D
解得 . ∴ .
O1
O C
A B
6测棱相等的锥体顶点的投影在底面外接圆心
例 7、.若三棱锥 S-ABC 的底面是以 AB 为斜边的等腰直角三角形，AB=2，
。正四面体（棱长为a）的外接球半径R
与内切球半径r之比为R：R r＝6 a3：1.外接
球半径：
4
r 6a
内切球半径1：2
结出论，：内正切四球面和r体外 14与接h 球球的的接两切个问球题心，是可重合通的过，线为面正关四系R 面证 3r 体高2、的正四多等面分体点的，内即切定球有和内外切接球球的的半球径心重合(为。正四面体3、的正高棱)，锥且的外内接切球球的和半外径接球．球心都在高线上，
球与多面体的内切、外接
球的半径r和正方体的棱长a有什么关系？
.r
a
一、球体的体积与表面积①来自V球43
R3
二、球与多面体的接、切
② S球面 4 R2
定义1：若一个多面体的各顶点都在一个球的球面上，
则称这个多面体是这个球的内接多面体，
这个球是这多个面体的外接球
。
定义2：若一个多面体的各面都与一个球的球面相切，则称这个多面体是这个球的外切多面体，这个球是这多个面体的内切球。
例4、正三棱锥的高为 1，底面边长为。求
棱锥的全面积和它的内切球的表面积。
A 解法1：过侧棱AB与球心O作截面( 如图 )
在正三棱锥中，BE 是正△BCD的高，
1
O1 是正△BCD的中心，且AE 为斜高
O
FD
B
O1
E
C 作 OF ⊥ AE 于 F 设内切球半径为 r，则 OA = 1 －r ∵ Rt △ AFO ∽ Rt △ AO1E
∴外接球的半径为
，∴球的表面积等于
.
解析：球内接多面体，利用圆内接多边形的性质求出小圆半径，通常用到余弦定理求余弦值，通过余弦值再利用正弦c 定 2理r 得到小圆半径，从而解决问题。 sinC
5 正棱锥的外接球的球心是在其高上
例 5 在三棱锥 P－ABC 中，PA＝PB=PC= ,侧棱 PA 与底面 ABC 所成的角为 60°，则该三棱锥外接球的体积为（）