高二数学课件 平面与平面垂直

2.1.2 两条直线平行和垂直的判定1.理解并掌握两条直线平行与垂直的条件；（重点）2.会运用条件判断两直线是否平行或垂直.（难点）能否通过斜率来判断两条直线的位置关系？xy 为了在平面直角坐标系内表示直线的倾斜程度，我们引入倾斜角的概念，再利用倾斜角与直线上点的坐标关系引入直线的斜率，从而把几何问题转化为代数问题.Ox y O1l 2l 两条直线平行的判定思考1 设两条直线l 1，l 2 的斜率分别为k 1，k 2，当l 1∥l 2 时， k 1 与k 2 满足什么关系？α1α212∥l l 11αα=11k k =1αxy O 2α斜率均不存在的两条直线平行1l 2l 思考2 设两条直线l 1，l 2 的斜率都不存在，两直线l 1 与l 2 有何位置关系？xy O 1l 2l 若两条直线l 1、l 2平行，则作用：1.判定两线平行2.证明三点共线121212∥，都不存在k k l l k k ⎧=⎪⇔⎨⎪⎩例1 已知A(2，3)，B(-4，0)，P(-3，1)，Q(-1，2)，试判断直线BA与PQ的位置关系，并证明你的结论.1. 已知四边形ABCD 的四个顶点分别为A (0，0)，B (2，－1)，C (4，2)，D (2，3)，试判断四边形ABCD 的形状，并给出证明.x O y AB DC1;23.2////.，四边形是平行四边形.解：AB CD BC DA k k k k AB CD BC DA ABCD==-==∴∴ 分析：判断两组对边是否分别平行.y l 1O xl 2α1α2两条直线垂直的判定思考3 设两条直线l 1，l 2的斜率分别为k 1，k 2，当 l 1⊥l 2 时， k 1 与k 2 满足什么关系？因为直线l 1，l 2的斜率分别为k 1，k 2，则直线l 1，l 2的方向向量分别是 ， ，于是即11(，)a k = 21(，)b k = 1212010l l a b a b k k ⊥⇔⊥⇔⋅=⇔+=121k k =-1l x y o 2l 若一条直线的倾斜角为90°,另一条直线的倾斜角为0°,则两直线互相垂直.思考4 若两条直线中有一条直线的斜率不存在，这两条直线可能垂直吗？y l 1O xl 2若两条直线l 1、l 2垂直，则作用：判定两线垂直12121210、中一个为，另一个不存在k k l l k k ⎧=-⎪⊥⇔⎨⎪⎩例2已知A(-6，0)，B(3，6)，P(0，3)，Q(6，-6)，试判断直线AB与PQ 的位置关系.分析：分别求出两直线的斜率，观察斜率之间的关系.2. 已知A (5，-1)，B (1，1)，C (2，3)三点，试判断△ABC 的形状.C O y A Bx分析：结合图形可猜想AB ⊥BC .△ABC 为直角三角形.1．下列说法正确的有( )①若不重合的两直线斜率相等，则它们平行；②若l1∥l2，则k1＝k2；③若两直线中有一条直线的斜率不存在，另一条直线的斜率为0，则两直线垂直；④若l1 与l2 的斜率都不存在，则l1∥l2.A．4个 B．3个C．2个 D．1个2.试确定m 的值，使过点的直线与过点 的直线：(1)平行； (2)垂直.(1)(1)A m B m -，，，(12)(50)P Q -，，，3.已知点M (2，2)和N (5，-2)，点P 在x 轴上，且∠MPN 为直角，求点P 的坐标.“几何问题代数化”的思想 1.两条直线平行的判定 2.两条直线垂直的判定121212=10k k l l k k ⋅-⎧⊥⇔⎨⎩、中一个为，一个不存在121212//k k l l k k =⎧⇔⎨⎩、都不存在。

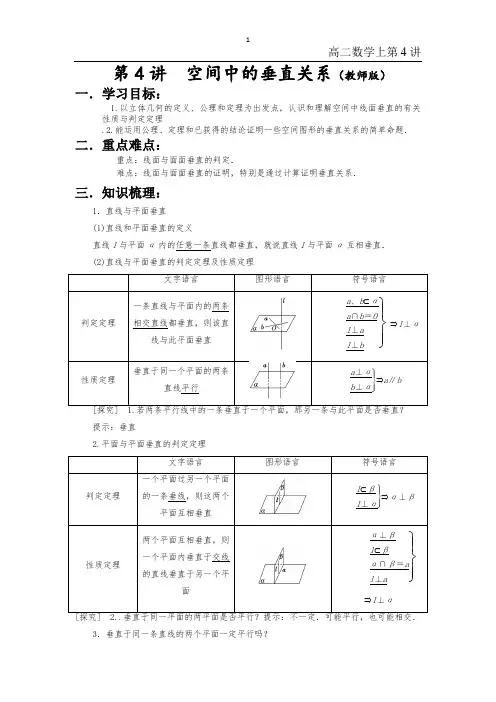
第4讲空间中的垂直关系（教师版）一．学习目标：1.以立体几何的定义、公理和定理为出发点，认识和理解空间中线面垂直的有关性质与判定定理.2.能运用公理、定理和已获得的结论证明一些空间图形的垂直关系的简单命题．二．重点难点：重点：线面与面面垂直的判定．难点：线面与面面垂直的证明，特别是通过计算证明垂直关系．三．知识梳理：1．直线与平面垂直(1)直线和平面垂直的定义直线l与平面α内的任意一条直线都垂直，就说直线l与平面α互相垂直．(2)直线与平面垂直的判定定理及性质定理一条直线与平面内的两条相交直线都垂直，则该直垂直于同一个平面的两条[探究] 1.若两条平行线中的一条垂直于一个平面，那另一条与此平面是否垂直？提示：垂直2.平面与平面垂直的判定定理一个平面过另一个平面的一条垂线，则这两个两个平面互相垂直，则一个平面内垂直于交线的直线垂直于另一个平[探究] 2..垂直于同一平面的两平面是否平行？提示：不一定．可能平行，也可能相交．3．垂直于同一条直线的两个平面一定平行吗？提示：平行．可由线面垂直的性质及面面平行的判定定理推导出．四．典例剖析：题型一线面、面面垂直判断题例1（1）下列命题中，正确的序号是________．①若直线l与平面α内的一条直线垂直，则l⊥α；②若直线l不垂直于平面α，则α内没有与l垂直的直线；③若直线l不垂直于平面α，则α内也可以有无数条直线与l垂直；④若平面α内有一条直线与直线l不垂直则直线l与平面α不垂直．[思路探索] 利用线面垂直的定义并结合反例法，反证法判断．解析当l与α内的一条直线垂直时，不能保证l与平面α垂直，所以①不正确；当l与α不垂直时，l可能与α内的无数条平行直线垂直，所以②不正确，③正确．根据线面垂直的定义，若l⊥α则l与α的所有直线都垂直，所以④正确．答案③④（2）(2012·浙江省名校新高考研究联盟第二次联考)下列错误的是( )A．如果平面α⊥平面γ，如果平面β⊥平面γ，α∩β＝l，那么l⊥γB．如果平面α⊥平面β，那么平面α内一定存在直线垂直于平面βC．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面βD．如果平面α⊥平面β，过α内任意一点作交线的垂线，那么此垂线必垂直β解析：D中当过交线上任意一点作交线的垂线不在平面α内时，此垂线不垂直β，故选D.（3）(教材习题改编)PD垂直于正方形ABCD所在的平面，连接PB、PC，PA、AC、BD，则一定互相垂直的平面有( )A．8对B．7对C．6对D．5对解析：选B 由于PD⊥平面ABCD.故平面PAD⊥平面ABCD，平面PDB⊥平面ABCD，平面PDC⊥平面ABCD，平面PDA⊥平面PDC，平面PAC⊥平面PDB，平面PAB⊥平面PAD，平面PBC⊥平面PDC，共7对．课堂小结：(1)线面垂直的定义不易用来判定线面垂直，但能利用它判定线面不垂直．(2)要注意定义的等价性．课堂练习1：（1）下列命题中正确的个数是( )①如果直线l与平面α内的无数条直线垂直，则l⊥α；②如果直线l与平面α内的一条直线垂直，则l⊥α；③如果直线l不垂直于α，则α内没有与l垂直的直线；④如果直线l不垂直于α，则α内也可以有无数条直线与l垂直．A．0 B．1 C．2 D．3答：B（2）下列命题错误的是________(填序号)．①若直线l与平面α内的两条直线垂直，则l⊥α；②若直线l与平面α内的两条相交直线垂直，则l与α的所有直线垂直；③过一点和已知直线垂直的平面有且只有一个；④a、b为异面直线，a∥α，b∥α，若l⊥a，l⊥b，则l⊥α.解析②③④正确，①不正确．答案①（3）(2012·金丽衢十二校第二次联考)已知平面α，β和直线m，给出条件：①m∥α；②m⊥α；③m⊂α；④α⊥β；⑤α∥β.当满足条件时，m⊥β.(填符合条件的序号)解析：当m⊥α且α∥β时，m⊥β，即应当填②⑤.题型二线面垂直的证明——————常运用线面垂直的判定定理证例2（等腰三角形中线即高证垂直）（2013年高考浙江卷（文））如图,在在四棱锥P-ABCD中,PA ⊥面ABCD,AB=BC=2,AD=CD=7,PA=3,∠ABC=120°,G 为线段PC 上的点.(Ⅰ)证明:BD ⊥面PAC ; （2）（3）（略）证明:(Ⅰ)由已知得三角形ABC 是等腰三角形,且底角等于30°,且6030AB CB AD CD ABD CBD ABD CBD BAC BD DB =⎫⎪=⇒∆≅∆⇒∠=∠=∠=⎬⎪=⎭且,所以;、BD AC ⊥,又因为PA ABCD BD PA BD PAC BD AC ⊥⇒⊥⎫⇒⊥⎬⊥⎭; 课堂练习2：（勾股定理证垂直）（2013年高考广东卷（文））如图4,在边长为1的等边三角形ABC 中,,D E 分别是,AB AC 边上的点,AD AE =,F 是BC 的中点,AF 与DE 交于点G ,将ABF ∆沿AF 折起,得到如图5所示的三棱锥A BCF -,其中BC =. (1) 证明:DE //平面BCF ;(2) 证明:CF ⊥平面ABF ;(3) 当23AD =时,求三棱锥F DEG -的体积F DEG V -.图 4【答案】(1)在等边三角形ABC中,AD AE=AD AEDB EC∴=,在折叠后的三棱锥A BCF-中也成立,//DE BC∴,DE⊄平面BCF,BC⊂平面BCF,//DE∴平面BCF;(2)在等边三角形ABC中,F是BC的中点,所以AF BC⊥①,12BF CF==.在三棱锥A BCF-中,2BC=,222BC BF CF CF BF∴=+∴⊥②BF CF F CF ABF⋂=∴⊥平面;(3)由(1)可知//GE CF,结合(2)可得GE DFG⊥平面.11111113232333F DEG E DFGV V DG FG GF--⎛∴==⋅⋅⋅⋅=⋅⋅⋅⋅=⎝⎭题型三线线垂直的证明——————常转化为证线面垂直例3：（2013年高考课标Ⅰ卷（文））如图,三棱柱111ABC A B C-中,CA CB=,1AB AA=, 160BAA∠= .(Ⅰ)证明:1AB AC⊥;(Ⅱ)若2AB CB==,16AC=,求三棱柱111ABC A B C-的体积.【答案】(I)取AB的中点O,连接OC O、1OA O、1A B,因为CA=CB,所以OC AB⊥,由于AB=A A1,∠BA A1=600,故,AA B∆为等边三角形,所以OA1⊥AB.因为OC⨅OA1=O,所以AB⊥平面OA1C.又A1CC平面OA1C,故AB⊥AC. (II)由题设知12ABC AA B∆∆与都是边长为的等边三角形，12AA B都是边长为的等边三角形，所以2211111.OC OA AC AC OA OA OC ==+⊥又，故111111111,--= 3.ABC ABCOC AB O OA ABC OA ABC A B CABC S A B C V S OA=⊥∆⨯=因为所以平面，为棱柱的高，又的面积ABC的体积课堂练习3：（2013年高考大纲卷（文））如图,四棱锥902,P ABCD ABC BAD BC AD PAB PAD-∠=∠==∆∆中，，与都是边长为2的等边三角形.(I)证明:;PB CD⊥(II)（略）【答案】(Ⅰ)证明:取BC的中点E,连结DE,则ABED为正方形.过P作PO⊥平面ABCD,垂足为O. 连结OA,OB,OD,OE.由PAB∆和PAD∆都是等边三角形知PA=PB=PD, [来源:学科网]所以OA=OB=OD,即点O为正方形ABED对角线的交点, OE BD⊥,从而PB OE⊥.因为O是BD的中点,E是BC的中点, 所以OE//CD.因此,PB CD⊥.题型四面面垂直的证明——————常转化为证线面垂直例4（2013年高考山东卷（文））如图,四棱锥中,,,分别为的中点(Ⅰ)求证:;(Ⅱ)求证:课堂练习4：（2013年高考北京卷（文））如图,在四棱锥P ABCD -中,//AB CD ,AB AD ⊥,2CD AB =,平面PAD ⊥底面ABCD ,PA AD ⊥,E 和F 分别是CD 和PC 的中点,求证:(1)PA ⊥底面ABCD ;(2)//BE 平面PAD ;(3)平面BEF ⊥平面PCD【答案】(I)因为平面PAD⊥平面ABCD,且PA垂直于这个平面的交线AD所以PA垂直底面ABCD.(II)因为AB∥CD,CD=2AB,E为CD的中点，所以AB∥DE,且AB=DE所以ABED为平行四边形,所以BE∥AD,又因为BE⊄平面PAD,AD⊂平面PAD ，所以BE∥平面PAD.(III)因为AB⊥AD,而且ABED为平行四边形所以BE⊥CD,AD⊥CD,由(I)知PA⊥底面ABCD,所以PA⊥CD,所以CD⊥平面PAD[来源:学§科§网]所以CD⊥PD,因为E和F分别是CD和PC的中点所以PD∥EF,所以CD⊥EF,所以CD⊥平面BEF,所以平面BEF⊥平面PCD.题型五线面、面面垂直探究问题例5（2012北京文）如图1,在Rt△ABC中,∠C=90°,D,E分别是AC,AB上的中点, 点F为线段CD上的一点.将△ADE沿DE折起到△A 1DE的位置,使A1F⊥CD,如图2.(1)求证:DE∥平面A1CB;(2)求证:A1F⊥BE;(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.【考点定位】本题第二问是对基本功的考查,对于知识掌握不牢靠的学生可能不能顺利解决.第三问的创新式问法,难度比较大.解:(1)因为D,E分别为AC,AB的中点,所以DE∥BC.又因为DE⊄平面A1CB,所以DE∥平面A1CB.(2)由已知得AC⊥BC且DE∥BC,所以DE⊥AC.所以DE⊥A1D,DE⊥CD.所以DE⊥平面A1DC.而A1F⊂平面A1DC,所以DE⊥A1F.又因为A1F⊥CD,所以A1F⊥平面BCDE.所以A1F⊥BE(3)线段A1B上存在点Q,使A1C⊥平面DEQ.理由如下:如图,分别取A1C,A1B的中点P,Q,则PQ∥BC.又因为DE∥BC,所以DE∥PQ.所以平面DEQ即为平面DEP.由(2)知DE⊥平面A1DC,所以DE⊥A1C.又因为P是等腰三角形DA1C底边A1C 的中点,所以A1C⊥DP,所以A1C⊥平面DEP,从而A1C⊥平面DEQ.故线段A1B上存在点Q,使得A1C⊥平面DEQ.课堂练习5：（2012北京理）如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB 上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.(1)求证:A1C⊥平面BCDE;(2)（略）(3)线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?说明理由.、、【考点定位】此题第二问是对基本功的考查,对于知识掌握不牢靠的学生可能不能顺利解答.第三问的创新式问法,难度非常大.解:(1) CD DE ⊥,1A E DE ⊥∴DE ⊥平面1A CD , 又 1AC ⊂平面1A CD , ∴1AC ⊥DE 又1AC CD ⊥, ∴1AC ⊥平面BCDE (3)设线段BC 上存在点P ,设P 点坐标为()00a ，，,则[]03a ∈，则(10A P a =- ，，,()20DP a = ，，设平面1A DP 法向量为()1111n x y z = ，，,则1111020ay x ay ⎧-=⎪⎨+=⎪⎩∴111112z x ay ⎧=⎪⎪⎨⎪=-⎪⎩∴()136n a =- ， 假设平面1A DP 与平面1A BE 垂直,则10n n ⋅=,∴31230a a ++=,612a =-,2a =-∵03a << ∴不存在线段BC 上存在点P ,使平面1A DP 与平面1A BE 垂直五．品味高考（家庭作业）：1.（2013年普通高等学校招生统一考试广东省数学（理）卷）设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是（ ）yCA ．若αβ⊥,m α⊂,n β⊂,则m n ⊥B ．若//αβ,m α⊂,n β⊂,则//m nC ．若m n ⊥,m α⊂,n β⊂,则αβ⊥D ．若m α⊥,//m n ,//n β,则αβ⊥ 【答案】D2．（2013年普通高等学校招生统一考试新课标Ⅱ卷数学（理））已知为异面直线,平面,平面.直线满足,,,l m l n l l αβ⊥⊥⊄⊄,则 （ ）A ．,且B ．,且C ．与相交,且交线垂直于 D ．与相交,且交线平行于【答案】D3.（2013年普通高等学校招生统一考试浙江数学（理）试题）在空间中,过点A 作平面π的垂线,垂足为B ,记)(A f B π=.设βα,是两个不同的平面,对空间任意一点P ,)]([)],([21P f f Q P f f Q βααβ==,恒有21PQ PQ =,则（ ）A ．平面α与平面β垂直B ．平面α与平面β所成的(锐)二面角为045C ．平面α与平面β平行D ．平面α与平面β所成的(锐)二面角为060【答案】A4.（2013年普通高等学校招生统一考试辽宁数学（理）试题）如图,AB 是圆的直径,PA 垂直圆所在的平面,C 是圆上的点.(I)求证:PAC PBC ⊥平面平面；(II) （略）【答案】（略）5.（2013年普通高等学校招生全国统一招生考试江苏卷）本小题满分14分.如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ，分别是棱SC SA ，的中点.求证:(1)平面//EFG 平面ABC ; (2)SA BC ⊥.【答案】证明:(1)∵AB AS =,SB AF ⊥∴F 分别是SB 的中点 ∵E.F 分别是SA.SB 的中点 ∴EF∥AB又∵EF ⊄平面ABC, AB ⊆平面ABC ∴EF∥平面ABC ，同理:FG∥平面ABC 又∵EF FG=F, EF.FG ⊆平面ABC∴平面//EFG 平面ABC(2)∵平面⊥SAB 平面SBC ，平面SAB 平面SBC =BCAF ⊆平面SABAF⊥SB ，∴AF⊥平面SBC 又∵BC ⊆平面SBC ∴AF⊥BC 又∵BC AB ⊥, AB AF=A, AB.AF ⊆平面SAB ∴BC⊥平面SAB 又∵SA ⊆平面SAB∴BC⊥SA6.（2013年普通高等学校招生统一考试广东省数学（理）卷）如图1,在等腰直角三角形ABC中,90A ∠=︒,6BC =,,D E 分别是,AC AB 上的点,CD BE ==O 为BC 的中点.将ADE ∆沿DE 折起,得到如图2所示的四棱锥A BCDE '-,其中A O '=. (Ⅰ) 证明:A O '⊥平面BCDE ; (Ⅱ)（略）【答案】(Ⅰ) 在图1中,易得3,OC AC AD ===.COBDEC DO BE'A 图1 图2ABCSGFE连结,OD OE ,在OCD ∆中,由余弦定理可得OD ==，由翻折不变性可知A D '=所以222A O OD A D ''+=,所以A O OD '⊥,理可证A O OE '⊥, 又OD OE O = ,所以A O '⊥平面BCDE .7.（2013年高考陕西卷（理））如图, 四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形, O为底面中心, A 1O ⊥平面ABCD, 1AB AA ==证明: A 1C ⊥平面BB 1D 1D ; (Ⅱ) （略）解:(Ⅰ) BD O A ABCD BD ABCD O A ⊥∴⊂⊥11,,面且面 ;又因为, 在正方形ABCD中，BD C A AC A C A AC A BD A AC O A BD AC ⊥⊂⊥=⋂⊥11111,，故面且面所以；且在正方形AB CD 中,AO = 1 . .111=∆O A OA A RT 中，在O E C A OCE A E D B 1111111⊥为正方形，所以，则四边形的中点为设.，所以由以上三点得且，面面又O O BD D D BB O D D BB BD =⋂⊂⊂111111E .E ,D D BB C A 111面⊥.(证毕)8.（2013年高考江西卷（理））如图,四棱锥P ABCD -中,PA ,ABCD E BD ⊥平面为的中点,G PD 为的中点，3,12DAB DCB EA EB AB PA ∆≅∆====，1AC D OB E'A H,连接CE 并延长交AD 于F .(1) 求证:AD CFG ⊥平面;解:(1)在ABD ∆中,因为E 是BD 的中点,所以1EA EB ED AB ====, 故,23BAD ABE AEB ππ∠=∠=∠=,因为DAB DCB ∆≅∆,所以EAB ECB ∆≅∆, 从而有FED FEA ∠=∠,故,EF AD AF FD ⊥=,又因为,PG GD =所以FG ∥PA . 又PA ⊥平面ABCD ,所以,GF AD ⊥故AD ⊥平面CFG .。

数学必修二第二章点直线平面之间的位置关系青岛天龙中学高二数学备课组数学必修二第二章点直线平面之间的位置关系青岛天龙中学高二数学备课组第 1 页共2 页第 2 页共2 页§2.3.1 直线与平面垂直的判定一、学习目标：1．正确理解和掌握“二面角”、“二面角的平面角”及“直二面角”、“两个平面互相垂直”的概念；2．掌握两个平面垂直的判定定理及其简单的应用；二、学习重、难点重点: 平面与平面垂直的判定；难点: 如何度量二面角的大小。

三、课前预习：阅读教材P67-69，注意逐字逐句仔细审题，认真思考、独立规范作答，不会的先绕过，做好记号。

,四、知识衔接：直线与平面垂直的定义：直线与平面垂直的判定定理：直线与平面所成的角：五、学习过程;一、二面角的定义问题1:半平面：二面角：二面角的表示:二面角的平面角:二面角的平面角∠AOB的特点：(1)角的顶点在棱上；(2)角的两边分别在二面角的两个面上；(3)角的两边分别和棱垂直。

特别指出：①二面角的大小是用平面角来度量的，其范围是[0，0 180）；②二面角的平面角的大小与棱上点（角的顶点）的选择无关，是有二面角的两个面的位置惟一确定；③二面角的平面角所在的平面和棱是垂直的直二面角:规律：求异面直线所成的角，直线与平面所成的角，平面与平面所成的角最终都转化为线与线相交构成的角。

例1：如图四面体ABCD的棱BD长为2，其余各棱长均为2，求二面角A-BD-C的大小。

二、两个平面互相垂直两个平面互相垂直：两个互相垂直的平面画法：平面α与β垂直，记作：判定定理:一个平面过另一个平面的垂线，则这两个平面垂直。

符号语言:AB AB=B ABββααβ⊥⋂⊂⇒⊥，，图形语言:思路:线面垂直⇒面面垂直判断对错:1.如果平面α内有一条直线垂直于平面β内的一条直线，则α⊥β.（）2.如果平面α内有一条直线垂直于平面β内的两条直线，则α⊥β.（）3.如果平面α内的一条直线垂直于平面β内的两条相交直线, 则α⊥β.（）例2、已知直线PA垂直于圆O所在的平面，A为垂足，AB为圆O的直径，C是圆周上异于A、B的一点。

高二数学两个平面垂直的判定和性质知识精讲人教版【基础知识精讲】1.二面角半平面：一个平面内的一条直线，把这个平面分为两部分，其中的每一部分都叫做半平面.二面角：从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱，这两个半平面叫做二面角的面.棱为AB，面为α，β的二面角，记作二面角α—AB—β，如果棱用a表示，则记作二面角α—a—β，有时也可以全用大写拉丁字母表示，例平面PAB与平面QAB形成的二面角记作P—AB—Q.注意：平面几何中可以把角理解为一个旋转量，同样一个二面角也可以看作以一个半平面以其棱为轴旋转而成的.2.二面角的平面角平面与平面的位置关系，总的来说只有相交或平行两种.为了对相交平面的相互位置作进一步的对探讨，有必要研究二面角的大小问题.如图，在二面角α—a—β的棱a上任取一点O，在半平面α和β内，从点O分别作垂直于棱a的射线OA，OB，射线OA和OB组成∠AOB，在棱a上另取一点O′，按同样方法作∠A′O′B′.因为OA和O′A′，OB和O′B′都垂直于棱a，所以∠AOB和∠A′O′B′的两边分别平行且方向相同，因此∠AOB＝∠A′O′B′，可见∠AOB的大小与点O在棱上的位置无关.二面角的平面角：以二面角的棱上任意一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角.注意：①它是一个“平面角”，因此两边必须在同一平面内.②二面角的平面角的两边都必须与棱垂直.画二面角和它的平面角，最常见的两种形式：(1)直立式(2)平卧式二面角的大小，可以用它的平面角来度量，二面角的平面角是几度，就说这个二面角是几度.特别地：平面角是直角的二面角叫做直二面角. 二面角Q 的X 围是［0，π］3.两个平面垂直的判定(i)定义：两个平面所成二面角为直二面角；如果α与β垂直，记作α⊥β，画两个互相垂直的平面，把直立平面的竖边画成和水平平面的横边垂直，如图：(ii)两个平面垂直的判定定理：如果一个平面经过另一个平面的垂线，那么这两个平面互相垂直.AB ⊥β，AB ⊂α⇒α⊥β.建筑工人在砌墙时，常用一端系有铅锤的线来检查所砌的墙面是否和水平面垂直，就是依据这个定理.(iii)垂直于平行平面中的一个平面必垂直于另一个平面. α∥β,r ⊥α⇒r ⊥β说明 平面与平面的垂直问题可以转化为直线与平面的垂直问题，即线面垂直可以导致面面垂直.4.两个平面垂直的性质(i)两个平面垂直的性质定理：如果两个平面垂直，那么在一个平面内垂直于交线的直线必垂直于另一个平面.α⊥β，α∩β＝a,b ⊂α,b ⊥a ⇒b ⊥β(ii)过一平面内一点而垂直于另一平面的直线必在这平面内. (iii)相交平面同时垂直于第三个平面，则交线垂直于第三平面. (iv)过不垂直于平面的一直线有且只有一个平面与已知平面垂直. 从两个平面垂直的性质可以看出面面垂直可以得出线面垂直.5.两条异面直线上两点的距离公式设a 、b 是异面直线，AA ′是a 、b 的公垂线，A ′∈b,A ∈b ，AA ′＝d.E ∈a,F ∈b ，A E '＝m,FA ＝n.且a 、b 成θ角，则EF ＝θcos 2222mn n m d ±++.说明 (i)两条异面直线公垂线的存在性.(ii)可证明两条异面直线的距离是异面直线上两点的距离.(iii)可以解决分别在二面角的面内两点的距离问题.【重点难点解析】二面角及其平面角是本节重点概念，应熟练掌握找平面角的各种基本办法，两个平面垂直的判定定理及性质定理，是本节的两个重要定理，应弄清定理内容，灵活使用定理处理综合问题.如何选取恰当位置作出二面角的平面角是本节的难点，应在掌握找平面角的各种方法之后，通过加强练习达到灵活熟练的程度.同时，异面直线上两点间距离的计算也是本节的一个难点.例1 直线a 、b 是异面直线，a ⊥平面α，b ⊥平面β，a ⊥b ，求证：α⊥β.证明 过b 上任意一点作直线a ′，使a ∥a ′.∵a ⊥b,∴a ′⊥b.设相交直线a ′、b 确定一个平面γ,γ∩β＝c.∵b ⊥β,c ⊂β,∴b ⊥c.在平面γ内，b ⊥c,b ⊥a ′,∴a ′∥c.∴a ∥a ′∥c.又∵a ⊥α,∴c ⊥α,c ⊂β，∴β⊥α例2 在三棱锥S —ABC 中，∠ASB ＝∠BSC ＝60°，∠ASC ＝90°，且SA ＝SB ＝SC ，求证：平面ASC ⊥平面ABC.证明 取AC 的中点O ，连SO 、BO ，由已知，得ΔSAB 、ΔSBC 都是正三角形.∴BC ＝AB ＝a,SA ＝SC ＝a,又SO ⊥AC ，BO ⊥AC ，∴∠SOB 就是二面角S —AC —B 的平面角.又∵SA ＝AB ＝a,SC ＝BC ＝a,AC ＝AC,∴ΔACS ≌ΔACB.∴SO ＝BO ＝22a.在ΔSOB 中，∵SB ＝a,∴∠SOB ＝90°. 即平面SAC ⊥平面ABC.另证：过S 作SO ⊥平面ABC ，垂足是O.∵SA ＝SB ＝SC ，∴S 在平面内的射影是ΔABC 的外心，同前面的证明，可知ΔABC 是直角三角形，∴O 在斜边AC 上.又∵平面SAC 经过SO ，∴平面SAC ⊥平面ABC说明 证明“面面垂直”的常用方法是根据定义证明平面角是90°，或利用判定定理证明一个平面经过另一个平面的垂线.例3 如图，四面体ABCD 的棱BD 长为2，其余各棱的长均是2，求：二面角A —BD—C 、A —BC —D 、B —AC —D 的大小.解 (1)取BD 的中点O ，连AO 、OC. 在ΔABD 中，∵AB ＝AD ＝2，BD ＝2，∴ΔABD 是等腰直角三角形，AO ⊥BD ，同理OC ⊥BD. ∴∠AOC 是二面角A —BD —C 的平面角 又AO ＝OC ＝1，AC ＝2，∴∠AOC ＝90°.即二面角A —BD —C 为直二面角.(2)∵二面角A —BD —C 是直二面角，AO ⊥BD ，∴AO ⊥平面BCD. ∴ΔABC 在平面BCD 内的射影是ΔBOC. ∵S ΔOCB ＝21,S ΔABC ＝23,∴cos θ＝33.即二面角A —BC —D 的大小是arccos33. (3)取AC 的中点E ，连BE 、DE. ∵AB ＝BC ，AD ＝DC ，∴BD ⊥AC ，DE ⊥AC ，∴∠BED 就是二面角的平面角. 在ΔBDE 中，BE ＝DE ＝26，由余弦定理，得cos α＝-31 ∴二面角B —AC —D 的大小是π—arccos31. 评析 本例提供了求二面角大小的方法：先作出二面角的平面角，再利用其所在的三角形算出角的三角函数值，或利用面积的射影公式S ′＝S ·cos θ求得.例4 如图所示，在三棱锥S —ABC 中，SA ⊥底面ABC ，AB ⊥BC ，DE 垂直平分SC ，且分别交AC 、SC 于D 、E.又SA ＝AB ，SB ＝SC.求以BD 为棱，以BDE 与BDC 为面的二面角的度数.解法一：由于SB ＝BC ，且E 是SC 中点，因此BE 是等腰三角形SBC 的底边SC 的中线，所以SC ⊥BE.又已知SC ⊥DE ，BE ∩DE ＝E ，∴SC ⊥平面BDE ， ∴SC ⊥BD ，又∵SA ⊥底面ABC ，BD 在底面ABC 上， ∴SA ⊥BD.而SA ∩SC ＝S ， 所以BD ⊥平面SAC.∵DE ＝平面SAC ∩平面BDE ，DC ＝平面SAC ∩平面BDC ， ∴BD ⊥DE ，BD ⊥DC.∴∠EDC 是所求二面角的平面角. ∵SA ⊥底面ABC ， ∴SA ⊥AB ，SA ⊥AC.设SA ＝a,则AB ＝a,BC ＝SB ＝2a. 又AB ⊥BC ，所以AC ＝3a.在Rt ΔSAC 中 tg ∠ACS ＝AC SA ＝31，所以∠ACS ＝30°. 又已知DE ⊥SC ，所以∠EDC ＝60°，即所求的二面角等于60°.解法二：由于SB ＝BC ，且E 是SC 的中点，因此BE 是等腰ΔSBC 的底边SC 的中线，所以SC ⊥BE.又已知SC ⊥DE ，BE ∩DE ＝E.∴SC ⊥平面BDE ，SC ⊥BD.由于SA ⊥底面ABC ，且A 是垂足，所以，AC 是SC 在平面ABC 上的射影，由三垂线定理的逆定理得BD ⊥AC ；又E ∈SC ，AC 是SC 在平面内的射影，所以E 在平面ABC 内的射影在AC 上，由于D ∈AC ，所以DE 在平面ABC 内的射影在AC 上，根据三垂线定理得BD ⊥DE.∵DE ⊂平面BDE ，DC ⊂平面BDC. ∴∠EDC 是所求二面角的平面角. 以下解法同解法一.例5 在直三棱柱ABC —A ′B ′C ′中，∠BAC ＝90°，AB ＝BB ′＝1，直线B ′C 与平面ABC 成30°的角.(如图所示)(1)求点C ′到平面AB ′C 的距离； (2)求二面角B —B ′C —A 的余弦值.解 (1)∵ABC —A ′B ′C ′是直三棱柱，∴A ′C ′∥AC ，AC ⊂平面AB ′C ，∴A ′C ′∥平面AB ′C ，于是C ′到平面AB ′C 的距离等于点A ′到平面AB ′C 的距离，作A ′M ⊥AB ′于M.由AC ⊥平面AB ′A ′A 得平面AB ′C ⊥平面AB ′A ′A ，∴A ′M ⊥平面AB ′C ，A ′M 的长是A ′到平面AB ′C 的距离.∵AB ＝BB ′＝1，∠B ′CB ＝30°，∴B ′C ＝2，BC ＝3，AB ′＝2，A ′M ＝AA AA B A ''⨯''＝22. 即C ′到平面AB ′C 的距离为22； (2)作AN ⊥BC 于N ，则AN ⊥平面B ′BCC ′，作NQ ⊥B ′C 于Q ，则CQ ⊥B ′C ，∴∠AQN 是所求二面角的平面角，AN ＝BCAC AB ⨯＝36，AQ ＝C B B A AC ''⨯＝1.∴sin ∠AQN ＝AQ AN ＝36,cos ∠AQN ＝33.说明 利用异面直线上两点间的距离公式，也可以求二面角的大小，如图，AB ＝BB ′＝1，∴AB ′＝2，又∠B ′CB ＝30°，∴BC ＝3,B ′C ＝2,AC ＝2.作AM ⊥B ′C 于M ，BN ⊥B ′C 于N ，则AM ＝1，BN ＝23，＝23，CM ＝1，∴MN ＝21.∵BN ⊥B ′C,AM ⊥B ′C ，∴BN 与AM 所成的角等于二面角B —B ′C —A 的平面角.设为θ.由AB 2＝AM 2+BN 2+MN 2-2AM ×BN ×cos θ得cos θ＝31＝33.例6 如图所示，四棱锥P —ABCD 的底面是边长为a 的菱形，∠A ＝60°，PC ⊥平面ABCD ，PC ＝a,E 是PA 的中点.(1)求证平面BDE ⊥平面ABCD. (2)求点E 到平面PBC 的距离.(3)求二面角A —EB —D 的平面角大小.解 (1)设O 是AC ，BD 的交点，连结EO. ∵ABCD 是菱形，∴O 是AC 、BD 的中点，∵E 是PA 的中点，∴EO ∥PC ，又PC ⊥平面ABCD ，∴EO ⊥平面ABCD ，EO ⊂平面BDE ，∴平面BDE ⊥平面ABCD. (2)EO ∥PC ，PC ⊂平面PBC ， ∴EO ∥平面PBC ，于是点O 到平面PBC 的距离等于E 到平面PBC 的距离.作OF ⊥BC 于F ， ∵EO ∥平面ABCD ，PC ⊂平面PBC ，∴平面PBC ⊥平面ABCD ，于是OF ⊥平面PBC ，OF 的长等于O 到平面PBC 的距离.由条件可知，OB ＝2a ,OF ＝2a×23＝43a ，则点E 到平面PBC 的距离为43a.(3)过O 作OG ⊥EB 于G ，连接AG∵OE ⊥AC ，BD ⊥AC ∴AC ⊥平面BDE∴AG ⊥EB(三垂线定理)∴∠AGO 是二面角A —EB —D 的平面角 ∵OE ＝21PC ＝21a,OB ＝23a∴EB ＝a.∴OG ＝EB OB OE ⋅＝43a 又AO ＝21a.∴tan ∠AGO ＝OG AO ＝332∴∠AGO ＝arctan332. 评析 本题考查了面面垂直判定与性质，以及利用其性质求点到面距离，及二面角的求法，三垂线定理及某逆定理的应用.例7 如图，矩形ABCD 中，AB ＝2，BC ＝23，以AC 为轴翻折半平面，使二平面角B —AC —D 为120°，求：(1)翻折后，D 到平面ABC 的距离；(2)BD 和AC 所成的角.分析 研究翻折问题，通常要画出翻折前的平面图形和翻折后的空间图形，对应点的字母要相同.解 分别过B 、D 作AC 的垂线，垂足是E 、F ，过F 作FB ′∥BE ，过B 作BB ′∥AC ，交点B ′，则四边形EFB ′B 是矩形.∵AC ⊥DF ，AC ⊥B ′F ，∴AC ⊥平面B ′FD ，即∠DF ′B 就是二面角B —AC —D 的平面角，亦即∠DFB ′＝120°.过D 作DO ⊥′BF ，垂足为O.∵DO ⊂平面DFB ′，AC ⊥平面DFB ′.∴DO ⊥AF ，DO ⊥平面ABC.在Rt ΔADC 中，CD ＝2，AD ＝23，∴DF ＝3，OD ＝OF ·sin60°＝23. (2)在ΔDFB ′中，DB ′＝︒⋅'⋅⋅-'+120cos 22F B DF F B DF ＝3.又由(1)可知，AC ∥BB ′，AC ⊥平面DFB ′.∴BB ′⊥平面DFB ′，∴ΔDBB ′是直角三角形，又BB ′＝EF ＝2.∴tan ∠DBB ′＝23. ∵AC ∥BB ′,∴AC 与BD 所成的角就是∠DBB ′，即为arctan23. 说明 处理翻折问题，只要过不在棱上的点作棱的垂直相交的线段，就可以化成基本题型处理，本题也可以这样考虑，即利用异面直线DF 、BE 上两点B 、D 间的距离，先求出BD 2＝EF 2+DF 2+BE 2-2DF ·BE ·cos120°＝13，从而得出∠DBB ′＝arccos132.【难题巧解点拨】例1 已知直线l ⊥平面α，直线m ⊂平面β，有下面四个命题： (1)α∥β⇒l ⊥m (2)α⊥β⇒l ∥m (3)l ∥m ⇒α⊥β (4)l ⊥m ⇒α∥β 其中正确的两个命题是( )A.(1)与(2)B.(3)与(4)C.(2)与(4)D.(1)与(3)分析：本题主要考查直线与平面、平面和平面的位置关系，以及空间想象能力和逻辑推理能力.解法一：在l ⊥α，m ⊂β的前提下，当α∥β时，有l ⊥β，从而l ⊥β，从而l ⊥m ，得(1)正确；当α⊥β时，l 垂直于α、β的交线，而m 不一定与该交线垂直，因此，l 与m 不一定平行，故(2)不正确.故应排除A 、C.依题意，有两个命题正确，不可能(3)，(4)都正确，否则连同(1)共有3个命题正确.故排除B ，得D.解法二：当断定(1)正确之后，根据4个选择项的安排，可转而检查(3)，由l ∥m,l ∥α知m ⊥α，从而由m ⊂α得α⊥β.即(3)正确.故选D.解法三：不从(1)检查起，而从(2)、(3)、(4)中任一命题检查起，如首先检查(4)；由l ⊥α,m ⊥β不能否定m 是α、β的交线，因此α∥β不一定成立，故(4)是不正确的，因此可排除B 、C.依据A 和D 的内容可知(1)必定是正确的，否则A 和D 也都排除，以下只要对(2)或(3)检查，只须检查一个便可以做出判断.例2 一X 正方形的纸ABCD ，BD 是对角线，过AB 、CD 的中点E 、F 的线段交BD 于O ，以EF 为棱，将正方形的纸折成直二面角，则∠BOD 等于( )A.120°B.150°C.135°D.90°分析：本题考查线面垂直，面面垂直，余弦定理，以及空间与平面问题的转化能力。