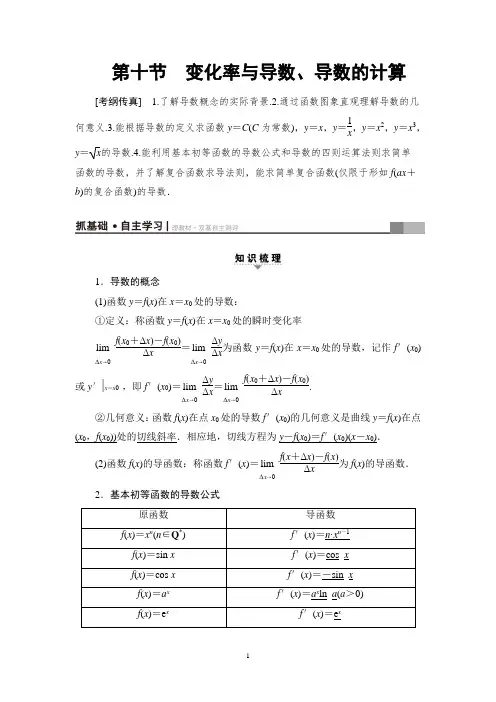
第十节变化率与导数、导数的计算[考纲传真] 1.了解导数概念的实际背景.2.通过函数图象直观理解导数的几何意义.3.能根据导数的定义求函数y＝C(C为常数)，y＝x，y＝1x，y＝x2，y＝x3，y＝x的导数.4.能利用基本初等函数的导数公式和导数的四则运算法则求简单函数的导数，并了解复合函数求导法则，能求简单复合函数(仅限于形如f(ax＋b)的复合函数)的导数．1．导数的概念(1)函数y＝f(x)在x＝x0处的导数：①定义：称函数y＝f(x)在x＝x0处的瞬时变化率lim Δx→0f(x0＋Δx)－f(x0)Δx＝limΔx→0ΔyΔx为函数y＝f(x)在x＝x0处的导数，记作f′(x0)或y′|x＝x0，即f′(x0)＝limΔx→0ΔyΔx＝limΔx→0f(x0＋Δx)－f(x0)Δx.②几何意义：函数f(x)在点x0处的导数f′(x0)的几何意义是曲线y＝f(x)在点(x0，f(x0))处的切线斜率．相应地，切线方程为y－f(x0)＝f′(x0)(x－x0)．(2)函数f(x)的导函数：称函数f′(x)＝limΔx→0f(x＋Δx)－f(x)Δx为f(x)的导函数．2．基本初等函数的导数公式(1)[f (x )±g (x )]′＝f ′(x )±g ′(x )； (2)[f (x )·g (x )]′＝f ′(x )g (x )＋f (x )g ′(x )； (3)⎣⎢⎡⎦⎥⎤f (x )g (x )′＝f ′(x )g (x )－f (x )g ′(x )[g (x )]2(g (x )≠0)．4．复合函数的导数复合函数y ＝f (g (x ))的导数和函数y ＝f (u )，u ＝g (x )的导数间的关系为y x ′＝y u ′·u x ′，即y 对x 的导数等于y 对u 的导数与u 对x 的导数的乘积．1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”) (1)f ′(x 0)与(f (x 0))′表示的意义相同．( ) (2)求f ′(x 0)时，可先求f (x 0)再求f ′(x 0)．( ) (3)曲线的切线与曲线不一定只有一个公共点．( ) (4)若f (x )＝e 2x ，则f ′(x )＝e 2x .( ) [答案] (1)× (2)× (3)√ (4)×2．(教材改编)有一机器人的运动方程为s (t )＝t 2＋3t (t 是时间，s 是位移)，则该机器人在时刻t ＝2时的瞬时速度为( )【导学号：01772075】A.194 B.174 C.154D.134D [由题意知，机器人的速度方程为v (t )＝s ′(t )＝2t －3t 2，故当t ＝2时，机器人的瞬时速度为v (2)＝2×2－322＝134.]3．(2016·天津高考)已知函数f (x )＝(2x ＋1)e x ，f ′(x )为f (x )的导函数，则f ′(0)的值为________．3 [因为f (x )＝(2x ＋1)e x ，所以f ′(x )＝2e x ＋(2x ＋1)e x ＝(2x ＋3)e x ， 所以f ′(0)＝3e 0＝3.]4．(2016·豫北名校期末联考)曲线y ＝－5e x ＋3在点(0，－2)处的切线方程为________．5x ＋y ＋2＝0 [∵y ′＝－5e x ，∴所求曲线的切线斜率k ＝y ′| x ＝0＝－5e 0＝－5，∴切线方程为y －(－2)＝－5(x －0)，即5x ＋y ＋2＝0.]4．(2015·全国卷Ⅰ)已知函数f (x )＝ax 3＋x ＋1的图象在点(1，f (1))处的切线过点(2,7)，则a ＝________.1 [∵f ′(x )＝3ax 2＋1， ∴f ′(1)＝3a ＋1. 又f (1)＝a ＋2，∴切线方程为y －(a ＋2)＝(3a ＋1)(x －1)．∵切线过点(2,7)，∴7－(a ＋2)＝3a ＋1，解得a ＝1.](1)y ＝e x ln x ； (2)y ＝x ⎝ ⎛⎭⎪⎫x 2＋1x ＋1x 3；(3)y ＝x －sin x 2cos x2； (4)y ＝ln(2x －9)．[解] (1)y ′＝(e x )′ln x ＋e x (ln x )′＝e x ln x ＋e x ·1x ＝e x ⎝ ⎛⎭⎪⎫ln x ＋1x . (2)∵y ＝x 3＋1＋1x 2，∴y ′＝3x 2－2x 3.(3)∵y ＝x －12sin x ，∴y ′＝1－12cos x . (4)令u ＝2x －9，y ＝ln u ，则y ′x ＝y ′u ·u ′x . 因此y ′＝12x －9·(2x －9)′＝22x －9. [规律方法] 1.熟记基本初等函数的导数公式及运算法则是导数计算的前提，求导之前，应利用代数、三角恒等式等变形对函数进行化简，然后求导，这样可以减少运算量提高运算速度，减少差错．2．如函数为根式形式，可先化为分数指数幂，再求导．3．复合函数求导，应先确定复合关系，由外向内逐层求导，必要时可换元处理．[变式训练1] (1)f (x )＝x (2 017＋ln x )，若f ′(x 0)＝2 018，则x 0等于( ) A ．e 2 B.1 C.ln 2D.e(2)(2015·天津高考)已知函数f (x )＝ax ln x ，x ∈(0，＋∞)，其中a 为实数，f ′(x )为f (x )的导函数．若f ′(1)＝3，则a 的值为________．(1)B (2)3 [(1)f ′(x )＝2 017＋ln x ＋x ×1x ＝2 018＋ln x ，故由f ′(x 0)＝2 018，得2 018＋ln x 0＝2 018，则ln x 0＝0，解得x 0＝1.(2)f ′(x )＝a ⎝ ⎛⎭⎪⎫ln x ＋x ·1x ＝a (1＋ln x )． 由于f ′(1)＝a (1＋ln 1)＝a ，又f ′(1)＝3，所以a ＝3.]☞角度1已知曲线y ＝13x 3＋43.(1)求曲线在点P (2,4)处的切线方程； (2)求曲线过点P (2,4)的切线方程．[思路点拨] (1)点P (2,4)是切点，先利用导数求切线斜率，再利用点斜式写出切线方程；(2)点P (2,4)不一定是切点，先设切点坐标为⎝ ⎛⎭⎪⎫x 0，13x 30＋43，由此求出切线方程，再把点P (2,4)代入切线方程求x 0.[解] (1)根据已知得点P (2,4)是切点且y ′＝x 2，∴在点P (2,4)处的切线的斜率为y ′| x ＝2＝4，3分 ∴曲线在点P (2,4)处的切线方程为y －4＝4(x －2)， 即4x －y －4＝0.5分(2)设曲线y ＝13x 3＋43与过点P (2,4)的切线相切于点A ⎝ ⎛⎭⎪⎫x 0，13x 30＋43，则切线的斜率为y ′| x ＝x 0＝x 20， ∴切线方程为y －⎝ ⎛⎭⎪⎫13x 30＋43＝x 20(x －x 0)， 即y ＝x 20·x －23x 30＋43.7分 ∵点P (2,4)在切线上，∴4＝2x 20－23x 30＋43， 即x 30－3x 20＋4＝0，9分 ∴x 30＋x 20－4x 20＋4＝0，∴x 20(x 0＋1)－4(x 0＋1)(x 0－1)＝0，∴(x 0＋1)(x 0－2)2＝0，解得x 0＝－1或x 0＝2， 故所求的切线方程为x －y ＋2＝0或4x －y －4＝0.12分 ☞角度2 求切点坐标若曲线y ＝x ln x 上点P 处的切线平行于直线2x －y ＋1＝0，则点P的坐标是________．【导学号：01772076】(e ，e) [由题意得y ′＝ln x ＋x ·1x ＝1＋ln x ，直线2x －y ＋1＝0的斜率为2.设P (m ，n )，则1＋ln m ＝2，解得m ＝e ，所以n ＝eln e ＝e ，即点P 的坐标为(e ，e)．]☞角度3 求参数的值(1)已知直线y ＝x ＋1与曲线y ＝ln(x ＋a )相切，则a 的值为( )A ．1 B.2 C.－1D.－2(2)(2017·西宁复习检测(一))已知曲线y＝x＋1x－1在点(3,2)处的切线与直线ax＋y＋1＝0垂直，则a＝()A．－2 B.2C.－12 D.12(1)B(2)A[(1)设直线y＝x＋1与曲线y＝ln(x＋a)的切点为(x0，y0)，则y0＝1＋x0，y0＝ln(x0＋a)．又y′＝1x＋a，所以y′|x＝x0＝1x0＋a＝1，即x0＋a＝1.又y0＝ln(x0＋a)，所以y0＝0，则x0＝－1，所以a＝2.(2)由y′＝－2(x－1)2得曲线在点(3,2)处的切线斜率为－12，又切线与直线ax＋y＋1＝0垂直，则a＝－2，故选A.][规律方法] 1.导数f′(x0)的几何意义就是函数y＝f(x)在点P(x0，y0)处的切线的斜率，切点既在曲线上，又在切线上，切线有可能和曲线还有其他的公共点．2．曲线在点P处的切线是以点P为切点，曲线过点P的切线则点P不一定是切点，此时应先设出切点坐标．易错警示：当曲线y＝f(x)在点(x0，f(x0))处的切线垂直于x轴时，函数在该点处的导数不存在，切线方程是x＝x0.[思想与方法]1．f′(x0)是函数f(x)在x＝x0处的导数值；(f(x0))′是函数值f(x0)的导数，而函数值f(x0)是一个常数，其导数一定为0，即(f(x0))′＝0.2．对于函数求导，一般要遵循先化简再求导的基本原则．在实施化简时，必须注意变换的等价性．[易错与防范]1．利用公式求导时要特别注意除法公式中分子的符号，防止与乘法公式混淆．复合函数的导数要正确分解函数的结构，由外向内逐层求导．2．曲线y＝f(x)“在点P(x0，y0)处的切线”与“过点P(x0，y0)的切线”的区别：前者P (x 0，y 0)为切点，而后者P (x 0，y 0)不一定为切点．3．曲线的切线与二次曲线的切线的区别：曲线的切线与曲线的公共点的个数不一定只有一个，而直线与二次曲线相切只有一个公共点．课时分层训练(七) 二次函数与幂函数A 组 基础达标 (建议用时：30分钟)一、选择题1．已知幂函数f (x )＝k ·x α的图象过点⎝ ⎛⎭⎪⎫12，22，则k ＋α＝( )【导学号：01772040】A.12 B.1 C.32D.2C [由幂函数的定义知k ＝1.又f ⎝ ⎛⎭⎪⎫12＝22，所以⎝ ⎛⎭⎪⎫12α＝22，解得α＝12，从而k ＋α＝32.]2．函数f (x )＝2x 2－mx ＋3，当x ∈[－2，＋∞)时，f (x )是增函数，当x ∈(－∞，－2]时，f (x )是减函数，则f (1)的值为( )A ．－3 B.13 C.7D.5B [函数f (x )＝2x 2－mx ＋3图象的对称轴为直线x ＝m4，由函数f (x )的增减区间可知m4＝－2，∴m ＝－8，即f (x )＝2x 2＋8x ＋3，∴f (1)＝2＋8＋3＝13.]3．若幂函数y ＝(m 2－3m ＋3)·xm 2－m －2的图象不过原点，则m 的取值是( )A ．－1≤m ≤2 B.m ＝1或m ＝2 C ．m ＝2D.m ＝1B [由幂函数性质可知m 2－3m ＋3＝1，∴m ＝2或m ＝1.又幂函数图象不过原点，∴m 2－m －2≤0，即－1≤m ≤2，∴m ＝2或m ＝1.]4．已知函数y ＝ax 2＋bx ＋c ，如果a >b >c 且a ＋b ＋c ＝0，则它的图象可能是( )【导学号：01772041】A B C DD [由a ＋b ＋c ＝0，a ＞b ＞c 知a ＞0，c ＜0，则ca ＜0，排除B ，C.又f (0)＝c ＜0，所以也排除A.]5．若函数f (x )＝x 2－ax －a 在区间[0,2]上的最大值为1，则实数a 等于( ) A ．－1 B.1 C.2D.－2B [∵函数f (x )＝x 2－ax －a 的图象为开口向上的抛物线， ∴函数的最大值在区间的端点取得． ∵f (0)＝－a ，f (2)＝4－3a ，∴⎩⎨⎧ －a ≥4－3a ，－a ＝1，或⎩⎨⎧－a ≤4－3a ，4－3a ＝1，解得a ＝1.] 二、填空题6．(2017·上海八校联合测试改编)已知函数f (x )＝ax 2－2ax ＋1＋b (a ＞0)．若f (x )在[2,3]上的最大值为4，最小值为1，则a ＝________，b ＝________.1 0 [因为函数f (x )的对称轴为x ＝1，又a ＞0， 所以f (x )在[2,3]上单调递增，所以⎩⎨⎧f (2)＝1，f (3)＝4，即⎩⎨⎧a ·22－2a ·2＋1＋b ＝1，a ·32－2a ·3＋1＋b ＝4，解方程得a ＝1，b ＝0.] 7．已知P ＝2，Q ＝⎝ ⎛⎭⎪⎫253，R ＝⎝ ⎛⎭⎪⎫123，则P ，Q ，R 的大小关系是________.【导学号：01772042】P ＞R ＞Q [P ＝2＝⎝ ⎛⎭⎪⎫223，根据函数y ＝x 3是R 上的增函数且22＞12＞25，得⎝ ⎛⎭⎪⎫223＞⎝ ⎛⎭⎪⎫123＞⎝ ⎛⎭⎪⎫253，即P ＞R ＞Q .] 8．已知函数f (x )＝x 2－2ax ＋5在(－∞，2]上是减函数，且对任意的x 1，x 2∈[1，a ＋1]，总有|f (x 1)－f (x 2)|≤4，则实数a 的取值范围是________．[2,3] [f (x )＝(x －a )2＋5－a 2，根据f (x )在区间(－∞，2]上是减函数知，a ≥2，则f (1)≥f (a ＋1)，从而|f (x 1)－f (x 2)|max ＝f (1)－f (a )＝a 2－2a ＋1， 由a 2－2a ＋1≤4，解得－1≤a ≤3， 又a ≥2，所以2≤a ≤3.] 三、解答题9．已知幂函数f (x )＝x (m 2＋m )－1(m ∈N *)经过点(2，2)，试确定m 的值，并求满足条件f (2－a )＞f (a －1)的实数a 的取值范围．[解] 幂函数f (x )经过点(2，2)， ∴2＝2(m 2＋m )－1，即2＝2(m 2＋m )－1，∴m 2＋m ＝2，解得m ＝1或m ＝－2.4分 又∵m ∈N *，∴m ＝1.∴f (x )＝x ，则函数的定义域为[0，＋∞)， 并且在定义域上为增函数．由f (2－a )＞f (a －1)，得⎩⎨⎧2－a ≥0，a －1≥0，2－a ＞a －1，10分解得1≤a ＜32.∴a 的取值范围为⎣⎢⎡⎭⎪⎫1，32.12分 10．已知函数f (x )＝x 2＋(2a －1)x －3，(1)当a ＝2，x ∈[－2,3]时，求函数f (x )的值域；(2)若函数f (x )在[－1,3]上的最大值为1，求实数a 的值．[解] (1)当a ＝2时，f (x )＝x 2＋3x －3，x ∈[－2,3]， 对称轴x ＝－32∈[－2,3]，2分 ∴f (x )min ＝f ⎝ ⎛⎭⎪⎫－32＝94－92－3＝－214，f (x )max ＝f (3)＝15， ∴值域为⎣⎢⎡⎦⎥⎤－214，15.5分(2)对称轴为x ＝－2a －12.①当－2a －12≤1，即a ≥－12时，f (x )max ＝f (3)＝6a ＋3，∴6a ＋3＝1，即a ＝－13满足题意；8分 ②当－2a －12＞1，即a ＜－12时，f (x )max ＝f (－1)＝－2a －1，∴－2a －1＝1，即a ＝－1满足题意． 综上可知a ＝－13或－1. 12分B 组 能力提升 (建议用时：15分钟)1．(2017·江西九江一中期中)函数f (x )＝(m 2－m －1)x 4m 9－m 5－1是幂函数，对任意的x 1，x 2∈(0，＋∞)，且x 1≠x 2，满足f (x 1)－f (x 2)x 1－x 2＞0，若a ，b ∈R ，且a＋b ＞0，ab ＜0，则f (a )＋f (b )的值( )【导学号：01772043】A ．恒大于0 B.恒小于0 C ．等于0D.无法判断A [∵f (x )＝(m 2－m －1)x 4m 9－m 5－1是幂函数， ∴m 2－m －1＝1，解得m ＝2或m ＝－1.当m ＝2时，指数4×29－25－1＝2 015＞0，满足题意．当m ＝－1时，指数4×(－1)9－(－1)5－1＝－4＜0，不满足题意， ∴f (x )＝x 2 015.∴幂函数f (x )＝x 2 015是定义域R 上的奇函数，且是增函数． 又∵a ，b ∈R ，且a ＋b ＞0，∴a ＞－b ， 又ab ＜0，不妨设b ＜0，则a ＞－b ＞0，∴f (a )＞f (－b )＞0， 又f (－b )＝－f (b )，∴f (a )＞－f (b )，∴f (a )＋f (b )＞0.故选A.]2．设f (x )与g (x )是定义在同一区间[a ，b ]上的两个函数，若函数y ＝f (x )－g (x )在x ∈[a ，b ]上有两个不同的零点，则称f (x )和g (x )在[a ，b ]上是“关联函数”，区间[a ，b ]称为“关联区间”．若f (x )＝x 2－3x ＋4与g (x )＝2x ＋m 在[0,3]上是“关联函数”，则m 的取值范围为________．⎝ ⎛⎦⎥⎤－94，－2 [由题意知，y ＝f (x )－g (x )＝x 2－5x ＋4－m 在[0,3]上有两个不同的零点．在同一直角坐标系下作出函数y ＝m 与y ＝x 2－5x ＋4(x ∈[0,3])的图象如图所示，结合图象可知，当x ∈[2,3]时，y ＝x 2－5x ＋4∈⎣⎢⎡⎦⎥⎤－94，－2，故当m ∈⎝ ⎛⎦⎥⎤－94，－2时，函数y ＝m 与y ＝x 2－5x ＋4(x ∈[0,3])的图象有两个交点．]3．已知二次函数f (x )＝ax 2＋bx ＋1(a ，b ∈R )，x ∈R .(1)若函数f (x )的最小值为f (－1)＝0，求f (x )的解析式，并写出单调区间； (2)在(1)的条件下，f (x )＞x ＋k 在区间[－3，－1]上恒成立，试求k 的范围． [解] (1)由题意知⎩⎪⎨⎪⎧－b 2a ＝－1，f (－1)＝a －b ＋1＝0，解得⎩⎨⎧a ＝1，b ＝2.2分所以f (x )＝x 2＋2x ＋1，由f (x )＝(x ＋1)2知，函数f (x )的单调递增区间为[－1，＋∞)，单调递减区间为(－∞，－1].6分(2)由题意知，x 2＋2x ＋1＞x ＋k 在区间[－3，－1]上恒成立，即k ＜x 2＋x ＋1在区间[－3，－1]上恒成立，8分令g (x )＝x 2＋x ＋1，x ∈[－3，－1]，由g (x )＝⎝ ⎛⎭⎪⎫x ＋122＋34知g (x )在区间[－3，－1]上是减函数，则g (x )min ＝g (－1)＝1，所以k ＜1，即k 的取值范围是(－∞，1).12分第三节 基本不等式[考纲传真] 1.了解基本不等式的证明过程.2.会用基本不等式解决简单的最大(小)值问题．1．基本不等式ab ≤a ＋b2(1)基本不等式成立的条件：a >0，b >0. (2)等号成立的条件：当且仅当a ＝b . 2．几个重要的不等式 (1)a 2＋b 2≥2ab (a ，b ∈R )； (2)b a ＋ab ≥2(a ，b 同号且不为零)； (3)ab ≤⎝⎛⎭⎪⎫a ＋b 22(a ，b ∈R )；(4)⎝⎛⎭⎪⎫a ＋b 22≤a 2＋b22(a ，b ∈R )． 3．算术平均数与几何平均数设a >0，b >0，则a ，b 的算术平均数为a ＋b2，几何平均数为ab ，基本不等式可叙述为：两个正数的算术平均数不小于它们的几何平均数．4．利用基本不等式求最值问题 已知x >0，y >0，则(1)如果xy 是定值p ，那么当且仅当x ＝y 时，x ＋y 有最小值是2p (简记：积定和最小)．(2)如果x ＋y 是定值q ，那么当且仅当x ＝y 时，xy 有最大值是q 24(简记：和定积最大)．1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”) (1)函数y ＝x ＋1x 的最小值是2.( )(2)函数f (x )＝cos x ＋4cos x ，x ∈⎝ ⎛⎭⎪⎫0，π2的最小值等于4.( )(3)x >0，y >0是x y ＋yx ≥2的充要条件．( ) (4)若a >0，则a 3＋1a 2的最小值为2a .( ) [答案] (1)× (2)× (3)× (4)×2．若a ，b ∈R ，且ab >0，则下列不等式中，恒成立的是( ) A ．a 2＋b 2>2ab B ．a ＋b ≥2ab C.1a ＋1b >2abD.b a ＋a b ≥2D [∵a 2＋b 2－2ab ＝(a －b )2≥0，∴A 错误；对于B ，C ，当a <0，b <0时，明显错误．对于D ，∵ab >0，∴b a ＋ab ≥2b a ·a b ＝2.]3．(2016·安徽合肥二模)若a ，b 都是正数，则⎝ ⎛⎭⎪⎫1＋b a ⎝ ⎛⎭⎪⎫1＋4a b 的最小值为( )A ．7 B.8 C ．9D.10C [∵a ，b 都是正数，∴⎝ ⎛⎭⎪⎫1＋b a ⎝ ⎛⎭⎪⎫1＋4a b ＝5＋b a ＋4a b ≥5＋2b a ·4ab ＝9，当且仅当b ＝2a >0时取等号，故选C.]4．若函数f (x )＝x ＋1x －2(x >2)在x ＝a 处取最小值，则a 等于( ) 【导学号：01772209】A ．1＋ 2 B.1＋ 3 C ．3D.4C [当x >2时，x －2>0，f (x )＝(x －2)＋1x －2＋2≥2(x －2)×1x －2＋2＝4，当且仅当x －2＝1x －2(x >2)，即x ＝3时取等号，即当f (x )取得最小值时，x ＝3，即a ＝3，选C.]5．(教材改编)若把总长为20 m 的篱笆围成一个矩形场地，则矩形场地的最大面积是__________m 2.25 [设矩形的一边为x m ，矩形场地的面积为y ， 则另一边为12×(20－2x )＝(10－x )m ， 则y ＝x (10－x )≤⎣⎢⎡⎦⎥⎤x ＋(10－x )22＝25， 当且仅当x ＝10－x ，即x ＝5时，y max ＝25.](1)(2015·湖南高考)若实数a ，b 满足1a ＋2b ＝ab ，则ab 的最小值为( )A.2B.2C ．2 2 D.4(2)(2017·郑州二次质量预测)已知正数x ，y 满足x 2＋2xy －3＝0，则2x ＋y 的最小值是__________．(1)C (2)3 [(1)由1a ＋2b ＝ab 知a >0，b >0，所以ab ＝1a ＋2b ≥22ab ，即ab ≥22，当且仅当⎩⎪⎨⎪⎧1a ＝2b ，1a ＋2b ＝ab ，即a ＝42，b ＝242时取“＝”，所以ab 的最小值为2 2.(2)由x 2＋2xy －3＝0得y ＝3－x 22x ＝32x －12x ，则2x ＋y ＝2x ＋32x －12x ＝3x 2＋32x≥23x 2·32x ＝3，当且仅当x ＝1时，等号成立，所以2x ＋y 的最小值为3.] [规律方法] 1.利用基本不等式求函数最值时，注意“一正、二定、三相等，和定积最大，积定和最小”．2．在求最值过程中若不能直接使用基本不等式，可以考虑利用拆项、配凑、常数代换、平方等技巧进行变形，使之能够使用基本不等式．[变式训练1] (1)(2016·湖北七市4月联考)已知a >0，b >0，且2a ＋b ＝1，若不等式2a ＋1b ≥m 恒成立，则m 的最大值等于( )A ．10 B.9 C ．8D.7(2)(2016·湖南雅礼中学一模)已知实数m ，n 满足m ·n >0，m ＋n ＝－1，则1m ＋1n 的最大值为__________．(1)B (2)－4 [(1)∵2a ＋1b ＝2(2a ＋b )a ＋2a ＋b b ＝4＋2b a ＋2a b ＋1＝5＋2⎝ ⎛⎭⎪⎫b a ＋a b ≥5＋2×2b a ×a b ＝9，当且仅当a ＝b ＝13时取等号．又2a ＋1b ≥m ，∴m ≤9，即m的最大值等于9，故选B.(2)∵m ·n >0，m ＋n ＝－1，∴m <0，n <0， ∴1m ＋1n ＝－(m ＋n )⎝ ⎛⎭⎪⎫1m ＋1n＝－⎝ ⎛⎭⎪⎫2＋n m ＋m n ≤－2－2n m ·mn ＝－4，当且仅当m ＝n ＝－12时，1m ＋1n 取得最大值－4.]已知a >0，b >0，a ＋b ＝1，求证： (1)1a ＋1b ＋1ab ≥8； (2)⎝ ⎛⎭⎪⎫1＋1a ⎝ ⎛⎭⎪⎫1＋1b ≥9. [证明] (1)1a ＋1b ＋1ab ＝2⎝ ⎛⎭⎪⎫1a ＋1b ，∵a ＋b ＝1，a >0，b >0，∴1a ＋1b ＝a ＋b a ＋a ＋b b ＝2＋a b ＋ba ≥2＋2＝4，3分 ∴1a ＋1b ＋1ab ≥8(当且仅当a ＝b ＝12时等号成立).5分 (2)法一：∵a >0，b >0，a ＋b ＝1，∴1＋1a ＝1＋a ＋b a ＝2＋b a ，同理1＋1b ＝2＋ab ， ∴⎝ ⎛⎭⎪⎫1＋1a ⎝ ⎛⎭⎪⎫1＋1b ＝⎝ ⎛⎭⎪⎫2＋b a ⎝ ⎛⎭⎪⎫2＋a b ＝5＋2⎝ ⎛⎭⎪⎫b a ＋a b ≥5＋4＝9，10分∴⎝ ⎛⎭⎪⎫1＋1a ⎝ ⎛⎭⎪⎫1＋1b ≥9(当且仅当a ＝b ＝12时等号成立).12分 法二：⎝ ⎛⎭⎪⎫1＋1a ⎝ ⎛⎭⎪⎫1＋1b ＝1＋1a ＋1b ＋1ab ，由(1)知，1a ＋1b ＋1ab ≥8，10分故⎝ ⎛⎭⎪⎫1＋1a ⎝ ⎛⎭⎪⎫1＋1b ＝1＋1a ＋1b ＋1ab ≥9.12分 [规律方法] 1.“1”的代换是解决问题的关键，代换变形后能使用基本不等式是代换的前提，不能盲目变形．2．利用基本不等式证明不等式，关键是所证不等式必须是有“和”式或“积”式，通过将“和”式转化为“积”式或将“积”式转化为“和”式，达到放缩的效果，必要时，也需要运用“拆、拼、凑”的技巧，同时应注意多次运用基本不等式时等号能否取到．[变式训练2] 设a ，b 均为正实数，求证：1a 2＋1b 2＋ab ≥2 2.【导学号：01772210】[证明] 由于a ，b 均为正实数， 所以1a 2＋1b 2≥21a 2·1b 2＝2ab ，3分当且仅当1a 2＝1b 2，即a ＝b 时等号成立， 又因为2ab ＋ab ≥22ab ·ab ＝22， 当且仅当2ab ＝ab 时等号成立， 所以1a 2＋1b 2＋ab ≥2ab ＋ab ≥22，8分 当且仅当⎩⎪⎨⎪⎧1a 2＝1b 2，2ab ＝ab ，即a ＝b ＝42时取等号.12分制50≤x ≤100(单位：千米/时)．假设汽油的价格是每升2元，而汽车每小时耗油⎝ ⎛⎭⎪⎫2＋x 2360升，司机的工资是每小时14元． (1)求这次行车总费用y 关于x 的表达式；(2)当x 为何值时，这次行车的总费用最低，并求出最低费用的值．[解](1)设所用时间为t＝130x(h)，y＝130x×2×⎝⎛⎭⎪⎫2＋x2360＋14×130x，x∈[50,100].2分所以这次行车总费用y关于x的表达式是y＝130×18x＋2×130360x，x∈[]50，100.(或y＝2 340x＋1318x，x∈[]50，100).5分(2)y＝130×18x＋2×130360x≥26 10，当且仅当130×18x＝2×130360x，即x＝1810，等号成立.8分故当x＝1810千米/时，这次行车的总费用最低，最低费用的值为2610元.12分[规律方法] 1.设变量时一般要把求最大值或最小值的变量定义为函数．2．根据实际问题抽象出函数的解析式后，只需利用基本不等式求得函数的最值．3．在求函数的最值时，一定要在定义域(使实际问题有意义的自变量的取值范围)内求解．[变式训练3]某化工企业2016年年底投入100万元，购入一套污水处理设备．该设备每年的运转费用是0.5万元，此外每年都要花费一定的维护费，第一年的维护费为2万元，由于设备老化，以后每年的维护费都比上一年增加2万元．设该企业使用该设备x年的年平均污水处理费用为y(单位：万元)．(1)用x表示y；(2)当该企业的年平均污水处理费用最低时，企业需重新更换新的污水处理设备．则该企业几年后需要重新更换新的污水处理设备．[解](1)由题意得，y＝100＋0.5x＋(2＋4＋6＋ (2x)x，即y＝x＋100x＋1.5(x∈N*).5分(2)由基本不等式得：y＝x＋100x＋1.5≥2x·100x＋1.5＝21.5，8分当且仅当x＝100x，即x＝10时取等号．故该企业10年后需要重新更换新的污水处理设备.12分[思想与方法]1．基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能，因此可以用在一些不等式的证明中，还可以用于求代数式的最值或取值范围．如果条件等式中，同时含有两个变量的和与积的形式，就可以直接利用基本不等式对两个正数的和与积进行转化，然后通过解不等式进行求解．2．基本不等式的两个变形：(1)a2＋b22≥⎝⎛⎭⎪⎫a＋b22≥ab(a，b∈R，当且仅当a＝b时取等号)．(2)a2＋b22≥a＋b2≥ab≥21a＋1b(a>0，b>0，当且仅当a＝b时取等号)．[易错与防范]1．使用基本不等式求最值，“一正”“二定”“三相等”三个条件缺一不可．2．“当且仅当a＝b时等号成立”的含义是“a＝b”是等号成立的充要条件，这一点至关重要，忽视它往往会导致解题错误．3．连续使用基本不等式求最值要求每次等号成立的条件一致．课时分层训练(七)二次函数与幂函数A组基础达标(建议用时：30分钟)一、选择题1．已知幂函数f (x )＝k ·x α的图象过点⎝ ⎛⎭⎪⎫12，22，则k ＋α＝( )【导学号：01772040】A.12 B.1 C.32D.2C [由幂函数的定义知k ＝1.又f ⎝ ⎛⎭⎪⎫12＝22，所以⎝ ⎛⎭⎪⎫12α＝22，解得α＝12，从而k ＋α＝32.]2．函数f (x )＝2x 2－mx ＋3，当x ∈[－2，＋∞)时，f (x )是增函数，当x ∈(－∞，－2]时，f (x )是减函数，则f (1)的值为( )A ．－3 B.13 C.7D.5B [函数f (x )＝2x 2－mx ＋3图象的对称轴为直线x ＝m4，由函数f (x )的增减区间可知m4＝－2，∴m ＝－8，即f (x )＝2x 2＋8x ＋3，∴f (1)＝2＋8＋3＝13.]3．若幂函数y ＝(m 2－3m ＋3)·xm 2－m －2的图象不过原点，则m 的取值是( )A ．－1≤m ≤2 B.m ＝1或m ＝2 C ．m ＝2D.m ＝1B [由幂函数性质可知m 2－3m ＋3＝1，∴m ＝2或m ＝1.又幂函数图象不过原点，∴m 2－m －2≤0，即－1≤m ≤2，∴m ＝2或m ＝1.]4．已知函数y ＝ax 2＋bx ＋c ，如果a >b >c 且a ＋b ＋c ＝0，则它的图象可能是( )【导学号：01772041】A B C DD [由a ＋b ＋c ＝0，a ＞b ＞c 知a ＞0，c ＜0，则c a ＜0，排除B ，C.又f (0)＝c ＜0，所以也排除A.]5．若函数f (x )＝x 2－ax －a 在区间[0,2]上的最大值为1，则实数a 等于( )A ．－1B.1C.2D.－2B [∵函数f (x )＝x 2－ax －a 的图象为开口向上的抛物线，∴函数的最大值在区间的端点取得．∵f (0)＝－a ，f (2)＝4－3a ，∴⎩⎨⎧ －a ≥4－3a ，－a ＝1，或⎩⎨⎧ －a ≤4－3a ，4－3a ＝1，解得a ＝1.] 二、填空题6．(2017·上海八校联合测试改编)已知函数f (x )＝ax 2－2ax ＋1＋b (a ＞0)．若f (x )在[2,3]上的最大值为4，最小值为1，则a ＝________，b ＝________.1 0 [因为函数f (x )的对称轴为x ＝1，又a ＞0，所以f (x )在[2,3]上单调递增，所以⎩⎨⎧ f (2)＝1，f (3)＝4， 即⎩⎨⎧a ·22－2a ·2＋1＋b ＝1，a ·32－2a ·3＋1＋b ＝4，解方程得a ＝1，b ＝0.] 7．已知P ＝2，Q ＝⎝ ⎛⎭⎪⎫253，R ＝⎝ ⎛⎭⎪⎫123，则P ，Q ，R 的大小关系是________. 【导学号：01772042】P ＞R ＞Q [P ＝2＝⎝ ⎛⎭⎪⎫223，根据函数y ＝x 3是R 上的增函数且22＞12＞25， 得⎝ ⎛⎭⎪⎫223＞⎝ ⎛⎭⎪⎫123＞⎝ ⎛⎭⎪⎫253，即P ＞R ＞Q .] 8．已知函数f (x )＝x 2－2ax ＋5在(－∞，2]上是减函数，且对任意的x 1，x 2∈[1，a ＋1]，总有|f (x 1)－f (x 2)|≤4，则实数a 的取值范围是________．[2,3] [f (x )＝(x －a )2＋5－a 2，根据f (x )在区间(－∞，2]上是减函数知，a ≥2，则f (1)≥f (a ＋1)，从而|f (x 1)－f (x 2)|max ＝f (1)－f (a )＝a 2－2a ＋1，由a 2－2a ＋1≤4，解得－1≤a ≤3，又a ≥2，所以2≤a ≤3.]三、解答题9．已知幂函数f (x )＝x (m 2＋m )－1(m ∈N *)经过点(2，2)，试确定m 的值，并求满足条件f (2－a )＞f (a －1)的实数a 的取值范围．[解] 幂函数f (x )经过点(2，2)， ∴2＝2(m 2＋m )－1，即2＝2(m 2＋m )－1，∴m 2＋m ＝2，解得m ＝1或m ＝－2.4分又∵m ∈N *，∴m ＝1.∴f (x )＝x ，则函数的定义域为[0，＋∞)，并且在定义域上为增函数．由f (2－a )＞f (a －1)，得⎩⎨⎧ 2－a ≥0，a －1≥0，2－a ＞a －1，10分解得1≤a ＜32.∴a 的取值范围为⎣⎢⎡⎭⎪⎫1，32.12分 10．已知函数f (x )＝x 2＋(2a －1)x －3， (1)当a ＝2，x ∈[－2,3]时，求函数f (x )的值域；(2)若函数f (x )在[－1,3]上的最大值为1，求实数a 的值．[解] (1)当a ＝2时，f (x )＝x 2＋3x －3，x ∈[－2,3]，对称轴x ＝－32∈[－2,3]，2分∴f (x )min ＝f ⎝ ⎛⎭⎪⎫－32＝94－92－3＝－214， f (x )max ＝f (3)＝15，∴值域为⎣⎢⎡⎦⎥⎤－214，15.5分 (2)对称轴为x ＝－2a －12.①当－2a－12≤1，即a≥－12时，f(x)max＝f(3)＝6a＋3，∴6a＋3＝1，即a＝－13满足题意；8分②当－2a－12＞1，即a＜－12时，f(x)max＝f(－1)＝－2a－1，∴－2a－1＝1，即a＝－1满足题意．综上可知a＝－13或－1. 12分B组能力提升(建议用时：15分钟)1．(2017·江西九江一中期中)函数f(x)＝(m2－m－1)x4m9－m5－1是幂函数，对任意的x1，x2∈(0，＋∞)，且x1≠x2，满足f(x1)－f(x2)x1－x2＞0，若a，b∈R，且a＋b＞0，ab＜0，则f(a)＋f(b)的值()【导学号：01772043】A．恒大于0 B.恒小于0C．等于0 D.无法判断A[∵f(x)＝(m2－m－1)x4m9－m5－1是幂函数，∴m2－m－1＝1，解得m＝2或m＝－1.当m＝2时，指数4×29－25－1＝2 015＞0，满足题意．当m＝－1时，指数4×(－1)9－(－1)5－1＝－4＜0，不满足题意，∴f(x)＝x2 015.∴幂函数f(x)＝x2 015是定义域R上的奇函数，且是增函数．又∵a，b∈R，且a＋b＞0，∴a＞－b，又ab＜0，不妨设b＜0，则a＞－b＞0，∴f(a)＞f(－b)＞0，又f(－b)＝－f(b)，∴f(a)＞－f(b)，∴f(a)＋f(b)＞0.故选A.]2．设f(x)与g(x)是定义在同一区间[a，b]上的两个函数，若函数y＝f(x)－g(x)在x ∈[a ，b ]上有两个不同的零点，则称f (x )和g (x )在[a ，b ]上是“关联函数”，区间[a ，b ]称为“关联区间”．若f (x )＝x 2－3x ＋4与g (x )＝2x ＋m 在[0,3]上是“关联函数”，则m 的取值范围为________．⎝ ⎛⎦⎥⎤－94，－2 [由题意知，y ＝f (x )－g (x )＝x 2－5x ＋4－m 在[0,3]上有两个不同的零点．在同一直角坐标系下作出函数y ＝m 与y ＝x 2－5x ＋4(x ∈[0,3])的图象如图所示，结合图象可知，当x ∈[2,3]时，y ＝x 2－5x ＋4∈⎣⎢⎡⎦⎥⎤－94，－2， 故当m ∈⎝ ⎛⎦⎥⎤－94，－2时，函数y ＝m 与y ＝x 2－5x ＋4(x ∈[0,3])的图象有两个交点．]3．已知二次函数f (x )＝ax 2＋bx ＋1(a ，b ∈R )，x ∈R .(1)若函数f (x )的最小值为f (－1)＝0，求f (x )的解析式，并写出单调区间；(2)在(1)的条件下，f (x )＞x ＋k 在区间[－3，－1]上恒成立，试求k 的范围．[解] (1)由题意知⎩⎪⎨⎪⎧ －b 2a＝－1，f (－1)＝a －b ＋1＝0，解得⎩⎨⎧a ＝1，b ＝2.2分 所以f (x )＝x 2＋2x ＋1，由f (x )＝(x ＋1)2知，函数f (x )的单调递增区间为[－1，＋∞)，单调递减区间为(－∞，－1].6分(2)由题意知，x 2＋2x ＋1＞x ＋k 在区间[－3，－1]上恒成立，即k ＜x 2＋x ＋1在区间[－3，－1]上恒成立，8分令g (x )＝x 2＋x ＋1，x ∈[－3，－1]，由g (x )＝⎝ ⎛⎭⎪⎫x ＋122＋34知g (x )在区间[－3，－1]上是减函数，则g (x )min ＝g (－1)＝1，所以k ＜1，即k 的取值范围是(－∞，1).12分。
