北师大中考数学专题复习之图形的相似专题练习

•中考总复习：图形的相似--巩固练习（提高）【巩固练习】一、选择题1．如图，四边形ABCD中，∠BAD=∠ADC=90°，AB=AD=2，CD=1，点P在四边形ABCD的边上．若P到BD 的距离为1，则点P的个数为（）．A．1B．2C．3D．42.如图，直角三角形纸片的两直角边长分别为6、8，按如图那样折叠，使点A与点B重合，折痕为D E，则△SB CE：△SB DE等于（）．A.2：5B.14:25C.16:25D.4:213.（2015•甘南州）如图，在平行四边形ABCD中，E是AB的中点，CE和BD交于点△O，设OCD的面积为△m，OEB的面积为，则下列结论中正确的是（）A．m=5B．m=4C．m=3D．m=104.如图所示，平地上一棵树高为6米，两次观察地面上的影子，第一次是当阳光与地面成60°时，第二次是阳光与地面成30°时，第二次观察到的影子比第一次长()．A．63-3 B.43 C.63 D.3-235．如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，四边形ACDE是平行四边形，连接CE交AD于点F，连接BD交CE于点G，连接BE．下列结论中：①CE=BD②△ADC是等腰直角三角形③∠ADB=∠AEB④CD•AE=EF•CG；一定正确的结论有（）．A．1个B．2个C．3个D．4个=，③∠B+∠2=90°④BC∶AC∶AB=3∶4∶5，⑤AC⋅BD=AC⋅C D，②6．如图，△A BC中，CD⊥AB于D，一定能确定△A BC为直角三角形的条件的个数是（）．①∠1=∠A，CD DBAD CDA．1B．2C．3D．4二、填空题7.如图已知△ABC的面积是3的等边三角形，△ABC∽△ADE，AB=2AD，∠BAD=45°，AC与DE相交于点△F，则AEF的面积等于__________（结果保留根号）.第7题第8题8.已知三个边长分别为2、3、5的正三角形从左到右如图排列，则图中阴影部分面积为．9.如图，等边三角形ABC的边长为3，点P为BC边上一点，且BP=1，点D为AC边上一点，若∠APD= 60°，则CD的长为．第9题第10题10．如图，在直角三角形ABC中（∠C=90°），放置边长分别3，4，x的三个正方形，则x的值为．11.如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S，S，则S+S的1212值为．3．．．．．．．．．．．．．． ．．12. （2015•湖州）已知正方形 ABC 1D 1 的边长为 1，延长 C 1D 1 到 A 1，以 A 1C 1 为边向右作正方形 A 1C 1C 2D 2，延 长 C 2D 2 到 A 2，以 A 2C 2 为边向右作正方形 A 2C 2C 3D （如图所示），以此类推…．若 A 1C 1=2，且点 A ，D 2，D 3，…，D 10 都在同一直线上，则正方形 A 9C 9C 10D 10 的边长是 ．三、解答题13.（2015•杭州模拟）如图，正方形 ABCD 的边长为 2，点 E ，F 分别是 DC 和 BC 两边上的动点且始终保 持∠EAF=45°，连接 AE 与 AF 交 DB 于点 N ，△M ．下列结论：① △A D M∽ NBA ；②△CEF 的周长始终保持 不变其值是 4；③AE×AM=AF×AN；④DN 2+BM 2=NM 2．其中正确的结论有哪些？14. 如图（△1）， ABC 与△EFD 为等腰直角三角形，AC 与 DE 重合，AB =EF =9，∠BAC ＝∠DEF ＝90°，固 定△ABC ，将△EFD 绕点 A 顺时针旋转，当 DF 边与 AB 边重合时，旋转中止.不考虑旋转开始和结束时重 合的情况，设 DE 、DF （或它们的延长线）分别交 BC （或它的延长线）于 G 、H 点，如图（2）. （△1）问：始终与 AGC 相似的三角形有及；（2）设 CG ＝x ，BH ＝y ，求 y 关于 x 的函数关系式（只要求根据 2 的情况说明理由）； （3）问：当 x 为何值时，△AGH 是等腰三角形？15.已知:直角梯形 OABC 中，BC∥OA，∠AOC=90°，以AB 为直径的圆 M 交 OC 于 D ．E ，连结 AD 、BD 、BE.(1)在不添加其他字母和线的前提下，直接写出图 1 中的两对相似三角形._____________________，______________________；(2)直角梯形OABC中，以O为坐标原点，A在x轴正半轴上建立直角坐标系（如图2），若抛物线y=ax2-2ax-3a(a<0)经过点A．B．D，且B为抛物线的顶点.①写出顶点B的坐标（用a的代数式表示）___________；②求抛物线的解析式；③在x轴下方的抛物线上是否存在这样的点P：过点P做PN⊥x轴于△N，使得PAN与△OAD相似？若存在，求出点P的坐标；若不存在，说明理由.16．（2011上海）在△R t ABC中，∠ACB=90°，BC=30，AB=50．点P是AB边上任意一点，直线PE⊥AB，与边AC或BC相交于E．点M在线段AP上，点N在线段BP上，EM=EN，sin∠EMP=1213．（1）如图1，当点E与点C重合时，求CM的长；（2）如图2，当点E在边AC上时，点E不与点A、C重合，设AP=x，BN=y，求y关于x的函数关系式，并写出函数的定义域；（△3）若AME∽△ENB（△AME的顶点A、M、E分别与△ENB的顶点E、N、B对应），求AP的长．图1图2备用图【答案与解析】一．选择题1．【答案】B．2．【答案】B．3．【答案】B；【解析】∵AB∥CD，∴△OCD∽△OEB，又∵E 是 AB 的中点， ∴2EB=AB=CD，∴=（ ）2，即=（ ）2，解得 m=4 ．故选 B ． 4．【答案】B ． 5．【答案】Ｄ；【解析】①利用 SAS 证明△BAD ≌△CAE ，可得到 CE=BD ，②利用平行四边形的性质可得 AE=CD ，再结合△ADE 是等腰直角三角形可得到△ADC 是等腰直角三角形； ③利用 SAS 证明△BAE ≌△BAD 可得到∠ADB=∠AEB ；④利用已知得出∠GFD=∠AFE ，以及∠GDF+∠GFD=90°，得出∠GCD=∠AEF ，进而得出△CGD ∽△EAF ，得 出比例式． 6．【答案】Ｃ；【解析】①因为∠A+∠2=90°，∠1=∠A ，所以∠1+∠2=90°，即△ABC 为直角三角形，故正确；②根据 CD 2=AD•DB 得到 AD CD =CD DB，再根据∠ADC=∠CDB=90°，则△ACD ∽△CBD ，∴∠1=∠A ，∠2=∠B ，根据三角形内角和定理可得：∠ACB=90°，故正确；③因为∠B+∠2=90°，∠B+∠1=90°，所以推出∠1=∠2，无法得到两角和为 90°，故错误；④设 BC 的长为 3x ，那么 AC 为 4x ，AB 为 5x ，由 9x 2+16x 2=25x 2，符合勾股定理的逆定理，故正确； ⑤由三角形的相似无法推出 AC•BD=AD•CD 成立，所以△ABC 不是直角三角形，故错误． 所以正确的有三个．故选 C ． 二．填空题7．【答案】 3 - 3 4．8．【答案】 3 8．29．【答案】 ；3【解析】∵△ABC 是等边三角形，∴∠B=∠C=60°， ∵∠APB=∠PAC+∠C ，∠PDC=∠PAC+∠APD ，∵∠APD=60°，∴∠APB=∠PAC+60°，∠PDC=∠PAC+60°，∴∠APB=∠PDC ， 又∵∠B=∠C=60°，∴△ABP ∽△PCD ，∴ AB BP 3 1 = ，即 = ，PC CD 2 CD2∴CD= ．310．【答案】７；【解析】根据已知条件可以推出△CEF ∽△OME ∽△PFN 然后把它们的直角边用含 x 的表达式表示出来， 利用对应边的比相等，即可推出 x 的值答题． 11.【答案】17；【解析】如图，设正方形 S 2 的边长为 x ，根据等腰直角三角形的性质知，AC= 2 x ，x= 2 CD ，∴AC=2CD ，CD=2，∴EC 2=22+22，即 EC=2 2 ，∴S 2 的面积为 EC 2=8， ∵S 1 的边长为 3，S 1 的面积为 3×3=9， ∴S 1+S 2=8+9=17．12．【答案】．【解析】延长 D 4A 和 C 1B 交于 O ， ∵AB∥A 2C 1，∴ AOB∽ D △2OC 2，∴ = ，∵AB=BC 1=1，DC 2=C 1C 2=2，∴==∴OC 2=2OB ， ∴OB=BC 2=3， ∴OC 2=6，设正方形 A 2C 2C 3D 3 的边长为 x 1， 同理证得： D △2OC △2∽ D 3OC 3，∴= ，解得，x 1=3，∴正方形 A 2C 2C 3D 3 的边长为 3，设正方形 A 3C 3C 4D 4 的边长为 x 2， 同理证得： D △3OC △3∽ D 4OC 4，∴=，解得 x 2= ，∴正方形 A 3C 3C 4D 4 的边长为 ；设正方形 A 4C 4C 5D 5 的边长为 x 3， 同理证得： D △4OC △4∽ D 5OC 5，∴= ，解得 x= ，∴正方形 A 4C 4C 5D 5 的边长为 以此类推…．；正方形 A n ﹣1C n ﹣1C n D n 的边长为 ； ∴正方形 A 9C 9C 10D 10 的边长为 ．故答案为．三.综合题 13．【解析】解：①∠ANB=∠NDA+∠NAD=45°+∠NAD，∠MAD=∠MAN+∠NAD=45°+∠NAD，∴∠ANB=∠MAD，又∠ADM=∠ABN=45°，∴△ADM∽△NBA，①正确；②如图△1，把ADE顺时针旋转90°得到△ABG，则BG=DE，∠FAG=∠FAB+∠DAE=45°，在△AEF和△AGF中，，∴△AEF≌△AGF，∴DG=EF，∴△CEF的周长=CE+CF+EF=CE+DE+CF+FG=4，②正确；③当MN∥EF时，AE×AM=AF×AN，∵MN与EF的位置关系不确定，∴③错误；④如图△2，把ADN顺时针旋转90°得到△ABH，则BH=DN，∠MAH=∠MAB+∠BAH=∠MAB+∠DAN45°，在△NAM和△HAM中，，∴△AEF≌△AGF，∴MN=MH，又∵∠MBH=∠MBA+∠ABH=90°，∴BH2+BM2=MH2，即DN2+BM2=NM2，④正确．∴正确的结论有：①②④.14．【解析】（△1）HGA及△HAB；（2）由（△1）可知AGC∽△HAB∴CG AC=AB BHx9，即=，9y所以，y=81 x 1（3）当CG＜BC时，∠GAC=∠H＜∠HAC，∴AC＜CH2∵AG＜AC，∴AG＜GH又AH＞AG，AH＞GH此时，△AGH不可能是等腰三角形；当CG=12BC时，G为BC的中点，H与C重合，△AGH是等腰三角形；99此时，GC=2，即x=2221当CG＞BC时，由（△1）可知AGC∽△HGA2所以，若△AGH必是等腰三角形，只可能存在AG=AH 若AG=AH，则AC=CG，此时x=9综上，当x=9或92时，△AGH是等腰三角形．2∴ DC∴1 = ， ∴ a2 = 1 ， ∴CP = = =24．在 Rt△CPM 中，∵sin ∠EMP = ，∴CM = CP = ⨯ 24 =26．，∴PE = x ． 在 Rt△MPE 中，∵sin∠EMP = ，∴ = ．∴EM = PE = ⨯ x = x ．∴PM =PN = ME2 - PE2 = x ⎪ - x ⎪ = x ． ∵AP +PN +NB =50，∴x + x +y =50．∴y = - x + 50 (0<x <32)．15．【解析】（△1）OAD∽△CDB.△ADB∽△ECB；（2）①（1，－4a ）；②∵△OAD ∽△CDBCB=OA OD∵ax 2－2ax －3a=0，可得 A （3，0）又 OC=－4a ，OD=－3a ，CD=－a ，CB=1，-a - 3a 3∵ a < 0 ，∴ a = -1．故抛物线的解析式为： y = - x 2 + 2x + 3 ．③存在，设 P （x ，－x 2+2x+3），∵△PAN 与△OAD 相似，且△OAD 为等腰三角形， ∴PN=AN ．当 x<0（x<－1）时，－x+3=－(－x 2+2x+3)，x 1=－2，x 2=3(舍去)， ∴P （－2，－5），当 x>0（x>3）时，x －3=－(－x 2+2x+3)，x 1=0，x 2=3(都不合题意舍去)， 符合条件的点 P 为（－2，－5）．16.【解析】（1）∵∠ACB =90°，∴AC = AB 2 - BC 2 = 502 - 302 =40．∵S = 1 ⋅ AB ⋅ CP = 21 2⋅ AC ⋅ BC ,AC ⋅ BC 40 ⨯ 30AB 501213CP 12 ∴ = ．CM 1313 1312 12（△2）由 APE ∽△ACB ，得 PE AP =BC AC ，即 PE x 3= 30 40 412 PE 1213 ME 1313 13 3 1312 12 4 16⎛ 13 ⎫2 ⎛ 3 ⎫25 ⎝ 16 ⎭ ⎝ 4 ⎭ 16 51621 16设AP=x，由（2）知EM=x，AM=x-PM=x-x=x，NB=-x+50．∴ x⎪=x⋅(-x+50)∴CE=AC=．设AP=x，易得BE=(50-x)，∴CE=30-(50-x)．（3）①当点E在线段AC上时，△AME∽△ENB，AM ME=EN NB．∵EM=EN，∴EM2=A M⋅NB．135112116161616⎛13⎫21121⎝16⎭1616解得x1=22，x2=0（舍去），即AP=22．②当点E在线段BC上时，根据外角定理，△ACE∽△EPM，∴AC EP12==．CE MP55501235353550∴30-(50-x)=．33解得x=42．即AP=42．∴AP的长为22或42．。

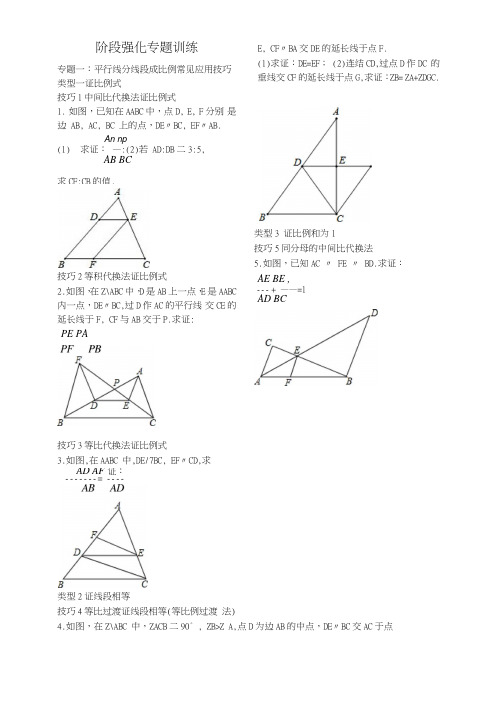
阶段强化专题训练专题一：平行线分线段成比例常见应用技巧类型一证比例式技巧1中间比代换法证比例式1.如图，已知在AABC中，点D, E, F分别是边AB, AC, BC 上的点，DE〃BC, EF〃AB.An np(1)求证：—:(2)若AD:DB二3:5,AB BC技巧2等积代换法证比例式2.如图，在Z\ABC中，D是AB上一点，E是AABC 内一点，DE〃BC,过D作AC的平行线交CE的延长线于F, CF与AB交于P.求证:PE PA类型3 证比例和为1技巧5同分母的中间比代换法5.如图，已知AC 〃FE 〃BD.求证：AE BE ,--- + ——=1AD BC技巧3等比代换法证比例式3.如图,在AABC 中,DE/7BC, EF〃CD,求类型2证线段相等技巧4等比过渡证线段相等(等比例过渡法)4.如图，在Z\ABC 中，ZACB二90° , ZB>Z A,点D为边AB的中点，DE〃BC交AC于点E, CF〃BA交DE的延长线于点F.(1)求证：DE=EF； (2)连结CD,过点D作DC 的垂线交CF的延长线于点G,求证：ZB= ZA+ZDGC. 求CF:CB的值.AD AF 证：------- = ----专题二：证明相似三角形的方法名师点金要找三角形相似的条件，关键抓住以下几点：(1)己知角相等时，找两对对应角相等，若只能找到一对对应角相等，判断夹相等的角的两边是否对应成比例；(2)无法找到角相等吋，判断三边是否对应成比例；(3)除此之外，也可考虑平行线分线段成比例定理及相似三角形的“传递性”.• • •方法1利用边或角的关系判定两直角三角形相似1.下面关于直角三角形相似叙述错误的是 ()A.有一锐角对应相等的两个直角三角形相似B.两直角边对应成比例的两个直角三角形相似C.有一条直角边相等的两个直角三角形相似D.两个等腰直角三角形相似2.如图，BC丄AD,垂足为C, AD二6. 4, CD=1. 6,BC=9. 3, CE=3. 1.求证：AABC^ADEC.方法2利用角判定两三角形相似3.如图，AABC是等边三角形，CE是外角平分线，点D在AC上，连接BD并延长，与CE 交于点 E. (1)求证：△ABDs/\CED； (2)方法3利用边角判定两三角形相似4.如图,AB=3AC, BD=3AE,又BD/7AC，点B, A,E在同一条直线上.求证：△ABDs^CAE.方法4利用三边判定两三角形相似5.如图，AD是△ABC的高，E, F分别是AB,ADEF^AABC.专训三巧作平行线构造相似三角形名师点金：解题吋，往往会遇到要证的问题与相似三角形联系不上或者说图中根本不存在相似三角形的情况，添加辅助线构造相似三角形是这类儿何证明题的一种重要方法.常作的辅助线有以下儿种：（1）由比例式作平行线；（2）有中点吋，作中位线；（3）根据比例式，构造相似三角形.训练角度1巧连线段的中点构造相似三角形1.如图，在Z\ABC中，E, F是边BC上的两个三等分点，D是AC的中点，BD分别交AE, AF 于点P, Q,求BP:PQ:QD・A训练角度2 过顶点作平行线构造相似三角形2.如图，在AABC中，AC=BC, F为底边AB 上一点，BF:AF = 3:2,取CF的中点D,连接AD并延长交BC于点E,求BE:EC的值. 4.如图，在厶ABC中,AB>AC,在边AB上取一点D,在AC上取一点E,使AD = AE,直线DE和BC 的延长线交于点P.求证: BP:CP=BD:EC.训练角度4 过一点作平行线构造相似三角形5.如图，在AABC中，点M为AC边的中点, 点E为八B上一点，且八E二丄AB,连接EM并4延长交BC的延长线于点D.求证：BC = 2CD. 作辅助线的方法一：作辅助线的方法二:3.如图，过AABC的顶点C任作一直线，与边AB 及中线AD分别交于点F和点E.求证:AE:ED=2AF:FB・训练角度3 过一边上的点作平行线构造相似三角形作辅助线的方法四: 作辅助线的方法三:9.如图，在口ABCD 中,AM 丄BC, AN 丄CD,垂 足分别为M, N.求证：全章整合提升密码专训一：证比例式或等积式的技巧 名师点金证比例式或等积式，若遇问题小无平行线或 相似三角形时，则需构造平行线或相似三角 形，得到等比例线段；若比例式或等积式中 的线段分布在两个三角形或不在两个三角 形中，可尝试证这两个三角形相似或先将它 们转化到两个三角形中再证两三角形相似， 若在两个明显不相似的三角形中，可运用中 I'可比代换.技巧1构造平行线法1.如图，在AABC 中，D 为AB 的中点，DF技巧3构造相似三角形法5.如图，在等边三角形ABC 中，点P 是BC 边上任意一点，AP 的垂直平分线分别交AB,交AC 于点E,交BC 的延长线于点F, 求证：AE ・CF=BF ・EC.技巧4等比过渡法6.如图，在ZkABC 中,AB=AC, DE//BC,点 F 在边AC 上，DF 与BE 相交于点G,且ZEDF =Z ABE.求证：⑴△ DEF s △ RDE ；⑵ DG ・ DF = DB ・EF.2.如图，已知Z\ABC 的边AB 上有一点D,边 BC的延长线上有一点E,且AD=CE, DE 交 AC 于点F,试证明：AB ・DF=BC ・EF.7.如图，CE 是RtAABC 斜边上的高，在EC 的延长线上任取一点P,连接AP,作BG 丄AP 于点G,技巧2三点找三角形相似法3.如图，在°ABCD 中，E 是AB 延长线上的一 点，DE 交BC 于F. 求证: DC_CFAE =AD*技巧5 8.如图，高，ZABC 的平分线BE 交AC 于E,交AD 于 卜.求证：BE _BC ，两次相似法在航△八BC 中，AD 是斜边BC 上的 4.如图，在△ABC 中，ZBAC=90° , M 为 BC 的中点，DM 丄BC 交CA 的延长线于D,交AB 于 E.求证：AM 2=MD • ME.AC 于点M, N.D(1) AAMB^AAND； (2)鑒=x-lD技巧6等积代换法10.如图,在ZkABC 中，AD丄BC 于D, DE1AB 于E, DF丄AC于F.求证：普=話A卜AB技巧7等线段代换法11.如图，等腰AABC 中，AB=AC, AD丄BC 于点D,点P是M）上一点，CF〃八B,延长BP交AC 于点E,交CF于点F,求证：BP2 =PE • PF.12.已知：如图，AD平分ZBAC, AD的垂直平分线EP交BC的延长线于点P.求证：PD2=PB - PC・MNAC专训二巧用“基本图形”探索相似条件名师点金：几何图形大多数由基本图形复合而成，因此熟悉三角形相似的基本图形，有助于快速、准确地识别相似三角形，从而顺利找到解题思路和方法.相似三角形的四类结构图：1.平行线型训练角度3子母型3.如图，在Z\ABC 中，ZBAC = 90° , AD丄BC于点D, E为AC的中点，ED的延长线交ABAR DR的延长线于点F.求证：話=环.训练角度4 旋转型4.如图，已知ZDAB=ZEAC, ZADE=ZABC. 求证：(1)Z\ADE S/\ABC； (2)学=架.AE CE训练角度1平行线型1.如图，在ZXABC中，BE平分ZABC交AC 于点E,过点E作ED〃BC交AB于点D. (1) 求证：AE ・BC=BD ・ AC； (2)如果S ZSADE=3,S ABDE=2, DE=6,求BC 的长.训练角度2 相交线型2.如图，点D, E分别为AABC的边AC, AB 上的点，BD, CE交于点0,且器=怜，试问AADE与AABC 相似吗？请说明理由.3.子母型A4.旋转型B C2.相交线型C DB专训三利用相似三角形巧证线段的数量和位置关系名师点金: 判断两线段之间的数量和位置关系是几何屮的基本题型z—.由角的关系推出“平行或垂直”是判断位置关系的常用方法，由相似三角形推出“相等”是判断数量关系的常用方法.训练角度1 证明两线段的数量关系类型1:证明两线段的相等关系1.如图，已知在AABC中，DE〃BC, BE与CD 交于点0,直线A0与BC边交于点M,与DE2.如图，一直线和AABC的边AB, AC分别交于点D,E,和BC的延长线交于点F,且AE:CE = BF:CF.求证：AD = DB.类型2证明两线段的倍分关系3.如图，在AABC中，BD丄AC于点D, CE丄AB 于点E, ZA=60° ,求证：DE=*BC. 训练角度2 证明两线段的位置关系类型证明两线段平行5.如图，已知点D为等腰直角三角形ABC的斜边AB上一点，连接CD, DE丄CD, DE=CD, 连接CE, AE.求证：AE〃BC・6.在AABC 中,D, E, F 分别为BC, AB, AC 上的点，EF//BC, DF〃AB,连接CE 和AD,分别交DF, EF于点N, M.(1)如图①，若E为AB的中点，图中与MN 平行的直线有哪几条？请证明你的结论；⑵如图②，若E不为AB的屮点，写出与MN 平行的直线，并证明.类型2证明两线垂直7.如图，在AABC中,D是AB上一点,AC2&如图，已知矩形ABCD, AD=|AB,点E, F 把AB 三等分，DF交AC于点G,求证：EG丄DF.4.如图，AM为AABC的角平分线，D为AB 的屮点,CE〃AB,CE交DM的延长线于E.求证：AC=2CE.专训四 巧用位似解三角形中的内接多边形问题名师点金位似图形是特殊位置的相似图形，它具有相 似图形的所有性质，位似图形必须具备三个 条件：（1）两个图形相似；（2）对应点的连线 相交于一点；（3）对应边互相平行或在同一 直线上.类型1三角形的内接正三角形问题 1•如图，用下血的方法可以画AAOB 的内接 等边三角形，阅读后证明相应问题.画法:①在AAOB 内画等边三角形CDE,使点 C 在0A 上，点D 在0B 上;②连接0E 并延长, 交AB于点E'，过点E'作E‘ C‘ 〃EC,交 0A 于点C'，作E‘ D' 〃ED,交0B 于点D'； ③连接C‘ D'，则2 D' E'是ZkAOB 的内 接等边三角形.求证：△（/ D‘ E'是等边三角形.类型2 三角形的内接矩形问题2.求作：内接于已知AABC 的矩形DEFG,使它 的边EF 在BC 上,顶点D, G 分别在AB, AC 上, 并且有 DE : EF=1 : 2.类型3 三角形的内接正形问题（方程思想）3.如图,AABC 是一块锐角三角形余料，边 BC= 120mm ,高AD 二80mm ,要把它加工成正方 形零件，使正方形的一边QM 在BC 上，其余 两个顶点P,N 分别在AB, AC 上，则这个正方 形零件的边长是多少？在 AB , AC , BC 上，且 DE //BC , AQ 交 DE 于 点 P.求证：DP ： BQ=PE ： QC.（2）在AABC 中,ZBAC =90°，正方形 DEFG 的四个顶点在AABC 的边上，连接AG ,AF , 分别交DE 于M ,N 两点.① 如图②，若AB=AC=1,直接写出MN 的长； ② 如图③，求证:MN 2 =DM ・EN.B专训五：图形的相似中的五种热门考点 名师点金：相似是初中数学的重要内容，也是中考重点 考查内容之一，而对于成比例线段、相似三 角形的判定与性质、位似图形等都是命题的 热点.考点一：比例线段及性质1. 下列各组长度的线段，成比例线段的是 () A. 2 cm, 4 cm, 4 cm, 8 cm B. 2 cm, 4 cm, 6 cm, 8 cmC. 1 cm, 2 cm, 3 cm, 4 cmD. 2. 1 cm, 3. 1 cm, 4. 3 cm, 5. 2 cm c “a b c d …“a+b + c + d2-若厂厂厂汙则—c —=3. 如图，乐器上的一-根弦AB=80 cm,两个端点A, B 固定在乐器板面上，支撑点C 是 靠近点B 的黄金分割点，则支撑点C 到端点 A 的距离约为 ___________ ・(&~2. 236,结果 精确到0.01)AC B考点二：平行线分线段成比例4. 如图，若AB 〃CD 〃EF,则下列结论中，与BC D — BEABC =60° ,以AC 为边向三角形外作正方形 ACDE,连接 BE 交 AC 于 F,若 BF=p5 cm, 则 EF=5.如图, 在 RtAABC 中，ZACB=90°AI) 环相等的是(CD EFA6.如图，在AABC 屮，AM : MD=4 : 1, BD : DC=2 : 3,求AE : EC 的值.考点三相似三角形的性质与判定7.己知△ABCs^DEF,若ZXABC 与Z\DEF 的相似比为3 : 4,则△八BC与ZXDEF 的面积之比为( ) A.4:3 B.3:4 C. 16:9D.9:16&在平行四边形ABCD中，点E在AD上，且AE : ED = 3 ： 1, CE的延长线与BA的延长线交于点F,贝|J S AA EF : S四边形ABCE为( ) A. 3 ： 4 B. 4 ： 3 C. 7 ： 9 D. 9 ： 79.若两个相似多边形的面积Z比为1 ： 4,周长之差为6,则这两个相似多边形的周长分另I」是______ .10.如图，AABC是直角三角形，ZACB = 90° , CD 丄AB于D, E是AC的中点,ED的延长线与CB 的延长线交于点F.⑴求证：FD'=FB・FC； (2)若FB = 5, BC =4,求FD的长.11.如图，四边形ABCD是正方形，BD是对角线，BE平分ZDBC交DC于点E,点F是BC 的延长线上一点，且CE=CF, BE的延长线交DF于点M.(1)求证：BM丄DF；(2)若正方形ABCD的边长为2,求ME・MB.考点四12.—天晚上，李明和张龙利用灯光下的影了长来测量一路灯的高度CD.如图，当李明⑵连接⑴中的AA',求四边形AA‘ C' C 的周长.（结果保留根号）走到点A处时，张龙测得李明直立时身高AM 与影子长AE正好相等；接着李明沿AC方向继续向前走，走到点B处时，李明直立时身高BN的影子恰好是线段AB,并测得AB = 1.25 m,已知李明直立时的身高为1.75 m,求路灯的高度CD.（结果精确到0. 1 m）// 1 // • :M// \ / ■■」E A B C13.某高中学校为高一新生设计的学生板凳的正面视图如图所示,其中BA=CD, BC=20 cm, BC, EF 平行于地面AD且到地面AD的距离分别为40 cm, 8 cm.为使板凳两腿底端A, D之间的距离为50 cm,那么横梁EF的长应为多少？（材质及其厚度等暂忽略不计）A D考点五图形的位似14.如图，已知正方形ABCD,以点A为位似中心，把正方形ABCD的各边缩小为原来的一半，得正方形A' B/C‘ D',则点C'的坐标为. 15.如图，在6X8的网格图中，每个小正方形的边长均为1,点0和AABC的顶点均在小正方形的顶点上.（1）以0为位似中心,在网格图中作AA，B z C'和△ABC位似，且相似比为1 ： 2；相似三角形的应用专训六全章热门考点整合应用名师点金：本章主要内容为：平行线分线段成比例，相似三角形的判定及性质，位似图形及其画法等，涉及考点、考法较多，是屮考的髙频考点.其主要考点可概括为：3个概念、2个性质、1个判定、2个应用、1个作图、1个技巧.考点一：3个概念概念1：成比例线段1.下列各组线段，是成比例线段的是()A. 3cm, 6cm,7cm,9cmB. 2cm,5cm,0.6dm, 8cmC・ 3cm, 9cm, 1. 8dnb 6cm D. icm, 2cnb 3cm, 4cm2.有一块三角形的草地，它的一条边长为25m,在图纸上，这条边的长为5cm,其他两条边的长都为4cm,则其他两边的实际长度都是___________ m.概念2：相似多边形3.如图，已知Z1' =Z1, Z2‘ =Z2, Z 3' =Z3, Z4‘ =Z4, ZD' =ZD,试判断四边形"B z C‘ D z 与四边形ABCD是否相似，并说明理由.概念3：位似图形4.如图，在AABC屮，A, B两个顶点在x轴的上方，点C的坐标是(一1, 0).以点C为位似中心，在x轴的下方作△ABC的位似图形，并把AABC的边放大到原来的2倍，记所得的像是AA' B' C.设点B的对应点L的坐标是(a, b),求点B的坐标.A j y/\ 1-o !7考点二：2个性质性质1：平行线分线段成比例的性质5.如图，在RtAABC 中，ZA=90° , AB=8, AC=6.若动点D从点B岀发，沿线段BA运动到点A 为止，运动速度为每秒2个单位长度.过点D 作DE〃BC交AC于点E,设动点D运动的时间为x秒，AE的长为y.(1)求出y关于x的函数解析式，并写出自变量x的取值范圉；(2)当x为何值时，ABDE的面积有最大值, 最大值为多少？性质2：相似三角形的性质6.如图，已知D是BC边上的中点，且AD=AC, DE丄BC, DE 与BA 相交于点E, EC 与AD相交于点F.(1)求证：AABC^AFCD； (2)若S AFCD=5,BC=10,求DE的长.考点三：1个判定一一相似三角形的判定7.如图，AACB为等腰直角三角形，点D为斜边AB上一点，连接CD, DE丄CD, DE=CD, 连接AE,过C作C0±AB于0.求证：△八CE s/XOCD.8.如图,在00的内接AABC中，ZACB= 90° , AC=2BC,过点C作AB的垂线/交00 于另一点、D,垂足为点E.设P是上异于点A,C的一个动点，射线AP交/于点F,连接PC 与PD, PD 交AB 于点G. (1)求证：Z\PACs △PDF；(2)若AB = 5,弧八卩=弧!3卩，求PD 的长.考点四：2个应用应用1：测高的应用9.如图，在离某建筑物CE 4 m处有一棵树AB,在某时刻，1.2 m的竹竿FG垂直地面放置，影子GH长为2 m,此时树的影子有一部分落在地而上，还有一部分落在建筑物的墙上，墙上的影子CD高为2 m,那么这棵树的高度是多少？例的技巧12.如图，已知AABC, ZB AC的平分线与Z DAC的平分线分别交BC及BC的延长线于点P, Q.⑴求ZPAQ的度数;（2）若点M为应用2：测宽的应用10.如图，一条小河的两岸有一段是平行的, 在河的一岸每隔6 m有一棵树，在河的对岸每隔60 m有一根电线杆，在有树的一岸离岸边30 m处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住，并且在这两棵树之间还有三棵树，求河的宽度.考点五：1个作图一一作一个图形的位似图形11.如图，在方格纸中（每个小方格的边长都是1个单位长度）有一点0和AABC.请以点0 为位似中心，把AABC缩小为原来的一半（不改变方向），画出AABC的位似图形.考点六：1个技巧一一证明四条线段成比IIIIIIIIIIIII r-i-7-r->-T-rn-r-rn-r-i。

第四章测试卷(时间:100分钟 满分:120分)一、选择题(每小题3分，共30分，)题号12345678910答案B C A D B C C C A C1.下列形状分别为正方形、矩形、正三角形、圆的边框，其中不一定是相似图形的是( )2.在比例尺为1：500000的交通地图上，玉林到灵山的长度约为 23.6cm ，则它的实际长度约为( )A.0.118km B.1.18km C.118km D.1180km3.如图，以A ，B ，C 为顶点的三角形与以D ，E ，F 为顶点的三角形相似，则这两个三角形的相似比为( )A.2:1B.3:1C.4:3D.3:24.在△ABC 中,D 是AB 中点,E 是AC 中点,若△ADE 的面积是3，则△ABC 的面积是 ( )A.3 B.6 C.9 D.125.如图,在△ABC 中,点D 在AB 边上,过点 D 作DE ∥BC 交AC 于点E,DF ∥AC 交BC 于F,若AE:DF=2:3,则BF:BC 的值是 ( )A. 23 B. 35 C. 12D. 256.如图,在四边形ABCD 中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC 和△BAC 相似的是 ( )A.∠DAC=∠ABC B. AC 是∠BCD 的平分线 C.AC²=BC ⋅CD D.ADAB =DCAC7. 若△ABC 的各 边都分别扩大到原来的 2 倍，得到△A ₁B ₁C ₁，下列结论正确的是 ( )A.△ABC 与△A ₁B ₁C ₁的对应角不相等 B.△ABC 与△A ₁B ₁C ₁不一定相似C.△ABC 与△A ₁B ₁C ₁的相似比为1:2 D.△ABC 与△A ₁B ₁C ₁的相似比为2:18.如图,点 E 是▱ABCD 的边 BC 延长线上的一点,AE 和CD 交于点G ，AC 是▱ABCD 的对角线，则图中相似三角形共有 ( )A.2 对B.3 对C.4 对D.5 对9.如图,已知E(-4,2),F(--2,--2),以O 为位似中心,把△EFO 缩小到原来的 12，则点E 的对应点的坐标为( )A.(2,一1)或(-2,1)B.(8,一4)或(一8,4)C.(2,-1)D.(8,-4)10.如图,在正方形 ABCD 中,点 E 、F 分别在边AD 和CD 上,AF ⊥BE,垂足为G,若 AEED =2,则 AGGF 的值为( )A. 45B. 56C.67D.78二、填空题(每小题3分，共15分)11.若△ABC ∽△A'B'C',且相似比为3:5,已知△ABC 的周长为21,则△A'B'C'的周长为 .12.如图是一架梯子的示意图，其中 AA₁‖BB₁‖CC₁‖DD₁,且AB=BC=CD.为使其更稳固，在A ，D ₁间加绑一条安全绳( 线段AD ₁),量得 AE=0.4m,则 AD₁= m13.如图，阳光通过窗口照到室内，在地上留下3m 宽的亮区.已知亮区一边到窗下的墙角的距离CE=7m ，窗口高AB=1.8m,那么窗口底边离地面的高BC 等于 m.14.如图，已知每个小方格的边长均为1，则△ABC 与△CDE 的面积比为 .15.如图,在正方形ABCD 中,E 是BC 的中点,F 是CD 上一点，且 CF =14CD,下列结论:①∠BAE=30°,②△ABE ∽△ECF,③AE ⊥EF,④△ADF ∽△ECF.其中正确的结论是 (填序号).三、解答题(本大题8个小题，共75 分)16.(8分)根据下列条件,判断△ABC 与△A'B'C'是否相似,并说明理由. AB =3,BC =4,AC =5,A 'B '=12,B 'C '=16,C 'A '=2017.(9分)如图,D 是△ABC 的边AC 上的一点,连接BD,已知∠ABD=∠C,BC=6,BD=4,如果△ABD 的面积为4,求△BC D 的面积.18.(9分)在平面直角坐标系中,△ABC 的三个顶点的坐标分别是 A(1，3)，B(4,1),C(1,1).(1)画出△ABC 关于x 轴成轴对称的△A ₁B ₁C ₁;(2)画出△ABC 以点O 为位似中心,相似比为 1:2的△A ₂B ₂C ₂.19.(9分)如图,四边形ABCD 是菱形,AF ⊥BC 交BD 于E,交 BC 于F.求证: AD 2=12DE ⋅DB.20.(10分)周末，小华和小亮想用所学的数学知识测量家门前小河的宽.测量时，他们选择了河对岸边的一颗大树，将其底部作为点 A，在他们所在的岸边选择了 B，使得AB与河岸垂直，并在B点竖起标杆BC，再在AB 的延长线上选择点 D 竖起标杆DE，使得点 E 与点C、A共线.已知:CB⊥AD,ED⊥AD,测得 BC=1m,DE=1.5m,BD=8.5m，测量示意图如图所示.请根据相关测量信息，求河宽 AB.21.(10分)如图,E是平行四边形ABCD的边 DA 延长线上一点,连结 EC 交AB 于 P.(1)写出图中的三对相似三角形(不添加辅助线)；(2)请在你所写的相似三角形中选一对，说明相似的理由.22.(10分)阅读与计算：请阅读以下材料，并完成相应的问题.角平分线分线段成比例定理：如图1，在△ABC中，AD平分∠BAC,则ABAC =BDCD.下面是这个定理的部分证明过程.证明:如图2,过点C作CE∥DA,交 BA的延长线于点 E⋯任务：(1)请按照上面的证明思路，写出该证明过程的剩余部分；(2)如图3,在△ABC中,AD是角平分线,AB=5cm ,AC=4 cm,BC=7 cm.求 BD的长.23.(10分)在矩形 ABCD中,点 E 是对角线AC 上一动点,连接 DE,过点 E 作EF⊥DE 交AB 于点 F.(1)如图1,当DE=DA时,求证:AF=EF;(2)如图2，点E 在运动过程中，DEEF的值是否发生变化?请说明理由.第四章测试卷答案一、选择题1、B2、C3、A4、D5、B6、C7、C8、C9、A 10、C 二、填空题11、35 12、1.2m 13、2.4m 14、4:1 15、②③三、解答题16、解：相似，理由： ∵AB A 'B '=312=14,BC B 'C '=416=14,AC A 'C '=520=14,∴ABA 'B'=BCB 'C '=ACA 'C ',∴ABC ∽A 'B 'C '.17、解:∵∠ABD=∠C,又∠A=∠A,∴△ABD ∽△ACB,S ABD S ACB=(BD CB )2=(46)2=49,18、解：如图所示19、证明:连接AC 交 BD 于点O,∵四边形ABCD 为菱形,∴AC ⊥BD,BO=OD,∵AE ⊥AD,∴△AOD ∽△EAD, ∴AD OD=ED AD,∴A D 2=ED ⋅OD,即 A D 2=12DE ⋅DB.20、解:∵CB ⊥AD,ED ⊥AD, ∴∠CBA =∠EDA =90°.∵∠CAB=∠EAD, ∴ABCOADE,∴AB AD=BC DE,∴AB AB +8.5=11.5,∴AB =17,.∴河宽为17m.21、解:(1)△EAP ∽△CBP,△AEP ∽△DEC,△BCP ∽△DEC.(2)选. △EAPO △CBP,理由如下:在▱ABCD 中AD ∥BC,∴∠EAP=∠B.又∵∠APE=∠BPC,∴△EAP ∽△CBP.22、解:(1)证明:如图2,过点C作CE∥DA,交BA的延长线于点E, ∵CEDA,∴BDCD =BAEA,∠CAD=∠ACE,∠BAD=∠E,∵AD平分∠BAC,∴∠BAD=∠CAD, ∠ACE=∠E,∴AE=AC,∴ABAC =BDCD；(2)∵AD是角平分线, ∴ABAC =BDCD,AB=5 cm,AC=4 cm,BC=7 cm, C.54=BD7−BD,解得BD=359cm.23、解:(1)证明:如图,连接 DF，在矩形ABCD 中,∠DAF=90°,又∵DE⊥EF,∴∠DEF=90°,∵AD=DE,DF=DF,∴Rt△DAF≌Rt△DEF(HL),∴AF=EF;(2)DEEF 的值不变.如图,过点E作EM⊥AD于点M,过点E 作EN⊥AB 于点 N,∵EM∥CD,EN∥BC,∴EMCD =AEAC,ENBC=AEAC,∴EMEN=CDBC,∵∠DEF=∠MEN=90°,∴∠DEM=∠FEN,又·∴∠DME=∠ENF=90°,∴△DME⊗△FNE,∴DEEF =EMEN,∴DEEF=CDBC,∵CD 与BC 的长度不变, ∴DEFF的长度不变.。

新北师大版九年级数学?图形的相像?同步练习题一、填空题1、实数x、y知足，那么=．2、如图，小明用长为 3m的竹竿 CD做丈量工具，丈量学校旗杆竹竿与旗杆的距离 DB=12m，那么旗杆 AB的高为 m．AB的高度，挪动竹竿，使3、如图， AB∥CD∥ EF，假如 AC：CE=2： 3，BF=10，那么线段 DF的长为．4、如图，在长 8cm，宽 4cm 的矩形中截去一个矩形〔暗影局部〕使留下的矩形与矩形相像，那么留下的矩形的面积为cm2．225、△ ABC∽△ DEF，且相像比为 3：4，S△ABC=2cm，那么 S△DEF=cm．6、两个相像三角形对应边的比为2：3，那么它们的周长比为．7、：△ ABC在直角坐标平面内，三个极点的坐标分别为A〔0，3〕、B〔3，4〕、C〔 2，2〕〔正方形网格中每个小正方形的边长是一个单位长度〕．〔1〕画出△ ABC向下平移 4个单位长度获得的△ A1B1 C1，点 C1的坐标是；〔2〕以点B为位似中心，在网格内画出△ A2B2C2，使△ A2B2C2与△ ABC位似，且位似比为2：1，点 C2的坐标是；〔 3〕△ A2B2C2的面积是平方单位．二、选择题8、如图，四边形 ABCD、CEFG都是正方形，点G在线段 CD上，连结 BG、DE，DE和 FG订交于点 O，设 AB=a，CG=b〔 a＞b〕．以下结论：①△ BCG≌△ DCE；② BG⊥DE；③= ；④22〕〔a﹣ b〕 ?S EFO=b ?S．此中结论正确的个数是〔△△ DGOA．4 个B．3个C．2 个D．1 个9、△ ABC与△ A′ B′ C′是位似图形，且△ ABC与△ A′ B′ C′的位似比是1：2，△ ABC的面积是 3，那么△ A′ B′ C′的面积是〔〕A． 3 B ． 6C． 9D． 1210、如图，在△ ABC中，点 D，E 分别在边 AB， AC上， DE∥BC， AE=6，，那么EC的长是〔〕A．B．8C D． 1411、如图，直线 l 1∥l 2∥ l 3，假定 AB=2， BC=3， DE=1，那么 EF 的值为〔〕A. B ．C．6D．12、△ ABC的三边长分别为，，2，△A′B′C′的两边长分别是 1 和，假如△ABC与△ A′B′C′相像，那么△ A′B′C′的第三边长应当是〔〕A． B ． C ．D．13、如图，△ ABC∽△ CBD， CD=2，AC=3，BC=4，那么 AB 的值等于〔〕A． 5 B ． 6 C 7 D ． 414、假如两个相像三角形的面积比是1：2，那么它们的周长比是〔〕：2B．1：4C．1：D．2 ：1DAG FB CE15、如图， ?ABCD中， E 是 AD延伸线上一点， BE交 AC于点 F，交 DC于点 G，那么以下结论中错误的选项是〔〕A．△ ABE∽△ DGEB ．△ CGB∽△ DGEC ．△ BCF∽△EAFD．△ ACD∽△ GCF16、如图，在△ ABC中，假如的是〔〕A. ∠ ADE=∠C DE与 BC不平行，那么以下条件中，不可以判B ．∠ AED=∠B断△ ADE∽△ ABCC．D．三、解答题17、如图，矩形ABCD为台球桌面，AD=260cm，AB=130cm，球当前在 E 点地点，AE=60cm．假如小丁对准BC边上的点 F 将球打过去，经过反弹后，球恰好弹到D点地点．〔 1〕求证：△BEF∽△ CDF；〔 2〕求 CF的长．18、如图，∠ MON=90°，A 是∠ MON内部的一点，过点 A 作 AB⊥ON，垂足为点 B，AB=3厘米，OB=4厘米，动点 E，F 同时从 O点出发，点 E 以 1.5 厘米 / 秒的速度沿 ON方向运动，点 F 以 2 厘米 / 秒的速度沿 OM方向运动， EF 与 OA交于点 C，连结 AE，当点 E 抵达点 B 时，点 F 随之停止运动．设运动时间为 t 秒〔 t ＞0〕．〔 1〕当 t=1 秒时，△ EOF与△ ABO能否相像？请说明原因；〔 2〕在运动过程中，不论 t 取何值时，总有 EF⊥OA．为何？〔 3〕连结 AF，在运动过程中，能否存在某一时辰t ，使得 S△AEF= S 四边形AEOF？假定存在，恳求出此时 t 的值；假定不存在，请说明原因．19、如图，在平行四边形 ABCD中，点 G是 BC延伸线上一点， AG与 BD交于点 E，与 DC交于点 F，假如 AB=m，CG= BC，求：〔 1〕 DF的长度；〔 2〕三角形ABE与三角形 FDE的面积之比．20、如图，△ ABC是等边三角形， AB=6，点 D在 AC上，AD=2CD，CM是∠ ACB的外角均分线，连结 BD并延伸与 CM交于点 E．〔 1〕求 CE的长；〔 2〕求∠ EBC的正切值．21、：如图，在平行四边形 ABCD中， E、F 分别是边 BC， CD上的点，且 EF∥ BD，AE、AF 分别交 BD与点 G和点 H，BD=12，EF=8．求：〔 1〕的值；〔 2〕线段 GH的长．22、如图，在△ ABC中，AD均分∠ BAC交 BC于点 D．点 E、F 分别在边 AB、AC上，且BE=AF， FG∥ AB交线段 AD于点 G，连结 BG、 EF．〔 1〕求证：四边形 BGFE是平行四边形；〔 2〕假定△ABG∽△ AGF，AB=10，AG=6，求线段 BE的长．23、如图，点 P 是菱形 ABCD的对角线 BD上一点，连结 CP并延伸，交 AD于 E，交 BA的延伸线点F．问：〔1〕图中△APD与哪个三角形全等？并说明原因；〔2〕求证：△APE∽△ FPA；〔 3〕猜想：线段 PC，PE， PF之间存在什么关系？并说明原因．24、如图．在△ ABC中，BC＞ AC，点 D 在 BC上，且 DC=AC，∠ACB的均分线 CF交 AD于点 F，点 E 是 AB的中点，连结 EF．〔 1〕求证： EF∥BC；〔 2〕假定四边形 BDFE的面积为 6，求△ ABD的面积．。

AC AD ＝，AB＝2，DC＝3，∴＝＝＝，∴＝，∴cos∠ACB＝＝，cos∠DAC＝＝，∴·＝×＝，∴＝，∵△4ABC与△DCA的面积比＝，∴△BCABC与△DCA的面积比92△1△1△1△1图形的相似综合复习题一、选择题(每小题6分，共24分)1．(重庆△)如图，ABC∽△DEF，相似比为1∶2，若BC＝1，则EF的长是(B)A．1B．2C．3D．42．(泰安△)在ABC和A△1B1C1中，下列四个命题：①若AB＝A B，AC＝A1C1，∠A＝∠A1，则ABC≌A B1C1；②若AB＝A1B1，AC＝A1C1，∠B＝∠B1，则ABC≌A B1C1；③若∠A＝∠A1，∠C＝∠C1，则ABC∽A△1B1C1；④若AC：A1C1＝CB：C1B1，∠C＝∠C1，则ABC∽A△1B1C1.其中真命题的个数为(B)A．4个B．3个C．2个D．1个3．(宁波)如图，梯形ABCD中，AD∥BC，∠B＝∠ACD＝90°，AB＝2，DC＝△3，则ABC 与△DCA的面积比为(C)A．2∶3B．2∶5C．4∶9D.2∶3BC AC 解析：∵AD∥BC，∴∠ACB＝∠DAC，又∵∠B＝∠ACD＝△90°，∴CBA∽△ACD，＝AB BC AC AB2BC2BC2AC2 DC AC AD DC3AC3AC3DA3 BC AC224BCAC DA339DA9DA4＝，故选：C4．孝感)在平面直角坐标系中，已知点E(－4，2)，F(－2，－2)，以原点O为位似中心，相似比为△1，把EFO缩小，则点E的对应点E′的坐标是(D)A．(－2，1)B．(－8，4)C．(－8，4)或(8，－4)D．(－2，1)或(2，－1)解析：如图二、填空题(每小题6分，共24分)5．(邵阳)如图，在ABCD中，F是BC上的一点，直线DF与AB的延长线相交于点E，BP∥DF，且与AD相交于点P，请从图中找出一组相似的三角形：__△ABP∽△AED(答案不唯一)__．AB2DE CD AF⎩,第5题图),第6题图)AD2 6．(滨州)如图，平行于BC的直线DE把△ABC分成的两部分面积相等，则＝____．7．(2013·安徽)如图，P为平行四边形ABCD边AD上一点，E，F分别为PB，PC的中点，△PEF，△PDC，△PAB的面积分别为S，S1，S2，若S＝2，则S1＋S2＝__8__．解析：过点P作PQ∥DC交BC于点Q，由DC∥AB，得到PQ∥AB，∴四边形PQCD与四边形APQB都为平行四边形，∴△PDC≌△CQP，△ABP≌△QPB，∴S△PDC＝△SCQP，S△ABP＝△SQ PB，∵1EF为△PCB的中位线，∴EF∥BC，EF＝2△BC，∴PEF∽△PBC，且相似比为1∶2，∴S△PEF∶S △PBC＝1∶4，△SPEF＝2，∴△SPBC＝△SC QP＋△SQ PB＝△SP DC＋△SA BP＝S1＋S2＝8,第7题图),第8题图) 8．(娄底)如图，小明用长为3m的竹竿CD做测量工具，测量学校旗杆AB的高度，移动竹竿，使竹竿与旗杆的距离DB＝12m，则旗杆AB的高为__9__m.三、解答题(共52分)9．(10分)(2013·巴中)如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为点E，连接DE，F为线段DE上一点，且∠AFE＝∠B.(1)求证：△ADF∽△DEC；(2)若AB＝8，AD＝63，AF＝43，求AE的长．(1)证明：∵▱ABCD，∴AB∥CD，AD∥BC，∴∠C＋∠B＝180°，∠ADF＝∠DEC.∵∠AFD⎧⎪∠AFD＝∠C，＋∠AFE＝180°，∠AFE＝∠B，∴∠AFD＝∠C.在△ADF与△DEC中，⎨∴△⎪∠ADF＝∠DEC，ADF∽△DECAD AF AD·CD(2)解：∵▱ABCD，∴C D＝AB＝8.由(1)知△ADF∽△DEC，∴＝，∴D E＝＝63×843＝12.在△R t ADE中，由勾股定理得AE＝DE2－AD2＝122－（63）2＝6 10．(10分)(巴中)如图，在平面直角坐标系xOy中，△ABC三个顶点坐标分别为A(－2，4)，B(－2，1)，C(－5，2)．(1)请画出△ABC关于x轴对称的A△1B1C1；(2)将A△1B1C1的三个顶点的横坐标与纵坐标同时乘以－2，得到对应的点A2，B2，C2，请画出A△2B2C2；AB LD 50 LDLC 4(3)求 A △1B 1C 1 与 A △2B 2C 2的面积比，即 △S A 1B 1C 1：△S A 2B 2C 2＝____(不写解答过程，直接写出结果)．解：(1)如图所示： A △1B 1C 1即为所求(2)如图所示： A △2B 2C 2即为所求(3)∵将 A △1B 1C 1的三个顶点的横坐标与纵坐标同时乘以－2，得到对应的点 A 2，B 2，C 2，∴ △A 1B 1C 1 与 A △2B 2C 2的相似比为 1∶2，∴S △A 1B 1C 1∶△S A 2B 2C 2＝1∶411．(10 分)(德宏州)如图，是一个照相机成像的示意图．(1)如果像高 MN 是 35 mm ，焦距是 50 mm ，拍摄的景物高度 AB 是 4.9 m ，拍摄点离景物 有多远？(2)如果要完整的拍摄高度是 2 m 的景物，拍摄点离景物有 4 m ，像高不变，则相机的 焦距应调整为多少毫米？LC 解：根据物体成像原理知：LMN∽ LBA ，∴△MN ＝ .(1)∵像高 MN 是 35 mm ，焦距是35 4.950 mm ，拍摄的景物高度 AB 是 4.9 m ，∴ ＝ ，解得 LD ＝7，∴拍摄点距离景物 7 米35 2(2)拍摄高度是 2 m 的景物，拍摄点离景物有 4 m ，像高不变，∴ ＝ ，解得 LC ＝70，∴相机的焦距应调整为 70 mm12．(10 分)(遵义)如图， ABCD 中，BD ⊥AD ，∠A ＝45°，E ，F 分别是 AB ，CD 上的点， 且 BE ＝DF ，连接 EF 交 BD 于点 O.(1)求证：BO ＝DO ；(2)若 EF⊥AB，延长 EF 交 AD 的延长线于点 G ，当 FG ＝1 时，求 AD 的长．⎧∠ODF＝∠OBE，DG FG 21⎧AB＝AC，⎧AB＝AC，AM AN(1)证明：∵四边形ABCD是平行四边形，∴DC＝AB，DC∥AB，∴∠ODF＝∠OBE，在△ODF⎪与△OBE中，⎨∠DOF＝∠BOE，∴△ODF≌△OBE(AAS)，∴BO＝DO⎪⎩DF＝BE，(2)解：∵BD⊥AD，∴∠ADB＝90°，∵∠A＝45°，∴∠DBA＝∠A＝45°，∵EF⊥AB，∴∠G＝∠A＝△45°，∴ODG是等腰直角三角形，∵AB∥CD，EF⊥AB，∴DF⊥OG，∴OF＝FG，△DFG是等腰直角三角形，∵△ODF≌△OBE(AAS)，∴OE＝OF，∴GF＝OF＝OE，即2FG＝EF，AD EF∵△DFG是等腰直角三角形，∴DF＝FG＝1，∴DG＝DF2＋FG2＝2，∵AB∥CD，∴＝，AD2即＝，∴AD＝2213．(12分)(衢州)(1)提出问题如图①，在等边△ABC中，点M是BC上的任意一点(不含端点B，C)，连接AM，以AM 为边作等边△AMN，连接CN.求证：∠ABC＝∠ACN.(2)类比探究如图②，在等边△ABC中，点M是BC延长线上的任意一点(不含端点C)，其他条件不变，(1)中结论∠ABC＝∠ACN还成立吗？请说明理由．(3)拓展延伸如图③，在等腰△ABC中，BA＝BC，点M是BC上的任意一点(不含端点B，C)，连接AM，以AM为边作等腰△AMN，使顶角∠AMN＝∠ABC.连接CN.试探究∠ABC与∠ACN的数量关系，并说明理由．(1)证明：∵△ABC，△AMN是等边三角形，∴AB＝AC，AM＝AN，∠BAC＝∠MAN＝60°，⎪∴∠BAM＝∠CAN，∵在△BAM和△CAN中，⎨∠BAM＝∠CAN，∴△BAM≌△CAN(SAS)，∴∠ABC⎪⎩AM＝AN，＝∠ACN(2)解：结论∠ABC＝∠ACN仍成立．理由如下：∵△ABC，△AMN是等边三角形，∴AB ＝AC，AM＝AN，∠BAC＝∠MAN＝60°，∴∠BAM＝∠CAN，∵在△BAM和△CAN中，⎪⎨∠BAM＝∠CAN，∴△BAM≌△CAN(SAS)，∴∠ABC＝∠ACN(3)解：∠ABC＝∠ACN.理由如下：⎪⎩AM＝AN，AB AC ∵BA＝BC，MA＝△M N，顶角∠ABC＝∠AMN，∴底角∠BAC＝∠MAN，∴ABC∽△AMN，∴＝，又∵∠BA M＝∠BAC－∠MAC，∠CAN＝∠MAN－∠MAC，∴∠BAM＝∠CAN，∴△BAM∽△CAN，∴∠ABC＝∠ACNR t ABC的斜边BC上异于B，C的一定点，过M点作直线截△ABC，使截1．如图，M是△得的三角形与△ABC相似，这样的直线共有(C)A．1条B．2条C．3条D．4条,第1题图),第2题图) 2．如图，在平面直角坐标系中，四边形OABC是边长为2的正方形，顶点A，C分别在x，y轴的正半轴上．点Q在对角线OB上，且QO＝OC，连接CQ并延长CQ交边AB于点P.则点P的坐标为__(2，4－22)__．。

图形的相似（压轴专练）（十大题型）题型1：相似三角形解答证明题1．在ABC V 中，AB AC =，点D 在线段CB 的延长线上，连接AD ，过点B 作BE BC ^交线段AD 于点,2120E BED BAC Ð+Ð=°．(1)如图1，求CAD Ð的度数．(2)如图2，若32DE AE =，求BD BC的值．(3)如图3，在（2）的条件下，连接,EC EC 交线段AB 于点F ，若BD =AF 的长．2．如图1，在ABC V 中，90BAC AB AC BD CD Ð=°=^,,于点D ，连接AD ，在CD 上截取CE ，使CE BD =，连接AE ．(1)直接判断AE 与AD 的位置关系(2)如图2，延长AD ，CB 交于点F ，过点E 作EG AF ∥交BC 于点G ，试判断FG 与AB 之间的数量关系，并证明；(3)在（2）的条件下，若2AE =，CE =EG 的长．题型2：相似三角形在特殊平行四边形中的应用3．如图1，四边形ABCD 是正方形，点E 在边BC 的延长线上，点F 在边AB 上，且AF CE =，连接EF 交DC 于点P ，连接AC 交EF 于Q ，连接DE DF 、．(1)求证：EQ FQ =；(2)连接BQ ，如图2，①若AQ DP ×=BQ 的长；②若FP FD =，则PE PQ = ．4．综合与实践已知：矩形ABCD ，M 是AD 边上一点．【基本图形】（1）如图1，AM MD =，BM 交AC 于F 点，BM 的延长线与CD 的延长线交于点E ，连AE ，求证：MF EM BF EB=；【类比探究】（2）如图2，AM MD =，过点D 任意作直线与BM ，BC 的延长线分别交于点E ，点P ，连AE ，求证：EAD PAD ÐÐ=；【扩展延伸】（3）如图3，E 是CD 延长线上一点，P 是BC 延长线上一点，AP 交CD 于Q 点，BE 交AD 于M 点，延长AD 交EP 于N 点，若M 是AN 的中点，且3AB =，4BC =，求AEP △的面积．题型3：翻折问题5．菱形ABCD 中，5AB =，点F 是AD 边上的点，点Q 是AB 边上的点．(1)如图1，若点F 是AD 的中点，CQ AB ^，连接CF 并延长交BA 的延长线于点P ，连接QF ，①求证：PAF CDF △≌△；②判定FCQ V 的形状，并说明理由；(2)若菱形面积为20，将菱形ABCD 沿CQ 翻折，点B 的对应点为点E ．①如图2，当点E 落在BA 边的延长线上时，连接BD ，交CQ 于R ，交EC 于点M ，求DR BM 的值；②如图3，当CE AD ^，垂足为点F ，交AD 于点N ，求四边形CFNQ 的面积．6．如图1，在矩形ABCD 中，3AB =，4=AD ，点E 在BC 上，连接AE ，把ABE V 沿直线AE 翻折得到AFE △，直线EF 与直线CD 交于点G ，连接DF ．(1)当DFG GEC Ð=Ð时，求BE 的长．小星看到把ABE V 沿直线AE 翻折得到AFE △，就想到翻折图形的特征特点，对应边相等，对应角相等，对应点连线被对称轴垂直平分，那么他就知道BE FE =，AB AF =，90ABE AFE Ð=Ð=°，根据DFG GEC Ð=Ð，他延长EG 与AD 的延长线相交于点H ，可证AD DF DH ==，AH EH =，再通过勾股定理即可求出BE 的长．请用小星的方法或自己的方法求BE 的长；(2)当G 是CD 的中点时，求BE 的长；(3)如图2，已知等边ABC V 的边长为6，点D 在边BC 上，连接AD ，把ABD △沿直线AD 翻折得到AED △，直线DE 与直线AC 交于点F ，若12CF =，求BD 的长．7．（1）发现：如图1，正方形ABCD 中，点E 在CD 边上，将ADE V 沿AE 对折得到AFE △，延长EF 交BC 边于点G ，连接AG ．证明：BG DE EG +=．（2）探究：如图2，矩形ABCD 中AD AB >，O 是对角线的交点，过O 任作一直线分别交BC AD 、于点M 、N ，四边形AMNE 是四边形CMND 沿MN 翻折得到的，连接CN ，若CDN △的面积与CMN V 的面积比为1:3，求MN DN的值．（3）拓展：如图3，在菱形ABCD 中，6AB =，E 为CD 边上的三等分点，60D Ð=°，将ADE V 沿AE 翻折得到AFE △，直线EF 交BC 于点P ，求PC 的长．题型4：旋转问题8．如图，ABC V 和ADE V 是有公共顶点的等腰直角三角形，90BAC DAE Ð=Ð=°．(1)如图1，连接BE 、CD ，BE 的延长线交AC 于F ，交CD 于点P ，求证：①ABE ACD V V ≌；②BP CD ^；(2)如图2，把ADE V 绕点A 顺时针旋转，当点D 落在AB 上时，连接BE 、CD ，CD 的延长线交BE 于点P ，若BC =3AD =．①求证：BDP CDA △∽△，②PDE △的面积是 ．9．问题背景：如图（1），在ABC V 和ADE V 中，AB AC AD AE ==，，BAC DAE Ð=Ð，求证：ABD ACE △△≌；尝试应用：如图（2），在ABC V 和ADE V 中，90ABC ADE Ð=Ð=°，30ACB AED Ð=Ð=°，连接CE ，点F 是CE 的中点．判定以B ，D ，F 为顶点的三角形的形状，并证明你的结论；拓展创新：如图（3），在ABC V 中，AC BC ＝AB 绕点A 逆时针旋转90°得到AD ，连接BD CD ，．若点E 是CD 的中点，连接BE ，直接写出BE 的最大值．10．如图，在V 锐角ABC 中，AB =3BC =，45ACB Ð=°，将ABC V 绕点B 按逆时针方向旋转得到11A BC V ．(1)如图①，当点1C 在线段CA 的延长线上时，求11CC A Ð的度数；(2)如图②，连接1AA ，1CC ，若1ABA △的面积为2，求1CBC △的面积；(3)如图③，点E 为线段AB 中点，点P 是线段AC 上的动点，在ABC V 绕点B 按逆时针方向旋转过程中，点P 的对应点是点1P ，求线段1EP 长度的最大值与最小值．题型5：最值问题11．如图，在ABC V 中，90,BAC AB AC Ð=°=，点D 为AC 一点，连接BD ．(1)如图1，若CD =，15ABD Ð=°，求AD 的长；(2)如图2，过点A 作AE BD ^于点E ，交BC 于点M ，AG BC ^于点G ，交BD 于点N ，求证：BM CM =；(3)如图3，将ABD △沿BD 翻折至BDE V 处，在AC 上取点F ，连接BF ，过点E 作EH BF ^交AC 于点G ，GE 交BF 于点H ，连接AH ，若:2GE BF =，AB =AH 的最小值．12．如图1和图2，平面上，四边形ABCD 中1582AB BC ==，，252CD =，6DA ＝，90A Ð=°，点M 在AD边上，且2DM =．点P 从点A 沿折线AB BC -上运动到点C ，将APM △沿MP 翻折，点A 的对应点为点A ¢，设点P 的运动路径长为x (0)x >．(1)如图1，连接BD ，①求CBD Ð的度数；②求证：AB CD ∥．(2)如图2，当点A ¢落到四边形ABCD 内部时，求x 的取值范围．(3)①当点A ¢落在AD 的延长线上时，请直接写出x 的值．②设点A ¢到边BC 所在直线的距离为h ，请直接写出h 的最小值．13．如图，在Rt ABC △中，90ACB Ð=°，AC BC =，点D 在直线AB 上，点E 在直线AC 上，连接BE ，DE ，且BE DE =，直线DE 交BC 于点F ．(1)如图①，当点D 在线段AB 上时，AD 4AC =，求BE 的长；(2)如图②，当D 是AB 的中点时，求证：CE CF BF +=；(3)如图③，连接CD ，将ADC △沿着CD 翻折，得到A CD ¢△，M 是AB 上一点，且37BM AB =，当A M ¢最短时，请直接写出DF BE 的值．题型6：比值问题14．如图1，在ABC D 中，AB AC =，点D 、E 分别在边AB 、AC 上，AD AE =，连接DC ，点F 、P 、G分别为DE 、DC 、BC 的中点，连接FP ，PG ．(1)图1中，求证：PF PG =；(2)当ADE V 绕点A 旋转到如图2所示的位置时，①PF PG =是否仍然成立？若成立请证明；若不成立，说明理由；②若:1:(1)AD AB n n =>，PDF △和PGC V 的面积分别是1S ，2S ，ABC V 的面积为3S ，求123S S S +的值．15．【特例感知】（1）如图1，在正方形ABCD 中，点P 在边AB 的延长线上，连接PD ，过点D 作DM PD ^，交BC 的延长线于点M ．求证：DP DM =．【变式求异】（2）如图2，在Rt ABC △中，90ABC Ð=°，点D 在边AB 上，过点D 作DQ AB ^，交AC 于点Q ，点P 在边AB 的延长线上，连接PQ ，过点Q 作QM PQ ^，交射线BC 于点M ．已知8BC =，10AC =，AD =2DB ，求PQ QM的值．【拓展应用】（3）如图3，在Rt ABC △中，90BAC Ð=°，点P 在边AB 的延长线上，点Q 在边AC 上（不与点A ，C 重合），连接PQ ，以Q 为顶点作PQM PBC Ð=Ð，PQM Ð的边QM 交射线BC 于点M ．若AC mAB =，CQ nAC =（m ，n 是常数），直接写出PQ QM的值（用含m ，n 的代数式表示）．题型7：“手拉手”模型16．在ABC V 中，90ACB Ð=°，AC BC =，点D 是BC 边上一动点，过点C 作CE AD ^交AB 于点E ．(1)如图1，若AC AE =，求ADB Ð的度数；(2)如图2，点F 是BD 上一点，连接EF 并延长交AD 的延长线于点G ．若点P 为AD 的中点，CP DG =，2G CAD Ð=Ð，求证：2CE EF FG +=；(3)点F 是BC 边上一点，射线EF 与射线AD 交于点G ，BFE ADC Ð=Ð，点H 是AC 上一点，且14CH AC =，连接HF ，H G ，点M 是射线AD 上一动点，连接MH ，MF ．在点D 的运动过程中，当GH 取得最小值m 时，在平面内将HFM △沿直线HM 翻折得到HNM V ，连接EN ．在点M 的运动过程中，若EN 的最大值为n ，直接写出n m的值．17．如图所示，在ABC V 中，D 、E 分别是AB 、AC 上的点，DE BC ∥，如图1，然后将ADE V 绕A 点顺时针旋转一定角度，得到图2，然后将BD 、CE 分别延长至M 、N ，使DM ＝12BD ，EN ＝12CE ，得到图3，请解答下列问题：(1)若AB AC =，请探究下列数量关系：①在图2中，BD 与CE 的数量关系是 ；②在图3中，猜想AM 与AN 的数量关系、MAN Ð与BAC Ð的数量关系，并证明你的猜想；(2)若·1AB k AC k =（＞），按上述操作方法，得到图4，请继续探究：AM 与AN 的数量关系、MAN Ð与BAC Ð的数量关系，直接写出你的猜想，不必证明．题型8：定值问题18．如图1，在ABCD Y 中，60A Ð=°，4=AD ，8AB =．Y的面积；(1)请计算ABCD△沿着AC翻折，D点的对应点为D¢，线段CD¢交AB于点M，请计算AM的长度；(2)如图2，将ADC^交AD¢的延(3)如图3，在（2）的条件下，点P为线段CM上一动点，过点P作PN AC^于点N，PG AD¢长线于点G．在点P PG+的长度是否为定值？如果是，请计算出这个定值；如果不是，请说明理由．题型9：情景探究题19．[问题情境]（1）王老师给爱好学习的小明和小颖提出这样一个问题：如图①，在ABC V 中，AB AC =，P 为边BC 上的任一点，过点P 作,PD AB PE AC ^^，垂足分别为D ，E ，过点C 作CF AB ^，垂足为F ．求证：PD PE CF +=．小明的证明思路是：如图①，连接AP ，由ABP V 与APC △面积之和等于ABC V 的面积可以证得：PD PE CF +=．小颖的证明思路是：如图②，过点P 作PG CF ^，垂足为G ，可以证得：,PD GF PE CG ==，则PD PE CF +=．请你选择小明、小颖两种证明思路中的任意一种，写出详细的证明过程．[变式探究]（2）如图③，当点Р在BC 延长线上时，问题情境中，其余条件不变，则PD PE CF 、、之间的数量关系是______．[结论运用]（3）如图④，将矩形ABCD 沿EF 折叠，使点D 落在点B 上，点C 落在点C ¢处，点P 为折痕EF 上的任一点，过点Р作,PG BE PH BF ^^，垂足分别为G ，H ，若18,5AD CF ==，求PG PH +的值．[迁移拓展]（4）图⑤是一个机器模型的截面示意图，在四边形ABCD 中，E 为AB 边上的一点，,ED AD EC CB ^^，垂足分别为D ，C ，且,3cm,AD CE DE BC AB AD BD ====××，M 、N 分别为AE BE ，的中点，连接DM CN ，，请直接写出DEM △与CEN V 的周长之和___________．题型10：相似三角形在平面直角坐标系的应用20．如图，在平面直角坐标系中；一次函数y kx b =+的图象与x 轴交于点A ，与y 轴交于点B (0,3)，与直线OC 交于点8,13C æöç÷èø．(1)求直线AB 的函数表达式；(2)过点C 作CD x ^轴于点D ，将ACD V 沿射线CB 平移得到的三角形记为A C D ¢¢¢△，点A ，C ，D 的对应点分别为A ¢，C ¢，D ¢，若A C D ¢¢¢△与BOC V 重叠部分的面积为S ，平移的距离CC m ¢=，当点A ¢与点B 重合时停止运动，当925S =时，求m 的值．21．综合运用如图1，在平面直角坐标系中，AOB V 是等腰直角三角形，AO BO =，点A 的坐标为()0,6．点C 是边OB 上一点，连接AC ，将线段AC 绕点C 顺时针旋转90°，得到线段CD ，连接AD ，BD ．(1)当AB 平分CAD Ð时，OAC Ð＝________°；(2)若13CO BO =，求BD 的长；(3)如图2，作点C 关于AD 的对称点E ，连接BE ，CE ，DE ．设BDE V 的面积S =，CO m =，求S 关于m 的函数表达式．。

中考数学《图形的相似》专项练习题及答案一、单选题1．一块含30°角的直角三角板（如图），它的斜边AB=8cm，里面空心△DEF的各边与△ABC的对应边平行，且各对应边的距离都是1cm，那么△DEF的周长是（）A．5cm B．6cm C．（6-√3）cm D．（3+√3）cm2．如图，DE△BC，EF△AB，现得到下列结论：AEEC=BFFC，ADBF=ABBC，EFAB=DEBC，CECF=EABF其中正确的比例式的个数有()A．4个B．3个C．2个D．1个3．如图，△ABC与△ADE成位似图形，位似中心为点A，若AD:AB=1:3，则△ADE与△ABC面积之比为（）A．1:2B．1:3C．1:9D．1:164．如图，△ABC中，三边互不相等，点P是AB上一点，有过点P的直线将△ABC切出一个小三角形与△ABC相似，这样的直线一共有（）A．5条B．4条C．3条D．2条5．如图，已知△ABC和△EDC是以点C为位似中心的位似图形，且△ABC和△EDC的位似比为1：2，△ABC面积为2，则△EDC的面积是（）A．2B．8C．16D．326．如图，△ADE△△ABC，若AD＝2，BD＝4，则△ADE与△ABC的相似比是（）A．1：2B．1：3C．2：3D．3：27．如图，以A为位似中心，将△ADE放大2倍后，得位似图形△ABC，若s1表示△ADE的面积，s2表示四边形DBCE的面积，则s1：s2=（）A．1︰2B．1︰3C．1︰4D．2︰38．如图，按如下方法，将△ABC的三边缩小到原来的12，任取一点O，连AO、BO、CO，并取它们的中点D、E、F得△DEF，则下列说法正确的是（）①△ABC与△DEF是相似图形；②△ABC与△DEF的周长比为2：1；③△ABC与△DEF的面积比为4：1．A．①、②B．②、③C．①、③D．①、②、③9．如图，已知AB是半圆O的直径，弦AD，CB相交于点P，若∠DPB=45°，则S△CDP：S△ABP 的值（）A．25B．23C．13D．1210．如图，AD△BE△CF，直线l1、l2这与三条平行线分别交于点A，B，C和点D，E，F．已知AB=1，BC=3，DE=2，则EF的长为（）A．4B．5C．6D．811．一个三角形的三边长分别为3,4,5,另一个与它相似的三角形中有一条边长为6.则这个三角形的周长不可能是()A．725B．18C．48D．2412．如图，小正方形的边长为均为1，下列各图（图中小正方形的边长均为1）阴影部分所示的三角形中，与△ABC相似的三角形是（）A．B．C．D．二、填空题13．勾股定理是一个基本的几何定理，有数百种证明方法．“青朱出入图”是我国古代数学家证明勾股定理的几何证明法．刘徽描述此图“勾自乘为朱方，股自乘为青方，令出入相补，各从其类，加就其余不动也，合成弦方之幂，开方除之，即弦也”．若图中BF=4，DF=2，则AE=．14．如图，矩形ABCD中，AB=3，BC=4，E是BC上一点，BE=1，AE与BD交于点F．则DF的长为．15．如图，点D在△ABC的边BC的延长线上，AD为△ABC的外角的平分线，AB＝2BC，AC＝3，CD＝4，则AB的长为．16．如图，在△ABC中，△BAC=90°，AD△BC于D，BD=3，CD=12，则AD的长为17．在某一时刻，测得一根高为1m的竹竿的影长为2m，同时测得一栋高楼的影长为40m，这栋高楼的高度是m．18．如图，已知路灯离地面的高度AB为4.8m，身高为1.6m的小明站在D处的影长为2m，那么此时小明离电杆AB的距离BD为m．三、综合题19．如图，已知△BAC=90°，AD△BC于D，E是AC的中点，ED的延长线交AB的延长线于点F．求证：（1）△DFB△△AFD；（2）AB：AC=DF：AF．20．一次小组合作探究课上，小明将两个正方形按如图1所示的位置摆放（点E、A、D在同一条直线上）.（1）发现BE与DG数量关系是，BE与DG的位置关系是.（2）将正方形AEFG绕点A按逆时针方向旋转（如图2），（1）中的结论还成立吗？若能，请给出证明；若不能，请说明理由.（3）把图1中的正方形分别改写成矩形AEFG和矩形ABCD，且AEAG=ABAD=23，AE=2，AB=4，将矩形AEFG绕点A按顺时针方向旋转（如图3），连接DE，BG.小组发现：在旋转过程中，DE2+BG2的值是定值，请直接写出这个定值.21．如图，已知点D在△ABC的外部，AD△BC，点E在边AB上，AB•AD＝BC•AE．（1）求证：△BAC＝△AED；（2）在边AC取一点F，如果△AFE＝△D，求证：ADBC=AFAC．22．如图，在▱ABCD中，对角线AC，BD相交于点O，过点O作BD的垂线与边AD，BC分别交于点E，F，连接BE交AC于点K，连接DF。

备战中考数学（北师大版）专项练习图形的相似（含解析）一、单选题1.如图，点G、F分别是△BCD的边BC、CD上的点，BD的延长线与GF的延长线相交于点A ，DE∥BC交GA于点E，则下列结论错误的是（）A.B.C. D.2.如图，△ABC中，D，E两点分别在AB，AC边上，且DE∥BC，假如，AC=6，那么AE的长为（）A.3B.4C.9D.123.一只蚂蚁沿直角三角形的边长爬行一周需2秒，假如将直角三角形的边长扩大1倍，那么这只蚂蚁再沿边长爬行一周需（）A.6秒B.5秒C.4秒D.3秒4.如图，△ABC中，∠BAC＝90°，AD⊥BC于D，若AB＝2，BC＝4，则CD的长是()A.1B.4C.3D.25.假如两个相似三角形的周长比为1：4，那么这两个三角形的相似比为（）A.1：2B.1：4C.1：8D.1：166.如图，已知在△ABC中，点D、E、F分别是边AB、AC、BC上的点，DE=BF，EF=BD，且AD：DB=3：5，那么CF：CB等于（）A.3：5B.3：8C.5：8D.2：57.如图，在△ABC中，点D、E分别在边AB、AC上，且DE不行于B C，则下列条件中不能判定△ABC∽△ADE的是（）A.∠AED＝∠BB.∠ADE＝∠CC.＝D.＝8.一张等腰三角形纸片，底边长15cm，底边上的高长22.5cm．现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条，如图所示．已知剪得的纸条中有一张是正方形，则这张正方形纸条是（）A.第4张B.第5张C.第6张D.第7张二、填空题9.在平面直角坐标系中，点A（2，3），B（5，﹣2），以原点O为位似中心，位似比为1：2，把△ABO缩小，则点B的对应点B′的坐标是___ _____10.如图，△ABC的内接正方形EFGH中，EH∥BC，其中BC=4，高A D=6，则正方形的边长为________．11.位似图形的相似比也叫做________12.如图，矩形中，点是边的中点，交对角线于点，则与的面积比等于________．13.如图，以点O为位似中心，将△ABC放大得到△DEF，若AD=OA，则△ABC与△DEF的面积之比为________14.如图，Rt△ABC中，∠A=90°，AB=6，AC=8，点E为边AB上一点，AE=2，点F为线段AB上一点，且BF=3，过点E作AC的平行线交B C于点D，作直线FD交AC于点G，则FG=________．15.如图，已知图中的每个小方格差不多上边长为1的小正方形，每个小正方形的顶点称为格点．若△ABC与△A1B1C1是位似图形，且顶点都在格点上，则位似中心的坐标是________．16.如图是小明在建筑物AB上用激光仪测量另一建筑物CD高度的示意图，在地面点P处水平放置一平面镜，一束激光从点A射出经平面镜上的点P反射后刚好射到建筑物CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB=15米，BP=20米，PD=32米，B、P、D在一条直线上，那么建筑物CD的高度是________米．三、解答题17.如图，在正方形ABCD中，E为边AD的中点，点F在边CD上，且CF=3FD，△ABE与△DEF相似吗？什么缘故？18.如图，△ABC中，点D在边AB上，满足∠ACD=∠ABC，若AC=，AD=1，求DB的长．四、综合题19.小明利用灯光下自己的影子长度来测量路灯的高度．如图，CD和E F是两等高的路灯，相距27m，身高1.5m的小明（AB）站在两路灯之间（D、B、F共线），被两路灯同时照耀留在地面的影长BQ=4m，BP=5m．（1）小明距离路灯多远？（2）求路灯高度．20.如图，在△ABC中，∠C=90°，AC=4，BC=3，点P从点A动身，以每秒4个单位长度的速度沿折线AC-CB运动，到点B停止．当点P不与△ABC的顶点重合时，过点P作其所在直角边的垂线交AB 于点Q，再以PQ为斜边作等腰直角三角形△PQR，且点R与△ABC的另一条直角边始终在PQ同侧，设△PQR与△ABC重叠部分图形的面积为S（平方单位）．点P的运动时刻为t（秒）．（1）求点P在AC边上时PQ的长，（用含t的代数式表示）；（2）求点R到AC、PQ所在直线的距离相等时t的取值范畴；（3）当点P在AC边上运动时，求S与t之间的函数关系式；（4）直截了当写出点R落在△ABC高线上时t的值．21.如图，在平面直角坐标系xOy中，△ABC三个顶点坐标分别为A（1，2），B（7，2），C（5，6）．（1）请以图中的格点为顶点画出一个△A1B1C ，使得△A1B1C ∽△ABC ，且△A1B1C与△ABC的周长比为1：2；（每个小正方形的顶点为格点）（2）依照你所画的图形，直截了当写出顶点A1和B1的坐标.22.如图，梯形ABCD中，AB∥DC ，∠B=90°，E为BC上一点，且AE⊥ED ．若BC=12，DC=7，BE：EC=1：2，（1）求AB的长．（2）求△AED的面积答案解析部分一、单选题1.【答案】C【考点】平行线分线段成比例【解析】解答：∵DE∥BC交GA于点E ，∴，，，A，B，D正确，故选C．分析：利用平行线分线段成比例定理即可得到答案．2.【答案】B【考点】平行线分线段成比例【解析】【解答】解：∵DE∥BC，∴，又AC=6，∴AE=4，故选：B．【分析】依照平行线分线段成比例定理，得到比例式，把已知数据代入运算即可．3.【答案】C【考点】相似三角形的应用【解析】【分析】本题依照放大后的三角形与三角形相似，故可依照相似三角形的性质求解，两个相似三角形对应边之比的比值叫做相似比．【解答】直角三角形各边的长度扩大一倍，周长扩大1倍，故爬行时刻扩大一倍．故只蚂蚁再沿边长爬行一周需4秒．故选C．【点评】熟练运用相似三角形的性质．4.【答案】C【考点】相似三角形的判定与性质【解析】【分析】先由∠BAC＝90°，AD⊥BC，∠B＝∠B证得△AB D∽△CBA，再依照相似三角形的性质求得BD的长，即可求得结果。

北师大版九年级上册数学第四章图形的相似含答案一、单选题(共15题，共计45分)1、如图，矩形的长和宽分别是4和3，等腰三角形的底和高分别是3和4，如果此三角形的底和矩形的宽重合，并且沿矩形两条宽的中点所在的直线自右向左匀速运动至等腰三角形的底与另一宽重合.设矩形与等腰三角形重叠部分（阴影部分）的面积为y，重叠部分图形的高为x，那么y关于x的函数图象大致应为（）A. B. C. D.2、如图，下列四个三角形中，与相似的是（）A. B. C. D.3、如图，在△ABC中，∠A=78°，AB=4，AC=6，将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（）A. B. C.D.4、小明是我校手工社团的一员，他在做折纸手工，如图所示在矩形ABCD中，AB=6，BC=8，点E是BC的中点，点F是边CD上的任意一点，△AEF的周长最小时，则DF的长为（）A.1B.2C.3D.45、如图，点D是△ABC的边BC的中点，且∠CAD＝∠B，若△ABC的周长为10，则△ACD的周长是（）A.5B.5C.D.6、如图，△ABC 内接于⊙ O ，AD 是△ABC 边 BC 上的高，D 为垂足.若 BD = 1，AD = 3，BC = 7，则⊙O 的半径是（）A. B. C. D.7、如图，△ABC中，∠BAC＝90°，AD⊥BC于D，若AB＝2，BC＝3，则CD的长是( )A. B. C. D.8、如图所示是△ABC位似图形的几种画法，其中正确的是个数是（）A.1B.2C.3D.49、如图，△ABC∽△ADE，则下列比例式正确的是（）A. B. C. D.10、如图，取一张长为、宽为的长方形纸片，将它对折两次后得到一张小长方形纸片，若要使小长方形与原长方形相似，则原长方形纸片的边应满足的条件是（）A. B. C. D.11、已知：如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE的长为（）A.6 cmB.4 cmC.3 cmD.2 cm12、在△ABC中，AB=12，BC=18，CA=24，另一个和它相似的△DEF最长的一边是36，则△DEF最短的一边是（）A.72B.18C.12D.2013、如图，已知AB是⊙O的直径，C是AB延长线上一点，BC=OB，CE是⊙O的切线，切点为D，过点A作AE⊥CE，垂足为E，则CD：DE的值是（）A. B.1 C.2 D.314、如图，AD=DF=FB，DE∥FG∥BC，且把三角形ABC分成面积为S1， S2， S3三部分，则S1：S2：S3=（）A.1：2：3B.1：4：9C.1：3：5D.无法确定15、已知：如图，在中，，则下列等式成立的是（）A. B. C. D.二、填空题(共10题，共计30分)16、如图，直线l1∥l2∥l3∥l4∥l5∥l6∥l7，且每相邻两条直线的距离相等.若直线l8分别与l1， l2， l5， l7相交于点A，B，C，D，则AB：BC：CD为________.17、在如图所示的正方形方格纸中，每个小的四边形都是相同的正方形，A、B、C、D都是格点，AB与CD相交于M，则AM：BM=________．18、已知，则的值为________.19、把一个矩形剪去一个正方形，若剩下的矩形与原矩形相似，则原矩形的长边与短边之比为________．20、上午某一时刻,身高1.7米的小刚在地面上的影长为3.4米,则影长26米的旗轩高度为________米21、如图所示，点E是平行四边形ABCD的边BC延长线上一点，连接AE，交CD 于点F，连接BF．写出图中任意一对相似三角形：________．22、如图，火焰的光线穿过小孔O，在竖直的屏幕上形成倒立的实像，像的长度BD=2 cm，OA=60 cm, OB=15 cm，则火焰的长度为________.23、将矩形纸片ABCD按如下步骤进行操作：（ 1 ）如图1，先将纸片对折，使BC和AD重合，得到折痕EF；（ 2 ）如图2，再将纸片分别沿EC，BD所在直线翻折，折痕EC和BD相交于点O.那么点O到边AB的距离与点O到边CD的距离的比值是________.24、如图，在直线l上摆放着三个正三角形：△ABC、△HFG、△DCE，已知BC ＝CE，F、G分别是BC、CE的中点，FM∥AC∥HG∥DE，GN∥DC∥HF∥AB．设图中三个四边形的面积依次是S1， S2， S3，若S1+S3＝20，则S1＝________，S2＝________．25、如图，在▱ABCD中，对角线AC、BD相交于点O，在BA的延长线上取一点E，连接OE交AD于点F．若CD=5，BC=8，AE=2，则AF=________．三、解答题(共5题，共计25分)26、解方程.534%－2x=0.5627、李航想利用太阳光测量楼高．他带着皮尺来到一栋楼下，发现对面墙上有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下：如示意图，李航边移动边观察，发现站到点E处时，可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠，且高度恰好相同．此时，测得李航落在墙上的影子高度CD=1.2m，CE=0.6m，CA=30m（点A、E、C在同一直线上）．已知李航的身高EF是1.6m，请你帮李航求出楼高AB．28、如图，两根电线杆相距Lm，分别在高10m的A处和15m的C处用钢索将两杆固定，求钢索AD与钢索BC的交点M离地面的高度MH．29、如图，在△PAB中，点C、D在AB上，PC＝PD＝CD，∠A ＝∠BPD，△APC 与△BPD相似吗？为什么？30、如图，Rt△ABC中，∠C=90°，BC=6，AC=8．点P，Q都是斜边AB上的动点，点P从B 向A运动（不与点B重合），点Q从A向B运动，BP=AQ．点D，E分别是点A，B以Q，P为对称中心的对称点，HQ⊥AB于Q，交AC于点H．当点E到达顶点A时，P，Q同时停止运动．设BP的长为x，△HDE的面积为y．（1）求证：△DHQ∽△ABC；（2）求y关于x的函数解析式并求y的最大值；（3）当x为何值时，△HDE为等腰三角形？参考答案一、单选题(共15题，共计45分)1、B2、C4、D5、B6、C7、D8、D9、D10、B11、C12、B13、C14、C15、C二、填空题(共10题，共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题，共计25分)26、29、。

第4章图形的相似章末拔尖卷【北师大版】参考答案与试题解析一．选择题（共10小题，满分30分，每小题3分）1．（3分）（2023秋·湖南永州·九年级校考期中）已知ab c =ba c=cb a=k，则直线y=kx+2k一定经过（ ）A．第一、二象限B．第二、三家限C．第三、四象限D．第一、四象限【答案】B【分析】对ab c =ba c=cb a=k关系式化简为a+b+c=2k(a+b+c)，分类讨论求出k的值即可找出经过的象限．【详解】∵ab c =ba c=cb a=k，∴a+b+c=2k(a+b+c)，当a+b+c=0时，a+b=−c，则k=−1，此时直线为y=−x−2，过二、三、四象限．当a+b+c≠0时，k=12，此时直线为y=12x+1，过一、二、三象限．综上所述，过二、三象限．故选B．【点睛】本题考查函数的象限，求出函数的表达式是解题的关键．本题的易错点在于忽略分类讨论的情况．2．（3分）（2023秋·湖南株洲·九年级校考期中）如图，已知∠1=∠2，添加下列条件后，仍无法判定△ABC∽△ADE的是（）A．ABAC =ADAEB．∠B=∠D C．∠C=∠AED D．ABAD=BCDE【答案】D【分析】根据相似三角形的判定方法：两角分别对应相等的两个三角形相似；两边成比例且夹角相等的两个三角形相似；三边成比例的两个三角形相似；一条直角边与斜边成比例的两个直角三角形相似；逐一判断即可．【详解】解∵∠1=∠2，∴∠DAE=∠BAC，若ABAD =ACAE，∠DAE=∠BAC，∴△ABC∼△ADE(SAS)，故A不符合题意；若∠DAE=∠BAC，∠B=∠D，∴△ABC~△ADE，故B不符合题意；若∠C=∠AED，∠DAE=∠BAC，∴△ABC~△ADE，故C不符合题意；∵AB AD =BCDE，∠DAE=∠BAC，∴无法判断△ABC与△ADE相似，故D符合题意；故选：D．【点睛】本题考查相似三角形的判定方法，熟记知识点是解题关键．3．（3分）（2023秋·江苏盐城·九年级校联考期末）如图，在▱ABCD中，点G在BC的延长线上，AG分别交BD、CD于点E、F，则图中相似三角形共有（）A．4对B．5对C．6对D．7对【答案】C【分析】本题根据平行四边形的对边平行，再根据平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似找出相似三角形即可得解．【详解】解：在▱ABCD中，∵AB∥CD，∴△ABE ∽△FDE ，△ABG ∽△FCG ；∵AD ∥BC ，∴△ADE ∽△GBE ，△FDA ∽△FCG ，∴△ABG ∽△FDA ，△ABD ∽△BCD ∴图中相似三角形有6对．故答案为6．【点睛】本题考查了相似三角形的判定，主要利用了平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似，要注意△ABG 与△FDA 都与△FCG 相似，所以也相似，这也是本题容易出错的地方．4．（3分）（2023·黑龙江哈尔滨·校考模拟预测）如图，在▱ABCD 中，点E 在CD 边上，连接AE 、BE ，AE 交BD 于点F ．则下列结论正确的是（ ）．A ．AF FE =CDDE B ．AF FE =DFBFC ．DE CE =DFBFD ．AF FE =ADBE【答案】A【分析】根据平行四边形的性质和平行线分线段成比例的性质进行解答即可．【详解】解：∵四边形ABCD 是平行四边形，∴AB =CD ，AB ∥CD ，∴AFFE =ABDE ，AFFE =BFDF ，故B 错误，不符合题意；∴AFFE =CDDE ，故A 正确，符合题意；如果AE ∥BC ，则有DECE =DFBF ，∵ AE 和BC 不平行，∴DECE ≠DFBF ，故C 错误，不符合题意；如果AD ∥BE ，则有AFFE =ADBE ，∵AD 和BE 不平行，∴AF FE ≠ADBE ，故D 错误，不符合题意；故选：A ．【点睛】本题考查了平行四边形的性质、平行线分线段成比例，熟练掌握平行线分线段成比例的性质定理是解题的关键．5．（3分）（2023·河北邯郸·校考三模）如图，正方形ABCD 的边长是10，在正方形外有E 、F 两点，满足AE =CF =6，BE =DF =8，则EF 的长是（ ）A ．B ．C ．14D ．【答案】B【分析】如图，过点F 作FH ⊥AD ,交AD 的延长线于点H ，过点E 作EI ⊥AD ，交DA 的延长线于点I ，过点E 作EG ⊥FH ,垂足为G ,则四边形EGHI 是矩形；运用勾股定理逆定理，求证∠AEB =90°，∠CFD =90°；求证△IAE ∽△EBA.从而求得IA =245,IE =185. HG =IE =185.同理可证△HDF ∽△FCD.求得HD =245,HF =325．EG =IH =985，GF =145. Rt △EFG 中，运用勾股定理求解．【详解】解：如图，过点F 作FH ⊥AD ,交AD 的延长线于点H ，过点E 作EI ⊥AD ，交DA 的延长线于点I ，过点E 作EG ⊥FH ,垂足为G ,则四边形EGHI 是矩形，∴EG =IH ．∵AE =6,BE =8,AB =10,∴AE 2+BE 2=AB 2.∴∠AEB =90°．同理，∠CFD =90°．∵∠IAE +∠EAB =90°,∠EBA +∠EAB =90°，∴∠IAE =∠EBA ．∴△IAE ∽△EBA.∴IAEB =IEEA =EAAB =610∴IA =610×8=245,IE =610×6=185.∴HG =IE =185.同理，可证△HDF ∽△FCD.∴HDFC =HFFD =DFCD =810．∴HD =810×6=245,HF =810×8=325．∴EG =IH =IA +AD +DH =245+10+245=985．GF =HF−HG =145.∴Rt △EFG 中，EF ==故选：B【点睛】本题考查正方形的性质，矩形的判定和性质，勾股定理及其逆定理，相似三角形；运用相似三角形工具求得线段间的数量关系是解题的关键．6．（3分）（2023·山东·统考中考真题）如图，四边形ABCD 是一张矩形纸片．将其按如图所示的方式折叠：使DA 边落在DC 边上，点A 落在点H 处，折痕为DE ；使CB 边落在CD 边上，点B 落在点G 处，折痕为CF ．若矩形HEFG 与原矩形ABCD 相似，AD =1，则CD 的长为（ ）A B C +1D 【答案】C【分析】先根据折叠的性质与矩形性质，求得DH =CG =1，设CD 的长为x ，则HG =x−2，再根据相似多边形性质得出EHCD =HGAD ，即1x =x−21，求解即可．【详解】解：，由折叠可得：DH=AD，CG=BC，∵矩形ABCD，∴AD=BC=1，∴DH=CG=1，设CD的长为x，则HG=x−2，∵矩形HEFG，∴EH=1，∵矩形HEFG与原矩形ABCD相似，∴EH CD =HGAD，即1x=x−21，解得：x=（负值不符合题意，舍去）∴CD=+1，故选：C．【点睛】本题考查矩形的折叠问题，相似多边形的性质，熟练掌握矩形的性质和相似多边形的性质是解题的关键．7．（3分）（2023秋·云南普洱·九年级统考期末）如图，△ADC是由等腰直角△EOG经过位似变换得到的，位似中心在x轴的正半轴，已知EO=1，D点坐标为D(2,0)，位似比为1:2，则两个三角形的位似中心P点的坐标是（）A,0B．(1,0)C．(0,0)D,0【答案】A【分析】先确定G点的坐标，再结合D点坐标和位似比为1：2，求出A点的坐标；然后再求出直线AG的解析式，直线AG与x的交点坐标，即为这两个三角形的位似中心的坐标．.【详解】解：∵△ADC与△EOG都是等腰直角三角形∴OE=OG=1∴G 点的坐标分别为（0，-1）∵D 点坐标为D （2，0），位似比为1：2，∴A 点的坐标为（2，2）∴直线AG 的解析式为y=32x-1∴直线AG 与x 的交点坐标为（23，0）∴位似中心P ,0．故答案为A ．【点睛】本题考查了位似中心的相关知识，掌握位似中心是由位似图形的对应顶点的连线的交点是解答本题的关键．8．（3分）（2023秋·浙江湖州·九年级统考期中）如图，将长方形纸片分别沿AB ，AC 折叠，点D ，E 恰好重合于点M ．记△COM 面积为S 1，△AOB 面积为S 2，且DEBC =75，则S 1S 2的值为（ ）A ．1:2B ．5:7C ．3:7D ．2:5【答案】D【分析】过点A 作AP ⊥BC 于P ，过点M 作MQ ⊥BC 于点Q ，则△APO ∽△MQO ，根据相似三角形的性质得出MQ AP=OMAO，设DE =7k ，则BC =5k ，根据折叠的性质及矩形的性质推出AM =AD =12DE =k ，CF =DE =7k ，OA =OB =OC =12BC =52k ，OM =AM−OA =k ，则MQAP =OMAO=25，根据三角形面积公式求解即可．【详解】解：如图，过点A 作AP ⊥BC 于P ，过点M 作MQ ⊥BC 于点Q ，∴∠APO =∠MQO =90°，∵∠AOP =∠MOQ ，∴△APO ∽△MQO ，∴MQ AP =OMAO ，∵ DEBC =75，∴设DE =7k ，则BC =5k ，由折叠可知，AE =AM =AD ，∠DAC =∠MAC ，∠BAE =∠BAM ，BF =BN ，∠AMC =∠D =∠E =∠N =90°，∴AM =AD =12DE =72k ，∵四边形CDEF 是矩形，∴CF =DE =7k ，CF∥DE ，∴BN =BF =DE−BC =2k ，∠DAC =∠BCA ，∠BAE =∠CBA ，∴∠BCA =∠MAC ，∠CBA =∠BAM ，∴OA =OB =OC ，∴OA =OB =OC =12BC =52k ，∴OM =AM−OA =72k−52k =k ，∴MQAP=OM AO=25，∵S 1=12OC ⋅MQ =12×52k ⋅MQ ，S 2=12OB ⋅AP =12×52k ⋅AP ，∴ S 1S 2=MQ AP=25=2:5，故选：D ．【点睛】此题考查了折叠的性质、矩形的性质，相似三角形的判定与性质，熟练掌握折叠的性质、矩形的性质是解题的关键．9．（3分）（2023秋·浙江湖州·九年级统考期末）如图△ACB ，∠ACB=90°，点O 是AB 的中点，CD 平分∠BCO 交AB 于点D ，作AE ⊥CD 分别交CO 、BC 于点G ，E ． 记△AGO 的面积为S 1，△AEB 的面积为S 2，当S 1S 2＝25时，则OGBC 的值是（ ）A ．25B ．13C ．411D ．38【答案】D【分析】连接BG ，过点O 作OT ∥AE 交BC 于点T ，首先证明AG EG =41，再利用平行线分线段成比例求解即可．【详解】解：如图所示，连接BG ，过点O 作OT ∥AE 交BC 于点T ，∵点O 是AB 的中点，∴AO =OB ，∴S ∆AOG =S ∆OBG ，∵S ∆AOGS ∆ABE =25，∴S ∆ABGS ∆BEG =41，∴AGEG =41，∵OT ∥AE ，AO =BO ，∴ET =TB ，∴OT =12AE ，∴GEOT =25，∵AE⊥CD，CD平分∠BCO，∴∠DCG=∠DCE，∴∠CGE+∠DCG=90°，∠CEG+∠DCB=90°，∴∠CGE=∠CEG，∴CG=CE，∵∠CGE=∠COT，∠CEG=∠CTD，∴∠COT=∠CTD，∴CO=CT，∴OG=ET，∵GE∥OT，∴CE CT =GEOT=25，∴CE ET =23，∴OG BC =38，故选：D．【点睛】题目主要考查平行线分线段成比例，三角形的面积，三角形中位线定理等，理解题意，学会添加辅助线，构造平行线是解题关键．10．（3分）（2023秋·全国·九年级专题练习）如图，在矩形ABCD中，点E是AD的中点，∠EBC的平分线交CD于点F将△DEF沿EF折叠，点D恰好落在EB上M点处，延长BC、EF交于点N，有下列四个结论：①BF垂直平分EN；②BF平分∠MFC；③△DEF∽△FEB；④S△BEF=3S△DEF．其中，将正确结论的序号全部选对的是（）A．①②③B．①②④C．②③④D．①②③④【答案】D【分析】由折叠的性质、矩形的性质与角平分线的性质，可证得CF＝FM＝DF；易求得∠BFE＝∠BFN，则可得BF⊥EN；证明∠EFM＝∠EBF即可证明△DEF∽△FEB；易求得BM＝2EM＝2DE，即可得EB＝3EM，根据等高三角形的面积比等于对应底的比，即可证明S△BEF=3S△DEF．【详解】解：∵四边形ABCD是矩形，∴∠D＝∠BCD＝90°，DF＝MF，由折叠的性质可得：∠EMF＝∠D＝90°，即FM⊥BE，CF⊥BC，∵BF平分∠EBC，∴CF＝MF，∴DF＝CF，在△DEF与△CFN中，∠D=∠FCN=90°DF=CF∠DFE=∠CFN∴△DFE≌△CFN，∴EF＝FN，∵∠BFM＝90°−∠EBF，∠BFC＝90°−∠CBF，∴∠BFM＝∠BFC，∴BF平分∠MFC；故②正确；∵∠MFE＝∠DFE＝∠CFN，∴∠BFE＝∠BFN，∵∠BFE＋∠BFN＝180°，∴∠BFE＝90°，即BF⊥EN，∴BF垂直平分EN，故①正确；∵∠BFE＝∠D＝∠FME＝90°，∴∠EFM＋∠FEM＝∠FEM＋∠FBE＝90°，∴∠EFM＝∠EBF，∵∠DFE＝∠EFM，∴∠DFE＝∠FBE，∴△DEF∽△FEB；故③正确；∵∠BFM＝∠BFC，BM⊥FM，BC⊥CF，∴BM＝BC＝AD＝2DE＝2EM，∴BE＝3EM，∴S△BEF＝3S△EMF＝3S△DEF；故④正确．综上所述：①②③④都正确，故答案选：D．【点睛】本题考查了折叠的性质、矩形的性质、角平分线的性质以及全等三角形的判定与性质，相似三角形的判断．此题难度适中，证得△DFE≌△CFN是解题的关键．二．填空题（共6小题，满分18分，每小题3分）11．（3分）（2023秋·山东菏泽·九年级校联考期中）如图，矩形ABCD中，BE⊥AC分别交AC，AD于点F、E，AF＝2，AC＝6，则AB的长为．【答案】【分析】根据题意，由矩形的性质综合判断得出∠ACB＝∠ABF，∠BAF＝∠BAC，从而证明△BFA∽△CBA，再利用相似三角形的性质列出方程，进而求解即可【详解】解：∵BE⊥AC，∴∠BAF+∠ABF＝90°，∵矩形ABCD中，∠ABC＝90°，∴∠ACB+∠BAF＝90°，∴∠ACB＝∠ABF，∵∠BAF＝∠BAC，∴△BFA∽△CBA，∴AB AF =ACAB，∴AB2＝AC•AF＝6×2＝12，∴AB=故答案为【点睛】本题主要考查了矩形性质与相似三角形的综合运用，熟练掌握相关概念是解题关键12．（3分）（2023·山西·统考一模）黄金分割具有严格的比例性，蕴藏着丰富的美学价值，这一比值能够引起人们的美感．如图，连接正五边形ABCDE 的各条对角线围成一个新的五边形MNPQR .图中有很多顶角为36°的等腰三角形，我们把这种三角形称为“黄金三角形”若MN 1，则AB ＝ ．1【详解】根据题意可知△DMN 与△AME 都是“黄金三角形”，AB=AE ，DM=EM ，∴MN DM ，EM AE∵，∴DM=2，∴，∴+1，+1.13．（3分）（2023春·浙江宁波·九年级校联考期末）如图，正方形ABCD 的边长为4，点E 在线段AD 上，以DE 为边构造正方形DEFG ，使G 在CD 的延长线上，连接CF ，取CF 中点H ，连接DH ．当E 为AD 中点时，△CDH 的面积为 ，当点E 在AD 边上运动（不含A ，D ）时，DH 的最小值为 ．【答案】 2 【分析】当E 为AD 中点时，过点H 作HN ⊥GC 于点N ，先证HN 是△CFG 的中位线，求出其长度，再根据三角形面积公式计算即可；连接GH ，EH ，AC ，BD ，AC 与BD 交于点O ，延长FE 到点M ，使EM =FE ，连接DM ，CM ，根据正方形的性质先证点D 、O 、M 、B 在一条直线上，再证EH 是△CFM 的中位线，并推出当CM ⊥BD 时，CM 最小，根据正方形的性质得出CO ⊥BD ，故点M 与点O 重合，求出对角线AC 的长，即可得出CO 的长，于是得出EH 的长，再根据正方形的性质证EH =DH ，即可得出DH 的最小值．【详解】解：当E 为AD 中点时，过点H 作HN ⊥GC 于点N ，如图1，∵正方形ABCD 的边长为4，∴AD =CD =4，∴AE =DE =2，∵四边形DEFG 是正方形，∴FG =DE =2，FG ⊥GC ，∴HN∥FG ，∴CH FH =CN NG ，∵点H 是CF 的中点，即CH FH =1，∴CN NG =1，∴点N 是GC 的中点，∴HN 是△CFG 的中位线，∴HN =12FG =12×2=1，∴S △CDH =12CD•HN =12×4×1=2；如图2，连接GH ，EH ，AC ，BD ，AC 与BD 交于点O ，延长FE 到点M ，使EM =FE ，连接DM ，CM ，∵四边形DEFG 是正方形，∴FE =DE ，∠FED =90°，∴DE =EM ，∠DEM =90°，∴△DEM 是等腰直角三角形，∴∠EDM =45°，∵四边形ABCD 是正方形，∴∠ADB =45°，AC ⊥BD ，∴点D 、O 、M 、B 在一条直线上，∵点E 是FM 的中点，点H 是CF 的中点，∴EH 是△CFM 的中位线，∴EH =12CM ，当CM 最小时，EH 最小，即当CM ⊥BD 时，CM 最小，∵CO ⊥BD ，∴M 点与O 点重合时，CM 最小，∵正方形ABCD 的边长为4，∴AD =CD =4，∠ADC =90°，AO =CO ，由勾股定理得AC =∴CO =12AC =12×=∴EH =12CO =12×=∵四边形DEFG 是正方形，∴∠FGC =90°，∵点H 是CF 的中点，∴GH =12CF =FH ，∴点H 在FG 的垂直平分线上，∵四边形DEFG 是正方形，∴点H 也在ED 的垂直平分线上，∴EH =DH ，∴DH =即DH故答案为：2【点睛】本题考查了正方形的性质，平行线分线段成比例，三角形中位线定理，熟练掌握正方形的性质及三角形中位线定理、正确添加辅助线是解题的关键，此题有点难度，需认真思考．14．（3分）（2023·江西南昌·校考二模）如图，在Rt△ABC中，∠ACB=90°，∠A=30°，BC=2，D为AB 的中点，F为线段AC上的动点，将AD沿过点D的射线DF折叠得到DE，若AB下方的DE与△ABC的边垂直，则AF的长度可能是．【答案】2或【分析】由直角三角形的性质和勾股定理可得AB=4，AC=AD=BD=2，分三种情况：当DE⊥AC 时，设垂足为G；当DE⊥AB时，作FH⊥AD交AD于H；当DE⊥BC时，分别进行计算即可得到答案．【详解】解：∵在Rt△ABC中，∠ACB=90°，∠A=30°，BC=2，∴AB=2BC=4，∴AC==∴D是AB的中点，∴AD=BD=2，如图1，当DE⊥AC时，设垂足为G，，由折叠可知，∠A=∠E=30°，∠EDF=∠FDA，EF=FA，∵∠DGA=90°，AD=1，∴DG=12∴AG=∵∠ADE =60°，∴∠EDF =∠FDA =30°=∠E ，∴DF =EF =FA ，GF =12DF ，∴AG =AF +GF =AF +12DF =AF +12AF =∴AF =如图2，当DE ⊥AB 时，，则∠ADE =90°，由折叠可知：∠ADF =∠EDF =45°，∠A =∠E =30°，∴∠AGD =90°−∠A =90°−30°=60°，∵∠AGD =∠E +∠EFG ，∴∠EFG =∠AGD−∠E =60°−30°=30°，∴∠E =∠EFG ，∴GE =GF ，在Rt △ADG 中，AD =2，DG =12AG ，∵DG 2+AD 2=AG 2，∴AG =DG 作FH ⊥AD 交AD 于H ，则HF ∥DG ，∵∠ADF =45°，∴ △DHF 是等腰直角三角形，∴DH =HF ，设DH =HF =x ，则AH =AD−DH =2−x ，∵HF ∥DG ，∴△AHF ∽△ADG ，∴HFDG =AHAD，即2−x2，解得：x=，∴DH=HF，在Rt△AHF中，∠AHF=90°，∠A=30°，∴AF=2HF=；如图3，当DE⊥BC时，，由折叠的性质可得：∠E=∠A=30°，∠EDF=∠ADF，∠AFD=∠EFD，∵AC⊥BC，∴DE∥AC，∴∠E=∠EFC=30°，∠BDE=∠A=30°，∵∠BDE+∠ADE=180°，∠AFE+∠EFC=180°，∴∠EDA=∠EFA，∴∠ADF=∠DFA，∴AD=AF=2，综上所述：AF的长为2或故答案为：2或【点睛】本题主要考查了折叠的性质、相似三角形的判定与性质、直角三角形的性质、勾股定理、等腰三角形的判定与性质等知识，熟练掌握以上知识点，添加适当的辅助线，采用分类讨论的思想解题，是解此题的关键．15．（3分）（2023秋·上海·九年级上海市文来中学校考期中）在△ABC中，若AD交BC于D，BE交AC于E，CF交BA于F，AD，BE，CF相交于一点，BDEA =2，CEFB=3，则AFDC=．【答案】16【分析】如图，先利用三角形的面积关系可得BDDC =S△ABDS△ACD=S△BPDS△CPD，S△ABPS△BPD=APPD=S△APCS△PDC，再结合比例的基本性质证明S △ABP S △APC =S △BPD S △PDC ，可得BD DC =S △ABD S △ACD =S △BPD S △CPD =S △ABP S △APC ，同理可得：CE EA =S △BPC S △APB ,AF FB =S △APC S △BPC ， 可得∴BD DC ⋅CE EA ⋅AF FB =S △ABPS △APC ⋅S △BPCS △APB ⋅S △APCS △BPC =1， 从而可得结论．【详解】解：如图，设AD ，BE ，CF 相交于点P ，∵BD DC =S △ABD S △ACD =S △BPD S △CPD ， S △ABP S △BPD =AP PD =S △APC S △PDC ，∴S △ABPS △APC =S △BPDS △PDC ，∴BD DC =S △ABDS △ACD =S △BPDS △CPD =S △ABPS △APC ，同理可得：CE EA =S △BPC S △APB ,AF FB =S △APC S △BPC ，∴BD DC ⋅CE EA ⋅AF FB =S △ABP S △APC ⋅S △BPC S △APB ⋅S △APC S △BPC =1，∵ BD EA =2，CE FB =3，∴2×3×AF DC =1，∴AF DC =16 ．故答案为：16【点睛】本题考查的是三角形的面积关系，比例的基本性质，掌握比例的基本性质进行比例的变形是解题的关键．16．（3分）（2023秋·湖南永州·九年级统考期末）已知菱形A 1B 1C 1D 1的边长为6，∠A 1B 1C 1=60°，对角线A 1C 1，B 1D 1相交于点O ，以点O 为坐标原点，分别以OA 1，OB 1所在直线为x 轴、y 轴，建立如图所示的直角坐标系．以B 1D 1为对角线作菱形B 1C 2D 1A 2~菱形A 1B 1C 1D 1，再以A 2C 2为对角线作菱形A 2B 2C 2D 2~菱形B 1C 2D 1A 2，再以B 2D 2为对角线作菱形B 2C 3D 2A 3~菱形A 2B 2C 2D 2，…，按此规律继续作下去，在x 轴的正半轴上得到点A 1，A 2，A 3，…，A n ，则点A n 的坐标为 ．【答案】An (3n ，0)【分析】先根据菱形的性质求出A 1的坐标，根据勾股定理求出OB 1的长，再由锐角三角函数的定义求出OA 2的长，故可得出A 2的坐标，同理可得出A 3的坐标，找出规律即可得出结论．【详解】解：∵ 菱形A 1B 1C 1D 1的边长为6，∠A 1B 1C 1=60°，∴OA 1=A 1B 1·sin 30°=6×12=3，OB 1=A 1B 1∴A 1(3，0)，∵ 菱形B 1C 2D 1A 2~菱形A 1B 1C 1D 1，∴OA 2= OB 1tan30°9，∴A 2(9，0)，同理可得A 3(27，0)，∴A n (3n ，0)，故答案为：A n (3n ，0)．【点睛】本题考查的是相似多边形的性质，熟知相似多边形的对应角相等是解答此题的关键．三．解答题（共7小题，满分52分）17．（6分）（2023秋·宁夏银川·九年级银川市第三中学校考期中）求值：(1)已知b a =34，求a−2b a 2b 的值；(2)已知a b =c d =e f =43，若b +d +f =9，求a +c +e 的值．【答案】(1)−15(2)12【分析】（1）先根据已知条件得到b =34a ，然后把b =34a 代入所求式子中进行求解即可；（2=43，再把b +d +f =9代入求解即可．【详解】（1）解：∵b a =34，∴b =34a ，∴a−2b a 2b =a−2×34a a 2×34a =a−32a 32=−15；（2）解：∵a b =c d =e f =43，∴a c e b d f =43，∵b +d +f =9，∴a c e9=43，∴a +c +e =12．【点睛】本题主要考查了比例的性质，熟知比例的性质是解题的关键，一般地，若有a b =c d =e f =k ，则a c eb d f =k (b +d +f ≠0)．18．（6分）（2023·浙江·一模）如图，在5×5的网格中，线段AB 的端点都在格点上（两条网格线的交点叫格点）．请用无刻度的直尺画出符合要求的图形，并保留画图痕迹（不要求写画法）．(1)在图1中画出一个以AB 为边的Rt △ABC ，使顶点C 在格点上．(2)在图2中的线段AB 上找出一点D ，使BD AD =32．【答案】(1)答案见解析(2)答案见解析【分析】（1）取格点C ，连接AC 和BC 即可；（2）取格点E ，F ，连接EF 交AB 于点D ，点D 即为所求．【详解】（1）解：如下图，取格点C ，连接AC 和BC ，由题意可知：∠ACB =90°，∴△ABC 为Rt △ABC ；（2）如下图，取格点E ，F ，连接EF 交AB 于点D ，由题意可知：△BDF ∽△ADE ，∵BF AE =32，∴BD AD =32，∴点D 即为所求．【点睛】本题考查了考查了作图，解题的关键是掌握相似三角形的判定与性质．19．（8分）（2023秋·全国·九年级专题练习）如图所示，在等腰三角形ABC 中，AB =AC ，点E ，F 在线段BC 上，CE =BF ，点Q 在线段AB 上，且AE 2=AQ ⋅AB ．求证：(1)∠CAE =∠BAF ；(2)△ACE ∽△AFQ ．【答案】(1)见解析(2)见解析【分析】（1）利用SAS证明△ACE≌△ABF即可；（2）根据△ACE≌△ABF得出AE=AF，∠CAE=∠BAF，根据AE²=AQ·AB，AC=AB，得出AEAQ =ACAF，利用相似三角形的判定得出结论即可．【详解】（1）证明：∵AB=AC，∴∠B=∠C，在△ACE和△ABF中，AC=AB∠C=∠B CE=BF，∴△ACE≌△ABF(SAS)，∴∠CAE=∠BAF；（2）证明：∵△ACE≌△ABF，∴AE=AF，∠CAE=∠BAF，∵AE²=AQ·AB，AC=AB，∴AE AQ =ABAE，即AEAQ=ACAF，∴△ACE∽△AFQ．【点睛】本题考查了等腰三角形的性质，全等三角形的判定和性质以及相似三角形的判定，熟练掌握相关判定定理和性质定理是解题的关键．20．（8分）（2023秋·河北保定·九年级统考期中）已知在平面直角坐标系中的位置如图所示：(1)在图中画出△ABC沿x轴翻折后的△A1B1C1；(2)以点M(1,2)为位似中心，作出△A1B1C1按2:1放大后的位似图形△A2B2C2；(3)点A2的坐标___________；△ABC与△A2B2C2的周长比是___________，△ABC与△A2B2C2的面积比是___________．【答案】(1)见解析(2)见解析(3)3，6；1:2；1:4【分析】（1）利用关于x轴对称的点的坐标特征得到A1、B1、C1的坐标，然后描点即可；（2）延长MA1到A2使MA2=2MA1，延长MB1到B2使MB2=2MB1，延长MC1到C2使MC2=2MC1，从而得到△A2B2C2；（3）先利用轴对称的性质得到△ABC≌△A1B1C1，再根据位似的性质得到△A1B1C1与△A2B2C2的相似比为1:2，所以△ABC与△A2B2C2的相似比为1:2，然后根据相似三角形的性质解决问题．【详解】（1）解：如图，△A1B1C1为所作；（2）解：如图，△A2B2C2为所作；（3）解：点A2的坐标为3，6，∵△ABC沿x轴翻折后的△A1B1C1，∴△ABC≌△A1B1C1，∵△A1B1C1按2:1放大后的位似图形△A2B2C2，∴△A1B1C1与△A2B2C2的相似比为1:2，∴△ABC与△A2B2C2的相似比为1:2，∴△ABC与△A2B2C2的周长的比为1:2，△ABC与△A2B2C2的面积的比为1:4．故答案为：3，6；1:2；1:4【点睛】本题考查了作图−位似变换：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或−k．也考查了轴对称变换．21．（8分）（2023秋·四川内江·九年级校考期中）如图，在△ABC中，∠ACB＝90°，CD是高，BE平分∠ABC．BE分别与AC，CD相交于点E，F．（1）求证：△AEB∽△CFB；（2）若CE＝5，EF=BD＝6．求AD的长．【答案】（1）见解析；（2）AD=323【分析】（1）根据两角对应相等两三角形相似即可判断；（2）解直角三角形求出FH，CH，利用相似三角形的性质求出DF，AD即可．【详解】（1）证明：∵∠ACB=90°，∴∠ACD+∠BCD=90°，∵CD为AB边上的高，∴∠ADC=90°，∴∠A+∠ACD=90°，∴∠A=∠BCD，∵BE是∠ABC的平分线，∴∠ABE=∠CBE，∴ΔAEB∽ΔCFB．（2）解：如图，作CH⊥EF于H．∵∠BFD+∠ABE=90°，∠CEB+∠CBE=90°，∠ABE=∠CBE，∴∠BFD=∠CEB，∵∠BFD=∠CFE，∴∠CEF=∠CFE，∴△CEF为等腰三角形，∴CE=CF，∵CH⊥EF，∴点H为EF的中点，∴EH=FH∴CH=∵∠BFD=∠CFH,∠CHF=∠BDF=90°，∴ΔBFD∽ΔCFH，∴DFHF =BDCH，∴∴DF=3，CD=CF+DF=8，∵∠ADC=CDB=90°，∵∠ECH=∠FCH,∠FBD=∠CBF，根据ΔBFD∽ΔCFH，即∠FCH=∠FBD，∴∠ACD=∠CBD，∴ΔACD∽ΔCBD，∴ADCD =CDBD，∴AD8=86，∴AD=323．【点睛】本题考查相似三角形的性质，解直角三角形等知识，解题的关键是正确寻找相似三角形解决问题．22．（8分）（2023·安徽滁州·统考二模）【证明体验】（1）如图1，AD为△ABC的角平分线，∠ADC=60°，点E在线段AB上，AE=AC，求证：DE平分∠ADB；【思考探究】（2）如图2，在（1）的条件下，F为AB上一点，连接FC交AD于点G．若FB=FC，求证：DE2=BD⋅DG；【拓展延伸】（3）如图3，在四边形ABCD中，对角线AC平分∠BAD，∠BCA=2∠DCA，点E在AC上，∠EDC=∠ABC，若BC=5，CD=AD=2AE，求AC的长．【答案】（1）见解析；（2）见解析；（3）AC=163【分析】（1）证△AED≌△ACD即可；（2）证△EBD∽△GCD即可；（3）在AB上取一点F，使得AF=AD，连接CF．证△AFC≌△ADC可推出∠DCE=∠BCF，可证△DCE∽△BCF，进一步可证△EAD∽△DAC，即可求解．【详解】（1）证明：∵AD为△ABC的角平分线∴∠EAD=∠CAD∵AE=AC，AD=AD∴△AED≌△ACD∴∠ADE=∠ADC=60°∴∠EDB=180°−∠ADE−∠ADC=60°∴DE平分∠ADB（2）证明：∵FB=FC∴∠EBD=∠GCD∵∠BDE=∠GDC=60°∴△EBD∽△GCD∴BD CD =DEDG，DE⋅CD=BD⋅DG由（1）可知：△AED≌△ACD∴DE=CD∴DE2=BD⋅DG（3）解：如图，在AB上取一点F，使得AF=AD，连接CF∵AC平分∠BAD∴∠FAC=∠DAC∵AF=AD,AC=AC∴△AFC≌△ADC∴CF=CD,∠ACF=∠ACD,∠AFC=∠ADC ∵∠ACF+∠BCF=∠ACB=2∠ACD∴∠DCE=∠BCF∵∠EDC=∠FBC∴△DCE∽△BCF∴CD CB =CECF,∠CED=∠BFC∵BC=5,CF=CD=∴CE=4∵∠AED=180°−∠CED=180°−∠BFC=∠AFC=∠ADC,∠EAD=∠DAC ∴△EAD∽△DAC∴AE AD =ADAC∵AD=2AE∴AE 2AE =2AE4AE解得：AE=43∴AC=CE+AE=163【点睛】本题考查了全等三角形的判定与性质、相似三角形的判定与性质．掌握相关内容进行几何推导是解题关键．23．（8分）（2023春·四川成都·九年级统考期末）如图1，△ABC是等腰直角三角形，∠ACB=90°,AC=BC，先将边BC沿过点B的直线l对折得到BD，连接CD，然后以CD为边在左侧作△CDE，其中∠CDE=90°，CD=DE，BD与CE交于点F，连接BE，AD．(1)求证：△ACD≌△BDE；(2)如图2，当点D在△ABC的斜边AB上时，请直接写出用BC,BE表示AB的关系式；(3)如图3，当点D在△ABC的内部时，若点F为BD的中点，且△ACD的面积为10，求△CDF的面积．【答案】(1)证明见解析(2)AB=BC+BE(3)15【分析】（1）折叠得到BC=BD，进而得到∠BCD=∠BDC，推出∠ACD=∠BDE，利用SAS证明△ACD≌△BDE，即可；（2）全等三角形的性质，得到AD=BE，进而得到AB=BD+AD=BD+BE，再根据BC=BD，即可得出结论；（3）设直线l交CD于点H，交CE于K，取DH的中点G，连接FG，得到FG∥BH，进而得到CKFK =CHGH，推出CK FK =2，再根据l⊥CD,CD⊥DE，得到FG∥DE，进而推出CFEF=3，得到S△CDF:S△DEF=3:1，根据全等三角形的面积相等，三角形的中线平分面积，求出S△DEF=12S△ACD=5，即可得解．【详解】（1）证明：∵边BC沿过点B的直线l对折得到BD，∴BC=BD，∴∠BCD=∠BDC，∵∠ACB=∠CDE=90°，∴∠ACB−∠BCD=∠CDE−∠BDC，∴∠ACD=∠BDE，∵AC=BC，∴BD =AC ，∵CD =DE ，∴△ACD≌△BDE (SAS)；（2）解：由（1）得：△ACD≌△BDE ，∴AD =BE ，∴AB =BD +AD =BD +BE ，∵BC =BD ，∴AB =BC +BE ；（3）解：如图，设直线l 交CD 于点H ，交CE 于K ，取DH 的中点G ，连接FG ，∵点F 是BD 的中点，∴FG ∥BH ，∴CK FK =CH GH ，由折叠得：CH =DH ，∴CH =2GH ，∴CK FK =2，∵l ⊥CD,CD ⊥DE ，∴FG ∥DE ，∴FK EF =GH DG =1，∴CF EF =3，∴S △CDF :S △DEF =3:1，由（1）知：△BDE≌△ACD ，∴S △BDE =S △ACD =10，∵点F是BD的中点，S△ACD=5，∴S△DEF=12∴S△CDF=15．【点睛】本题考查全等三角形的判定和性质，折叠的性质，等腰三角形的判定和性质，三角形的中位线定理，平行线分线段成比例．本题的综合性强，难度较大，熟练掌握折叠的性质，证明三角形全等，是解题的关键．。

第四章图形的相似单元测试北师大版2024—2025学年秋季九年级上册考生注意：本试卷共三道大题，23道小题，满分120分，时量120分钟注意事项:1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。

笞卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2.回答第I卷时，选出每小题答案后，把答案填写在答题卡上对应题目的位置，填空题填写在答题卡相应的位置写在本试卷上无效。

3.回答第II卷时，将答案写在第II卷答题卡上。

4.考试结束后，将本试卷和答题卡一并交回。

第I卷一、选择题（每题只有一个正确选项，每小题3分，满分36分）1.在比例尺是1：8000的地图上，中山路的长度约为25cm，该路段实际长度约为（）A．3200m B．3000m C．2400m D．2000m2.如图，用放大镜将贺兰山旅游图标放大，这两个图形之间属于以下哪种图形变换（）A．相似B．平移C．轴对称D．旋转3．已知＝，则下列式子中正确的是（）A．a：b＝c2：d2B．a：d＝c：bC．a：b＝（a+c）：（b+d）D．a：b＝（a﹣d）：（b﹣d）4．下列说法中，不正确的是（）A．等边三角形都相似B．等腰直角三角形都相似C．矩形都相似D．正八边形都相似5．以下四组线段中，成比例的是（）A．3，4，6，8B．2，3，4，5C．1，2，3，4D．5，6，7，8 6．如果两个相似三角形的相似比是1：2，那么它们的周长比是（）A．2：1B．1：4C．1：D．1：27．如图，每个小正方形边长均为1，则下列图中的三角形（阴影部分）与图中△ABC相似的是（）A．B．C．D．8．如图，在平面直角坐标系中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为，点A，B，E在x轴上．若正方形ABCD的边长为2，则点F坐标为（）A．（8，6）B．（9，6）C．D．（10，6）9．如图，在▱ABCD中，E是AB边的中点，则S△AEG：S平行四边形ABCD的值为（）A．B．C．D．10．如图，在矩形ABCD中，E、F分别在BC、CD上运动（不与端点重合），连接BF、AE，交于点P，且满足．连接CP，若AB＝4，BC＝6，则CP的最小值为（）A．2﹣3B．2﹣2C．5D．3二．填空题（6小题，每题3分，共18分）11．若，则＝．12．如图，已知AC∥EF∥BD，如果AE：EB＝2：3，CD＝6，那么DF的长等于.13．如图，在▱ABCD中，AD＝16，∠ABC的平分线交AD于点F，交CD的延长线于点E，若S△EDF：S四边形FBCD＝9：55，则AB＝．14．若，则k＝．15．如图，△ABC∽△CBD，AB＝9，BD＝25，则BC＝．16．如图，矩形ABCD中，AB＝3，BC＝10，点P是AD上的一个动点，若以A，P，B为顶点的三角形与△PDC相似，则AP＝．第II卷第四章图形的相似单元测试北师大版2024—2025学年秋季九年级上册姓名：____________ 学号：____________准考证号：___________一、选择题12345678910题号答案二、填空题11、_______ 12、______13、_______ 14、______15、_______ 16、______三、解答题解答题（17、18、19题每题6分，20、21每题8分，22、23每题9分，24、25每题10分，共计72分，解答题要有必要的文字说明）17．已知，求的值．18．如图，AB∥CD∥EF，BF＝20．（1）若AC＝3，CE＝5，求DF的长；（2）若AC：CE＝2：3，求DF的长．19.在△ABC中，∠BAC＝90°，AB＝AC，点D是BC边上一点，过点D作∠ADE＝45°，DE交AC于点E，求证：△ABD∽△DCE．20.如图，在△ABC中，AD是角平分线，点E在边AC上，且AD2＝AE•AB，连接DE．（1）求证：△ABD∽△ADE；（2）若CD＝3，CE＝2，求AE的长．21.如图，△ABC中，D、E两点分别在BC、AD上，且AD为∠BAC的角平分线，若∠ABE＝∠C，＝．（1）求证：△AEB∽△ADC．（2）求△BDE与△ABC的面积比．22.如图，在正方形ABCD中，点E在边AD上，过点D作DK⊥BE于K，且DK＝．（1）若AE＝ED，求正方形ABCD的周长；（2）若∠EDK＝22.5°，求正方形ABCD的面积．23.如图，AB＝4，CD＝6，F在BD上，BC、AD相交于点E，且AB∥CD∥EF．（1）若AE＝3，求ED的长．（2）求EF的长．24.如图，四边形ABCD中，AC平分∠DAB，∠ADC＝∠ACB＝90°，E为AB的中点．（1）求证：AC2＝AB•AD；（2）求证：CE∥AD；（3）若AD＝8，AB＝12．求的值．25．问题1：如图①，在△ABC中，AB＝4，D是AB上一点（不与A，B重合），DE∥BC，交AC于点E，连接CD．设△ABC的面积为S，△DEC的面积为S′．（1）当AD＝3时，＝；（2）设AD＝m，请你用含字母m的代数式表示．问题2：如图②，在四边形ABCD中，AB＝4，AD∥BC，AD＝BC，E是AB上一点（不与A，B重合），EF∥BC，交CD于点F，连接CE．设AE＝n，四边形ABCD的面积为S，△EFC的面积为S′．请你利用问题1的解法或结论，用含字母n的代数式表示．。

图形的相似及相似图形的性质--巩固练习 【巩固练习】 一．选择题 1. 在比例尺为1︰1 000 000的地图上，相距3cm 的两地，它们的实际距离为（ ）A.3kmB.30kmC.300kmD.3 000km2. 下列四条线段中，不能成比例的是 （ ）A. a ＝2，b ＝4，c ＝3，d ＝6B. a ＝，b ＝，c ＝1，d ＝C. a ＝6，b ＝4，c ＝10，d ＝5D. a ＝，b ＝2，c ＝，d ＝23. 下列命题正确的是( )A ．所有的等腰三角形都相似B ．所有的菱形都相似C ．所有的矩形都相似D ．所有的等腰直角三角形都相似4. 某学习小组在讨论“变化的鱼”时，知道大鱼与小鱼是相似图形，如图所示，则小鱼上的点(a ，b)对应大鱼上的点( )A ．(-2a ，-2b)B ．(-a ，-2b)C ．(-2b ，-2a)D ．(-2a ，-b)5. 若a ：b=2：3，则下列各式中正确的式子是（ ）A ．2a=3bB ．3a=2bC ．32=a bD ．31=-b b a 6. 对一个图形进行放缩时，下列说法中正确的是（ ）A ． 图形中线段的长度与角的大小都保持不变B ． 图形中线段的长度与角的大小都会改变C ． 图形中线段的长度保持不变、角的大小可以改变D ． 图形中线段的长度可以改变、角的大小保持不变二. 填空题7. 在比例尺为1：40000的地图上，某条道路的长为7cm ，则该道路的实际长度是 km ． 8. 若，则________9．已知若-3=,=____;4x y x y y则若5-4=0,x y 则x :y =___. 10. 有一块三角形的草地，它的一条边长为25m ．在图纸上，这条边的长为5cm ，其他两条边的长都为4cm ，则其他两边的实际长度都是 m ．11. 用一个放大镜看一个四边形ABCD ，若四边形的边长被放大为原来的10倍，下列结论①放大后的∠B 是原来∠B 的10倍；②两个四边形的对应边相等；③两个四边形的对应角相等，则正确的有 .12. 如图：梯形ADFE 相似于梯形EFCB,若AD=3，BC=4，则______.AE BE = 三 综合题13. 如果a b c d k b c d a c d a b d a b c====++++++++，一次函数y kx m =+经过点（-1,2）， 求此一次函数解析式.14. 一个矩形ABCD 的较短边长为2．（1）如图①，若沿长边对折后得到的矩形与原矩形相似，求它的另一边长；（2）如图②，已知矩形ABCD 的另一边长为4，剪去一个矩形ABEF 后，余下的矩形EFDC 与原矩形相似，求余下矩形EFDC 的面积．【答案与解析】一、选择题1．【答案】B ．【解析】图上距离︰实际距离＝比例尺．2．【答案】C ．【解析】求出最大与最小的两数的积，以及余下两数的积，看所得积是否相等来鉴别它们是否成比例．3．【答案】 D4．【答案】 A【解析】 由图可知，小鱼和大鱼的相似比为1：2，若将小鱼放大1倍，则小鱼和大鱼关于原点对称.5.【答案】B6．【答案】D【解析】根据相似多边形的性质：相似多边形的对应边成比例，对应角相等，∴对一个图形进行收缩时，图形中线段的长度改变，角的大小不变，故选D ．二、填空题7.【答案】2.88.【答案】【解析】由可得，故填. 9.【答案】74;.4510.【答案】20.11.【答案】 ③12.【答案】 32.【解析】因为梯形ADFE 相似于梯形EFCB ，所以AD EF EF BC=,即EF=所以AE AD BE EF === 三、 解答题 13.【解析】∵a b c d k b c d a c d a b d a b c====++++++++ 则分两种情况：（1）+++=0a b c d ，即+1=0k ,=-1k(2)++=++=++=++b c d a c d a b d a b c ,即===,a b c d 1=3k 则 所以当=-1k ，过点（-1,2）时，=-+1y x 当1=3k ，过点（-1,2）时，17=+33y x .。

初中数学试卷 第四章图形的相似一、单选题1．如图，l 1，l 2，l 3，l 4是一组平行线，l 5，l 6与这组平行线依次相交于点A ，B ，C ，D和E ，F ，G ，H ．若AB ∶BC ∶CD=2∶3∶4，EG=10，则EH 的长为（ ）A ．14B ．16C ．18D ．202．如图是著名画家达·芬奇的名画《蒙娜丽莎》.画中的脸部被包在矩形ABCD 内，点E 是AB 的黄金分割点，BE ＞AE ，若AB ＝2a ，则BE 长为（ ）A ．（ +1）aB ．（﹣1）a C ．（3﹣）a D ．（﹣2）a3．如图，已知AB ∥CD ，AC 与BD 交于点O ，则下列比例中成立的是( )A ．O C O A O DO B=B ．OC O B OD O D =C ．O C O D A CO B=D ．B D OC A CO D=4．如图，小明为了测量一凉亭的高度AB （顶端A 到水平地面BD 的距离），在凉亭的旁边放置一个与凉亭台阶BC 等高的台阶DE （ 0.5m D E B C == ，A ，C ，B 三点共线），把一面镜子水平放置在平台上的点G 处，测得 15m C G = ，然后沿直线 C G 后退到点E 处，这时在镜子里恰好看到凉亭的顶端A ，测得 3m E G = ．若小明身高1.6m ，则凉亭的高度AB 约为（ ）A ．8.5mB ．9mC ．9.5mD ．10m5．如图，ABC 与DEF 位似，点O 是位似中心，若OE=3OB ，A B CS =4，则D E FS=（ ）A ．9B ．12C ．16D ．366．如图，A B C 与D E F 位似，位似中心为点O ，A B C 与D E F 的周长之比为49∶，则A O O D ∶的比为（ ）A ．2：3B ．2：5C ．4：9D ．4：137．如图，在ΔABC 中,D 、E 分别是AB 、AC 边上的中点，连接DE ，那么ΔADE 与ΔABC 的面积之比是（ ）A ．1:16B ．1:9C ．1:4D ．1:28．已知：如图，在△ABC 中，B E A C ⊥于点G ，C D A B ⊥于点F ，B A B E =，C A CD =，以下结论：①DE ∠=∠，②DFG E =，③A F A C A GA B=，④D FE G C FB G=，其中正确的是（ ）A．①②③B．①②④C．①③④D．②③④9．如图，△OAB与△OCD是以点0为位似中心的位似图形，相似比为1：2，∠OCD=90 ︒，CO=CD．若B(2，0)，则点C的坐标为()A．(2，2)B．(1，2)C．（，2 ）D．(2，1)10．如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，OC在y轴上，如果矩形OA'B'C'与矩形OABC关于点O位似，且矩形OA'B'C'的面积等于矩形OABC面积的14，那么点B'的坐标是（）A．（3，2）B．（－2，－3）C．（2，3）或（－2，－3）D．（3，2）或（－3，－2）二、填空题11．已知△ABC∽△A'B'C'，AD和A'D'是它们的对应角平分线，若AD：A'D'=4：3，△ABC的周长为16，则△A'B'C'的周长是．12．如图，////A C E FB D，若:2:3A E E B=，10C D=，则C F=.13．如图，将矩形O A B C置于平面直角坐标系中，4=，点D在B C边O A=，O C m上，且1D C=，将矩形O A B C沿A D折叠，使点B对应点E落在坐标平面内（1）当3m=时，O E的长度为．（2）若点E恰好落在x轴上，则m的值为．14．如图，已知AB⊥BD，ED⊥BD，C是线段BD的中点，且AC⊥CE，ED=1，BD=4，那么AB=.15．已知线段AB＝4，点P是线段AB的黄金分割点，则AP的长为．三、解答题16．如图所示，点D、E分别在AB、AC上，连接DE，△ADE∽△ABC，已知△ADE和△ABC的相似比是1：2，且△ADE的面积是1，求四边形DBCE的面积.17．如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条直角边DE＝40cm，EF＝20cm，测得边DF离地面的高度AC＝1.5m，CD＝10m，求树高AB．18．如图（图形不全），等边三角形A B C中，3A B=，点D在直线B C上，点E在直线A C上，且B A DC B E∠=∠，当1B D=时，求A E的长．几位同学通过探究得出结论：此题有多种结果．有同学已经得出两个符合题意结论：①当点D在边B C上、点E在边A C上时，2A E=；②当点D在边B C上、点E在A C的延长线上时，92A E=．要求：请针对其它情况，继续求出A E的长，并写出总的正确结论．19．如图，在矩形ABCD中，AB=18，AD=12，点M是边AB的中点，连结DM，DM与AC交于点G。

图形的相似知识点1 比例的性质一、单项选择题1. 53 x2 =，那么的值是A .B .C .D .2. 3x=4y(xy≠0)，那么以下比例式成立的是()3. 不为0的四个实数a、b ，c、d满足，改写成比例式错误的选项是〔〕A .B .C .D .4. 如果，那么的值是〔〕.A .B .C .D .5. 假设y3x2=，那么以下各式不成立的是〔〕6. 假设=，那么2x yx y-+的值为〔〕A .B .C . 1D .7. 2x=3y〔xy≠0〕，那么以下各式中错误的选项是〔〕8. =，a-ba+b那么的值是〔〕A . -B . -C . -D . -9. 假设a35b=，那么a+bb的值为〔〕A .B .C .D .10. x ：y=3：2，那么以下各式中不正确的选项是〔 〕二、解答题11. a ：b ：c=2：3：4，且2a+3b ﹣2c=10，求a ﹣2b+3c 的值． 12.== ， 且x+y ﹣z=6，求x 、y 、z 的值．13.=≠0，求代数式5a-2ba 2b+的值．14.= ， 且x ﹣y=2，求22x yy -+ 的值．15. a+b+c=60，且a 345b c==， 求a 、b 、c 的值． 16.32a b =， 求以下算式的值．17.023a b =≠，求代数式522a ba b-+的值． 18.234x y z ==， 〔1〕求2x y z-的值；〔2〕如果y z =-， 求x 的值．19. a+b+c=60，且345a b c==， 求a 、b 、c 的值． 20. ： = =，x ﹣y+z=6，求：代数式3x ﹣2y+z 的值．三、填空题 21. 假设12x y =， 那么x yy += .22. a:b=3:2，那么(a-b):a= ． 23. 如果x ：y=4：3，那么x yy-= ． 24. 34a b =，那么 2aa b+的值为 ． 25. 如果x ：y=1：2，那么+x yy= 26.24x y= ，那么32x y x y -=- ． 27. 如果=，那么a bb- 1 〔填“=〞“＞〞“＜〞〕 28. 假设 = =，那么4a bc+= 。