倍长中线法12.10

中考数学几何添加辅助线：倍长中线中线或中点是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线。

所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法。

此法常用于构造全等三角形，利用中线的性质、辅助线、对顶角进而用“SAS”证明对应边之间的关系。

常规的倍长中线可以出全等，但需要证明“三点共线”，遇到“中点+平行”，我们“延长出全等”，而非“倍长出全等”. 用“倍长中线法”作辅助线解几何题，是一种重要的技巧套路。

它可以有效地生发出全等、平行等基本条件，关联好多基本图形，帮助解题，大家务必好好掌握。

也给我们解题的启示：抓住核心，找到关键，才能快速解题。

逢中点，便倍长，全等观，平行现.倍长中线法:是指加倍延长中线，使所延长部分与中线相等，然后连接相应的顶点，构造“8字形”的全等三角形。

在与中点有关的线段尤其是涉及线段的等量关系时，倍长中线应用较常见，常见添加如图（AD是底边中线）典例1．已知：AD是ΔABC的中线，AE=EF．求证：AC=BF．名师指点：延长AD到M，使AD＝DM，连接BM，根据SAS证△ADC≌△MDB，推出BM＝AC，∠CAD＝∠M，根据AE＝EF，推出∠CAD＝∠AFE＝∠BFD，求出∠BFD＝∠M，再根据等腰三角形的性质证明即可．满分解答：证明：延长AD 到M ，使AD ＝DM ，连接BM ，∵AD 是△ABC 中线，∴CD ＝BD ，∵在△ADC 和△MDB 中，{CD ＝BD∠ADC ＝∠MDB AD ＝DM，∴△ADC ≌△MDB （SAS ），∴BM ＝AC ，∠CAD ＝∠M ，∵AE ＝EF ，∴∠CAD ＝∠AFE ，∵∠AFE ＝∠BFD ，∴∠BFD ＝∠CAD ＝∠M ，∴BF ＝BM ＝AC ，即AC ＝BF ．名师点评：倍长中线是常见的辅助线、全等中相关的角、线段的代换是解决问题的关键． 1．如图，在平行四边形ABCD 中，28CD AD ==，E 为AD 上一点，F 为DC 的中点，则下列结论中正确的是（ ）A ．4BF =B ．2ABC ABF ∠>∠。

倍长中线法
倍长中线的意思是：延长底边的中线，使所延长部分与中线相等，然后往往需要连接相应的顶点，则对应角对应边都对应相等。

此法常用于构造全等三角形，进而证明边之间的关系。

倍长中线法
中文名倍长中线
思想方法构造全等三角形领域平面几何外文名nethod of times the length of line 目的证明边之间的关系
1定义
所谓“倍长中线”，就是加倍延长中线，使所延长部分与中线相等，
然后往往需要连接相应的顶点，则对应角对应边都对应相等。

常用于构造全等三角形。

中线倍长法多用于构造全等三角形和证明边之间的关系（一般都是原题已经有中线时用，不太会有自己画中线的时候）。

说简单一点，倍长中线就是指：延长中线，使所延长部分与中线相等，然后往往需要连接相应的顶点，构造全等三角形。

倍长中线与截长补短模块一倍长中线中线是三角形中的重要线段之一，当题目的条件中有中线时，我们常采用“倍长中线法”添加辅助线，构造一组旋转型的全等，利用全等的结论来解决问题．倍长中线法，就是将三角形的中线延长一倍，以便构造出“8字型”全等．但是给出的条件并不一定要仅限于三角形的中线才可以，有些时候，只要已知条件中有中点就可以运用“倍长中线法”来解决问题．倍长中线（1）如图，AD为△ABC的中线，延长AD至E，使DE=AD，连接CE，求证：AB=CE，且AB//CE.G FEDCBA（2D 是BC 边中点，，求的取值范围.ABCD（3）如图，在ABC ∆中，AD 是BC 边上的中线，E 是AD 上一点，延长BE 交AC 于F ，AF =EF ，求证：AC =BE ．【答案】延长AD 到G ，使DG =AD ，连结BG ∵BD =CD ，BDG CDA ∠=∠，AD =GD ∴ADC GDB ≅∴AC =GB ．G EAF ∠=∠又∵AF =EF ，∴EAF AEF ∠=∠ ∴G BED ∠=∠∴BE =BG ，∴BE =AC ．倍长类中线如图，在ABC ∆中，AD 交BC 于点D ，点E 是BC 中点，EF AD ∥交CA 的延长线于点F ，交AB 于点G ，若BG CF =，求证：AD 为ABC ∆的角平分线．BCFEDC BAHAF GBE DC【答案】延长FE 到点H ，使HE FE =，连结BH ． 在CEF ∆和BEH ∆中 CE BE CEF BEH FE HE =⎧⎪∠=∠⎨⎪=⎩∴CEF BEH ∆∆≌∴EFC EHB ∠=∠，CF BH BG == ∴EHB BGE ∠=∠，而BGE AGF ∠=∠ ∴AFG AGF ∠=∠ 又∵EF AD ∥∴AFG CAD ∠=∠，AGF BAD ∠=∠ ∴CAD BAD ∠=∠∴AD 为ABC ∆的角平分线．提示：也可延长GE 至H ，使EH GE =，连接CH倍长三角形中线进阶已知，ABC ∆中，AB =AC ，CE 是AB 边上的中线，延长AB 到D ，使BD =AB ． 求证：（1）CD =2CE ；（2）D ACE ∠=∠．【答案】(1) 延长CE 到F ，使EF =CE ，连结BF ． ∵CE 是AB 的中线，∴AE =EB ，∴EBF EAC ≅ ∴BF =AC =BD ，EBF EAC ∠=∠，∴FBC FBE EBC A ACB DBC ∠=∠+∠=∠+∠=∠，∴FBC DBC ≅ ∴CD =CF =2CE ．∠FCB =∠BCD ．（2）解法一：又∵AB =AC ∴∠ACB =∠ABC ，∴∠ACB =∠FCB +∠ACE ，F GE DCBAE D CBA FCA EB DFE NABD C∠ABC =∠BCD +∠D ，∴∠D =∠ACE ． 解法二：由①中的两个全等，可以得到： F ACE F D ∠=∠∠=∠，，∴D ACE ∠=∠．倍长中线与角平分线综合已知AD 为ABC ∆的中线，ADB ∠，ADC ∠的平分线分别交AB 于E 、交AC 于F ． 求证：BE CF EF +>．【答案】延长FD 到N ，使DN DF =，连接BN 、EN ． 易证BND ∆≌CFD ∆，∴BN CF =，又∵ADB ∠，ADC ∠的平分线分别交AB 于E 、交AC 于F ，∴90EDF EDN ∠=∠=，利用SAS 证明EDN ∆≌EDF ∆，∴EN EF =， 在EBN ∆中，BE BN EN +>，∴BE CF EF +>．模块二 截长和补短截长补短（1）如图，在ABC △中，2B C ∠=∠，BAC ∠的平分线AD 交BC 与D ． 求证：AB +BD =AC ．【答案】方法一：在AC 上取一点E ，使得AB =AEFE AB D CDC B AABCDEED C B A FM AB CDE ED CB A连结DE ．在ABD △和AED △中 AB =AE ，BAD EAD ∠=∠AD =AD∴ABD AED ≅∴BD =ED ，B AED ∠=∠又∵2AED EDC C B C ∠=∠+∠=∠=∠EDC C ∠=∠，ED =EC ∴AB +BD =AC ．方法二：在AB 的延长线上取一点E 使得AC =AE ，连结DE ．在AED △和ACD △中，AE =AC EAD CAD ∠=∠，AD =AD∴AED ACD ≅，∴C E ∠=∠又∵22ABC E BDE C BDE ∠=∠+∠=∠=∠ ∴E BDE ∠=∠∴BE =BD ，∴AB +BD =AC ．方法三：延长DB 到点E 使得AB =BE ，连结AE 则有EAB E ∠=∠ 2ABC E EAB E ∠=∠+∠=∠又∵2ABC C ∠=∠，∴AE =AC 又∵EAD EAB BAD E DAC C DAC ADE ∠=∠+∠=∠+∠=∠+∠=∠∴AE =DE ，∴AB +BD =EB +BD =ED =AE =AC方法四：如图，作BF 平分ABC ∠交AD 、AC 于E 、F 点 延长BF 到M ，使FM =FA ，连结AM ∴ABF FBC ∠=∠∵2ABC C ∠=∠，∴FBC C ∠=∠．∴FB =FC ∵AF =FM ，∴M FAM ∠=∠ ∵AFE FBC C ∠=∠+∠，又AFE M FAM ∠=∠+∠ 即22AFE M C ∠=∠=∠．∴C M ∠=∠ ∴M ABM DBF C ∠=∠=∠=∠．∴AB =AM ∵ADB C DAC ∠=∠+∠ 且DEB EBA BAE ∠=∠+∠∵BAD DAC ∠=∠，∴ADB DEB ∠=∠．∴BD =BE 同理MA =ME∵AF =FM ，FB =FC ，∴AC =BM ．∴AC =AB +BD（2）如图所示，在ABC △中，AD BC ⊥于点D ，2B C ∠=∠．求证：AB BD CD +=．E DCBAABDECMFEDCB A【答案】由AD BC ⊥，2B C ∠=∠知：如果在CD 上截取DE DB =，连接AE ，就可以构造出两个等腰三角形ABE △和AEC △． 如图，在CD 上截取DE DB =，连接AE ． 因为AD BC ⊥，DE DB =，所以AE AB =，于是B AEB ∠=∠，又因为AEB C CAE ∠=∠+∠，2B C ∠=∠， 所以CAE C ∠=∠， 于是AE EC =，故AB BD AE ED EC ED CD +=+=+=．（3）如图，AC 平分BAD ∠，CE AB ⊥，且AE AD BE =+， 求证：180B D ∠+∠=︒．【答案】在AE 上截取一点F ，使得AD =AF ， 证ACD ≌ACF 即可． （4）已知：如图，四边形ABCD 是正方形，FAD FAE ∠=∠．求证：BE +DF =AE ．【答案】延长CB 至M ，使得BM =DF ，连接AM ． ∵AB =AD ，AD CD ⊥，AB BM ⊥，BM =DF ，∴，∴AFD AMB ∠=∠，DAF BAM ∠=∠， ∵AB CD ，∴ADF BAF EAF BAE BAE BAM EAM ∠=∠=∠+∠=∠+∠=∠， ∴AMB EAM ∠=∠，∴AE =EM =BE +BM =BE +DF ．C D BAFEDCBAABM ADF △≌△FEDCA截长补短进阶如图所示，在ABC △中，100A ∠=，40ABC ∠=，BD 是ABC ∠的平分线，延长BD 至E ，使DE =AD ．求证：BC =AB +CE【答案】在BC 上取一点F ，使得BF =BA 易证得ADB FDB ≅ ∴DF =AD ， 又∵DA =DE ∴DF =DE∵100A ∠=，AB =AC ∴40ABC ∠= ∵BD 平分ABC ∠， ∴20ABD ∠= ∴60ABD FDB ∠=∠=∵60CDE ADB ∠=∠= ∴ 60FDC EDC ∠=∠= ∴DCF DCE ≅ ∴FC =EC∴BC =BF +FC =AB +CE截长补短应用进阶如图，ABC △中，AB =AC ，108A ∠=，BD 平分ABC ∠交AC 于D 点．求证：BC =AC +CD ．【答案】方法一：在BC 上截取E 点使BE =BA ，连结DE ． ∵BD 平分ABC ∠，∴ABD EBD ∠=∠．EDCBAAB CDE DCB ADCBAF在ABD △与EBD △中∵AB =EB ，ABD EBD ∠=∠， BD =BD ∴ABD EBD ≅，∴A DEB ∠=∠∵108A ∠=， ∴108DEB ∠=∴72DEC ∠=． 又∵361854ADB ∠=+= ∴72CDE ∠=∴CDE DEC ∠=∠ ∴CD =CE∵BC =BE +EC ，∴BC =AC +CD方法二：如图，延长CA 到F ，使CF =CB ，连结BF ． ∵AB =AC ，且108BAC ∠=， ∴36ABC C ∠=∠=． ∵CB =CF ，∴F FBC ∠=∠．∴FAB C ABC ∠=∠+∠． ∴72FAB ∠=．∵12ADB C ABC ∠=∠+∠，∴54ADB ∠=．又∵54FDB ∠= ∴BF =AB =AC =FD ．∴AF =CD ．∴BC =AC +CD ．类型之一 轴对称及轴对称图形1．[2017·盐城]下列图形中，不是轴对称图形的是( C )A B C D【解析】选项A，B，D均可以沿一条直线折叠使图形左右两边的部分重合，故均为轴对称图形，只有C选项不是轴对称图形，故选C.2．[2018·武汉]点A(2，－5)关于x轴对称的点的坐标是( A )A．(2，5) B．(－2，5)C．(－2，－5) D．(－5，2)类型之二线段的垂直平分线3．如图13－1，把一张长方形纸片ABCD沿EF折叠后，点A落在CD边上的点A′处，点B落在点B′处，若∠2＝40°，则图中∠1的度数为( A )图13－1A．115°B．120°C．130°D．140°【解析】由题意知∠B′FC＝90°－∠2＝50°，由折叠知∠1＝12(180°＋50°)＝115°.4．[2018·黄冈]如图13－2，在△ABC中，DE是AC的垂直平分线，且分别交BC，AC于点D和E，∠B＝60°，∠C＝25°，则∠BAD为( B )图13－2A．50°B．70°C．75°D．80°【解析】∵DE是AC的垂直平分线，∴DA＝DC，∴∠DAC＝∠C＝25°，∵∠B＝60°，∴∠BAC＝95°，∴∠BAD＝∠BAC－∠DAC＝70°.5．[2018·南充]如图13－3，在△ABC中，AF平分∠BAC，AC的垂直平分线交BC于点E，∠B＝70°，∠FAE＝19°，则∠C＝__24__°.图13－3【解析】∵DE是AC的垂直平分线，∴EA＝EC，∴∠EAC＝∠C，∴∠FAC＝∠EAC＋19°，∵AF平分∠BAC，∴∠FAB＝∠EAC＋19°，∵∠B＋∠BAC＋∠C＝180°，∴70°＋2(∠C＋19°)＋∠C＝180°，解得∠C＝24°.6．[2018春·丹东期末改编]如图13－4，在△ABC中，边AB的垂直平分线交AB，BC于点M，E，边AC的垂直平分线交AC，BC于点N，F，△AEF的周长为10.图13－4(1)BC＝__10__；(2)若∠B＋∠C＝45°，则△AEF是什么特殊三角形？解：(1)∵ME是边AB的垂直平分线，∴AE＝BE，∵NF是边AC的垂直平分线，∴AF＝FC，∵△AEF的周长为10，∴AE＋EF＋AF＝BE＋EF＋FC＝BC＝10，则BC＝10；(2)由(1)知∠B＝∠BAE，∠C＝∠FAC，∵∠B＋∠C＝45°，∴∠B＋∠C＋∠BAE＋∠FAC＝90°，∴∠FAE＝90°，∴△AEF是直角三角形．7．[2017·连云港]如图13－5，等腰三角形ABC中，AB＝AC，点D，E分别在边AB，AC上，且AD＝AE，连接BE，CD，交于点F.图13－5(1)判断∠ABE与∠ACD的数量关系，并说明理由；(2)求证：过点A，F的直线垂直平分线段BC.解：(1)∠ABE＝∠ACD.理由：∵AB＝AC，∠BAE＝∠CAD，AE＝AD，∴△ABE≌△∠ACD.∴∠ABE＝∠ACD；(2)证明：∵AB＝AC，∴∠ABC＝∠ACB.由(1)可知，∠ABE＝∠ACD，∴∠FBC＝∠FCB，∴FB＝FC.又∵AB＝AC，∴点A，F均在线段BC的垂直平分线上，即直线AF垂直平分线段BC.类型之三等腰三角形的性质与判定8．[2018·邵阳]如图13－6，在等腰三角形ABC中，AB＝AC，∠A＝36°，将△ABC中的∠A沿DE向下翻折，使点A落在点C处．若AE＝3，则BC的长是__3__．图13－6【解析】∵AB＝AC，∠A＝36°，∴∠B＝∠BCD＝72°.∵将△ABC 中的∠A 沿DE 向下翻折，使点A 落在点C 处， ∴根据折叠的性质，得△AED ≌△CED ， ∴AE ＝CE ，∠A ＝∠ECD ＝36°， ∴∠BCE ＝∠BCD －∠ECD ＝36°， ∴∠BEC ＝180°－∠B －∠BCE ＝72°， ∴∠BEC ＝∠B ，∴BC ＝CE . ∵AE ＝3，∴BC ＝CE ＝AE ＝ 3.9．[2018·镇江]如图13－7，△ABC 中，AB ＝AC ，点E ，F 在边BC 上，BE ＝CF ，点D 在AF 的延长线上，AD ＝AC .图13－7(1)求证：△ABE ≌△ACF ；(2)若∠BAE ＝30°，则∠ADC 的度数是多少？ 解： (1)证明：∵AB ＝AC ， ∴∠B ＝∠ACF .在△ABE 和△ACF 中，⎩⎪⎨⎪⎧AB ＝AC ，∠B ＝∠ACB ，BE ＝CF ，∴△ABE ≌△ACF ；(2)∵△ABE ≌△ACF ，∠BAE ＝30°， ∴∠CAF ＝∠BAE ＝30°，∵AD ＝AC ，∴∠ADC ＝∠ACD ， ∴∠ADC ＝180°－30°2＝75°.10．如图13－8，在△ABC 中，∠ACB ＝90°，CD ⊥AB 于点D ，AE 平分∠BAC 交CD 于点F ，交BC 于点E ，试说明△CEF 是等腰三角形．图13－8解： 由已知得∠DAF ＋∠AFD ＝90°， ∠FAC ＋∠CEF ＝90°，又∵∠AFD ＝∠CFE ，∠FAC ＝∠DAF ， ∴∠CFE ＝∠CEF ，即△CEF 是等腰三角形．11．如图13－9，△ACB 和△DCE 均为等腰三角形，点A ，D ，E 在同一直线上，连接BE .图13－9(1)若∠CAB ＝∠CBA ＝∠CDE ＝∠CED ＝50°，求证：AD ＝BE ； (2)在(1)的条件下，求∠AEB 的度数．解： (1)∵∠CAB ＝∠CBA ＝∠CDE ＝∠CED ＝50°， ∴∠ACB ＝∠DCE ＝180°－2×50°＝80°.∵∠ACB ＝∠ACD ＋∠DCB ， ∠DCE ＝∠DCB ＋∠BCE ， ∴∠ACD ＝∠BCE .∵△ACB 和△DCE 均为等腰三角形， ∴AC ＝BC ，DC ＝E C.在△ACD 和△BCE 中，⎩⎪⎨⎪⎧AC ＝BC ，∠ACD ＝∠BCE ，DC ＝EC ，∴△ACD ≌△BCE (SAS)，∴AD ＝BE ； (2)∵△ACD ≌△BCE ，∴∠ADC ＝∠BEC . ∵点A ，D ，E 在同一直线上，且∠CDE ＝50°， ∴∠ADC ＝180°－∠CDE ＝130°，∴∠BEC ＝130°. ∵∠BEC ＝∠CED ＋∠AEB ，且∠CED ＝50°， ∴∠AEB ＝∠BEC －∠CED ＝130°－50°＝80°.类型之四 等边三角形的判定与性质12．[2018·福建A 卷]如图13－10，等边三角形ABC 中，AD ⊥BC ，垂足为D ，点E 在线段AD 上，∠EBC ＝45°，则∠ACE 等于( A )图13－10A．15°B．30°C．45°D．60°【解析】∵△ABC是等边三角形，∴∠ABC＝∠ACB＝60°，∵AD⊥BC，∴BD＝CD，AD是BC的垂直平分线，∴BE＝CE，∴∠EBC＝∠ECB＝45°，∴∠ACE＝60°－45°＝15°.类型之五含30°角的直角三角形的性质的运用13．如图13－11，在△ABC中，∠C＝90°，∠B＝30°，AD平分∠CAB，交BC于点D，若CD＝1，则BD＝__2__．图13－11【解析】∵∠C＝90°，∠B＝30°，∴∠CAB＝60°，∵AD平分∠CAB，∴∠CAD＝30°，∴BD＝AD＝2CD＝2.14．如图13－12，在△ABC中，BA＝BC，∠B＝120°，线段AB的垂直平分线MN交AC于点D，且AD＝8 cm.求：图13－12 第14题答图(1)∠ADG 的度数； (2)线段DC 的长度．解： (1)∵在△ABC 中，BA ＝BC ， ∴∠A ＝∠C ，又∵∠B ＝120°， ∴∠A ＝12×(180°－120°)＝30°，∵MN ⊥AB ，∴∠AGD ＝90°， ∴∠ADG ＝90°－30°＝60°； (2)如答图，连接BD . ∵MN 是AB 的垂直平分线，∴AD ＝BD ，∠A ＝∠ABD ＝30°，∴∠CBD ＝90°， 由(1)知∠A ＝∠C ＝30°，∴BD ＝12CD ，∴DC ＝2BD ＝2AD ，又∵AD ＝8 cm ，∴DC ＝16 cm.类型之六 等腰三角形探究型问题15．[2017·莱芜]已知△ABC 与△DEC 是两个大小不同的等腰直角三角形． (1)如图13－13①，连接AE ，DB .试判断线段AE 和DB 的数量和位置关系，并说明理由；(2)如图②，连接DB ，将线段DB 绕D 点顺时针旋转90°到DF ，连接AF ，试判断线段DE 和AF 的数量和位置关系，并说明理由．图13－13解：(1)AE＝DB，AE⊥DB.理由：∵CA＝CB，CE＝CD，∠ACE＝∠BCD＝90°，∴Rt△ACE≌Rt△BCD，∴AE＝DB.如答图①，延长DB交AE于点M，∵Rt△ACE≌Rt△BCD，∴∠AEC＝∠BDC.又∵∠AEC＋∠EAC＝90°，∴∠BDC＋∠EAC＝90°，∴在△AMD中，∠AMD＝180°－90°＝90°，∴AE⊥DB；(2)DE＝AF，DE⊥AF.第15题答图理由：如答图②，设ED与AF相交于点N，由题意可知BE＝AD. ∵∠EBD＝∠C＋∠BDC＝90°＋∠BDC，∠ADF＝∠BDF＋∠BDC＝90°＋∠BDC，∴∠EBD＝∠ADF，又∵DB＝DF，A EF∴△EBD ≌△ADF ，∴DE ＝AF ，∠E ＝∠FAD ＝45°， ∵∠EDC ＝45°，∴∠AND ＝90°，∴DE ⊥AF .类型之七 倍长中线与截长补短（选做）16. 如图，已知在ABC ∆中，AD 是BC 边上的中线，E 是AD 上一点，且BE AC =，延长BE交AC 于F ，AF 与EF 相等吗？为什么？【答案】延长AD 到G ，使DG AD =，连结BG ∵BD CD =，BDG CDA ∠=∠，AD GD = ∴ADC GDB ∆∆≌．∴AC GB =．G EAF ∠=∠ 又∵BE AC =，∴BE BG =∴G BED ∠=∠，而BED AEF ∠=∠ ∴AEF FAE ∠=∠，故FA FE =．17. 已知，如图，ABC 中，D 是BC 的中点，DE DF ⊥，试判断BE +CF 与EF 的大小关系，并证明你的结论.【答案】BE +CF >EF过点B 作AC 的平行线，交FD 的延长线于点G ∵BG AC ≤（已知）∴1C ∠=∠（两直线平行，内错角相等） ∵D 是BC 中点（已知）FED CBA FEDCBAED CBA∴BD =CD （中点定义） 在BGD 和CFD 中，123CBD CD ∠=∠⎧⎪=⎨⎪∠=∠⎩（已证）（已证）（已知） ∴()BGD CFD ASA ∆∆≌∴BG =CF ，GD =FD 全等三角形对应边相等） ∵DE DF ⊥（已知）∴（垂直定义） 在EDG 和EDF 中，4ED EDEDG GD FD =⎧⎪∠=∠⎨⎪=⎩（公共边）（已证）（已证） ∴()EDG EDF SAS ∆∆≌∴EG =EF （全等三角形对应边相等）∵在BEG 中，BE +BG >EG （三角形中两边之和大于第三边） ∴BE +CF >EF （等量代换）18. 如图，在ABC 中，AB +BD =AC ，BAC ∠的平分线AD 交BC 与D ．求证：2B C ∠=∠．【答案】在AC 上取一点E ，使得AB =AE ，连结DE ．在ABD 和AED 中， AB =AE ，BAD EAD ∠=∠， AD =AD ．∴ABD AED ∆∆≌，∴BD =ED ，B AED ∠=∠又∵AB +BD =AC ，∴EC =BD =ED2AED EDC C C B ∠=∠+∠=∠=∠．其他方法参考例题．490EDG ∠=∠=°D CB A。

全等三角形辅助线之倍长中线法倍长中线法：遇中线，要倍长，倍长之后有全等．当倍长后，连接方式不一样，可以产生更多结论如下：与倍长中线法类似的辅助线作法AD E DE=AD BE ADC EDB AD=DE ADC=EDB BD=CDADC EDB(SAS)AC BE∆∆∠∠∆≅∆延长至使，连接在和中，，故与此相关的重要结论AD ABC ∆为的中线D CB AEAD ABC ∆为的中线DC BAEAD E AD=DE CE BE CE ABEC 延长至，使，当连接时，结论相似；　当连接、，则为平行四边形M ABCDEMD E MD=DE CE BDM CDE BM CE∆≅∆延长至，使，连接可证，举例：FE G FE=GE EGC ()EFD ∆≅∆延长至，使可证平行线夹中点F EDCBA G如图，在△ABC 中，AD 为BC 边上的中D CB AEAD E DE=AD BE ADC EDB AD=DE ADC=EDB BD=CDADC EDB(SAS)AB-BE AE AB+BE AE <AD<∆∆∠∠∆≅∆<<<<延长至使，连接在和中，，故即２８１４654321FAB C DE如图，CB 是△AEC 的中线，CD 是△ABC 的中线，且AB=AC ． 求证：△CE=2CD ；△CB 平分△DCE ．E DCB A如图，在△ABC 中，D 是BC 的中点，E 是AD 上一点，BE=AC ，BE 的延长线交AC 于点F ．求证：△AEF=△EAF ．F EDCBA321MA BCD EF如图，在正方形ABCD 中，CD=BC ，△DCB=90°，点E 在CB 的延长线上，过点E 作EF △BE ，且EF=BE ．连接BF ，FD ，取FD 的中点G ，连接EG ，CG ．求证：EG=CG 且EG △CG ．GF EDCB AM2134GFDA1. 如图，在△ABC 中，AD 为BC 边上的中线．（1）按要求作图：延长AD 到点E ，使DE =AD ；连接BE ． （2）求证：△ACD ≌△EBD ． （3）求证：AB +AC >2AD ．（4）若AB =5，AC =3，求AD 的取值范围．2. 如图，在△ABC 中，AD 平分∠BAC ，且BD =CD ．求证：AB =AC ．3. 如图，CB 是△AEC 的中线，CD 是△ABC 的中线，且AB =AC ．求证：①CE =2CD ；②CB 平分∠DCE ．4. 如图，在△ABC 中，D 是BC 的中点，E 是AD 上一点，BE =AC ，BE 的延长线交AC 于点F ． 求证：∠AEF =∠EAF ．5. 如图，在△ABC 中，AD 交BC 于点D ，点E 是BC 的中点，EF ∥AD 交CA 的延长线于点F ，交AB 于点G ，BG =CF ． 求证：AD 为△ABC 的角平分线．GFE DCB AE DCB AF E DBAGFEDCBAFED CBA6. 如图，在四边形ABCD 中，AD ∥BC ，点E 在BC 上，点F 是CD 的中点，且AF ⊥AB ，已知AD =2.7，AE =BE =5，求CE 的长．7. 如图，在正方形ABCD 中，CD =BC ，∠DCB =90°，点E 在CB 的延长线上，过点E 作EF ⊥BE ，且EF=BE ．连接BF ，FD ，取FD 的中点G ，连接EG ，CG ．求证：EG =CG 且EG ⊥CG ．【参考答案】➢ 课前预习1. （1）相等，SSS ；夹角，SAS ；夹边，ASA ；对边，AAS ；直角，HL（2）全等，三，边 2. （1）证明：如图∵O 是AB 的中点 ∴AO =BO在△AOC 和△BOD 中AO BO AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩∴△AOC ≌△BOD （SAS ） （2）证明：如图 ∵O 是AB 的中点 ∴AO =BO ∵AC ∥BD ∴∠A =∠B在△AOC 和△BOD 中A B AO BOAOC BOD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△AOC ≌△BOD （ASA ）GF EDCBA➢ 典型题型1. 解：（1）如图，（2）证明：如图，∵AD 为BC 边上的中线 ∴BD =CD在△BDE 和△CDA 中12BD CD ED AD =⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA （SAS ） （3）证明：如图， ∵△BDE ≌△CDA ∴BE =AC ∵DE =AD ∴AE =2 AD在△ABE 中，AB +BE >AE ∴AB +AC >2AD （4）在△ABE 中，AB -BE <AE <AB +BE由（3）得 AE =2AD ，BE =AC ∵AC =3，AB =5 ∴5-3<AE <5+3 ∴2<2AD <8 ∴1<AD <42. 证明：如图，延长AD 到E ，使DE =AD ，连接BE在△ADC 和△EDB 中CD BD ADC EDB AD ED =⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△EDB （SAS ） ∴AC =EB ，∠2=∠E ∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E ∴AB =BE∴AB =AC3. 证明：如图，延长CD 到F ，使DF =CD ，连接BF∴CF =2CD∵CD 是△ABC 的中线21EDCBA 21EBCDA在△BDF 和△ADC 中BD AD ADC BDF DF DC =⎧⎪∠=∠⎨⎪=⎩∴△BDF ≌△ADC （SAS ） ∴BF =AC ，∠1=∠F ∵CB 是△AEC 的中线 ∴BE =AB ∵AC =AB ∴BE =BF ∵∠1=∠F ∴BF ∥AC∴∠1+∠2+∠5+∠6=180° 又∵AC =AB ∴∠1+∠2=∠5 又∵∠4+∠5=180° ∴∠4=∠5+∠6 即∠CBE =∠CBF 在△CBE 和△CBF 中CB CB CBE CBF BE BF =⎧⎪∠=∠⎨⎪=⎩∴△CBE ≌△CBF （SAS ） ∴CE =CF ，∠2=∠3 ∴CE =2CD CB 平分∠DCE4. 证明：如图，延长AD 到M ，使DM =AD ，连接BM∵D 是BC 边的中点 ∴BD =CD在△ADC 和△MDB 中CD BD ADC MDB AD MD =⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△MDB （SAS ） ∴∠1=∠M ，AC =MB ∵BE =AC ∴BE =MB ∴∠M =∠3321MA BCDEF∴∠1=∠2 即∠AEF =∠EAF5. 证明：如图，延长FE 到M ，使EM =EF ，连接BM∵点E 是BC 的中点 ∴BE =CE在△CFE 和△BME 中FE ME CEF BEM CE BE =⎧⎪∠=∠⎨⎪=⎩∴△CFE ≌△BME （SAS ） ∴CF =BM ，∠F =∠M ∵BG =CF ∴BG =BM ∴∠1=∠M ∴∠1=∠F ∵AD ∥EF∴∠3=∠F ，∠1=∠2 ∴∠2=∠3即AD 为△ABC 的角平分线6. 解：如图，延长AF 交BC 的延长线于点G∵AD ∥BC ∴∠3=∠G∵点F 是CD 的中点 ∴DF =CF在△ADF 和△GCF 中3G AFD GFC DF CF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADF ≌△GCF （AAS ）∴AD =CG ∵AD =2.7 ∴CG =2.7 ∵AE =BE ∴∠1=∠B ∵AB ⊥AF ∴∠1+∠2=90° ∠B +∠G =90°321MABCD EFG∴CE =EG -CG=5-2.7 =2.37. 证明：如图，延长EG 交CD 的延长线于点M由题意，∠FEB =90°，∠DCB =90°∴∠DCB +∠FEB =180° ∴EF ∥CD ∴∠FEG =∠M ∵点G 为FD 的中点 ∴FG =DG在△FGE 和△DGM 中1M FGE DGM FG DG ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△FGE ≌△DGM （AAS ） ∴EF =MD ，EG =MG ∵△FEB 是等腰直角三角形 ∴EF =EB ∴BE =MD在正方形ABCD 中，BC =CD ∴BE +BC =MD +CD 即EC =MC∴△ECM 是等腰直角三角形 ∵EG =MG∴EG ⊥CG ，∠3=∠4=45° ∴∠2=∠3=45° ∴EG =CG三角形全等之倍长中线（实战演练）1. 在△ABC 中，AC =5，中线AD =4，则边AB 的取值范围是_______________． 思路分析：①画出草图，标注条件：②根据题目条件，见_________，考虑_____________；添加辅助线是______________________________________；③倍长之后证全等：__________≌___________（ ），证全等转移边：______=_______； ④全等转移条件后，利用三角形三边关系可以得到AB 的取值范围．2. 如图，在正方形ABCD 中，AD ∥BC ，E 为AB 边的中点，G ，F 分别为AD ，BC 边上的点，且AG =1，BF =2．若GE ⊥EF ，则GF 的长为多少？【参考答案】1. 3<AB <13①图略②中线AD 倍长中线 延长AD 到点E ，使DE =AD ，连接CE ③△ADC △EDB SAS AC EB ④略2. AD ∥BC ，E 为AB 边的中点，平行夹中点；AG =BH ，GE =HE ；到线段两端点的距离相等，FH ，AG +BF 解：如图，延长GE 交CB 的延长线于点H ∵AD ∥BC ∴∠GAE =∠HBE ∵E 为AB 边的中点 ∴AE =BE在△AGE 和△BHE 中，AEG BEH AE BEGAE HBE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△AGE ≌△BHE （ASA ） ∴BH =AG ，HE =GE ∵GE ⊥EF ∴GF =HF ∵BF =2，AG =1 ∴GF =HF =BF +BH =BF +AG =2+1 =3G FEAD BC三角形全等之倍长中线（作业）➢ 例题示范例1：已知：如图，在△ABC 中，AB ≠AC ，D ，E 在BC 上，且DE =EC ，过D 作DF ∥BA 交AE 于点F ，DF =AC ． 求证：AE 平分∠BAC ．【思路分析】读题标注：见中线，要倍长，倍长之后证全等．结合此题，DE =EC ，点E 是DC 的中点，考虑倍长，有两种考虑方法： ①考虑倍长FE ，如图所示： ②考虑倍长AE ，如图所示：（这个过程需要考虑倍长之后具体要连接哪两个点）倍长中线的目的是为了证明全等：以方法①为例，可证△DEF ≌△CEG ，由全等转移边和角，重新组织条件证明即可． 【过程书写】证明：如图，延长FE 到G ，使EG =EF ，连接CG ．A D CE FA B DCE FGFE CD B A FE CD B AA B DCE FG在△DEF 和△CEG 中，ED EC DEF CEG EF EG =⎧⎪∠=∠⎨⎪=⎩∴△DEF ≌△CEG （SAS ） ∴DF =CG ，∠DFE =∠G ∵DF =AC ∴CG =AC ∴∠G =∠CAE ∴∠DFE =∠CAE ∵DF ∥AB ∴∠DFE =∠BAE ∴∠BAE =∠CAE ∴AE 平分∠BAC➢ 巩固练习1. 已知：如图，在△ABC 中，AB =4，AC =2，点D 为BC 边的中点，且AD 是整数，则AD =________．2. 已知：如图，BD 平分∠ABC 交AC 于D ，点E 为CD 上一点，且AD =DE ，EF ∥BC 交BD 于F ．求证：AB =EF ．3. 已知：如图，在△ABC 中，AD 是BC 边上的中线，分别以AB ，AC 为直角边向外作等腰直角三角形，AB =AE ，AC =AF ，∠BAE =∠CAF =90°． 求证：EF =2AD ．4. 如图，在△ABC 中，AB >AC ，E 为BC 边的中点，AD 为D CBAF E DCBAFED CBA G FE D CBA∠BAC 的平分线，过E 作AD 的平行线，交AB 于F ，交CA 的延长线于G ． 求证：BF =CG ．5. 如图，在四边形ABCD 中，AD ∥BC ，点E 在BC 上，点F是CD 的中点，连接AF ，EF ，AE ，若∠DAF =∠EAF ，求证：AF⊥EF ．➢ 思考小结1. 如图，在△ABC 中，AD 平分∠BAC ，且BD =CD ．求证：AB =AC ．比较下列两种不同的证明方法，并回答问题． 方法1：如图，延长AD 到E ，使DE =AD ，连接BE 在△BDE 和△CDA 中BD CD BDE CDA DE DA =⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA （SAS ） ∴AC =BE ，∠E =∠2 ∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E ∴AB =BE ∴AB =AC 方法2：如图，过点B 作BE ∥AC ，交AD 的延长线于点E ∵BE ∥AC ∴∠E =∠2在△BDE 和△CDA 中FE DB CA21ECDB A 21ECDBA DBA2E BDE CDA BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA （AAS ） ∴BE =AC ∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E ∴AB =BE ∴AB =AC 相同点：两种方法都是通过辅助线构造全等，利用全等转移条件进而解决问题．方法1是看到中点考虑通过___________构造全等，方法2是通过平行夹中点构造全等． 不同点：倍长中线的方法在证明全等时，利用的判定是________，实质是构造了一组对应边相等；利用平行夹中点证明全等时，利用的判定是_____，实质是利用平行构造了一组_____相等．2. 利用“倍长中线”我们就可以证明直角三角形中非常重要的一个定理：直角三角形斜边中线等于斜边的一半．请你尝试进行证明．已知：如图，在Rt △ABC 中，∠BCA =90°，CD 是斜边AB 的中线．求证：CD 12=AB ．【参考答案】➢ 巩固练习 1. 22. 证明略（提示：延长FD 到点G ，使得DG =DF ，连接AG ，证明△ADG ≌△EDF ，转角证明AB =EF ）3. 证明略（提示：延长AD 到点G ，使得GD =AD ，连接CG ，证明△ABD ≌△GCD ，△EAF ≌△GCA ）4. 证明略（提示：延长FE 到点H ，使得EH =FE ，连接CH ，证明△BFE ≌△CHE ，转角证明BF =CG ）5. 证明略（提示：延长AF 交BC 的延长线于点G ，证明△ADF ≌△GCF ，转角证明AF ⊥EF ） ➢ 思考小结 1. 倍长中线 SAS AAS 角2. 证明略DCB A。

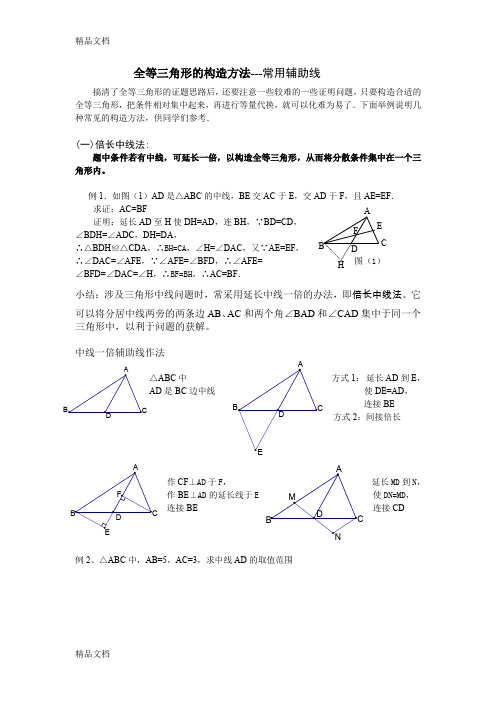
全等三角形的构造方法---常用辅助线搞清了全等三角形的证题思路后，还要注意一些较难的一些证明问题，只要构造合适的全等三角形，把条件相对集中起来，再进行等量代换，就可以化难为易了．下面举例说明几种常见的构造方法，供同学们参考．(一)倍长中线法:题中条件若有中线，可延长一倍，以构造全等三角形，从而将分散条件集中在一个三角形内。

例1．如图（1）AD 是△ABC 的中线，BE 交AC 于E ，交AD 于F ，且AE=EF ．求证：AC=BF 证明：延长AD 至H 使DH=AD ，连BH ，∵BD=CD ， ∠BDH=∠ADC ，DH=DA ， ∴△BDH ≌△CDA ，∴BH=CA ，∠H=∠DAC ，又∵AE=EF ， ∴∠DAC=∠AFE ，∵∠AFE=∠BFD ，∴∠AFE=图（1） ∠BFD=∠DAC=∠H ，∴BF=BH ，∴AC=BF ．小结：涉及三角形中线问题时，常采用延长中线一倍的办法，即倍长中线法。

它可以将分居中线两旁的两条边AB 、AC 和两个角∠BAD 和∠CAD 集中于同一个三角形中，以利于问题的获解。

中线一倍辅助线作法△ABC 中 方式1： 延长AD 到E ，AD 是BC 边中线 使DE=AD ，连接BE 方式2：间接倍长作CF ⊥AD 于F ，延长MD 到N ， 作BE ⊥AD 的延长线于使DN=MD ， 连接BE 连接CD例2、△ABC 中，AB=5，AC=3，求中线AD 的取值范围E AB C DF H例3、已知在△ABC 中，AB=AC ，D 在AB 上，E 在AC 的延长线上，DE 交BC 于F ，且DF=EF ，求证：BD=CE课堂练习：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF例4、已知：如图，在ABC ∆中，AC AB ≠，D 、E 在BC 上，且DE=EC ，过D 作BA DF //交AE 于点F ，DF=AC.求证：AE 平分BAC ∠课堂练习：已知CD=AB ，∠BDA=∠BAD ，AE 是△ABD 的中线，求证：∠C=∠BAE第 1 题图 A B F D EC作业：1、在四边形ABCD 中，AB ∥DC ，E 为BC 边的中点，∠BAE=∠EAF ，AF 与DC 的延长线相交于点F 。

全等三角形的类型题常见辅助线的作法有以下几种：1)遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”．2)遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转”．3)遇到角平分线，可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理．4)过图形上某一点作特定的平分线，构造全等三角形，利用的思维模式是全等变换中的“平移”或“翻转折叠”5)截长法与补短法，具体做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，是之与特定线段相等，再利用三角形全等的有关性质加以说明．这种作法，适合于证明线段的和、差、倍、分等类的题目．特殊方法：在求有关三角形的定值一类的问题时，常把某点到原三角形各顶点的线段连接起来，利用三角形面积的知识解答．倍长中线法1.已知：AB=4，AC=2，D是BC中点，AD是整数，求AD2、已知：D是AB中点，∠ACB=90°，求证：12 CD AB3、已知：∠1=∠2，CD=DE，EF//AB，求证：EF=AC4、已知，E是AB中点，AF=BD，BD=5，AC=7，求DCADB CDABCBACDF21E截长补短法1、已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C2、如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

求证：BC=AB+DC 。

3、如图，已知AD ∥BC ，∠PAB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．4、已知∠ABC=3∠C ，∠1=∠2，BE ⊥AE ，求证：AC-AB=2BE边加减的问题1、已知：点A 、F 、E 、C 在同一条直线上， AF ＝CE ，BE∥DF，BE ＝DF ．求证：△ABE≌△CDF．2、如图：DF=CE ，AD=BC ，∠D=∠C 。

全等三角形基本判定条件：1、三边对应相等(SSS)。

2、两边夹角对应相等(SAS)。

3、两角夹边对应相等(ASA)。

4、两角对边对应相等(AAS)。

5、直角三角形全等条件：①斜边及一直角边对应相等（HL）；②一直角边及一锐角对应相等（ASA）或斜边及一锐角对应相等（AAS）；③两直角边对应相等(SAS) 。

★注意：直角三角形全等，除边边边（SSS），边角边（SAS），角边角（ASA），角角边（AAS）对应相等外，还有直角边及斜边（HL）、一直角边及一锐角（ASA)、斜边及一锐角（AAS）、两直角边（SS）等对应相等。

除以上基本判定外，全等三角形另外判定条件：1、三条中线对应相等，两个三角形全等。

2、三条高线对应相等，两个三角形全等。

3、三条角平分线对应相等，两个三角形全等。

4、两个角及第三个角的角平分线对应相等，两个三角形全等。

5、两条边及第三条边上的中线对应相等，两个三角形全等。

6、钝角三角形中，一钝角和其一邻边对应相等，钝角所对的较大边也相等，两个三角形全等。

或两边及其中一边的对角(钝角)对应相等，两个三角形全等。

（SSA）7、等腰三角形中，底边和顶角分别对应相等，两个等腰三角形全等。

8、等腰直角三角形中，周长相等，两个等腰直角三角形全等。

（因为等腰直角三角形三边之比为1：1：√2，故周长相等时，等腰直角三角形的对应角相等，对应边相等，故全等）。

9、等边三角形中，有一边对应相等，两个三角形全等。

★特别提示：在三角形全等的判定中，一定有边相等，一定没有AAA和SSA（除非此角为钝角），这两种情况都不能唯一确定三角形的形状。

三角形全等的性质：1.全等三角形的对应角相等。

4. 全等三角形的对应边上的中线相等。

2.全等三角形的对应边相等。

5.全等三角形的对应角的角平分线相等。

3.全等三角形面积周长相等。

6.全等三角形的对应边上的高对应相等。

等腰三角形的性质1、等腰三角形的两个底角度数相等（简写“等边对等角”）。

倍长中线法知识网络详解：中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么（延长的那一条），用SAS 证全等（对顶角）倍长中线最重要的一点，延长中线一倍，完成SAS 全等三角形模型的构造。

【方法精讲】常用辅助线添加方法——倍长中线△ABC 中 方式1： 延长AD 到E ，AD 是BC 边中线 使DE=AD ，连接BE方式2：间接倍长作CF ⊥AD 于F ， 延长MD 到N ，作BE ⊥AD 的延长线于E 使DN=MD ， 连接BE 连接CN经典例题讲解：例1：△ABC 中，AB=5，AC=3，求中线AD 的取值范围D ABCEDAB C F EDC B AN D C B AM例2：已知在△ABC 中，AB=AC ，D 在AB 上，E 在AC 的延长线上，DE 交BC 于F ，且DF=EF ，求证：BD=CE例3：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF例4：已知：如图，在ABC ∆中，AC AB ≠，D 、E 在BC 上，且DE=EC ，过D 作BA DF //交AE 于点F ，DF=AC.求证：AE 平分BAC ∠FE DA B CFEC ABD AB F D E C例5：已知CD=AB ，∠BDA=∠BAD ，AE 是△ABD 的中线，求证：∠C=∠BAE自检自测：1、如图，△ABC 中，BD=DC=AC,E 是DC 的中点，求证，AD 平分∠BAE.2、在四边形ABCD 中，AB ∥DC ，E 为BC 边的中点，∠BAE=∠EAF ，AF 与DC 的延长线相交于点F 。

试探究线段AB 与AF 、CF 之间的数量关系，并证明你的结论.E D ABCF EAB C D3、如图，AD 为ABC ∆的中线，DE 平分BDA ∠交AB 于E ，DF 平分ADC ∠交AC 于F. 求证：EF CF BE >+4、已知：如图，∆ABC 中，∠C=90︒，CM ⊥AB 于M ，AT 平分∠BAC 交CM 于D ，交BC 于T ，过D 作DE//AB 交BC 于E ，求证：CT=BE.第 14 题图DF CBEADABCMTE。