构件的基本变形
- 格式:pptx
- 大小:819.30 KB
- 文档页数:26



构件的基本变形教案教案标题:构件的基本变形教案教学目标:1. 理解构件的基本变形概念和原因。
2. 掌握构件的基本变形计算方法。
3. 能够应用所学知识解决实际问题。
教学内容:1. 构件的基本变形概念和分类:a. 弹性变形和塑性变形的区别。
b. 构件的弯曲变形、剪切变形、扭转变形和轴向变形。
2. 构件的变形计算方法:a. 弹性变形计算:- 应变-应力关系的简介。
- 弹性模量的定义和计算方法。
- 弹性变形的计算公式和示例。
b. 塑性变形计算:- 屈服点和屈服强度的概念。
- 塑性变形的计算方法和示例。
3. 实际问题的解决:a. 根据已知条件计算构件的变形。
b. 分析构件的设计是否满足变形要求。
c. 提出改进措施以减小构件的变形。
教学步骤:第一步:导入介绍构件的基本变形概念和重要性,引发学生对主题的兴趣。
第二步:知识讲解详细讲解构件的基本变形概念和分类,强调弹性变形和塑性变形的区别。
第三步:计算方法讲解以弹性变形为例,讲解应变-应力关系、弹性模量的定义和计算方法,并通过示例演示弹性变形的计算。
第四步:塑性变形计算讲解屈服点和屈服强度的概念,介绍塑性变形的计算方法,并通过示例演示塑性变形的计算。
第五步:实际问题解决引导学生根据已知条件计算构件的变形,分析设计是否满足变形要求,并提出改进措施以减小构件的变形。
第六步:总结与拓展总结本节课的重点内容,提供相关拓展资料供学生深入学习。
教学资源:1. PowerPoint演示文稿。
2. 构件的实物样本或图片。
3. 计算公式和示例题。
4. 相关拓展资料。
评估方式:1. 课堂练习:布置一些计算题,考察学生对构件变形计算方法的掌握程度。
2. 小组讨论:要求学生在小组内讨论一个实际构件的变形问题,并提出解决方案。
3. 个人作业:要求学生独立完成一道综合性的构件变形计算题。
教学反思:在教案撰写过程中,我充分考虑了学生的学习需求和实际应用能力培养。
通过理论讲解、计算方法演示和实际问题解决等多种教学手段,旨在帮助学生全面理解构件的基本变形概念和计算方法,并能够运用所学知识解决实际问题。

机械构件的变形形式1. 弹性变形:机械构件在受到外力作用后,能够在一定范围内发生弹性变形。
简单来说,弹性变形是指构件受力后能够恢复到原始形状和尺寸的变形形式。
这种变形是可逆的,也就是说当外力消失时,构件能够恢复到原来的状态。
2. 塑性变形:机械构件在受到外力作用后,超过了其弹性限度范围,发生了塑性变形。
与弹性变形不同的是,塑性变形是不可逆的,构件无法通过去除外力来恢复到原来的形状和尺寸。
塑性变形常见的形式包括拉伸、压缩、弯曲和扭转等。
3. 破坏:机械构件在受到外力作用后,超过其强度极限,无法再承受更大的力而发生破坏。
破坏可以是断裂、裂纹扩展、脱落等形式。
破坏是构件无法再继续使用的严重变形形式,需要进行修复或更换。
4. 压缩变形:机械构件在受到垂直于其轴线方向的外力作用下,发生的沿轴线方向的压缩变形。
压缩变形使构件缩短,同时也会增加其横截面积。
这种变形形式常见于柱状构件或弹簧等。
5. 拉伸变形:机械构件在受到垂直于其轴线方向的外力作用下,发生的沿轴线方向的拉伸变形。
拉伸变形使构件延长,同时也会减小其横截面积。
这种变形形式常见于拉索、钢丝绳等。
6. 弯曲变形:机械构件在受到垂直于其轴线方向的外力作用下,发生的沿轴线方向的弯曲变形。
弯曲变形使构件在某个点上的一侧伸展,而在另一侧压缩。
这种变形形式常见于梁、梯形板等。
7. 扭转变形:机械构件在受到扭矩作用下,发生的在其轴线周围的旋转变形。
扭转变形使构件在轴线周围发生扭曲,同时也会引起构件截面的形变。
这种变形形式常见于轴、螺旋弹簧等。
8. 疲劳变形:机械构件在长时间、反复地受到交变载荷作用后,发生的逐渐积累的变形。
疲劳变形是一种渐进的过程,常导致构件的损坏和失效。
这种变形形式常见于高速旋转部件、机械连接等。
以上是机械构件的一些常见变形形式的解释,通过理解这些变形形式,可以更好地设计和使用机械构件,避免因变形而导致的故障和事故发生。



第八章组合变形§8-1 组合变形和叠加原理一、组合变形的概念:构件的基本变形:拉压、剪切挤压、扭转、弯曲。
由两种或两种以上基本变形的组合---称为组合变形。
如:梁的弯曲和拉压变形的组合。
轴的扭转和弯曲变形的组合。
梁的弯曲与剪切变形的组合(横力弯曲)。
李禄昌liluchang二、叠加法---解决组合变形问题的基本方法*:1、叠加原理:复杂外力进行简化、分解为几组静力等效载荷。
→ →每一组载荷对应着一种基本变形。
→ →分别计算一种基本变形的内力、应力、应变、挠度。
→ →将所有结果叠加,便是构件发生组合变形时的内力、应力、应变、挠度。
2、叠加原理的几个原则*:⑴、分量(内力、应力、应变、位移)与外力成线性关系。
⑵、与外力加载的先后顺序无关,⑶、材料服从胡克定律(线弹性变形)。
⑷、应用原始尺寸原理。
注意:各分量叠加时,同方向的相同分量可以用代数和叠加。
如:正应力与正应力、切应力与切应力。
3、叠加原理应用的基本步骤:xxσ(1) 、将载荷进行分解,产生几种基本变形;(2)、分析每种基本变形,确定危险截面;(3)、计算构件在每种基本变形情况下的危险截面内的应力;(4)、将各基本变形情况下的应力叠加,确定最危险点;**(5)、计算主应力,选择适合的强度理论,进行强度校核。
而不同方向的分量,应采用不同的求和方法,如:正应力与切应力之间。
σσσ'''=+τττ'''=+22p στ=+xτ不要用这个公式。
斜弯曲PϕyzxyzlP zP yP 不考虑剪应力Kk σσσ'''=+y z z y M z M y I I -sin cos z yP z P y I I ϕϕ=--cos y yyM z P zI I σϕ''=-=-sin ,z z zM y P y I I σϕ'=-=-如果是圆截面?§8-2 弯曲与拉伸的组合变形一、受力及变形特点:xyzlFF轴向拉伸F偏心拉伸zMyM附加力偶1、轴向力:产生拉压正应力:()()12x x zN x M x yA I σσσ=+=+注意两个应力正负号。
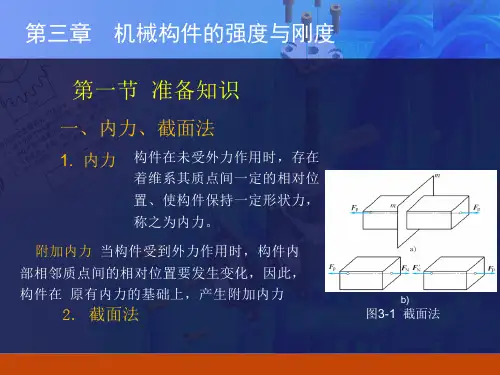
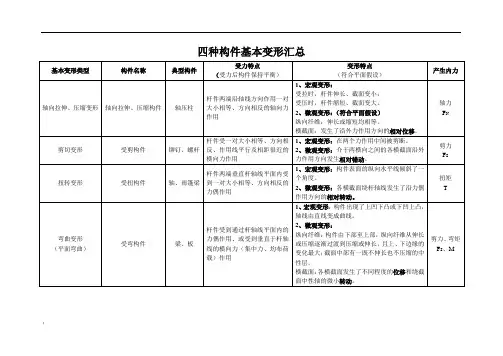


构件变形的四种基本形式
构件变形是结构工程中非常重要的一部分。
变形会影响到结构的正常运行和安全性。
下面是构件变形的四种基本形式。
1. 弯曲变形
弯曲变形是指在结构中,由于承受的力的作用,构件从直线变形成曲线的现象。
弯曲变形是结构中常见的一种变形形式,常见的例子包括弯曲梁、弯曲柱等。
弯曲变形会导致构件的剪切应力和弯曲应力增大,从而可能导致构件破坏。
因此,在结构设计中需要考虑弯曲变形的影响,并采取相应的措施。
2. 拉伸变形
3. 压缩变形
4. 扭转变形
总之,构件变形是结构中不可避免的一部分。
当设计结构时,需要考虑构件变形的影响,并采取相应的措施来保证结构的安全和稳定性。
材料力学中的四种基本变形举例
1.拉伸变形:
拉伸变形是指在外力的作用下,物体的长度增加或变长的过程。
这种
变形常见于拉伸试验中的拉力加载中,例如在拉伸试验机上施加外力,拉
伸材料直至材料的断裂点。
一个常见的例子是橡皮筋,当我们拉伸橡皮筋时,它的长度会增加。
2.压缩变形:
压缩变形是指在外力的作用下,物体的长度减少或变短的过程。
这种
变形常见于承受压力的构件中,例如梁柱结构承受竖向荷载时会产生压缩
变形。
一个典型的例子是弹簧,当我们用力将弹簧压缩时,它的长度会变短。
3.剪切变形:
剪切变形是指在外力的作用下,物体的平行侧面发生相对位移的过程。
这种变形常见于切削和金属加工中,例如在使用剪切机切割金属板材时,
金属板材的平行侧面会产生相对的移动。
另一个例子是在泥土工程中,当
土壤受到剪切力时,会发生剪切变形。
4.扭转变形:
扭转变形是指在外力作用下,物体沿纵轴发生旋转的过程。
这种变形
常见于旋转机械中,例如在使用螺旋桨驱动船只前进时,船体会发生扭转
变形。
另一个例子是在汽车悬挂系统中,当车辆转弯时,车身会发生扭转
变形。
这四种基本变形在材料力学中都具有重要的意义,并广泛应用于工程设计和材料选型过程中。
通过对这些变形的认识和理解,我们能够更好地预测和控制材料的行为和性能。