洛伦兹曲线与基尼系数的区别和联系

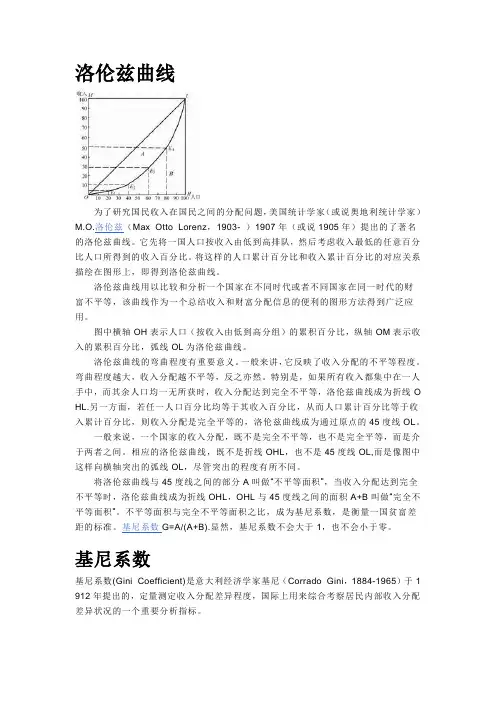
洛伦兹曲线为了研究国民收入在国民之间的分配问题，美国统计学家（或说奥地利统计学家）M.O.洛伦兹（Max Otto Lorenz，1903- ）1907年（或说1905年）提出的了著名的洛伦兹曲线。

它先将一国人口按收入由低到高排队，然后考虑收入最低的任意百分比人口所得到的收入百分比。

将这样的人口累计百分比和收入累计百分比的对应关系描绘在图形上，即得到洛伦兹曲线。

洛伦兹曲线用以比较和分析一个国家在不同时代或者不同国家在同一时代的财富不平等，该曲线作为一个总结收入和财富分配信息的便利的图形方法得到广泛应用。

图中横轴OH表示人口（按收入由低到高分组）的累积百分比，纵轴OM表示收入的累积百分比，弧线OL为洛伦兹曲线。

洛伦兹曲线的弯曲程度有重要意义。

一般来讲，它反映了收入分配的不平等程度。

弯曲程度越大，收入分配越不平等，反之亦然。

特别是，如果所有收入都集中在一人手中，而其余人口均一无所获时，收入分配达到完全不平等，洛伦兹曲线成为折线O HL.另一方面，若任一人口百分比均等于其收入百分比，从而人口累计百分比等于收入累计百分比，则收入分配是完全平等的，洛伦兹曲线成为通过原点的45度线OL。

一般来说，一个国家的收入分配，既不是完全不平等，也不是完全平等，而是介于两者之间。

相应的洛伦兹曲线，既不是折线OHL，也不是45度线OL,而是像图中这样向横轴突出的弧线OL，尽管突出的程度有所不同。

将洛伦兹曲线与45度线之间的部分A叫做“不平等面积”，当收入分配达到完全不平等时，洛伦兹曲线成为折线OHL，OHL与45度线之间的面积A+B叫做“完全不平等面积”。

不平等面积与完全不平等面积之比，成为基尼系数，是衡量一国贫富差距的标准。

基尼系数G=A/(A+B).显然，基尼系数不会大于1，也不会小于零。

基尼系数基尼系数(Gini Coefficient)是意大利经济学家基尼（Corrado Gini，1884-1965）于1 912年提出的，定量测定收入分配差异程度，国际上用来综合考察居民内部收入分配差异状况的一个重要分析指标。

请简述洛伦兹曲线和基尼系数。

洛伦兹曲线和基尼系数是两个经济学中常用的工具，用于衡量收入分配的不平等程度。

本文将分别介绍这两个工具的概念、计算方法以及应用。

一、洛伦兹曲线洛伦兹曲线是一种图形，用于表示收入分配的不平等程度。

它的横轴表示人口比例，纵轴表示收入比例。

如果收入完全平等分配，那么洛伦兹曲线就是一条45度直线。

但是，在现实中，收入分配往往不平等，因此洛伦兹曲线会呈现出一定的弯曲。

洛伦兹曲线的计算方法如下：1. 将人口按照收入从低到高排序，得到一个序列。

2. 计算每个收入段的人口比例和收入比例。

3. 将每个收入段的人口比例和收入比例画在坐标系上，得到洛伦兹曲线。

洛伦兹曲线的应用：1. 衡量收入不平等程度。

洛伦兹曲线越弯曲，说明收入分配越不平等。

2. 比较不同国家或地区的收入分配情况。

不同国家或地区的洛伦兹曲线可以进行比较，从而了解其收入分配的差异。

3. 制定政策。

洛伦兹曲线可以帮助政策制定者了解收入分配的情况，从而制定相应的政策。

二、基尼系数基尼系数是一种用于衡量收入分配不平等程度的指标。

它的取值范围在0到1之间，数值越大，说明收入分配越不平等。

基尼系数的计算方法如下：1. 将人口按照收入从低到高排序，得到一个序列。

2. 计算每个收入段的人口比例和收入比例。

3. 计算基尼系数。

基尼系数的计算公式为：G = (n + 1) / n - 2 * (A1 + A2 + ... + An) / n其中，n表示人口数量，A1、A2、...、An表示每个收入段的人口比例和收入比例的乘积之和。

基尼系数的应用：1. 衡量收入不平等程度。

基尼系数越大，说明收入分配越不平等。

2. 比较不同国家或地区的收入分配情况。

不同国家或地区的基尼系数可以进行比较，从而了解其收入分配的差异。

3. 制定政策。

基尼系数可以帮助政策制定者了解收入分配的情况，从而制定相应的政策。

洛伦兹曲线和基尼系数是两个常用的工具，用于衡量收入分配的不平等程度。

洛伦兹曲线和基尼系数的含义
罗伦兹曲线
1、定义：
罗伦兹曲线是描述一个经济体或经济体组合特定时期内平均对外投资所在的收益率与投资单位的风险的关系的曲线。

它是由美国投资银行家Harry Markowitz于1950年提出的。

2、公式：
罗伦兹曲线的公式为：F=f(R，Rm)。

在该公式中，F是投资者在某一特定投资收益率水平下所能取得的期望收益；R是投资者投资单位的风险率；Rm是市场平均收益率，为各种经济体的平均收益率。

3、分析：
罗伦兹曲线表明，随着投资收益率的增加，投资单位的风险回报比也会随之增涨。

而当投资收益率达到某一水平以上时，将不会有太多的风险收益比收益比，就达到罗伦兹曲线的最高点，不再有收益能够通过调整投资组合而获得。

基尼系数
1、定义：
基尼系数是由美国经济学家Robert Gini提出的，衡量一个社会或某个就业机会的非对称和不公平程度的一个指标，也可以用来衡量一个经济体的社会不平等程度。

2、公式：
基尼指数的公式为：G=R/Rm，其中，R是某个投资单位的收益率，Rm是市场平均收益率。

3、分析：
基尼指数可以分析投资者投资单位的收益，并与市场平均收益率相比较，基尼指数越大，表明投资单位的收益率较低，也就是说，如果投资单位的收益低于市场平均收益，基尼指数会变得更大。

基尼系数与洛伦茨曲线测定不同国家，或同一国家不同阶段的社会收入不平等程度，主要方法是描绘洛伦茨曲线（Lorenz Curve）和计算基尼系数（Gini Coefficient）。

洛伦茨曲线、基尼系数还可以用来判断政府为履行其收入分配职能而推行的社会收入再分配政策的基本效果。

洛伦茨曲线（Lorenz Curve）洛伦茨曲线是用来描述一国财富或收入分配状况的统计工具，它表示各阶层人民（从最贫困的开始）收入的累积部分占整个国民收入中的百分比。

在国民收入分配完全均等情况下，它是一条45度角直线；在国民收入分配绝对不平等情况下，则构成正方形的底边和右边。

由于任何国家实际收入分配状况都介于上述两种极端情况之间，故洛伦茨曲线一般为一条向下弯曲的曲线，其偏离45度角直线越小，表明该社会收入分配状况的平等化程度越高，其偏离45度角直线越大，表明该社会收入分配状况的平等化程度越低。

描绘洛伦茨曲线的一般方法是：先画一个正方形，其底边作为洛伦茨曲线图的横轴，按家庭收入水平的高低把全国家庭划分为5组，即最低收入的20％家庭、次低收入的20％家庭、中等收入的20％家庭、高收入的20％家庭和最高收入的20％家庭；该正方形的左边为洛伦茨曲线图的纵轴，用于比较各组家庭合计收入占全国总收入的百分比。

如果每个家庭组别的合计收入均占全国总收入的20％，连接对应纵坐标与横坐标的各点恰好为一条45度角直线，表明该国该时期社会收入分配状况最平等。

在洛伦茨曲线图中，该45度角直线就成为收入分配平等化的标准，此后，人们就可以根据实际标绘出的洛伦茨曲线对该45度角直线的偏离程度，大致地判断各种收入分配不平等状况的严重程度。

图2-1是根据表2-1中提供的意大利1977年和1986年的有关数据，描绘的反映该国70年代与80年代社会收入分配状况变化的洛伦茨曲线。

比如1977年意大利洛伦茨曲线画法，将正方形底边均等的分为五份，每份20%，左边均等分成100份，第一个20%对应的是6.2，在图中找到相应位置，确定一点，第二个20%对应的纵坐标为17.5（6.2+11.3），第三个点对应的是33.4（6.2+11.3+15.9），第四点对应56.1（6.2+11.3+15.9+22.7），第五个点对应100（6.2+11.3+15.9+22.7+43.9），然后将这五点用光滑的曲线连接起来。

洛伦兹曲线与基尼系数的区别和联系图中横轴OH表示人口（按收入由低到高分组）的累积百分比，纵轴OM表示收入的累积百分比，弧线OL为洛伦兹曲线。

洛伦兹曲线的弯曲程度有重要意义。

一般来讲，它反映了收入分配的不平等程度。

弯曲程度越大，收入分配越不平等，反之亦然。

特别是，如果所有收入都集中在一人手中，而其余人口均一无所获时，收入分配达到完全不平等，洛伦兹曲线成为折线OHL.另一方面，若任一人口百分比均等于其收入百分比，从而人口累计百分比等于收入累计百分比，则收入分配是完全平等的，洛伦兹曲线成为通过原点的45度线OL。

一般来说，一个国家的收入分配，既不是完全不平等，也不是完全平等，而是介于两者之间。

相应的洛伦兹曲线，既不是折线OHL，也不是45度线OL,而是像图中这样向横轴突出的弧线OL，尽管突出的程度有所不同。

将洛伦兹曲线与45度线之间的部分A叫做“不平等面积”，当收入分配达到完全不平等时，洛伦兹曲线成为折线OHL，OHL与45度线之间的面积A+B叫做“完全不平等面积”。

不平等面积与完全不平等面积之比，成为基尼系数，是衡量一国贫富差距的标准。

基尼系数G=A/(A+B).显然，基尼系数不会大于1，也不会小于零。

通过络伦兹曲线，可以直观地看到一个国家收入分配平等或不平等的状况。

整个的洛伦兹曲线是一个正方形，正方形的底边即横轴代表收入获得者在总人口中的百分比，正方形的左边即纵轴显示的是各个百分比人口所获得的收入的百分比。

从坐标原点到正方形相应另一个顶点的对角线为均等线，即收入分配绝对平等线，这一般是不存在的。

实际收入分配曲线即洛伦兹曲线都在均等线的右下方（如吉尼系数解释中的图）。

洛伦兹曲线就是，在一个总体（国家、地区）内，以“最贫穷的人口计算起一直到最富有人口”的人口百分比对应各个人口百分比的收入百分比的点组成的曲线。

基尼系数和洛伦兹曲线基尼系数和洛伦兹曲线是衡量收入分配差距的常用工具。

下面将分别从定义、计算方法和应用方面进行介绍。

基尼系数:定义: 基尼系数也常被称为基尼系数(Gini coefficient)，是一种用来衡量收入分配(或财富分配)不平等程度的指数。

该指数取值范围为0-1之间，0表示完全平等，1表示完全不平等。

计算方法: 基尼系数的计算方法是，将所有收入按照从小到大的顺序排序，然后画出累计收入分布图(也称洛伦兹曲线)，再计算洛伦兹曲线下方的面积(S)和洛伦兹曲线与对角线之间的面积(T)，基尼系数等于G=T/(S+T)。

应用: 基尼系数的应用范围较广，可以用来衡量国家、地区、城市、产业等层面的收入分配不平等程度。

该指数常被用来评估一个国家的社会经济发展状况，并且可以作为制定财政税收政策、社会保障政策、教育卫生政策等方案的参考指标。

洛伦兹曲线:定义: 洛伦兹曲线是一种用来表示收入(或财富)分配情况的图形工具。

该曲线是由意大利经济学家洛伦兹(Giuseppe Lorenz)于1905年首次提出，并被广泛用于衡量收入(或财富)分配的不平等程度。

计算方法: 洛伦兹曲线的计算方法是，将个人或家庭的收入按照从小到大的顺序排序，然后将排序后的个人或家庭的累计收入分别用横、纵坐标表示，得到一个累计收入分布图。

然后在同一个坐标系中画出对角线(也就是y=x的直线)，得到的线段与对角线之间的面积就是洛伦兹曲线下方的面积。

应用: 洛伦兹曲线通常与基尼系数同时使用，可以更准确地评估收入分配的不平等程度。

此外，洛伦兹曲线还可以用来比较不同国家、不同地区、不同产业之间的收入分配情况，为决策者制定政策提供参考依据。

总结:基尼系数和洛伦兹曲线都是衡量收入分配不平等程度的常用工具，二者通常被同时使用。

基尼系数是一个0-1之间的指数，越大表明收入分配越不平等；洛伦兹曲线是一个累计收入分布图，越靠近对角线表明收入分配越平等。

应用方面，二者均可以用来评估社会经济发展状况，作为政府制定政策的参考指标。

洛伦兹曲线基尼系数
洛伦兹曲线指的是一种用来描述收入或财富分布不公平程度的图形。

该曲线以意大利经济学家洛伦佐·洛伦兹（Lorenzo Lorenz）的名字命名，经常用于衡量一个国家或地区的收入分
配的不平等程度。

在洛伦兹曲线中，横轴表示累计收入或财富份额的累积百分比，纵轴表示对应的累计人口份额的累积百分比。

曲线的形状描述了收入或财富如何分配给人口的不平等程度。

如果所有人的收入或财富完全相等，则洛伦兹曲线将是一条45度的直线，在
这种情况下，洛伦茨曲线下方的面积与上方的面积相等，表明完全的收入或财富平等。

基尼系数是衡量洛伦茨曲线的不平等程度的指标。

它定义为洛伦茨曲线下方的面积与整个正方形面积之间的比例差异，其取值范围从0到1。

基尼系数越接近0，表示收入或财富分配越
平等；而基尼系数越接近1，表示收入或财富分配越不平等。

洛伦兹曲线和基尼系数的含义洛伦兹曲线与基尼系数是经济学中非常重要的统计指标，它们主要用于衡量国家或地区内贫富差距等社会经济状况，广泛应用于社会、经济和政治等不同领域。

本文将对洛伦兹曲线和基尼系数的历史、定义、应用等方面进行系统介绍。

洛伦兹曲线是由哥伦比亚大学经济学教授威廉洛伦兹（William Lorenz）于1905年提出，其初衷是通过将社会经济收入等级放置在一起，展示社会贫富不均的实际情况，后来洛伦兹曲线被用作经济学研究贫富不均的主要量化工具。

它是一条S型曲线，衡量社会贫富不均程度的指标，对贫富差距分布有很好的反映性，社会收入分布越均匀，曲线越接近一条水平线，社会收入分布越不均匀，曲线越趋向垂直。

而基尼系数是经济学学者瓦尔特基尼（Gini）在1912年提出，它是衡量社会贫富不均程度的重要统计指标，主要表示一个国家或地区内贫富差距的程度，基尼系数越高，则收入差距越大，排序越不同，表明收入分配状况越不公平；基尼系数越低，贫富差距越小，排序越一致，表明收入分配状况越趋向公平。

基尼系数的范围为0-1，基尼系数约为0时，表示收入完全均等，1时表示收入完全不均等。

洛伦兹曲线和基尼系数一般用于测量发达国家和发展中国家的社会经济状况，以便研究贫富差距的程度和趋势变化，衡量政策效果如何，以及这些政策如何影响不同级别的人。

因此，洛伦兹曲线和基尼系数经常被广泛应用于社会、经济和政治等不同领域，如经济增长、贫困治理、发展战略、社会福利及倾向性等，在一定程度上能够反映一个国家或地区的发展水平和收入分配的公平性，从而为相关政策决策提供依据。

虽然洛伦兹曲线和基尼系数具有广泛的应用前景，但由于存在一定的局限性，也遭遇到了一定的批评。

批评者认为，其数据准确性依赖于统计水平，而数据收集本身就存在一定难度，如果存在误差，则会影响其精确性。

此外，这两个指标只能衡量收入分配状况，无法衡量财富或实物财富生产水平、幸福指标等，因此也受到限制。

洛伦兹曲线,基尼系数的含义洛伦兹曲线和基尼系数是两个不同的概念，但它们之间有一定的联系。

洛伦兹曲线是一种比较不同人群收入悬殊情况的可视化曲线，而基尼系数则是通过计算洛伦兹曲线两端收入差异来衡量一个国家的社会不平等状况的。

洛伦兹曲线是由美国经济学家威尔弗雷德洛伦兹（Wilfredo Lopez）在1976年首次提出的，他在《经济文献》（Economic Record）杂志上发表的文章中提出了这一概念，为我们提供了一种新的来解释收入分配的方式。

洛伦兹曲线是一种可视化表示收入分布情况的图表，它通过把不同社会群体的收入支点放在水平轴上，把人口数量放在垂直轴上，把收入两端和收入中心的点用曲线连接起来，就形成了洛伦兹曲线。

在这个曲线上，收入的中心点就是曲线的波峰，而收入的两端就是曲线的最低点。

洛伦兹曲线可以反映出一个国家的收入分布情况。

如果洛伦兹曲线的波峰很低，说明一个国家的收入分布极不均衡，说明在这个国家里，具有较低收入的群体比较多；反之，洛伦兹曲线的波峰越高，说明这个国家的收入分布是比较均衡的，说明这个国家里拥有较高收入的群体越多。

基尼系数是一种比较不同收入水平的社会悬殊状态，也称作基尼不平等指数，是由美国经济学家基尼（James K. Kini）在1912年提出的。

基尼系数是一个分数型的数字，它反映的是一个国家收入分配的不平等程度，基尼系数越大，说明这个国家的收入分配差异越大，收入不均导致的贫富差距也越大。

基尼系数是通过计算洛伦兹曲线最低点和最高点的收入差异来计算的，这两个点分别代表了收入最高、最低的社会群体，也代表了一个国家的收入和财富悬殊程度。

一般来说，如果基尼系数高于1，说明这个国家的收入分布非常不均衡，贫富悬殊差距非常大；如果基尼系数低于1，说明这个国家的收入分布比较均衡，贫富悬殊差距也比较小。

洛伦兹曲线和基尼系数是两个不同的概念，但它们之间存在着一定的联系。

洛伦兹曲线是一种可视化表示不同收入水平群体收入悬殊情况的图表，而基尼系数则是通过计算洛伦兹曲线两端收入差异来衡量一个国家社会不平等状况的指标。

基尼系数与洛伦兹曲线的关系
基尼系数和洛伦兹曲线是经济学中常用的两个指标，用于衡量收入或财富的不平等程度。

基尼系数是一个介于0和1之间的数值，越接近1表示不平等程度越高；而洛伦兹曲线则是一条反映收入或财富分配情况的曲线，越靠近对角线表示分配越公平。

基尼系数和洛伦兹曲线之间的关系是密切的。

基尼系数实际上是洛伦兹曲线下的面积与对角线下的面积之比。

也就是说，洛伦兹曲线的形态越弯曲，基尼系数就越高，反之亦然。

因此，通过观察洛伦兹曲线的形态可以推断出收入或财富分配的不平等程度，而通过计算基尼系数可以更加准确地衡量这种不平等程度的大小。

基尼系数和洛伦兹曲线的应用范围非常广泛，不仅被经济学家广泛用于研究收入或财富分配问题，也被政策制定者用来制定财政和社会政策。

因此，了解基尼系数和洛伦兹曲线的关系以及如何使用它们对经济现象进行分析和评估，对于经济学学生和从事经济研究和政策制定的人员都非常重要。

- 1 -。