从一道中考数学试题谈起

时光荏苒，转眼间已经度过了紧张的中考。

回顾这段备考的日子，我深知数学试卷对于中考的重要性。

在这次备考过程中，我积累了一些关于数学试卷学习的经验和心得，以下是我的一些感悟。

首先，要重视基础知识的学习。

数学试卷中，基础知识占据了很大比重。

要想在数学考试中取得好成绩，就必须打好基础。

因此，我在备考期间，对课本上的知识点进行了系统复习，对公式、定理、性质等进行了归纳总结。

同时，我还注重提高自己的运算能力，通过大量练习题来巩固所学知识。

其次，要掌握解题技巧。

在备考过程中，我发现很多同学在考试中失分，很大程度上是因为解题技巧不足。

为了提高自己的解题能力，我认真分析了历年的中考数学试卷，总结出了一些解题技巧。

例如，遇到选择题时，要学会运用排除法；遇到填空题时，要学会从已知条件出发，逐步推导出答案；遇到解答题时，要学会分步骤进行解答，注意审题和计算。

再次，要培养良好的做题习惯。

在数学考试中，良好的做题习惯对于提高成绩至关重要。

我在备考期间，养成了以下几种习惯：一是审题要仔细，避免因粗心而失分；二是做题要规范，书写要工整，避免因书写不规范而失分；三是遇到难题要冷静，不要慌张，先从简单题目入手，逐步提高信心。

此外，要注重模拟考试。

在备考过程中，模拟考试是检验自己学习成果的重要手段。

通过模拟考试，我发现了自己存在的不足，并及时进行了调整。

在模拟考试中，我注重以下几点：一是模拟考试的时间要充足，确保在规定时间内完成所有题目；二是模拟考试的环境要安静，避免外界干扰；三是模拟考试后要及时总结，找出自己的不足之处。

最后，要保持良好的心态。

在备考过程中，心态对于考试成绩有着重要影响。

我始终保持积极向上的心态，相信自己能够取得好成绩。

在考试中，遇到困难时，我学会了调整心态，以平和的心态面对考试。

总之，通过这次中考数学试卷的学习，我深刻认识到，要想在数学考试中取得好成绩，必须重视基础知识，掌握解题技巧，培养良好的做题习惯，注重模拟考试，并保持良好的心态。

几何解题研究的方法与思考——以一道中考试题为例胡坚波收稿日期：2020-09-23作者简介：胡坚波（1981—），男，中学一级教师，主要从事初中数学课堂教学研究.摘要：解题教学是必不可少的一种课堂教学形式，教师解题研究的能力直接影响到学生对问题理解的深度.教师只有掌握了解题研究的一般方法，才能在课堂中引导学生抓住问题的本质，从而优化解法，并进一步带领学生发现问题、提出问题、解决问题，进而得到一般性的结论，最终提高学生的解题能力、培养学生的数学学科核心素养.文章以2020年中考浙江杭州卷第14题的研究为例，谈谈几何解题研究的一般方法．关键词：中考试题；解题研究；一般方法中考试题的命制往往有其意义，一道看似不起眼的试题，其中很可能蕴含着丰富的内容.如果继续探究下去，或许就能发现试题背后隐藏的深意，从而体现解题的育人价值.本文以2020年中考浙江杭州卷第14题为例，谈谈应该怎样进行几何解题的研究.题目（2020年浙江·杭州卷）如图1，已知AB 是⊙O 的直径，BC 与⊙O 相切于点B ，连接AC ，OC.若sin ∠BAC =13，则tan ∠BOC 的值为.COAB图1作为填空题的第4道题，试题本身不难，主要考查了三角函数的相关知识.不妨设BC =1，则AC =3.解得AB =22，OB =2.则tan ∠BOC作为填空题，此题的求解到这里就结束了，但是作为解题研究，现在才刚刚开始.一、获得研究对象研究图形要抓住图形的本质，为了更容易抓住本质，几何研究要做减法，即去掉非关键因素.此题中，可以隐去圆，那么题目条件等价于“如图2，∠ABM =90°，点C 在射线BM 上，O 是AB 的中点”.观察图形的结构，不难发现，若点C 的位置确定了，则整个图形的形状就随之确定，即∠BOC ，∠BAC ，∠ACO ，∠BCO 的度数也随之确定.原试题就是在确定的条件下进行的定量研究，而研究图形变化过程中的规律性也是几何研究的常见问题.在图2中，当点C 的位置变化时，∠BOC ，∠BAC ，∠ACO ，∠BCO 的大小也随之改变.当点C 从点B 向射线BM 的方向移动时，容易发现∠BOC 和∠BAC 的度数变大，∠OCB 的度数变小，但无法很快确定∠ACO 的变化情况.接下来，我们进一步探究∠ACO 的变化情况.CO ABM 图2··56二、借助技术获得初步猜想几何问题的研究一般要经历画图、测量、计算、猜想、证明的过程.几何画板软件为我们画图、测量、计算提供了很好的辅助.利用几何画板软件对复杂的问题进行初步研究、获得猜想，是常见的研究起点.利用几何画板软件，发现当点C 从点B 向射线BM 的方向移动时，∠ACO 的度数先变大后变小，且∠ACO 取到的最大值约为19.47°（如图3）.进一步计算，发现此时sin ∠ACO ≈0.33.∠OCA =19.47°∠CAO =35.58°sin∠OCA =0.33M ABCO图3猜想：如图3，当∠ABM =90°，点O 是AB 的中点时，射线BM 上存在点C ，使得∠ACO 取到最大值，此时sin ∠ACO ＝13.三、从“数”的角度验证猜想通过利用几何画板软件进行探究，发现点C 的位置决定了∠ACO 的大小，而点C 的位置可以用BC 的长度来刻画，所以继续探究的思路是用BC 的长度表示sin ∠ACO.为了研究方便，不妨设AB =2，BC =x ，根据勾股定理，得OC 2=1+x 2，AC 2=4+x 2.因为S △ACO =12AC ·OC ·sin ∠ACO =12AO ·BC ，所以sin ∠ACO =x x 4+5x 2+4=14因为x 2＋4x 2≥4，所以当x 2=4x 2，即x =2时，x 2＋4x 2的最小值为4.所以得到sin ∠ACO ≤13，即当BC =2时，sin ∠ACO 取最大值13，猜想得证.四、从“形”的角度验证猜想前面我们从“数”的角度验证了猜想，接下来我们从“形”的角度来思考.抓住变化过程中不变的关系是研究几何问题的常用方法.进一步观察图形，我们发现当点C 的位置发生改变时，∠ACO 所对的边AO 的长度始终没有发生变化.即角度在变，角度所对的边不变.这让我们联想到了圆中同弦所对的角.构造过A ，C ，O 三点的⊙D.如图4，若⊙D 与射线BM 相交，设另一个交点为点E.在线段CE 上任意取一点F （除点C ，E 外），连接AF ，OF ，根据圆内角大于同弧所对的圆周角，可得∠AFO ＞∠ACO.故可知此时∠ACO 的度数并没有取得最大值.图4图5如图5，若⊙D 与射线BM 相切于点C ，在射线BM 上任意取一点G （除点C 外），连接AG ，OG ，根据圆外角小于同弧所对的圆周角，可得∠AGO ＜∠ACO.故此时∠ACO 取到最大值，于是得到第一个有价值的结论.结论1：∠ACO 取到最大值的充要条件是过A ，C ，O 三点的⊙D 与射线BM 相切.接下来，求此时∠ACO 的正弦值及BC 的长.可以沿用前面的解题思路，分别求出线段AO ，OC ，AC ，BC 的长度，再利用△ACO 的面积求解.解法1：如图6，连接DC ，AD ，作DH ⊥AO.H O ABCDM图6不妨设AO =BO =1，则AH =OH =12，BH =32.因为⊙D 与射线BM 相切于点C ，所以DC ⊥BC.因为∠B =90°.··57所以四边形BCDH为矩形.所以AD=DC=BH=32.在Rt△ADH中，由勾股定理，得DH=2.所以BC=DH=2.由勾股定理，得OC=3，AC=6.由S△ACO=12AC·OC·sin∠ACO=12AO·BC，代入解得sin∠ACO=13.显然，求解过程还是有些复杂，不妨进一步思考，此图形还有什么特殊性可以应用？从圆的视角看，⊙D与射线BM相切，∠ACO为圆周角，解法豁然开朗.解法2：利用圆周角定理，可以转化到圆心角进行求解，可得∠ADH=∠ACO.所以sin∠ACO=sin∠ADH=AHAD=13.利用圆幂定理，可得BC2=BO·BA.解得BC=2.解法2抓住了问题的本质，解法也更优化、更简洁.“数”和“形”两种思考方法都能验证猜想，可见这也是我们解决几何问题的一般思路.对比两种思路，从“数”的角度思考，往往需要设未知变量，再利用勾股定理、相似、面积关系、三角函数等，列出未知变量与所求量之间的关系，然后用代数的方法求解；从“形”的角度思考，往往需要根据图形的结构，抓住图形中不变的关系，构建出几何模型，再根据图形性质求解.用“数”的方法容易想到，但计算较复杂；用“形”的方法比较直观，计算也相对简单，但是要弄清楚几何模型结构有一定的难度，需要的知识综合度高，也需要一定的逻辑推理.数形结合的思想方法在教学中有其育人价值，在解题教学中我们应让学生经历基本的活动经验，这样才能培养学生必需的基本数学思想.五、追本溯源其实，本问题在数学史中已经存在，称为“米勒问题”.德国数学家米勒于1471年提出“塑像问题”：有一个高a米的塑像立在一个高b米的底座上，一个人朝它走去（人的高度忽略不计），问此人应站在离塑像底座多远的地方，才能使塑像看上去最大（即视角最大）？根据题意画出图形，如图7，AO为雕像，BO为底座，点C表示人，求∠ACO最大时，BC的长.ABO图7这与我们研究的问题非常相似，只是点O的位置不再是中点，这为我们进一步研究问题提供了思路，即可以改变图形的条件，使之更具一般性，进而获得一般性的结论，这是我们进一步研究几何问题的方向.六、改变条件进一步探究1.改变点O的位置受“米勒问题”的启发，我们可以改变点O的位置，使之一般化，为了研究的连贯性，不妨设AB=2，AO=n（0＜n＜2），这样点O在线段AB上就具有一般性了，本质上与“米勒问题”是等价的.因为结论1与点O在线段AB上的位置无关，所以结论1仍成立.如图8，当⊙D与射线BM相切于点C时，∠ACO取得最大值.此时，易得AH=n2，DC=BH=2－n2.所以AD=DC= 2－n2，sin∠ACO=sin∠ADH=AH AD=n4-n.根据圆幂定理，得BC=BO·BA=4-2n.显然当n=1，即点O是AB的中点时，sin∠ACO的最大值为13，此时BC=2.但是这只是其中的一种特殊情况，于是得到第二个有价值的结论.HOA BCDM图8··58结论2：如图8，设∠ABM =90°，AB =2，点O 是线段AB 上一点，AO =n （0＜n ＜2），则在射线BM 上存在点C ，使得∠ACO 取到最大值，且此时sin∠ACO =n 4-n，BC =4-2n.2.改变∠ABM 的大小此题条件里动点C 所在的射线BM 与AB 垂直，显然条件中的位置比较特殊.若从这个角度改变条件，当射线BM 与AB 不垂直，即∠ABM ≠90°时，相当于“米勒问题”中的雕像及底座与地面不垂直时，那么结论2是否仍成立？因为∠ABM ≠90°，所以四边形DCBH 不再是矩形，即DC ≠BH.求半径的解法相应会有所改变，猜想sin ∠ACO 的值与∠ABM 的度数有关.因为结论1与∠ABM 的大小无关，所以结论1仍然成立.∠ACO 取到最大值时，过A ，C ，O 三点的⊙D 与射线BM 相切，故圆幂定理仍然适用，所以BC =BO ·BA =4-2n.所以可得第三个有意义的结论.结论3：设∠ABM =α（0°＜α＜180°），AB =2，点O 是线段AB 上一点，AO =n （0＜n ＜2），则射线BM 上存在点C ，使得∠ACO 取到最大值，且此时BC =4-2n ，sin ∠ACO 的值与∠ABM 的度数无关.接下来，求sin ∠ACO.因为∠ABM 有锐角和钝角两种情况，所以要分两种情形分类进行研究.情形1：如图9，当0°＜α＜90°时，⊙D 与射线BM相切于点C.根据前面的猜想sin ∠ACO 会与α有关，为了将α用上，所以考虑作垂线构造直角三角形.作DH ⊥AO 于点H ，BE ⊥AB 交DC 的延长线于点E ，作DF ⊥BE 于点F.M O AB CD EF GH图9易证∠CBE =∠EDF =90°-α，DF =BH =2-n 2.所以DE =DF cos ()90°－α=4-n 2sin α，CE =BC ·tan ()90°－α=4-2n ·tan ()90°－α，AD =DC =DE -CE =4-n 2sin α-4-2n ·tan ()90°－αsin∠ACO =sin∠ADH =AH AD =n sin α4-n -24-2n cos α.情形2：如图10，当90°＜α＜180°时，⊙D 与射线BM 相切于点C.同样作DH ⊥AO 于点H ，作BE ⊥AB 交DC 于点E ，作DF ⊥BE 交BE 的延长线于点F.H A B CDOEF M图10易证∠CBE =∠EDF =α-90°，DF =BH =2-n 2.所以DE =DF cos ()α－90°=4-n 2sin α，CE =BC ·tan ()α-90°=4-2n ·tan ()α-90°，AD =DC =DE +CE =4-n 2sin α＋4-2n ·tan()α-90°sin∠ACO =sin∠ADH =AH AD 发现两种情形最后结果的表达式是一致的，而把α=90°代入，得sin∠ACO =n 4-n.与之前的计算结果一致，可见角度在变，结果的表达式不变，得到了变化过程中不变关系的本质，于是得到了问题的一般性结论.结论4：设∠ABM =α（0°<α<180°），AB =2，点O 是线段AB 上一点，AO =n （0＜n ＜2），则射线BM 上存在点C ，使得∠ACO 取到最大值，且此时BC =4-2n ，sin∠ACO =3.当射线BM 改为直线BM 时，相当于“米勒问题”中人可以站到雕像的背面进行观察.如图11，当点C 在直线BM 上移动时，由前面的研究可知，当点C 在射线BM 1和BM 2上时，分别有一个点C 1和点C 2，使得∠AC 1O 和∠AC 2O 在各自的射线上取到最大值，那么∠AC 1O 和∠AC 2O 哪个更大一些呢？显然，当BM ⊥AB 时，BC 1=··59BC 2，由对称性可知∠AC 1O =∠AC 2O.当BM 与AB 不垂直时，不妨设∠ABC 1=α（0°<α<90°），则∠ABC 2=180°-α.根据结论4，可以得到sin ∠AC 1O =sin ∠AC 2O =因为0<cos α<1，所以sin ∠AC 1O ＞sin ∠AC 2O.所以∠AC 1O ＞∠AC 2O.得到结论5.M 2OAB MC 1C 2M 1图11结论5：如图11，当点C 在直线BM 上时，设AB =2，点O 是线段AB 上一点，AO =n （0＜n ＜2），如果直线BM 与线段AB 所成的较小的夹角为∠ABM 1（0°＜∠ABM 1≤90°），则点C 一定在射线BM 1上，使得∠ACO 取到最大值，且此时BC =4-2n ，sin∠ACO =七、解后思考回顾整个研究过程，通过图形的变化将一个确定的图形变为不确定的图形，从而获得研究对象.而对于变化中规律的研究，入手比较难，这时信息技术为化解难点提供了帮助.借助几何画板软件，不仅能方便地展示图形变化的过程，而且可以通过教师有意识地控制帮助学生观察影响变化的要素及其关系，从而获得初步的猜想.接着，从“数”和“形”两个角度验证了该猜想，进一步体会到几何问题在“数”和“形”上的统一，体会到数形结合思想在解题中的重要作用.在引出“米勒问题”后，通过进一步改变条件——点的位置变化、角度的大小变化、射线变为直线等，发现了在条件变化过程中不变的结论.通过这样的解题教学研究可以让学生进一步体会到研究几何问题的一般方法——从简单到复杂，从特殊到一般.整个研究过程，具备学习素材的真实性，问题的开放性，学习过程的探索性，学习手段的操作性，探索过程的动态化、可视化，学习体验的形象化、可表达，学习结果的创造性.这些都有利于在今后的学习中，提高学生发现问题和解决问题的能力，进而实现几何解题教学的育人价值.参考文献：［1］王红权.“高考真题分析”习题课的教学实践与思考［J ］.中小学数学（高中版），2015（4）：20-23.［2］章建跃.研究三角形的数学思维方式［J ］.数学通报，2019，58（4）：1-10.··60。

中考数学试卷真题分析中考数学试卷一直被认为是考生们晋级高中所必须要面对的一道关卡。

通过对中考数学试卷的真题分析，我们可以更好地了解试卷的出题趋势和考察重点，为备考提供有效的参考。

本文将针对历年中考数学试卷进行真题分析，以帮助考生们在备考中更为有针对性地进行复习。

第一部分：选择题分析在中考数学试卷中，选择题是考察考生基础知识和解题能力的重要部分。

通过对选择题的真题分析，我们可以发现一些规律和特点。

以2019年某地区中考数学试卷为例，其中选择题部分如下：1. 已知函数 y = -2x + c，若点 (2, 5) 在图像上，则 c = ？A. -9B. -1C. 1D. 92. 如果一个整数 x 满足 x^2 - 5x - 14 = 0，则 x = ？A. -2B. 7C. -7D. 2通过分析上述两道题目，我们可以发现选择题的题目类型主要包括函数与方程、几何和概率统计等。

在备考中，我们需要重点掌握这些知识点，并能够熟练运用。

同时，在解题过程中，要注意审题、排除法和推理等解题技巧的运用，以提高解题正确率。

第二部分：填空题分析填空题是中考数学试卷的另一个重要组成部分。

通过填空题的真题分析，我们可以发现一些解题技巧和常见考点。

以2018年某地区中考数学试卷为例，其中填空题部分如下：1. 根据(x-2)(x+7)的展开式，得到二次项的系数是____。

2. 8的平方根是____。

3. 用分数表示0.875，得到的分数为____。

通过分析上述三道题目，我们可以发现填空题主要考察基础知识和计算能力。

在备考中，我们需要熟练掌握数的运算、代数式的展开等基础知识，并能够迅速准确地计算填空内容。

第三部分：解答题分析解答题在中考数学试卷中占有一定比重，需要考生们具备较强的分析和推理能力。

通过对解答题的真题分析，我们可以找出一些解题技巧和注意事项。

以下是2017年某地区中考数学试卷中的一道解答题例题：某商店的一些商品以七折出售，张三用140 元购买了其中的一部分，问：如果他再多花 10 元，还可以买到商品的数量是多少？解题步骤：1. 根据七折出售的信息，可以得到商品的原价是x元，折扣价是0.7x元。

随着初三中考试卷的揭晓，我对于这次数学考试有了更加深刻的认识。

在这场考试中，我虽然取得了一定的成绩，但也暴露出很多不足。

通过这次听课，我对数学学习有了更深的感悟，以下是我的一些心得体会。

一、基础知识的重要性在这次考试中，我发现很多题目都是围绕基础知识展开的。

要想在数学考试中取得好成绩，首先要打好基础。

基础知识是整个数学体系的基石，只有掌握了基础知识，才能在更高层次上进行思考。

因此，在今后的学习中，我要加强对基础知识的掌握，做到熟练运用。

二、解题方法的多样化在数学学习中，解题方法的选择至关重要。

这次考试中，我发现很多同学在解题时，只限于一种方法，导致解题效率低下。

实际上，对于同一道题目，我们可以从多个角度去思考，运用不同的解题方法。

在今后的学习中，我要努力拓宽解题思路，学会从多个角度分析问题，提高解题能力。

三、审题能力的提升在这次考试中，我发现有些题目失分是因为审题不仔细。

审题是解题的第一步，只有准确把握题意，才能找到解题的关键。

在今后的学习中，我要注重培养自己的审题能力，提高对题目的敏感度，避免因审题失误而失分。

四、时间管理能力的提高在考试中，时间管理能力对于取得好成绩至关重要。

这次考试中，有些同学因为时间分配不合理，导致题目解答不完整。

在今后的学习中，我要合理安排时间，做到心中有数，确保在考试中能够充分发挥自己的水平。

五、团队合作的重要性在数学学习中，团队合作同样重要。

通过听课，我发现很多优秀的同学都善于与同学交流学习心得，共同进步。

在今后的学习中，我要积极参与团队合作，与同学们共同探讨问题，共同提高。

六、坚持不懈的精神数学学习是一个漫长的过程，需要我们坚持不懈地努力。

在这次考试中，我认识到自己的不足，但我相信，只要我坚持不懈地努力，就一定能够取得更好的成绩。

总之，通过这次初三中考试卷的听课，我对数学学习有了更深的认识。

在今后的学习中，我将努力打好基础，拓宽解题思路，提高审题能力，合理安排时间，积极参与团队合作，坚持不懈地努力，争取在数学学习中取得更好的成绩。

中考数学试卷心得体会（经典版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的经典范文，如演讲致辞、总结报告、心得体会、合同协议、条据文书、规章制度、自我介绍、策划方案、职业规划、其他范文等等，想了解不同范文格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample texts for everyone, such as speeches, summary reports, insights, contract agreements, policy documents, rules and regulations, self introduction, planning plans, career planning, and other sample texts. If you want to learn about different formats and writing methods of sample texts, please stay tuned!中考数学试卷心得体会中考数学试卷心得体会【精选5篇】中考数学试卷心得体会怎么写好？本为精选优秀的中考数学试卷心得体会范文，都是标准的书写参考模板。

由一道中考题引出的数学课堂教学的思考中考数学题目：小明家有一口水井，他第一次探测水井深度时用了一根 2 米长的绳子，坠入绳子底部的重物刚好抵住井底，此时绳子正好垂直，小明测得距离井口顶端 1.5 米深处，第二次探测深度时，他用了同样的绳子，重物靠近绳子一端，然后绕着重物转了一圈抛出去落在井底，此时绳子在井边紧绷，小明测得距离井口顶端2 米深处。

试计算此井的深度（取$ \pi \approx 3.14 $）。

这一道中考题是一个典型的应用题，考察了学生对三角函数、相似三角形和勾股定理等知识点的掌握程度。

在数学教学中，应用题可以帮助学生将抽象的数学知识转化为实际生活中的应用场景，提高学生对数学的兴趣和学习积极性。

数学教学应该以学生为中心，注重学生的学习兴趣和自主学习能力的培养。

在教学过程中，教师应该及时调整教学策略，结合学生的实际情况，巧妙设计教学活动，增强学生的参与感和学习体验。

在教学此题时，教师可以采取以下教学方法：一、情境教学法教师可以通过讲述实际生活中的水井问题，引发学生对数学问题的兴趣和探索欲望，将抽象的数学知识转化成具体的场景，提高学生的学习积极性。

二、案例教学法教师可以通过展示相关案例，让学生了解实际生活中的应用案例，激发学生探究问题的好奇心和兴趣，帮助学生更深入地理解数学知识。

三、探究性学习法教师可以给学生每一个环节都进行探究性学习，让学生在体验中学习，让学生自我探索，有个人的领悟，这样学生才有机会真正掌握数学所需要的概念和技能。

四、合作学习法教师可以将学生分为小组，给每个小组分配任务，让小组成员相互协作，互相帮助，让学生在小组中体验合作学习的过程，发现知识的互通，增强对数学知识的理解。

五、启发式教学法教师可以在教学中巧妙地引导学生思考，提出问题，让学生自我探究，通过解决问题，增强学生的发散思维和创新能力。

通过以上教学方法的运用，可以帮助学生更好地掌握中考数学题目，提高学生的数学素养和解决实际问题的能力。

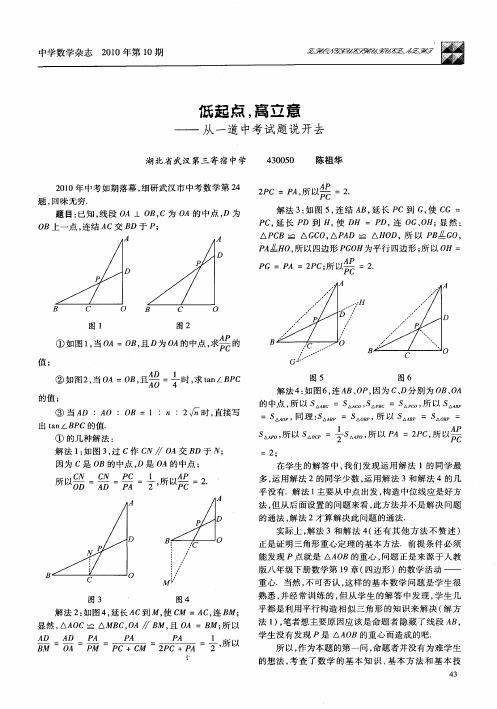
从一道中考题说起重庆市渝高中学周秀娟中考数学压轴题历来是初三师生关注的焦点，它一般有动态问题、开放性题型、探索性题型、存在性题型等类型，涉及到代数、几何多个知识点，囊括初中重要的数学思想和方法。

对于考生而言，中考压轴题是一根标尺，可以比较准确的衡量学生综合解题能力以及数学素养，同时它的得失，可以直接影响到学生今后的发展。

从2010年至2014年，重庆市中考都考查了在动态问题下的存在性问题，A卷其中有三年考查了等腰三角形存在性问题，今天我就2014年重庆市数学中考A卷第26题第3问进行说题。

一、原题再现26．（12分）(2014年重庆市)已知：如图①，在矩形ABCD中，AB=5，AD=，AE⊥BD，垂足是E．点F是点E关于AB的对称点，连接AF、BF．（1）求AE和BE的长；（2）若将△ABF沿着射线BD方向平移，设平移的距离为m（平移距离指点B沿BD方向所经过的线段长度）．当点F分别平移到线段AB、AD上时，直接写出相应的m的值．（3）如图②，将△ABF绕点B顺时针旋转一个角α（0°＜α＜180°），记旋转中的△ABF为△A′BF′，在旋转过程中，设A′F′所在的直线与直线AD交于点P，与直线BD交于点Q．是否存在这样的P、Q两点，使△DPQ为等腰三角形？若存在，求出此时DQ的长；若不存在，请说明理由．二.审题分析本题是运动型综合题，涉及的知识点有：旋转变换、矩形、勾股定理、等腰三角形存在性等知识考点．从条件上看，第（3）小题有Rt△ABF旋转过程中，直线A′F′与直线AD、直线BD 的交点位置变化，讨论等腰三角形存在性的各种情况。

通过观察旋转变换的过程中，图形发生的变化，构造出等腰三角形的条件，利用勾股定理性质的运用，融进矩形，对学生分析问题的能力要求较高，不失一道好的压轴题。

由于此旋转图形是直角三角形，因此解决问题的突破口和切入点就在于此。

画出旋转过程中的图形变化情况，并识别旋转过程中的不变量是解决此问题的难点，学生难于将分散的条件集中到有效的图形变化上进行解决，总有无从下手的感觉。