苏教科版初中数学八年级下册：7-3频数和频率 导学案

7.3频数与频率教学反思在新课改的形式下，如何激发教师的教研热情，提升教师的教研能力和学校整体的教研实效，是摆在每一个学校面前的一项重要的“校本工程”。

所以在学习上级的精神下，本期个人的研修经历如下：1.自主学习：我积极参加网课和网上直播课程.认真完成网课要求的各项工作.教师根据自己的专业发展阶段和自身面临的专业发展问题，自主选择和确定学习书目和学习内容，认真阅读，记好读书笔记；学校每学期要向教师推荐学习书目或文章，组织教师在自学的基础上开展交流研讨，分享提高。

2.观摩研讨：以年级组、教研组为单位，围绕一定的主题，定期组织教学观摩，开展以课例为载体的“说、做、评”系列校本研修活动。

3.师徒结对：充分挖掘本校优秀教师的示范和带动作用，发挥学校名师工作室的作用，加快新教师、年轻教师向合格教师和骨干教师转化的步伐。

4.实践反思：倡导反思性教学和教育叙事研究，引导教师定期撰写教学反思、教育叙事研究报告，并通过组织论坛、优秀案例评选等活动，分享教育智慧，提升教育境界。

5.课题研究：立足自身发展实际，学校和骨干教师积极申报和参与各级教育科研课题的研究工作，认真落实研究过程，定期总结和交流阶段性研究成果，及时把研究成果转化为教师的教育教学实践，促进教育质量的提高和教师自身的成长。

6.专题讲座：结合教育教学改革的热点问题，针对学校发展中存在的共性问题和方向性问题，进行专题理论讲座。

7.校干引领：从学校领导开始，带头出示公开课、研讨课，参与本校的教学观摩活动，进行教学指导和引领。

8.网络研修：充分发挥现代信息技术，特别是网络技术的独特优势，借助教师教育博客等平台，促进自我反思、同伴互助和专家引领活动的深入、广泛开展。

我们认识到：一个学校的发展，将取决于教师观念的更新，人才的发挥和校本培训功能的提升。

多年来，我们学校始终坚持以全体师生的共同发展为本，走“科研兴校”的道路，坚持把校本培训作为推动学校建设和发展的重要力量，进而使整个学校的教育教学全面、持续、健康发展。

课题：频数与频率教学目标1、通过掷硬币的实验，理解频数与频率的概念。

2、会计算实验中某个对象出现的频数与频率。

3、知道多次重复试验中，各试验结果的频数之和等于实验的总次数，各试验结果的频率之和等于1。

教学重点、难点重点： 1、频数和频率的概念及相互联系，频率的计算。

2、知道多次重复试验中，各试验结果的频数之和等于实验的总次数，各试验结果的频率之和等于1.难点：频数与频率的联系和区别。

教学过程一创设情境，导入新课在一次国际象棋比赛中，有两个最优秀的选手始终是平局，于是决定用掷硬币的方法来确定谁是第一名。

把硬币抛掷地面，只有两种可能性，有国徽的一面朝上或者另一面朝上，出现哪种情形的可能性大，假设你是这两个选手中的一员，你会选择“正面”还是“反面”？下面就让我们来通过试验感受抛掷硬币时，出现有国徽的一面朝上的可能性。

二合作交流，探究新知1 掷一枚硬币的试验（1）体会频数与频率的概念两人一组，一人抛硬币，一人记录，花面为正面，字面为反面，第一人抛掷10次后，两人次数 1 2 3 4 5 6 7 8 9 10结果统计：在这10次试验中，正面朝上的有__ __次，反面朝上的有____次。

指出：正面朝上的次数也叫正面朝上的频数，反面朝上的次数也叫反面朝上的频数。

思考：正面朝上的次数和反面朝上的次数以及总次数有什么关系？指出：在一组多次重复实验中，各结果的频数之和等于试验的总次数。

在这10次试验中，正面朝上的次数占总次数的几分之几？反面朝上的次数占总次数的几分之几？指出：正面朝上的次数占总次数的比例叫正面朝上的频率，反面朝上的次数占总次数的比频数频率正面朝上反面朝上和发现：正面朝上的的频率和反面朝上的频率之和等于______频率=( )/( )小结：频数：某个对象重复出现的次数。

频率：某个对象的频数与实验总次数的比值。

在一组多次重复实验中，频数之和等于试验的总次数，频率之和等于1。

频率=频数/总次数 (2)统计10位同学的结果填入下表（体会正面朝上和反面朝上的频率差距大不大？）频数频率正面朝上反面朝上说一说：上面用抛掷硬币的实验来决定冠军时，哪面朝上的可能性大？三课堂练习，巩固提高1、红黑蓝三色小球各一个，形状大小不同，放在同一个不透明的袋子里，每次从中任意摸出两个，然后放回袋中再摸。

2020年八年级数学下册 7.3 频数和频率教案（新版）苏科版
教学目标：1．掌握频数、频率的概念；会求一组数据的频数与频率；
2．通过统计数据，制成各种图表，增强学生对生活中所见到的统计图表进行数据处理和评判的主动意识；
3．培养学生实事求是的科学态度，并通过对数据的整理，提高学生的责任心与耐心细致的工作态度．
重点、难点：频数与频率的概念，会计算频数与频率．在合作探究中，通过频数和频率的计算对一些简单的事情作出合理的推测，识别各种图表的优缺点。

教学过程：
一.【预学指导】
1、调查中产生的数据表示方式有
2、为了增强环保意识，学校规定每个班级选举1名学生当“环保卫士”．八年级（1）班有4名同学参加竞选，你有什么好办法？
二.【问题探究】
问题1：
1、在上述竞选过程中，能出现哪些数据？
2、根据什么数据确定当选同学？
归纳：
为了使用的方便对于上述数据我们给出相应的名称
频数：
频率：
上述调查中4名同学的频数是： 4名同学的频率是：
问题2：
小组讨论：
1．选举“环保卫士”用的是哪种调查方法？
2．每个候选对象得票的频数指的是什么？频数是多少？
3．每个候选对象得票的频率指的是什么？频率是多少？
个人复备4．通过选举产生的“环保卫士”与指定某同学为“环保卫士”这两种方法，你认为哪一种更好些？
三.【拓展提升】
课本尝试P22
此调查中的总数是多少？
按污染指数完成各级的数据。

四.【课堂小结】
通过这节课的学习，你有什么感受呢？【板书设计】
【教学反思】。

课题：7.3 频数和频次课时：1课型：新讲课教课目的：
1．能说出频数、频次的意义，知道频数与频次都能反应每个对象出现的屡次程度.
2．经历检查、采集、整理、剖析数据的活动过程，领会数据在解决实质问题中的
作用，发展数感和统计观点
教课要点：
正确理解频数、频次的意义
教课难点：
正确理解频数、频次的意义
教课方案：设计说明及增补：情课本 P22数学实验室
境
导
入
教
1、观点
学
（1）频数：（2）频次：
过
2、议一议：
程
（1）选举“环保小卫士”用的是哪一种检查方法?
（2）每位候选人得票的频数指的是什么?
（3）每位候选人得票的频次指的是什么?
（4）你以为．经过选举产生“环保小卫士”与指定某同学
为“环保小卫士”这两种方法，哪一种更好 ?
讲堂练习： P22--23试试、练习
小结回首本节课所学内容，说说自己的收获与领会作业增补习题
板书设计 :
教课反省：。

7.3 频数和频率学习目标：1．掌握频数、频率的概念；会求一组数据的频数与频率；2．通过统计数据，制成各种图表，增强学生对生活中所见到的统计图表进行数据处理和评判的主动意识；3．培养学生实事求是的科学态度，并通过对数据的整理，提高学生的责任心与耐心细致的工作态度．重点、难点：频数与频率的概念，会计算频数与频率．在合作探究中，通过频数和频率的计算对一些简单的事情作出合理的推测，识别各种图表的优缺点。

学习过程：一.【预学指导】1、调查中产生的数据表示方式有2、为了增强环保意识，学校规定每个班级选举1名学生当“环保卫士”．八年级（1）班有4名同学参加竞选，你有什么好办法？二.【问题探究】问题1：1、在上述竞选过程中，能出现哪些数据？2、根据什么数据确定当选同学？归纳：为了使用的方便对于上述数据我们给出相应的名称频数：频率：上述调查中4名同学的频数是： 4名同学的频率是：问题2：小组讨论：1．选举“环保卫士”用的是哪种调查方法？2．每个候选对象得票的频数指的是什么？频数是多少？3．每个候选对象得票的频率指的是什么？频率是多少？4．通过选举产生的“环保卫士”与指定某同学为“环保卫士”这两种方法，你认为哪一种更好些？三.【拓展提升】课本尝试P22此调查中的总数是多少？按污染指数完成各级的数据。

四.【课堂小结】通过这节课的学习，你有什么感受呢？五.【反馈练习】1、下列说法中，正确的是（）A．频数表示每个对象出现的次数与总次数的比值B.频率表示每个对象出现的次数C.频数与总次数的比值是频率D．频率与总次数的比值是频数2、●○●○○●○○○●○○○○●○○○○○，出现实心圆的频数是，频率是，出现空心圆的频数是，频率是3、某班有50名学生，如果将他们按出生月份分成4组，其中4～6月份组的频率为0.32，则这个组有名同学。

5．下表是对某班50名学生如何到校问题进行的～次调查结果，根据表中已知数据填表：。

7.3 频数与频率-苏科版八年级数学下册教案课程内容概要本节课主要介绍频数和频率的定义及计算方法，通过例题和练习掌握两个概念并能够灵活运用。

教学目标1.了解频数和频率的概念和计算方法；2.掌握频数和频率的计算技巧；3.能够在实际问题中应用频数和频率。

教学重难点1.频数的定义和计算；2.频率的定义和计算；3.频数和频率的联系和区别。

教学内容及方法1.概念讲解–进行简要的概念解释，引导学生理解频数和频率的基本概念和含义。

2.案例演示–搭配典型的例题或问题，演示如何计算频数和频率，并帮助学生理解实际应用中的相关计算方法。

3.问题练习–设计重心在于拓展学生思维和应用能力的问题，使学生能够深刻理解并熟练掌握频数和频率的计算方法。

4.总结提高–课堂结束前进行简单的总结，并结合练习题的答案和解法，对上述知识点进行巩固和提高。

教学过程1. 概念解释首先，让我们来了解一下频数和频率的概念：•频数：在一组数据中某一数值出现的次数。

•频率：某个数值在总频数中所占的比例。

2. 案例演示假设班级有 40 名学生，他们的考试成绩分别为：成绩频数80 1290 18100 10现在，我们可以通过这张表计算出这组数据的总频数，以及每个数值的频率。

•总频数：12 + 18 + 10 = 40•80 的频率：12 ÷ 40 = 0.3（30%）•90 的频率：18 ÷ 40 = 0.45（45%）•100 的频率：10 ÷ 40 = 0.25（25%）通过这个例子，我们可以看出，频数和频率是计算数据分布情况的两个重要参数，能够很好地反映数据的集中趋势和离散程度。

3. 问题练习接下来，我们进行一些练习，加深对频数和频率的理解和掌握。

问题 1某班级进行了一次月考，英语成绩的分布情况如下：成绩频数60 665 870 1075 1280 14请计算出英语成绩的总频数，并求出 65 分的频率。

问题 2某市场调查机构对某市某项商品的销售情况进行了调查，得到如下数据：销售额频数0~10 2010~20 3020~30 1530~40 5请计算出该项商品的总销售额，并求出销售额在 20 元以上的频率。

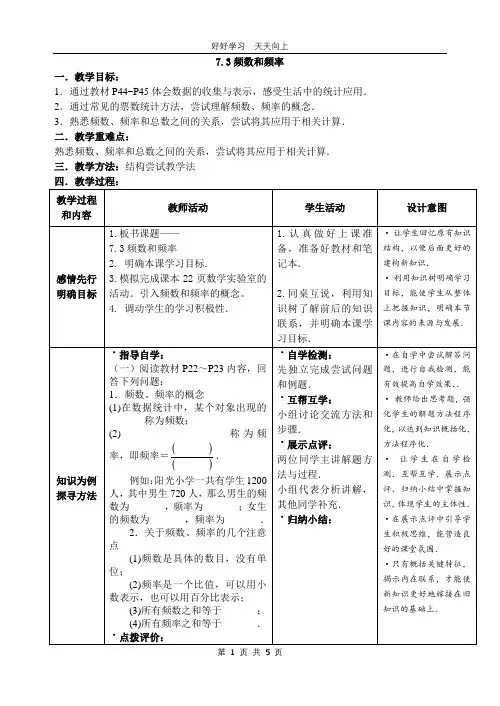
7.3频数和频率一．教学目标：1．通过教材P44~P45体会数据的收集与表示，感受生活中的统计应用．2．通过常见的票数统计方法，尝试理解频数、频率的概念．3．熟悉频数、频率和总数之间的关系，尝试将其应用于相关计算．二．教学重难点：熟悉频数、频率和总数之间的关系，尝试将其应用于相关计算．三．教学方法：结构尝试教学法四．教学过程：教师对学生展示．点评．提问等情况作出积极的评价．˙归纳小结变式训练感悟验证1、某班学生一次数学测验的成绩如下（单位：分）：64 85 92 54 70 8262 70 92 79 82 81 6877 82 80 95 62 70 9590 71 71 88 82 8791 89 86 68 72 97 5467 75 78 84 88 76 88请你根据上面的数据填表（含最小值和最大值）．点评：计算各个频率后，发现各频率之和等于1．2、未成年人的思想道德建设越来越受到社会的关注．某青少年研究所随机调查了泰州市内某校100名学生寒假用零花钱的数量（取整数元），以便引导学生树立正确的消费观．根据调查数据制成如下统计表：根据表中信息，解答下列问题：(1)将表格填写完整；(2)这次调查的样本容量是_______；(3)研究所认为，应对寒假用零花钱150元以上的学生提出勤俭节约的建议，试估计应对该校1 000名学生中的多少名学生提出这项建议？点评：解决此题的关键是准确地理解基本概念以及频率、频数、样本容量之间的计算关系和一些常用的结论，如各小组的频数之和等于样本容量，各小组的频率之和等于1．分组完成．同学黑板板演．完成后相互检查，并指出错误，及时订正．提示：与同学合作，采用“唱票”的方法统计数据，频率等于各分数段的人数与总人数的比值解答：填表如下：提示：根据频率的总和为1，很容易计算出100.5～150.5这一小组的频率为0.25，再根据频率计算公式就可以求出各小组的频数，把表格补全．样本容量是指样本中个体的数目，没有单位．第(3)题是通过样本的情况去估计总体的情况．解答：(1)由题意，第一组的频数为0.1×100＝10；第三组的频率为1－0.1－0.2－0.3－0.1－0.05＝0.25；第三组的频数为100×0.25＝25；频率合计为1；(2) 100；(3)(0.3＋0.1＋0.05)×1000＝450（人）．∴估计应对该校1000名学生中的·强化方法．·写出并说出解题方法和步骤，用好“出声思维”的同时，使学生更好的加深对知识概念的理解．·再练一组加强方法的理解。

频数和频次【学习目标】1．掌握频数、频次的观点；会求一组数据的频数与频次；2．经过统计数据，制成各样图表，加强学生对生活中所见到的统计图表进行数据办理和评判的主动意识；3．培育学生脚踏实地的科学态度，并经过对数据的整理，提升学生的责任心与耐心仔细的工作态度。

【学习重难点】频数与频次的观点，会计算频数与频次。

在合作研究中，经过频数和频次的计算对一些简单的事情做出合理的推断，辨别各样图表的优弊端。

【学习过程】一、预学指导1．检查中产生的数据表示方式有2．为了加强环保意识，学校规定每个班级选举1名学生当“环捍卫士”。

八年级（1）班有4名同学参加竞选，你有什么好方法？二、问题研究问题1：1．在上述竞选过程中，能出现哪些数据？2．依据什么数据确立入选同学？概括：为了使用的方便关于上述数据我们给出相应的名称频数：频次：上述检查中4名同学的频数是：名同学的频次是：问题2：小组议论：1．选举“环捍卫士”用的是哪一种检查方法？2．每个候选对象得票的频数指的是什么？频数是多少？3．每个候选对象得票的频次指的是什么？频次是多少？4．经过选举产生的“环捍卫士”与指定某同学为“环捍卫士”这两种方法，你以为哪一种更好些？三、讲堂小结经过这节课的学习，你有什么感觉呢？四、反应练习1．以下说法中，正确的选项是（）．频数表示每个对象出现的次数与总次数的比值B．频次表示每个对象出现的次数C．频数与总次数的比值是频次D．频次与总次数的比值是频数2．●○●○○●○○○●○○○○●○○○○○，出现实心圆的频数是，频次是，出现空心圆的频数是，频次是3．某班有50名学生，假如将他们按出生月份分红4组，此中4～6月份组的频次为0 .32，则这个组有名同学。

4．下表是对某班 50名学生怎样到校问题进行的～次检查结果，依据表中已知数据填表：。