最新重庆中考数学几何证明题--(专题练习+答案详解)

2021年重庆中考数学第26题几何证明专题训练1.如图1，在Rt△ACB中，AC=BC，过B点作BD⊥CD于D点，AB交CD于E．(1)如图1，若AC=6，tan∠ACD=2，求DE的长；(2)如图2，若CE=2BD，连接AD，在AD上找一点F，使CF=DF，在FD上取一点G，使∠EGF=∠CFG，求证：AF=EG；(3)如图3，D为线段BC上方一点，且∠BDC=90°，AC=6，连接AD，将AD绕A点逆时针旋转90°，D点对应点为E点，H为DE中点，求当AH有最小值时，直接写出△ACH 的面积．2.在△ABC中，∠BAC=90°，点E为AC上一点，AB=AE，AG⊥BE，交BE于点H，交BC于点G，点M是BC边上的点．(1)如图1，若点M与点G重合，AH=2，BC=√26，求CE的长；(2)如图2，若AB=BM，连接MH，∠HMG=∠MAH，求证：AM=2√2HM；(3)如图3，若点M为BC的中点，作点B关于AM的对称点N，连接AN、MN、EN，请直接写出∠AMH、∠NAE、∠MNE之间的角度关系．3.如图，在△ABC和△DEF中，AB=AC，DE=DF，∠BAC=∠EDF=120°，线段BC与EF相交于点O．(1)若点O恰好是线段BC与线段EF的中点．①如图1，当点D在线段BC上，A、F、O、E四点在同一条直线上时，已知BC=4√3，DE=√3，求AD的长；②如图2，连接AD，CF相交于点G，连接OG，BG，当BG⊥OG时，求证：BG=√3CG．2(2)若点D与点A重合，CF//AB，H、K分别为OC、AF的中点，连接HK，直接写出HKAE−OF 的值．AC，连接4.在△ABC和△AEF中，∠AFE=∠ABC=90°，∠AEF=∠ACB=30°，AE=12 EC，点G是EC中点，将△AEF绕点A顺时针旋转．(1)如图1，若E恰好在线段AC上，AB=2，连接FG，求FG的长度；(2)如图2，若点F恰好落在射线CE上，连接BG，证明：GB=√3AB+GC；2GC最大时，直接写出直线AB，(3)如图3，若AB=3，在△AEF旋转过程中，当GB−12AC，BG所围成三角形的面积．5.如图，四边形ABCD为正方形，△AEF为等腰直角三角形，∠AEF=90°，连接FC，G为FC的中点，连接GD，ED．(1)如图①，E在AB上，直接写出ED，GD的数量关系．(2)将图①中的△AEF绕点A逆时针旋转，其它条件不变，如图②，(1)中的结论是否成立？说明理由．(3)若AB=5，AE=1，将图①中的△AEF绕点A逆时针旋转一周，当E，F，C三点共线时，直接写出ED的长．6.如图1，在四边形ABCD中，AC交BD于点E，△ADE为等边三角形．(1)若点E为BD的中点，AD=4，CD=5，求△BCE的面积；(2)如图2，若BC=CD，点F为CD的中点，求证：AB=2AF；(3)如图3，若AB//CD，∠BAD=90°，点P为四边形ABCD内一点，且∠APD=90°，连接BP，取BP的中点Q，连接CQ.当AB=6√2，AD=4√2，tan∠ABC=2时，求CQ+√10BQ的最小值．107.已知△ABC中，∠ACB=90°，AC=2BC．(1)如图①，若AB=BD，AB⊥BD，求证：CD=√2AB；(2)如图②，若AB=AD，AB⊥AD，BC=1，求CD的长；(3)如图③，若AD=BD，AD⊥BD，AB=2√5，求CD的长．8.在△ABC中，∠ABM=45°，AM⊥BM，垂足为M，点C是BM延长线上一点，连接AC．(1)如图1，若AB=3√2，BC=5，求AC的长；(2)如图2，点D是线段AM上一点，MD=MC，点E是△ABC外一点，EC=AC，连接ED并延长交BC于点F，且点F是线段BC的中点，求证：∠BDF=∠CEF．9.在平行四边形ABCD中，对角线AC、BD交于点O，过点A作AE⊥BC于E，过点C作CF⊥CD交AE于点F，连接OF.以OF为直角边作Rt△OFG，其中∠OFG=90°，连接AG．(1)如图1，若∠EAB=30°，OA=2√3，AB=6，则求CE的长度；(2)如图2，若CF=CD，∠FGO=45°，求证：EC=√2AG+2EF；(3)如图3，动点P从点A运动到点D(不与点A、点D重合)，连接FP，过点P作FP的垂线，又过点D作AD的垂线交FP的垂线于点Q，点A′是点A关于FP的对称点，连接A′Q.若AE=2EC，FG=2OF，EF=1，AG=√5，则在动点P的运动过程中，直接写出A′Q的最小值．10.在正方形ABCD中，E为边CD上一点(不与点C、D重合)，垂直于BE的一条直线MN分别交BC、BE、AD于点M、P、N，正方形ABCD的边长为6．(1)如图1，当点M和点C重合时，若AN=4，求线段PM的长度；(2)如图2，当点M在边BC上时，判断线段AN、MB、EC之间的数量关系，并说明理由；(3)如图3，当垂足P在正方形ABCD的对角线AC上运动时，连接NB，将△BPN沿着BN翻折，点P落在点P′处，AB的中点为Q，直接写出P′Q的最小值．11.如图1，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F．(1)求∠CPE的度数；(2)如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°时，连接CE，试探究线段AP与线段CE的数量关系，并说明理由．12. 如图，在菱形ABCD 中，∠ABC =60°，分别过点B 作BC 的垂线，过点D 作CD 的垂线，两垂线相交于点E ．(1)如图1，若AD =4，连接AE ，BD ，求三角形ADE 的面积；(2)如图2，点F 是DE 延长线上的一点，点G 为EB 延长线上的一点，且EF =BG ，连接BF ，DG ，DG 交FB 的延长线于点H ，连接AH ，试猜想线段AH ，BH ，HD 的数量关系并证明你的结论；(3)如图3，在(2)的条件下，在AH 上取得一点P ，使得HP =3AP ，已知Q 为直线ED 上一点，连接BQ ，连接QP ，当BQ +QP 最小时，直接写出S △QDC S 菱形ABCD 的值．13. 如图，已知△ABC 中，∠ABC =45°，CD 是边AB 上的高线，E 是AC 上一点，连接BE ，交CD 于点F ．(1)如图1，若∠ABE =15°，BC =√3+1，求DF 的长；(2)如图2，若BF =AC ，过点D 作DG ⊥BE 于点G ，求证：BE =CE +2DG ；(3)如图3，若R 为射线BA 上的一个动点，以BR 为斜边向外作等腰直角△BRH ，M 为RH 的中点.在(2)的条件下，将△CEF 绕点C 旋转，得到△CE′F′，E ，F 的对应点分别为E′，F′，直线MF′与直线AB 交于点P ，tan∠ACD =13，直接写出当MF′取最小值时RMPF′的值．14. 如图△ABC 为等腰直角三角形，∠A =90°，D 、E 分别为AB 、AC 边上的点，连接DE ，以DE 为直角边向上作等腰直角三角形DEF ，连接BE 、BF ．(1)如图1，当CE =AD 时，求证：BF ⊥BD ；(2)如图2，H 为BE 的中点，过点D 作DG ⊥BC 于点G ，连接GH.求证：BF =2HG ；(3)如图3，BE 与DF 交于点R ，延长BF 交AC 于点P ，∠APB 的角平分线交BE 于点Q.若点E 为AC 上靠近点A 的三等分点，且tan∠AED =67，请直接写出BR QR 的值．15. 如图，△ABC 是等边三角形，△BDE 是顶角为120°的等腰三角形，BD =DE ，连接CD ，AE ．(1)如图1，连接AD ，若∠ABE =60°，AB =BE =√3，求CD 的长；(2)如图2，若点F 是AE 的中点，连接CF ，DF.求证：CD =2DF ；(3)如图3，在(2)的条件下，若AB =2√3，BD =2，将△BDE 绕点B 旋转，点H 是△AFC 内部的一点，当DF 最大时，请直接写出2HA +HF +√5HC 的最小值的平方．16.如图，点B，C，D在同一条直线上，△BCF和△ACD都是等腰直角三角形.连接AB，DF，延长DF交AB于点E．(1)如图1，若AD=BD，DE是△ABD的平分线，BC=1，求CD的长度；(2)如图2，连接CE，求证：DE=√2CE+AE；(3)如图3，改变△BCF的大小，始终保持点F在线段AC上(点F与点A，C不重合).将ED绕点E顺时针旋转90°得到EP.取AD的中点O，连接OP.当AC=2时，直接写出OP 长度的最大值．17.如图，已知△ABC为等腰直角三角形，AB=AC且∠CAB=90°，E为BC上一点，且BE=AC，过E作EF⊥BC且EF=EC，连接CF．(1)如图1，已知AB=2，连接AE、AF，求△AEF的面积；(2)如图2所示，D为AB上一点，连接DB，作∠DBH=45°交EF于H点，求证：CD=HF+√2CE；(3)已知△ABC面积为8+4√2，D为射线AC上一点，作∠DBH=45°，交射线EF于H，连接DH，点M为DH的中点，当CM有最小值时，请直接写出△CMD的面积．18.如图，Rt△ABC中，∠ABC=90°，AB=BC，点E是边BC上的一个动点，点D是射线AC上的一个动点；连接DE，以DE为斜边，在DE右侧作等腰Rt△DFE，再过点D 作DH⊥BC，交射线BC于点H．(1)如图1，若点F恰好落在线段AE上，且∠DEH=60°，CD=3√2，求出DF的长；(2)如图2，若点D在AC延长线上，此时，过F作FG⊥BC于点G，FG与AC边的交点记为M，当AE=DE时，求证：FM+√2MD=AB；(3)如图3，若AB=4√10，点D在AC延长线上运动，点E也随之运动，且始终满足AE=DE，作点E关于DF的对称点E′，连接CF、FE′、DE′，当CF取得最小值时，请直接写出此时四边形CFE′D的面积．19.如图1，在Rt△ABC中，∠BAC=90°，AB=AC，点D是BC边上一动点，连接AD，把AD绕点A顺时针旋转90°，得到AE，连接DE．(1)如图1所示，若BC=4，在D点运动过程中，当tan∠BDE=8时，求线段CD的长；11(2)如图2所示，点F是线段DE的中点，连接BF并延长交CA延长线于点M，连接DM，交AB于点N，连接CF，AF，当点N在线段CF上时，求证：AD+BF=CF；(3)如图3，若AB=2√3，将△ABC绕点A顺时针旋转得△AB′C′，连接CC′，P为线段CC′上一点，且CC′=√3PC′，连接BP，将BP绕点B顺时针旋转60°得到BQ，连接PQ，K 为PQ的中点，连接CK，请直接写出线段CK的最大值．20.在△ABC中，AC=BC，D为△ABC外一点，连接CD．(1)如图1，若∠ACB=60°，CD//AB，连接BD交AC于点E，且CD=2AB=2，求S△BCE．EC，(2)如图2，CE=CD，∠ECB=∠DCA，ED交AB于点F，FG垂直平分EC，且FG=12BF．M，N分别为AF，CD中点，连接MN，求证：MN=12(3)如图3，若∠ACB=90°，CD//AB，将AD绕着A点顺时针旋转60°得到AD′，连接DD′，BD′，且AC=√6，求BD′的最小值．21.已知，等腰直角△ABC中，AC=BC，∠ACB=90°，D为AB边上的一点，连接CD，以CD为斜边向右侧作直角△CDE，连接AE并延长交BC的延长线于点F．(1)如图1，当∠CDE=30°，AD=1，BD=3时，求线段DE的长；(2)如图2，当CE=DE时，求证：点E为线段AF的中点；(3)如图3，当点D与点A重合，AB=4时，过E作EG⊥BA交直线BA于点G，EH⊥BC交直线BC于点H，连接GH，求GH长度的最大值．22.如图，在锐角△ABC中，∠ACB=45°，点D是边BC上一动点，连接AD，将线段AD绕点A逆时针旋转90°得到线段AE，连接DE交AC于点F．(1)如图1，若∠ADC=60°，求证：DF=AF+EF；(2)如图2，在点D运动的过程中，当∠ADC是锐角时，点M在线段DC上，且AM=AD，连接ME，猜想线段ME，MD，AC之间存在的数量关系，并证明你猜想的结论；(3)在点D运动的过程中，当∠ADC是钝角时，点N是线段DE上一动点，连接CN，若AF=m，请直接用含m的代数式表示2CN+√2NE的最小值．CF=3523.如图1，在Rt△ABC与Rt△ABD中，∠ACB=∠ADB=90°，∠BAC=60°，CE⊥AB交AB于点E，AE=AD，点F在线段BD上，连接AF．(1)若AC=4，求线段BD的长；(2)如图2，若∠DAF=60°，点M为线段BF的中点，连接CM，证明：2CM=BF+√3AC；(3)如图3，在(2)的条件下，将△ADF绕点A旋转得△AD′F′，连接BF′，点M为线段BF′的中点，连接D′M，当D′M长度取最小时，在线段AB上有一动点N，连接MN，将线段MN绕点M逆时针旋转60°至MN′，连接D′N′，若AC=4，请直接写出(2MN′−√2D′N′)的最小值．。

重庆中考24题几何证明专题训练1、如图，△ABC 中，∠ABC=45°，过点C 作CD ⊥AB 于点D ，过点B 作BM ⊥AC 于点M ，BM 交CD 于点E ，且点E 为CD 的中点，连接MD ，过点D 作ND ⊥MD 于点D ，DN 交BM 于点N ． 1）若BC= ，求△BDE 的周长； 2）求证：NE －ME=CM ．2、如图,正方形ABCD 的边长为6, 点E 在边AB 上，连接ED ,过点D 作FD ⊥DE 与BC 的延长线相交于点F , 连接EF 与边CD 相交于点G 、与对角线BD 相交于点H ． (1)若BD ＝BF ，求BE 的长；(2)若∠2＝2∠1,求证：HF ＝HE ＋HD ．3、如图，△ABC 中，∠BAC=90°，AB=AC ，AD ⊥BC ，垂足是D ，AE 平分∠BAD ，交BC 于点E.在△ABC 外有一点F ，使FA ⊥AE ，FC ⊥BC.（1）求证：BE=CF ；（2）在AB 上取一点M ，使BM=2DE ，连接MC ，交AD 于点N ，连接ME.求证：①ME ⊥BC ；②DE=DN.4、在正方形ABCD 中，E 为CD 上一点，连接AE ，过点C 作CF⊥AE 的延长线于点F ，连接DF ，过点D 作DG⊥DF 交AE 于点G ． （1）求证：△AGD≌△CFD ；（2）若E 为CD 的中点，求证：CF+EF=GE ．5、如图，在正方形ABCD 中，点E 是AB 中点，点F 是AD 上一点，且DE ＝CF ，ED 、FC 交于点G ，连接BG ，BH 平分∠GBC 交FC 于H ，连接DH 。

（1）若DE ＝10，求线段AB 的长；（2）求证：DE －HG ＝EG 。

6．如图，矩形ABCD 中，点E 是∠ABC 的平分线上一点，且AE ⊥CE 于点E ，连接ED ，BE 与边AD 边相交于点F 。

（1）求证：EF=ED ；（2）若AB=3，BC=5，求四边形BCDE 的面积。

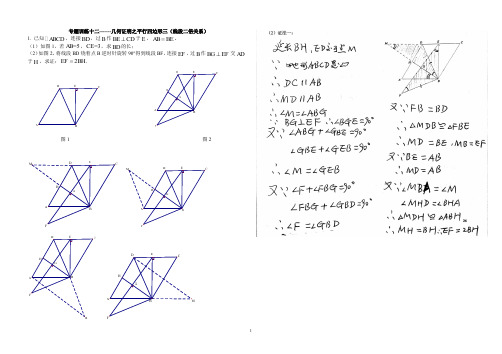
专题训练十二-------几何证明之平行四边形三（线段二倍关系）1. 已知ABCD ，连接BD ，过B 作BE CD ⊥于E ，AB BE =。

（1）如图1，若=5AB ，=3CE ，求BD 的长； （2）如图2，将线段BD 绕着点B 逆时针旋转90°得到线段BF ，连接EF ，过B 作BG EF ⊥交AD 于H ，求证：2.EF BH =图1 图22.已知平行四边形ABCD,过点A作BC的垂线,垂足为点E,且满足AE=EC,过点C作AB 的垂线,垂足为点F,交AE于点G,，连接BG.(1)如图1，若4AC CD=,求BG的长度;(2)如图2，取AC上一点Q,连接EQ,在△QEC内取一点,连接QH，EH，过点H作AC的垂线,垂足为点P，若QH=EH，∠QEH=45°，求证:AQ=2HP.3.如图，在ABCD中，连接AC，AB=AC，点E为BC一点，连接AE，且BE AE=，延长AE至F，使AF CE=，连接BF.（1）如图1，若0120BAC∠=，AC=求EF的长；（2）如图2，若BF＝2CE，连接CF并延长，交AB于点G，求证：2.CF FG=图1 图2证明：如图，过A作AH∥BC，∵EB＝EA，AB＝AC，∴∠BAE＝∠ABC，∠ABC＝∠ACB，∴∠BAE＝∠ACB，∵AF EC=，在△ABF和△CAE中AB ACBAE ACBAF EC=⎧⎪∠=∠⎨⎪=⎩∴△ABF≌△CAE（SAS），∴BF＝AE，∵BF＝2CE，∴AE＝2CE＝2AF，∴AF＝FE，∵AH∥BC，∴∠G＝∠ECF，∠GAF＝∠CEF，B在△AGE和△DCE中GAF CEFG ECF AF FE∠∠∠∠⎧⎪⎨⎪⎩＝＝＝∴△AHF≌△ECF（AAS），∴HF＝CF，AH＝CE＝AF，∴△AHF为等腰三角形，∴∠HAG＝∠ABC＝∠BAE，∴G为HF的中点，∴CF＝HF=2FG，4. 如图，在ABCD中，连接AC，BC＝AC，E为线段BC上一点，，且BE＝AE，过B作BF⊥AC于点F，取BC的中点G，连接AG．（1）如图1，若BF=AF=AG的长；（2）如图2，若∠BA,E＝∠CAG，求证：AC＝2AG.B图1 图2（2）证法一：（2）证法二：（2）证法三：5.如图，在四边形ABCD中，线段DE与四边形的边BC交于点E，对角线相交于点O，AG、CF分别垂直DE于点G和点F，连接OG．（1）如图1，若四边形ABCD为正方形，BC＝6，BE＝2EC，求DG的长；（2）如图2，若四边形ABCD为平行四边形，DE平分∠ADC，其它条件不变，求证：BE＝2OG．解：（1）如图1，∵四边形ABCD为正方形，∴AD＝CD＝BC＝6，∠ADC＝∠BCD＝90°∵BE＝2EC，∴EC＝2∴DE ＝＝＝2∵AG、CF分别垂直DE于点G和点F，∴∠AGD＝∠CFD＝90°∵∠DAG+∠ADG＝∠CDE+∠ADG＝90°∴∠DAG＝∠CDE∴△ADG∽△DEC∴＝，即＝∴DG ＝．（2）证明：如图2，延长AB、DE交于点H，∵DE平分∠ADC，∴∠ADH＝∠CDE∵四边形ABCD为平行四边形，∴AB∥CD，AD∥BC，OB＝OD∴∠CED＝∠ADH，∠H＝∠CDE∴∠H＝∠ADH＝∠CDE＝∠CED＝∠BEH∴BE＝BH，AH＝AD，∵AG⊥DH，∴DG＝GH，∴OG ＝BH∴OG ＝BE，即BE＝2OG．6.如图，在平行四边形ABCD中，CE⊥BC交AD于点E，连接BE，点F是BE上一点，连接CF．（1）如图1，若∠ECD＝30°，BC＝BF＝4，DC＝2，求EF的长；（2）如图2，若BC＝EC，过点E作EM⊥CF，交CF延长线于点M，延长ME、CD相交于点G，连接BG交CM于点N，若CM＝MG，求证：EG＝2MN．（1）解：如图1中，∵四边形ABCD是平行四边形，∴AD∥BC，∵EC⊥BC，∴AD⊥EC，∴∠BCE＝∠CED＝90°，∵∠ECD＝30°，CD＝2，∴CE ＝，在Rt△BCE中，BE ＝＝，∵BC＝CF＝4，∴EF＝BE﹣BF ＝﹣4．（2）证法一：如图2中，延长GM到H，使得MH＝MG，连接CH，BH．∵CM＝MG＝MH，CM⊥GH，∴∠HCG＝90°，CH＝CG，∴∠HCG＝∠BCE，∴∠BCH＝∠ECG，∵CB＝CE，∴△BCH≌△ECG（SAS），∴BH＝EG，∠CHB＝∠CGE＝45°，∵∠CHG＝45°，∴∠BHG＝90°，∴∠BHG＝∠CMG＝90°，∴MN∥BH，∵HM＝HG，∴BN＝NG，∴BH＝2MN，∴EG＝2MN．证法二：7.如图所示，在ABCD中，AC BC⊥，点E是CD的中点，连接AE，作AF AE⊥交BC于点F．（1）若2AC=，BC，求AE的长；（2）点G为BC延长线上一点，且AG CG BC+=，求证：2EG AF=．（1）解：AC BC⊥，90ACB∴∠=︒，2AC =，BC=，3AB∴=，四边形ABCD是平行四边形，3CD AB∴==，//AD BCCA AD∴⊥，90CAD∴∠=︒，CE ED=，1322AE CD∴==．（2）证法一：如答图1，延长AE交BC的延长线于M．//AD CM，DAE M∴∠=∠，AED MEC∠=∠，DE EC=，第25题图DAE MCE ∴∆≅∆， AE EM CM AD ∴==，，又AD BC =，AM CD AB ∴==， BC CM ∴=，又AG CG BC +=， AG GM ∴=， GE AM ∴⊥，090,GEM ∴∠=又AF AE ⊥，090,FAE ∴∠=,FAE GEM ∴∠=∠ //EG AF ∴AE EM =，FG GM ∴=EG ∴是AFM ∆的中位线， 2EG AF ∴=．证法二：如答图2，延长GE 交AD 的延长线于M ．//,AD BCD ECG ∴∠=∠，又MED CEG ∠=∠，DE EC =，GEC MED ∴∆≅∆，,CG MD ∴= 又AG CG BC +=AD BC =，AG AM ∴=， AE GM ∴⊥，AF AE ∴⊥ //MG AF ∴又//AM FG∴四边形AFGM 是平行四边形，2AF GM GE ∴==，8.已知如图，平行四边形ABCD 中，连接BD ，点E 、F 是BC 上两点，且BE CF =，过点E 作EG DF ⊥，交DC 于点G ,交DF 于点.H（1） 如图1，若,2DH EH DE HG ===，求DG 的长；（2） 如图2，若090,BD C ∠=D B D C =，过点F 作FM DC ⊥于点M ，连接AG ，求证：2.DG CM =AA图1 图2A答图2BD9.在ABCD中，BH平分∠ABC交AD于H，交AC于E，过点A作AG⊥BC于点G，过点E作FE⊥EC交BC于F，连接GE.(1)如图1,若G为BF中点, BG=5, AG=12,2BC AH=，求FC长度；(2)如图2,若AG=EG,∠BAE+∠EFC=180°,求证:HD=2AG.B图1 图210.如图，ABCD中，连接AC，090,BACAB AC∠==,点E是边BC上一点，（1）如图1，若4,AB CE==BE；（2）如图2，过点A作AF AE⊥且=AF AE，连接CF，过点A作AG CF⊥交BC于点H，求证：2.CF AH=DD图1 图211.如图，ABCD的对角线AC、BD相交于点O，AC=BC.（1）如图1，过点B作BE⊥AC于点E，若AC=8，BE=6，求OE的长；（2）如图2，若∠BDC=045,过点C作CF⊥CD交BD于F，过B作BG⊥BC，且BG=BC,.连接AG、DG，求证：AG=2OF.B图1 图2HB12. 已知，在▱ABCD中，AB⊥AC，点E是AC上一点，连换BE，延长BE交AD于点F，BE＝CE．（1）如图1，当∠AEB＝60°，BF＝2时，求▱ABCD的面积；（2）如图2，点G是过点E且与BF垂直的直线上一点，连接GF，GC，FC，当GF＝GC时，求证：AB＝2EG．（1）解：如图1中，∵四边形ABCD是平行四边形，∴AD∥BC，∴∠EAF＝∠ECB，∠AFE＝∠EBC，∵EB＝EC，∴∠EBC＝∠ECB，∴∠EAF＝∠EF A，∴EA＝EF，∴AC＝BF＝2，∵∠AEB＝∠EBC+∠ECB＝60°，∴∠ACB＝∠ECB＝30°，∴AB＝AC•tan30°＝，∴S 平行四边形ABCD ＝AB •AC＝．（2）证明：如图2中，作GH ⊥CF 于H ．∵CA ＝BF ，∠ACB ＝∠FBC ＝30°，BC ＝CB ， ∴△ACB ≌△FBC （SAS ），∴∠BFC ＝∠BAC ＝90°，AB ＝CF ， ∵GE ⊥BF ，GH ⊥CF ，∴∠GEF ＝∠EFH ＝∠GHF ＝90°， ∴四边形EFHG 是矩形， ∴EG ＝FH ，∵GE ＝GC ，GH ⊥CF ， ∴FH ＝HC ， ∴CF ＝2EG ， ∴AB ＝2EG ．11.如图，ABCD 的对角线AC 、BD 相交于点O ，AC=BC.（1）如图1，过点B 作BE ⊥AC 于点E ，若AC=8，BE=6，求OE 的长；（2）如图2，若∠BDC=045,过点C 作CF ⊥CD 交BD 于F ，过B 作BG ⊥BC ，且BG=BC,. 连接AG 、DG ，求证：AG=2OF.图1 图2HB12. 已知，在▱ABCD 中，AB ⊥AC ，点E 是AC 上一点，连换BE ，延长BE 交AD 于点F ，BE ＝CE ．11 （1）如图1，当∠AEB ＝60°，BF ＝2时，求▱ABCD 的面积；（2）如图2，点G 是过点E 且与BF 垂直的直线上一点，连接GF ，GC ，FC ，当GF ＝GC 时，求证：AB ＝2EG ．（1）解：如图1中，∵四边形ABCD 是平行四边形， ∴AD ∥BC ，∴∠EAF ＝∠ECB ，∠AFE ＝∠EBC ， ∵EB ＝EC ，∴∠EBC ＝∠ECB ， ∴∠EAF ＝∠EF A ， ∴EA ＝EF ， ∴AC ＝BF ＝2，∵∠AEB ＝∠EBC +∠ECB ＝60°， ∴∠ACB ＝∠ECB ＝30°， ∴AB ＝AC •tan30°＝，∴S 平行四边形ABCD ＝AB •AC＝．（2）证明：如图2中，作GH ⊥CF 于H ．∵CA ＝BF ，∠ACB ＝∠FBC ＝30°，BC ＝CB ， ∴△ACB ≌△FBC （SAS ），∴∠BFC ＝∠BAC ＝90°，AB ＝CF ， ∵GE ⊥BF ，GH ⊥CF ，∴∠GEF ＝∠EFH ＝∠GHF ＝90°，∴四边形EFHG 是矩形， ∴EG ＝FH ，∵GE ＝GC ，GH ⊥CF ， ∴FH ＝HC ， ∴CF ＝2EG ， ∴AB ＝2EG ．。

重庆中考数学几何专题训练（一）及答案1. （2019年重庆南开初三（下）半期考试题）在平行四边形ABCD 中，E 为AD 上一点,连接BE 、CE ，满足BC=BE=CE 。

（1）如图1，已知∠ABC=90°，BC=4，求AC 的长；（2）如图2，过点A 作AF ⊥BE 于点F,交CE 于点G ，连接BG ，在BG 上取点M ，使得∠AMG=60°，延长AM 交BC 于点N,求证：CN=2AE.图1 图2(1)解:ΘBC=BE=CE,∴o EBC 60=∠Θ ∠ABC=90° ∴ o ABE 30=∠Θ平行四边形ABCD,∴AD//BC ,∴ ∠EAB=90°∴AB=BE 23=3223=BC ∴AC=72281216==+（2）过点E 作EK//AN ，交BC 于点KΘBC=BE=CE,∴o BEC EBC 60=∠=∠Θ平行四边形ABCD ，∴AD//BC ，∴ 四边形 ANKE 是平行四边形∴o EBC BEA 60=∠=∠，o AEC 120=∠Θ∠AMG=60°，∴o o o o MGE MAE 180********=--=∠+∠∴ANB EAM CGB ∠=∠=∠，ΘEK//AN ，∴CEK EKB ANB CGB o ∠+=∠=∠=∠60又ΘEBG EBG BEC CGB o ∠+=∠+∠=∠60，∴CEK EBG =∠ΘBC=BE=CE,∴o BEG BCE 60=∠=∠，∴EKC BGE ∆≅∆（ASA ）∴CK=EG 又Θo BEC BEA 60=∠=∠，AF ⊥BE ，∴AE=EG=CKΘ四边形 ANKE 是平行四边形，∴AE=NK=CK ，∴CN=2AE2. （2019年西南大学附属中学校初三下月考试题）在菱形ABCD 中,∠ABC=60°,BD 为菱形的一条对角线.(1) 如图1,过A 作AE ⊥BC 于点E,交BD 于点F,若EF=2,求菱形ABCD 的面积；(2)如图2,M 为菱形ABCD 外一点,过A 作AN ⊥BM 交BM 的延长线于点M,连接AM ，DM ，AG ⊥DM 于点G,且∠AMN=∠AMD,求证:(图1)F E D C A (图2)GN M D C B A（2）解答：因为∠AMN=∠AMD ，AN ⊥BM ，AG ⊥DM ∴AN=AG ，∠ANB=∠AGD=90︒，MN ＝MG 因为菱形ABCD∴AB=AD∴ABN ≅ADG （HL ） ∴D Ｇ＝ＢＮ，∠ABM ＝∠ADM ∴∠BMD=∠BAD=180︒-∠ABC=120︒∴∠AMN=∠AMG=12∠DMN=30︒ ∴MN=MG=123AM ∴DM=DG+MG=BN+MG=BM+MN+MG=BM+3AM 即：DM=BM+3AM （1）解答:因为在菱形ABCD 中,∠ABC=60°,BD 为菱形的一条对角线 所以AB=BC ，∠ABD=∠CBD=30︒, 又因为AE ⊥BC ，所以∠AEB=90︒，∠BAE=30︒ 所以AF=BF=2EF=4，AE=6，所以BC=AB=43， 所以菱形ABCD 的面积是24 3.3.如图，在等腰Rt△ABC中，O为斜边AC的中点，连接BO，以AB为斜边向三角形内部作Rt△ABE,且∠AEB=90°，连接EO.求证：（1）∠OAE=∠OBE; （2）AE=BE+2OE.（1）证明：因为O为等腰Rt∆ABC斜边AC的中点, 所以∠ABO=∠BAO=45︒所以∠OAE=45︒-∠BAE因为AB为斜边作Rt∆ABE，所以∠ABE=90︒所以∠OBE=90︒-∠OBA-∠BAE=45︒-∠BAE即∠OAE=∠OBE（2）证明：在AE上取AF=BE，连接OF因为O为等腰Rt∆ABC斜边AC的中点, ∴∠ABO=∠BAO=45︒，∠AOB=90︒，∴AO=BO 因为∠OAE=∠OBE，∴∆AFO≅∆BEO（SAS）∴∠AOF=∠BOE，OF=OE∴∠EOF=∠AOB=90︒，∴EF=2OE因为AE=AF+EF∴AE=BE+2OEC A。

专题02 全等模型--半角模型全等三角形在中考数学几何模块中占据着重要地位，也是学生必须掌握的一块内容，本专题就半角模型进行梳理及对应试题分析，方便掌握。

模型1.半角模型【模型解读】过等腰三角形顶点 两条射线，使两条射线的夹角为等腰三角形顶角的一半这样的模型称为半角模型。

【常见模型及证法】常见的图形为正方形，正三角形，等腰直角三角形等，解题思路一般是将半角两边的三角形通过旋转到一边合并成新的三角形，从而进行等量代换，然后证明与半角形成的三角形全等，再通过全等的性质得到线段之间的数量关系。

半角模型（题中出现角度之间的半角关系）利用旋转——证全等——得到相关结论. 1．（2022·湖北十堰·中考真题）【阅读材料】如图①，四边形ABCD 中，AB AD =，180B D ∠+∠=︒，点E ，F 分别在BC ，CD 上，若2BAD EAF ∠∠=，则EF BE DF =+．【解决问题】如图②，在某公园的同一水平面上，四条道路围成四边形ABCD ．已知100m CD CB ==，60D ∠=︒，120ABC ∠=︒，150BCD ∠=︒，道路AD ，AB 上分别有景点M ，N ，且100m DM =，)501m BN =，若在M ，N 之间修一条直路，则路线M N →的长比路线M A N →→的长少_________m 1.7）．【答案】370【分析】延长,AB DC 交于点E ，根据已知条件求得90E ∠=︒,进而根据含30度角的直角三角形的性质，求得,EC EB ，,AE AD ，从而求得AN AM +的长，根据材料可得MN DM BN =+，即可求解．【详解】解：如图，延长,AB DC 交于点E ，连接,CM CN ，60D ∠=︒，120ABC ∠=︒，150BCD ∠=︒，30A ∴∠=︒，90E ∠=︒，100DC DM ==DCM ∴是等边三角形，60DCM ∴∠=︒,90BCM ∴∠=︒,在Rt BCE 中，100BC =，18030ECB BCD ∠=︒-∠=︒，1502EB BC ==，EC ==100DE DC EC ∴=+=+Rt ADE △中，2200AD DE ==+150AE ==， ∴200100100AM AD DM =-=+=+()AN AB BN AE EB BN =-=--())15050501=--150=，100150250AM AN ∴+=+=+Rt CMB △中，BM =)50501EN EB BN EC =+=+=ECN ∴是等腰直角三角形()1752NCM BCM NCB BCM NCE BCE DCB ∴∠=∠-∠=∠-∠-∠=︒=∠由阅读材料可得))100501501MN DM BN =+=+=，∴路线M N →的长比路线M A N →→的长少)250501200370+=+≈m ．答案：370． 【点睛】本题考查了含30度角的直角三角形的性质，勾股定理，理解题意是解题的关键．2．（2022·河北邢台·九年级期末）学完旋转这一章，老师给同学们出了这样一道题：“如图1，在正方形ABCD 中，∠EAF ＝45°，求证：EF ＝BE ＋DF ．”小明同学的思路：∠四边形ABCD 是正方形，∠AB ＝AD ，∠B ＝∠ADC ＝90°．把∠ABE 绕点A 逆时针旋转到ADE '△的位置，然后证明AFE AFE '≌△△，从而可得=EF E F '． E F E D DF BE DF ''=+=+，从而使问题得证．(1)【探究】请你参考小明的解题思路解决下面问题：如图2，在四边形ABCD 中，AB ＝AD ，∠B ＝∠D ＝90°，12EAF BAD ∠=∠，直接写出EF ，BE ，DF 之间的数量关系．(2)【应用】如图3，在四边形ABCD 中，AB ＝AD ，∠B ＋∠D ＝180°，12EAF BAD ∠=∠，求证：EF ＝BE ＋DF ．(3)【知识迁移】如图4，四边形ABPC 是O的内接四边形，BC 是直径，AB ＝AC ，请直接写出PB ＋PC 与AP 的关系． ADE ，证明∠AEF EAF ='E AF ∠，先利用圆内接四边形的性质证明为等腰直角三角形，等量代换即得结论．重合，点ADE=180°知，BAD，∠∠BAF=∠EAF=E∠，∠EF=E F'∠ABE绕点腰直角三角形的判定及性质等知识点．解题关键是利用旋转构造全等三角形．3．（2022·福建·龙岩九年级期中）（1）【发现证明】如图1，在正方形ABCD 中，点E ，F 分别是BC ，CD 边上的动点，且45EAF ∠=︒，求证：EF DF BE =+．小明发现，当把ABE △绕点A 顺时针旋转90°至ADG ，使AB 与AD 重合时能够证明，请你给出证明过程．（2）【类比引申】①如图2，在正方形ABCD 中，如果点E ，F 分别是CB ，DC 延长线上的动点，且45EAF ∠=︒，则（1）中的结论还成立吗？若不成立，请写出EF ，BE ，DF 之间的数量关系______（不要求证明） ②如图3，如果点E ，F 分别是BC ，CD 延长线上的动点，且45EAF ∠=︒，则EF ，BE ，DF 之间的数量关系是_____（不要求证明）.（3）【联想拓展】如图1，若正方形ABCD 的边长为6，AE =求AF 的长．45EAF ∠=︒，45BAE FAD ∴∠+∠=︒，45DAG FAD ∴∠+∠=︒，EAF FAG ∴∠=∠，AF AF =，()EAF GAF SAS ∴∆≅∆，EF FG DF DG ∴==+，EF DF BE ∴=+；（2）①不成立，结论：EF DF BE =-；证明：如图2，将ABE ∆绕点A 顺时针旋转90︒至ADM ∆，EAB MAD ∴∠=∠，AE AM =，90EAM =︒∠，BE DM =，45FAM EAF ∴∠=︒=∠，AF AF =，()EAF MAF SAS ∴∆≅∆，EF FM DF DM DF BE ∴==-=-；②如图3，将ADF ∆绕点A 逆时针旋转90︒至ABN ∆，AN AF ∴=，90NAF ∠=︒，45EAF ∠=︒，45NAE ∴∠=︒，NAE FAE ∴∠=∠，AE AE =，()AFE ANE SAS ∴∆≅∆，EF EN ∴=，BE BN NE DF EF ∴=+=+．即BE EF DF =+．故答案为：BE EF DF =+．正方形Rt EFC中，2CF CE+解得：2x=．2DF∴=，226AF AD DF=+=【点睛】本题属于四边形综合题，主要考查了正方形的性质、旋转的性质、全等三角形的判定与性质以及勾股定理的综合应用，解题的关键是作辅助线构造全等三角形，根据全等三角形的对应边相等进行推导．4．（2022·山东省青岛第二十六中学九年级期中）【模型引入】当几何图形中，两个共顶点的角所在角度是公共大角一半的关系，我们称之为“半角模型”【模型探究】（1）如图1，在正方形ABCD中，E、F分别是AB、BC边上的点，且∠EDF＝45°，探究图中线段EF，AE，FC之间的数量关系．【模型应用】（2）如图2，如果四边形ABCD中，AB＝AD，∠BAD＝∠BCD＝90°，∠EAF＝45°，且BC＝7，DC＝13，CF＝5，求BE的长．【拓展提高】（3）如图3，在四边形ABCD中，AB＝AD，∠ABC与∠ADC互补，点E、F分别在射线CB、DC上，且∠EAF12=∠BAD．当BC＝4，DC＝7，CF＝1时，CEF的周长等于．（4）如图4，正方形ABCD中，AMN的顶点M、N分别在BC、CD边上，AH∠MN，且AH＝AB，连接BD分别交AM、AN于点E、F，若MH＝2，NH＝3，DF＝EF的长．（5）如图5，已知菱形ABCD中，∠B=60°，点E、F分别是边BC，CD上的动点（不与端点重合），且∠EAF=60°．连接BD分别与边AE、AF交于M、N，当∠DAF＝15°时，求证：MN2+DN2=BM2．又AH=AN，AB=AD，∠∠ABH∠∠ADN（SAS），∠DN=BH，∠ABH=∠ADN，∠∠B=60°，且∠EAF=60°．∠∠BAD=120°，∠∠DAF+∠BAE=∠EAF=60°，∠∠BAG+∠BAE=∠EAF，即∠MAH=∠MAN，而AH=AN，AM=AM，∠∠AMH∠∠AMN（SAS），∠MN=MH，∠AMN=∠AMH，∠菱形ABCD，∠B=60°，∠∠ABD=∠ADB=30°，∠∠HBD=∠ABH+∠ABD=60°，∠∠DAF=15°，∠EAF=60°，∠∠ADM中，∠DAM=∠AMD=75°，∠∠AMN=∠AMH=75°，∠∠HMB=180°-∠AMN-∠AMH=30°，∠∠BHM=90°，∠BH2+MH2=BM2，∠DN2+MN2=BM2．【点睛】本题是四边形综合题，主要考查了旋转的性质、正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识，解题关键是学会用旋转法添加辅助线，构造全等三角形解决问题，学会利用探究的结论解决新的问题，属于中考压轴题．课后专项训练：1．（2022·重庆市育才中学二模）回答问题（1）【初步探索】如图1：在四边形ABCD中，AB=AD，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且EF=BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG=BE．连接AG，先证明△ABE∠∠ADG，再证明△AEF∠∠AGF，可得出结论，他的结论应是_______________；（2）【灵活运用】如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°．E、F分别是BC、CD上的点，且EF=BE+FD，上述结论是否仍然成立，并说明理由；（3）【拓展延伸】知在四边形ABCD中，∠ABC+∠ADC=180°，AB=AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF=BE+FD，请直接写出∠EAF与∠DAB的数量关系．2．（2022·江西九江·一模）如图（1），在四边形ABCD 中，180B D ∠+∠=︒，AB AD =，以点A 为顶点作EAF ∠，且12EAF BAD ∠=∠，连接EF ．(1)观察猜想 如图（2），当90BAD B D ∠=∠=∠=︒时，①四边形ABCD 是______（填特殊四边形的名称）；②BE ，DF ，EF 之间的数量关系为______．(2)类比探究 如图（1），线段BE ，DF ，EF 之间的数量关系是否仍然成立？若成立，请加以证明；若不成立，请说明理由．(3)解决问题 如图（3），在ABC 中，90BAC ∠=︒，4AB AC ==，点D ，E 均在边BC 上，且45DAE ∠=︒，若BD =，求DE 的长．证得ABE ADG ≌，得出证得AEF AGF ≌，之间的数量关系；（2）同（1）②即可得出，证得ABD ACM ≌，同（证得AEF AGF ≌，在Rt ECM 中，由勾股定理可解得90BAD B D =∠=∠=︒，ABCD 是矩形，又∠AB AD ，∠矩形CD 至点G ，使得DG=BE 90ADG ADF =∠=︒，∠∠，∠ABE ADG ≌，DG ，BAE DAG ∠=∠1BAD ∠，∠BAE DAF ∠+∠∠AEF AGF ≌，∠EF DG EF =∠BE FD +在ABC 中，B ACB ∠=∠∠ABD ACM ≌，同（1）②的证明方法得DE ME =， 2BD =，22+BC AB AC ==DE ME =x -，Rt ECM 中，2EM ，2(2)(32+【点睛】本题考查了特殊的平行四边形的判定、全等三角形的性质和判定及勾股定理的应用，熟练应用相关定理和性质是解决本题的关键．3．（2022·山东聊城·九年级期末）（1）如图1，点E ，F 分别在正方形ABCD 的边BC ，CD 上，45EAF ∠=︒，连接EF ，求证：EF BE DF =+，试说明理由．（2）类比引申：如图2，四边形ABCD 中，AB AD =，90BAD ∠=︒，点E ，F 分别在边BC ，CD 上，∠EAF =45°，若B 、D ∠都不是直角，则当B 与D ∠满足等量关系______时，仍有EF BE DF =+，试说明理由．（3）联想拓展：如图3，在∠ABC 中，90BAC ∠=︒，AB AC =，点D ，E 均在边BC 上，且∠DAE =45，若1BD =，2EC =，求DE 的长．AB AD =∠ADC =∠B =90°∠则DAG ∠∠F AG =∠F AD理由：AB AD==∠BAE DAG∠=︒，BAD90∠+∠=ADC B在∠AFE和∠AFG∴=EF FG()3将∠ACE∠=BAC又∠∠F AB=∠则在∠ADF∠∠ADF∠∠∠∠C+∠ABD4．（2022·黑龙江九年级阶段练习）已知：正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N．当∠MAN绕点A旋转到BM=DN时，（如图1），易证BM+DN=MN．(1)当∠MAN 绕点A 旋转到BM ≠DN 时（如图2），线段BM 、DN 和MN 之间有怎样的数量关系？写出猜想，并加以证明；(2)当∠MAN 绕点A 旋转到如图3的位置时，线段BM 、DN 和MN 之间又有怎样的数量关系？请直接写出你的猜想． 【答案】(1)BM DN MN +=，理由见解析；(2)DN BMMN -=，理由见解析【分析】（1）把ADN ∆绕点A 顺时针旋转90︒，得到ABE ∆，然后证明得到AEM ANM ∆∆≌，从而证得ME MN =，可得结论；（2）首先证明ADQ ABM ∆∆≌，得DQ BM =，再证明AMN AQN ∆∆≌，得MN QN =，可得结论； （1）解：BM DN MN +=．理由如下：如图2，把ADN ∆绕点A 顺时针旋转90︒，得到ABE ∆，90ABE ADN ∴∠=∠=︒，AE AN =，BE DN =，180ABE ABC ∴∠+∠=︒，∴点E ，点B ，点C 三点共线，90904545EAM NAM ∴∠=︒-∠=︒-︒=︒，又45NAM ∠=︒，在AEM ∆与ANM ∆中，AE AN EAM NAM AM AM =⎧⎪∠=∠⎨⎪=⎩，AEM ANM ∴∆∆≌（SAS ），ME MN ∴=， ME BE BM DN BM =+=+，DN BM MN ∴+=；（2）解：DN BM MN -=．理由如下：在线段DN 上截取DQ BM =，在ADQ ∆与ABM ∆中，AD AB ADQ ABM DQ BM =⎧⎪∠=∠⎨⎪=⎩，ADQ ABM ∴∆∆≌（SAS ），DAQ BAM ∴∠=∠，QAN MAN ∴∠=∠．在AMN ∆和AQN ∆中，AQ AM QAN MAN AN AN =⎧⎪∠=∠⎨⎪=⎩，AMN AQN ∴∆∆≌（SAS ），MN QN ∴=，DN BM MN ∴-=．【点睛】本题是四边形综合题，考查正方形的性质，旋转变换，全等三角形的判定和性质，勾股定理等知识，解题的关键是学会利用旋转法添加辅助线，构造全等三角形解决问题．5．（2022·重庆南川·九年级期中）如图，正方形ABCD 中，45MAN ∠=︒，MAN ∠绕点A 顺时针旋转，它的两边分别交BC 、DC （或它们的延长线）于点M 、N ．(1)当MAN ∠绕点A 旋转到BM DN =时（如图1），证明：2MN BM =；(2)绕点A 旋转到BM DN ≠时（如图2），求证：MN BM DN =+；(3)当MAN ∠绕点A 旋转到如图3位置时，线段BM 、DN 和MN 之间有怎样的数量关系？请写出你的猜想并证明．【答案】(1)见解析(2)见解析(3)DN BM MN -=，见解析【分析】（1）把ADN △绕点A 顺时针旋转90︒，得到ABE △，证得B 、E 、M 三点共线，即可得到AEM △∠ANM ，从而证得ME MN =；（2）证明方法与（1）类似；（3）在线段DN 上截取DQ BM =，判断出ADQ△∠ABM ，同（2）的方法，即可得出结论．（1）证明：如图1，∠把ADN △绕点A 顺时针旋转90︒，得到ABE △，ABE ∴∠ADN △，AE ANM ∴=，ABE D ∠=∠，四边形ABCD 是正方形，90ABC D ∴∠=∠=︒，90ABE ABC ∴∠=∠=︒，∴点E 、B 、M 三点共线．90904545EAM NAM ∴∠=︒-∠=︒-︒=︒，又45NAM ∠=︒，在AEM △与ANM 中，AE AN EAM NAM AM AM =⎧⎪∠=∠⎨⎪=⎩，AEM ∴△∠()ANM SAS ，ME MN ∴=，ME BE BM DN BM =+=+，DN BM MN ∴+=，BM DN =，2MN BM ∴=．（2）证明：如图2，把ADN △绕点A 顺时针旋转90︒，得到ABE △，ABE ∴∠ADN △，AE ANM ∴=，ABE D ∠=∠，四边形ABCD 是正方形，90ABC D ∴∠=∠=︒，90ABE ABC ∴∠=∠=︒，∴点E 、B 、M 三点共线．90904545EAM NAM ∴∠=︒-∠=︒-︒=︒，又45NAM ∠=︒，在AEM △与ANM 中，AE AN EAM NAM AM AM =⎧⎪∠=∠⎨⎪=⎩，AEM ∴△∠()ANM SAS ，ME MN ∴=，ME BE BM DN BM =+=+，DN BM MN ∴+=． （3）解：DN BM MN -= 理由如下：如图3，在线段DN 上截取DQ BM =，连接AQ ，在ADQ △与ABM中，AD AB ADQ ABM DQ BM =⎧⎪∠=∠⎨⎪=⎩，ADQ ∴∠()ABM SAS ，DAQ BAM ∴∠=∠，QAN MAN ∴∠=∠．在AMN 和AQN △中，AQ AM QAN MAN AN AN =⎧⎪∠=∠⎨⎪=⎩，AMN ∴∠()AQN SAS ，MN QN ∴=，DN BM MN ∴-=．【点睛】本题是四边形综合题，考查正方形的性质，旋转变换，全等三角形的判定和性质，勾股定理等知识，学会利用旋转法添加辅助线，构造全等三角形是解题的关键．6．（2022·江西景德镇·九年级期中）（1）【特例探究】如图1，在四边形ABCD 中，AB AD =，90ABC ADC ∠=∠=︒，100BAD ∠=︒，50EAF ∠=︒，猜想并写出线段BE ，DF ，EF 之间的数量关系，证明你的猜想；（2）【迁移推广】如图2，在四边形ABCD 中，AB AD =，180ABC ADC ∠+∠=︒，2BAD EAF ∠∠=．请写出线段BE ，DF ，EF 之间的数量关系，并证明；（3）【拓展应用】如图3，在海上军事演习时，舰艇在指挥中心（O 处）北偏东20°的A 处．舰艇乙在指挥中心南偏西50°的B 处，并且两舰艇在指挥中心的距离相等，接到行动指令后，舰艇甲向正西方向以80海里/时的速度前进，同时舰艇乙沿北偏西60°的方向以90海里/时的速度前进，半小时后，指挥中心观测到甲、乙两舰艇分别到达C ，D 处，且指挥中心观测两舰艇视线之间的夹角为75°．请直接写出此时两舰艇之间的距离．【答案】（1）EF =BE +DF ，理由见解析；（2）EF =BE +DF ，理由见解析；（3）85海里【分析】（1）延长CD 至点G ，使DG =BE ，连接AG ，可证得∠ABE ∠∠ADG ，可得到AE =AG ，∠BAE =∠DAG ，再由100BAD ∠=︒，50EAF ∠=︒，可证得∠AEF ∠∠AGF ，从而得到EF =FG ，即可求解；（2）延长CD 至点H ，使DH =BE ，连接AH ，可证得∠ABE ∠∠ADH ，可得到AE =AH ，∠BAE =∠DAH ，再由2BAD EAF ∠∠=，可证得∠AEF ∠∠AHF ，从而得到EF =FH ，即可求解；（3）连接CD ，延长AC 、BD 交于点M ，根据题意可得∠AOB =2∠COD ，∠OAM +∠OBM =70°+110°=180°，再由（2）【迁移推广】得：CD =AC +BD ，即可求解．【详解】解：（1）EF =BE +DF ，理由如下：如图，延长CD 至点G ，使DG =BE ，连接AG ，∠90ABC ADC∠=∠=︒，∠∠ADG=∠ABC=90°，∠AB=AD，∠∠ABE∠∠ADG，∠AE=AG，∠BAE=∠DAG，∠100BAD∠=︒，50EAF∠=︒，∠∠BAE+∠DAF=50°，∠∠F AG=∠EAF=50°，∠AF=AF，∠∠AEF∠∠AGF，∠EF=FG，∠FG=DG+DF，∠EF=DG+DF=BE+DF；（2）EF=BE+DF，理由如下：如图，延长CD至点H，使DH=BE，连接AH，∠180ABC ADC∠+∠=︒，∠ADC+∠ADH=180°，∠∠ADH=∠ABC，∠AB=AD，∠∠ABE∠∠ADH，∠AE=AH，∠BAE=∠DAH，∠2BAD EAF∠∠=∠∠EAF=∠BAE+∠DAF=∠DAF+∠DAH，∠∠EAF=∠HAF，∠AF=AF，∠∠AEF∠∠AHF，∠EF=FH，∠FH=DH+DF，∠EF=DH+DF=BE+DF；（3）如图，连接CD，延长AC、BD交于点M，根据题意得：∠AOB=20°+90°+40°=150°，∠OBD=60°+50°=110°，∠COD=75°，∠OAM=90°-20°=70°，OA=OB，∠∠AOB=2∠COD，∠OAM+∠OBM=70°+110°=180°，∠OA=OB，∠由（2）【迁移推广】得：CD=AC+BD，∠AC=80×0.5=40，BD=90×0.5=45，∠CD=40+45=85海里．即此时两舰艇之间的距离85海里．【点睛】此题是三角形综合题，主要考查了全等三角形的判定和性质、勾股定理的运用、等腰直角三角形的性质，题目的综合性较强，难度较大，解题的关键是正确的作出辅助线构造全等三角形，解答时，注意类比思想的应用．7．（2022·上海·九年级专题练习）小明遇到这样一个问题：如图1，在Rt∠ABC中，∠BAC＝90°，AB＝AC，点D，E在边BC上，∠DAE＝45°．若BD＝3，CE＝1，求DE的长．小明发现，将∠ABD 绕点A 按逆时针方向旋转90º，得到∠ACF ，联结EF （如图2），由图形旋转的性质和等腰直角三角形的性质以及∠DAE ＝45°，可证△F AE ∠△DAE ，得FE ＝DE ．解△FCE ，可求得FE （即DE ）的长．(1)请回答：在图2中，∠FCE 的度数是 ，DE 的长为 ．参考小明思考问题的方法，解决问题：(2)如图3，在四边形ABCD 中，AB ＝AD ，∠B ＋∠D ＝180°．E ，F 分别是边BC ，CD 上的点，且∠EAF ＝12∠BAD ．猜想线段BE ，EF ，FD 之间的数量关系并说明理由． ）根据旋转的性质，可得ADB AFC ≌，勾股定理解按逆时针方向旋转，使AB 与AD 重合，FG ＝DG ＋FD ＝BE ＋按逆时针方向旋转90º，得到∠ACF ∠ADB AFC ≌ACF ∴∠,90AB AC BAC ∠==45ACF ABD ∴∠=∠=在Rt FCE 中，BD 2EF CF ∴=+(2)猜想：EF =BE 如图，将∠ABE8．（2022·黑龙江·哈尔滨市九年级阶段练习）已知四边形ABCD 是正方形，一个等腰直角三角板的一个锐角顶点与A 点重合，将此三角板绕A 点旋转时，两边分别交直线BC ，CD 于M ，N ．(1)如图1，当M ，N 分别在边BC ，CD 上时，求证：BM +DN =MN(2)如图2，当M ，N 分别在边BC ，CD 的延长线上时，请直接写出线段BM ，DN ，MN 之间的数量关系(3)如图3，直线AN 与BC 交于P 点，MN =10，CN =6，MC =8，求CP 的长．【答案】（1）见解析；（2）BM DN MN -=；（3）3【分析】（1）延长CB 到G 使BG DN=，连接AG ，先证明AGB AND ≅△△，由此得到AG AN =，GAB DAN ∠=∠，再根据45MAN ∠=︒，90BAD ∠=︒，可以得到45GAM NAM ∠=∠=︒，从而证明AMN AMG △≌△，然后根据全等三角形的性质即可证明BM DN MN +=；（2）在BM 上取一点G ，使得BG DN =，连接AG ，先证明AGB AND ≅△△，由此得到AG AN =，GAB DAN ∠=∠，由此可得90GAN BAD ∠=∠=︒，再根据45MAN ∠=︒可以得到45GAM NAM ∠=∠=︒，从而证明AMN AMG △≌△，然后根据全等三角形的性质即可证明BM DN MN -=；（3）在DN 上取一点G ，使得DG BM =，连接AG ，先证明ABM ADG ≌，再证明AMN AGN △≌△，设DG BM x ==，根据DC BC =可求得2x =，由此可得6AB BC CD CN ====，最后再证明ABP NCP △≌△，由此即可求得答案．【详解】（1）证明：如图，延长CB 到G 使BG DN =，连接AG ，∠四边形ABCD 是正方形，∠AB AD =，90ABG ADN BAD ∠=∠=∠=︒，在ABG 与ADN △中，AB AD ABG ADN BG DN =⎧⎪∠=∠⎨⎪=⎩， ()AGB AND SAS ∴△≌△，AG AN ∴=，GAB DAN ∠=∠，45MAN ∠=︒，90BAD ∠=︒，∠45DAN BAM BAD MAN ∠+∠=∠-∠=︒，45GAM GAB BAM DAN BAM ∴∠=∠+∠=∠+∠=︒，GAM NAM ∴∠=∠，在AMN 与AMG 中，AM AM GAM NAM AN AG =⎧⎪∠=∠⎨⎪=⎩， ()AMN AMG SAS ∴△≌△，MN GM ∴=，又∠BM GB GM +=，BG DN =，BM DN MN ∴+=；（2）BM DN MN -=，理由如下：如图，在BM 上取一点G ，使得BG DN =，连接AG ，∠四边形ABCD 是正方形，∠AB AD =，90ABG ADN BAD ∠=∠=∠=︒，在ABG 与ADN △中，AB AD ABG ADN GB DN =⎧⎪∠=∠⎨⎪=⎩，()AGB AND SAS ∴△≌△，AG AN ∴=，GAB DAN ∠=∠，∠GAB GAD DAN GAD ∠+∠=∠+∠，∠90GAN BAD ∠=∠=︒，又45MAN ∠=︒，45GAM GAN MAN MAN ∴∠=∠-∠=︒=∠，在AMN 与AMG 中，AM AM GAM NAM AN AG =⎧⎪∠=∠⎨⎪=⎩，()AMN AMG SAS ∴△≌△，MN GM ∴=，又∠BM BG GM -=，BG DN =，∠BM DN MN -=，故答案为：BM DN MN -=；（3）如图，在DN 上取一点G ，使得DG BM =，连接AG ，∠四边形ABCD 是正方形，∠AB AD BC CD ===，90ABM ADG BAD ∠=∠=∠=︒，//AB CD ，在ABM 与ADG 中，AB AD ABM ADG BM DG =⎧⎪∠=∠⎨⎪=⎩， ()ABM ADG SAS ∴△≌△，AM AG ∴=，MAB GAD ∠=∠，∠MAB BAG GAD BAG ∠+∠=∠+∠，∠90MAG BAD ∠=∠=︒，又45MAN ∠=︒，45GAN MAG MAN MAN ∴∠=∠-∠=︒=∠，在AMN 与AGN 中，AM AG MAN GAN AN AN =⎧⎪∠=∠⎨⎪=⎩， ()AMN AGN SAS ∴△≌△，10MN GN ∴==，设DG BM x ==，∠6CN =，8MC =，∠1064DC DG GN CN x x =+-=+-=+，8BC MC BM x =-=-， ∠DC BC =，∠48x x +=-，解得：2x =，∠6AB BC CD CN ====，∠//AB CD ，∠BAP CNP ∠=∠，在ABP △与NCP 中，APB NPC BAP CNP AB CN ∠=∠⎧⎪∠=∠⎨⎪=⎩， ()ABP NCP AAS ∴△≌△，9．（2022·浙江·九年级阶段练习）如图1，等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合，将此三角板绕点A旋转，使三角板中该锐角的两条边分别交正方形的两边BC，DC于点E，F，连接EF．（1）猜想BE、EF、DF三条线段之间的数量关系，并证明你的猜想；（2）在图1中，过点A作AM∠EF于点M，请直接写出AM和AB的数量关系；∠BAD，（3）如图2，将Rt∠ABC沿斜边AC翻折得到Rt∠ADC，E，F分别是BC，CD边上的点，∠EAF=12连接EF，过点A作AM∠EF于点M，试猜想AM与AB之间的数量关系．并证明你的猜想．10．（2022·北京四中九年级期中）如图，在∠ABC中，∠ACB=90°，CA=CB，点P在线段AB上，作射线CP （0°＜∠ACP＜45°)，射线CP绕点C逆时针旋转45°，得到射线CQ，过点A作AD∠CP于点D，交CQ于点E，连接BE．(1)依题意补全图形；(2)用等式表示线段AD，DE，BE之间的数量关系，并证明．【答案】(1)作图见解析．(2)结论：AD+BE=DE．证明见解析．【分析】（1）根据要求作出图形即可．（2）结论：AD+BE=DE．延长DA至F，使DF=DE，连接CF．利用全等三角形的性质解决问题即可．（1）解：如图所示：（2）结论：AD+BE=DE．理由：延长DA至F，使DF=DE，连接CF．∠AD∠CP，DF=DE，∠CE=CF，∠∠DCF=∠DCE=45°，∠∠ACB=90°，∠∠ACD+∠ECB=45°，∠∠DCA+∠ACF=∠DCF=45°，∠∠FCA=∠ECB，在∠ACF和∠BCE中，CA CB ACF BCE CF CE =⎧⎪∠=∠⎨⎪=⎩，∠∠ACF ∠∠BCE （SAS ），∠AF =BE ，∠AD +BE =DE ．【点睛】本题考查作图-旋转变换，全等三角形的判定和性质，等腰直角三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．。

专题复习：几何证明综合型问题——针对题型：24题（10分）☆核心：考虑构造辅助线，考虑证明全等专项突破1：特殊四边形（矩菱正）特殊性质与判定1.菱形A.性质①四边相等②对角线互相垂直，每一条对角线平分每一组对角S对角线乘积的一半③B.判定①一组邻边相等的平行四边形②两对角线垂直的平行四边形③四边相等的四边形2.矩形A.性质①四个角为直角②对角线相等B.判定①有一个角是直角的平行四边形②对角线相等的平行四边形③有三个角是直角的四边形注意：“三个角相等的四边形是矩形”是假命题3.正方形满足所有平矩菱的性质与判定专项突破2：角的转化（必考）✧ 1.和差角，用外角✧ 2.内角和（对角互补模型）✧ 3.平行线转角（倍长中线有平行）※注意：倍长中线无法证角时，考虑延长平行线和截线，构造三线八角✧ 4.同角（或等角）的余角（或补角）相等✧ 5.等量±等量✧ 6.以算代证，字母表示角✧7.八字模型（倒角重点图形）✧8.给角度算角度（67.5°，22.5°，45°，30°，60°，75°，120°······）✧9.利用四边形本身的平行（内错或同位或同旁内角）、对角特点（相等）倒角✧10.双垂图形，必有角等（相似）△11.四点共圆12.······专项突破3：四边形中常见辅助线☆可结合考查等边三角形、等腰（Rt ）三角形、平矩菱正等特殊平行四边形的性质和判定✧ 1.截长补短：截谁相等，证谁全等（第一对全等容易出现）✧ 2.“几个等式”：①矩形+中点==斜边中线②平分+平行（或垂直）==等腰③中点+平行（四边形）==延长相交④Rt+等腰==斜边中点✧ 3.一边一角构全等✧ 4.手拉手模型✧ 5.依靠60°构造等边三角形✧ 6.特殊角度的转化60°（120°）、22.5°（45°、135°、67.5°）、15°（75°、150°、105°）、90°······✧7.半角模型【条件】如图，四边形ABCD 中，AB =AD ，180BAD BCD ABC ADC ︒∠+∠=∠+∠=，12EAF BAD E BC F CD ∠=∠，点在直线上,点在直线上【结论】BE DF EF 、、满足截长补短关系✧8.正方形中：①CFDE CF DE ⊥⇔=②对角线上有一点，构造对称型全等③旋转型全等④半角模型⑤旋转型全等✧9.以等腰Rt ∆斜边为斜边构造Rt ∆10.······考点突破（24题第1问）考点一：几何计算⎪⎩⎪⎨⎧③勾股定理②三角函数①相似“三板斧”（24题第2问）☆考点二：中点问题（一）已知中点（2倍/倍半关系）1.倍长中线法※注意：平行条件为后续证明提供条件2.中位线①有多个中点时，用中位线②有1个中点，再延长另一边使之成为中点，构造中位线※注意：必出平行条件，进而进行角的转化3.Rt ∆斜边中线等于斜边一半※注意：逆定理：如果一个三角形一边上的中线等于这边一半，那么这个三角形是直角三角形4.等腰（或等边）∆的三线合一5.中垂线※注意：常向两端把线连6.······（二）证明中点1.作平行，证平行2.有等腰，证两线（平分或垂直）3.······【例1】如图，在菱形ABCD 中，点E 、F 分别是BC 、CD 上一点，连接DE 、EF ，且AE =AF ，BAF DAE ∠=∠．（1）求证：CE =CF ；（2）若︒=∠120ABC ，点G 是线段AF 的中点，连接DG ，EG ．求证：DG ⊥GE ．☆考点三：角平分线问题（一）有角平分线1.“两等腰”：角平分+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧平行（内错）垂直（延长）⇒等腰2.“两全等”：角平分+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧等）截相等（构造对称型全引垂线⇒全等3.等腰三角形“三线合一”AB CDE F G4.······（三）证角平分线作垂直考点四：截长补短☆核心：截谁相等，证谁全等，第一对全等容易出现，易出等腰三角形等特殊图形切记不要死脑筋！！！！【例2】正方形ABCD 中，M 在CD 上，N 在DA 延长线上，AN CM =，点E 在BD 上，NE 平分DNM ∠.过E 作MN EF ⊥于F ，求证：EF AD MN 22-=.考点五：综合型试题【例3】正方形ABCD 中，连接其对角线AC ，∠BCA 的平分线CF 交AB 于点F ，过点B 作BM ⊥CF 于点N ，交AC 于点M ，过点C 作CP ⊥CF ，交AD 延长线于点P ．（1）若正方形ABCD 的边长为4，求△ACP 的面积；（2）求证：CP=BM+2FN ．【练习1】如图，正方形ABCD 中，对角线AC 与BD 相交于O ，︒=∠15ADE ，过D 作ED DG ⊥DG 于D ，且AD AG =，过G 作AC GF //交ED 的延长线于F ．（1）若64=ED ，求AG ；（2）求证：BD ED DF =+2．【练习2】如图，正方形ABCD 中，E 为AB 边上一点，过点D 作DF ⊥DE ，与BC 延长线交于点F ．连接EF ，与CD 边交于点G ，与对角线BD 交于点H ．（1）若BF=BD =2，求BE 的长；（2）若∠ADE=2∠BFE ，求证：FH=HE+HD ．【练习3】如图，AC 为正方形ABCD 的一条对角线，点E 为DA 边延长线上的一点，连接BE ，在BE 上取一点F ，使BC BF =，过点B 作BE BK ⊥于B ，交AC 于点K ，连接CF ，交AB 于点H ，交BK 于点G ．（1）求证：BG BH =；（2）求证：AE BG BE +=．备注：。

重庆中考几何一、有关几何的基本量：线段、角度、全等、面积、四边形性质1、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，E为AB延长线上一点，连接ED，与BC 交于点H．过E作CD的垂线，垂足为CD上的一点F，并与BC交于点G．已知G为CH的中点，且∠BEH=∠HEG．（1）若HE=HG，求证：△EBH≌△GFC；（2）若CD=4，BH=1，求AD的长．（1）证明：∵HE=HG，∴∠HEG=∠HGE，∵∠HGE=∠FGC，∠BEH=∠HEG，∴∠BEH=∠FGC，∵G是HC的中点，∴HG=GC，∴HE=GC，∵∠HBE=∠CFG=90°．∴△EBH≌△GFC；（2）解：过点H作HI⊥EG于I，∵G为CH的中点，∴HG=GC，∵EF⊥DC，HI⊥EF，∴∠HIG=∠GFC=90°，∠FGC=∠HGI，∴△GIH≌△GFC，∵△EBH≌△EIH（AAS），∴FC=HI=BH=1，∴AD=4-1=3．2、已知，Rt△ABC中，∠ACB=90°，∠CAB=30°．分别以AB、AC为边，向形外作等边△ABD 和等边△ACE．（1）如图1，连接线段BE、CD．求证：BE=CD；（2）如图2，连接DE交AB于点F．求证：F为DE中点．证明：（1）∵△ABD和△ACE是等边三角形，∴AB=AD，AC=AE，∠DAB=∠EAC=60°，∴∠DAB+∠BAC=∠EAC+∠BAC，即∠DAC=∠BAE，在△DAC和△BAE中，AC=AE ∠DAC=∠BAE AD=AB ，∴△DAC≌△BAE（SAS），∴DC=BE；（2）如图，作DG∥AE，交AB于点G，由∠EAC=60°，∠CAB=30°得：∠FAE=∠EAC+∠CAB=90°，∴∠DGF=∠FAE=90°，又∵∠ACB=90°，∠CAB=30°，∴∠ABC=60°，又∵△ABD为等边三角形，∠DBG=60°，DB=AB，∴∠DBG=∠ABC=60°，在△DGB和△ACB中，∠DGB=∠ACB ∠DBG=∠ABC DB=AB ，∴△DGB≌△ACB（AAS），∴DG=AC，又∵△AEC为等边三角形，∴AE=AC，∴DG=AE，在△DGF和△EAF中，∠DGF=∠EAF ∠DFG=∠EFA DG=EA ，∴△DGF≌△EAF（AAS），∴DF=EF，即F为DE中点．3、如图，在直角梯形ABCD中，AD⊥DC，AB∥DC，AB=BC，AD与BC延长线交于点F，G是DC延长线上一点，AG⊥BC于E．（1）求证：CF=CG；（2）连接DE，若BE=4CE，CD=2，求DE的长．解答：（1）证明：连接AC，∵DC ∥AB ，AB=BC ，∴∠1=∠CAB ，∠CAB=∠2， ∴∠1=∠2；∵∠ADC=∠AEC=90°，AC=AC ， ∴△ADC ≌△AEC ， ∴CD=CE ；∵∠FDC=∠GEC=90°，∠3=∠4， ∴△FDC ≌△GEC ，∴CF=CG ．（2）解：由（1）知，CE=CD=2， ∴BE=4CE=8，∴AB=BC=CE+BE=10，∴在Rt △ABE 中，AE= AB 2-BE 2 =6， ∴在Rt △ACE 中，AC= AE 2+CE 2 =102 由（1）知，△ADC ≌△AEC ， ∴CD=CE ，AD=AE ，∴C 、A 分别是DE 垂直平分线上的点， ∴DE ⊥AC ，DE=2EH ；（8分） 在Rt △AEC 中，S △AEC =21 AE •CE=21AC •EH ， ∴EH=AC CEAE ⋅ =10226⨯ =5103∴DE=2EH=2×5103=5106 4、如图，AC 是正方形ABCD 的对角线，点O 是AC 的中点，点Q 是AB 上一点，连接CQ ，DP ⊥CQ 于点E ，交BC 于点P ，连接OP ，OQ ；求证：（1）△BCQ ≌△CDP ； （2）OP=OQ ．证明：∵四边形ABCD 是正方形， ∴∠B=∠PCD=90°，BC=CD ， ∴∠2+∠3=90°，又∵DP ⊥CQ ， ∴∠2+∠1=90°， ∴∠1=∠3，在△BCQ 和△CDP 中，∠B=∠PCD BC=CD ∠1=∠3 ． ∴△BCQ ≌△CDP ． （2）连接OB ． 由（1）：△BCQ ≌△CDP 可知：BQ=PC ， ∵四边形ABCD 是正方形， ∴∠ABC=90°，AB=BC ， 而点O 是AC 中点， ∴BO=21AC=CO ，∠4=21∠ABC=45°=∠PCO ， 在△BCQ 和△CDP 中， BQ=CP ∠4=∠PCO BO=CO∴△BOQ ≌△COP ， ∴OQ=OP ．5、在等腰梯形ABCD 中，AD ∥BC ，AB=AD=CD,∠ABC=60°,延长AD 到E,使DE=AD,延长DC 到F ，使DC=CF,连接BE 、BF 和EF.⑴求证：△ABE ≌△CFB; ⑵如果AD=6,tan ∠EBC 的值. 解：（1）证明：连结CE ， 在△BAE 与△FCB 中，∵ BA=FC ，∠A=∠BCF ，， AE=BC ， ∴△BAE ≌△FCB ；（2）延长BC 交EF 于点G ，作AH ⊥BG 于H ，作AM ⊥BG ，∵△BAE ≌△FCB ，∴∠AEB=∠FBG ，BE=BF ，∴△BEF 为等腰三角形，又∵AE ∥BC ， ∴∠AEB=∠EBG ，∴∠EBG=∠FBG ，∴BG ⊥EF ，∵∠AMG=∠EGM=∠AEG=90°， ∴四边形AMGE 为矩形，∴AM=EG ， 在Rt △ABM 中，AM=AB •sin60°=6×23=33 ，∴EG=AM=33， BG=BM+MG=6×2+6×cos60°=15，∴tan ∠EBC=531533==BG EG 6、如图，在梯形ABCD 中，AD ∥BC ，∠C=90°，E 为CD 的中点，EF ∥AB 交BC 于点F（1）求证：BF=AD+CF ；ABDECF（2）当AD=1，BC=7，且BE平分∠ABC时，求EF的长．（1）证明：如图（1），延长AD交FE的延长线于N∵∠NDE=∠FCE=90°∠DEN=∠FEC DE=EC∴△NDE≌△FCE ∴DN=CF ∵AB∥FN，AN∥BF∴四边形ABFN是平行四边形∴BF=AD+DN=AD+FC（2）解：∵AB∥EF，∴∠ABN=∠EFC，即∠1+∠2=∠3，又∵∠2+∠BEF=∠3，∴∠1=∠BEF，∴BF=EF，∵∠1=∠2，∴∠BEF=∠2，∴EF=BF，又∵BC+AD=7+1∴BF+CF+AD=8而由（1）知CF+AD=BF∴BF+BF=8∴2BF=8，∴BF=4，∴BF=EF=47、已知：AC是矩形ABCD的对角线，延长CB至E，使CE=CA，F是AE的中点，连接DF、CF分别交AB于G、H点（1）求证：FG=FH；（2）若∠E=60°，且AE=8时，求梯形AECD 的面积．（1）证明：连接BF∵ABCD为矩形∴AB⊥BC AB⊥AD AD=BC∴△ABE为直角三角形∵F是AE的中点∴AF=BF=BE∴∠FAB=∠FBA∴∠DAF=∠CBF∵AD=BC, ∠DAF=∠CBF ,AF=BF ,∴△DAF≌△CBF∴∠ADF=∠BCF∴∠FDC=∠FCD∴∠FGH=∠FHG ∴FG=FH ；（2）解：∵AC=CE ∠E=60° ∴△ACE 为等边三角形 ∴CE=AE=8 ∵AB ⊥BC ∴BC=BE=CE 21=4 ∴根据勾股定理AB=34 ∴梯形AECD 的面积=21×(AD+CE)×CD=21×(4+8)×34=3248、如图，直角梯形ABCD 中，AD ∥BC ，∠BCD=90°，且CD=2AD ，tan ∠ABC=2，过点D作DE ∥AB ，交∠BCD 的平分线于点E ，连接BE ． （1）求证：BC=CD ；（2）将△BCE 绕点C ，顺时针旋转90°得到△DCG ，连接EG ．求证：CD 垂直平分EG ； （3）延长BE 交CD 于点P ．求证：P 是CD 的中点． 证明：（1）延长DE 交BC 于F ，∵AD ∥BC ，AB ∥DF ，∴AD=BF ，∠ABC=∠DFC ． 在Rt △DCF 中，∵tan ∠DFC=tan ∠ABC=2， ∴CFCD=2， 即CD=2CF ，∵CD=2AD=2BF ， ∴BF=CF ， ∴BC=BF+CF=21CD+21CD=CD ． 即BC=CD ．（2）∵CE 平分∠BCD ，∴∠BCE=∠DCE ， 由（1）知BC=CD ， ∵CE=CE ，∴△BCE ≌△DCE ， ∴BE=DE ，由图形旋转的性质知CE=CG ，BE=DG ， ∴DE=DG ，∴C ，D 都在EG 的垂直平分线上， ∴CD 垂直平分EG ． （3）连接BD ， 由（2）知BE=DE ， ∴∠1=∠2． ∵AB ∥DE ，∴∠3=∠2．∴∠1=∠3．∵AD ∥BC ，∴∠4=∠DBC ．由（1）知BC=CD ，∴∠DBC=∠BDC ，∴∠4=∠BDP ． 又∵BD=BD ，∴△BAD ≌△BPD(ASA)∴DP=AD ． ∵AD=21CD ，∴DP=21CD ．∴P 是CD 的中点． 9．(2011南岸二诊)如图，已知点P 是正方形ABCD 的对角线AC 上一点，过点P 作EF ⊥DP ，交AB 于点E ，交CD 于点G ，交BC 的延长线于点F ，连接DF ．（1）若23=DF ，求DP 的长； （2）求证：CF AE =.10．如图，正方形CGEF 的对角线CE 在正方形ABCD 的边BC 的延长线上（CG ＞BC ），M 是线段AE 的中点，DM 的延长线交CE 于N ． （1）线段AD 与NE 相等吗？请说明理由； （2）探究：线段MD 、MF 的关系，并加以证明．11、如图，梯形ABCD 中，AD ∥BC ，AB=DC=10cm ，AC 交BD 于G ，且∠AGD=60°，E 、F 分别为CG 、AB 的中点．（1）求证：△AGD 为正三角形； （2）求EF 的长度．G 24题图PFEDCBA解答：（1）证明：连接BE，∵梯形ABCD中，AB=DC，∴AC=BD，可证△ABC≌△DCB，∴∠GCB=∠GBC，又∵∠BGC=∠AGD=60°∴△AGD为等边三角形，（2）解：∵BE为△BCG的中线，∴BE⊥AC，在Rt△ABE中，EF为斜边AB上的中线，∴EF=AB=5cm．12、如图，梯形ABCD中，AD∥BC，DE=EC，EF∥AB交BC于点F，EF=EC，连接DF．（1）试说明梯形ABCD是等腰梯形；（2）若AD=1，BC=3，DC=，试判断△DCF的形状；（3）在条件（2）下，射线BC上是否存在一点P，使△PCD是等腰三角形，若存在，请直接写出PB的长；若不存在，请说明理由．解答：解：（1）证明：∵EF=EC，∴∠EFC=∠ECF，∵EF∥AB，∴∠B=∠EFC，∴∠B=∠ECF，∴梯形ABCD是等腰梯形；（2）△DCF是等腰直角三角形，证明：∵DE=EC，EF=EC，∴EF=CD，∴△CDF是直角三角形（如果一个三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形），∵梯形ABCD是等腰梯形，∴CF=（BC﹣AD）=1，∵DC=，∴由勾股定理得：DF=1，∴△DCF是等腰直角三角形；（3）共四种情况：∵DF⊥BC，∴当PF=CF时，△PCD是等腰三角形，即PF=1，∴PB=1；当P与F重合时，△PCD是等腰三角形，∴PB=2；当PC=CD=（P在点C的左侧）时，△PCD是等腰三角形，∴PB=3﹣；当PC=CD=（P在点C的右侧）时，△PCD是等腰三角形，∴PB=3+．故共四种情况：PB=1，PB=2，PB=3﹣，PB=3+．（每个1分）13．在梯形ABCD中，AD∥BC，AB=CD，且DE⊥AD于D，∠EBC=∠CDE,∠ECB=45°．⑴求证：AB=BE ；⑵延长BE ，交CD 于F ．若CE =2，tan ∠CD E =31，求BF 的长． 13．⑴证明：延长DE ，交BC 于G ．∵DE ⊥AD 于D ，∴∠ADE =90°又AD ∥BC ， ∴∠DGC =∠BGE =∠ADE =90°， 而∠ECB =45°, ∴△EGC 是等腰直角三角形， ∴EG=CG在△BEG 和△DCG 中，EBG CDG EGB CGD EG CG ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BEG ≌△DCG (AAS ) ∴BE=CD=AB ⑵连结BD ．∵∠EBC=∠CDE ∴∠EBC +∠BCD =∠CDE +∠BCD =90°，即∠BFC =90° ∵CE=2，∴EG=CG=1又tan ∠CDE =31，∴13CG DG =，∴DG =3 ∵△BEG ≌△DCG ，∴BG=DG=3∴2210BE BG EG =+=∴CD=BE=10法一：∵1122BCDSBC DG CD BF ==，11431022BF ⨯⨯=⨯∴6105BF = 法二：经探索得，△BEG ∽△BFC ，∴BE BCBG BF=，∴1043BF = ∴6105BF = 14．如图，直角梯形ABCD 中，,90,45,AD BC ADC ABC AB ∠=∠=∥的垂直平分线EG 交BC 于F ，交DC 的延长线于.G求证：(1)CG CF =；(2).BC DG =AB CDEF证明：(1) ,AB EF ⊥ 45B ∠=904545EFB ∴∠=-=45CFG ∴∠=//,90AD BC ADC ∠=90FCG ∴∠=45,FCG ∴∠= CG CF =∴(2)连接AF ， EF 是AB 的中垂线,AF BF FE AB ∴=⊥45=∠=∠∴BFE AFE90=∠∴AFB DCB AFB ∠=∠∴BC AD CD AF //,// ∴,AF DC BF DC ∴=∴=由(1)知CG CF = ,CG DC CF BF +=+∴即：DG BC =二、有关“截长补短”题型1、在ABCD 中，对角线,BD BC G BD ⊥为延长线上一点且ABG ∆为等边三角形，BAD ∠、CBD ∠的平分线相交于点E ，连接AE BD F 交于，连接GE 。

类型三向角两边作垂线1. 如图，在正方形ABCD中，F是CD的中点，E是BC边上的一点，且AF平分∠DAE.(1)若正方形ABCD的边长是4，BE＝3, 求EF的长；(2)求证：AE＝EC＋CD.第1题图2. (2017重庆育才一模)已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE .(1)如图①，若∠ABE ＝15°，O 为BE 中点，连接AO ，且AO ＝1，求BC 的长；(2)如图②，F 也为AC 上一点，且满足AE ＝CF ，过A 作AD ⊥BE 交BE 于点H ，交BC 于点D ，连接DF 交BE 于点G ，连接AG .若AG 平分∠CAD ，求证：AH ＝12AC .第2题图答案1. (1)解：∵正方形ABCD ，∴AD＝CD＝BC, ∠D＝∠C＝90°.∵BE＝3，∴EC＝1.∵F是CD的中点，∴DF＝CF＝2.在Rt△EFC中，由勾股定理得EF＝CE2＋CF2＝12＋22＝ 5. (2)证明：如解图，过点F作FG⊥AE于点G，∵AF平分∠DAE，∠D＝90°，∴FG＝DF.在Rt△ADF和△AGF中，∵AF＝AF，DF＝GF，∴△ADF≌△AGF(HL)，∴AG＝AD.∵DF＝FC＝FG，EF＝EF，∠C＝∠FGE＝90°，∴△FCE≌△FGE(HL)，∴CE＝GE.∵AE＝AG＋GE，AG＝AD＝CD，GE＝CE，∴AE＝EC＋CD.第1题解图2. (1)解：如解图①，在AB上取一点M，使得BM＝ME，连接ME. 在Rt△ABE中，∵OB＝OE，∴BE ＝2OA ＝2，∵MB ＝ME ，∴∠MBE ＝∠MEB ＝15°，∴∠AME ＝∠MBE ＋∠MEB ＝30°，设AE ＝x ，则ME ＝BM ＝2x ，AM ＝3x ， ∵AB 2＋AE 2＝BE 2，∴(2x ＋3x )2＋x 2＝22，∴x ＝6－22或－6＋22(舍)，∴AB ＝AC ＝(2＋3)·6－22，∴BC ＝2AB ＝3＋1.第2题解图①(2)证明：如解图②， 过点G 作GM ⊥AC 于M .∵AG 平分∠CAD , GH ⊥AD ，∴GH ＝GM .在Rt △GAH 和Rt △GAM 中，⎩⎪⎨⎪⎧AG ＝AG GH ＝GM ，∴△GAH ≌△GAM (HL ),∴AH ＝AM .过点C 作CP ⊥AC ，交AD 的延长线于P ，∵BE ⊥AP ，∴∠AHB ＝90°，∴∠ABH ＋∠BAH ＝90°，∵∠BAH ＋∠PAC ＝90°，∴∠ABE ＝∠PAC ，在△ABE 和△CAP 中，⎩⎪⎨⎪⎧∠ABE ＝∠CAP AB ＝AC ∠BAE＝∠ACP，∴△ABE ≌△CAP (ASA )，∴AE ＝CP ＝CF ，∠AEB ＝∠P , 在△DCF 和△DCP 中，⎩⎪⎨⎪⎧CD ＝CD ∠DCF＝∠DCP CF ＝CP，∴△DCF ≌△DCP (SAS )，∴∠DFC ＝∠P ，∴∠GFE ＝∠GEF ， ∴GE ＝GF ，∵GM ⊥EF ，∴FM ＝ME ，∵AE ＝CF ，∴AF ＝CE ，∴AM ＝CM ，∴AH ＝AM ＝CM ＝12AC .第2题解图②。

1.(10分)如图，已知ABC △满足AB BC AC <<．(1)用尺规作图在边AC 上确定一点P ，使得PB PC =(不写作法和证明，保留作图痕迹)；(2)若AB AP =，37ABC A ︒∠-∠=，求C ∠的大小．2. 如图，在钝角中，.（1) 作AC 的重直平分线，与边BC 、AC 分别交于点D 、E(要求：尺规作图，不写作法，保留作图痕迹）,（2)在（1)的条件下，过点B 作BHLAC 交CA 的延长线于点H. 连接AD,求证3.如图，在平行四边形ABCD 中，AE 平分交BD 于点E,交BC 于点M.（1)尺规作图：作的平分线CN,交BD 于点F.（基本作图，保留作图痕迹，不写作法，并标明字母）（2)求证：AE=CF.ABC ∆090BAC ∠>ADE HBC ∠=∠BAD ∠BCD∠4.(10分）如图，在平行四边形ABCD 中，AC 是对角线。

（1)尺规作图：过点A 作BC 的垂线交BC 于点E（不写作法，保留作图痕迹，并标明字母）； （2)在（1)的条件下，若BC=5,求,平行四边形ABCD 的面积。

5. 如图，在平行四边形ABCD 中，AB=AC,.（1)使用直尺和圆规，作的平分线AE 交CD 于点F(保留作图痕迹）；（2)在（1)的条件下，求的度数。

6.如图，在矩形ABCD 中，点E 是BC 边上一点，AD=DE （1)过A 作于点F,(基本作图，保留作图痕迹，不写作法，要下结论）；（2)求证：AF=CD.50B ∠=DAC ∠AFC ∠AF DE ⊥3tan 2ACB ∠=045B ∠=7.20.如图，已知三角形ABC,CD 平分（1)以D 为顶点，在边AB 右侧作,交AC 于点E. (要求：尺规作图，不写做法，保留作图痕迹）（2)在（1)所作的图中，求证：DE=CE8.如图，已知ΔABC,在BC 的延长线上取一点D 使得AD=AC.（1)在AC 左侧，求作点E,使得AE=AB,CE=DB,连接AE 、CE.(用基本作图，保留作图痕迹，不写作法、结论）（2)求证：9. 如图，在平行四边形ABCD 中，CF 平分交BD 于点F.（1)尺规作图：过点A 作AE 平分交BD 于点E,注意：不写作法，保留作图痕迹，并标明字母，（2)求证：AE=CF.ACB ∠ADE ABC ∠=∠EAB CAD ∠=∠BCD ∠BAD ∠10.(10分）如图，菱形ABCD 的对角线AC,BD 交于点O.尺规作图：过点A 作直线BC 的垂线（不写作法和证明，保留作图痕迹），该垂线与BC 交于点E,F 为AD 边上一点，DF=AE,连接OF,若OD=2AO,请猜想CE 与OF 的数量关系，并证明你的猜想。