安徽省宿州市砀山县梨都中学2015届高三上学期第三次月考数学(文)试卷

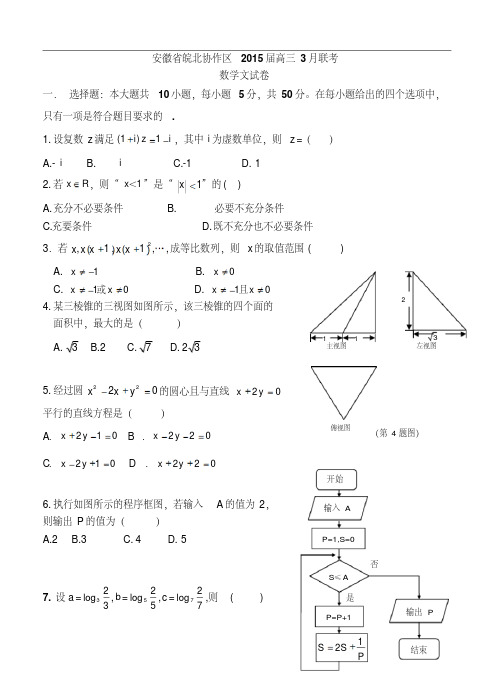
***学校高三（上期）第三次月考数学试卷一、选择题（本大题共9小题，共45.0分）)1. 已知全集U=R，集合A={x||x−1|<1}，B={x|2x−5x−1≥1}，则A∩∁U B=( )A.{x|1<x<2}B.{x|1<x≤2}C.{x|1≤x<2}D.{x|1≤x<4}2. 设m∈R，则“m＝−3”是“直线l1:mx+3y＝2−m与l2:x+(m+2)y＝1平行”的（）A.充分但不必要条件B.必要但不充分条件C.充要条件D.既不充分也不必要的条件3. 函数f(x)=e x+1x3(e x−1)（其中e为自然对数的底数）的图象大致为（）A. B.C. D.4. 已知棱长为的正方体ABCD−A1B1C1D1的一个面A1B1C1D1在半球底面上，四个顶点A，B，C，D都在半球面上，则半球体积为（）A.4B.2C.D.5. 已知△ABC的内角A，B，C的对边分别为a，b，c，满足2acos A =3c−2bcos B，且b=√5sin B，则a＝（）A.5 3B.23C.35D.2√536. 已知函数y＝f(x)是定义在R上的偶函数，且当x∈[0, +∞)时，f(x)+xf′(x)>0，若a ＝0.76f(0.76)，b＝(log0.76)f(log0.76)，c＝60.6⋅f(60.6)，则a，b，c的大小关系是（）A.c>a>bB.a>c>bC.b>a>cD.a>b>c7. 设F1，F2分别是椭圆E:x2a2+y2b2=1(a>b>0)的左、右焦点，过点F1的直线交椭圆E于A，B两点，|AF1|＝3|BF1|，若cos∠AF2B=35，则椭圆E的离心率为（）A.1 2B.23C.√32D.√228. 已知函数f(x)＝cos(2x−）+2sin(x−）sin(x+）(x∈R)．给出下面四个结论：①f(x)是最小正周期为π的奇函数；②f(x)图象的一条对称轴是；③f(x)图象的一个对称中心是；④f(x)的单调递增区间为．其中正确的结论是（）A.①③B.②③C.②③④D.①②③9. 已知函数f(x)={x2+4a,x>01+log a|x−1|,x≤0(a>0，且a≠1)在R上单调递增，且关于x的方程|f(x)|＝x+3恰有两个不相等的实数解，则a的取值范围是（）A.(34, 1316] B.(0, 34]∪{1316}C.[14, 34)∪{1316} D.[14, 34]∪{1316}二、填空题（本大题共6小题，共30.0分）)10. 若，则z的共轭复数为________．11. 如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为________．12. 已知圆C的圆心在直线x+y＝0上，圆C与直线x−y＝0相切，且在直线x−y−3＝0上截得的弦长为√6，则圆C的方程为________．13. 已知a∈R，设函数f(x)＝，若关于x的不等式f(x)≥0在R上恒成立，则a的取值范围为________．14. 在直角三角形ABC中，∠ACB＝90∘，AC＝4，＝2，＝3，则＝________．15. 已知正数x，y满足x2y+4xy2+6xy＝x+4y，则xyx+4y 的最大值为________18．三、解答题（本大题共5小题，共75.0分）)16. 在△ABC中，内角A，B，C所对的边分别为a，b，c，sin B2=√66，b sin A=√6a sin C，c=1．（1）求a的值和△ABC的面积；（2）求sin(2A+π3)的值．17. 在四棱锥P−ABCD中，PD⊥平面ABCD，AB // DC，AB⊥AD，DC＝AD＝1，AB＝2，∠PAD＝45∘，E是PA的中点，F在线段AB上，且满足＝0．(Ⅰ)求证：DE // 平面PBC；(Ⅱ)求二面角F−PC−B的余弦值；(Ⅲ)在线段PA上是否存在点Q，使得FQ与平面PFC所成角的余弦值是，若存在，求出AQ的长；若不存在，请说明理由．18. 如图，在平面直角坐标系xOy中，椭圆C：＝1(a>b>0)的离心率为，短轴长是2．(Ⅰ)求椭圆C的方程；(Ⅱ)设椭圆C的下顶点为D，过点D作两条互相垂直的直线l1，l2，这两条直线与椭圆C的另一个交点分别为M，N．设l1的斜率为k(k≠0)，△DMN的面积为S，当时，求k的取值范围．19. 已知等比数列{a n}的公比q>0，且满足a1+a2＝6a3，a4＝4a32，数列{b n}的前n项和S n＝，n∈N∗．(Ⅰ)求数列{a n}和{b n}的通项公式；(Ⅱ)设c n＝，求数列{c n}的前2n项和T2n．20. 已知f(x)＝x2−4x−6ln x．(Ⅰ)求f(x)在（1, f(1)）处的切线方程以及f(x)的单调性；(Ⅱ)对∀x∈(1, +∞)，有xf′(x)−f(x)>x2+6k(1−）−12恒成立，求k的最大整数解；(Ⅲ)令g(x)＝f(x)+4x−(a−6)ln x，若g(x)有两个零点分别为x1，x2(x1<x2)且x0为g(x)的唯一的极值点，求证：x1+3x2>4x0．参考答案与试题解析**8学校高三（上）第三次月考数学试卷一、选择题（本大题共9小题，共45.0分）1.【答案】C【考点】交、并、补集的混合运算【解析】可解出集合A，B，然后进行补集、交集的运算即可．【解答】解：A={x|0<x<2}，B={x|x<1或x≥4}；∴∁U B={x|1≤x<4}，∴A∩∁U B={x|1≤x<2}．故选C.2.【答案】C【考点】充分条件、必要条件、充要条件【解析】由直线l1:mx+3y＝2−m与l2:x+(m+2)y＝1平行，可得且，解出即可判断出．【解答】直线l1:mx+3y＝2−m与l2:x+(m+2)y＝1平行，则且，解得m＝−3，因此“m＝−3”是“直线l1:mx+3y＝2−m与l2:x+(m+2)y＝1”平行的充要条件．3.【答案】D【考点】函数的图象与图象的变换【解析】由函数为偶函数，排除AC；由x→+∞时，f(x)→0，排除B，由此得到答案．【解答】f(−x)=e−x+1(−x)3(e−x−1)=−1+e xx3(1−e x)=e x+1x3(e x−1)=f(x)，故函数f(x)为偶函数，其图象关于y轴对称，故排除A，C；当x→+∞时，x3(e x−1)>>e x+1，f(x)→0，故排除B．4.【答案】B【考点】柱体、锥体、台体的体积计算球的表面积和体积棱柱的结构特征【解析】先求正方体的底面对角线的长，再求球的半径，然后求半球的体积．【解答】正方体的顶点A、B、C、D在半球的底面内，顶点A1、B1、C1、D1在半球球面上，底面ABCD的中心到上底面顶点的距离就是球的半径＝，半球的体积：×π×（）3＝2π．5.【答案】A【考点】正弦定理【解析】由正弦定理及两角和的正弦函数公式，三角形内角和定理可得3sin C cos A＝2sin C，结合sin C≠0，可得cos A，利用同角三角函数基本关系式可求sin A，由正弦定理可求a的值．【解答】∵2acos A =3c−2bcos B，可得：2a cos B＝3c cos A−2b cos A，∴由正弦定理可得：2sin A cos B＝3sin C cos A−2sin B cos A，可得3sin C cos A＝2(sin A cos B+ sin B cos A)＝2sin C，∵sin C≠0，可得：cos A=23，∴sin A=√1−cos2A=√53，又∵b=√5sin B，∴由正弦定理asin A =bsin B，可得：√53=bsin B=√5，可得：a=53．6.【答案】A【考点】利用导数研究函数的单调性【解析】此题暂无解析【解答】此题暂无解答7.【答案】D【考点】椭圆的离心率椭圆的定义余弦定理【解析】设|F1B|＝k(k>0)，则|AF1|＝3k，|AB|＝4k，由cos∠AF2B=35，利用余弦定理，可得a＝3k，从而△AF1F2是等腰直角三角形，即可求椭圆E的离心率．【解答】设|F1B|＝k(k>0)，则|AF1|＝3k，|AB|＝4k，∴|AF2|＝2a−3k，|BF2|＝2a−k∵cos∠AF2B=35，在△ABF2中，由余弦定理得，|AB|2＝|AF2|2+|BF2|2−2|AF2|⋅|BF2|cos∠AF2B，∴(4k)2＝(2a−3k)2+(2a−k)2−65(2a−3k)(2a−k)，化简可得(a+k)(a−3k)＝0，而a+k>0，故a＝3k，∴|AF2|＝|AF1|＝3k，|BF2|＝5k，∴|BF2|2＝|AF2|2+|AB|2，∴AF1⊥AF2，∴△AF1F2是等腰直角三角形，∴c=√22a，∴椭圆的离心率e=ca =√22，8.【答案】B【考点】命题的真假判断与应用三角函数中的恒等变换应用【解析】本题考查两角和与差的三角函数及辅助角公式，同时考查函数y＝A sin(ωx+φ)的图象与性质，利用两角和与差的三角函数及辅助角公式化简f(x)，然后由正弦函数的性质，逐一分析求解即可．【解答】∵＝，∴f(x)不是奇函数，故①不正确．∵，∴直线是f(x)图象的一条对称轴，故②正确．∵，∴点是f(x)图象的一个对称中心，故③正确，令，可得，所以f(x)的单调递增区间为，故④不正确．所以正确的结论为②③．9.【答案】D【考点】分段函数的应用【解析】由题意可知f(x)在两段上均为增函数，且f(x)在(0, +∞)上的最小值大于或等于f(0)，作出|f(x)|和y＝x+3的图象，根据交点个数判断4a与3的大小关系，以及直线和抛物线相切的条件，列出不等式组解出．【解答】由1+loga |x−1|＝0，解得x＝1−1a≤−3，即x≤0时，有且只有一解．则a的范围是[14, 34]∪{1316}．故选：D．二、填空题（本大题共6小题，共30.0分）10.【答案】1−3i【考点】复数的运算【解析】利用复数的运算法则求出z，由此能求出z的共轭复数．【解答】＝，∴z的共轭复数为1−3i．11.【答案】43【考点】柱体、锥体、台体的体积计算由三视图求外接球问题【解析】本题主要考查空间几何的体积．【解答】解：正方体的棱长为2，以其所有面的中心为顶点的多面体是正八面体，其中正八面体的所有棱长都是√2，则该正八面体的体积为1 3×(√2)2×2=43．故答案为：43．12.【答案】(x−1)2+(y+1)2＝2【考点】直线与圆的位置关系【解析】设圆心为C(a, b)，半径为r，由题意可得关于a，b，r的方程组，求解可得a，b，r的值，则圆的方程可求．【解答】设圆心为C(a, b)，半径为r，由题意可得，{a+b=0 r=√2(√2)2+(√62)2=r2，解得{a=1b=−1r=√2．∴圆C的方程为(x−1)2+(y+1)2＝2．13.[0, 2e]【考点】函数恒成立问题分段函数的应用【解析】按照x≤1与x>1分类讨论，分别分离变量、求最值即可．【解答】当x<1时，f(x)≥0化为恒成立，，∵x<1，∴x−1<0，∴，∴，当且仅当即x＝0时取等号．∴a≥0(1)当x>1时，f(x)≥0化为恒成立．设，，∴当∈(1, e)时，，g(x)单调递减，当∈(e, +∞)时，，g(x)单调递增，∴g(x)≥g(e)＝e+e＝2e，∴a≤2e．综上，a∈[0, 2e]．故答案为[0, 2e]．14.【答案】【考点】数量积表示两个向量的夹角如图所示，设B(0, a)，利用向量的线性运算和数量积运算即可得出．【解答】建立如图所示的坐标系，则由题意可得A(4, 0)，C(0, 0)，设B(0, a)．又∵＝2，∴＝（，）；∵＝3，∴＝+＝+•＝(−2，），∴则＝4×−2×4＝，15.【答案】18【考点】基本不等式及其应用【解析】令x+4y＝t，则由条件可得xyx+4y =1t+6，然后根据条件出t的范围，进一步求出xyx+4y的最大值．【解答】∵正数x，y满足x2y+4xy2+6xy＝x+4y，∴xy(x+4y+6)＝x+4y，∴xy=x+4yx+4y+6．令x+4y＝t，则xy=tt+6且t>0，∵x+4y≥2√4xy=4√xy，当且仅当x＝4y时取等号，∴t≥4√tt+6，即t2+6t−16≥0，∴t≥2或t≤−8（舍），∴xyx+4y =1t+6≤18，∴xyx+4y 的最大值为18．三、解答题（本大题共5小题，共75.0分）16.【答案】解：(1)△ABC中，sin B2=√66，∴cos B2=√1−sin2B2=√306，∴sin B=2sin B2cos B2=√53，cos B=1−2sin2B2=23，∴B为锐角．∵b sin A=√6a sin C，利用正弦定理可得sin B sin A=√6sin A sin C，∴sin C=√6=√3018<sin B，故C为锐角，cos C=√1−sin2C=7√618，∴sin A=sin(B+C)=sin B cos C+cos B sin C=√53×7√618+23×√3018=√306．再根据c=1，利用正弦定理asin A =csin C，可得√306=√3018，求得a=3，故△ABC的面积为S=12ac⋅sin B=12×3×1×√53=√52．（2）∵cos A=−cos(B+C)=sin B sin C−cos B cos C=√53×√3018−23×7√618=−√66，∴sin A=√1−cos2A=√306，cos2A=1−2sin2A=1−2×3036=−23，∴sin(2A+π3)=sin2A cosπ3+cos2A sinπ3=√306×12−23×√32=√30−4√312．【考点】求两角和与差的正弦两角和与差的余弦公式【解析】（1）△ABC中，由条件利用同角三角函数的基本关系、二倍角公式求得sin B、cos B的值，再利用正弦定理求得sin C的值，可得cos C的值，可得sin A=sin(B+C)的值，再利用正弦定理求得a的值．（2）求得cos A=−cos(B+C)的值，可得sin A的值，求得sin2A、cos2A的值，再利用两角和的正弦公式求得sin(2A+π3)的值．【解答】解：(1)△ABC中，sin B2=√66，∴cos B2=√1−sin2B2=√306，∴sin B=2sin B2cos B2=√53，cos B=1−2sin2B2=23，∴B为锐角．∵b sin A=√6a sin C，利用正弦定理可得sin B sin A=√6sin A sin C，∴sin C=√6=√3018<sin B，故C为锐角，cos C=√1−sin2C=7√618，∴sin A=sin(B+C)=sin B cos C+cos B sin C=√53×7√618+23×√3018=√306．再根据c=1，利用正弦定理asin A =csin C，可得√306=√3018，求得a=3，故△ABC的面积为S=12ac⋅sin B=12×3×1×√53=√52．（2）∵cos A=−cos(B+C)=sin B sin C−cos B cos C=√53×√3018−23×7√618=−√66，∴sin A=√1−cos2A=√306，cos2A=1−2sin2A=1−2×3036=−23，∴sin(2A+π3)=sin2A cosπ3+cos2A sinπ3=√306×12−23×√32=√30−4√312．17.【答案】证明：(Ⅰ)证法一：取PB的中点M，AB的中点N，连结EM，CM，∵在四棱锥P−ABCD中，PD⊥平面ABCD，AB // DC，AB⊥AD，DC＝AD＝1，AB＝2，∠PAD＝45∘，E是PA的中点，F在线段AB上，∴CD // AB，且CD＝，EM // AB，且EM＝，∴EM // CD，且EM＝CD，四边形CDEM为平行四边形，∴DE // CM，∵CM⊂平面PBC，DE⊄平面PBC，∴DE // 平面PBC．（1）证法二：由题意得DA、DC、DP两两垂直，如图，以D为原点，DA、DC、DP分别为x，y，z轴，建立空间直角坐标系，则A(1, 0, 0)，B(1, 2, 0)，C(0, 1, 0)，P(0, 0, 1)，E（），＝(−1, −1, 0)，＝(0, −1, 1)，设平面PBC的法向量为＝(x, y, z)，则，取y＝1，得＝(−1, 1, 1)，又＝（），∴＝0．又DE⊄平面PBC，∴DE // 平面PBC．（2）设点F(1, t, 0)，则＝(1, t−1, 0)，＝(1, 2, 0)，∵＝0，∴＝1+2(t−1)＝0．解得t＝，∴F(1，，0)，，＝(0, 1, −1)，设平面FPC的法向量＝(x, y, z)，由，得，取x＝1，得＝(1, 2, 2)，设二面角F−PC−B的平面角为θ，则cosθ＝＝，∴二面角F−PC−B的余弦值为．(Ⅲ)设＝＝(−λ, 0, λ)，λ∈[0, 1]，∴＝，∴＝λ−1，∴cos<>＝＝，∵FQ与平面PFC所成角的余弦值是，∴其正弦值为，∴||＝，解得，或（舍），∴在线段PA上是否存在点Q，使得FQ与平面PFC所成角的余弦值是，＝（-），|AQ|＝．【考点】二面角的平面角及求法直线与平面平行【解析】(Ⅰ)证法一：取PB的中点M，AB的中点N，连结EM，CM推导出四边形CDEM为平行四边形，从而DE // CM，由此能证明DE // 平面PBC．证法二：由题意得DA、DC、DP两两垂直，以D为原点，DA、DC、DP分别为x，y，z轴，建立空间直角坐标系，利用向量法能证明DE // 平面PBC．(Ⅱ)设点F(1, t, 0)，求出平面FPC和平面PCB的法向量，利用向量法能求出二面角F−PC−B的余弦值．(Ⅲ)设＝＝(−λ, 0, λ)，λ∈[0, 1]，利用向量法能求出在线段PA上是否存在点Q，使得FQ与平面PFC所成角的余弦值是，|AQ|＝．【解答】证明：(Ⅰ)证法一：取PB的中点M，AB的中点N，连结EM，CM，∵在四棱锥P−ABCD中，PD⊥平面ABCD，AB // DC，AB⊥AD，DC＝AD＝1，AB＝2，∠PAD＝45∘，E是PA的中点，F在线段AB上，∴CD // AB，且CD＝，EM // AB，且EM＝，∴EM // CD，且EM＝CD，四边形CDEM为平行四边形，∴DE // CM，∵CM⊂平面PBC，DE⊄平面PBC，∴DE // 平面PBC．（1）证法二：由题意得DA、DC、DP两两垂直，如图，以D为原点，DA、DC、DP分别为x，y，z轴，建立空间直角坐标系，则A(1, 0, 0)，B(1, 2, 0)，C(0, 1, 0)，P(0, 0, 1)，E（），＝(−1, −1, 0)，＝(0, −1, 1)，设平面PBC的法向量为＝(x, y, z)，则，取y＝1，得＝(−1, 1, 1)，又＝（），∴＝0．又DE⊄平面PBC，∴DE // 平面PBC．（2）设点F(1, t, 0)，则＝(1, t−1, 0)，＝(1, 2, 0)，∵＝0，∴＝1+2(t−1)＝0．解得t＝，∴F(1，，0)，，＝(0, 1, −1)，设平面FPC的法向量＝(x, y, z)，由，得，取x＝1，得＝(1, 2, 2)，设二面角F−PC−B的平面角为θ，则cosθ＝＝，∴二面角F−PC−B的余弦值为．(Ⅲ)设＝＝(−λ, 0, λ)，λ∈[0, 1]，∴＝，∴＝λ−1，∴cos<>＝＝，∵FQ与平面PFC所成角的余弦值是，∴其正弦值为，∴||＝，解得，或（舍），∴在线段PA上是否存在点Q，使得FQ与平面PFC所成角的余弦值是，＝（-），|AQ|＝．18.【答案】（1）设椭圆C的半焦距为c，则由题意得，又a2＝b2+c2，联立解得a＝2，b＝1．∴椭圆方程为+y2＝1，（2）由(Ⅰ)知，椭圆C的方程为+y2＝1，所以椭圆C与y轴负半轴交点为D(0, −1)．因为l1的斜率存在，所以设l1的方程为y＝kx−1，代入+y2＝1，得M（，），从而DM＝＝．用-代k得DN＝，所以△DMN的面积S＝•×＝．则＝，因为，即>，整理得4k4−k2−14<0，解得-<k2<2所以0<k2<2，即-<k<0或0<k<．从而k的取值范围为（-，0)∪(0，）．【考点】椭圆的标准方程椭圆的应用直线与椭圆的位置关系【解析】(Ⅰ)根据椭圆C的离心率为，短轴长是2，结合a2＝b2+c2，即可求出a，b的值；(Ⅱ)设l1的方程为y＝kx−1，代入入+y2＝1，求出M的坐标，可得DM，用-代k得DN＝，求出△DMN的面积，＝，可得>，从而可求k的取值范围．【解答】（1）设椭圆C的半焦距为c，则由题意得，又a2＝b2+c2，联立解得a＝2，b＝1．∴椭圆方程为+y2＝1，（2）由(Ⅰ)知，椭圆C的方程为+y2＝1，所以椭圆C与y轴负半轴交点为D(0, −1)．因为l1的斜率存在，所以设l1的方程为y＝kx−1，代入+y2＝1，得M（，），从而DM＝＝．用-代k得DN＝，所以△DMN的面积S＝•×＝．则＝，因为，即>，整理得4k4−k2−14<0，解得-<k2<2所以0<k2<2，即-<k<0或0<k<．从而k的取值范围为（-，0)∪(0，）．19.【答案】（1）依题意，由a1+a2＝8a3，a4＝2a32，可得，解得q＝，a1＝，∴a n＝•（）n−1＝（）n，n∈N∗，对于数列{b n}：当n＝1时，b3＝S1＝1，当n≥7时，b n＝S n−S n−1＝-＝n，∵当n＝6时，b1＝1也满足上式，∴b n＝n，n∈N∗．（2）由题意及(Ⅰ)，可知当n为奇数时，c n＝•a n+7＝×（）n+3＝-，当n为偶数时，c n＝a n⋅b n＝n⋅（）n，令A＝c5+c3+...+c2n−2，B＝c2+c4+...+c8n，则A＝c1+c3+...+c4n−1＝-+-+…+-＝-＝-，B＝c6+c4+c6+...+c2n＝2⋅（）2+4⋅（）4+2⋅（）8+...+2n⋅（）2n，∴（）2B＝2⋅（）4+2⋅（）2+...+(2n−2)⋅（）2n+7n⋅（）7n+2，两式相减，可得B＝2⋅（）2+2⋅（）4+3⋅（）2+...+2⋅（）2n−2n⋅（）2n+6，＝（）3+（）7+（）5+...+（）3n−1−2n⋅（）2n+2，＝−2n⋅（）2n+7，＝−(n+）•（）2n+2+，∴B＝-•（）2n−6+，∴T8n＝c1+c2+...+c5n＝(c1+c3+...+c8n−1)+(c2+c3+c6+...+c2n)＝A+B＝--•（）2n−1+＝-（+）2n−2．【考点】数列递推式数列的求和【解析】此题暂无解析【解答】此题暂无解答20.【答案】（1）f(x)＝x2−4x−6ln x的导数为f′(x)＝2x−4−，可得f′(1)＝−8，f(1)＝−3，所以f(x)在（1, f(1)）处的切线方程为y+3＝−8(x−1)即y＝−8x+5；由f′(x)＝(x+1)(x−3)，由f′(x)>0，可得x>3；由f′(x)<0，可得0<x<3，所以f(x)的单调递减区间为(0, 3)，单调递增区间为(3, +∞)；（2）xf′(x)−f(x)>x2+6k(1−）−12等价于k<（）min，可令ℎ(x)＝，ℎ′(x)＝，记m(x)＝x−2−ln x，m′(x)＝1−>0，所以m(x)为(1, +∞)上的递增函数，且m(3)＝1−ln3<0，m(4)＝2−ln4>0，所以∃x0∈(3, 4)，m(x0)＝0，即x0−2−ln x0＝0，所以ℎ(x)在(1, x0)上递减，在(x0, +∞)上递增，且ℎ(x)min＝ℎ(x0)＝＝x0∈(3, 4)，所以k的最大整数解为3；(Ⅲ)证明：g(x)＝x2−a ln x，g′(x)＝2x−＝＝0，可得x0＝，当x∈(0，），g′(x)<0，x∈（，+∞)，g′(x)>0，所以g(x)在(0，）上单调递减，（，+∞)上单调递增，而要使g(x)有两个零点，要满足g(x0)<0，即g（）＝（）2−a ln<0可得a>2e，因为0<x1<，x2>，令＝t(t>1)，由f(x1)＝f(x2)⇒x12−a ln x1＝x22−a ln x2，即x12−a ln x1＝t2x12−a ln tx1⇒x12＝，而x1+3x2>4x0⇔(3t+1)x1>2⇔(3t+1)2x12>8a，即(3t+1)2•>8a，由a>0，t>1，只需证(3t+1)2ln t−8t2+8>0，令ℎ(t)＝(3t+1)2ln t−8t2+8，则ℎ′(t)＝(18t+6)ln t−7t+6+，令n(t)＝(18t+6)ln t−7t+6+，则n′(t)＝18ln t+11+>0(t>1)，故n(t)在(1, +∞)上递增，n(t)>n(1)＝0；故ℎ(t)在(1, +∞)上递增，ℎ(t)>ℎ(1)＝0；∴x1+3x2>4x0．【考点】利用导数研究函数的最值利用导数研究函数的单调性【解析】(Ⅰ)求得f(x)的导数，可得切线的斜率和切点，由点斜式方程可得切线方程；由导数大于0，可得增区间；导数小于0，可得减区间，注意定义域；(Ⅱ)xf′(x)−f(x)>x2+6k(1−）−12等价于k<（）min，可令ℎ(x)＝，求得导数，再构造函数，求得导数，判断单调性可得ℎ(x)的单调性，以及最小值，即可得到所求k的最大整数解；(Ⅲ)求得g(x)的导数和单调性，由极小值小于0，可得a>2e，再由分析法，注意构造函数，求得导数和单调性，即可得证．【解答】（1）f(x)＝x2−4x−6ln x的导数为f′(x)＝2x−4−，可得f′(1)＝−8，f(1)＝−3，所以f(x)在（1, f(1)）处的切线方程为y+3＝−8(x−1)即y＝−8x+5；由f′(x)＝(x+1)(x−3)，由f′(x)>0，可得x>3；由f′(x)<0，可得0<x<3，所以f(x)的单调递减区间为(0, 3)，单调递增区间为(3, +∞)；（2）xf′(x)−f(x)>x2+6k(1−）−12等价于k<（）min，可令ℎ(x)＝，ℎ′(x)＝，记m(x)＝x−2−ln x，m′(x)＝1−>0，所以m(x)为(1, +∞)上的递增函数，且m(3)＝1−ln3<0，m(4)＝2−ln4>0，所以∃x0∈(3, 4)，m(x0)＝0，即x0−2−ln x0＝0，所以ℎ(x)在(1, x0)上递减，在(x0, +∞)上递增，且ℎ(x)min＝ℎ(x0)＝＝x0∈(3, 4)，所以k的最大整数解为3；(Ⅲ)证明：g(x)＝x2−a ln x，g′(x)＝2x−＝＝0，可得x0＝，当x∈(0，），g′(x)<0，x∈（，+∞)，g′(x)>0，所以g(x)在(0，）上单调递减，（，+∞)上单调递增，而要使g(x)有两个零点，要满足g(x0)<0，即g（）＝（）2−a ln<0可得a>2e，因为0<x1<，x2>，令＝t(t>1)，由f(x1)＝f(x2)⇒x12−a ln x1＝x22−a ln x2，即x12−a ln x1＝t2x12−a ln tx1⇒x12＝，而x1+3x2>4x0⇔(3t+1)x1>2⇔(3t+1)2x12>8a，即(3t+1)2•>8a，由a>0，t>1，只需证(3t+1)2ln t−8t2+8>0，令ℎ(t)＝(3t+1)2ln t−8t2+8，则ℎ′(t)＝(18t+6)ln t−7t+6+，令n(t)＝(18t+6)ln t−7t+6+，则n′(t)＝18ln t+11+>0(t>1)，故n(t)在(1, +∞)上递增，n(t)>n(1)＝0；故ℎ(t)在(1, +∞)上递增，ℎ(t)>ℎ(1)＝0；∴x1+3x2>4x0．。

高三第三次月考数学（文）试题时间：120分钟 满分：180分一、选择题（本大题共11小题，每小题5分，满分55分） 1、设n S 是等差数列{}n a 的前n 项和，若735S =，则4a =（ ）A ．8B ．7C ．6D ．5 2、函数y x x x =+∈30sin cos ([,])π的值域是 （ ）（A ）[-2，2] （B ）[-1，2] （C ）[-1，1] （D ）[-3，2] 3、已知|a |＝6，|b |＝3，a ·b ＝－12，则向量a 在向量b 方向上的投影是( )． A ．－4B ．4C ．－2D ．24、两座灯塔A 和B 与海洋观察站C 的距离都等于a km ，灯塔A 在观察站C 的北偏东20°，灯塔B 在观察站C 的南偏东40°，则灯塔A 与灯塔B 的距离为( ) A ．a km B.2a km C ．2a km D.3a km5、已知ΔABC 的三个顶点A 、B 、C 及所在平面内一点P 满足=++，则点P 与ΔABC 的关系是A 、P 在ΔABC 内部B 、P 在ΔABC 外部C 、P 在直线AB 上D 、P 在ΔABC 的AC 边的一个三等分点上 6、函数y= sin(2x+4π)的一个增区间是( ) A. [-4,4ππ] B. [-8,83ππ] C. [-0,2π] D. [-83,8ππ]7、在等比数列｛a n ｝中，a 1＝1，a 10＝3，则a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 = （ ） A. 81 B. 27527 C. 3 D. 2438、在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若a cos A ＝b sin B ，则sin A cos A ＋cos 2B 等于( )．A ．－12 B.12C ．－1D ．19、在平行四边形ABCD 中，AC 与BD 交于点O ，E 是线段OD 的中点，AE 的延长线与CD 交于点F. 若=, =,则=AF （ ）A ．1142a b +r rB. 2133a b +r rC. 1124a b +r rD. 1233a b +r r10、数列1，1＋2，1＋2＋22，…，1＋2＋22＋…＋2n －1，…的前n 项和为 （ ）A.2n －n －1B.2n +1－n －2C.2nD.2n +1－n 11、设S n 为等差数列{a n }的前n 项和，若a 1＝1，公差d ＝2，S k ＋2－S k ＝24，则k ＝( )．A ．8B ．7C ．6D ．5二、填空题（本大题8小题，每小题5分，满分40分）12、已知复数z 满足z (1i)2i ⋅-=-（i 为虚数单位），则复数z=13、两个等差数列的前n 项和之比为5n ＋102n －1，则它们的第7项之比为________．14、若cos(α＋β)＝15，cos(α－β)＝35，则tan αtan β＝________.15、已知各项不为0的等差数列{a n }，满足2a 3－a 27＋2a 11＝0，数列{b n }是等比数列，且b 7＝a 7，则b 6b 8＝________.16、等比数列{a n }的前n 项和S n ＝2n－1，则a 21＋a 22＋…＋a 2n ＝________.17、在正项等比数列{}n a 中，11=a ，1642=a a ，则=-++-+-121212821a a a Λ---------18、关于函数()(),32sin 4R x x x f ∈⎪⎭⎫ ⎝⎛+=π有下列命题： ① 由()()021==x f x f 可得21x x -必是π的整数倍；② ()x f y =的表达式可改写为()⎪⎭⎫ ⎝⎛-=62cos 4πx x f ；③ ()x f y =的图象关于点⎪⎭⎫ ⎝⎛-0,6π 对称；④ ()x f y =的图象关于直线6π-=x 对称.以上命题成立的序号是__________________.19、（选做）若M 为△ABC 内一点，且满足AM →＝34AB →＋14AC →，则△ABM 与△ABC 的面积之比为________．三、解答题（本小题共6小题，满分85分）20、（本题14分）在ABC ∆中，角,,A B C 所对的边分别为,,a b c ，已知cos cos A b B a =，且23C π∠=． （Ⅰ）求角,A B 的大小；（Ⅱ）设函数()sin()cos f x x A x =++，求()f x 在[,]63ππ-上的值域．21、（本题14分）.已知向量a ρ＝(cos 23x ，sin 23x )，b ϖ＝(2sin 2cos x x ，-)，且x ∈[0，2π]． （1）求b a ϖϖ+（2）设函数b a x f ϖϖ+=)(+b a ϖϖ⋅，求函数)(x f 的最值及相应的x 的值。

数学参考答案（文科）一.选择题1.B2. D3. A4.C 5 .A 6 . C 7.B 8. A 9. C 10. D二.填空题11. c a b >> 12 . 16 13 .22488+ 14. 3115 ②⑤ 三．解答题16 解：（1）∵ 0cos sin =-C a A c ，由正弦定理得： 0cos sin sin sin =-C A A C又 ∵ A 为三角形的一内角， ∴ 0sin ≠A ∴ 0cos sin =-C C∵ π<<C 0 ∴ 4π=C …………………………6分（2）设)4cos(2cos 2sin32π+-=B A A y A A A A cos sin 3)cos(sin 3+=--=π )6sin(2π+=A ………………………………………………9分又 ∵ 430π<<A ， ∴ 当3π=A 时，2max =y∴ 125)43(ππππ=+-=B . …………………………………12分17 解：（1）∵ 25.05=M∴ 20=M ∴ 2=m ∴1.0=p ，6.0=n∴ 12.0=a ……………………………………………………6分（2）4326.0720=⨯（人） ………………………………………9分（3） 样本中可评为“优秀学生”的频率为203=p ， ∴ 估计小明被评为“优秀学生”的概率为203. …………12分18.解（I ）n n na S n n )1(2--=2≥n 时，)1)(2(2)1()1(211--+----=-=--n n a n n n na S S a n n n n n}{41n n n a a a ⇒=-⇒-为11=a ，4=d 的等差数列 344)1(1-=-+=⇒n n a n …………6分（II ）12)12()1(2-=⇒-=--=n nS n n n n na S nn n 2212)12(121n n n n S S S n =-+=+++⇒10082015)1(22=⇒=--⇒n n n 存在 ………………12分19. 解：(1)取CE 的中点M ，连结MF,MB ， ∵F 是CD 的中点 ∴MF ∥DE 且MF =21DE ∵AB ⊥平面ACD ，DE ⊥平面ACD ∴AB ∥DE ，MF ∥AB ∵AB=21DE ∴MF=AB ∴ 四边形ABMF 是平行四边形 AF ∥BM,AF ⊄平面BCE ，BM ⊆平面BCE ∴BCE 平面/AF/…………4分 (2) ∵AC=AD∴AF ⊥CD,又∵DE ⊥平面ACD AF ⊆平面ACD ∴AF ⊥DE ，又CD ⋂DE=D ∴AF ⊥平面CDE又∵BM ∥AF ∴BM ⊥平面CDE ∵BM ⊄平面BCE∴CDE BCE 平面平面⊥……………8分 (3)作DH ⊥CE 于H,则DH ⊥平面CBE 由已知得：22,6,2,2====AF CE DE CD 在Rt △CDE 中，32=⋅=CE DE CD DH232121=⋅=⋅=∆AF CE BM CE S BCE ∴3131=⋅=∆-DH S V CBE CBE D ………13分 20.解:(1)2()321g x x ax '=+- 由题意01232<-+ax x 的解集是⎪⎭⎫ ⎝⎛-1,31即01232=-+ax x 的两根分别是1,31-.将1=x 或31-代入方程01232=-+ax x 得1-=a . ()223+--=∴x x x x g . …………4分(2)由(Ⅰ)知：2()321g x x x '=--，(1)4g '∴-=，∴点(1,1)P -处的切线斜率k =(1)4g '-=， ∴函数y=()x g 的图像在点(1,1)P -处的切线方程为：14(1)y x -=+，即450x y -+=. …………8分(3) 2)()(2'+≤x g x f 对()+∞∈,0x 上恒成立，即：123ln 22++≤ax x x x 对()+∞∈,0x 上恒成立，可得xx x a 2123ln --≥对()+∞∈,0x 上恒成立， 设()x x x x h 2123ln --=, 则()()()22'213121231x x x x x x h +--=+-=令()0'=x h ,得31,1-==x x (舍)当10<<x 时,()0'>x h ;当1>x 时, ()0'<x h∴当1=x 时,()x h 取得最大值, ()x h max =-2 2-≥∴a .a ∴的取值范围是[)+∞-,2. …………13分21解：（1）由已知得： 62=a ∴ 3=a 223-=-c a ,22=c ,1=b∴ 椭圆C 的方程为：1922=+y x ………………………………4分 （2）设AM l ：)3(-=x k y 不失一般性，设0>k ∵0=⋅， 则 AN l ：)3(1--=x ky 由098154)19(99)3(222222=-+-+⇒⎩⎨⎧=+-=k x k x k y x x k y ∵ 点)03(，A 在AM 上， 设)(11y x M ，∴ 199813221+-=k k x ∴ 19327221+-=k k x ……………6分 ∴ 1961|3|1||2212+⋅+=-+=k k x k AM用k1-替换k 得： 96119611||2222+⋅+=+⋅+=k k k kk AN ……………………… …8分 ∴ ||||21AN AM S ⋅= )19)(9(36)1(21222++⋅+=k k kk 222224264)1(9)1(189829)1(18kk k k k k k k +++=+++= ………………………10分 83649218164)1(91822=⨯≤+++=k k k k 当且仅当222)1(964+=k k ，即：374+=k 成立. ∴ 83max =S .……………………………………………………………13分。

安徽省宿州市2015届高三第三次质量检测数学试题（文科）一、选择题（本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1. 若，为虚数单位，则=（ ）A. B. C. D.2.命题“任意，都有”的否定，叙述正确的是（ ）A.存在，使得B.任意，都有C.存在，使得D.存在，使得3. “”是“双曲线的离心率大于”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4. 有以下四种变换方式：① 向左平移个单位长度，再将每个点的横坐标缩短为原来的倍；② 向右平移个单位长度，再将每个点的横坐标缩短为原来的倍；③ 每个点的横坐标缩短为原来的倍，再向右平移个单位长度；④ 每个点的横坐标缩短为原来的倍，再向左平移个单位长度.其中能将的图像变为的图像的是（ ）A．②和④ B．①和③ C．①和④ D．②和③开始是奇数？输出结束是是否否5.等比数列中，若，，则（ ）A．4 B．-4 C． D．56.如图，程序框图的输出值（ ）A．10 B．11C．12 D．137. 设是两条不同的直线，是两个不同的平面，给出下列命题：① 若，，则； ② 若，，则；③ 若，，则； ④ 若，，则；⑤ 若，，，则.其中真命题的个数为（ ）A. 1个B. 2个C. 3个D. 4个8.若函数在区间是单调函数，则实数的取值范围是（ ）A. B. C. D.9.设是函数图像上的任意两点，点满足,其中是坐标原点，若点的横坐标是，则点的纵坐标是（ ）A.—1B. 0C. 1D.310. 已知函数是定义在上周期为3的周期函数，当时，，则函数在上的零点的个数为（ ）A．8 B．7 C．6 D．5二、填空题（本大题共5小题，每小题5分，共25分．）11.已知，，，则，，的大小关系为____________；12.若样本数据，…，的方差为4，则数据，…，的方差是____________；13.一个几何体的俯视图如图所示,主视图是底边长为8，86高为4的等腰三角形，左视图是底边长为6，高为4的等腰三角形，那么该几何体的全面积是____________；14.已知点,,,，若平面区域由满足 (）的点组成，现从梯形平面区域内任取一点，则点落在区域内的概率为___________；15.已知圆，直线，以下结论成立的有___________.（写出所有正确结分组频数频率[10,15）50.25[15,20）12[20,25）[25,30]10.05合计1论的编号）①对任意实数与，直线和圆相切；②对任意实数与，直线和圆有公共点；③存在实数与，直线和圆相离；④对任意实数，必存在实数，使得直线和圆相切；⑤对任意实数，必存在实数，使得直线和圆相切.三、解答题（本大题共6小题，满分75分．解答应写出文字说明、证明过程或演算步骤．）16. (本小题满分12分)在中，角所对的边分别为，且满足：.（Ⅰ）求角的大小；（Ⅱ）求的最大值，并求出取得最大值时角的值.17. (本小题满分12分)对某校高一年级学生参加“社区志愿者”活动次数进行统计，随机抽取名学生作为样本，得到这个学生参加“社区志愿者”活动的次数.据此作出频数和频率统计表及频率分布直方图如下：（Ⅰ）求出表中及图中的值；（Ⅱ）若该校高一学生有720人，试估计他们参加“社区志愿者”活动的次数在[15,20）内的人数；（Ⅲ）若参加“社区志愿者”活动的次数不少于20次的学生可评为“优秀志愿者”，试估计小明被评为“优秀志愿者”的概率.18．（本小题满分12分）设数列的前项和为（I）求数列的通项公式（II）是否存在正整数使得…成立？若存在，求出的值；若不存在，请说明理由．19．（本小题满分13分）如图：在多面体中，,,FECBAD,是的中点.（Ⅰ）求证：;（Ⅱ）求证:;（Ⅲ）求三棱锥的体积.20.（本小题满分13分）已知函数．（I）如果函数的单调递减区间为，求函数的解析式；（II）在(Ⅰ)的条件下,求函数y=的图像在点处的切线方程；（III）若不等式恒成立，求实数的取值范围.21.（本小题满分13分）已知椭圆（）上的动点到两个焦点的距离之和为6，且到右焦点距离的最小值为.（Ⅰ）求椭圆的方程；（Ⅱ）若直线和椭圆交于两点，为椭圆的右顶点，,求面积的最大值.安徽省宿州市2015届高三第三次质量检测数学参考答案（文科）一.选择题1.B2. D3. A4.C 5 .A 6 . C 7.B 8. A 9. C 10. D二.填空题11. 12 . 16 13 . 14. 15 ②⑤三．解答题16 解：（1）∵ ，由正弦定理得：又 ∵ 为三角形的一内角， ∴∴∵ ∴ …………………………6分（2）设………………………………………………9分又 ∵ ， ∴ 当时，∴ . …………………………………12分17 解：（1）∵ ∴∴ ∴ ，∴ ……………………………………………………6分（2）（人） ………………………………………9分（3） 样本中可评为“优秀学生”的频率为，∴ 估计小明被评为“优秀学生”的概率为. (12)分18.解（I）时，为，的等差数列…………6分（II）存在 ………………12分19. 解：(1)取CE的中点M，连结MF,MB，MFECBAD∵F是CD的中点∴MF∥DE且MF=DE∵AB⊥平面ACD，DE⊥平面ACD∴AB∥DE，MF∥AB∵AB=DE∴MF=AB∴四边形ABMF是平行四边形AF∥BM,AF平面BCE，BM平面BCE∴…………4分(2) ∵AC=AD∴AF⊥CD,又∵DE⊥平面ACD AF平面ACD ∴AF⊥DE，又CDDE=D ∴AF⊥平面CDE又∵BM∥AF∴BM⊥平面CDE∵BM平面BCE∴……………8分(3)作DH⊥CE于H,则DH⊥平面CBE由已知得：在Rt△CDE中，∴………13分20.解:(1)由题意的解集是即的两根分别是.将或代入方程得.. …………4分(2)由(Ⅰ)知：，，点处的切线斜率，函数y=的图像在点处的切线方程为：，即. …………8分(3)对上恒成立，即：对上恒成立，可得对上恒成立，设, 则令,得(舍)当时,;当时,当时,取得最大值,=-2.的取值范围是. …………13分21解：（1）由已知得： ∴,,∴ 椭圆的方程为： ………………………………4分 （2）设： 不失一般性，设∵， 则 ：由∵ 点在上， 设∴ ∴ ……………6分∴用替换得：……………………… …8分∴………………………10分当且仅当，即：成立.∴ . ……………………………………………………………13分注：用其他方法求解，可酌情给分。

安徽省示范高中2015届高三数学第三次联考试题文（扫描版）金榜教育·2015届安徽省示范高中高三第三次联考数学（文科）参考答案一：选择题 1 【答案】C2 【答案】A 【解析】2x =时，(1,1)a =-r ，(3,3)b =r，a b ⊥r r 。

反之不成立，2a =-也可以。

故选A 。

3 【答案】B【解析】5127cos sin -+131313αα-==. 4 【答案】A 【解析】由11(1)(1)n n na n n n n n n +-==+-+++-，所以12(21)(32)(1)5n a a a n n +++=-+-+++-=L L ， 即115n +-=，即16n +=，解得136,35n n +==.选A.5 【答案】D【解析】2=∴=ϖπT Θ 由五点作图法知232πϕπ=+⨯，ϕ= -6π 6 【答案】D【解析】依题意，函数2()f x x bx c =++对称轴为12x =,且在1[,)2+∞上为增函数，因为(0)(1)f f =，(2)(3)f f -=，123<<，所以(1)(2)(3)f f f <<,即)2()2()0(-<<f f f 选择D.7【答案】A【解析】特称命题的否定为：对任意实数x ，都有210x x +-≥，选A ； 8【答案】A【解析】000000026sin sin 75sin(3045)sin 30cos 45sin 45cos304A +==+=+=由62a c ==+可知,075C ∠=,所以030B ∠=,1sin 2B =由正弦定理得261sin 2sin 2264ab B A+=⋅=⨯=+,故选A9【答案】D【解析】建立如图所示的直角坐标系，则()()()()0,0,0,4,2,4,4,0A B C D ，从而()3,2P ，故()()3,2,3,2PA PB =--=-u u u r u u u r ，从而PA PB ⋅=u u u r u u u r945-=。

正视图俯视图侧视图安庆2015届高三年级第三次模拟考试数学(文科)试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分,共150分,考试时间120分钟。

注意事项：1．答题前，务必在试题卷答题卡规定的地方填写自己的班级、姓名、考场号、座位号。

2．答第Ⅰ卷时，每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦擦干净后，再选涂其他答案标号。

3．答第Ⅱ卷时，必须使用0.5毫米的黑色墨水签字笔在答题卡上书写，要求字体工整、笔迹清晰。

作图题可先用铅笔在答题卡规定的位置绘出，确认后再用0.5毫米的黑色墨水签字笔描清楚。

必须在题号所指示的答题区域作答，超出答题区域书写的答案无效，在试题卷、草稿纸上答题无效。

4．保持卡面清洁，不折叠，不破损。

第I 卷（选择题，共50分）一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的.1．设i 是虚数单位，则复数324321i i i -+-等于（ ） A ．i 62-- B ．i 22+- C ．i 24+ D ．i 64-2．已知集合{}04|2>-=x x A ，{}02|<-=x x B ，则()B A C R ⋂等于（ ） A ．)2,(-∞B ．[]2,2-C ．()2,2-D ．)2,2[-3．“3=m ”是“函数m x x f =)(为实数集R 上的奇函数”的（ ）.A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件4．在区间[]0,π上随机取一个实数x ，使得1sin 0,2x ⎡⎤∈⎢⎥⎣⎦的概率为（ ）A ．1πB ．2πC ．13D ．235．将函数π()sin(2)3f x x =+的图象向右平移ϕ个单位，得到的图象关于原点对称，则ϕ的最小正值为（ ）A ．π6B ．π3C ．5π12 6．已知某几何体的三视图，则该几何体的体积是（A ．12B ．24C ．36D ．482 3 5 5 7 920 1 4 810 3 3 4 534 1 2 2 56 97．直线10x my ++=与不等式组30,20,20x y x y x +-≥⎧⎪-≥⎨⎪-≤⎩表示的平面区域有公共点，则实数m 的取值范围是（ ）A ．14,33⎡⎤⎢⎥⎣⎦B ．41,33⎡⎤--⎢⎥⎣⎦C ．3,34⎡⎤⎢⎥⎣⎦D ．33,4⎡⎤--⎢⎥⎣⎦8．已知圆心为O ，半径为1的圆上有不同的三个点C B A ,,，其中0=⋅OB OA ，存在实数,λμ满足0=++OB u OA OC λ，则实数,λμ的关系为（ ） A ．221λμ+= B ．111λμ+= C ．1λμ= D ．1λμ+=9．已知抛物线28y x =的准线与双曲线()222210,0x y a b a b-=>>相交于A 、B 两点，双曲线的一条渐近线方程是y x =，点F 是抛物线的焦点，且△FAB 是等边三角形，则该双曲线的标准方程是（ ）A ．183222=-y xB ．221163x y -=C ．221632x y -=D ．221316x y -= 10．对于函数()x f x ae x =-，若存在实数,m n ，使得()0f x ≤的解集为[](),m n m n <，则实数a 的取值范围是（ ）A ． ()1,00,e ⎛⎫-∞⋃ ⎪⎝⎭B ． ()1,00,e ⎛⎤-∞⋃ ⎥⎝⎦C ．10,e ⎛⎫⎪⎝⎭D ． 10,e ⎛⎤⎥⎝⎦第II 卷（非选择题，共100分）二、填空题：本大题共5小题，每小题5分，共25分，把答案填在题中横线上。

高中数学学习材料马鸣风萧萧*整理制作教育·2015届安徽省示范高中高三第三次联考金榜教育·2015届安徽省示范高中高三第三次联考数学（文科）参考答案一：选择题1 【答案】C2 【答案】A 【解析】2x =时，(1,1)a =-，(3,3)b =，a b ⊥。

反之不成立，2a =-也可以。

故选A 。

3 【答案】B【解析】5127cos sin -+131313αα-==. 4 【答案】A【解析】由11(1)(1)n n na n n n n n n +-==+-+++-，所以12(21)(32)(1)5n a a a n n +++=-+-+++-=，即115n +-=，即16n +=，解得136,35n n +==.选A.5 【答案】D【解析】2=∴=ϖπT 由五点作图法知232πϕπ=+⨯，ϕ= -6π 6 【答案】D【解析】依题意，函数2()f x x bx c =++对称轴为12x =,且在1[,)2+∞上为增函数，因为(0)(1)f f =，(2)(3)f f -=，123<<，所以(1)(2)f ff <<,即)2()2()0(-<<f f f 选择D.7【答案】A【解析】特称命题的否定为：对任意实数x ，都有210x x +-≥，选A ； 8【答案】A【解析】026sin sin 75sin(3045)sin 30cos 45sin 45cos304A +==+=+=由62a c ==+可知,075C ∠=,所以030B ∠=,1sin 2B =由正弦定理得261sin 2sin 2264ab B A+=⋅=⨯=+,故选A9【答案】D【解析】建立如图所示的直角坐标系，则()()()()0,0,0,4,2,4,4,0A B C D ， 从而()3,2P ，故()()3,2,3,2PA PB =--=-，从而PA PB ⋅=945-=。

2015年安徽省某校高考数学三模试卷（文科）一、选择题：每小题5分，共50分．在四个选项中只有一项是正确的． 1. 若复数z 满足z +2=(z −2)⋅i ，则复数z 的共轭复数z ¯=( )A −2iB 2iC 2+ID 2−i2. 已知全集U =R ，集合A ={x|x 2−2x −3<0}，B ={x|0<x <3}，则（ ） A A ∪B =B B A ∩∁U B =⌀ C B ⊆A D A ⊆B3. 计算(log 32−log 318)÷81−14=( ) A −32B −6C 32D 64. 如图所示的程序框图的输出结果是（ ）A 2B 12C −12D −15. 某几何体的三视图如图所示，则该几何体的体积等于（ ）A 203 B 223 C 243 D 2636. 已知命题p:∀x ∈R ，2x >x 2；命题q:∃x(−2, +∞)，使得(x +1)⋅e x ≤1，则下列命题中为真命题的是（ ）A p ∧qB p ∨(￢q)C (￢p)∧qD (￢p)∧(￢q) 7. 在边长为1的正三角形ABC 中任取一点M ，则AM <√32的概率为（ ）A√3π18 B √3π12 C √3π9 D √3π68. 等比数列{a n }满足a 3=16，a 15=14，则a 6=( )A ±2B 2C 4√2D ±4√29. 已知函数y =2sin(ωx +φ)(ω>0)与直线y =a(a >0)相切，且y =a 与x 轴及函数的对称轴围成的图形面积为π，则ω的值不可能是（ ） A 1 B 2 C 4 D 810. 在平面直角坐标系中xOy 中，圆C 的方程为x 2+y 2−4y +3=0，若直线x −ty +2=0上至多存在一点使得以该点为圆心，1为半径的圆与圆C 相切，则t 的范围为（ ）A (−∞, 0)B (−∞, 0]C (0, +∞)D [0, +∞)二、填空题：每小题5分．11. 已知平面向量a →，b →满足|a →|=|b →|=|a →−b →|=1，则|a →+b →|=________． 12. 若x ，y 满足约束条件{y ≥0x +3y ≤33x +y ≥3，则z =8x −4y 的最小值为________．13. 若函数f(x)=2x +ax 在[1, +∞)上为增函数，则实数a 的取值范围是________．14. 已知F 是抛物线x 2=2py 的焦点，A 、B 是该抛物线上的两点，且满足|AF|+|BF|=3p ，则线段AB 的中点到x 轴的距离为________． 15. 下列命题：①已知函数f(x)={2x−2，x ≥02−x ，x <0，则f[f(−2)]=4；②已知O 为平面内任意一点，A 、B 、C 是平面内互不相同的三点，且满足OA →=xOB →+yOC →．x +y =1，则A 、B 、C 三点共线；③已知平面α∩平面β=l ，直线a ⊂α且a ⊥直线l ，直线b ⊂β，则a ⊥b 是α⊥β的充要条件；④若△ABC 是锐角三角形，则cosA <sinB ；⑤若f(x)=sin(2x +φ)−cos(2x −φ)的最大值为1，且φ∈(0, π2)，则f(x)的单调递增区间为[kπ−π8, kπ+3π8](k ∈Z)．其中真命题的序号为________（填写所有真命题的序号）．三、解答题：共75分．解答应写出必要的文字说明、证明过程及演算步骤． 16. △ABC 中，角A 、B 、C 所对额定边分别为a ，b ，c ，且b <c ； （1）若a =c ⋅cosB ，求角C ；（2）若cosA =sin(B −C)，求角C ．17. 如图，四棱锥P −ABCD 的底面ABCD 为平行四边形，且满足：BD =BA ，BD ⊥BA ，AD =2√2，又PA =PD =√6，M 、N 分别为AD 、PC 的中点． （1）求证：MN // 平面PAB ．（2）连接PM 、BM ，若∠PMB =45∘， (I)证明：平面PBC ⊥平面ABCD ； (II)求四面体N −ABD 的体积．18. 某校高三年级有1200人，在期末统考中，某学科得分的频率分布直方图如图所示；已知频率分布直方图的前四个小长方形上端的中点都在曲线y=1100⋅2110(x−55)上，且题干频率分布直方图中各组中间值估计总体的平均分为72.5分．（1）分别求分数在[80, 90),[90, 100]范围内的人数；（2）从分数在[40, 50)和[90, 100]内的学生中，按分层抽样抽取6人，再从这6人中任取两人，求这两人平均分不超过60分的概率．19. 已知函数f(x)=13x3−2ax2+3a2x−2．（1）若的单调递减区间为(−3, −1)，求a的值；（2）若f(x)在(0, 2a)上有两个零点，求a3的取值范围．20. 下列数表中各数均为正数，且各行依次成等差数列，各列依次成等比数列，公比均相等，已知a11=1，a23=14，a32=16；a11a12a13 (1)a21a22a23 (2)…a n1a n2a n3…a nm（1）求数列{a n1}的通项公式；（2）设b n=a1na n1，T n为数列{b n}的前n项和，若T n<m2−7m对一切nN∗都成立，求最小的正整数m的值．21. 已知椭圆C:x2a2+y2b2=1(a>b>0)的焦距为2c，离心率为e，左焦点为F，点M(√2c, √2ce)在椭圆C上，O是坐标原点．（1）求e的大小；（2）若C上存在点N满足|FN|等于C的长轴长的34，求直线ON的方程．2015年安徽省某校高考数学三模试卷（文科）答案1. B2. C3. B4. D5. A6. C7. D8. D9. A 10. B11. √3 12. 313. (−∞, 2] 14. p15. ①②④ 16. 解：（1）由a =c ⋅cosB 及正弦定理，可得sinA =sinCcosB ， 既有：sinBcosC +cosBsinC =sinCcosB ， 故：sinBcosC =0，而在△ABC 中，sinB ≠0，所以cosC =0，既得C =90∘．…6分（2）由cosA =sin(B −C)得−cos(B +C)=sinBcosC −cosBsinC ， 即有：sinBsinC −cosBcosC =sinBcosC −cosBsinC ， 从而：(sinB +cosB)(sinC −cosC)=0， 又因为b <c ，所以B <C ， 所以(sinB +cosB)≠0， 既有sinC −cosC =0， 故解得：C =45∘．…12分17. （1）证明：取PB 的中点E ，连接AE ，NE ．又M 、N 分别为AD 、PC 的中点．∴ NE = // 12BC = // AM ，∴ 四边形AMNE 是平行四边形， ∴ MN // AE ，又MN ⊄平面PAB ，∴ AE ⊂平面PAB ． ∴ MN // 平面PAB ．(2)(I)证明：∵ PA =PD ，AM =MD ，∴ PM ⊥AD ，∴ PM =√PA 2−AM 2=2．在△PMB 中，由余弦定理可得：PB 2=PM 2+BM 2−2PM ⋅BMcos45∘=2， ∴ PB 2+BM 2=PM 2，∴ PB ⊥AB ． 同理可得PB ⊥DB ，BD ∩BM =B ， ∴ PB ⊥平面ABCD ，∴ 平面PBC ⊥平面ABCD ；(II)解：∵ N 是PC 的中点，PB ⊥平面ABCD ， ∴ 点N 到平面ABCD 的距离ℎ=12PB ．∴ V N−ABD =13⋅12PB ⋅S △ABD =13×12×√2×12×22=√23． 18. 解：（1）由题意可知前四组的频率分别为120，110，15，25， ∴ 分数在[80, 90),[90, 100]两组的频率是15和120，∴ 分数在[80, 90)内的人数是15×1200=240，分数在[90, 100)内的人数是120×1200=60；（2）由（1）知抽出的分数在[40, 50)和[90, 100]内的学生人数均为3人， 分别记为a 、b 、c 和1、2、3，从中抽取2人的情形为(a, b)，(a, c)，(a, 1)， (a, 2)，(a, 3)，(b, c)，(b, 1)，(b, 2)，(b, 3)，(c, 1)， (c, 2)，(c, 3)，(1, 2)，(1, 3)，(2, 3)共15种，其中两人平均分不超过60分的有(a, b)，(a, c)，(b, c)共3种， ∴ 所求概率为P =315=15．19. 解：（1）∵ f(x)=13x 3−2ax 2+3a 2x −2，∴ f′(x)=x 2−4ax +3a 2=(x −3a)(x −a)， ∵ 函数f(x)的单调递减区间为(−3, −1)， ∴ {3a =−3a =−1，即a =−1；（2）∵ f(x)在(0, 2a)上有两个零点， ∴ a >0，且{f(a)>0f(0)<0f(2a)<0，解得32<a 3<3 故a 3的取值范围为(32, 3)20. 解：（1）由题意可设第一行的等差数列的公差为d ，各列依次成等比数列，公比相等设为q >0．∵ a 11=1，a 23=14，a 32=16，∴ {(1+2d)q =14(1+d)q 2=16，解得d =3，q =2．∴ a n1=2n−1．（2）由（1）可得a 1n =a 11+3(n −1)=3n −2． ∴ b n =a 1n a n 1=3n−22n−1，∴ T n =1+42+722+...+3n−22n−1， 12T n =12+422+...+3n−52n−1+3n−22n，∴ 12T n =1+3(12+122+⋯+12n−1)−3n−22n=3×1−12n 1−12−3n−22n−2=4−3n+42n，∴ T n =8−3n+42n−1．∵ T n <m 2−7m 对一切n ∈N ∗都成立，∴ m2−7m>(T n)max，∴ m2−7m≥8，m>0，解得m≥8，∴ 最小的正整数m的值是8．21. 解：（1）∵ 点M(√2c, √2ce)在椭圆C上，∴ 2c2a2+2c2e2b2=1，∴ b2=2c2，∴ a2=3c2，∴ e=ca =√33；（2）由（1）C的方程可化为x 23c2+y22c2=1，设N(x1, y1)，则∵ |FN|等于C的长轴长的34，∴ |FN|2=(x1+c)2+y12=(34×2√3c)2，∴ 4x12+24cx1−45c2=0，∴ x1=32c，∴ y1=±√22c，∴ 直线ON的方程为y=±√23x．。

2017-2018学年安徽省宿州市砀山县梨都中学高二（上）第二次月考数学试卷（文科）一、选择题1．已知椭圆上的一点P到椭圆一个焦点的距离为3，则P到另一个焦点的距离（）A． 2 B． 3 C． 5 D． 72．抛物线y=﹣2x2的焦点坐标是（）A． B．（﹣1，0） C． D．3．“对任意的x∈R，x3﹣x2+1≤0”的否定是（）A．不存在x∈R，x3﹣x2+1≤0 B．存在x∈R，x3﹣x2+1≤0C．存在x∈R，x3﹣x2+1＞0 D．对任意的x∈R，x3﹣x2+1＞04．设定点F1（0，﹣3），F2（0，3），满足条件|PF1|+|PF2|=6，则动点P的轨迹是（） A．椭圆 B．线段C．椭圆或线段或不存在 D．不存在5．若椭圆的两焦点为（﹣2，0）和（2，0），且椭圆过点，则椭圆方程是（）A． B． C． D．6．顶点在原点，坐标轴为对称轴的抛物线过点（﹣2，3），则它的方程是（）A． x2=y或y2=﹣x B． x2=±8y或x2=yC． x2=y D． y2=﹣x7．已知抛物线y2=2px（p＞0）的准线与圆（x﹣3）2+y2=16相切，则p的值为（）A． B． 1 C． 2 D． 48．方程表示焦点在y轴上的椭圆，则k的取值范围是（）A．﹣16＜k＜25 B． C． D．9．若椭圆+=1的离心率e=，则m的值为（）A． 1 B．或 C． D． 3或10．已知双曲线﹣=1的右焦点与抛物线y2=12x的焦点重合，则该双曲线的焦点到其渐近线的距离等于（）A． B． C． 3 D． 5二．填空题（共5小题，每题5分，共25分）11．已知抛物线y2=2px（p＞0）过焦点的弦AB两端点为A（x1，y1），B（x2，y2），则关系式为定值．12．若“∀x∈R，x2﹣2x﹣m＞0”是真，则实数m的取值范围是．13．若双曲线﹣=1（b＞0）的渐近线方程式为y=，则b等于．14．已知抛物线y2=4x上一点到焦点的距离为5，这点的坐标为．15．在椭圆+=1内以点P（﹣2，1）为中点的弦所在的直线方程为．三、解答题：16．（1）求过点（2，）且与椭圆+=1有相同焦点的椭圆方程；（2）求与双曲线﹣=1有共同的渐近线，并且经过点（﹣3，3）的双曲线方程．17．若△ABC的两个顶点坐标A（﹣4，0）、B（4，0），△ABC的周长为18，则顶点C的轨迹方程为．18．若点A的坐标为（3，2），F为抛物线的焦点，点P是抛物线y2=2x上一动点，求|PA|+|PF|的最小值并求此时点P的坐标．19．P为椭圆+=1上一点，F1，F2为左右焦点，若∠F1PF2=60°．（1）求△F1PF2的面积；（2）求P点的坐标．20．已知p：|M+1|≤2成立．q：方程x2﹣2mx+1=0有实数根．若￢p为假，p∧q为假，求实数m的取值范围．21．已知椭圆+=1（a＞b＞0）的离心率为，右焦点为F（1，0）．（1）求此椭圆的标准方程；（2）若过点F且倾斜角为的直线与此椭圆相交于A、B两点，求|AB|的值．2014-2015学年安徽省宿州市砀山县梨都中学高二（上）第二次月考数学试卷（文科）参考答案与试题解析一、选择题1．已知椭圆上的一点P到椭圆一个焦点的距离为3，则P到另一个焦点的距离（）A． 2 B． 3 C． 5 D． 7考点：椭圆的简单性质．专题：圆锥曲线的定义、性质与方程．分析：先根据条件求出a=5；再根据椭圆定义得到关于所求距离d的等式即可得到结论．解答：解：设所求距离为d，由题得：a=5．根据椭圆的定义得：2a=3+d⇒d=2a﹣3=7．故选D．点评：本题主要考查椭圆的定义．在解决涉及到圆锥曲线上的点与焦点之间的关系的问题中，圆锥曲线的定义往往是解题的突破口．2．抛物线y=﹣2x2的焦点坐标是（）A． B．（﹣1，0） C． D．考点：抛物线的简单性质．专题：计算题．分析：先把抛物线的方程化为标准形式，再利用抛物线 x2=﹣2p y 的焦点坐标为（0，﹣），求出物线y=﹣2x2的焦点坐标．解答：解：∵在抛物线y=﹣2x2，即 x2=﹣ y，∴p=，=，∴焦点坐标是（0，﹣），故选 D．点评：本题考查抛物线的标准方程和简单性质的应用，抛物线 x2=﹣2p y 的焦点坐标为（0，﹣）．3．“对任意的x∈R，x3﹣x2+1≤0”的否定是（）A．不存在x∈R，x3﹣x2+1≤0 B．存在x∈R，x3﹣x2+1≤0C．存在x∈R，x3﹣x2+1＞0 D．对任意的x∈R，x3﹣x2+1＞0考点：的否定．分析：根据“对任意的x∈R，x3﹣x2+1≤0”是全称，其否定是对应的特称，从而得出答案．解答：解：∵“对任意的x∈R，x3﹣x2+1≤0”是全称∴否定为：存在x∈R，x3﹣x2+1＞0故选C．点评：本题主要考查全称与特称的相互转化．要注意两点：1）全称变为特称；2）只对结论进行否定．4．设定点F1（0，﹣3），F2（0，3），满足条件|PF1|+|PF2|=6，则动点P的轨迹是（） A．椭圆 B．线段C．椭圆或线段或不存在 D．不存在考点：椭圆的定义．专题：计算题．分析：根据题意可得|PF1|+|PF2|=6，由于|F1F2|=6，所以可得点P在线段F1F2上运动，进而得到答案．解答：解：由题意可得：动点P满足条件|PF1|+|PF2|=6，又因为|F1F2|=6，所以点P的轨迹是线段F1F2．故选B．点评：本题考查椭圆的定义，在判断是否是椭圆时要注意前提条件．考查计算能力．5．若椭圆的两焦点为（﹣2，0）和（2，0），且椭圆过点，则椭圆方程是（）A． B． C． D．考点：椭圆的标准方程．专题：待定系数法；圆锥曲线的定义、性质与方程．分析：先由条件求出半焦距和焦点所在的坐标轴，待定系数法设出椭圆的方程，把椭圆经过的点的坐标代入椭圆的方程，即可求出待定系数，从而得到椭圆的标准方程．解答：解：由题意知，c=2，焦点在 x 轴上，∴a2=b2+4，故可设椭圆的方程为+=1，把点代入椭圆的方程可求得 b2=6，故椭圆的方程为+=1，故选D．点评：本题考查用待定系数法求椭圆的标准方程，以及椭圆方程中a、b、c之间的关系．6．顶点在原点，坐标轴为对称轴的抛物线过点（﹣2，3），则它的方程是（）A． x2=y或y2=﹣x B． x2=±8y或x2=yC． x2=y D． y2=﹣x考点：抛物线的标准方程．专题：计算题；圆锥曲线的定义、性质与方程．分析：由题意可得，可设抛物线的方程为 x2=2py，或 y2=﹣2px，p＞0，把点（﹣2，3）代入方程求得p的值，即可求得抛物线的方程．解答：解：（1）抛物线的顶点在坐标原点，对称轴是x轴，并且经过点（﹣2，3），设它的标准方程为y2=2px（p＞0）∴9=﹣4p，解得p=﹣，∴y2=﹣x．（2）抛物线的顶点在坐标原点，对称轴是y轴，并且经过点（﹣2，3），设它的标准方程为x2=﹣2py（p＞0）∴4=﹣6p，解得：p=．∴x2=﹣y故选A．点评：本题主要考查求抛物线的标准方程的方法，体现了分类讨论的数学思想，属于中档题．7．已知抛物线y2=2px（p＞0）的准线与圆（x﹣3）2+y2=16相切，则p的值为（）A． B． 1 C． 2 D． 4考点：抛物线的简单性质．专题：计算题；压轴题．分析：根据抛物线的标准方程可知准线方程为，根据抛物线的准线与圆相切可知求得p．解答：解：抛物线y2=2px（p＞0）的准线方程为，因为抛物线y2=2px（p＞0）的准线与圆（x﹣3）2+y2=16相切，所以；故选C．点评：本题考查抛物线的相关几何性质及直线与圆的位置关系．8．方程表示焦点在y轴上的椭圆，则k的取值范围是（）A．﹣16＜k＜25 B． C． D．考点：椭圆的简单性质；椭圆的标准方程．专题：计算题．分析：焦点在y轴上的椭圆，满足y2的分母大于x2的分母，建立不等式可求k的取值范围解答：解：由题意，16+k＞25﹣k＞0∴故选C．点评：本题以椭圆的标准方程为载体，考查椭圆的性质，利用焦点在y轴上的椭圆，满足y2的分母大于x2的分母，是解题的关键．9．若椭圆+=1的离心率e=，则m的值为（）A． 1 B．或 C． D． 3或考点：椭圆的简单性质．专题：计算题．分析：分别看焦点在x轴和y轴时长半轴和短半轴的长，进而求得c，进而根据离心率求得m．解答：解：当椭圆+=1的焦点在x轴上时，a=，b=，c=由e=，得=，即m=3当椭圆+=1的焦点在y轴上时，a=，b=，c=由e=，得=，即m=．故选D点评：本题主要考查了椭圆的简单性质．解题时要对椭圆的焦点在x轴和y轴进行分类讨论．10．已知双曲线﹣=1的右焦点与抛物线y2=12x的焦点重合，则该双曲线的焦点到其渐近线的距离等于（）A． B． C． 3 D． 5考点：双曲线的简单性质；抛物线的简单性质．专题：计算题．分析：确定抛物线y2=12x的焦点坐标，从而可得双曲线的一条渐近线方程，利用点到直线的距离公式，即可求双曲线的焦点到其渐近线的距离．解答：解：抛物线y2=12x的焦点坐标为（3，0）∵双曲线的右焦点与抛物线y2=12x的焦点重合∴4+b2=9∴b2=5∴双曲线的一条渐近线方程为，即∴双曲线的焦点到其渐近线的距离等于故选A．点评：本题考查抛物线的性质，考查时却显得性质，确定双曲线的渐近线方程是关键．二．填空题（共5小题，每题5分，共25分）11．已知抛物线y2=2px（p＞0）过焦点的弦AB两端点为A（x1，y1），B（x2，y2），则关系式为定值﹣4 ．考点：抛物线的简单性质．专题：计算题．分析：先根据题意设出A、B点的坐标，结合A，F，B三点共线可得到4ab=﹣1，再由==代入可得到答案．解答：解：由题设，可设点A（2pa2，2pa），B（2pb2，2pb）．因三点A，F，B共线，∴4ab=﹣1．易知，===﹣4．故答案为：﹣4．点评：本题主要考查抛物线的简单性质．考查基础知识的灵活应用，属于基础题．12．若“∀x∈R，x2﹣2x﹣m＞0”是真，则实数m的取值范围是（﹣∞，﹣1）．考点：全称．专题：函数的性质及应用．分析：根据全称的定义和性质即可得到结论．解答：解：若“∀x∈R，x2﹣2x﹣m＞0”是真，则满足判别式△=4+4m＜0，解得m＜﹣1，故答案为：（﹣∞，﹣1）点评：本题主要考查全称的应用，结合一元二次函数的性质是解决本题的关键．13．若双曲线﹣=1（b＞0）的渐近线方程式为y=，则b等于 1 ．考点：双曲线的简单性质；函数解析式的求解及常用方法．专题：计算题．分析：根据双曲线的性质求得渐近线方程的表达式求得b．解答：解：由双曲线方程可得渐近线方程为y=±，又双曲线的渐近线方程式为y=，∴，解得b=1．故答案为1点评：本小题考查双曲线的几何性质、待定系数法，属基础题．14．已知抛物线y2=4x上一点到焦点的距离为5，这点的坐标为（4，4）或（4，﹣4）．考点：抛物线的简单性质．专题：圆锥曲线的定义、性质与方程．分析：先设出该点的坐标，根据抛物线的定义可知该点到准线的距离与其到焦点的距离相等，进而利用点到直线的距离求得x的值，代入抛物线方程求得y值，即可得到所求点的坐标．解答：解：∵抛物线方程为y2=4x，∴焦点为F（1，0），准线为l：x=﹣1设所求点坐标为P（x，y）作PQ⊥l于Q根据抛物线定义可知P到准线的距离等于P、Q的距离即x+1=5，解之得x=4，代入抛物线方程求得y=±4故点P坐标为：（4，±4）故答案为：（4，4）或（4，﹣4）．点评：本题主要考查了抛物线的简单性质．在涉及焦点弦和关于焦点的问题时常用抛物线的定义来解决．15．在椭圆+=1内以点P（﹣2，1）为中点的弦所在的直线方程为x﹣2y+4=0 ．考点：直线与圆锥曲线的综合问题．专题：计算题．分析：设以点P（﹣2，1）为中点的弦所在的直线与椭圆+=1交于A（x1，y1），B（x2，y2），由点P（﹣2，1）是线段AB的中点，知，把A（x1，y1），B（x2，y2）代入椭圆x2+4y2=16，由点差法得到k==，由此能求出以点P（﹣2，1）为中点的弦所在的直线方程．解答：解：设以点P（﹣2，1）为中点的弦所在的直线与椭圆+=1交于A（x1，y1），B（x2，y2），∵点P（﹣2，1）是线段AB的中点，∴，把A（x1，y1），B（x2，y2）代入椭圆x2+4y2=16，得，①﹣②得（x1+x2）（x1﹣x2）+4（y1+y2）（y1﹣y2）=0，∴﹣4（x1﹣x2）+8（y1﹣y2）=0，k==，∴以点P（﹣2，1）为中点的弦所在的直线方程为，整理，得x﹣2y+4=0．故答案为：x﹣2y+4=0．点评：本题主要考查椭圆标准方程，简单几何性质，直线与椭圆的位置关系．考查运算求解能力，推理论证能力．解题时要认真审题，注意点差法的合理运用．三、解答题：16．（1）求过点（2，）且与椭圆+=1有相同焦点的椭圆方程；（2）求与双曲线﹣=1有共同的渐近线，并且经过点（﹣3，3）的双曲线方程．考点：椭圆的简单性质；双曲线的简单性质．专题：圆锥曲线的定义、性质与方程．分析：（1）要求的椭圆与椭圆+=1有相同焦点，因此可设要求的椭圆方程为：（m＞0），把点（2，）代入解出即可．（2）要求的双曲线与双曲线﹣=1有共同的渐近线，并且经过点（﹣3，3），因此可设要求的双曲线方程为=1，λ＞0，把点（﹣3，3）代入即可得出．解答：解：（1）∵要求的椭圆与椭圆+=1有相同焦点，∴可设要求的椭圆方程为：（m＞0），把点（2，）代入可得=1，解得m=5．∴要求的椭圆方程为：=1．（2）∵要求的双曲线与双曲线﹣=1有共同的渐近线，并且经过点（﹣3，3），∴可设要求的双曲线方程为=1，λ＞0，把点（﹣3，3）代入可得：=1，解得λ=．∴要求的双曲线方程为：=1．点评：本题考查了椭圆与双曲线的标准方程及其性质，属于基础题．17．若△ABC的两个顶点坐标A（﹣4，0）、B（4，0），△ABC的周长为18，则顶点C的轨迹方程为（y≠0）．考点：轨迹方程．专题：圆锥曲线的定义、性质与方程．分析：根据三角形的周长和定点，得到点A到两个定点的距离之和等于定值，得到点A的轨迹是椭圆，椭圆的焦点在y轴上，写出椭圆的方程，去掉不合题意的点．解答：解：（1）∵△ABC的两顶点A（﹣4，0），B（4，0），周长为18，∴AB=8，BC+AC=10，∵10＞8，∴点C到两个定点的距离之和等于定值，∴点C的轨迹是以A，B为焦点的椭圆，∵2a=10，2c=8，∴b=3，所以椭圆的标准方程是（y≠0）．故答案为：（y≠0）点评：本题考查直线与圆锥曲线的综合应用能力，综合性强，是高考的重点．本题具体涉及到轨迹方程的求法，注意椭圆的定义的应用．18．若点A的坐标为（3，2），F为抛物线的焦点，点P是抛物线y2=2x上一动点，求|PA|+|PF|的最小值并求此时点P的坐标．考点：抛物线的简单性质．专题：圆锥曲线的定义、性质与方程．分析：利用抛物线的定义，将点P到其焦点的距离转化为它到其准线的距离即可．解答：解：根据题意，作图如下，设点P在其准线x=﹣上的射影为M，有抛物线的定义得：|PF|=|PM|，∴欲使|PA|+|PF|取得最小值，就是使|PA|+|PM|最小，∵|PA|+|PM|≥|AM|=（当且仅当M，P，A三点共线时取“=”），∴|PA|+|PF|取得最小值时（M，P，A三点共线时）点P的纵坐标y0=2，设其横坐标为x0，∵P（x0，2）为抛物线y2=2x上的点，∴x0=2，∴点P的坐标为P（2，2）．点评：本题考查抛物线的简单性质，将点P到其焦点的距离转化为它到其准线的距离是关键，考查转化思想的灵活应用，属于中档题．19．P为椭圆+=1上一点，F1，F2为左右焦点，若∠F1PF2=60°．（1）求△F1PF2的面积；（2）求P点的坐标．考点：椭圆的简单性质．专题：圆锥曲线的定义、性质与方程．分析：（1）设|PF1|=m，|PF2|=n，由椭圆的定义可得m+n=2a=10，由余弦定理可得：82=m2+n2﹣2mncos60°=（m+n）2﹣3mn=100﹣3mn，解得mn．再利用三角形的面积计算公式即可得出．（2）设P（x，y），可得=，=，由于∠F 1PF2=60°．可得=±tan60°=，化为﹣8y=（x2+y2﹣16），与联立解得即可．解答：解：（1）由椭圆+=1可得a=5，b=3，c=4．设|PF1|=m，|PF2|=n，则m+n=2a=10，由余弦定理可得：82=m2+n2﹣2mncos60°=（m+n）2﹣3mn=100﹣3mn，解得mn=12．∴△F1PF2的面积S==．（2）设P（x，y），则．F1（﹣4，0），F2（4，0）．∴=，=，∵∠F1PF2=60°．∴=±tan60°=，化为﹣8y=（x2+y2﹣16），与联立解得：，．点评：本题考查了椭圆的定义及其标准方程、余弦定理、三角形的面积计算公式、到角公式，考查了推理能力与计算能力，属于难题．20．已知p：|M+1|≤2成立．q：方程x2﹣2mx+1=0有实数根．若￢p为假，p∧q为假，求实数m的取值范围．考点：复合的真假．专题：简易逻辑．分析：若“¬p”为假，则p为真，“p∧q”为假得q为假，由此关系求实数m的取值范围即可．解答：解：因为“¬p”为假，所以p是真．又由“p∧q”为假，所以q是假．当p为真时，则得﹣3≤m≤1；当q为假时，则△=4m2﹣4＜0，得：﹣1＜m＜1，当p是真且q是假时，得﹣1＜m＜1．点评：本题考查的真假判断与运用，解答本题的关键是根据“¬p”为假，“p∧q”为假判断出p为真q为假，熟练掌握复合真假的判断方法很重要．21．已知椭圆+=1（a＞b＞0）的离心率为，右焦点为F（1，0）．（1）求此椭圆的标准方程；（2）若过点F且倾斜角为的直线与此椭圆相交于A、B两点，求|AB|的值．考点：椭圆的简单性质．专题：计算题；直线与圆；圆锥曲线的定义、性质与方程．分析：（1）运用离心率公式，由c=1，求得a，再由a，b，c的关系，可得b，进而得到椭圆方程；（2）求出直线方程，联立椭圆方程，消去y，得到x的方程，解得交点A，B，再由两点的距离公式，即可得到弦长．解答：解：（1）由于右焦点为F（1，0），则c=1，离心率为，则有e==，即有a=，b2=a2﹣c2=2﹣1=1，则椭圆的标准方程为：+y2=1；（2）过点F且倾斜角为的直线为：y=x﹣1，联立椭圆方程，消去y，得3x2﹣4x=0，解得，x=0或，则交点分别为A（0，﹣1），B（）．则|AB|==．点评：本题考查椭圆的方程和性质，考查直线和椭圆方程联立，求交点和弦长，考查运算能力，属于基础题．。