山东省单县希望初级中学_八年级数学下学期第一次月考试题(精选资料)青岛版

八下数学月考试卷一、选择题（共12小题；共60分）1. 若直角三角形的三边长分别为2，4，x，则x的可能值有 ( )A. 1个B. 2个C. 3个D. 4个2. 下列说法中正确的有 ①负数没有平方根，但负数有立方根；②49的平方根是±23；③827的立方根是±23；④−8的立方根是−2．A. 1个B. 2个C. 3个D. 4个3. 如图，将正方形OABC放在平面直角坐标系xOy中，O是原点，若点A的坐标为1,3，则点C的坐标为 ( )A. 1B. −1,C. −1D. −−14. 如图所示，如果将矩形纸沿虚线①对折后，沿虚线②剪开，剪出一个直角三角形，展开后得到一个等腰三角形，则展开后的等腰三角形周长是 ( )A. 12B. 18C. 2+10D. 2+2105. 在数轴上标注了四段范围，如图，则表示8的点落在 ( )A. 段①B. 段②C. 段③D. 段④6. 如图，每个小正方形的边长为1，点A，B，C是小正方形的顶点，连接AB，BC，则∠ABC的度数为 A. 90∘B. 60∘C. 45∘D. 30∘7. 如图，已知△ABC中，AB=10，AC=8，BC=6，DE是AC的垂直平分线，DE交AB于点D，连接CD，则CD= A. 3B. 4C. 4.8D. 58. 下列说法错误的是 A. 16的平方根是±2B. 2是无理数C. 3是有理数D. 22是分数9. 如图，在菱形ABCD中，AB=5，对角线AC=6，若过点A作AE⊥BC，垂足为E，则AE的长为 ( )A. 4B. 125C. 245D. 510. 一个正方体的水晶砖的体积为100，它的棱长大约在 ( )A. 4和5之间B. 5和6之间C. 6和7之间D. 7和8之间11. 如图，在四边形ABCD中，E是BC边上的中点，连接DE并延长，交AB的延长线于点F，AB=BF，添加一个条件，使四边形ABCD是平行四边形，你认为下面四个条件中可选择的是 A. AD=BCB. CD=BFC. ∠A=∠CD. ∠F=∠CDE12. 如图所示，在矩形ABCD中，AB=2，BC=4，对角线AC的垂直平分线分别交AD，AC于点E，O，连接CE，则CE的长为 ( )A. 3B. 3.5C. 2.5D. 2.8二、填空题（共6小题；共30分）13. 把下列各数分别填在相应的括号内：5，−3，0， 43，0.3，227，−1.732， 25， −163，− 27，−π2，0.101001⋯整数集合： ⋯ ；分数集合： ⋯ ；有理数集合： ⋯ ； 无理数集合： ⋯ ．14. 如图所示，正方形 A 的面积（阴影部分）是 ，其边长的整数部分是 ，这个正方形的边长是 （填有理数或无理数）．15. 如图，在 △ABC 中，∠ACB =90∘，CD ⊥AB 于 D ，∠A =30∘，E 为 AB 的中点，则 ∠ECD为 ．16. 如图，在平行四边形 ABCD 中，\（AB=2\sqrt{13}\space{\mathrm {cm}}\），\（AD=4\space{\mathrm {cm}}\），\（AC\perp BC\），则 \（\triangle DBC\） 比 \（\triangle ABC\） 的周长长 cm ．17. 如图，△ABC 中，AD 是中线，AE 是角平分线，CF ⊥AE 于 F ，AB =5,AC =2，则 DF 的长为 ．18. 计算： 9−2−1+ 83− −2 + −13 0= ．三、解答题（共9小题；共117分）19. 计算Ⅰ − 36+ 214+ 2733−π−3.140+1−2Ⅱ820. 求x的值．Ⅰx−12=25Ⅱx+33=−2721. 已知2a+1的平方根是±3，3a+2b−4的立方根是−2，求4a−5b+8的立方根．22. 如图，O是△ABC内一点，连接OB，OC，并将AB，OB，OC，AC的中点D，E，F，G依次连接，得到四边形DEFG．求证：四边形DEFG是平行四边形．23. 如图所示，在四边形ABCD中，∠BAD=90∘，∠CBD=90∘，AD=4，AB=3，BC=12，求正方形DCEF的面积．24. 如图，已知AD=4，CD=3，∠ADC=90∘，AB=13，BC=12，求四边形ABCD的面积．25. 如图，在正方形ABCD中，边长为4，点E、F分别在边AD和CD上，其中AE=2,DF=1．判断BE与EF的位置关系并说明理由.26. （1）分别计算下列各式的值：=；52=．①22=；23②−22=； −232=；−52=．Ⅱ根据计算的结果，可以得到：①当a≥0时，2=；②当a<0时， a2=．Ⅲ应用所得的结论解决：如图，已知a，b在数轴上的位置，化简 a2− b2−a−b2．27. 如图，在△ABC中，∠ACB=90∘，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，且AF=CE=AE．Ⅰ说明四边形ACEF是平行四边形；Ⅱ当∠B满足什么条件时，四边形ACEF是菱形，并说明理由．答案第一部分1. B2. C3. C4. D5. C6. C7. D8. D9. C 10. A11. D 12. C第二部分13. −3，0，25；0.3，227，−1.732；−3，0，0.3，227，−1.732，25；5，43，−163，−27，−π2，0.101001⋯14. 69；8；无理数15. 30∘16. 417. 3218. 312第三部分19. （1）原式=−6+32+3=−32.（2）原式=2−1+2−1= 2.20. （1）由x−12=25得x−1=±5，解得x1=6，x2=−4．（2）由x+33=−27得x+3=−3，解得x=−6．21. ∵2a+1的平方根是±3，3a+2b−4的立方根是−2，∴2a+1=9,3a+2b−4=−8,解得a=4,b=−8,∴4a−5b+8=4×4−5×−8+8=64，∴4a−5b+8=64=8，∴4a−5b+8的立方根为83=2．22. ∵D，G分别是AB，AC的中点，∴DG∥BC，DG=12BC．∵E，F分别是OB，OC的中点，∴EF∥BC，EF=12BC，∴DG∥EF，DG=EF，∴四边形DEFG是平行四边形．23. ∵∠BAD=90∘，AD=4，AB=3，∴BD= AD2+AB2=42+32=5．∵∠CBD=90∘，BC=12，∴CD2=BD2+BC2=52+122=169，即正方形DCEF的面积为169．24. 如图，连接AC．因为AD=4，CD=3，∠ADC=90∘，所以AC=32+42=5△ACD的面积=6，在△ABC中，因为AC=5，BC=12，AB=13，∴AC2+BC2=AB2，即△ABC为直角三角形，且∠ACB=90∘，所以直角△ABC的面积=30，所以四边形ABCD的面积=30−6=24．四边形ABCD的面积为24．25. BE⊥EF．理由：∵正方形ABCD中，边长为4，AE=2，DF=1∴ED=2，CF=3，BC=4在Rt△ABE中，BE=42+22=25，在Rt△BCF中，BF=42+32=5，在Rt△EDF中，EF=2+12=5，在△BEF中，∴△BEF是直角三角形，且∠BEF=90∘，∴BE⊥EF．；526. （1）①2；23②2；2；53（2）a；−a（3）由题意知a<0，b>0，所以a−b<0，原式=a2−b2− a−b2=−a−b+ a−b=−a−b+b−a=−2a.27. （1）由题意知∠FDC=∠DCA=90∘，∴EF∥CA．∴∠AEF=∠EAC．∵AF=CE=AE，∴∠F=∠AEF=∠EAC=∠ECA．又AE=EA，∴△AEC≌△EAF．∴EF=CA．∴四边形ACEF是平行四边形．（2）当∠B=30∘时，四边形ACEF是菱形．理由是：∵∠B=30∘，∠ACB=90∘，AB．∴AC=12∵DE垂直平分BC，∴BE=CE．又AE=CE，∴CE=1AB．2∴AC=CE．∴四边形ACEF是菱形．。

山东省八年级（下）月考数学试卷一、选择题（本大题共10小题，每小题4分，共40分）1．已知函数y=kx+b的图象如图所示，则一元二次方程x2+x+k﹣1=0根的存在情况是（）A．没有实数根B．有两个相等的实数根C．有两个不相等的实数根D．无法确定2．把二次函数y=﹣x2﹣x+3用配方法化成y=a（x﹣h）2+k的形式（）A．y=﹣（x﹣2）2+2 B．y=（x﹣2）2+4 C．y=﹣（x+2）2+4 D．y=2+33．若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根，则k的取值范围是（）A．k＞﹣1 B．k＞﹣1且k≠0 C．k＜1 D．k＜1且k≠04．若关于x的一元二次方程为ax2+bx+5=0（a≠0）的解是x=1，则2013﹣a﹣b的值是（）A．2021 B．2008 C．202X D．20125．方程x2﹣9x+18=0的两个根是等腰三角形的底和腰，则这个三角形的周长为（）A．12 B．15 C．12或15 D．不能确定6．将抛物线y=3x2向左平移2个单位，再向下平移1个单位，所得抛物线为（）A．y=3（x﹣2）2﹣1 B．y=3（x﹣2）2+1 C．y=3（x+2）2﹣1 D．y=3（x+2）2+17．二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论正确的是（）A．a＜0 B．b2﹣4ac＜0C．当﹣1＜x＜3时，y＞0 D．﹣8．如图，抛物线y=x2+bx+c与x轴交于A、B两点，与y轴交于点C，且∠OBC=45°，则下列各式成立的是（）A．b﹣c﹣1=0 B．b+c﹣1=0 C．b﹣c+1=0 D．b+c+1=09．已知实数a，b分别满足a2﹣6a+4=0，b2﹣6b+4=0，且a≠b，则的值是（）A．7 B．﹣7 C．11 D．﹣1110．在同一坐标系内，一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是（）A．B．C．D．二、填空题（本大题共6小题，每小题4分，共24分）11．若函数y=（m﹣3）是二次函数，则m=．12．抛物线y=2x2﹣bx+3的对称轴是直线x=1，则b的值为．13．已知2是关于x的一元二次方程x2+4x﹣p=0的一个根，则该方程的另一个根是．14．如图，已知二次函数y=ax2+bx+c的图象与x轴交于A（1，0），B（3，0）两点，与y 轴交于点C（0，3），则二次函数的图象的顶点坐标是．15．若|b﹣1|+=0，且一元二次方程kx2+ax+b=0有两个实数根，则k的取值范围是．16．二次函数y=﹣x2+bx+c的图象如图所示，则一次函数y=bx+c的图象不经过第象限．三、解答题（一）（本大题共3小题，每小题5分，共15分）17．用配方法解方程：x2﹣4x+1=018．解方程：（y﹣1）2+2y（1﹣y）=0．19．用12米长的木料，做成如图的矩形窗框，则当长和宽各多少米时，矩形窗框的面积最大？最大面积是多少？四、解答题（二）（本大题共4小题，9+10+10+12分）20．如图所示，要在20米宽，32米长的矩形耕地上修筑同样宽的三条小路（两条纵向，一条横向，横向与纵向互相垂直），把耕地分成大小不等的六块花田，要使花田面积为570m2，则道路应修多宽？21．（10分）（2002•鄂州）某工厂大门是一抛物线形水泥建筑物（如图），大门地面宽AB=4米，顶部C离地面高度为4.4米．现有一辆满载货物的汽车欲通过大门，货物顶部距地面2.8米，装货宽度为2.4米．请通过计算，判断这辆汽车能否顺利通过大门？22．（10分）（2010•青海）某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克．经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克．（1）现该商场要保证每天盈利6 000元，同时又要顾客得到实惠，那么每千克应涨价多少元？（2）若该商场单纯从经济角度看，每千克这种水果涨价多少元，能使商场获利最多？23．（12分）（202X春•广饶县校级月考）已知，如图，抛物线y=ax2+3ax+c（a＞0）与y轴交于点C，与x轴交于A，B两点，点A在点B左侧．点B的坐标为（1，0），OC=3OB．（1）求抛物线的解析式；（2）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值．山东省八年级（下）月考数学试卷参考答案与试题解析一、选择题（本大题共10小题，每小题4分，共40分）1．已知函数y=kx+b的图象如图所示，则一元二次方程x2+x+k﹣1=0根的存在情况是（）A．没有实数根B．有两个相等的实数根C．有两个不相等的实数根D．无法确定考点：根的判别式；一次函数图象与系数的关系．分析：先根据函数y=kx+b的图象可得；k＜0，再根据一元二次方程x2+x+k﹣1=0中，△=12﹣4×1×（k﹣1）=5﹣4k＞0，即可得出答案．解答：解：根据函数y=kx+b的图象可得；k＜0，b＜0，则一元二次方程x2+x+k﹣1=0中，△=12﹣4×1×（k﹣1）=5﹣4k＞0，则一元二次方程x2+x+k﹣1=0根的存在情况是有两个不相等的实数根，故选：C．点评：此题考查了一元二次方程根的判别式，用到的知识点是一次函数图象的性质，关键是根据函数图象判断出△的符号．2．把二次函数y=﹣x2﹣x+3用配方法化成y=a（x﹣h）2+k的形式（）A．y=﹣（x﹣2）2+2 B．y=（x﹣2）2+4 C．y=﹣（x+2）2+4 D．y=2+3考点：二次函数的三种形式．专题：配方法．分析：利用配方法先提出二次项系数，在加上一次项系数的一半的平方来凑完全平方式，把一般式转化为顶点式．解答：解：y=﹣x2﹣x+3=﹣（x2+4x+4）+1+3=﹣（x+2）2+4故选C．点评：二次函数的解析式有三种形式：（1）一般式：y=ax2+bx+c（a≠0，a、b、c为常数）；（2）顶点式：y=a（x﹣h）2+k；（3）交点式（与x轴）：y=a（x﹣x1）（x﹣x2）．3．若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根，则k的取值范围是（）A．k＞﹣1 B．k＞﹣1且k≠0 C．k＜1 D．k＜1且k≠0考点：根的判别式．专题：计算题．分析：方程的根的情况，只要看根的判别式△=b2﹣4ac的值的符号就可以了．注意考虑“一元二次方程二次项系数不为0”这一条件．解答：解：因为方程kx2﹣2x﹣1=0有两个不相等的实数根，则b2﹣4ac＞0，即（﹣2）2﹣4k×（﹣1）＞0，解得k＞﹣1．又结合一元二次方程可知k≠0，故选：B．点评：总结：一元二次方程根的情况与判别式△的关系：（1）△＞0⇔方程有两个不相等的实数根；（2）△=0⇔方程有两个相等的实数根；（3）△＜0⇔方程没有实数根．本题容易出现的错误是忽视k≠0这一条件．4．若关于x的一元二次方程为ax2+bx+5=0（a≠0）的解是x=1，则2013﹣a﹣b的值是（）A．2021 B．2008 C．202X D．2012考点：一元二次方程的解．分析：将x=1代入到ax2+bx+5=0中求得a+b的值，然后求代数式的值即可．解答：解：∵x=1是一元二次方程ax2+bx+5=0的一个根，∴a•12+b•1+5=0，∴a+b=﹣5，∴2013﹣a﹣b=2013﹣（a+b）=2013﹣（﹣5）=2021．故选：A．点评：此题主要考查了一元二次方程的解，解题的关键是把已知方程的根直接代入方程得到待定系数的方程即可求得代数式a+b的值．5．方程x2﹣9x+18=0的两个根是等腰三角形的底和腰，则这个三角形的周长为（）A．12 B．15 C．12或15 D．不能确定考点：解一元二次方程-因式分解法；三角形三边关系；等腰三角形的性质．专题：计算题．分析：利用因式分解法求出方程的解得到x的值，分类讨论腰与底，利用三角形边角关系判断即可确定出周长．解答：解：方程变形得：（x﹣3）（x﹣6）=0，解得：当x=3或x=6，当3为腰，6为底时，三角形三边为3，3，6，不能构成三角形，舍去；当3为底，6为腰时，三角形三边为6，6，3，周长为6+6+3=15，故选B点评：此题考查了解一元二次方程﹣因式分解法，熟练掌握分解因式的方法是解本题的关键．6．将抛物线y=3x2向左平移2个单位，再向下平移1个单位，所得抛物线为（）A．y=3（x﹣2）2﹣1 B．y=3（x﹣2）2+1 C．y=3（x+2）2﹣1 D．y=3（x+2）2+1考点：二次函数图象与几何变换．分析：先求出平移后的抛物线的顶点坐标，再利用顶点式写出抛物线解析式即可．解答：解：抛物线y=3x2向左平移2个单位，再向下平移1个单位后的抛物线顶点坐标为（﹣2，﹣1），所得抛物线为y=3（x+2）2﹣1．故选C．点评：本题考查了二次函数图象与几何变换，求出平移后的抛物线的顶点坐标是解题的关键．7．二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论正确的是（）A．a＜0 B．b2﹣4ac＜0C．当﹣1＜x＜3时，y＞0 D．﹣考点：二次函数图象与系数的关系．专题：存在型．分析：根据二次函数的图象与系数的关系对各选项进行逐一分析即可．解答：解：A、∵抛物线的开口向上，∴a＞0，故选项A错误；B、∵抛物线与x轴有两个不同的交点，∴△=b2﹣4ac＞0，故选项B错误；C、由函数图象可知，当﹣1＜x＜3时，y＜0，故选项C错误；D、∵抛物线与x轴的两个交点分别是（﹣1，0），（3，0），∴对称轴x=﹣==1，故选项D正确．故选D．点评：本题考查的是二次函数的图象与系数的关系，能利用数形结合求解是解答此题的关键．8．如图，抛物线y=x2+bx+c与x轴交于A、B两点，与y轴交于点C，且∠OBC=45°，则下列各式成立的是（）A．b﹣c﹣1=0 B．b+c﹣1=0 C．b﹣c+1=0 D．b+c+1=0考点：二次函数图象与系数的关系．分析：根据∠OBC=45°，有OB=OC，可设点C，B的坐标为（0，c），（c，0），把点B（c，0）代入二次函数y=x2+bx+c，得c2+bc+c=0，从而求出关系式．解答：解：∵∠OBC=45°，∴OB=OC，∴点C，B的坐标为（0，c），（c，0）；把点B（c，0）代入二次函数y=x2+bx+c，得c2+bc+c=0，即c（c+b+1）=0，∵c≠0，∴b+c+1=0．故选D．点评：此题考查了学生的综合应用能力，考查了二次函数的点与函数的关系，考查了直角三角形的性质，考查了数形结合思想．9．已知实数a，b分别满足a2﹣6a+4=0，b2﹣6b+4=0，且a≠b，则的值是（）A．7 B．﹣7 C．11 D．﹣11考点：根与系数的关系．专题：计算题．分析：根据已知两等式得到a与b为方程x2﹣6x+4=0的两根，利用根与系数的关系求出a+b与ab的值，所求式子通分并利用同分母分式的加法法则计算，再利用完全平方公式变形，将a+b与ab的值代入计算即可求出值．解答：解：根据题意得：a与b为方程x2﹣6x+4=0的两根，∴a+b=6，ab=4，则原式===7．故选A点评：此题考查了一元二次方程根与系数的关系，熟练掌握根与系数的关系是解本题的关键．10．在同一坐标系内，一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是（）A．B．C．D．考点：二次函数的图象；一次函数的图象．分析：令x=0，求出两个函数图象在y轴上相交于同一点，再根据抛物线开口方向向上确定出a＞0，然后确定出一次函数图象经过第一三象限，从而得解．解答：解：x=0时，两个函数的函数值y=b，所以，两个函数图象与y轴相交于同一点，故B、D选项错误；由A、C选项可知，抛物线开口方向向上，所以，a＞0，所以，一次函数y=ax+b经过第一三象限，所以，A选项错误，C选项正确．故选C．点评：本题考查了二次函数图象，一次函数的图象，应该熟记一次函数y=kx+b在不同情况下所在的象限，以及熟练掌握二次函数的有关性质：开口方向、对称轴、顶点坐标等．二、填空题（本大题共6小题，每小题4分，共24分）11．若函数y=（m﹣3）是二次函数，则m=﹣5．考点：二次函数的定义．分析：根据二次函数的定义解答．解答：解：∵y=（m﹣3）是二次函数，∴，解得m=﹣5．故答案为﹣5．点评：本题考查了二次函数的定义，要知道，形如x+c（a、b、c是常数，a≠0）的函数，叫做二次函数．其中x、y是变量，a、b、c是常量，a是二次项系数，b是一次项系数，c 是常数项．y═ax2+bx+c（a、b、c是常数，a≠0）也叫做二次函数的一般形式．12．抛物线y=2x2﹣bx+3的对称轴是直线x=1，则b的值为4．考点：二次函数的性质．分析：已知抛物线的对称轴，利用对称轴公式可求b的值．解答：解：∵y=2x2﹣bx+3，对称轴是直线x=1，∴=1，即﹣=1，解得b=4．点评：主要考查了求抛物线的顶点坐标的方法：公式法：y=ax2+bx+c的顶点坐标为（，），对称轴是x=．13．已知2是关于x的一元二次方程x2+4x﹣p=0的一个根，则该方程的另一个根是﹣6．考点：根与系数的关系；一元二次方程的解．分析：根据根与系数的关系：x1+x2=﹣，x1•x2=，此题选择两根和即可求得．解答：解：∵2是关于x的一元二次方程x2+4x﹣p=0的一个根，∴2+x1=﹣4，∴x1=﹣6，∴该方程的另一个根是﹣6．点评：此题主要考查了一元二次方程的根与系数的关系．14．如图，已知二次函数y=ax2+bx+c的图象与x轴交于A（1，0），B（3，0）两点，与y 轴交于点C（0，3），则二次函数的图象的顶点坐标是（2，﹣1）．考点：待定系数法求二次函数解析式；二次函数的性质．分析：已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．解答：解：设解析式为：y=a（x﹣x1）（x﹣x2）（a≠0），即y=a（x﹣1）（x﹣3）把点C（0，3），代入得a=1．则y=（x﹣1）（x﹣3）=x2﹣4x+3．所以图象的顶点坐标是（2，﹣1）．点评：主要考查了用待定系数法求二次函数的解析式．15．若|b﹣1|+=0，且一元二次方程kx2+ax+b=0有两个实数根，则k的取值范围是k≤4且k≠0．考点：根的判别式；非负数的性质：绝对值；非负数的性质：算术平方根．专题：计算题．分析：首先根据非负数的性质求得a、b的值，再由二次函数的根的判别式来求k的取值范围．解答：解：∵|b﹣1|+=0，∴b﹣1=0，=0，解得，b=1，a=4；又∵一元二次方程kx2+ax+b=0有两个实数根，∴△=a2﹣4kb≥0且k≠0，即16﹣4k≥0，且k≠0，解得，k≤4且k≠0；故答案为：k≤4且k≠0．点评：本题主要考查了非负数的性质、根的判别式．在解答此题时，注意关于x的一元二次方程的二次项系数不为零．16．二次函数y=﹣x2+bx+c的图象如图所示，则一次函数y=bx+c的图象不经过第四象限．考点：二次函数图象与系数的关系；一次函数图象与系数的关系．专题：计算题．分析：由抛物线的对称轴在y轴右侧，得到a与b异号，根据抛物线开口向下得到a小于0，故b大于0，再利用抛物线与y轴交点在y轴正半轴，得到c大于0，利用一次函数的性质即可判断出一次函数y=bx+c不经过的象限．解答：解：根据图象得：a＜0，b＞0，c＞0，故一次函数y=bx+c的图象不经过第四象限．故答案为：四．点评：此题考查了二次函数图象与系数的关系，以及一次函数图象与系数的关系，熟练掌握一次、二次函数的图象与性质是解本题的关键．三、解答题（一）（本大题共3小题，每小题5分，共15分）17．用配方法解方程：x2﹣4x+1=0考点：解一元二次方程-配方法．专题：配方法．分析：首先把方程移项变形为x2﹣4x=﹣1的形式，然后在方程的左右两边同时加上一次项系数一半的平方，左边就是完全平方式，右边就是常数，然后利用平方根的定义即可求解．解答：解：移项，得：x2﹣4x=﹣1，配方，得：x2﹣4x+（﹣2）2=﹣1+（﹣2）2，即（x﹣2）2=3，解这个方程，得：x﹣2=±；即x1=2+，x2=2﹣．点评：配方法的一般步骤：（1）把常数项移到等号的右边；（2）把二次项的系数化为1；（3）等式两边同时加上一次项系数一半的平方．选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．18．解方程：（y﹣1）2+2y（1﹣y）=0．考点：解一元二次方程-因式分解法．分析：先变形，再分解因式，即可得出两个一元一次方程，求出方程的解即可．解答：解：变形得：（y﹣1）2﹣2y（y﹣1）=0，（y﹣1）（y﹣1﹣2y）=0，y﹣1=0，y﹣1﹣2y=0，y1=1，y2=﹣1．点评：本题考查了解一元二次方程的应用，解此题的关键是能把一元二次方程转化成一元一次方程．19．用12米长的木料，做成如图的矩形窗框，则当长和宽各多少米时，矩形窗框的面积最大？最大面积是多少？考点：二次函数的应用．分析：设长为xm，表示出宽，然后根据矩形的面积公式列式并整理成顶点式形式，再根据二次函数的最值问题求解．解答：解：设长为xm，则宽为：（12﹣3x）=（4﹣x）m，面积=x（4﹣x）=﹣x2+4x=﹣（x﹣2）2+4，所以，当x=2m时，窗框有最大面积4m2．点评：本题考查了二次函数的应用，矩形的面积，主要利用了二次函数的最值问题，难点在于用长表示出宽．四、解答题（二）（本大题共4小题，9+10+10+12分）20．如图所示，要在20米宽，32米长的矩形耕地上修筑同样宽的三条小路（两条纵向，一条横向，横向与纵向互相垂直），把耕地分成大小不等的六块花田，要使花田面积为570m2，则道路应修多宽？考点：一元二次方程的应用．专题：几何图形问题．分析：本题中，试验地的面积=矩形耕地的面积﹣三条道路的面积+道路重叠部分的两个小正方形的面积．如果设道路宽x，可根据此关系列出方程求出x的值，然后将不合题意的舍去即可．解答：解：设道路为x米宽，由题意得：20×32﹣20x×2﹣32x+2x2=570，整理得：x2﹣36x+35=0，解得：x=1，x=35，经检验是原方程的解，但是x=35＞20，因此不合题意舍去．答：道路为1m宽．点评：本题考查了一元二次方程的应用，对于面积问题应熟记各种图形的面积公式．另外，整体面积=各部分面积之和；剩余面积=原面积﹣截去的面积．21．（10分）（2002•鄂州）某工厂大门是一抛物线形水泥建筑物（如图），大门地面宽AB=4米，顶部C离地面高度为4.4米．现有一辆满载货物的汽车欲通过大门，货物顶部距地面2.8米，装货宽度为2.4米．请通过计算，判断这辆汽车能否顺利通过大门？考点：二次函数的应用．专题：压轴题．分析：本题只要计算大门顶部宽2.4米的部分离地面是否超过2.8米即可．如果设C点是原点，那么A的坐标就是（﹣2，﹣4.4），B的坐标是（2，﹣4.4），可设这个函数为y=kx2，那么将A的坐标代入后即可得出y=﹣1.1x2，那么大门顶部宽2.4m的部分的两点的横坐标就应该是﹣1.2和1.2，因此将x=1.2代入函数式中可得y≈﹣1.6，因此大门顶部宽2.4m部分离地面的高度是4.4﹣1.6=2.8m，因此这辆汽车正好可以通过大门．解答：解：根据题意知，A（﹣2，﹣4.4），B（2，﹣4.4），设这个函数为y=kx2．将A的坐标代入，得y=﹣1.1x2，∴E、F两点的横坐标就应该是﹣1.2和1.2，∴将x=1.2代入函数式，得y≈﹣1.6，∴GH=CH﹣CG=4.4﹣1.6=2.8m，因此这辆汽车正好可以通过大门．点评：本题主要结合实际问题考查了二次函数的应用，得出二次函数式进而求出大门顶部宽2.4m部分离地面的高度是解题的关键．22．（10分）（2010•青海）某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克．经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克．（1）现该商场要保证每天盈利6 000元，同时又要顾客得到实惠，那么每千克应涨价多少元？（2）若该商场单纯从经济角度看，每千克这种水果涨价多少元，能使商场获利最多？考点：二次函数的应用；二次函数的最值．专题：应用题．分析：本题的关键是根据题意列出一元二次方程，再求其最值．解答：解：（1）设每千克应涨价x元，则（10+x）（500﹣20x）=6 000（4分）解得x=5或x=10，为了使顾客得到实惠，所以x=5．（6分）（2）设涨价z元时总利润为y，则y=（10+z）（500﹣20z）=﹣20z2+300z+5 000=﹣20（z2﹣15z）+5000=﹣20（z2﹣15z+﹣）+5000=﹣20（z﹣7.5）2+6125当z=7.5时，y取得最大值，最大值为6 125．（8分）答：（1）要保证每天盈利6000元，同时又使顾客得到实惠，那么每千克应涨价5元；（2）若该商场单纯从经济角度看，每千克这种水果涨价7.5元，能使商场获利最多．（10分）点评：求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法，常用的是后两种方法，当二次系数a的绝对值是较小的整数时，用配方法较好，如y=﹣x2﹣2x+5，y=3x2﹣6x+1等用配方法求解比较简单．23．（12分）（202X春•广饶县校级月考）已知，如图，抛物线y=ax2+3ax+c（a＞0）与y轴交于点C，与x轴交于A，B两点，点A在点B左侧．点B的坐标为（1，0），OC=3OB．（1）求抛物线的解析式；（2）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值．考点：二次函数的性质；待定系数法求二次函数解析式．分析：（1）已知了B点坐标，易求得OB、OC的长，进而可将B、C的坐标代入抛物线中，求出待定系数的值，即可得出抛物线的解析式．（2）根据A、C的坐标，易求得直线AC的解析式．由于AB、OC都是定值，则△ABC的面积不变，若四边形ABCD面积最大，则△ADC的面积最大；可过D作x轴的垂线，交AC于M，x轴于N；易得△ADC的面积是DM与OA积的一半，可设出N点的坐标，分别代入直线AC和抛物线的解析式中，即可求出DM的长，进而可得出四边形ABCD的面积与N点横坐标间的函数关系式，根据所得函数的性质即可求出四边形ABCD的最大面积．解答：解：（1）∵B（1，0），∴OB=1；∵OC=3BO，∴C（0，﹣3）；（1分）∵y=ax2+3ax+c过B（1，0）、C（0，﹣3），∴；解这个方程组，得，∴抛物线的解析式为：y=x2+x﹣3；（2）过点D作DM∥y轴分别交线段AC和x轴于点M、N在y=x2+x﹣3中，令y=0，得方程x2+x﹣3=0解这个方程，得x1=﹣4，x2=1∴A（﹣4，0）设直线AC的解析式为y=kx+b∴，解这个方程组，得，∴AC的解析式为：y=﹣x﹣3，∵S四边形ABCD=S△ABC+S△ADC=+•DM•（AN+ON）=+2•DM设D（x，x2+x﹣3），M（x，﹣x﹣3），DM=﹣x﹣3﹣（x2+x﹣3）=﹣（x+2）2+3，当x=﹣2时，DM有最大值3此时四边形ABCD面积有最大值．点评：此题考查了二次函数解析式的确定、图形面积的求法、平行四边形的判定和性质、二次函数的应用等知识，综合性强，难度较大．。

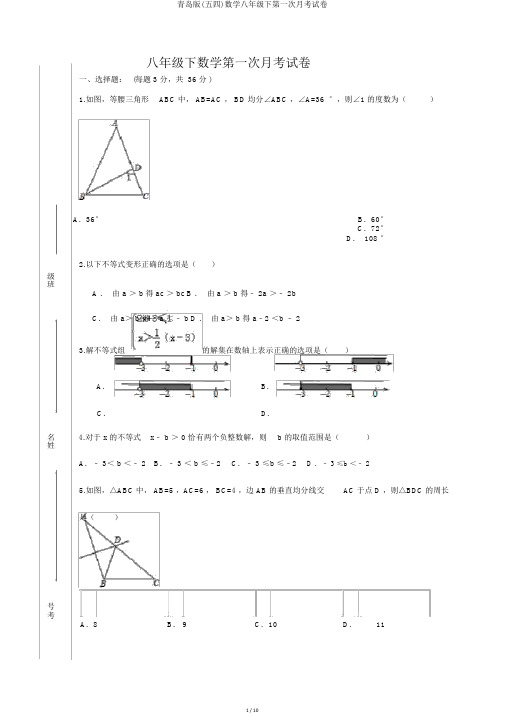
八年级下数学第一次月考试卷一、选择题：(每题 3 分，共 36 分 )1.如图，等腰三角形ABC 中， AB=AC ， BD 均分∠ABC ，∠A=36 °，则∠1 的度数为（）A．36°B．60°C．72°D． 108 °2.以下不等式变形正确的选项是（）级班A ．由 a ＞ b 得 ac ＞ bcB ．由 a ＞ b 得﹣ 2a ＞﹣ 2bC．由 a＞ b 得﹣ a ＜﹣ b D ．由 a＞ b 得 a﹣2 ＜b ﹣ 23.解不等式组的解集在数轴上表示正确的选项是（）A．B．C．D．名 4.对于 x 的不等式x﹣ b ＞ 0 恰有两个负整数解，则 b 的取值范围是（）姓A．﹣ 3＜ b ＜﹣ 2 B．﹣ 3 ＜ b ≤﹣2C．﹣ 3 ≤b ≤﹣2 D ．﹣ 3 ≤b ＜﹣ 25.如图，△ABC 中， AB=5 ，AC=6 ， BC=4 ，边 AB 的垂直均分线交AC 于点 D ，则△BDC 的周长是（）号考A．8B． 9C．10D．11金戈铁制卷6.不等式组 的整数解的个数是（ ）A ． 3B ． 5C ． 7D ．无数个7. 当 0 ＜ x ＜ 1 时， x ， ， x 2的大小次序是（）A ． ＜ x ＜ x2B ． x ＜ x 2＜C ． x 2＜ x ＜ D ． ＜ x 2＜ x8. 如图， △ABC 中，BD 均分∠ABC ，BC 的中垂线交 BC 于点 E ，交 BD 于点 F ，连结 CF ．若∠A=60 °，∠ABD=24 °，则∠ACF 的度数为（）A ．48°B ．36°C ．30°D ． 24 °9.对于 x 的不等式组 的解集为 x ＜3 ，那么 m 的取值范围为（ ）A ． m =3B ． m ＞ 3C ． m ＜ 3D ．m ≥310. . 以下命题中，正确的选项是()A ．一腰相等的两个等腰三角形全等.B ．等腰三角形底边上的随意一点到两腰距离之和都大于一腰上的高 .C ．有一角相等和底边相等的两个等腰三角形全等 .D ．等腰三角形的角均分线、中线和高共7 条或 3 条.11. 已知：在△ABC 中，AB ≠AC ，求证： ∠B ≠∠C ．若用反证法来证明这个结论， 能够假定()A ．∠A ＝∠BB ．AB ＝ BCC ．∠B ＝∠CD ．∠A ＝∠C12. 如下图，一次函数y ＝kx ＋ b （ k 、 b 为常数，且 k 0 ）与正比率函数 y ＝ ax （a 为常数，且 a0 ）订交于点 P ，则不等式 kx+b>ax 的解集是（）A ． x>1B ． x<1C ． x>2D ． x<2二、填空题（每题 3 分，共 24 分）13. 等腰三角形一腰上的高与另一腰的夹角的度数为20 °，则顶角的度数是．14. 边长为 a 的等边三角形的面积是．15. 各边长度都是整数、最大边长为8 的三角形共有个16.如图，在 Rt △ABC 中，∠ACB=90 °，点D 在 AB 边上，将△CBD 沿 CD 折叠，使点 B 恰巧落在AC 边上的点 E 处．若∠ A=26 °，则∠CDE=．（16 题）（17题）17. 如图， AB＝ AC ，FD ⊥BC 于 D ，DE⊥ AB 于 E，若∠AFD ＝ 145 °，则∠EDF＝．18. 若不等式组恰有两个整数解，则m 的取值范围是19. 假如三角形的三边长度分别为3a ， 4a ，14，则a的取值范围是______三、解答题20 、解不等式组并把解集在数轴上表示出来．（每题5分，共20分）．．4x2x 61 x2 x 2 4 x 1x 1 ， 3 1 2x2 39x321. 实验学校为初一寄宿学生安排宿舍，若每间4 人，则有 20 人没法安排，若每间8人，则有一间不空也不满，求宿舍间数和寄宿学生人数。

青岛版数学八年级下册第一次月考测试题及答案解析（根据第六单元和第七单元编写）一、选择题1.已知▱ABCD的周长为32,AB=4,则BC等于( )A. 4B. 12C. 24D. 282.已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD 四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是（）A. 选①②B. 选①③C. 选②④D. 选②③3.下列条件中，不能判定四边形是平行四边形的是（）A. 两组对边分别平行B. 一组对边平行，另一组对边相等C. 两组对边分别相等D. 一组对边平行且相等4.如图所示，在平行四边形ABCD中，∠ABE=∠AEB，AE∥DF，DC是∠ADF的角平分线．下列说法正确的是（）①BE=CF ②AE是∠DAB的角平分线③∠DAE+∠DCF=120°．A. ①B. ①②C. ①②③D. 都不正确5.如图，D、E、F分别为Rt△ABC中AB、AC、BC的中点，AB=2，则DC和EF的大小关系是（）A. DC＞EFB. DC＜EFC. DC=EFD. 无法比较6.如图，在梯形ABCD 中，∠ABC=90º，AE ∥CD 交BC 于E ，O 是AC 的中点，AB=，AD=2，BC=3，下列结论：①∠CAE=30º；②AC=2AB ；③S △ADC =2S △ABE ；④BO ⊥CD ，其中正确的是（）A. ①②③B. ②③④C. ①③④D. ①②③④7．下列说法中，不正确的是（ ）．A 3是2)3(-的算术平方根B ±3是2)3(-的平方根C －3是2)3(-的算术平方根 D.－3是3)3(-的立方根8. 在-1.414，2，π，3.14，2+3，3.212212221…，这些数中，无理数的个数为( ).A.5B.2C.3D.49. 已知下列结论：①在数轴上的点只能表示无理数；②任何一个无理数都能用数轴上的点表示；③实数与数轴上的点一一对应；④有理数有无限个，无理数有有限个.其中正确的结论是( ).A.①②B.②③C.③④D.②③④10. 若225a =，3b =，则a b +=（ ）A ．-8B ．±8C ．±2D ．±8或±211. 已知一个直角三角形的两边长分别为3和4，则第三边长是（ ）A ．5B ．25C ．7D ．5或712. 若a 、b 为实数，且满足│a －2│+2b -=0，则b －a 的值为( )A ．2B ．0C ．－2D ．以上都不对二、填空题13.矩形ABCD 的对角线AC 、BD 相交于点O ，∠AOD=120°，AC+BD=16，则该矩形的面积为________14.如图，剪两张等宽对边平行的纸条，随意交叉叠放在一起，转动其中的一张，重合的部分构成了一个四边形，这个四边形是________．C B ADE F15.如图，▱ABCD 的对角线交于点O ，且AB=5，△OCD 的周长为13，则▱ABCD 的两条对角线长度之和为________．16.如图，▱ABCD 中，∠A=50°AD ⊥BD ，沿直线DE 将△ADE 翻折，使点A 落在点A′处，AE 交BD 于F ，则∠DEF=________17．等腰三角形的腰长为5，底边长为8，则它底边上的高为_____，面积为____．18.如图，小莹用一张长方形纸片ABCD 进行折纸，已知该纸片宽AB 为8cm ，•长BC•为10cm ．当小莹折叠时，顶点D 落在BC 边上的点F 处（折痕为AE ）．则此时EC= •19．有一长、宽、高分别为5cm 、4cm 、3cm 的木箱，在它里面放入一根细木条（木条的粗细、形变忽略不计），要求木条不能露出木箱，请你算一算，•能放入的细木条的最大长度是_________cm ．20. 如图7，已知在Rt ABC △中，Rt ACB ∠=∠，4AB =，分别以AC ，BC 为直径作半圆，面积分别记为1S ，2S ，则1S +2S 的值等于 ．三、解答题22．求x 值（每题4分，共8分） (1)126942-=x (2) 16461)21(3=-+x23.已知：如图，E 、F 分别为▱ABCD 中AD 、BC 的中点，分别连接AF 、BE 交于G ，连接CE 、DF 交于点H ．求证：EF 与GH 互相平分．24.如图，已知△ABC 的中线BD 、CE 相交于点O 、M 、N 分别为OB 、OC 的中点． （Ⅰ）求证：MD 和NE 互相平分；（Ⅱ）若BD ⊥AC ，EM=2 ，OD+CD=7，求△OCB 的面积．25.如图，△ABC 中，点O 为AC 边上的一个动点，过点O 作直线MN ∥BC ，设MN 交∠BCA 的外角平分线CF 于点F ，交∠ACB 内角平分线CE 于E ．C A BDE 10 15 （1）求证：EO=FO ；（2）当点O 运动到何处时，四边形AECF 是矩形？并证明你的结论；（3）若AC 边上存在点O ，使四边形AECF 是正方形，猜想△ABC 的形状并证明你的结论 。

青岛版八年级下册数学第一次月考试卷一．选择题（共12小题） 1．函数x32y 中自变量x 的取值范围是（ ）A ．x ＞3B ．x ＜3C ．x ≤3D ．x ≥﹣32．如图，某电信公司提供了A ，B 两种方案的移动通讯费用y （元）与通话时间x （元）之间的关系，则下列结论中正确的有（ ）（1）若通话时间少于120分，则A 方案比B 方案便宜20元； （2）若通话时间超过200分，则B 方案比A 方案便宜12元；（3）若通讯费用为60元，则B 方案比A 方案的通话时间多； （4）若两种方案通讯费用相差10元，则通话时间是145分或185分． A ．1个 B ．2个 C ．3个 D ．4个3．已知y=（m ﹣3）x |m|﹣2+1是一次函数，则m 的值是（ ） A ．﹣3 B ．3C ．±3D ．±24．正比例函数y=2kx 的图象如图所示，则y=（k ﹣2）x+1﹣k 图象大致是（ ）A ．B ．C ．D ．5．在一次函数y=ax ﹣a 中，y 随x 的增大而减小，则其图象可能是（ ）A ．B ．C ．D ．6．在下列图象中，能作为一次函数y=﹣x+1的图象的是（ ）A．B．C．D．7．若不等式组无解，则m的取值范围是（ ）A．m＞2 B．m＜2 C．m≥2 D．m≤28．如果（a+1）x＜a+1的解集是x＞1，那么a的取值范围是（ ）A．a＜0 B．a＜﹣1 C．a＞﹣1 D．a是任意有理数9．已知不等式4x﹣a≤0的正整数解是1，2，则a的取值范围是（ ）A．8＜a＜12 B．8≤a＜12 C．8＜a≤12 D．8≤a≤1210．对于实数x，我们规定表示不大于x的最大整数，例如=1，=3，=﹣3，若=5，则x的取值可以是（ ）A．36 B．40 C．45 D．4611．泰安市出租车的收费标准是：起步价8元（即行驶距离不超过3千米都需付8元车费），超过3千米以后，每增加1千米，加收1.5元（不足1千米按1千米计）．某人从甲地到乙地经过的路程是x千米，出租车费为15.5元，那么x的最大值是（ ）A．11 B．8 C．7 D．512．某医院为了提高服务质量，进行了下面的调查：当还未开始挂号时，有N个人已经在排队挂号，开始挂号后排队的人数平均每分钟增加M人．假定挂号的速度是每窗口每分钟K个人，当开放一个窗口时，40分钟后恰好不会出现排队现象；若同时开放两个窗口时，则15分钟后恰好不会出现排队现象．根据以上信息，若要求8分钟后不出现排队现象，则需要同时开放的窗口至少应有（ ）A．4个B．5个C．6个D．7个二．填空题（共5小题）13．若定义：f（x）=﹣x，g（y）=y2，例如f（3）=﹣3，g（2）=4，则g[f（2）]=．14．执行图所示的程序框图，若输入x=10，则输出y的值为 ．15．拖拉机工作时，油箱中的余油量Q（升）与工作时间t（时）d关系式为Q=40﹣5t．当t=4时，Q=升，从关系式可知道这台拖拉机最多可工作 小时．16．若是正整数，则最小的整数n是 ．17．已知a，b，c在数轴上的位置如图，化简代数式的值为 ．三．解答题（共9小题）18．已知一次函数图象如图：（1）求一次函数的解析式；（2）若点P为该一次函数图象上一点，且点A为该函数图象与x轴的交点，若S△PAO=6，求点P的坐标．19．若直线分别交x轴、y轴于A、B两点，点P是该直线上的一点，PC⊥x轴，C为垂足．（1）求△AOB的面积．（2）如果四边形PCOB的面积等△AOB的面积的一半，求出此时点P的坐标．20．计算：（1）2﹣6+3（2）（﹣）（+）+（2﹣3）2．21．解不等式：，并写出它的所有正整数解．22．解不等式组，并把它们的解集表示在数轴上．23．如图，有一张边长为6cm的正方形纸板，现将该纸板的四个角剪掉，制作一个有底无盖的长方体盒子，剪掉的四个角是面积相等的小正方形，此小正方形的边长为cm．求：（1）剪掉四个角后，制作长方体盒子的纸板的面积；（2）长方体盒子的体积．24．哈市某花卉种植基地欲购进甲、乙两种君子兰进行培育，若购进甲种2株，乙种3株，则共需要成本1700元；若购进甲种3株，乙种1株，则共需要成本1500元．（1）求甲乙两种君子兰每株成本分别为多少元？（2）该种植基地决定在成本不超过30000元的前提下购进甲、乙两种君子兰，若购进乙种君子兰的株数比甲种君子兰的3倍还多10株，求最多购进甲种君子兰多少株？25．某水果店计划购进苹果和丑桔共140千克，这两种水果的进价、售价如表所示：（1）若该水果店购进这两种水果的进货款为1000元，求水果店购进这两种水果各多少千克．（2）若该水果店决定丑桔的进货量不超过苹果进货量的3倍，应怎样安排进货才能使水果店在销售完这批水果时获利最多？26．如图①，正方形ABCD，EFGH的中心P，Q都在直线l上，EF⊥l，AC=EH．正方形ABCD以1cm/s的速度沿直线l向正方形EFGH移动，当点C与HG的中点I重合时停止移动．设移动时间为x s时，这两个正方形的重叠部分面积为y cm2，y与x的函数图象如图②．根据图象解答下列问题：（1）AC=cm；（2）求a的值，并说明点M所表示的实际意义；（3）当x取何值时，重叠部分的面积为1cm2？八年级数学学科能力展示参考答案一．选择题（共12小题）题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B C A B B A D B B B B A二．填空题（共5小题）13．914．﹣1.2515．20；816．317．﹣a三．解答题（共9小题）18．已知一次函数图象如图： （1）求一次函数的解析式；（2）若点P 为该一次函数图象上一点，且点A 为该函数图象与x 轴的交点，若S △PAO =6，求点P 的坐标．解：（1）设一次函数解析式为y=kx+b ，根据题意得，解得，所以一次函数解析式为y=x+2； （2）把y=0代入y=21x+2得21x+2=0，解得x=﹣4，则A 点坐标为（﹣4，0）， 设P 点坐标为（x ，y ），∴S △PAO =21•OA •|y|， ∵S △PAO =6，∴21•4•|y|=6，解得y=±3， 当y=3时，则y=21x+2=3，解得x=2；当y=﹣3时，则y=21x+2=﹣3，解得x=﹣10；∴P 点坐标为（2，3）或（﹣10，﹣3）．19．若直线分别交x 轴、y 轴于A 、B 两点，点P 是该直线上的一点，PC ⊥x 轴，C 为垂足．（1）求△AOB 的面积．（2）如果四边形PCOB 的面积等△AOB 的面积的一半，求出此时点P 的坐标．解：（1）由y=21x+2可知A （﹣4，0），B （0，2）， ∴OA=4，OB=2，∴S △AOB =21OA •OB=4； （2）设P （m ，21m+2），∵四边形PCOB 的面积等△AOB 的面积的一半，S △AOB =4， ∴四边形PCOB 的面积为2， ∴21（21m+2+2）（﹣m ）=2， 解得m=2±2，∴P （2﹣2，3﹣）或（2+2，3+2）．20．计算：（1）2﹣6+3（2）（﹣）（+）+（2﹣3）2．解：（1）2﹣6+3=4﹣6×+3×4=2+12=14；（2）（﹣）（+）+（2﹣3）2=6﹣5+12+18﹣12=31﹣12．21．如图，有一张边长为6cm的正方形纸板，现将该纸板的四个角剪掉，制作一个有底无盖的长方体盒子，剪掉的四个角是面积相等的小正方形，此小正方形的边长为cm．求：（1）剪掉四个角后，制作长方体盒子的纸板的面积；（2）长方体盒子的体积．解：（1）长方体盒子的纸板的面积：（6）2﹣4×（）2=64cm2；（2）长方体盒子的体积：（6﹣2）（6﹣2）×=32cm3．22．解不等式：，并写出它的所有正整数解．解：去分母，得3（x+3）﹣2（2x﹣1）＞6，去括号，得3x+9﹣4x+2＞6，移项，得3x﹣4x＞6﹣9﹣2，合并同类项，得﹣x＞﹣5，系数化成1得x＜5．则正整数解是1，2，3，4．23．解不等式，并把它们的解集表示在数轴上．解：，解①得x＜2，解②得x≥﹣1，所以不等式组的解集为﹣1≤x＜2．用数轴表示为：．24．哈市某花卉种植基地欲购进甲、乙两种君子兰进行培育，若购进甲种2株，乙种3株，则共需要成本1700元；若购进甲种3株，乙种1株，则共需要成本1500元．（1）求甲乙两种君子兰每株成本分别为多少元？（2）该种植基地决定在成本不超过30000元的前提下购进甲、乙两种君子兰，若购进乙种君子兰的株数比甲种君子兰的3倍还多10株，求最多购进甲种君子兰多少株？解：（1）设甲种君子兰每株成本为x元，乙种君子兰每株成本为y元，依题意有，解得．故甲种君子兰每株成本为400元，乙种君子兰每株成本为300元．（2）设购进甲种君子兰a株，则购进乙种君子兰（3a+10）株，依题意有400a+300（3a+10）≤30000，解得a≤．∵a为整数，∴a最大为20．故最多购进甲种君子兰20株．25．某水果店计划购进苹果和丑桔共140千克，这两种水果的进价、售价如表所示：（1）若该水果店购进这两种水果的进货款为1000元，求水果店购进这两种水果各多少千克．（2）若该水果店决定丑桔的进货量不超过苹果进货量的3倍，应怎样安排进货才能使水果店在销售完这批水果时获利最多？解：（1）设购进苹果x千克，则购进丑桔（140﹣x）千克，依题意得：5x+9（140﹣x）=1000，解得：x=65，则140﹣65=75（千克），答：水果店购进苹果65千克，丑桔75千克．（2）设购进苹果x千克时售完这批水果将获利y元，由题意得：140﹣x≤3x，解得：x≥35．获得利润y=（8﹣5）x+（13﹣9）（140﹣x）=﹣x+460．故当x=35时，y有最大值，最大值为425元．140﹣35=105（千克）．答：购进苹果35千克，丑桔105千克时水果店在销售完这批水果时获利最多．26．如图①，正方形ABCD，EFGH的中心P，Q都在直线l上，EF⊥l，AC=EH．正方形ABCD以1cm/s的速度沿直线l向正方形EFGH移动，当点C与HG的中点I重合时停止移动．设移动时间为x s时，这两个正方形的重叠部分面积为y cm2，y与x的函数图象如图②．根据图象解答下列问题：（1）AC=4cm；（2）求a的值，并说明点M所表示的实际意义；（3）当x取何值时，重叠部分的面积为1cm2？解：（1）当这两个正方形的重叠部分面积为8时，也就是小正方形的面积为8，得出小正方形的边长为2cm，所以AC=×2=4cm．故答案为：4．（2）当x=4时，点A与点I重合，y===8，∴a的值为8．点M所表示的实际意义为：当x=4s时，重叠部分面积最大，最大面积为8cm2；（3）由题意，可知：当0≤x≤2时，y=x2，此时y的取值范围是0≤y≤4；当2≤x≤6时，y=﹣（x﹣4）2+8，此时y的取值范围是4≤y≤8；当6≤x≤8时，y=（8﹣x）2，此时y的取值范围是0≤y≤4．当y=1时，得x2=1，解得x=1（负值舍去），或（8﹣x）2=1，解得x=7或x=9（不合题意，舍去），∴当x的值为1或7时，重叠部分的面积为1．11。

山东省菏泽市单县希望初级中学2023-2024学年八年级下学期第一次月考数学试题一、单选题1．矩形的两条对角线的夹角为60度，对角线长为15，则矩形的较短边长为（ ） A ．12 B ．10 C ．7.5 D ．52．16的算术平方根是（ ）A ．4B ．4-C ．4±D ．8±3．如图，在四边形ABCD 中，点P 是对角线BD 的中点，点E 、F 分别是AB 、CD 的中点，AD BC =，30PEF ∠=︒，则PFE ∠的度数是（ ）A ．15︒B ．20︒C ．25︒D ．30︒4．在Rt ABC △中，90C ∠=︒，12a =，16b =，则c 的长为（ ）A ．26B ．18C ．20D ．215．四边形ABCD 的对角线AC 、BD 交于点O ，能判定它是正方形的是（ ） A ．AO ＝OC ，OB ＝ODB ．AO ＝BO ＝CO ＝DO ，AC ⊥BD C ．AO ＝OC ，OB ＝OD ，AC ⊥BD D ．AO ＝OC ＝OB ＝OD6．如图，平行四边形ABCD 的对角线AC 、BD 相交于点O ，下列结论正确的是（ ）A ．S Y ABCD =4S △AOBB ．AC=BDC ．AC ⊥BDD ．Y ABCD 是轴对称图形7．如图，已知矩形ABCD 沿着直线BD 折叠，使点C 落在C '处，BC '交AD 于E ，AD =8，AB =4，则DE 的长为（ ）A ．3B ．4C ．5D ．68．如果一个实数的平方根与它的立方根相等，则这个数是（ ）A ．0B ．正实数C ．0和1D ．19．如图，在平行四边形ABCD 中，BD 为对角线，E 、F 分别是AD 、BD 的中点，连结EF ．若EF=3，则CD 的长为( )A ．2B ．3C ．4D ．610．下列四种说法：①负数的立方根仍为负数；②1的平方根与立方根都是1； ③4的平方④互为相反数的两个数的立方根仍为相反数，正确的有（ ）.A ．1个B ．2个C ．3个D ．4个二、填空题11．若一个数的立方根就是它本身，则这个数是．12．25的平方根是；64的立方根是．13．如图，矩形ABCD 中，8AB =，4BC =，将矩形沿AC 折叠，点D 落在点D ¢处，则重叠部分AFC V 的面积为．14．如图，131243AD CD AB BC CD AD ⊥====，，，，，则四边形ABCD 的面积是．15．如图，已知□ABCD 的对角线AC 、BD 相交于点O ， 点E 是CD 的中点，若BD=12cm ，△DOE 的周长为15cm ，则□ABCD 的周长为cm ．16．如图，ABCD Y 中，E 、F 分别为BC 、AD 边上的点，要使BF DE =，需添加一个条件：．17．如图，四边形ABCD 的对角线相交于O 点，且有AB DC AD BC ∥,∥，则图中有对全等三角形.18．如图，在ABCD Y 中，AE CD ⊥于点E ，如果65B ∠=︒，则DAE ∠=．三、解答题19．如图，已知E 、F 分别是□ABCD 的边BC 、AD 上的点，且BE=DF ⑴求证：四边形AECF 是平行四边形；⑵若BC=10，∠BAC=90°，且四边形AECF 是菱形，求BE 的长．20．已知四边形ABCD 是矩形，对角线AC 和BD 相交于点P ，若在矩形的上方加一个DEA △，且使DE AC ∥，AE BD ∥．(1)求证：四边形DEAP 是菱形；(2)若AE CD =，求DPC ∠的度数．21．如图，在Rt ABC V 中，90B ??，3AB =，4BC =，12CD =，13AD =，求四边形ABCD 的面积．22．如图，在ABC V 中，904B AB BC ∠=︒==，，点E 在BC 上，将ABC V 沿AE 折叠，使点B 落在AC 边上的点F 处．(1)求BE的长；(2)判断CEF△是什么特殊三角形．23．如图，在△ABC中，AB＝BC，D、E、F分别是BC、AC、AB边上的中点．（1）求证：四边形BDEF是菱形；（2）若AB＝12cm，求菱形BDEF的周长．24．在ABCV中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF BD=，连接BF．(1)求证：BD CD=．(2)如果AB AC=，试判断四边形AFBD的形状，并证明你的结论．。

山东省青岛市八年级下学期数学第一次月考试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分） (2017八下·江海期末) 使式子有意义的条件是（）.A .B .C .D .2. （2分） (2019九上·乐山月考) 下列各式中的最简二次根式是（）A .B .C .D .3. （2分）在二次根式①、②、③、④中与是同类二次根式的是（）A . ①和③B . ②和③C . ①和④D . ③和④4. （2分）计算+6，结果为（）A . 5B .C . 4D . 95. （2分）已知关于x的一元二次方程x2+ x-1=0有两个不相等的实数根，则k的取值范围是（）A . k>－1B . k≥－1C . k≥1D . k≥06. （2分） (2018八上·阜宁期末) 要使有意义，的取值范围是（）A .B .C .D .7. （2分）下列计算正确的是（）A . （﹣）2=-3B . =π-3.2C .D . =-38. （2分） (2019九上·江阴期中) 如图.在矩形ABCD中，AB=6，BC=8.E是边AD的一个动点，将△BAE沿BE 对折至△BFE的位置，则线段DF的最小值为（）A . 2B . 4C . 6D . 89. （2分） (2020八上·昌平期末) 下列是勾股数的有（）① 3、4、5；② 5、12 、13；③ 9、40 、41；④ 13、14、15；⑤ ；⑥ 11 、60 、61A . 6组B . 5组C . 4组D . 3组10. （2分）(2018·建湖模拟) 如图，在直角坐标系中，四边形 OABC 为菱形，对角线 OB、AC 相交于 D 点，已知 A点的坐标为（10，0），双曲线 y= （ x＞0 ）经过 D 点，交 BC 的延长线于 E 点，且OB•AC=120（OB ＞AC），有下列四个结论：①双曲线的解析式为y=（x＞0）；②E 点的坐标是（4，6）；③sin∠COA= ；④EC= ；⑤AC+OB=8 ．其中正确的结论有（）A . 4 个B . 3 个C . 2 个D . 1 个11. （2分） (2019八上·哈尔滨月考) 如图，中，是高，，若，则的长是（）A .B .C .D .12. （2分）(2017·抚顺模拟) 如图，△P1OA1 ，△P2A1A2都是等腰直角三角形，点P1 ， P2都在函数y=（x＞0）的图象上，斜边OA1、A1A2都在x轴上，则点P2的坐标是（）A . （4 ，）B . （4+2 ，4﹣2 ）C . （2+2 ，2 ﹣2）D . （4+2 ，2+2 ）二、填空题 (共6题；共6分)13. （1分） (2019九上·新蔡期中) 计算的结果是________.14. （1分）(2017·东河模拟) 等腰三角形一条边的边长为3，它的另两条边的边长是关于x的一元二次方程x2﹣12x+k=0的两个根，则k的值是________．15. （1分）已知：x= ，y= ，那么x2+y2的值为________．16. （1分） (2016八上·河源期末) 如图，将边长为6的等边△ABC放置在平面直角坐标系中，则A点坐标为________．17. （1分）将一张矩行纸片按图中方式折叠,若∠1 =50°，则∠2为________度.18. （1分）(2013·宁波) 如图，AE是半圆O的直径，弦AB=BC=4 ，弦CD=DE=4，连结OB，OD，则图中两个阴影部分的面积和为________．三、解答题 (共6题；共39分)19. （10分） (2019八下·交城期中) 计算：（1）（2）20. （5分） (2017八下·高密期中) 在Rt△ABC中，a为直角边，c为斜边，且满足 +2 =a ﹣4，求这个三角形的周长和面积．21. （5分）(2017·安丘模拟) 如图，一枚运载火箭从地面O处发射，当火箭到达A点时，从地面C处的雷达站测得AC的距离是6km，仰角是43°，1s后，火箭到达B点，此时测得仰角为45.5°，这枚火箭从点A到点B的平均速度是多少？（结果精确到0.01）22. （5分） (2019八上·河南月考) 如图，一块铁皮（图中阴影部分），测得，，，， .求阴影部分面积.23. （9分）(2012·绍兴) 小明和同桌小聪在课后复习时，对课本“目标与评定”中的一道思考题，进行了认真的探索．【思考题】如图，一架2.5米长的梯子AB斜靠在竖直的墙AC上，这时B到墙C的距离为0.7米，如果梯子的顶端沿墙下滑0.4米，那么点B将向外移动多少米？（1）请你将小明对“思考题”的解答补充完整：解：设点B将向外移动x米，即BB1=x，则B1C=x+0.7，A1C=AC﹣AA1= ﹣0.4=2而A1B1=2.5，在Rt△A1B1C中，由得方程________，解方程得x1=________，x2=________，∴点B将向外移动________米．（2）解完“思考题”后，小聪提出了如下两个问题：【问题一】在“思考题”中，将“下滑0.4米”改为“下滑0.9米”，那么该题的答案会是0.9米吗？为什么？【问题二】在“思考题”中，梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离，有可能相等吗？为什么？请你解答小聪提出的这两个问题．24. （5分） (2018八上·长春期末) 一座建筑物发生了火灾，消防车到达现场后，发现最多只能靠近建筑物底端5米，消防车的云梯最大升长为13米，求云梯可以达到该建筑物的最大高度.参考答案一、选择题 (共12题；共24分)答案：1-1、考点：解析：答案：2-1、考点：解析：答案：3-1、考点：解析：答案：4-1、考点：解析：答案：5-1、考点：解析：答案：6-1、考点：解析：答案：7-1、考点：解析：答案：8-1、考点：解析：答案：9-1、考点：解析：答案：10-1、考点：解析：答案：11-1、考点：解析：答案：12-1、考点：解析：二、填空题 (共6题；共6分)答案：13-1、考点：解析：答案：14-1、考点：解析：答案：15-1、考点：解析：答案：16-1、考点：解析：答案：17-1、考点：解析：答案：18-1、考点：解析：三、解答题 (共6题；共39分)答案：19-1、答案：19-2、考点：解析：答案：20-1、考点：解析：答案：21-1、考点：解析：答案：22-1、考点：解析：答案：23-1、答案：23-2、考点：解析：答案：24-1、考点：解析：。

八年级数学第一次月考试题 姓名： 考号：一、选择题：（每题3分 共30分）1.下列式子一定是二次根式的是 （ ） A.2--x B.x C.22+x D.22-x2、若b b -=-3)3(2，则 （ ） A.b>3 B.b<3 C.b ≥3 D.b ≤3 3.化简)22(28+-得 （ ）A.—2B.22- C.2 D.224-4.若x ＜2，化简x x -+-3)2(2的正确结果是（ ） A.-1 B.1 C.2x-5 D.5-2x5.若最简二次根式a a 241-+与是同类二次根式，则a 的值为 （ ） A.43-=a B.34=a C.1=a D.1-=a6、下列二次根式中，与32是同类二次根式的是：（ ） A ）12 B ）24 C ）27 D ）507.下列计算正确的是（ ）==4=8.下列二次根式中，最简二次根式是（ ）．(A)；．9.如图，已知∠1＝∠2，则不一定．．．能使△ABD ≌△ACD 的条件是（ ） A ．AB ＝AC B ．BD ＝CD C ．∠B ＝∠C D ．∠ BDA ＝∠CDA10.如图，已知△ABC ≌△DEF ，∠A ＝∠D ，则下列结论正确的．．．．．．．是（ ） A ．AB ＝DF B ．AC ＝DE C ．∠B ＝∠E D ．AC ＝DC 二、填空题 （每题4分 共20分）11. 若0)3(12=++-+y y x ，则y x -的值为 12.计算-÷的结果是 ．13.aa 的取值范围为__________________．14、如图，∠B=∠D ，要使△ABC ≌△ADC ，那么还需一个条件 （填一个即可） 15、如图在△ABC 和△ADE 中，∠B=∠D ，AB=AD ，BC=DE ，则ΔADC ≌ΔABE 的根据是（14题）（15题）三、解答题16.计算(20分) （1）)212(8-⨯ （2）÷（3）、221－631＋8） （4）3231+821－5051A B EDAC17（10分）先化简，再求值：（aa a a -+-112）÷a ，其中a =12+.18、(10分)如图，已知点E C ，在线段B F 上，BC=EF ，AB ∥DE ，∠ACB=∠F ． △ABC 和△DEF 全等吗？为什么？19（10分）、已知，如图所示，B 、E 、F 、C 四点在同一条直线上，AB=DC ，BE=CF ，∠B=∠C ，线段 AF 和DE 相等吗？为什么？一、选择题答案卡：CE BF DAOFEBAD。

试卷第1页，总3页初二数学单元测试题 一． 选择题（每题3分将答案填在后面的表格内） 1．下列说法正确的是（ ） A ．一组对边相等，另一组对边平行的四边形是平行四边形 B ．对角线互相垂直的四边形是菱形 C ．对角线相等的四边形是矩形 D ．有三个角是直角的四边形是矩形 2．下列平行四边形中，其图中阴影部分面积不一定等于平行四边形面积一半的是（ ） A ． B ．C ．D ． 3．如图，平行四边形ABCD 中，DE ⊥AB 于E ，DF ⊥BC 于F ，若平行四边形ABCD 的周长为48，DE=5，DF=10，则平行四边形ABCD 的面积等于（ ） A ．87.5 B ．80 C ．75 D ．72.5 3题图4题图 6题图 4．如图，在平行四边形ABCD 中，对角线AC 、BD 相交于点O ，E 、F 是对角线AC 上的两点，给出下列四个条件：①AE=CF ；②DE=BF ；③∠ADE=∠CBF ；④∠ABE=∠CDF ．其中不能判定四边形DEBF 是平行四边形的有（ ） A ．1个 B ．2个 C ．3个 D ．4个 5．以三角形的一条中位线和第三边上的中线为对角线的四边形是（ ） A ．梯形 B ．平行四边形 C ．菱形 D ．矩形 6．如图，△ABC 的面积是12，点D 、E 、F 、G 分别是BC 、AD 、BE 、CE 的中点，则△AFG 的面积是（ ） A ．4.5 B ．5 C ．5.5 D ．6 7题图 8题图 9题图 10题图 7．如图，△ABC 中，D 、E 分别是BC 、AC 的中点，BF 平分∠ABC ，交DE 于点F ，若BC=6，则DF 的长是（ ） A ．3 B ．2 C ． D ．4 8．如图，在矩形ABCD 中，AB=8，BC=4，将矩形沿AC 折叠，则重叠部分△AFC 的面积为（ ） A ．12 B ．10 C ．8 D ．6 9．如图，O 是菱形ABCD 的对角线AC 、BD 的交点，E 、F 分别是OA 、OC 的中点．下列结论：①S △ADE =S △EOD ；②四边形BFDE 也是菱形；③四边形ABCD 的面积为EF ×BD ；④∠ADE=∠EDO ；⑤△DEF 是轴对称图形．其中正确的结论有（ ） A ．1个 B ．2个 C ．3个 D ．4个 10．如图，在Rt △ABC 中，∠BAC=90°，AB=6，AC=8，P 是斜边BC 上一动点，PE ⊥AB 于E ，PF ⊥AC 于F ，EF 与AP 相交于点O ，则OF 的最小值为（ ） A ．4.8 B ．1.2 C ．3.6 D ．2.4 11．如图，已知某菱形花坛ABCD 的周长是24m ，∠BAD=120°，则花坛对角线BD 的长是（ ） A ．6m B ．6m C ．3m D ．3m11题图12题图12．将n个边长都为1cm的正方形按如图所示的方法摆放，点A1，A2，…，An分别是正方形对角线的交点，则n个正方形重叠形成的重叠部分的面积和为（）A．cm2B．cm2 C ．cm2D ．（）n cm2二．填空题（每题3分）13．平行四边形的一个内角平分线将该平行四边形的一边分为2cm和3cm两部分，则该平行四边形的周长为．14．如图所示，在▱ABCD中，对角线AC、BD相交于点O，已知△BOC与△AOB的周长之差为4，▱ABCD的周长为28，则BC的长度为．14题图16题图17题图18题图15．已知菱形的一条对角线长为6cm，面积为24cm2，则菱形的周长是cm．16．如图，连接四边形ABCD各边中点，得到四边形EFGH，还要添加条件，才能保证四边形EFGH是矩形．17．E为▱ABCD边AD上一点，将△ABE沿BE翻折得到△FBE，点F在BD上，且EF=DF．若∠C=52°，那么∠ABE=．18．如图，将正方形OABC放在平面直角坐标系中，O是原点，A的坐标为（1，），则点C的坐标为．三．解答题（共5小题）19（12分）．如图，AD是△ABC的中线，AE∥BC，BE交AD于点F，交AC于G，F是AD的中点．（1）求证：四边形ADCE是为平行四边形；（2）若EB是∠AEC的角平分线，请写出图中所有与AE相等的边．20．（12分）如图，在△ABC中，AB=AC，D为边BC的中点，四边形ABDE是平行四边形，AC，DE相交于点O．（1）求证：四边形ADCE是矩形；（2）若∠AOE=60°，AE=2，求矩形ADCE对角线的长．试卷第2页，总3页试卷第3页，总3页21、（12分）已知：如图，在 △ABC 中，AB=AC ，AD 是BC 边上的中线， E 是 AC 的中点， BF ⊥CA 延长线于点F ，求证：∠CBF=∠ADE . 22．（15分）如图，在Rt △ABC中，∠ACB=90°，过点C 的直线MN ∥AB ，D 为AB 边上一点，过点D 作DE ⊥BC ，交直线MN 于E ，垂足为F ，连接CD 、BE ． （1）求证：CE=AD ； （2）当D 在AB 中点时，四边形BECD 是什么特殊四边形？说明你的理由； （3）若D 为AB 中点，则当∠A 的大小满足什么条件时，四边形BECD 是正方形？请说明你的理由． 23．（15分）如图（1），BD 、CE 分别是△ABC 的外角平分线，过点A 作AF ⊥BD ，AG ⊥CE ，垂足分别为F 、G ，连接FG ，延长AF 、AG ，与直线BC 相交于M 、N ． （1）试说明：FG=（AB +BC +AC ）； （2）①如图（2），BD 、CE 分别是△ABC 的内角平分线；②如图（3），BD 为△ABC 的内角平分线，CE 为△ABC 的外角平分线． 则在图（2）、图（3）两种情况下，线段FG 与△ABC 三边又有怎样的数量关系？请写出你的猜想，并对其中的一种情况说明理由．1。

山东省单县希望初级中学 2015-2016 学年八年级数学下学期第一次月考试题一、选择题（每题 3 分，共 30 分）1、不能判定四边形 ABCD 是平行四边形的是（ ）A.AB ∥ CD ， AB=CDB.AB=CD ， AD=BCC.AD=BC ，∠ A=∠ CD.AB∥CD ，∠ B=∠ D2、在下列各式中正确的是（）A. ( 2)2＝－ 2 B. 9 ＝ 3 C. 16 ＝ 8 D.22 ＝23、 □ ABCD 的周长为 32cm , △ ABC 的周长为 22cm,则 AC 的长为（）A. 11cmB. 4cmC. 6cmD. 5cmE4、如图，在四边形 ABCD 中， AC 、BD 互相平分于点 O ，AD∠AEC=∠BED =90°，则四边形 ABCD 是（ )A. 平行四边形B. 菱形OC. 矩形D.正方形BC5、下列各组数中，不能构成直角三角形的一组是（）A ． 1，2，5 B ．1，2，3C．3，4，5D． 6，8， 126、 81 的算术平方根是（）A. ±9B.9C.3D.8127、如图， E 、 F 是 ABCD对角线 AC 上两点，且 AECF ，连结 DE 、 BF ，则图中共有全等三角形的对数是（ ）DCＡ．1对Ｂ． 2 对Ｃ．3对Ｄ．4 对F8、如图， DE 是△ ABC 的中位线， DE=2,AB+AC=12,E则四边形 BCED 的周长为（ ）A第 7 题BA.18B.12C.16D.209、如图 3 所示，平行四边形ABCD 中，对角线 AC 、 BD 交于点 O ，点 E 是 BC 的中点．若 OE=3 cm ，则 AB 的长为 ()A ． 3 cmB． 6 cmAC ． 9 cmD ． 12 cm DE ABCD 为平行四边10、已知四边形 ABCD 中 , AC 交 BD 于点 O , 如果只给条件“ AB ∥ CD ” , 那么还不能判定四形 形 , 给出以下四种说法 :B C(1) 如果再加上条件“ BC=AD ” , 那么四边形 ABCD 一定是平行四边形 ;(2) 如果再加上条件“BADBCD ” , 那么四边形一定是平行四边形 ;ABCD (3) 如果再加上条件“ AO=OC ” , 那么四边形 ABCD 一定是平行四边形 ;(4) 如 果再加上条件“ DBACAB ” , 那么四边形 一定是平行四边形ABCD 其中正确的说法是 ( ) A.(1)(2) B.(1)(3)(4) C.(2)(3) D.(2)(3)(4)填空题（每题 3分，共 24分） 11、如果 2a18 0 ，那么 a 的算术平方根是．12、如果三角形的三边之比为 5:12 ： 13，且周长为 60 厘米，那么这个三角形的面积为．13、 E 、 F 、 G 、 H 分别为菱形 ABCD 四边的中点，则四边形 EFGH 为．14、如图，在平面直角坐标系中，四边形 ABCD 是菱形， ∠ABC =60°， AB =4, 则点 B 坐标，点 C坐标为，点 D 坐标为.- 1 -15、（ 2a+3）2+ b2=0,则 ab=___________。