实验一 信号的表示、可视化及时域运算

《信号与系统》仿真作业实验一：连续信号的表示及可视化：f(t)=δ(t); f(t)=ε(t); f(t)=e at(分别取a>0与a<0);f(t)=R(t); f(t)=Sa(wt); f(t)=sin(2πft);(分别画出不同周期个数的波形)解：（1）f(t)=δ(t)的matlab表示：程序清单如下：》t=-5:0.01:5;k=(0-(-5))/0.01+1;y=zeros(size(t));y(k)=1/(0.01-(-0.01));plot(t,y);title('冲击函数f(t)=δ(t)')画出冲击函数的图形如下：冲击函数f(t)=δ(t)t（2） f(t)=ε(t )的matlab 表示及图形： 程序清单如下： 》t=-5:0.01:5; y=heaviside(t) plot(t,y)画出阶跃函数的图形如下：(3) f(t)=e at 的matlab 表示及图形： 程序清单如下： 》t=-10:0.01:10;y1=exp(0.1*t); y2=exp(-0.1*t); plot(t,y1,'r',t,y2,'b') 画出指数函数的图形如下：tf (t )=ε(t )(4) f(t)=R(t)的matlab 表示及图形： 程序清单如下： 》t=-5:0.01:5;y=heaviside(t+2)-heaviside(t-2); plot(t,y,'b') 画出窗函数的图形如下：(5) f(t)=Sa(wt) 的matlab 表示及图形： 程序清单如下：》ezplot('sin(t)./t',[-20,20]) grid ontf (t )=e atty =R 9t )画出抽样函数的图形如下：sin(t)/tt（6）f(t)=sin(2πft)的matlab表示及图形：程序清单如下：》ezplot('sin(2*pi*50*t)',[-.02,.02])grid on画出正弦函数的图形如下：实验二：离散信号的表示及可视化：f(t)=δ(n ); f(t)=ε(n ); f(t)=e an (分别取a>0与a<0); f(t)=R N (n ); f(t)=Sa(nw); f(t)=sin(nw );(分别取不同的w 值) 解：（1） 冲击序列f(n)=δ(n )的matlab 实现： 程序清单如下： 》n0=0; ns=-10; nf=10; n=[ns:nf];y=[zeros(1,n0-ns),1,zeros(1,nf-n0)];-0.02-0.015-0.01-0.00500.0050.010.0150.02-1-0.50.51tsin(2 50 t)stem(n,y);title('冲击序列f(n)=δ(n)')画出冲击序列的图形如下：冲击序列f(n)=δ(n)n（2）阶跃序列f(n)=ε(n)的matlab实现：程序清单如下：》n0=0;ns=-10;nf=10;n=[ns:nf];y=[zeros(1,n0-ns),ones(1,nf-n0+1)];stem(n,y);title('阶跃序列f(n)=ε(n)')阶跃序列的图形如下：（3） 指数序列f(t)=e an (分别取a>0与a<0)的matlab 实现： 程序清单如下： 》n=-10:10; y1=exp(0.1*n); y2=exp(-0.1*n); plot(n,y1,'ro',n,y2,'bo') 指数序列的图形如下：（4） 门序列f(n)=R N (n )的matlab 实现：程序清单如下： 》n1=-3;n2=3;ns=-15;nf=15;阶跃序列f(n)=ε(n)nnf (t )=e a nn=[ns:nf];y=[zeros(1,n1-ns),ones(1,n2-n1+1),zeros(1,nf-n2)]; stem(n,y);title('窗序列f(n)=R N (n )') 窗序列的图形如下：（5） 抽样序列f(t)=Sa(nw)的matlab 实现： 》n=-20:0.5:20; y=sin(n)./n; plot(n,y,'o'); title('f(t)=Sa(nw)')窗函数f(n)=R N (n)n抽样序列的图形如下：（6） 正弦序列f(t)=sin(nw )(分别取不同的w 值)的matlab 实现： 》n=-0.1:0.002:0.1 w=100 y=sin(w*n) plot(n,y,'o') grid on正弦序列的图形如下：f (t)=Sa(nw)nny =s i n (w *n )实验三：系统的时域求解1、设h(n)=(0.9)n u(n),x(n)=u(n)-u(n-10),求：y(n)=x(n)*h(n),并画出x(n),h(n),y(n)波形。

实验一信号的表示、可视化及时域运算实验一信号的表示、可视化及时域运算一、实验目的：熟悉MATLAB 软件的使用，学会信号的表示及用MATLAB 来产生信号，实现信号的可视化。

二、实验时数：2学时三、实验内容：信号按照自变量的取值是否连续可分为连续时间信号和离散时间信号。

信号与系统的仿真运算对信号与系统课程的学习有着重要意义。

MATLAB 以其科学与技术计算通用的交互系统和编程语言，具有良好的交互数学计算和易于使用的集成图形，编程简单，功能连贯，成为信号与系统的仿真运算首选。

本次实验完成以下内容：1．熟悉MATLAB 语言。

A ）双击快捷图标，启动MATLAB 。

B ）了解界面功能。

主界面包括标题栏、菜单栏、工具栏和输入输出区等。

C ）简单的信号处理可以通过在Command Window 中输入相关指令按Enter 键执行来达到处理目的。

复杂的信号处理可以通过编写M 文件，执行M 文件达到处理目的。

M 文件的编写类似于Word 文档编写。

选中命令窗口File 菜单中M-File 打开M 文件编辑器或单击命令窗口工具栏中New M-File 图标编辑M-文件。

D ）M-文件可以在命令窗口输入已保存的M-文件名回车执行，也可使用M-文件编辑器窗口中选择Debug 菜单中的RUN 运行M-文件。

2．连续信号的表示与可视化。

MATLAB 提供了大量的生成基本信号的函数，一种常用的方法是调用相关函数及运算通过向量形式来表示信号，用适当的MATLAB 语句表示信号后，可以利用MATLAB 的绘图命令绘制出直观的信号波形。

本次实验完成指数信号at Ae ，正弦信号)sin(0?ω+t A ，)cos(0?ω+t A ，抽样函数tt t Sa ππ)sin()(=，矩形脉冲函数（产生以t=o 为中心的宽度为width 的矩形波）),(width t rectpuls ，三角波脉冲函数),,(skew width t tripuls 。

实验一信号的时域分析一、实验目的：1. 熟悉MATLAB 软件的使用2. 学会信号的多种表示形式和信号的可视化；3. 熟悉MATLAB中信号的基本运算和卷积运算。

二、实验时数：2学时三、实验相关知识：信号按照自变量的取值是否连续可分为连续时间信号和离散时间信号。

对一维时间信号进行时域分析，首先需要将信号随时间变化的规律用二维曲线表示出来。

对于简单信号可以通过手工绘制其波形，但对于复杂的信号，手工绘制信号波形显得十分困难，且难以绘制精确的曲线。

1、连续时间信号的描述在 MATLAB中通常用三种方法来产生并表示连续时间信号，即采用符号运算工具箱来描述信号；采用向量表示法来描述信号；采用Simulink工具来描述并产生信号。

(1)采用MATLAB软件符号运算工具箱来描述信号方法一：符号函数图形计算器在MATLAB 环境下输入命令funtool，则会产生三个视窗，如所示。

图1 符号函数图形计算器●figure No.1：可轮流激活，显示f函数的计算结果。

●figure No.2：可轮流激活，显示g函数的计算结果。

●figure No.3 ：函数运算器，其功能有：f，g 可输入函数表达式；x 是自变量，在缺省时绘制在[-2pi，2pi]的范围内的函数图形，在figure No.1 或figure No.2产生相应的波形。

方法二：符号运算表示法如果信号可以用一个表达式来表示它，则我们可用ezplot命令（缺省的区间为[-2*pi, 2*pi]）绘制出信号的波形，例如对于连续信号f(t)=sin(πt/4),我们可以用符号表达式表示为：f=sym('sin(pi/4*t)');然后用 ezplot命令绘制其波形：ezplot(f,[-16,16]);该命令绘制的信号波形如错误!未找到引用源。

所示。

图 1 符号运算表示法表示信号(2)采用向量表示法来描述信号用适当的MATLAB 中的向量来表示信号，该信号可以利用MATLAB 的绘图命令绘制出直观的信号波形。

成绩评定表课程设计任务书目录一、引言1二、Matlab入门22.1 Matlab7.0介绍 (2)2.2利用Matlab7.0编程完成习题设计 (3)三、Matlab7.0实现连续时间信号时移、反褶、尺度变换的设计43.1常用连续时间信号的类别及原理43.2编程设计及实现43.3运行结果及其分析6四、结论17五、参考文献 (18)一、引言近年来，计算机多媒体教序手段的运用逐步普及，大量优秀的科学计算和系统仿真软件不断涌现，为我们实现计算机辅助教案和学生上机实验提供了很好的平台。

通过对这些软件的分析和对比，我们选择MATLAB语言作为辅助教案工具，借助MATLAB强大的计算能力和图形表现能力，将《信号与系统》中的概念、方法和相应的结果，以图形的形式直观地展现给我们，大大的方便我们迅速掌握和理解老师上课教的有关信号与系统的知识。

MATLAB是当前最优秀的科学计算软件之一，也是许多科学领域中分析、应用和开发的基本工具。

MATLAB全称是Matrix Laboratory,是由美国Mathworks公司于20世纪80年代推出的数学软件，最初她是一种专门用于矩阵运算的软件，经过多年的发展，MATLAB已经发展成为一种功能全面的软件，几乎可以解决科学计算中的所有问题。

而且MATLAB编写简单、代码效率高等优点使得MATLAB在通信、信号处理、金融计算等领域都已经被广泛应用。

它具有强大的矩阵计算能力和良好的图形可视化功能，为用户提供了非常直观和简洁的程序开发环境，因此被称为第四代计算机语言。

MATLAB 强大的图形处理功能及符号运算功能，为我们实现信号的可视化及系统分析提供了强有力的工具。

MATLAB 强大的工具箱函数可以分析连续信号、连续系统，同样也可以分析离散信号、离散系统，并可以对信号进行各种分析域计算，如相加、相乘、移位、反折、傅里叶变换、拉氏变换、Z 变换等等多种计算。

人们之间的交流是通过消息的传播来实现的，信号则是消息的表现形式，消息是信号的具体内容。

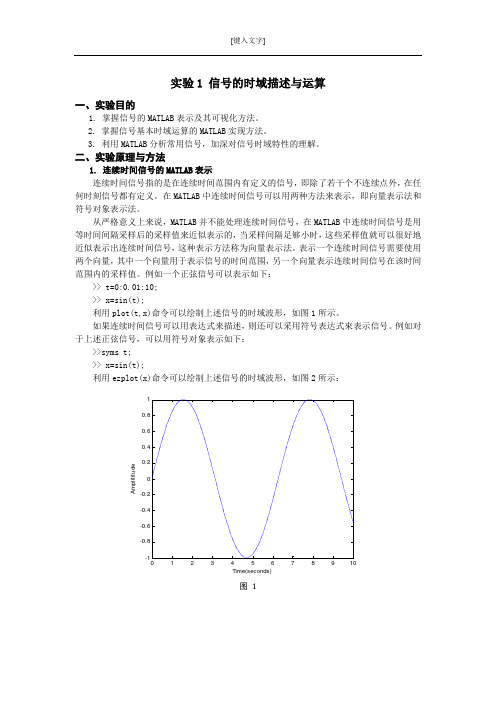
实验1 信号的时域描述与运算一、实验目的1. 掌握信号的MATLAB 表示及其可视化方法。

2. 掌握信号基本时域运算的MATLAB 实现方法。

3. 利用MATLAB 分析常用信号，加深对信号时域特性的理解。

二、实验原理与方法1. 连续时间信号的MATLAB 表示连续时间信号指的是在连续时间范围内有定义的信号，即除了若干个不连续点外，在任何时刻信号都有定义。

在MATLAB 中连续时间信号可以用两种方法来表示，即向量表示法和符号对象表示法。

从严格意义上来说，MATLAB 并不能处理连续时间信号，在MATLAB 中连续时间信号是用等时间间隔采样后的采样值来近似表示的，当采样间隔足够小时，这些采样值就可以很好地近似表示出连续时间信号，这种表示方法称为向量表示法。

表示一个连续时间信号需要使用两个向量，其中一个向量用于表示信号的时间范围，另一个向量表示连续时间信号在该时间范围内的采样值。

例如一个正弦信号可以表示如下：>> t=0:0.01:10; >> x=sin(t);利用plot(t,x)命令可以绘制上述信号的时域波形，如图1所示。

如果连续时间信号可以用表达式来描述，则还可以采用符号表达式來表示信号。

例如对于上述正弦信号，可以用符号对象表示如下：>>syms t; >> x=sin(t);利用ezplot(x)命令可以绘制上述信号的时域波形，如图2所示：图 1Time(seconds)A m p l i t i t u d e图表 2matlab 提供了一些函数用于常用信号的产生，例如阶跃信号、脉冲信号、指数信号、正弦信号等，表中列出了一些常用的基本函数。

常用的信号产生函数2.连续时间信号的时域运算对连续时间信号的运算包括两信号相加、相乘、微分、积分，以及位移、反转、尺度变换（尺度伸缩）等。

1）相加和相乘信号相加和相乘指两信号对应时刻的值相加和相乘，对于两个采用向量表示的可以直接使用算术运算的运算符“+”和“*”来计算，此时要求表示两信号的向量时间范围和采样间隔相同。

实验一连续时间信号的时域和频域分析一. 实验目的：1. 熟悉MATLAB 软件平台。

2. 掌握MATLAB 编程方法、常用语句和可视化绘图技术。

3. 编程实现常用信号及其运算MATLAB 实现方法。

4. 编程实现常用信号的频域分析。

二. 实验原理：1、连续时间信号的描述：（1）向量表示法连续信号是指自变量的取值范围是连续的，且对于一切自变量的取值，除了有若干个不连续点之外，信号都有确定的值与之对应。

严格来说，MATLAB 并不能处理连续信号，而是用等时间间隔点的样值来近似表示连续信号。

当取样时间间隔足够小时，这些离散的样值就能较好地近似连续信号。

矩阵是MATLAB 进行数据处理的基本单元，矩阵运算是MATLAB 最重要的运算。

通常意义上的数量（也称为标量）在MATLAB 系统中是作为1×1 的矩阵来处理的，而向量实际上是仅有一行或者一列的矩阵。

通常用向量表示信号的时间取值范围，如t = -5:5，但信号x(t)、向量t 本身的下标都是从1 开始的，因此必须用一个与向量x 等长的定位时间变量t，以及向量x，才能完整地表示序列x(t)。

在MATLAB 可视化绘图中，对于以t 为自变量的连续信号，在绘图时统一用plot 函数；而对n 为自变量的离散序列，在绘图时统一用stem 函数。

（2）符号运算表示法符号对象(Symbolic Objects 不同于普通的数值计算)是Matlab 中的一种特殊数据类型，它可以用来表示符号变量、表达式以及矩阵，利用符号对象能够在不考虑符号所对应的具体数值的情况下能够进行代数分析和符号计算(symbolic math operations)，例如解代数方程、微分方程、进行矩阵运算等。

符号对象需要通过sym 或syms 函数来指定, 普通的数字转换成符号类型后也可以被作为符号对象来处理.我们可以用一个简单的例子来表明数值计算和符号计算的区别: 2/5+1/3 的结果为0.7333(double 类型数值运算), 而sym(2)/sym(5)+sym(1)/sym(3)的结果为11/15, 且这里11/15 仍然是属于sym 类型, 是符号数。

姓名： 周强 班级： 电信1004班 学号： 201004135136实验1 时域连续信号的表示及运算一、 实验目的1．掌握常用时域连续信号的MA TLAB 表示方法。

2．掌握连续信号的基本运算，包括信号相加与相乘、微分与积分、平移、反转、尺度变换、奇偶分解、卷积积分等。

二、 实验原理及方法MATLAB 利用连续信号在等时间间隔点的采样值来近似表示连续信号。

三、 实验内容及步骤1. 利用MATLAB 命令画出下列连续信号的波形图。

（1）)()2(t u e t--源代码 （1 ） )()2(t u e t -- 图像 t=0:0.001:8;y=(2-exp(-t)).*heaviside(t);plot(t,y);grid onaxis([0 8 1 2])波形图（2）)(cos t u源代码：t=0:0.01:2*pi;y=heaviside(cos(t));plot(t,y);grid onaxis([0 2*pi 0 1])波形图（3）产生幅度为1、周期为1、占空比为0.5的周期矩形信号。

源代码t=0:0.01:8; 波形图y=heaviside(sin(2*pi*t));plot(t,y);grid onaxis([0 4 0 1.2]);2. 已知)(t f 的波形如图1-15所示，做出)()(t f t f +、)()(t f t f ⋅、)(t f 的微分、)(t f 的积分、)43(t f -的波形。

)(t f 的图像代码syms t yy=t*(heaviside(t)-heaviside(t-1))+heaviside(t-2)-heaviside(t-1);ezplot(t ,y);grid onaxis([0 4 -1.5 1.5]))(t f 的图像t )(t f 01121-图1-15)()(t f t f +源代码syms t y y1y1=t*(heaviside(t)-heaviside(t-1))+heaviside(t-2)-heaviside(t-1);y=y1+y1; )()(t f t f +波形图ezplot(t,y);grid onaxis([0 4 -2.1 2.1]))()(t f t f ⋅源代码syms t yy=t*(heaviside(t)-heaviside(t-1))+heaviside(t-2)-heaviside(t-1);ezplot(t ,y*y);grid onaxis([0 4 -2.1 2.1])波形图)(t f 的微分syms t y fy=t*(heaviside(t)-heaviside(t-1))+heaviside(t-2)-heaviside(t-1);f=diff(y,'t');t=0:0.01:4; )(tf的微分波形图ezplot(f,t);grid onf的积分)(t源代码syms t y f y1y=t*(heaviside(t)-heaviside(t-1))+heaviside(t-2)-heaviside(t-1);f=int(y,'t');t=0:0.01:4;ezplot(f,t);grid on波形图3(tf4)源代码syms t y1 yy1=t*(heaviside(t)-heaviside(t-1))+heaviside(t-2)-heaviside(t-1);y=subs(y1,t,3-4*t);ezplot(t ,y);grid onaxis([0 1.2 -1.2 1.2])波形图实验心得与小结：（1）学会了单位阶跃函数heaviside()的使用，掌握了用matlab画一些连续信号的波形图（2）掌握了对一些基本的函数求微分，积分，翻转，平移的方法，还有一些符号变量的使用（3）学会了如何利用三角函数的周期性画出周期性的单位阶跃函数体会：在学习的过程中只有不断的尝试，才能从其中学到一些东西，在上机的过程中，我们不能只会画几个图像就以为学会了，从理解到自己能熟练运用还有一段距离，只有不断的从实验中发现错误才能提高自己，才能有收获。

《信号与系统》上机实验实验一连续时间信号的表示及可视化一．实验目的熟练掌握连续时间信号的表示及可视化处理。

二．实验源程序δf(t))=)(tf=@(t)dirac(t) %定义函数ezplot(f,[-5:5]); %利用ezplot( )命令绘制连续图形xlabel('(t)'); %横坐标ylabel('(f)'); %纵坐标f(t)= ε(t)（f=Heaviside(n)）f=@(t)heaviside(t) %定义函数ezplot(f,[-5:5]); %利用ezplot( )命令绘制连续图形xlabel('(t)'); %横坐标ylabel('(f)'); %纵坐标f(t)=at e(分别取a>0及a<0)a=1时f=@(t)exp(t) %定义函数ezplot(f,[-5:5]); %利用ezplot( )命令绘制连续图形xlabel('(t)'); %横坐标ylabel('(f)'); %纵坐标a=-1时f=@(t)exp(-t) %定义函数ezplot(f,[-5:5]); %利用ezplot( )命令绘制连续图形xlabel('(t)'); %横坐标ylabel('(f)'); %纵坐标f(t)=R(t)t=-5:0.01:5; %设定时间变量t的范围及步长y=rectpuls(t,2); %用rectpuls（t a)命令表示门函数，默认以零点为中心，宽度为aplot(t,y); %用plot函数绘制连续函数grid on; %显示网格命令title('门函数'); %用title函数设置图形的名称axis([-5 5 -0.5 1.5]);f(t)=Sa(wt)w=5时，f=Sa(5*t)f=@(t)Sinc(5*t) %定义函数ezplot(f,[-5:5]); %利用ezplot( )命令绘制连续图形xlabel('(t)'); %横坐标ylabel('(f)'); %纵坐标axis([-5 5 -1.2 1.2])w=8时，f=Sa(8*t)f=@(t)sinc(8*t) %定义函数ezplot(f,[-4:4]); %利用eaplot( )命令绘制连续图形xlabel('(t)'); %横坐标ylabel('(f)'); %纵坐标f(t)=Sin(2πft)(分别画出不同周期个数的波形)f(t)=Sin(t)f=@(t)sin(t) %定义函数ezplot(f,[-15:15]); %利用eaplot( )命令绘制连续图形xlabel('(t)'); %横坐标ylabel('(f)'); %纵坐标axis([-15 15 -1.2 1.2])三．程序运行结果(1)(2)（3）-5-4-3-2-1012345-1-0.8-0.6-0.4-0.200.20.40.60.81(t)dirac(t)(f )-5-4-3-2-101234500.20.40.60.81(t)heav iside(t)(f )（4）-5-4-3-2-1012345010********607080(t)exp(t)(f )-5-4-3-2-1012345010********607080(t)exp(-t)(f )（5）-5-4-3-2-1012345-1-0.8-0.6-0.4-0.200.20.40.60.81(t)Sinc(5 t)(f )(6)-4-3-2-101234 -1-0.8-0.6-0.4-0.20.20.40.60.81(t)sinc(8 t)(f)-15-10-5051015 -1-0.8-0.6-0.4-0.20.20.40.60.81(t)sin(t)(f)实验二离散时间信号的表示及可视化一．实验目的学会对离散时间信号进行标识和可视化处理。

北京理工大学信号与系统实验实验报告信号与系统实验报告姓名:肖枫学号:1120111431班号:05611102专业:信息对抗技术学院:信息与电子学院12实验1 信号的时域描述与运算一、实验目的1. 掌握信号的MATLAB表示及其可视化方法。

2. 掌握信号基本时域运算的MATLAB实现方法。

3. 利用MATLAB分析常用信号，加深对信号时域特性的理解。

二、实验原理与方法1. 连续时间信号的MATLAB表示连续时间信号指的是在连续时间范围内有定义的信号，即除了若干个不连续点外，在任何时刻信号都有定义。

在MATLAB中连续时间信号可以用两种方法来表示，即向量表示法和符号对象表示法。

从严格意义上来说，MATLAB并不能处理连续时间信号，在MATLAB中连续时间信号是用等时间间隔采样后的采样值来近似表示的，当采样间隔足够小时，这些采样值就可以很好地近似表示出连续时间信号，这种表示方法称为向量表示法。

表示一个连续时间信号需要使用两个向量，其中一个向量用于表示信号的时间范围，另一个向量表示连续时间信号在该时间范围内的采样值。

例如一个正弦信号可以表示如下:>> t=0:0.01:10;>> x=sin(t);利用plot(t,x)命令可以绘制上述信号的时域波形，如图1所示。

如果连续时间信号可以用表达式来描述，则还可以采用符号表达式來表示信号。

例如对于上述正弦信号，可以用符号对象表示如下:>> x=sin(t);>> ezplot(X);利用ezplot(x)命令可以绘制上述信号的时域波形10.80.60.40.2-0.2-0.4-0.6-0.8-1012345678910Time(seconds)图1 利用向量表示连续时间信号3sin(t)10.5-0.5-1-6-4-20246t图 2 利用符号对象表示连续时间信号常用的信号产生函数函数名功能函数名功能 heaviside 单位阶跃函数 rectpuls 门函数 sin 正弦函数 tripuls 三角脉冲函数 cos 余弦函数 square 周期方波 sinc sinc函数 sawtooth 周期锯齿波或三角波 exp 指数函数2.连续时间信号的时域运算对连续时间信号的运算包括两信号相加、相乘、微分、积分，以及位移、反转、尺度变换(尺度伸缩)等。