初二数学练习反比例函数2013-03-03

反比例函数测试题一、选择题1．反比例函数y ＝－4x 的图象在 （）A ．第一、三象限B ．第二、四象限C ．第一、二象限D ．第三、四象限2．已知关于x 的函数y ＝k （x +1）和y ＝－k x （k ≠0）它们在同一坐标系中的大致图象是（• ）3．已知反比例函数y ＝xk 的图象经过点（m ，3m ），则此反比例函数的图象在 （ ） A ．第一、二象限 B ．第一、三象限C ．第二、四象限D ．第三、四象限4.函数x k y =的图象经过点（－4，6），则下列各点中在xk y =图象上的是（ ） A 、（3，8） B 、（3，－8） C 、（－8，－3） D 、（－4，－6） 5.正比例函数kx y =和反比例函数x k y =在同一坐标系内的图象为（ ）B 6.在同一直角坐标平面内，如果直线x k y 1=与双曲线xk y 2=没有交点，那么1k 和2k 的关系一定是（ ） A 、1k <0，2k >0 B 、1k >0，2k <0 C 、1k 、2k 同号 D 、1k 、2k 异号7.已知 一次函数y=kx+b 的图像经过第一二四象限 则反比例函数xkb y =的图像在（ ）A 第一二象限B 第三 四象限C 第一三象限D 第二三象限y o y o y o yo二、填空题：（3分×10=30分）1、y 与x 成反比例，且当y ＝6时，31=x ，这个函数解析式为 ；2、当路程s 一定时，速度v 与时间t 之间的函数关系是 ；（填函数类型）3、函数2x y -=和函数xy 2=的图象有 个交点； 4、反比例函数xk y =的图象经过（－23，5）点、（a ，－3）及（10，b ）点， 则k ＝ ，a ＝ ，b ＝ ； 5、若函数()()414-+-=m x m y 是正比例函数，那么=m ，图象经过 象限；6、已知y 与x -2成反比例，当x =3时，y =1，则y 与x 间的函数关系式为 ；7、右图3是反比例函数x k y 2-=的图象，则k 的取值范围是 . 8、函数xy 2-=的图象，在每一个象限内，y 随x 的增大而 ； 9、反比例函数xy 2=在第一象限内的图象如图，点M 是图象上 一点，MP 垂直x 轴于点P ，则△MOP 的面积为 ； 10、()522--=m x m y 是y 关于x 的反比例函数，则m 值为 ；（三）解答题1、已知一次函数b kx y +=与反比例函数xm y =的图像交于A （—2 ，1） B （1 ，n ）俩点。

反比例函数测试题一、选择题4〔〕1．反比例函数y＝－的图象在xA．第一、三象限B．第二、四象限C．第一、二象限D．第三、四象限2．关于x的函数y＝k〔x+1〕和y＝－k〔k≠0〕它们在同一坐标系中的大致图象是x〔?〕3．反比例函数y＝k的图象经过点〔m，3m〕，那么此反比例函数的图象在〔〕xA．第一、二象限 B ．第一、三象限C．第二、四象限 D ．第三、四象限4.函数y k4，6〕，那么以下各点中在yk〕的图象经过点〔－图象上的是〔x xA、〔3，8〕B、〔3，－8〕C、〔－8，－3〕D、〔－4，－6〕5.正比例函数y kx和反比例函数k在同一坐标系内的图象为〔〕yy y x y yo x ox o x o xA B C D6.在同一直角坐标平面内，如果直线y k1x与双曲线y k2没有交点，那么k1和k2的x关系一定是〔〕A、k1<0，k2>0B、k1>0，k2<0C、k1、k2同号D、k1、k2异号7.一次函数y=kx+b的图像经过第一二四象限那么反比例函数kby的图像在x〔〕A 第一二象限B第三四象限C第一三象限D第二三象限二、填空题：〔3分×10=30分〕1、y 与x 成反比例，且当 y ＝6时，x1；，这个函数解析式为32、当路程s 一定时，速度 v 与时间t 之间的函数关系是；〔填函数类型〕3、函数yx2的图象有 个交点；和函数y x24、反比例函数 yk的图象经过〔－ 3，5〕点、〔a ，－3〕及〔10，b 〕点，那么k ＝x，b ＝ 2，a ＝；5y 4m 1xm 4是正比例函数，那么m，图象经过象、假设函数限；6、y 与x-2成反比例，当 x=3时，y=1，那么y 与x 间的函数关系式为；7、右图3是反比例函数y k 2的图象，那么k 的取值范围是.x28、函数y的图象，在每一个象限内，y 随x 的增大x而；9、反比例函y 2M 是图象数x 在第一象限内的图象如图，点上一点，MP垂直x轴于点P，那么△MOP的面积为；y10、y m2x m25是y关于x的反比例函数，那么m值为；MO P x 〔三〕解答题1、一次函数y kxb与反比例函数y m的图像交于A〔—2，1〕B〔1，n〕x俩点。

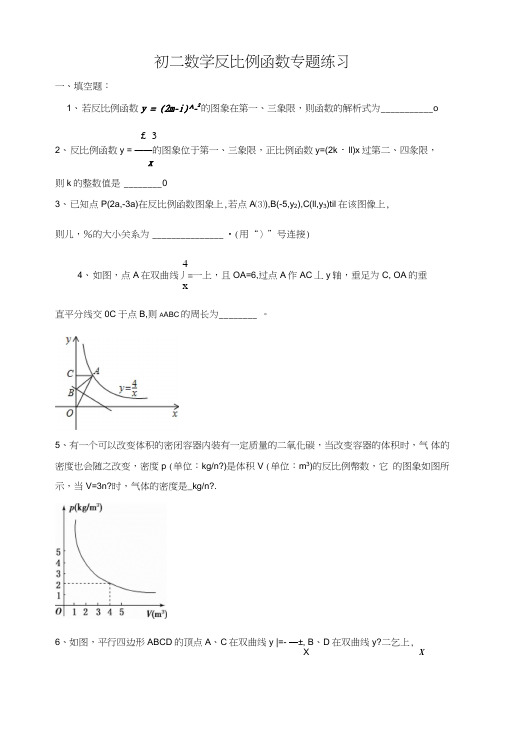
初二数学反比例函数专题练习一、填空题：1、若反比例函数y = (2m-i)^-2的图象在第一、三象限，则函数的解析式为___________ o£_32、反比例函数y = ——的图象位于第一、三象限，正比例函数y=(2k・ll)x过第二、四彖限，x则k的整数值是________ 03、已知点P(2a,-3a)在反比例函数图象上,若点A⑶),B(-5,y2),C(ll,y3)til在该图像上,则儿，％的大小关系为_______________ •(用“〉”号连接)44、如图，点A在双曲线丿=一上，且OA=6,过点A作AC丄y轴，垂足为C, OA的垂x直平分线交0C于点B,则A ABC的周长为________ 。

5、有一个可以改变体积的密闭容器内装有一定质量的二氧化碳，当改变容器的体积时，气体的密度也会随之改变，密度p (单位：kg/n?)是体积V (单位：m3)的反比例幣数，它的图象如图所示，当V=3n?时，气体的密度是_kg/n?.6、如图，平行四边形ABCD的顶点A、C在双曲线y |=- —±, B、D在双曲线y?二乞上,X X7、己知A（xp yj, B（X2, y2）是反比例函数y」图象上的两点，且x r x2=-2, Xi *x2=3, yi-y2=-^»X 3当・3vxWl时，y的取值范围是_______________ .138、如图，直线）^ = -x-3交坐标轴于A、B两点，交双曲线y =—于点D（D在笫一象限），过D2x作两坐标轴的垂线DC、DE,连接0D•将直线AB沿x轴平移，使得四边形OBCD为平行四边形,则平移后直线AB的解析式为________k9、如图，反比例函数y = - （x>0 ）的图象经过矩形OABC对角线的交点，分别与AB、xBC交于点D. E,若四边形ODBC的而积为9,则《的值为（）。

10•函数yi二x （x>0） , y2=-（x>0）的图象如图6所示，则:X(1) 两函数图象的交点A的坐标为(2,2);(2) 当x>2 吋,y2>yi；(3) 当x=l 时,BC=3;⑷当x逐渐增大时,yi随着x的增大而增大,y?随着x的增大而减小.其中正确结论的序号是____________ 11.如图7,己知点A,C在反比例函数尸牛(">0)的图象上，点B,D在反比例函数yg(bv())的图象上，AB//CD//X轴，AB, CD在x轴的两侧，AB二3, CD=2, AB与CD的距离为5,如图8,将边长为8的正三角形OAB放置于平面直角坐标系xOy屮，C是AB边上的动点 (不与端点A, B重合)，作CD丄0B于点D,若点C, D都在双曲线y二£上(k>0, x>0), 则k的值为. 13.己知反比例函数y= ----- 的图象过点(xi，y】)、(X2，y?)，若xi<0<x2时，yi>y2,则k的X取值范围是()A- k<4 B- k>4 C k>0D.无法确定止加热，水温开始下降，此时水温(°C )与开机后用时(min)成反比例关系.直至水温降至30°C, 饮水机关机•饮水机关机后即刻自动开机，重复上述自动程序•若在水温为30°C吋,接通电源后, 水温y (°C)和时间(min)的关系如图，为了在上午第一节下课时(8:45)能喝到不超过50°C 的水，则接通电源的时间可以是当天上午的()A. 7:50B.7:30C.7:45D.7:20三、解答题16.已知双曲线y」与直线丫二衣相交于A、B两点。

初二数学反比例函数复习题班级 姓名典型例题： 一、函数关系式：1.当m= 时，y = m+3x 是反比例函数，任取一个m 值写出这个反比例函数2.已知y 与x+2成反比例，且当x=2时,y=3，求：（1）y 关于x 的函数解析式； （2）当x=-2时的y 值3. 一定质量的二氧化碳，当它的体积时，它的密度（1）求与V 的函数关系式；（2）求当时二氧化碳的密度.二、图像：1.设函数y=（m －2）25m x．（1）当m 取何值时，它是反比例函数？ （2）画出它的图象；2. 甲乙两地相距100km ，一辆火车从甲地开往乙地，把火车到达乙地所用的时间y(h)表示为汽车的平均速度x(km/h)的函数，则这个函数的图象大致是（ ）3．一次函数y=kx －k 与反比例函数xky =在同一直角坐标系内的图象大致( )三、图像的性质1．已知反比例函数xky =的图象经过点A （2，—4）. (1)求k 的值； (2)点B （21，—16）、C （—3，5）在这个函数的图象上吗？(3)画出函数示意图，并指出函数的图象在哪几个象限？y 随x 的增大怎样变化？2．函数xky =与y=ax 的图象的一个交点A 的坐标是(-1，-3)，(1)求这两个函数的解析式；(2)在同一直角坐标系内，画出它们的图象；(3)你能求出这两个图象的另一个交点B 的坐标吗？怎样求？3．如图所示,一个反比例函数的图象在第二象限内,点 A 是图象上的任意一点,AM ⊥x 轴于M,O 是原点,若S △AOM=3,求该反比例函数的解析式,并写出自变量的取值范围.4.如图，是反比例函数y =2- mx的图象的一支．(1) 函数图象的另一支在第几象限？(2) 求常数m 的取值范围．(3) 点A （－3，y1）、B （－1，y2）、C （2，y3）都在这个反比例函数的图象上，比较y1、、y2和y3的大小．（图象法、代人法、增减性法）O A Mxy5.已知反比例函数 y = kx 与一次函数y=mx+b 的图象交于P(－2,1)和Q （1，n ）两点．(1) 求k 、n 的值；(2) 求一次函数y=mx+b 的解析式． (3) 求△POQ 的面积．典型练习：（5分钟）1．（1）下列函数，① 1)2(=+y x ②. 11+=x y ③21x y =④.x y 21-=⑤2x y =-⑥13y x=；其中是y 关于x 的反比例函数的有：_________________． 2．如果反比例函数xmy 31-=的图象位于第二、四象限，那么m 的范围为 ．3. 如图，直线y ＝mx 与双曲线xky =交于A 、B 两点，过点A 作AM ⊥x 轴，垂足为M ，连结BM,若ABM S ∆＝2，则k 的值是（ ） A ．2 B 、m －2 C 、m D 、44.知反比例函数y=xk,当x=1时，y=-8.（1）求k 值，并写出函数关系式； （2）点P 、Q 、R 在反比例函数图象上，填空：P(1， ), Q(2， ), R( ,-8)； （3）点P ′、Q ′、R ′分别是（2）题中点P 、Q 、R 关于原点的中心对称点，写出点P ′、Q ′、 R ′的坐标；课后练习：一、填空1．反比例函数2y x=（0 x ）的图象在第 象限．图象经过P （－2，m ），则 m ＝ . 2．已知反比例函数(0)ky k x=≠的图象经过点(12)-，，则这个函数的表达式是 ___．3．写出一个m 使得反比例函数xm y 3-=的图象在第二、四象限 ．4．若y 是 x 的反比例函数，且当 x ＝3 时，y ＝8，则 y 与 x 的函数关系式为 ．5．已知反比例函数y=kx (k ≠0)与一次函数y=x 的图象有交点, 则k 的范围是______ .6．已知反比例函数xm y 23-=，当______m 时，其图象的两个分支在第二、四象限内；当______m 时，其图象在每个象限内y 随x 的增大而减小．7.对于反比例函数y = kx （k>0），当x 1 < 0< x 2 <x 3时，其对应的值y 1、y 2、y 3的大小关系是 ．8．一个直角三角形的两直角边长分别为y x ，，其面积为2，则y 与x 之间的关系是 。

第一课时[A 组]1、下列函数中，哪些是反比例函数？( )（1）y=-3x ； （2）y=2x+1； （3） y=-x 2；（4）y=3(x-1)2+1； 2、下列函数中，哪些是反比例函数（x 为自变量）？说出反比例函数的比例系数：（1） x y 1-= ；（2）xy=12 ；（3） xy=-13 （4）y=3x3、列出下列函数关系式，并指出它们是分别什么函数．说出比例系数①火车从安庆驶往约200千米的合肥，若火车的平均速度为60千米／时，求火车距离安庆的距离S(千米)与行驶的时间t(时)之间的函数关系式 ②某中学现有存煤20吨，如果平均每天烧煤x 吨，共烧了y 天，求y 与x 之间的函数关系式． 4、.已知一个长方体的体积是100立方厘米，它的长是ycm ，宽是5cm ，高是xcm ． （1） 写出用高表示长的函数式； （2） 写出自变量x 的取值范围； （3） 当x ＝3cm 时，求y 的值5、已知y 与x 成反比例，并且x ＝3时y ＝7，求： （1）y 和x 之间的函数关系式；（2）当13x =时，求y 的值； (3)y ＝3时，x 的值。

7、写出一个经过点（－3，6）的反比例函数 你还能写出另外一个也经过点（－3，6）的双曲线吗？8、当m 为何值时，函数224-=m x y 是反比例函数，并求出其函数解析式．9、已知y 成反比例，且当4b =时，1y =-。

求当10b =时，y 的值。

10:画出下列函数双曲线，y=-x 2的图象，已知点A （-3，a ）、B （－2，b ）,C(4，c)在双曲线，y=-x 2的图象令上，请把[B 组]11、已知函数221()m y m m x -=+，当m 取何值时（1）是正比例函数；（2）是反比例函数。

12、（1）已知y ＝y1＋y2，y1与x 成正比例，y2与x 成反比例， 并且x ＝2和x ＝3时，y 的值都等于 19．求y 和x 之间的函数关系式（2）若y 与2x －2成反比例，且当x=2时，y=1，则y 与x 之间的关系式为13、(03广东)如图1，某个反比例函数的图像经过点P ．则它的解析式（ ）（A ）xy 1=（x ＞0） （B ）x y 1-= （x ＞0）（C ）xy 1=（x ＜0) （D ）x y 1-= （x ＜0)第二课时[A 组]1、xy 3-=的图像叫 ，图像位于 象限，在每一象限内，当x 增大时，则y ；函数4y x=图象在第象限，在每个象限内y 随x 的减少而 2:、根据下列表格中x 与y 的对应值：（1）在直角坐标系中，描点画出图象；（2）试求式。

反比例函数（附答案）一．选择题1、如图，直线l 和双曲线ky x=（0k >）交于A 、B 两点，P 是线段AB 上的点（不与A 、B 重合），过点A 、B 、P 分别向x 轴作垂线，垂足分别为C 、D 、E ，连接OA 、OB 、OP ，设△AOC 的面积为1S 、△BOD 的面积为2S 、△POE 的面积为3S ，则 ( )A ．S S S <<B ．S S S >>C ． S S S =>D ．S S S =<），则此反比例函数表达式为（A ．y x =； B ．y x =-；C ．12y x=；D ．12y x=-.7、已知k ＞0 ，那么函数y=kx的图象大致是 （ 8、在反比例函数y=xm21-的图象上有两点A （x 1,y 1）,B (x 2,y 2),当x 1＜0＜x 2时，有y 1＜y 2,则m 的取值范围是（C ）第6题图第5题A 、m ＜0B 、m ＞0C 、m ＜21 D 、m ＞219、在同一直角坐标系中，函数y=kx+k ，与y=xk-（k 0≠）的图像大致为（ ）10. 如图,某个反比例函数的图象经过点(－1,1),则它的解析式为（ ）A .)0(1>=x x y B .)0(1>-=x x y C .)0(1<=x x y D .)0(1<-=x xy 11. 在函数21-=x y 中，自变量x 的取值范围是（ ）X BC16.函数(0)ky k x=≠的图象过点(22)-，，则此函数的图象在平面直角坐标系中的（ ） A ．第一、三象限 B ．第三、四象限C ．第一、二象限D ．第二、四象限17如图，平面直角坐标系中，OB 在x 轴上，∠ABO ＝90o ，点A 的坐标为(1，2)．将△AOB 绕点A 逆时针旋转90o ，点O 的对应点C 恰好落在双曲线y ＝kx(x ＞0)上，则k ＝（ ）A ．2B ．3C ．4D ．6218.） A ．()m n -，B ．(n ，)nD ．()m n ，19. 在平面直角坐标系中，反比例函数)0(<=k xy 图象的两支曲线分别在（ ）. A. 第一、三象限； B. 第二、四象限； C. 第一、二象限； D. 第三、四象限． 且 ） C.25. 函数xky-=1与x y 2=的图象没有交点，则k 的取值范围为（ ）A ．0<kB ．1<kC ．0>kD ．1>k26.双曲线x 10y=与x6y =在第一象限内的图象依次是M 和N ，设点P 在图像M 上，PC 垂直于X 轴于点C 交图象N 于点A 。

数学反比例函数测试题及试卷答案（时间90分钟 满分100分）班级 学号 姓名 得分一、选择题（每小题3分，共24分）1．如果x 、y 之间的关系是10(0)ax y a -+=≠，那么y 是x 的 （ ） A ．正比例函数 B ．反比例函数 C ．一次函数D ．二次函数2．函数y ＝－4x的图象与x 轴的交点的个数是 （ ）A ．零个B ．一个C ．两个D ．不能确定3．反比例函数y ＝－4x的图象在 （ ）A ．第一、三象限B ．第二、四象限C ．第一、二象限D ．第三、四象限 4．已知关于x 的函数y ＝k （x +1）和y ＝－kx（k ≠0）它们在同一坐标系中的大致图象是（• ）5．已知反比例函数y ＝xk的图象经过点（m ，3m ），则此反比例函数的图象在 （ ） A ．第一、二象限 B ．第一、三象限 C ．第二、四象限 D ．第三、四象限6．某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P （ kPa ） 是气体体积V （ m 3） 的反比例函数，其图象如图所示．当气球内的气压大于120 kPa 时，气球发将爆炸．为了安全起见，气球的体积应 （ ） A ．不小于54m 3B ．小于54m 3C ．不小于45m 3D ．小于45m 33)第6题7．如果点P 为反比例函数xy 4=的图象上一点，PQ ⊥x 轴，垂足为Q ，那么△POQ 的面 积为 （ ） A ．2 B ． 4 C ．6 D ． 8 8．已知：反比例函数xmy 21-=的图象上两点A （x 1，y 1），B （x 2， y 2）当x 1＜0＜x 2时， y 1＜y 2，则m 的取值范围 （ ）A ．m ＜0B ．m ＞0C ．m ＜21 D ．m ＞21二、填空题（每小题2分，共20分）9．有m 台完全相同的机器一起工作，需m 小时完成一项工作，当由x 台机器（x 为不大于m 的正整数）完成同一项工作时，所需的时间y 与机器台数x 的函数关系式是____. 10．已知y 与x 成反比例，且当x 32=-时，y =5，则y 与x 的函数关系式为__________. 11．反比例函数xy 3=的图象在第一象限与第 象限. 12．某食堂现有煤炭500吨，这些煤炭能烧的天数y 与平均每天烧煤的吨数x 之间的函数关系式是 . 13．若nxm y ++=2)5(是反比例函数，则m 、n 的取值是 .14．两位同学在描述同一反比例函数的图象时，甲同学说：这个反比例函数图象上任意一点到两坐标轴的距离的积都是3；乙同学说：这个反比例函数的图象与直线y =x 有两 个交点，你认为这两位同学所描述的反比例函数的解析式是 . 15．在ABC △的三个顶点A （2，－3）、B （－4，－5）、C （－3，2）中，可能在反比例函数(0)ky k x=>的图象上的点是 ． 16．如果反比例函数4ny x-=的图象位于第二、四象限，则n 的取值范围是_______；如果图象在每个象限内，y 随x 的增大而减小，则n 的取值范围是 . 17．如图，△P 1OA 1、△P 2A 1 A 2是等腰直角三角形，点P 1、P 2在函数4(0)y x x=>的图象上，斜边OA 1、A 1 A 2都在x 轴上，则点A 2的坐标是 . 18．两个反比例函数k y x =和1y x=在第一象限内的图象如图所示，点P 在k y x =的图象上，PC ⊥x 轴于点C ，交1y x =的图象于点A ，PD ⊥y 轴于点D ，交1y x =的图象于点B ，当点P 在k y x =的图象上运动时，以下结论： ①△ODB 与△OCA 的面积相等；②四边形PAOB 的面积不会发生变化；③PA 与PB 始终相等；O 12 第17题④当点A 是PC 的中点时，点B 一定是PD 的中点．其中一定正确的是 （把你认为正确结论的序号都填上，少填或错填不给分）． 三、解答题（共56分） 19．（4分）反比例函数xky =的图象经过点A （2 ，3）. （1）求这个函数的解析式；（2）请判断点B （1 ，6）是否在这个反比例函数的图象上，并说明理由.20．（4分）已知三角形的一边为x ，这条边上的高为y ，三角形的面积为3，写出y 与x的函数表达式，并画出函数的图象.21．（4分）如图，一次函数y =kx ＋b 的图像与反比例函数xmy =的图像相交于A 、B 两点， （1）利用图中条件，求反比例函数和一次函数的解析式（2）根据图像写出使一次函数的值大于反比例函数的值的x 的取值范围.22．（6分）某蓄水池的排水管每时排水8 m 3，6h 可将满池水全部排空． （1）蓄水池的容积是多少？（2）如果增加排水管，使每时排水量达到Q （m 3），那么将满池水排空所需的时间t （h ）将如何变化？（3）写出t 与Q 之间的函数关系式．（4）如果准备在5小时之内将满水池排空，那么每时的排水量至少为多少？ （5）已知排水管的最大排水量为每时12m 3，那么最少多长时间可将满池水全部排空？23．（6分）双曲线5y x在第一象限的一支上有一点C （1，5），过点C 的直线y =kx ＋b （k >0）与x 轴交于点A （a ，0）.（1）求点A 的横坐标a 与k 之间的函数关系式；（2）当该直线与双曲线在第一象限内的另一交点D 的横坐标是9时，求△COA 的面积.第21题图24．（6分）已知反比例函数xmy 3-=和一次函数1-=kx y 的图象都经过点m P (，)3m - （1）求点P 的坐标和这个一次函数的解析式；（2）若点M （a ，1y ）和点N （1+a ，2y ）都在这个一次函数的图象上．试通过计算或利用一次函数的性质，说明1y 大于2y25．（6分）近视眼镜的度数y （度）与镜片焦距x （米）成反比例，已知800度近视眼镜镜片的焦距为0.125米， （1）求y 与x 的函数关系；（2）若张华同学近视眼镜镜片的焦距为0.25米，你知道他的眼睛近视多少度吗？26．（6分）对于取消市场上使用的杆秤的呼声越来越高，原因在于一些不法商贩在卖货时将秤砣挖空，或更换较小称砣，使砣较轻，从而欺骗顾客.（1）如图，对于同一物体，哪个图用的是标准秤砣，哪个用的是较轻的秤砣？ （2）在称同一物体时，所称得的物体质量y （千克）与所用秤砣质量x （千克）之间满足关系.（3）当砣较轻时，称得的物体变重，这正好符合哪个函数的哪些性质？27．（6分）联想电脑公司新春期间搞活动，规定每台电脑0.7万元，交首付后剩余的钱数y 与时间t 的关系如图所示：（1）根据图象写出y 与t 的函数关系式. （2）求出首付的钱数.（3）如果要求每月支付的钱数不少于400元，那么还至少几个才能将所有的钱全部还清？图1图2月)y (）28．（8分）如图，直线b kx y +=与反比例函数xk y '=（x ＜0）的图象相交于点A 、点B ，与x 轴交于点C ，其中点A 的坐标为（－2，4），点B 的横坐标为－4. （1）试确定反比例函数的关系式；（2）求△AOC 的面积.新人教八年级（下）第17章《反比例函数》答案一、选择题1．B；2． A；3． B；4． A ；5． B ；6． C ；7．A ；8． C．二、填空题9．y ＝x m 210．152y x=- 11．三 12．y ＝x 500 13．m ≠－5 n ＝－3 14．y ＝x 3 15．B16.n ＞4，n ＜4 17．（0） 18．①②④ 三、解答题 19．（1）y ＝x 6；（2）在 20． y ＝6x ，图像略 21．（1）2y x=-，1y x =--;（2） 2x <-或0x <<1 22．（1）348m ；（2）t 将减小；（3）48t Q=；（4）4859.6Q Q==，；（5）48412t ==23．（1）51a k =-+， （2） 25 24．（1）12--=x y ；（2）略 25．（1）100y x=，（2）400度 26．（1）图②是用与秤配套的秤砣，图①则使用较轻的秤砣.（2）反比例. （3）函数y =x k（k ＞0），当x 变小时，y 增大 27．（1）y ＝t6000 ；（2）7000－6000＝1000（元）；（3）400＝t6000，t ＝15 28．（1）8xy =-；（2）126。

完整版)反比例函数练习题含答案测试1 反比例函数的概念一、填空题1.一般的，形如 y=k/x 的函数称为反比例函数，其中x是自变量，y是因变量。

自变量x的取值范围是x≠0.2.写出下列各题中所要求的两个相关量之间的函数关系式，并指出函数的类别。

1) 商场推出分期付款购电脑活动，每台电脑元，首付4000元，以后每月付y元，x个月全部付清，则y=(8000+)/x，是反比例函数。

2) 某种灯的使用寿命为1000小时，它的使用天数y与平均每天使用的小时数x之间的关系式为 y=1000/x，是反比例函数。

3) 设三角形的底边、对应高、面积分别为a、h、S。

当a=10时，S与h的关系式为 S=10h/2，是正比例函数；当S=18时，a与h的关系式为 h=36/a，是反比例函数。

4) 某工人承包运输粮食的总数是w吨，每天运x吨，共运了y天，则 y=w/x，是反比例函数。

3.下列各函数 y=1/(k2+1)、y=x/(x5+x12)、y=14-3x、y=2x和y=3x-1 中，是y关于x的反比例函数的有：①y=1/(k2+1)、② y=x/(x5+x12)、③ y=2x。

4.若函数 y=m/(x-1) (m是常数) 是反比例函数，则 m=1，解析式为 y=1/(x-1)。

5.近视眼镜的度数y(度)与镜片焦距x(m)成反比例，已知400度近视眼镜片的焦距为0.25m，则 y=1000/x。

二、选择题6.已知函数 y=3x/(kx+1)，当x=1时，y=-3，那么这个函数的解析式是 y=3x/(3k+1)。

(解析：由 y=-3=3/(3k+1) 可得 k=-1/3，代入原式得 y=3x/(3x-1)。

)7.已知 y 与 x 成反比例，当 x=3 时，y=4，那么 y=3 时，x 的值等于 4/3.三、解答题8.已知 y 与 x 成反比例，当 x=2 时，y=3.1) 求y 与x 的函数关系式：y=k/x，代入已知条件得k=6，因此函数关系式为 y=6/x。

第17章反比例函数单元复习测试(时间：120分钟分数：120分) 得分_______ 一、精心选一选，想信你一定能选对！（每题3分，共30分）1．下列函数，①y=2x，②y=x，③y=x-1，④y=11x是反比例函数的个数有（）．A．0个 B．1个 C．2个 D．3个2．反比例函数y=2x的图象位于（）A．第一、二象限 B．第一、三象限 C．第二、三象限 D．第二、四象限3．已知矩形的面积为10，则它的长y与宽x之间的关系用图象表示大致为（）4．已知关于x的函数y=k（x+1）和y=-kx（k≠0）它们在同一坐标系中的大致图象是（• ）．5．已知点（3，1）是双曲线y=kx（k≠0）上一点，则下列各点中在该图象上的点是（）．A．（13，-9） B．（3，1） C．（-1，3） D．（6，-12）6．某气球充满一定质量的气体后，当温度不变时，气球内的气体的气压P（kPa）是气体体积V（m3）的反比例函数，其图象如图所示，当气球内的气压大于140kPa时，•气球将爆炸，为了安全起见，气体体积应（）．A．不大于2435m3 B．不小于2435m3 C．不大于2437m3 D．不小于2437m3(第6题) (第7题)7．某闭合电路中，电源电压为定值，电流I（A）与电阻R（Ω）成反比例，如右图所表示的是该电路中电流I 与电阻R之间的函数关系的图象，则用电阻R表示电流I•的函数解析式为（）．A．I=6RB．I=-6RC．I=3RD．I=2R8．函数y=1x与函数y=x的图象在同一平面直角坐标系内的交点个数是（）．A．1个 B．2个 C．3个 D．0个9．若函数y=（m+2）|m|-3是反比例函数，则m 的值是（ ）．A ．2B ．-2C ．±2D ．×210．已知点A （-3，y 1），B （-2，y 2），C （3，y 3）都在反比例函数y=4x的图象上，则（ ）． A ．y 1<y 2<y 3 B ．y 3<y 2<y 1 C ．y 3<y 1<y 2 D ．y 2<y 1<y 3二、细心填一填，相信你填得又快又准！（每题3分，共27分） 11．一个反比例函数y=k x（k ≠0）的图象经过点P （-2，-1），则该反比例函数的解析式是________． 12．已知关于x 的一次函数y=kx+1和反比例函数y=6x 的图象都经过点（2，m ），则一次函数的解析式是________． 13．一批零件300个，一个工人每小时做15个，用关系式表示人数x•与完成任务所需的时间y 之间的函数关系式为________．14．正比例函数y=x 与反比例函数y=1x的图象相交于A 、C 两点，AB ⊥x 轴于B ，CD•⊥x 轴于D ，如图所示，则四边形ABCD 的为_______．(第14题) (第15题) (第19题)15．如图，P 是反比例函数图象在第二象限上的一点，且矩形PEOF 的面积为8，则反比例函数的表达式是_________．16．反比例函数y=21039n n x --的图象每一象限内，y 随x 的增大而增大，则n=_______．17．已知一次函数y=3x+m 与反比例函数y=3m x -的图象有两个交点，当m=_____时，有一个交点的纵坐标为6． 18．若一次函数y=x+b 与反比例函数y=k x 图象，在第二象限内有两个交点，•则k______0，b_______0，（用“>”、“<”、“＝”填空）19．两个反比例函数y=3x ，y=6x 在第一象限内的图象如图所示，点P 1，P 2，P 3……P 2005，在反比例函数y=6x的图象上，它们的横坐标分别是x 1，x 2，x 3，…x 2005，纵坐标分别是1，3，•5•……，•共2005年连续奇数，过点P 1，P 2，P 3，…，P 2005分别作y 轴的平行线与y=3x 的图象交点依次是Q 1（x 1，y 1），Q 2（x 2，y 2），Q 3（x 3，y 3），…，Q 2005（x 2005，y 2005），则y 2005=________．三、耐心选一选，千万别漏选！（每题4分，共8分，错选一项得0分，•对而不全酌情给分）20．当>0时，两个函数值y ，一个随x 增大而增大，另一个随x 的增大而减小的是（ •）．A ．y=3x 与y=1x B ．y=-3x 与y=1xC ．y=-2x+6与y=1xD ．y=3x-15与y=-1x21．在y=1x的图象中，阴影部分面积为1的有（）．四、用心做一做，培养你的综合运用能力．22．（8分）如图，已知一次函数y=kx+b（k≠0）的图象与x轴、y轴分别交于A、B•两点，且与反比例函数y=mx （m≠0）的图象在第一象限交于C点，CD垂直于x轴，垂足为D，•若OA=OB=OD=1．（1）求点A、B、D的坐标;（2）求一次函数和反比例函数的解析式．23．（10分）如图，已知点A（4，m），B（-1，n）在反比例函数y=8x的图象上，直线AB•分别与x轴，y轴相交于C、D两点，（1）求直线AB的解析式．（2）C、D两点坐标．（3）S△AOC：S△BOD是多少？24．（11分）已知y=y1-y2，y1y与x成反比例，且当x=1时，y=-14，x=4时，y=3．求（1）y与x之间的函数关系式．（2）自变量x的取值范围．（3）当x=14时，y的值．25．（12分）如图，一次函数y=kx+b的图象与反比例函数y=mx的图象交于A、B两点．（1）利用图中的条件，求反比例函数和一次函数的解析式．（2）根据图象写出使一次函数的值大于反比例函数的值的x的取值范围．26．（14分）如图，双曲线y=5x在第一象限的一支上有一点C（1，5），•过点C•的直线y=kx+b（k>0）与x轴交于点A（a，0）．（1）求点A的横坐标a与k的函数关系式（不写自变量取值范围）．（2）当该直线与双曲线在第一象限的另一个交点D的横坐标是9时，求△COA•的面积．答案:1．B 2．D 3．A 4．A 5．B 6．B 7．A 8．B 9．A 10．D11．y=2x 12．y=x+1 13．y= 14．2 15．y=-8x16．n=-3 17．m=5 18．<，> 19．2004．5 20．A 、B 21．A 、C 、D22．解：（1）∵OA=OB=OD=1，∴点A 、B 、D 的坐标分别为A （-1，0），B （0，1），D （1，0）．（2）∵点AB 在一次函数y=kx+b （k ≠0）的图象上， ∴ 解得 ∴一次函数的解析式为y=x+1，∵点C 在一次函数y=x+1的图象上，•且CD ⊥x 轴，∴C 点的坐标为（1，2），又∵点C 在反比例函数y=m x（m ≠0）的图象上， ∴m=2，•∴反比例函数的解析式为y=2x ． 23．（1）y=2x-6；（2）C （3，0），D （0，-6）；（3）S △AOC ：S △BOD =1：1．（2）自变量x 取值范围是x>0．25．解：（1）由图中条件可知，双曲线经过点A （2，1）∴1=，∴m=2，∴反比例函数的解析式为y=2x． 又点B 也在双曲线上，∴n==-2，∴点B 的坐标为（-1，-2）． ∵直线y=kx+b 经过点A 、B ．∴ 解得 ∴一次函数的解析式为y=x-1． （2）根据图象可知，一次函数的图象在反比例函数的图象的上方时，•一次函数的值大于反比例函数的值，即x>2或-1<x<0．26．解：（1）∵点C （1，5）在直线y=-kx+b 上，∴5=-k+b ，又∵点A （a ，0）也在直线y=-kx+b 上，∴-ak+b=0，∴b=ak将b=ak 代入5=-k+a 中得5=-k+ak ，∴a=+1． （2）由于D 点是反比例函数的图象与直线的交点20x 01k b b -+=⎧⎨=⎩11k b =⎧⎨=⎩2m 21-122k b k b =+⎧⎨-=-+⎩11k b =⎧⎨=-⎩5k∴ ∵ak=5+k ，∴y=-8k+5 ③ 将①代入③得：=-8k+5，∴k=，a=10． ∴A （10，0），又知（1，5），∴S △COA =12×10×5=25． 599y y k ak⎧=⎪⎨⎪=-+⎩5959。

初二数学反比例函数练习题反比例函数是数学中的重要概念之一，初二学生在学习数学时常常会遇到反比例函数，并需要解答与之相关的练习题。

本文将为初二数学学习者提供一些关于反比例函数的练习题，帮助他们巩固相关知识点。

练习题1：已知y与x成反比例关系，且当x为2时，y为5.求当x为10时，y的取值。

解答：我们知道反比例关系可以表示为y = k / x，其中k为常数。

根据题目中的条件，我们可以得出：5 = k / 2解方程可得k = 10。

因此反比例函数为y = 10 / x。

当x为10时，代入上述函数中可得：y = 10 / 10y = 1因此，当x为10时，y的取值为1。

练习题2：已知y与x成反比例关系，且当x为3时，y为4.求当y为6时，x的取值。

解答：根据反比例关系的表示式y = k / x，我们可以利用已知条件列方程：4 = k / 3解方程可得k = 12。

因此反比例函数为y = 12 / x。

当y为6时，代入上述函数中可得：6 = 12 / x解方程可得x = 2因此，当y为6时，x的取值为2。

练习题3：已知y与x成反比例关系，且当x为2时，y为10.求当y为3时，x的取值。

解答：根据反比例关系的表示式y = k / x，我们可以利用已知条件列方程：10 = k / 2解方程可得k = 20。

因此反比例函数为y = 20 / x。

当y为3时，代入上述函数中可得：3 = 20 / x解方程可得x = 20 / 3因此，当y为3时，x的取值为20 / 3。

练习题4：已知y与x成反比例关系，且当x为5时，y为7.求当x为8时，y的取值。

解答：根据反比例关系的表示式y = k / x，我们可以利用已知条件列方程：7 = k / 5解方程可得k = 35。

因此反比例函数为y = 35 / x。

当x为8时，代入上述函数中可得：y = 35 / 8因此，当x为8时，y的取值为35 / 8。

通过以上的反比例函数练习题，我们可以巩固和理解反比例关系的概念和求解方法。