脉冲核磁共振实验讲义PPT讲稿

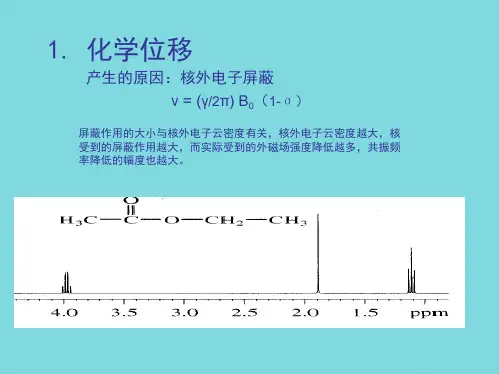
附件材料二脉冲核磁共振实验基本原理核磁共振（NMR ）是一种磁共振现象，是原子核在核能级上的共振跃迁。

利用核磁共振可以测定原子核的磁矩，精确地测量磁场，研究物质结构。

1922年斯特恩（Otto Stern 1888—1969）通过实验，用分子束方法证明了原子核磁矩空间量子化，并为进一步测定质子之类的亚原子粒子的磁矩奠定了基础。

此后，拉比(Isidor Isaac Rabi 1898—1988)发展了分子束磁共振方法，可以精密测量核磁矩和光谱的超精细结构。

1946年布洛赫（Felix Bloch 1905—1983）实现了原子核感应，现称核磁共振（具有磁矩的原子核位于恒定磁场中时，将以一定的角速度围绕磁场轴作进动并最终沿磁场方向趋向。

如果垂直于该恒定磁场外加一弱交变磁场,且当交变磁场的圆频率和恒定磁场满足一定的关系时，核磁矩将会沿着固定轨道绕恒定磁场进动，同时出现能量的最大吸收）。

当年年底，塞尔(Edward Mills Purcell 1912—1997)首次报告了在凝聚态物质中观察到的核磁共振现象。

1943年斯特恩因在发展分子束方法上所作的贡献和发现了质子的核磁矩获得诺贝尔物理学奖。

1944年拉比因用共振方法记录了原子核的磁特性获诺贝尔物理学奖。

1952年布洛赫和塞尔因发展了核磁精密测量的新方法及由此所作的发现分享诺贝尔物理学奖。

在稳态核磁共振的基础上，1950年代出现了脉冲核磁共振方法，得到高灵敏度、高分辨率的核磁共振信号。

核磁共振与计算机结合，发展了许多高新技术。

一般地，连续波核磁共振波谱仪在任一瞬间，只有一种核处于共振状态，而其他核都处于“等待”状态，因此扫描速度慢，这就不利于对一些量小的样品和某些天然丰度小的核进行测定，由于它们必须采取累加的方法，而连续波核磁共振波谱仪扫描速度慢，耗时长，且难于保证信号长期不漂移；脉冲核磁共振波谱仪仪器工作的方式是利用短而强的射频脉冲，使所有的核同时都共振，从而在很短的时间内完成一张谱图的记录。

核磁共振及其成像实验一、引言核磁共振指受电磁波作用的原子核系统在外磁场中磁能级之间发生共振跃迁的现象，1939年首次被拉比在高真空中的氢分子束实验中观察到，之后广泛运用于医学成像领域。

本实验旨在掌握核磁共振基本原理，并利用核磁共振研究硬脉冲及其回波，测量横向弛豫时间，了解几种成像参数对图像的影响。

二、实验原理2.1核磁共振基本原理当一个样品被放在外磁场0B 中时，样品就会被磁化，产生能级分裂现象，所产生的能级间距为：0E B ћγ∆= (1) 若在该样品系统上加上一个射频磁场，当射频场能量等于能级间距时，样品对外加射频能量吸收达到最大，因此得到核磁共振产生的基本条件：00h ћB ћυωγ==(2) 因此得到拉莫尔方程00B ωγ= (3)其中0ω就是产生核磁共振的拉莫尔频率，γ为样品物质的磁旋比，0B 为外加磁场的磁场强度。

2.2自旋回波考虑一个90°-τ-180°-τ采样的脉冲序列。

把一个包含大量自旋数的样品分为610个系综，在每个区域，外磁场分布在一个很窄的范围，每个系综内有一确定的净磁化强度，它们都对总的磁化强度做出贡献。

第一个90°脉冲后，每一个这样的磁化矢量均以稍稍不同的频率作进动，彼此逐渐散相。

经过时间τ后，施之一个双倍宽度的180°脉冲，相位差全部反转，再经过适当时间τ后，所有系综回到同相位状态，总磁化强度达到最大值。

在样品线圈里，感应出“自旋回波”信t存在着采样时间较长的缺点，号，幅度一般小于FID信号。

由于此回波序列测量2故采用90°-τ-180°-2τ-180°-…序列。

2.3弛豫过程t表征由横向弛豫时间：起因于自旋-自旋之间的相互作用。

横向弛豫时间2于非平衡态进动相位相关产生的不为0的磁化强度横向分量M恢复到平衡态时t描述了垂直于磁场方向的核自旋磁矩相位无关所需特征时间。

即横向弛豫时间2恢复到热平衡态的快慢程度。

脉冲核磁共振实验核磁共振技术来源于1939年美国物理学家拉比（I.I.Rabi ）所创立的分子束共振法，他使用这种方法首先实现了核磁共振这一物理思想，精确德测定了一些原子核的磁矩，从而获得了1944年度的诺贝尔物理奖.此后,磁共振技术迅速发展,经历了半个多世纪的而长盛不衰,孕育了多个诺贝尔奖获得者,它还渗透到化学、生物、医学、地学和计量等学科领域,以及众多的生产技术部门,成为分析测试中不可缺少的实验手段.所谓核磁共振,是指磁矩不为零的原子核处于恒定磁场中,由射频或者微波电磁场引起塞曼能级之间的共振跃迁现象.核磁共振现象具有其特点,因此,我们先介绍一些核磁共振的基础知识.一、核磁共振基础知识1． Bloch 方程:1946年Bloch 采用正交线圈感应法观察水的核磁共振信号后就根据经典理论力学推导出Bloch 方程建立核磁共振的唯象理论。

长久以来大量的实验表明Bloch 方程在液体中完全精确，同时还发现Bloch 方程在其他能级跃迁理论也高度吻合，比如激光的瞬态理论中Bloch 方程同样适用。

所以Bloch 方程已经超越了半经典的陀螺模型，现在已经推广到磁共振以外的能级跃迁系统。

在激光物理中采用密度矩阵和Maxwell 方程组推导出Bloch 方程又称为Maxwell-Bloch 方程(有的书称为FHV 表象理论)。

所以Bloch 方程促进了量子力学的发展是非常重要的公式。

由于Maxwell-Bloch 方程推导涉及高等量子力学和量子电动力学等复杂的理论和繁琐的数学基础所以本文采用Bloch 半经典的唯象理论。

（1）半经典理论:将原子核等效为角动量为 L 的陀螺和具有磁矩为L γμ=磁针。

其中γ称为旋磁比。

原子核在外磁场作用下受到力矩 B T⨯=μ (1)并且产生附加能量B E⋅=μ (2)根据陀螺原理 T dt L d=和Lγμ=得B dtd⨯=μγμ(3) 其分量式)()()(y x x y zx z z x y z y y Z xB B dtd B B dt d B B dt d μμγμμμγμμμγμ-=-=-= (4)（2）驰豫过程:驰豫过程是原子核的核磁矩与物质相互作用产生的。

第三章 NMR 实验技术基础4 脉冲技术a 频偏效应(off-resonance effects)由于射频场为单色波，而样品中的化学位移有一定的范围，因此不同的核感受到的有效场也不同。

(1) 脉冲作用对象为Z 磁化向量 在off-resonance 状态，相位y 的脉冲作用于平衡态的z 磁化向量后：M M M M M M x y z ==-=+000221sin sin ;(cos )sin cos ;(cos cos sin )αθαθθθαθ当频偏大时有明显的相位及强度的畸变：tan (cos )cos sin (cos )sin sin βαθααθαγ==-=-⋅-M M B yx 111Ω这个式子适合于分析相位与频偏的关系。

当频偏不大于射频场频率时，90度脉冲后的水平分量的相位与频偏基本上是线性关系，βγτγττπ=-=-=-ΩΩΩB B 190190902 因此不太大的频偏下，实际的90度脉冲可以当成理想的90度脉冲，后跟一段演化期，时间长度为ττπ=290相比之下，有频偏时180度脉冲的效果要差的多，通常需要其他技术来弥补。

90度脉冲的激发曲线的第一个零点位于Ω=±151γB180度脉冲的激发曲线的第一个零点位于Ω=±31γB如蛋白质中C α的化学位移平均在56ppm 左右,而CO 的化学位移在174ppm 左右，若要激发其中之一同时对另一个影响最小，180度方波的功率应选择为1181256738562⨯=.Hz ,对应的脉冲宽度大约58.4μs.(2) 脉冲作用对象为水平磁化向量(nonresonant effects) 频偏较大时射频场的有效磁场接近Z 向，因此横向磁化向量在脉冲期间绕Z 轴有额外的进动，产生相移：φωτNR pt =<>122()Ω此处<>对脉冲串作平均，在多维谱中当τp 随间接维时间变化时（如去偶序列），这个相移在对应的间接维中表现为一个频移ωωNR t =<>122()Ω该图显示的是脉冲宽度58.4 s 的180度脉冲对横向磁化产生的额外相移。