单位脉冲函数及傅里叶变换的性质

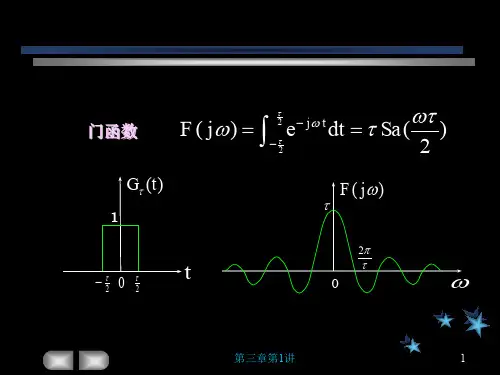
傅⾥叶变换三部曲（⼆）·傅⾥叶变换的定义Part1:傅⾥叶级数的复数形式设f(x)是周期为l的周期函数,若f(x)∼a02+∞∑n=1(a n cosnπxl+bn sinnπxl),an=1l∫l−lf(x)cosnπxl d x,(n=0,1,2,…)bn=1l∫l−lf(x)sinnπxl d x.(n=1,2,…)记ω=πl,引进复数形式:cos nωx=e i nωx+e−i nωx2,sin nωx=e i nωx−e−i nωx2i级数化为f(x)∼a02+∞∑n=1(a ne i nωx+e−i nωx2+bne i nωx−e−i nωx2i)=a02+∞∑n=1(a n−ib n2e i nωx+a n+ib n2e−i nωx)令c0=a02,cn=a n−ib n2,dn=a n+ib n2,则c0=12l∫l−lf(x)d x,c n=12l∫l−lf(x)(cos nωx−isin nωx)d x=12l∫l−lf(x)e−i nωx d x,d n=12l∫l−lf(x)(cos nωx+isin nωx)d x=12l∫l−lf(x)e i nωx d x≜c−n=¯c n,(n=1,2,…)合并为c n=12l=∫l−lf(x)e−i nωx d x,(n∈Z)级数化为+∞∑n=−∞c n e−i nωx=12l+∞∑n=−∞∫l−l f(x)e−i nωx d x e i nωx我们称c n为f(x)的离散频谱(discrete spectrum),|c n|为f(x)的离散振幅频谱(discrete amplitude spectrum),arg c n为f(x)的离散相位频谱(discrete phase spectrum).对任何⼀个⾮周期函数f(t)都可以看成是由某个由某个周期为l的函数f(x)当l→∞时得来的.Part2:傅⾥叶积分和傅⾥叶变换傅⾥叶积分公式设f T(t)是周期为T的周期函数,在[−T2,T2]上满⾜狄利克雷条件,则f T(t)=1T∞∑n=−∞∫T2−T2f T(t)e−j nωt d t e j nωt,ω=2πT(上式中j是虚数单位,在傅⾥叶分析中我们不⽤i⽽通常记作j)由limT→∞f T(t)=f(t)知,f(t)=limT→∞1T∞∑n=−∞[∫T2−T2f T(t)e−j nωt d t]e j nωt记Δω=2πT,则Δω→0⇔T→∞,则f(t)=limT→∞1T∞∑n=−∞[∫T2−T2f T(t)e−j nωt d t]e j nωt=limΔω→012π+∞∑n=−∞∫T2T2f T(t)e−j nωt d t e j nωtΔω[][][]令F T(nω)=∫T2−T2f T(t)e−j nωt d t,则f(t)=limΔω→012π+∞∑n=−∞F T(nω)e j nωtΔω,F T(t)→∫+∞−∞f(t)e−jωt d t≜F(ω)(T→∞),由定积分定义f(t)=12π∫+∞−∞F(ω)e jωt dω,即f(t)=12π∫+∞−∞∫+∞−∞f(t)e−jωt d t e jωt dω上述公式称为傅⾥叶积分公式.傅⾥叶积分存在定理若f(t)在任何有限区间上满⾜狄利克雷条件,且在R上绝对可积,则12π∫+∞−∞∫+∞−∞f(t)e−jωt d t e jωt dω=f(t),t为连续点,f(t−)+f(t+)2,t为间断点.傅⾥叶变换设f(t)满⾜傅⾥叶积分存在定理,定义F(ω)=∫+∞−∞f(t)e−jωt d t 为f(t)的傅⾥叶变换(Fourier Transform)(实际上是⼀个实⾃变量的复值函数),记作F(ω)=F[f(t)]类似地,定义f(t)=12π∫+∞−∞F(ω)e−jωt dω为F(ω)的傅⾥叶逆变换(Inverse Fourier Transform),记作f(t)=F−1[F(ω)]在⼀定条件下,有F[f(t)]=F(ω)⇒F−1[F(ω)]=f(t);F−1[F(ω)]=f(t)⇒F[f(t)]=F(ω). f(t)与F(ω)在傅⽒变换意义下是⼀个⼀⼀对应,称f(t)与F(ω)构成⼀个傅⽒变换对,记作f(t)F↔F(ω)在不引起混淆的情况下,简记为f(t)↔F(ω).f(t)称为原象函数(original image function),F(ω)称为象函数(image function).在频谱分析中,F(ω)⼜称为f(t)的频谱(密度)函数(spectrum function),|F(ω)|称为f(t)的振幅频谱(amplitude spectrum),arg F(ω)称为f(t)的相位频谱(phase spectrum).下⾯我们来求⼏个常见信号函数的傅⽒变换.例1 求矩形脉冲函数(rectangular pulse function)R(t)=1,|t|≤1, 0,|t|>1的傅⽒变换及其频谱积分表达式.解:F(ω)=F[R(t)]=∫+∞−∞R(t)e−jωt d t=∫1−1R(t)e−jωt t=e−jωt−jω1−1=−e−jω−e jωjω=2sinωω;R(t)=12π∫∞−∞F(ω)e jωt dω=1π∫+∞F(ω)cosωt dω=1π∫+∞2sinωωcosωt dω=2π∫+∞sinωcosωtωdω=1,|t|<1, 12,|t|=1, 0,|t|>1因此可知,当t=0时,有[] []{{ []{∫+∞0sin t xd t =π2例2 求指数衰减函数(exponential decay function)E (t )=0,t <0,e −βt ,t ≥0的傅⽒变换及其频谱积分表达式,其中β>0为常数.解:F (ω)=F [E (t )]=∫+∞−∞E (t )e −j ωt d t=∫+∞0e −βt e −j ωtd t =∫+∞0e (β+j ω)t d t =1β+j ωβ−j ωβ2+ω2E (t )=12π∫+∞−∞F (ω)e j ωt ω=12π∫+∞−∞β−j ωβ2+ω2e j ωtω=1π∫+∞βcos ωt +ωsin ωtβ2+ω2d ω=0,t <0,12,t =0,e −βt ,t >0Part3:单位脉冲函数我们记电流脉冲函数q (t )=0,t ≠0,1,t =0,严格地,由于q (t )在t =0出不连续,所以q (t )在t =0点是不可导的.但是,如果我们形式地计算这个导数,有q ′(0)=limΔt →0q (0+Δt )−q (0)Δt=limΔt →0−1Δt=∞我们引进这样⼀个函数,称为单位脉冲函数(unit pulse function)或狄拉克(Dirac)函数,简记为δ−函数,即δ(t )=0,t ≠0,∞,t =0,⼀般地,给定⼀个函数序列δε(t )=0,t <0,1ε,0≤t ≤ε,0,t >ε则有δ(t )=lim ε→0δε(t )=0,t ≠0,∞,t =0于是∫+∞−∞δ(t )d t =limε→0∫+∞−∞δεd t =limε→0∫ε01εd t =1若设f (t )为连续函数,则δ−函数有以下性质:∫+∞−∞δ(t )f (t )d t =f (0);∫+∞−∞δ(t −t 0)f (t )d t =f (t 0)于是我们可得:F [δ(t )]=∫+∞−∞δ(t )e −j ωt t =e −j ωt t =0=1于是δ(t )与常数1构成了⼀对傅⾥叶变换对.例3: 证明:e j ω0t ↔2πδ(ω−ω0)其中ω0是常数.证:{{{{{{|f(t)=F−1[F(ω)]=12π∫+∞−∞2πδ(ω−ω0)e jωt dω=e jωtω=ω=e jω0t在物理学和⼯程技术中,有许多重要函数不满⾜傅⽒积分定理中的绝对可积条件,即不满⾜条件∫+∞−∞|f(t)|d t<∞例如常数,符号函数,单位阶跃函数以及正,余弦函数等, 然⽽它们的⼴义傅⽒变换也是存在的,利⽤单位脉冲函数及其傅⽒变换就可以求出它们的傅⽒变换.所谓⼴义是相对于古典意义⽽⾔的,在⼴义意义下,同样可以说,原象函数f(t)和象函数F(ω)构成⼀个傅⽒变换对.例求正弦函数f(t)=sinω0t的傅⽒变换.解:F(ω)=F[f(t)]=∫+∞−∞f(t)e−jωt d t=∫+∞−∞e jω0t−e−jω0t2je−jωt d t=12j∫+∞−∞e−j(ω−ω0)t−e−j(ω+ω0)t d t=jπδ(ω+ω0)−δ(ω−ω0)同样我们易得F(cosω0t)=πδ(ω+ω0)+δ(ω−ω0)例证明:单位阶跃函数(unit step function)u(t)=0,t<0, 1,t>0的傅⽒变换为F[u(t)]=1jω+πδ(ω)证:F−11jω+πδ(ω)=12π∫+∞−∞1jω+πδ(ω)e jωt dω=12π∫+∞−∞[πδ(ω)]e jωt dω+12π∫+∞−∞1jωe jωt dω=12+12π∫+∞−∞cosωt+jsinωtjωdω=12+12π∫+∞−∞sinωtωdω=12+1π∫+∞sinωtωdω∫+∞0sinωtωdω=π2,t>0,−π2,t<0⇒F−11jω+πδ(ω)=12+1π−π2=0,t<012,t=0,12+1ππ2=1,t>0=u(t).本⽂完|()[][]{[][][][][][] { []{()()。

f(t)=δ(t)求导的傅里叶变换傅里叶变换（Fourier Transform）是一个重要的数学工具，可以将一个函数从时域（时间域）转换到频域（频率域），并且傅里叶变换的性质在信号与系统、图像处理、通信等领域具有广泛的应用。

本文将讨论函数f(t) = δ(t)的傅里叶变换。

首先，我们需要了解一下脉冲函数δ(t)。

脉冲函数是一种非常特殊的函数，它在原点处为无穷大，其他位置为零，且满足积分等于1。

简单地说，脉冲函数在原点处集中了无穷小的能量。

脉冲函数在信号处理中有很多应用，例如用于描述一个瞬间发生的事件、用于模拟信号的表示等。

在实际应用中，由于脉冲函数在无穷小时间间隔内具有无穷大的幅度，因此脉冲函数是一个理论构建的函数，并不能在物理上实现。

然而，脉冲函数的数学表示和性质非常重要，并且可以通过极限过程近似实现。

现在，我们来计算f(t) = δ(t)的傅里叶变换。

根据傅里叶变换的定义，我们可以得到函数F(ω)的表达式：F(ω) = ∫[f(t)·e^(-jωt)]dt其中，j是虚数单位，ω是频率变量。

对于我们要计算的f(t) = δ(t)，将其代入上述公式中，可以得到：F(ω) = ∫[δ(t)·e^(-jωt)]dt现在，我们需要解决积分中的问题。

脉冲函数δ(t)在原点处是无穷大，那么如何处理这个积分呢？事实上，脉冲函数δ(t)具有一个重要的性质，即它在积分号下的函数中，只有在t = 0时才有非零值。

这意味着在实际积分过程中，我们只需要关注t = 0的情况即可。

因此，将t = 0代入积分式中，可以得到：F(ω) = ∫[δ(t)·e^(-jωt)]dt= δ(0)·e^(-jω·0)= e^0= 1由此可见，函数f(t) = δ(t)的傅里叶变换结果为F(ω) = 1。

这意味着在频域中，目标函数f(t) = δ(t)的幅度为常数1，与频率无关。

值得注意的是，由于脉冲函数δ(t)在原点处只有一个非零值，因此f(t) = δ(t)在时间域中的长度为零，也即是一个无限短的脉冲。

傅里叶变换基础知识1•傅里叶级数展幵最简单有最常用的信号是谐波信号，一般周期信号利用傅里叶级数展开成多个乃至无穷多个不同频率的谐波信号，即一般周期信号是由多个乃至无穷多个不同频率的谐波信号线性叠加而成。

1.1周期信号的傅里叶级数在有限区间上，任何周期信号双/）只要满足狄利克雷（dmclilet）条件，都可以展开成傅里叶级数。

1・1・1狄利克雷（duichlet）条件狄利克雷（duichlet）条件为：（1）信号双/）在一个周期内只有有限个第一类间断点（当t从左或右趋向于这个间断点时，函数有左极限值和右极限值）；（2 ）信号/ （t）在一周期内只有有限个极人值和极小值；（3 ）信号在一个周期内是绝对可积分的，即应为有限值。

1.1.2间断点在非连续函数y二f{・x）中某点处心处有中断现彖，那么，兀就称为函数的不连续点。

（1）第一类间断点（有限型间断点）：a.可去间断点：函数在该点左极限、右极限存在且相等，但不等于该点函数值或函数在该点无定义（兀令分母为零时等情况）；b.跳跃间断点：函数在该点左极限、右极限存在，但不相等（y = lxl/x°在点x = 0处等情况）。

（2）第二类间断点：除第一类间断点的间断点。

1.13傅里叶级数三角函数表达式傅里叶级数三角函数表达式为X X0=仇+乞（①cos“q/ +加• • •J1-1式中：心为信号的常值分量；色为信号的余弦信号幅值：你为信号的正弦信号幅值。

％、心、》分别表示为：==J ：） cosncootdtx{ t ）sinncootdt式中：7；为信号的周期；。

为信号的基频，即角频率，$=2龙/7；「=1,2,3...。

合并同频项也可表示为X （t）二％ + 艺 A cos （gf + q）H-l式中：信号的幅值人和初相位q分别为人=虫+丐2 =arcnm （・b” /心）1.1.4频谱的相矢概念（1） 信号的频谱（三角频谱）：构成信号的各频率分量的集合，表征信号的幅值和相位随频率的变化矢系，即信号的结构，是（或&・/）和q 厂3 （或2・/）的统称；（2） 信号的幅频谱：周期信号幅值人随e （或/）的变化尖系，用（或A ・/>表示； （3） 信号的相频谱：周期信号相位仇随e （或f ）的变化矢系，用0,弋。

第 6 章 积分变换积分变换就是通过含参变量积分 ()(,)()d baF s K s x f x x=ò 将一个已知函数 ) (x f 变为 另一个函数 ) (s F ．积分变换理论不仅在数学诸多分支中得到广泛应用，而且在许多科学技 术领域中，例如：物理学，力学，现代光学，无线电技术和信号处理等方面，作为一种研究 工具发挥着重要作用．傅里叶变换和拉普拉斯变换是最重要的积分变换．6.1 傅里叶变换在讨论傅里叶变换之前，我们有必要先来回顾一下傅里叶级数展开．6.1.1 傅里叶级数1804 年，傅里叶首次提出“在有限区间上由任意图形定义的任意函数都可以表示为单纯的正弦与余弦之和” ，但并没有给出严格的证明．1829 年，由法国数学家狄利克雷 （Dirichlet ）证明了下面的定理，为傅里叶级数奠定了理论基础．定理 6．1 设 ) (t f T 是以T 为周期的实值函数，且在[ 2,2 TT - ]上满足狄利克雷条件， 即 ) (tf T 在[ 2,2 TT - ]上满足 （1） 连续或只有有限个第一类间断点， （2） 至多只有有限个极值点． 则在 ) (tf T 连续点处有 å +¥= + + = 10 0 0) sin cos ( 2 ) ( n n n T t nb t n a a t f w w ， （6­1）其中Tp w 2 0 = ，2 0 22 ()d TT T a f t t T - = ò ，2 0 2 2 ()cos d TT n T a f t n t t T - = ò w ， 2 0 22 ()sin d TT n T b f t n t t T - = ò w (1,2,) n = L ．在间断点 0 t 处，（6­1）式左端为 00 1[(0)(0)] 2T T f t f t ++- ．我们称（6­1）式为傅里叶级数的三角形式．由于正弦函数与余弦函数可以统一地由指数函数表示， 因此我们可以得到另外一种更为 简洁的形式，即傅里叶级数的复指数形式，具体形式如下0 () jn t T n n f t c e w +¥=-¥= å ，（6­2）2 21 ()d T jn tT n T c f t et T w - = ò (0,1,2) n =±± L ．（6­3）其中 n a ， n b ， n c 的关系由欧拉公式 0 00 cos sin jn ten t j n t ± =± w w w (1) j =- 可知： 00 , 2a c =2 n n n a jb c - =， 2n nna jbc - + = (1,2,) n = L ．傅里叶级数有非常明确的物理意义．事实上，在（6．1）式中，令0 2a A =， 22 n n n A a b =+ ， cos nn n a A q =， sin n n n b Aq - = (1,2,) n = L ，则（6­1）式变为å+¥= - + = 10 0 0 ) sin sin cos (cos ) ( n n n T t n t n A t f w q w q å +¥= + + = 10 0 ) cos(n n n t n A A q w ． 如果以 ) (t f T 代表信号，则上式说明，一个周期为T 的信号可以分解成无穷多种频率成 份的简谐波的叠加．这些谐波的频率基频 0 w 的倍数．由此可见，信号 ) (t f T 本身不含有各 种频率成份，而仅由一系列具有离散频率的谐波所构成，其中 n A 反映了频率为 0 n w 的谐波 在 ) (t f T 中所占的份额，称为振幅； n q 则是频率为 0 n w 的谐波沿时间轴移动的大小，称为相 位．这两个指标完全刻画了信号 ) (tf T 的形态． 再来看看（6­2）式，由 n c 与 n a 及 n b 的关系可得00 c A = ，arg arg n n n c c q - =-= ，221 22n n n A c c a b - ==+= (1,2,) n = L ．因此 n c 作为一个复数，其模与辐角正好反映了频率为 0 n w 的简谐波的振幅与相位，其 中振幅 n A 被平均分配到正负频率上，而负频率的出现完全是为了数学表示的方便，它与正 频率一起构成同一个简谐波． 因此， 仅由系数 n c 就可以完全刻画了信号 ) (t f T 的频率特性． 我 们称 n c 为周期函数 ) (t f T 的离散频谱， n c 为离散振幅谱，arg n c 为离散相位谱．为进一步 明确 n c 与频率 0 n w 的对应关系，常常记 0 () n F n c w = ．例 1 脉冲矩形波的信号函数 ) (t f 是以2p 为周期的周期函数，它在[,] p p - 上的表达 式为1,0() 1,0 t f t t p p ì--£< ï = í<£ ï î如何将函数展开为傅里叶级数的三角形式．解由定理 6．1 可得1 0 = w ， 0 0 = a ， 0 = n a (1,2,) n =L ， 0 12 ()sin sin n b f t ntdt ntdt ppp p p- ==òò 0 22 (cos )(1cos ) nt n n n =-=- pp p p4,1,3,5,, 2 [1(1)] 0,2,4,6,. n n n n n ì = ï =--= í ï = îLL p p 于是，函数 ) (t f 的傅里叶级数的三角形式为 å ¥= - - =1 1 2) 1 2 sin( 4) ( n n tn t f p ． 例 2 求以T 为周期的脉冲信号函数0,20 () 2,02 T T t f t t T ì -<< ï = í<< ï î的离散频谱和它的傅里叶级数的复指数形式．解 令 Tpw 2 0 =，当 0 = n 时， = = ) 0 ( 0F c 220211 ()d 2d 1; T TT T f t t t TT - == òò ;当 0 ¹ n 时，) ( 0 w n Fc n = 0 2 2 1 ()d Tjn tT T f t e t T - - = ò w 0 202 d T jn t e t T w - = ò (1) jn j e n p p - =- 2 ,1,3,5,, 0,2,4,6,. jn n n pì -= ï = í ï = îL L 脉冲信号函数 ) (tf T 的傅里叶级数的复指数形式为 0 (21) 2 ()1 (21) j n t T n jf t e n w p +¥- =-¥ - =+ -å． 6.1.2 傅里叶积分与傅里叶变换通过前面的的讨论，我们知道了一个周期函数可以展开为傅里叶级数，那么，对非周期 函数是否同样适用呢？请看下面的案例分析．[引例 6．1] 如何将非周期函数 ) (t f 展开为傅里叶级数呢？ 分析对于一般的非周期函数 ) (t f ，我们可以另外定义一个相应的周期函数 ) (t f T ，使它在一个周期 ]2,2 [ TT - 上与周期函数 ) (t f 完全相同，其余区间上按周期T 延拓出去，即 (),[2,2], () (),[2,2].T T f t t T T f t f t T t T T ì Î- ï = í+Ï- ï î 显然，其周期T 取得越长，周期函数 ) (t f T 越接近非周期函数 ) (t f ，设想让周期T 趋于无 穷大时，我们定义的周期函数 ) (tf T 就完全等于非周期函数 ) (t f ，即 ()lim () T T f t f t ®+¥= ．可 见非周期函数可以看作周期为无穷大周期函数．这是解决问题的核心思想．1．傅里叶积分公式将非周期函数 ) (t f 看作是由周期函数 ) (t f T 当T ®+¥时转化来的， 有 （6­2） 式与 （6­3） 式有()lim () T T f t f t ®+¥ = 00 22 1 lim [()d ] T jn jn tT T T n f e e T+¥- - ®+¥=-¥ = å ò w t w t t 02 02 lim[()d ] 2T jn jn t T T T n f e e +¥- - ®+¥=-¥= å ò w t w w t t p ．当T 趋于无穷大时，频率间隔 Tpw 2 0 =变成无穷小的频率微分d w ，离散频率 0 n w 变 成连续变化的频率 n w ，记 0 w w =D ， 0 n n w w = ，得2 20 1()lim [()d ] 2 n n T j jn t T T n f t f e e w t w w t t w p +¥ - - D ® =-¥ =× D å ò ．这是一个和式的极限，按照积分定义，在一定条件下，上式可写为1 ()[()d ]d2 j j tf t f e e wt w t t w p+¥+¥ - -¥-¥ =òò ． （6­4）由此得到下面的定理．定理 6．2（傅氏积分定理） 如果 ) (t f 在 ) , ( +¥ -¥ 上的任一有限区间满足狄利克雷条件， 且在 ) , ( +¥ -¥ 上绝对可积（即()d f t t +¥-¥<+¥ ò），则（6．4）式成立．在 ) (t f 的间断点 处，（6­4）式的左端应为 00 1 [(0)(0)] 2T T f t f t ++- ．称（6­4）式为傅里叶积分，简称傅氏积分． 2． 傅里叶变换 从（6­4）式出发，令()()d j t F f t e t w w +¥- -¥= ò ,（6­5）则有1 ()()d2 j t f t F e w w w p +¥-¥= ò ．（6­6）可以看出，由（6­5）式与（6­6）式定义了一个变换对，即对于任一已知函数 ) (t f ，通 过指定的积分运算，可以得到一个与之对应的函数 () F w ； 而由 () F w 通过类似的积分运算， 可以回复到 ) (t f ．它们具有非常优美的对称形式，并且还具有明确的物理意义和极好的数 学性质．由于它们是从傅里叶级数得来的，因此我们给出如下定义．定义 6．1 称（6­5）式为傅里叶变换（简称傅氏变换），其中函数 () F w 称为 ) (t f 的 像函数，记为 ()[()] F f t w =F ；称（6­6）式为傅里叶逆变换（简称傅氏逆变换），其中函 数 ) (t f 称为 () F w 像原函数，记为 1 ()[()] f t F - =w F ．这样， ) (t f 与 () F w 构成一个傅氏变换对．与傅里叶级数一样，傅氏变换也明确的物理意义． 在频谱分析中， 傅氏变换 () F w 又称 ) (t f 的频谱函数， 而它的模 () F w 称为 ) (t f 的 振幅谱，称arg () F w 为 ) (t f 的相位谱．由于傅氏变换这种特殊的物理意义，因而在工程实 际中得到广泛地应用．例 3 求矩形脉冲函数 1,1 () 0,1 t f t t ì £ ï= í > ï î的傅氏变换与傅氏表达式．解 1111()()d d j tj t j t eF f t e t e t j - +¥-- -¥- - ===- òò w w w w w ( ) 12sin j j e e j - =--= w w ww w． 1 ()()d 2 j tf t F e w w w p +¥ -¥ =ò 12sin d 2 j t e w w w p w +¥ -¥ = ò 12sin 2sin cos d sin d 22 j t t +¥+¥ -¥-¥ =+ òò w w w w w w p w p w 02sin cos d t +¥ = ò w w w pw．由傅氏积分定理可知 0 2,||1,sin cos d 4,||1, 0,|| 1.t tt t +¥ ì < ï == í ï > îò p w w w p w 上式中当 0 t = 可得重要积分公式 0 sin d 2x x x +¥ = ò p． 例 4 求单边指数衰减函数 0,0 () ,0t t f t e t -b ì < ï= í ³ ï î (0) b > 的频谱函数、振幅谱、相位谱．解 由傅氏变换物理意义可知，) (t f 的频谱函数()[()]()d j t F f t f t e t+¥-w -¥w == ò F () 0d j te t+¥-b+w = ò 22 1 j j b -w == b +w b +w,) (t f 的振幅谱 221 () F w =b +w，) (t f 的相位谱arg ()arg() F w =-w b ．6.1.3 单位脉冲函数（d 函数）及其傅里叶变换傅里叶级数与傅里叶变换以不同的形式反映了周期函数与非周期函数的频谱特性， 是否 可以借助某种手段将它们统一起来呢？更具体地说， 是否能够将离散频谱以连续频谱的方式 表现出来呢？这就需要引入下面将要介绍的单位脉冲函数及其傅里叶变换． 在物理和工程技 术中, 常常会碰到单位脉冲函数． 因为有许多物理现象具有脉冲性质, 如在电学中, 要研究 线性电路受具有脉冲性质的电势作用后产生的电流; 在力学中, 要研究机械系统受冲击力作 用后的运动情况等． 而这些物理量都不能用通常的函数形式来表示．[引例 6.2] 在原来电流为零的电路中, 某一瞬时(设为 0 t = )进入一单位电量的脉冲, 现在要确定电路上的电流 ) (t i ．分析以 ) (t q 表示上述电路中的电荷函数, 则0,0; () 1,0.t q t t ¹ ì= í= î 0 d ()()() ()lim d t q t q t t q t i t t tD ® +D - == D , 当 0 t ¹ 时, 0 ) ( = t q , 由于 ) (t q 是不连续的, 从而在普通导数意义下, ) (t q 在这一点是不 能求导数的．如果我们形式地计算这个导数, 则得00 (0)(0)1 (0)limlim t t q t q i t t D ®D ® +D - æö==-=¥ ç÷ D Dèø ．这表明在通常意义下的函数类中找不到一个函数能够表示这样的电流强度．为了确定这样的电流强度, 我们需要引入一个新的函数，即所谓的单位脉冲函数，又称 为狄拉克函数或d 函数：0,0; () ,0.t t t ¹ ì = í¥= î d 有了这种函数, 对于许多集中于一点或一瞬时的量, 例如点电荷, 点热源, 集中于一点 的质量及脉冲技术中的非常窄的脉冲等, 就能够象处理连续分布的量那样, 以统一的方式加 以解决．对于函数 0,0()1,0, ,0 t t t t e ì < ïd =e ££e í ï ¥> î我们定义 0 0,0, ()lim () ,0 t t t t ® ¹ ì == í ¥= î e e d d ．此时有 0 00 1 ()d lim ()d lim d 1 t t t t t +¥+¥ e e -¥-¥ e®e® d =d == e òòò．在图形上，人们常常用一个从原点出发长度等于 1的有向线段表示d 函数, 这个线段的 长度表示d 函数的积分值, 称为d 函数的冲击强度．1．d 函数的性质：性质 6.1 设 ) (t f 是定义在 ) , ( +¥ -¥ 上的有界函数，且在 0 t = 处连续，则()()d (0) t f t t f +¥-¥d = ò ．（6­7）一般地，若 ) (t f 在 0 t t = 点连续，则00 ()()d () t t f t t f t +¥-¥d -= ò．（6­8）性质 6．2 d 函数为偶函数，即 ()() t t =- d d ．2． d 函数的傅氏变换根据d 函数的定义及性质，我们可以容易得出d 函数的傅氏变换为()[()]()d 1 j t j tt F t t e t e+¥-w -w = -¥ w =d =d == ò F ．显然， () t d 与常数 1 构成了一傅氏变换对，按逆变换公式有1 1 ()[()]d2 j tt F e w d w w p+¥ - -¥ ==ò F ． 由上式可得d 2() j te t w w pd +¥-¥= ò．（6­9）这是一个关于d 函数的重要公式．例 5 证明：1和2() pd w 构成傅氏变换对． 证 由傅氏变换的定义及（6­9）式得[ ] ()11d d 2() j t j F e t e +¥+¥-w wt -¥-¥w ==×=t =pd w òò F ．例 6 求函数 0 () j tf t e= w 的傅氏变换．解 由傅氏变换的定义及（6­9）式得0 ()[()]d j t j t F f t e e t+¥- -¥== ò w w w F 0 () 0 d 2()j t e t +¥- -¥==- ò w w pd w w 0 2() =- pd w w ．例 7 求正弦函数 0 ()sin f t t =w 的傅氏变换．解0 ()[()]sin dj t F f t e t t +¥- -¥== ò w w w F 00 1 ()d 2 j tj t j t e e e t j+¥- - -¥ =- ò w w w 00 ()() 1 ()d 2 j t j te e t j+¥ --+ -¥ =- ò w w w w 00 [()()]j =+-- p d w w d w w ． 例 8 试证单位阶跃函数 0,0 () 1,0t u t t ì < ï= í> ï î的傅氏变换为1() j +pd w w． 证 设 1()() F j w =+pd w w， 1 ()[()] u t F - =w F ，则 11()(())d 2j t u t e j w pd w w p w+¥-¥=+ ò111 ()d d 22j tj te e j w w d w w w p w+¥+¥-¥-¥=+ òò11sin d 2 t+¥=+ òw w pw．由例 3 可知sin d 2 x x x +¥= òp ，所以有 0,0, () 1,0.t u t t ì < ï= í > ï î6.1.4 傅里叶变换的性质这里介绍傅氏变换的几个重要性质, 为了叙述方便起见, 假定在这些性质中, 凡是需要 求傅氏变换的函数都满足傅氏积分定理中的条件, 在证明这些性质时, 不再重述这些条件．1．线性性质设 ()[()] F f t w =F ， ()[()] G g t w =F ， , a b 为常数，则[()()]()() f t g t F G +=+ a b a w b w F ， 1 [()()]()() F G f t g t - +=+ a w b w a b F ．2．位移性质设 ()[()] F f t w =F ， 00 , t w 为实常数，则0 0 [()]() j t f t t e F - -= w w F ,（6­10）0 1 0 [()]() j tF ef t - -= w w w F ． （6­11）证 由定义有00 [()]()d j t f t t f t t e t +¥-¥-=- òw F ，作变量替换 10 t t t =- 得10 () 011 [()]()d j t t f t t f t e t+¥-- -¥-= ò w F 0 1 11 ()d j t j t e f t e t+¥- - -¥= ò w w 0() j t e F - = w w ．类似可证（6­11）式．3．相似性质设 ()[()] F f t w =F ，a 为非零实常数，则1 [()]() f at F a aw=F ． （6­12）证1 ()d ,0 [()]()d 1 ()d ,0sj a s at j t s j a f s e s a af at f at e t f s e s a a - +¥= +¥ -¥ - -¥- -¥ +¥ì > ï ï = í ï < ï î ò = ò ò w w w F 11 ()d () jsaf s es F aa a- +¥-¥==òw w． 例 9 计算 [(52)] u t - F ．解法 1 （先用相似性，再用平移性）令 ()(2) g t u t =- ，则 (5)(52) g t u t =- ，得51[(52)][(5)][()] 5 u t g t g t -== wF F F 2 5 511 [(2)][()] 55 j u t e u t - æö=-= ç÷ èø w w wF F 2 511 () 5 j e j w w pd w w - ìü éù =+ íý êú ëû îþ2 5 15 () 55 j e j - éù =+ êú ëû ww pd w． 解法 2 （先用平移性，再用相似性）令 ()(5) g t u t = ，则 2 ()(52) 5g t u t -=- ，得2[(52)][()] 5u t g t -=- F F 2 5 [()] j e g t - = w F ( )25 [(5)] j e u t - = w F 2 551 [()] 5 j eu t - æö= ç÷ èø ww F 25 511 () 5 j e j - éù =+ êú ëû w wpd w w 25 15 () 55 j e j - æö=+ ç÷ èøw w pd w ． 4．微分性质若 [()]() f t F = w F ，且 lim ()0 t f t ®+¥= ，则[()]()f t j F ¢ = w w F （6­13）一般地，若 ()lim ()0 k t ft ®+¥= (0,1,2,1) k n =- L ，则() [()]()() n n f t j F = w w F ．（6­14）同样还能得到像函数的导数公式为' ()[()] F j tf t w =- F ，一般地，有() ()()[()] n n n F j t f t w =- F ．当 () f t 的傅氏变换已知时，上式可用来求 () n t f t 的傅氏变换．5．积分性质设 [()]() f t F = w F ，且 lim()d 0 tt f t t -¥®¥ = ò，则有1[()d ]() tf t t F j-¥=ò w w F ． 6．帕塞瓦尔（Parseval ）等式 设 [()]() f t F = w F ，则有22 1 ()d ()d 2 f t t F +¥+¥ -¥-¥ =w w pòò ． （6­15）例 10 求积分2 2sin d +¥òww w的值．解 由例 3 可知函数1,1 () 0,1 t f t t ì £ ï = í> ï î 所对应的像函数为 2sin () F = ww w，则由（6­15）式可得212 112sin d 1d 2 2t +¥-¥- æö== ç÷ èøòò w w p w , 由于被积函数是偶函数，故2 2sin d 2+¥= òwpw w ． 实际上, 只要记住下面五个傅里叶变换对, 则所有的傅里叶变换都无须用公式直接计算 而可由傅里叶变换的性质导出．()1 t d « ,1()() j u t «+pd w w , 1() j tu t e - «+ b b w,0 j 0 e 2() t «- w pd w w ,224 e e t - - «w b bpb．例 11 利用傅氏变换的性质求 0 () t t d - ， 0 j et w ， () tu t 的傅氏变换 解 因()1 t « d ，由位移性质得 0j 0()e tt t -w d -« ; 由12() « pd w ，得 0 j 0 e 2()t w «pd w -w ; 由 1 ()() j u t«+pd w w ，得 2 d 1 ()()() d j j jtu t j j éù ¢ «+pd w =-+pd w êú w w w ëû2 1()j () tu t ¢ «-+pd w w．例 12 若 0 ()cos () f t t u t =w × , 求其傅氏变换． 解1()() j u t pd w w«+ , 00 j j e e()() 2t t f t u t w w - + =«00 00 111()()() 2j()j() F éù w =+pd w -w ++pd w +w êúw -w w +w ëû00 220 j [()()] 2w pd w w d w w w w =+-++ - ． 习题 6.11． 试求 ()sin f t t = 的离散频谱和它的傅里叶级数的复指数形式． 2． 求下列函数的傅氏变换：(1) 1,10, ()1,01, 0,;t f t t --<< ìï=<< í ï î其它 (2) ,0, () 0,0;t e t f t t ì £ = í> î(3) 1,0, sgn 1,0;t t t -< ì= í> î (4) ()cos sin f t t t = ．6.2 拉普拉斯变换6.2.1 拉普拉斯变换的基本概念[引例 6.3] 弹簧的机械振动机械振动是工程技术上常遇到的现象.例如,振动沉桩机利用振动来克服土壤和桩之间 的摩擦以及桩前部的阻力,使桩打入土中.混凝土振动台利用振动来克服混凝土颗粒的起始移 动阻力和内磨擦力, 使混凝土捣实.另一方面,工程技术中也要考虑减弱不必要的振动,以保证 机械的稳定性,保证操作人员的安全.下面我们举一个弹簧振动的例子.有一个弹簧，它的上端固定.质量为m 的物体挂在弹簧上(如图 6-1), 弹簧的弹性系数 为k ，取物体的平衡位置为坐标原点O , 取x 轴铅直向下. 给物体一个离开平衡 位置冲击力 () A t d ，那么物体便在平衡 位置附近作上下振动,在振动过程中, 物体的位置x 随时间t 变化,即x 是t 的 函数.这个函数反映了物体的运动规律. 问:该物体的运动规律怎样？分析 要求物体的运动规律,首先要建立描述物体离开平衡位置的位移 () x t 的数学模型.根据胡克定律,物体离开平衡位置的位 移 () x t 满足的微分方程为：, ) ( kx t A x m - = ¢ ¢ d 且 0) 0 ( , 0 ) 0 ( = ¢ = x x 解此线性微分方程满足初始条件的解即得物体的运动规律. [引例 6.4] R­C 电路的电磁振荡图 6-2 是 R­C 串联电路图，其中，电阻 2 R =W ， 电容 0.1 C F = ，电源电动 势 100sin 5 E t V = ， (0)0 C u = .当开关 K 合上后，电路中有电流通过.现在我们来研究电容器两极板间电压 C u 随时间t 的变化规 律.分析 根据回路电压定律，有()100sin 5 R C u u e t t+== 由于 d (),() d CR u u Ri t i t Ct== ,从而可以求得电压 C u 满足的微分方程： d ()100sin 5 d CC u RCu t t t+= 解此线性微分方程，即可知电容器两极板间电压 C u 随时间t 的变化规律.图6-2CO xOx图6-1从上述两个实际问题可以看到， 弹簧的机械振动，多个动态元件电路的电磁振荡的数学 模型可以用一个线性微分方程来描述.若反映事物运动的数学模型可以用一个线性微分方程 来描述，这样的物理系统称为线性系统.线性系统在工程技术与科学领域的研究中，占有很 重要的地位.对线性系统进行研究和分析，就应该求出线性微分方程满足初始条件的解.当然可以用 常规方法求出线性微分方程满足初始条件的解，但方法比较复杂.人们在寻找微分方程的一 种简捷的求解方法时，采用了将问题进行变换的思想方法,从而产生了拉普拉斯变换.拉普拉斯变换是一种积分变换， 能把微积分运算转化为代数运算， 因而使常系数线性微 分方程变换为代数方程.于是在寻求常系数线性微分方程(组)的特解时,无须按常规先求通 解,然后再求特解,只要借助于变换表即可求出特解.从而使计算简化.拉普拉斯变换还具有 特殊的物理意义，因而在许多领域被广泛的应用．下面就拉普拉斯变换的一些概念，基本性质及几个常用的拉普拉斯变换作一简略介绍.定义 6．2 设函数 () f t 的定义域为[) 0,+¥ ，若积分 0()e d st f t t+¥- ò对于s 在某一范围内的值存在， 则此积分就确定了一个参数为s 的函数，记为 () F s ， 即()()e d st F s f t t+¥- = ò函数 ) (s F 称为 ) (t f 的拉普拉斯(Laplacs)变换 (简称为拉氏变换，或称为 () f t 的象 函数)， 0()()d st F s f t e t +¥- = ò称为函数 () f t 的拉普拉斯变换式，用记号 [()] L f t 表示,即()[()]F s L f t = 若 () F s 是 () f t 的拉普拉斯变换，则 () f t 称为 () F s 的拉普拉斯逆变换（或称为 ) (t f 的象原函数)，记为 1 [()] L F s - ，即1 ()[()]f t L F s - = 拉普拉斯变换中的参数s ，一般不限于是实数，可以为复数.不过在本书中，为简单起 见,本节我们把s 当作正的实数来讨论.但这并不影响对拉普拉斯变换的性质的研究,对于解 决实际问题也已经足够了.[说明] (1) 在物理、力学和工程上的问题，都是在某一时刻起进行分析讨论，也就是 以开始瞬间进行分析讨论. 因此，在拉普拉斯变换定义中，只要求函数 () f t 当 0 t ³ 时有定 义，並假定在 0 t < 时， ()0 f t = .(2) 拉普拉斯变换是将给定的函数 () f t 经过广义积分变换成新的一个函数 () F s ，一般 说来 ，在实际中遇到的函数，它的拉普拉斯变换总是存在的.下面介绍如何用定义求拉普拉斯变换. 例 1 求函数 () ea tf t = ( 0 t ³ , a 是常数)的拉普拉斯变换.解 () 0[]e e d e d at a t st a s t L e t t+¥+¥-- == òò 这个积分在s a > 时收敛，所以 () () 0 0e 1[e ]e d []()a s t ata s t L t s a a s s a- +¥-+¥ ===> -- ò 所以1[e ]() at L s a s a=> - .例 2 求函数 ()sin f t kt = 的拉普拉斯变换.解 0[sin ]sin e d stL t kt t +¥- =ò22 0e (sin cos ) st kt k kt s k +¥- - = + 22k s k = + (0) s > .例 3 求狄拉克（Dirac）函数的拉普拉斯变换 解 00 001[()]()e d ()e d e d lim lim st st st L t t t t t t tt t t d d d t +¥+¥--- ®® === òòò 0e d e 1limlim sts t ttt t t- - ®® === ò 所以有[()]1L t d = 为了求得较为复杂的函数的拉普拉斯变换,下面我们介绍拉普拉斯变换的几个基本性质.6.2.2 拉普拉斯变换的基本性质1 . 线性性质 对于函数 () f t 和 () g t ，任意常数a 和b ，若 [()] L f t 和 [()] L g t 存 在，则有关系式[()()][()][()]L f t g t L f t L g t a b a b +=+利用拉普拉斯变换的定义，容易直接验证这个关系式.根据这个性质，可以推出一系列 函数的拉普拉斯变换.例 4 求函数 1 ()(1) e atf ta- =- 的拉普拉斯变换. 解 由线性性质可得11 [(1e )][1e ] 11 [1][e ] 1111 () ()at at at L L a aL L a a a s s a s s a -- - -=- =- =-=++ 2. 平移性质 若 [()]() L f t F s = ,则[e ()]()at L f t F s a =- 这个性质表明,象原函数乘以 ate 等于其象函数作位移a ，因此这个性质称为平移性质.（证明从略,留给读者做练习）.例 5 求 [e )] atL t 解 因为 2 1[], L t s=由平移性质可得 21[e ] ()at L t s a =- 3. 延滞性质若 [()]() L f t F s = ,则[()]()e asL f t a F s - -= ( ) 0 a > .（证明从略,留给读者做练习.） 这个性质表明, 函数 () f t a - 表示函 数 () f t 在时间上滞后a 个单位(图 6­3), 因此这个性质称为延滞性质. 延滞性质也 表示为[()()]()e a sL u t a f t a F s - --= Oa)( a t f - 图6-3.)(t f t)(t f4. 微分性质若 [()]() L f t F s = ,则[()]()(0)L f t sF s f ¢ =- 特别当 (0)0 f = 时，有 [()]()L f t sF s ¢ = 证[()]()e d st L f t f t t+¥- ¢¢ = ò 0()()e d est st f t s f t t+¥- +¥- =+ ò （ 0 s > ）()(0)sF s f =- 此性质可推广到n 阶导数,()12(1) [()]()[(0)(0)(0)]n n n n n L f t s F s s f s f f --- ¢ =-+++ L 特别当初始值 (1)(0)(0)(0)(0) n f f ff - ¢ ==== L 就有() [()]() n n L f t s F s = （n 为自然数）[说明] 对原函数的微分运算, 通过拉普拉斯变换便化为用s 乘它的象函数的乘运算,拉 拉斯变换的微分性质使我们可以把 () f t 的常系数微分方程转化为 () F s 的代数方程，因此它 在解微分方程中起着重要的作用. 拉普拉斯变换有一系列性质，在这里我们只介绍了几个简 单而基本的普拉斯变换的性质.例 6 求函数 () n f t t = 的拉普拉斯变换 （n 为自然数） 解 因为 12() (),()(1),,()!.n n n f t nt f t n n t f t n -- ¢¢¢ ==-= L 所以 (1) (0)(0)(0)0 n f f f - ¢ ==== L 因为 () [()]() n n L f t s F s = 又 ![!] n L n s=所以1!![()][] n n n n n L f t L t s s s + === × 5 . 积分性质若 [()]()(0), L f t F s s =¹ 并且 () f t 连续,则()[()d ] tF s L f t t s=ò 证 设 0()()d , tt f t t j =ò 显然 (0)0,()().t f t j j ¢ ==所以 [()][()](0)[()]. L t sL t sL t j j j j ¢ =-= 因为 [()][()](). L t L f t F s j ¢ == 所以 0 ()[()][()d ],tF s sL t sL f t t j == ò 即()[()d ] tF s L f t t s=ò 积分性质表明： 一个函数积分后再取拉普拉斯变换， 等于这个函数的象函数除以参数 . s 为方便应用起见，现将求解常系数线性微分方程的初值问题时经常遇到的拉普拉斯变 换列成一简表如下.表 6-1 常用函数的拉普拉斯变换表序号 原函数 ()f t 象函数 ()F s 1 ()t d 1 2 ()u t 1s 3 t 2 1 s 4 (1,2,)n t n = L 1 ! n n s + 5 eat1 s a- 61eat - - () a s s a + 7e a tt 2 1 () s a - 8e (1,2,)n at t n = L 1!()n n s a + - 9 sin tw 22s w w + 10 cos tw 22s s w + 11 sin() t w j + 22sin cos s s j w jw + + 12cos()t w j + 22cos sin s s j w jw - +13sin t tw 2222 ()ss w w + 14cos t tw 22222()s s w w - + 15e sin at tw - 22() s a w w ++ 16e cos at tw - 22 () s a s a w + ++ 172 1(1cos ) t w w- 22 1 () s s w + 18e eat bt- ()()a b s a s b - -- 192t p 1s s201 tp 1 s6.2.3 拉普拉斯逆变换在运用拉普拉斯变换求解常系数线性方程时，我们要碰到如何根据已知象函数 () F s 去求 它的原函数 () f t问题，也就是要讨论拉普拉斯逆变换问题.拉普拉斯变换和拉普拉斯逆变换 是一一对应的，对于常用的象函数的求取可以通过查本书的拉普拉斯变换表求得结果.对一 些象函数不能直接利用拉普拉斯变换表求得逆变换时，要结合使用拉普拉斯逆变换性质,为 此，把常用的拉普拉斯变换的几个主要性质用逆变换形式列出.1.线性性质 1 [()()]()()(,)L aF s bG s af t bg t a b - +=+ 为常数 2.平移性质 11 [()][()]() at at L F s a e L F s e f t -- -== 3.延滞性质1 [()]()()as L e F s f t a u t a -- =-´- 例 7 求下列象函数的拉普拉斯逆变换：(1)225 () s F s s- = ； (2)23() 32s F s s s + = ++ ；解 (1) 由性质1 及常用函数的拉普拉斯变换表,得111 22 2511 ()[]2[]5[] s f t L L L s s s--- - ==- 2()5 u t t =- (2 ) 首先用部分分式展开法，将所给的象函数展开2 321() 3212s F s s s s s + ==-++++ 于是由拉普拉斯变换表立即查得123 ()[] 32 s f t L s s - + = ++ 11 21 [][] 12L L s s -- =- ++ 2 2e e t t-- =- 6.2.4 拉普拉斯变换的应用举例下面举例说明拉普拉斯变换在解常系数线性微分方程(组)中的应用. 例 8 求微分方程 4120 y y y ¢¢¢ +-= 满足初始条件 (0)1,(0)0 y y ¢ == 的解. 解 对方程两边取拉普拉斯变换，因为 [0]0 L = ，所以[412]0L y y y ¢¢¢ +-= 由拉普拉斯变换的线性性质，得[]4[]12[]0L y L y L y ¢¢¢ +-= 再由拉普拉斯变换的微分性质得2 [](0)(0)4[[](0)]12[]0s L y sy y sL y y L y ¢ --+--= 设 []() L y Y s = 并将初始条件代入，得2 (412)()40s s Y s s +---= 即2 4() 412s Y s s s + =+- 下面通过拉普拉斯逆变换求 ) (t y 先将 ) (s F 分解为部分分式之和.2 41/43/4() 41262s Y s s s s s + ==++-+- 于是 111 1/43/4 ()[()][][] 62y t L Y s L L s s --- ==+ +- 62 13 e e 44 t t - =+ 即所求微分方程的解是 62 13 ()e e44t ty t - =+ [注意] 从上例可以看出，拉普拉斯变换解常系数线性微分方程的步骤如下： 1. 对方程两边取拉普拉斯变换，设 []() L y Y s = ，得出关于 () Y s 的代数方程； 2. 解此方程，求出 () Y s ；3. 对 ) (s Y 作拉普拉斯逆变换，即可求出微分方程的解.例 9 求微分方程组 200 x y x x y ¢¢¢ --= ì í ¢-= î满足初始条件 (0)0,(0)1,(0)1 x x y ¢ === 的解.解 对方程组两边取拉普拉斯变换，得2 [](0)(0)]2([](0))[]0[](0)][]0 s L x sx x sL y y L x sL x x L y ¢ ì -----= í--= î设 []() L x X s X == ，设 []() L y Y s Y == 并将初始条件 (0)0,(0)1,(0)1 x x y ¢ === 代 入，得2 (1)210 0 s X sY sX Y ì --+= í-= î解此方程，得2 2 1 1.1 X s s Y s ì = ï ï + íï =ï + î作拉普拉斯逆变换，得微分方程组的解()sin , ()cos . x t t y t t= ì í= î 从上述各例可以到， 应用拉普拉斯变换求解常系数线性微分方程(组)的初始问题是比较简 单的.但遗憾的是,它对方程中强迫的要求比较高.因此,并非任何常系数线性微分方程(组)都 能用拉普拉斯变换求解,这一点要注意.现在我们来解前面提出的弹簧机械振动问题和 RC 电路的电磁振荡问题. 例 10 弹簧机械振动问题我们知道弹簧振动的微分方程为 (), mx A t kx d ¢¢=- 且 (0)0,(0)0x x ¢ == 设 [()](),(0)0 L x T X S x ¢ == ，对 () mx A t kx d ¢¢=- 两边取拉普拉斯变换，并将初始条 件 (0)0,(0)1 x x ¢ == 代入，得2 () AX s ms k=+ 作拉普拉斯逆变换，得()sin A k x t tm km=可见，振动物体按正弦规律运动,振幅为A km角频率为 k m .例 11 电路的电磁振荡问题我已经知道 RC 电路的电磁振荡方程为d ()100sin 5 d cc u RCu t t t+= 设 [()]() C C L u t U s = ，对上式两边取拉普拉斯变换，并将初始条件和已知条件代入， 化简得2 2500() (5)(25)Uc s s s =++ 作拉普拉斯逆变换，得5 ()50(e cos 5sin 5)t C u t t t - =-+ 拉普拉斯（Laplace ）变换在电学、光学、力学等工程技术与科学领域中有着广泛的应 用．由于它的像原函数的条件比傅里叶变换的条件要弱，因此在某些问题上，它比傅里叶变 换的适用面要广．练习题 6.21.求函数 ()3f t t = 当 0 t ³ 的拉普拉斯变换. 2.求函数 ()1e tf t t =+ 的拉普拉斯变换.3.求 1() 3 F s s =+ 的拉普拉斯逆变换 . 4.求 2 1() 49F s s = + 的拉普拉斯逆变换 .5.求微分方程组 e0 ty y x x x - ¢ ì +-= í ¢+= î满足初始条件 (0)0,(0)1 y x == 的解.趣味阅读（六）刑事侦察中时间的推断自从人类使用科学方法介入司法侦破以来，如何确定死亡时间一直困扰着人们．当一次 谋杀发生后，尸体的温度从原来的 37℃开始下降，如果两个小时后尸体温度变为 35℃，并 且假定周围空气的温度保持 20℃不变，试求出尸体温度u 随时间 t 的变化规律．又如果尸 体发现时的温度是 30℃，时间是下午 6点整，那么谋杀是何时发生的？为了解决上述问题，需要了解有关热力学的一些基本规律．例如，热量总是从温度高的 物体向温度低的物体传导的；在一定的温度范围内， 一个物体的温度变化速度与这一物体的 温度和其所在介质温度的差值成正比．这是已为实验证实了的牛顿（Newton）冷却定律．现将牛顿冷却定律应用于刑事侦察中死亡时间的鉴定．设尸体在时刻t 的温度为 ) (t u u = (t 从谋杀后计)， 则尸体的冷却速度以d d ut来表示． 注 意到热量总是从温度高的物体向温度低的物体传导的，因而 20 u > ．所以温度差 20 u - 恒 正；又因尸体将随时间而逐渐冷却，故温度变化速度d d ut恒负．故有： d d ut(20) k u =-- 这里 0 > k 是比例常数． 上述方程就是尸体冷却过程的数学模型， 初始条件为 (0)37 u = ． 为了解出物体的温度u 和时间t 的关系， 我们对 d d ut(20) k u =-- 两边取拉普拉斯变换， 设 []() L u U s = ，得出关于 () U s 的代数方程．20 ()(0)() ksU s u kU s s-=-+再根据初始条件 (0)37 u = ，于是20 ()()37 ks k U s s+=+解出：1720() U s s k s=+ + 对 () U s 作拉普拉斯逆变换，即可求出微分方程的解．()2017ektu t - =- 根据两小时后尸体温度为 35℃这一条件，有2 352017ek- =- 得 0.063 k » ，于是0.063 2017etu - =- 将 30 u = 代入上式 ， 即得 8.4 t = ． 于是， 可以判定谋杀发生在下午 6点尸体被发现前的 8． 4 小时，即谋杀是在上午 9 点 36分发生的．复习题六 A 组（基础层次）1. 已知信号函数 ) (t f 是以2p 为周期的周期函数，它在[,] p p - 上的表达式为1,0 () ,0 t f t t t p p ì -£< ï = í <£ ï î，如何将函数展开为傅里叶级数的三角形式．2． 求下列函数的傅氏变换：(1) 2 1,||1, () 0,||1;t t f t t ì -£ ï = í> ï î (2) sin 2,0, () 0,0; t e t t f t t - ì ³ ï= í< ï î(3) 3 ()sin f t t = ；(4) ()sin(5)3f t t p=+ ．3． 已知 00 ()[()()] F w p d w w d w w =++- 为函数 () f t 的傅氏变换，求 () f t ． 4． 求下列各函数的拉普拉斯变换：(1) 2 ()34 f t t t =+- ; (2) ()3cos 25sin 2 f t t t =- ;(3) 1,04, () 1,4;t f t t -£< ì = í³ î 5． 求下列象函数的拉普拉斯逆变换：(1) 2() 2F s s = - ; (2) 31() (1)F ss = - ; (3) 223() s F s s- = ; (4) 243() 4s F s s - =+ ; (5) () (3)(5)sF ss s = ++ .6． 用拉普拉斯变换解下列常系数线性微分方程：(1) 20 y y ¢+= ， (0)3 y = ；.(2) 324, y y y ¢¢¢ -+= (0)0, y = (0)1 y ¢ = .7． 用拉普拉斯变换解微分方程组20,(0)0,(0)1,(0) 1. 0,x y x x y y x y ¢¢+= ì ¢ === í¢++= î 复习题六 B 组（提高层次）1． 求下列函数的傅氏变换．(1) 1,||1, () 0,|| 1.t f t t ì £ ï = í> ï î(2) sin ,||, () 0,||. t t f t t £ ì= í> îp p 2． 设 ()[()] F f t w =F ，证明： 1 ()()e d 2 j tf F t t w w p+¥ - -¥ ±= ò m ． 3． 求函数 1 ()[()()()()] 222a af t t a t a t t d d d d =++-+++- 的傅氏积分变换．4． 求下列函数的傅氏变换．(1) 0 ()sin (); f t t u t w =×(2) 0()() j t f t e tu t w = ．5． 证明：若 ) ( )] ( [ s F t f L = ，则当 0 > a 时，有 ) ( 1)] ( [ as F a at f L = 6． 求下列象函数的拉普拉斯逆变换(1) )1 ( 1) (2+ = s s s F ;(2) 22 )1 ( 24 ) ( + - =s s s F . 7． 用拉普拉斯变换解下列常系数线性微分方程(1) 22, xy y y e - ¢¢¢ ++= (0)(0)0; y y ¢¢ == (2) 3 83216 y y t t ¢¢¢+=- , (0)(0)(0)0;y y y ¢¢¢¢ === 8． 用拉普拉斯变换解常系数线性微分方程组;5 6) 0 ( , 0 ) 0 ( , 0 ) 0 ( ,5 1 ) 0 ( , 2 sin 3 4 , 2 cos 3 = ¢ = = ¢ = îíì = + ¢ - ¢ ¢ = + ¢ + ¢ ¢ y y x x t y x y t x y x 9． 在如图 6­4 所示的 L R - 电路中，电阻 ) ( 10 W = R ，电感 ) ( 2 H L = ，电源电动势) ( 5 sin 50 V t E = ，当开关K 合上后，电路中有电流通过．求电流强度 ) (t i 的变化规律．图6-4．。

单位脉冲函数的傅里叶变换是多少
摘要：
1.单位脉冲函数的概念及性质
2.单位脉冲函数的傅里叶变换公式
3.单位脉冲函数傅里叶变换的意义
4.结论
正文：
单位脉冲函数是一种特殊的数学函数，它在某个时间点上具有无限大的值，而在其他时间点上具有零值。

这个时间点通常称为脉冲的“中心点”，单位脉冲函数的傅里叶变换可以用来分析其频谱特性。

单位脉冲函数的傅里叶变换公式可以表示为：
F{δ(t)} = ∫δ(t)e^-jωtdt
其中，F 表示傅里叶变换，δ(t) 表示单位脉冲函数，ω表示角频率，t 表示时间。

根据傅里叶变换的定义，我们知道傅里叶变换是将一个信号从时域转换到频域的过程。

对于单位脉冲函数来说，其在时域上的取样性质使得其频谱具有特殊的性质。

具体来说，单位脉冲函数的频谱密度在-∞到+∞区间内处处相等，常称为均匀谱或白色噪声。