当前位置：文档之家 › 随机变量方差的概念及性质

随机变量方差的概念及性质

  • 格式：ppt
  • 大小：1.75 MB
  • 文档页数：48

下载文档原格式

  / 48

合集下载

随机变量方差的概念及性质

随机变量方差的概念及性质


= ( n 2 n) p 2 + np.
D( X ) = E ( X 2 ) [ E ( X )]2
= ( n 2 n) p 2 + np ( np )2
= np(1 p ) ).
3. 泊松分布
设 X ~ π(λ ), 且分布律为
P{ X = k } =
λk
k!
e λ , k = 0,1,2,
π π 2 = 3π + 24 2 4 16
4 2
2
= 20 2π 2 .
2 0 例4 设 X ~ 1 1 3 2
1 3 , 求 D( 2 X 3 + 5). 1 1 12 12
解
D( 2 X 3 + 5) = D( 2 X 3 ) + D( 5)
= 4 D( X )
= E[ X E ( X )]2 + E[Y E (Y )]2 ± 2 E {[ X E ( X )][Y E (Y )]}
= D( X ) + D(Y ).
推广 若 X 1 , X 2 ,
D( X1 ± X 2 ±
, X n 相互独立 , 则有 + D( X n ).
± X n ) = D( X1 ) + D( X 2 ) +
= C E {[ X E ( X )] }
2 2
= C 2 D( X ).
(3) 设 X, Y 相互独立, D(X), D(Y) 存在, 则
D( X ± Y ) = D( X ) + D(Y ).
证明
D( X ± Y ) = E {[( X ± Y ) E ( X ± Y )]2 } = E {[ X E ( X )] ± [Y E (Y )]}2
随机变量方差的定义及性质

随机变量方差的定义及性质

方差与期望值的离散程度有关。如果一个随机变量的取值比较离散，即取值比较分散，那么其方差就比较大；如果一个随机 变量的取值比较集中，即取值比较接近期望值，那么其方差就比较小。
02
CATALOGUE
方差的性质
方差的非负性
总结词
方差具有非负性，即对于任何随机变量X，其方差Var(X)总是非负的。
详细描述
方差的独立性
要点一
总结词
如果两个随机变量X和Y是独立的，那么Var(X+Y) = Var(X) + Var(Y)。
要点二
详细描述
这是方差的一个重要性质，表明如果两个随机变量相互独 立，那么它们的和的方差等于它们各自方差的和。这个性 质在概率论和统计学中非常重要，因为它允许我们通过独 立随机变量的方差来计算复合随机变量的方差。
度。
方差主要关注数据点的离散程度 ，而峰态则关注数据点的集中趋
势。
如果数据分布更加尖锐，即数据 点更加集中在平均值附近，则方 差可能会减小，因为数据点之间
的差异较小。
THANKS
感谢观看
方差还可以表示为
Var(X)=E(X^2)-[E(X)]^2。这个公式可以用来计算方差，其中E(X^2)表示随机变量X的平方的期望值 ，E(X)表示随机变量X的期望值。
方差与期望值的关系
方差的大小与期望值有关。如果一个随机变量的期望值越大，其方差也越大；如果一个随机变量的期望值越小，其方差也越 小。
03
CATALOGUE
方差的应用
方差在统计学中的应用
描述数据分散程度
方差是衡量随机变量取值分散程度的量，用于描述数 据的离散程度。
检验假设
在统计学中，方差分析（ANOVA）等方法用于检验 多个总体均值是否相等，从而判断假设是否成立。
随机变量的方差和标准差

随机变量的方差和标准差


0
2
0
xe
x2 2a2
dx
2a
2
e
x2 2a2
d
0
x2 2a2
2a
2
e
x2 2a2
0
2a2
；
DX EX 2 EX 2a2 πa2 a2 (4 π)．
22
DXY EX 2Y 2 (EXY )2 EX 2EY 2 (EX )2 (EY )2 [DX (EX )2 ][DY (EY )2 ] (EX )2 (EY )2
证明 事实上，有 其中
二、切贝绍夫不等式
1
2
xi
( X EX )2 P
X xi
DX 2
,
1
2
xi EX
( X EX )2 P
X xi
P X EX PX xi xi EX
证明 (1) 设X是非负离散 型随机变量，其一切可能 值为{Xi}，
则对于任意ε>0，有
设随机变量X的数学期望和方差都存在，则对于任意ε>0， 事件{|X－EX|≥ε}的概率有如下估计式——切贝绍夫不等式：
其中前两个和式∑表示对于满足| xi －EX|≥ε的X 的一切可能 值xi求和，后一个和式∑表示对于X 的一切可能值xi求和．
设X 是连续型随机变量，其概率密度
P
| x EX |
f
|xEX |
( x)dx
1 2
(x
EX )2
例为f (4fx.)(1dx1x) ，设则D随X2机 变 量 X 的 数 学 期 望 为 μ ，
方差为
，则由切
贝绍夫不等式，有
PX E X
P
3
X
3
连续型随机变量的数学期望与方差

连续型随机变量的数学期望与方差


(1)D( )
E[
E( )]2
[x
E( )]2
p( x)dx
(2)方差的简便计算公式
D( )=E（ 2） E（2 ）
x2 p(x)dx
x p( x)dx
例2 随机变量的概率密度函数
6x(1 x)，当0 x 1
p(x)
0
当x 0或x 1时
求随机变量的方差。
12
4、方差的性质 设 k ,b,c均为常数，则有
E( ) xp(x)dx
15
2、数学期望的性质
(1)EaX b aEX b
(2)EaX aEX
(3)EX b EX b
(4)Eb b
(5)EX Y EX EY
(6)E( f ( )) f (x)p(x)dx
(6)E f ( ) f (xk )PK
k
16
（二）连续型随机变量ξ取值的方差
(1)D(c) 0
(2)D(k ) k 2D( ) (3)D( b) D( )
(4)D(k b) k 2D( )
13
下页
三、练习
• 课本第90页 第6题
14
四、小结 （一）连续型随机变量ξ取值的数学期望
1、连续型随机变量的数学期望的定义 p(x) 设连续型随机变量 的密度函数为
若积分 xp(x绝)d对x 收敛，则 的数学期望为：
x0 x1 x2 L xn
xi xi1 xi
b i
【xi
,
xi
）
+1
y p(x)
o
x0b0 x1 xi bi xi1
xn x
6
连续型随机变量ξ的概率分布
ξ 【x0 , x1）【x1, x2）
高斯随机变量的均值和方差

高斯随机变量的均值和方差

高斯随机变量的均值和方差高斯随机变量的均值和方差概述：高斯随机变量是一种常见的概率分布，也被称为正态分布。

它在各个科学领域中都有广泛的应用，具有很强的实用价值。

均值和方差是高斯随机变量的两个重要统计特征，对于了解它的分布特性和应用具有重要意义。

一、高斯随机变量的定义和性质高斯随机变量的定义是指数学上服从正态分布的随机变量。

它的概率密度函数可以表示为一个钟形曲线，呈现出对称性和峰值集中的特点。

正态分布的概率密度函数可由均值和方差唯一确定。

1. 对称性：高斯随机变量的概率密度函数关于均值对称，即曲线在均值处达到峰值。

2. 峰值集中：均值是高斯随机变量的分布特征之一，它确定了曲线的中心位置。

方差则衡量了数据相对于均值的离散程度，决定了曲线的宽窄。

二、高斯随机变量的均值均值是一个概率分布的集中趋势的度量标准，对于高斯分布来说，均值是分布的中心位置。

1. 数学期望：高斯随机变量的均值也被称为数学期望，表示了随机变量的平均值。

对于高斯分布，其数学期望即为分布的均值。

2. 均值的性质：高斯随机变量的均值具有线性性质，即对于两个独立的高斯随机变量X和Y，它们的线性组合aX + bY的均值就是a和b的加权平均值。

三、高斯随机变量的方差方差是用来衡量数据的离散程度，对于高斯分布来说，方差决定了数据的分布宽度。

1. 方差的定义：高斯随机变量的方差是其概率分布关于均值的平均偏离程度的度量。

方差的数学定义为随机变量与均值的差的平方的期望。

2. 方差的性质：高斯随机变量的方差有以下几个性质：（1）方差非负，即方差的值大于等于0。

（2）方差为0表示所有数据都是相同的，即没有离散度。

（3）方差具有线性性质，对于两个独立的高斯随机变量X和Y，它们的线性组合aX + bY的方差为a^2Var(X) + b^2Var(Y)。

结论：高斯随机变量的均值和方差是衡量它分布特性的重要统计量。

均值决定了分布的中心位置，方差则表征了对中心位置的离散程度。

3.2随机变量的方差

3.2随机变量的方差


一样的，还必须考虑这两个班级学生的两极分
化情况.为了反映随机变量的这种离散程度，我
们引入方差概念.
一、方差的概念
1．定义1 定义3.2.1 设 是一个随机变量，数学期望 E
2 为随机 存在，则称 E ( E ) E ( E ) 存在，如果
2
变量的方差,并记为. D 或Var
这个结论的充分性是显然的，下面证明必要性：
1 1 D 0 P( E 0) P( E ) P( E ) 0 n n 1 n n 1 1 2 n 1 ( ) n
由此知
P( E ) 0
更一般地，若 1 , 2
, n 两两独立，则
D1 n D1 D n
性质4 对任意的常数 C E ，则有 D E( C) 2 事实上 E ( C )2 E ( E E C ) 2
E ( E ) 2 2( E C ) E ( E ) ( E C ) 2 D ( E C ) 2 .
E 2
a
2 2 x a ab b x 2 p ( x)dx 4(b a ) a 3 2 2 2
(b a ) D E ( E ) . 12
7) 指数分布 设 ~ E( ) ，已知 E , 因为
E x p( x)dx x e dx x 2d (e x )
契贝晓夫不等式也可以表示成
P( a ) 1 D
2
由切比雪夫不等式看出， D 越小，事件 发生的概率越小， 越是集中在 的附近取值.由
此可见，方差刻划了随机变量取值的离散程度.
方差概念及计算公式

方差概念及计算公式

quad88样条newton-cotes公式 最常用
trapz梯形法定积分
cumtrapz梯形法区间积分
sum等宽矩阵法定积分
cumsum等宽矩阵法区间积分
fnint样条的不定积分
多重数值积分
dblquad('fun',inmin,inmax,outmin,outmax,tol,method) 定积分
问题1：函数f(x)在什么条件下可以表示成幂级数 ；
问题2：如果f(x)能表示成如上形式的幂级数，那末系数cn(n=0,1,2,3,…)怎样确定？
下面我们就来学习这两个问题。
泰勒级数
我们先来讨论第二个问题.假定f(x)在a的邻区内能表示成 这种形式的幂级数，其中a是事先给定某一常数，我们来看看系数cn与f(x)应有怎样的关系。
积分限为函数时 先求G(y)={x2(y),x1(y)}f(x,y)dx 再求I={y2,y1}G(y)dy 这里用{}表示豆芽符
数值微分
多项式求导 polyder
差分算积分 diff(X)
6.符号微积分
约定变量x 系数a,b
极限
limit(f,x,a)求x->a时f值、
limit(f,x,a,'right') 右极限 limit(f,x,a,'left')左极限
超定求最小二乘解 用A\B %基于奇异值分解；用pinv(A)*B %基于householder变换
欠定由qr分解求得
非负最小二乘解 X=nnls(A,b,TOL) TOL指定误差，可缺省
零点法求解方程
fzero一元 fsolve多元
x=fzero(fun,x0)
[x,fval,exitflag]=fzero(fun,x0,options,P1,P2,...)
一随机变量方差的定义及性质

一随机变量方差的定义及性质


(1p)/ p2
ab ab 2 (ba)2 12
0
1/
1 / 2
μ,σ0
μ
σ2
分布
Gamma分布
参数 , 0
数学期望
/
方差
/2
三、例题讲解
例1 设随机变量X 具有概率密度
求D(X).
1 x, 1 x 0, p(x) 1 x, 0 x 1,
2(X),即 D(X) 2(X) E{[XE(X)]2}.
称 D(X)为标准差或均,记 方为 差σ(X).
2. 方差的意义
方差描述了随机变量X取值对于数学 期望的分散程度.如果D(X)值大, 表示X 取 值分散程度大, E(X)的代表性差;而如果 D(X) 值小, 则表示X 的取值比较集中,以 E(X)作为随机变量的代表性好.
k
则有
0p1.
EX k n 0kk npk(1p)nknp
E (X 2 ) E [X (X 1 ) X ]
E [X (X 1 ) ] E (X )
n
k(k1)Cn kpk(1p)nknp
k0
nk(k1)n!pk(1p)nknp k0k!(nk)!
xexdx
0
1/.
D (X ) E (X 2 ) [E (X )2]
0 x2exdx1/2
2/21/2
1 2 指 数 分 布 的 期 望 分和 别方 1为 /差和1/2.
6. 正态分布
设X~N(μ,σ2),其概率密度为
f(x )1e (x 2 σ μ 2 )2, σ 0 , x . 2 σ
D (X ) E (X 2 ) [E (X )2]
bx2 1 dxab2 a ba 2 ((bb aa)2 .
随机变量的方差

随机变量的方差

概率与统计
随机变量的方差
1
4.2 方差
一. 定义与性质 方差是衡量随机变量取值波动 程度 的一个数字特征。
如何定义？
2
1.(p121)定义 若E(X2)存在，则称 E[X-E(X)]2 为随机变量 X的方差，记为D(X),或Var(X).
称 ( X ) D( X ) 为随机变量X的标准差
可见
2 [ x E ( X )] P{ X xk }, 离散型情形 k D( X ) k 1 2 [ x E ( X )] f ( x )dx, 连续型情形
3
2.推论
D(X)=E(X2)-[E(X)]2.
例1：设随机变量X的概率密度为 1 x 1 x 0 f ( x) 1 x 0 x 1 0 其它


5. 正态分布N(, 2)：
D X 2
6
1.请给出一个离散型随机变量X和一个连续 型随机变量Y，使它们的期望都是2， 方差都是1。
2.已知随机变量X1,X2,…,Xn相互独立，
且每个Xi的期望都是0，方差都是1， 令Y= X1+X2+…+Xn ，求E（Y2）
7
三.切比雪夫不等式 若随机变量X的期望和方差存在，则对任意 D( X ) 0，有 P{| X E( X ) | } ; 2 这就是著名的切比雪夫(Chebyshev)不等式。 它有以下等价的形式：
i 1 i 1 n n5Βιβλιοθήκη 二.几个常用随机变量的方差
1. 二项分布B(n, p)： 2. 泊松分布p()：
D X np(1 p) D X
1 2 D X b a 12 1 D X 2
072随机变量的均值与方差

072随机变量的均值与方差

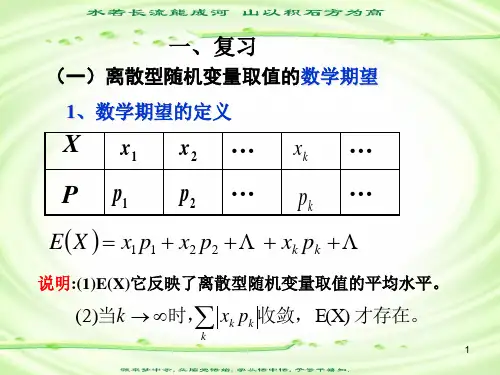
§16.1 随机变量的均值与方差1.所示，则称n n 2211为离散型随机变量X 的均值或数学期望，记为E(X)或μ，即E(X)=n n p x p x p x +++ 2211，其中i x 是随机变量X 的可能取值，i p 是概率，i p ≥0；n i ,,2,1 =，121=+++n p p p性质：①E(C)=C ；②E(aX)=aE(X)；③E(aX+b)=aE(X)+b ；④超几何分布X ～H(n,M,N)的数学期望为NnM X E =)(，二项分布X ～B(n ，p)的数学期望为np X E =)(。

2.X 的概率分布如表所示，则称n n p x p x p x 22211)()()(μ-++-+- 为离散型随机变量X 的方差，记为V(X)或2σ，即V(X)= n n p x p x p x 2222121)()()(μμμ-++-+- （其中)(X E =μ，i p ≥0；n i ,,2,1 =，121=+++n p p p ），方差也可用公式212)(μ-=∑=i ni i p x X V ，即22)()()(X E X E X V -=，V(X)的算术平方根称为X 的标准差，即)(X V =σ。

性质：①0)(=C V ；②)()(2X V a b aX V =+；③超几何分布X ～H(n,M,N)的方差为)1())(()(2---=N N n N M N nM X V ，二项分布X ～B(n ，p)的方差为)1()(p np X V -=。

注：随机变量的方差和标准差都反映了随机变量的取值偏离于均值的平均程度。

方差或标准差越小，随机变量偏离于均值的平均程度越小。

三、典型例题例1：有10张卡片，其中8张标有数字2，有2张标有数字5，从中随即地抽取3张卡片，设3 张卡片上的数字之和为随机变量ξ，求E(ξ)、V(ξ)例2：假定某射手每次射击命中目标的概率为32，且只有3发子弹。

方差概念及计算公式

方差概念及计算公式

方差概念及计算公式-CAL-FENGHAI.-(YICAI)-Company One1方差概念及计算公式一．方差的概念与计算公式例1两人的5次测验成绩如下：X： 50，100，100，60，50 E(X )=72；Y： 73， 70， 75，72，70 E(Y )=72。

平均成绩相同，但X不稳定，对平均值的偏离大。

方差描述随机变量对于数学期望的偏离程度。

单个偏离是消除符号影响方差即偏离平方的均值，记为D(X )：直接计算公式分离散型和连续型，具体为：这里是一个数。

推导另一种计算公式得到：“方差等于平方的均值减去均值的平方”，即，其中分别为离散型和连续型计算公式。

称为标准差或均方差，方差描述波动程度。

二．方差的性质1．设C为常数，则D(C) = 0（常数无波动）；2．D(CX )=C2D(X ) （常数平方提取）；证：特别地D(-X ) = D(X ), D(-2X ) = 4D(X )（方差无负值）3．若X、Y相互独立，则证：记则前面两项恰为D(X )和D(Y )，第三项展开后为当X、Y 相互独立时，，故第三项为零。

特别地独立前提的逐项求和，可推广到有限项。

三．常用分布的方差1．两点分布2．二项分布X ~ B( n, p )引入随机变量X i（第i次试验中A出现的次数，服从两点分布），3．泊松分布（推导略）4．均匀分布另一计算过程为5．指数分布（推导略）6．正态分布（推导略）~正态分布的后一参数反映它与均值的偏离程度，即波动程度（随机波动），这与图形的特征是相符的。

例2求上节例2的方差。

解根据上节例2给出的分布律，计算得到求均方差。

均方差的公式如下：（xi为第i个元素）。

S = ((x1-x的平均值)^2 + (x2-x的平均值)^2+(x3-x的平均值)^2+...+(xn-x的平均值)^2)/n)的平方根大数定律表表明：事件发生的频率依概率收敛于事件的概率p，这个定理以严格的数学形式表达了频率的稳定性。

连续型随机变量的方差计算公式

连续型随机变量的方差计算公式1. 前言在概率论和统计学中，方差是用来衡量一个随机变量在其平均值附近的离散程度的一个重要指标。

连续型随机变量的方差计算方法与离散型随机变量略有不同，本文将详细介绍连续型随机变量的方差的计算方法。

2. 连续型随机变量的方差的定义连续型随机变量X的方差定义为：$$ Var(X)=E\left((X-E(X))^2\right) $$其中E表示期望，即：$$ E(X)=\int_{-\infty}^{\infty}x f(x)dx $$其中f(x)是X的概率密度函数。

方差实际上是随机变量和其期望的差的平方的期望。

3. 连续型随机变量方差计算的步骤计算连续型随机变量方差的一般步骤如下：3.1 计算期望首先需要计算随机变量的期望E(X)，即：$$ E(X)=\int_{-\infty}^{\infty}x f(x)dx $$3.2 常规计算然后计算(X-E(X))^2，即将X的每个值减去期望，然后平方：$$(X-E(X))^2$$3.3 期望计算再把(X-E(X))^2乘以概率密度函数f(x)，然后对x从负无穷到正无穷进行积分，即可得到方差，即：$$ Var(X)=E\left((X-E(X))^2\right)=\int_{-\infty}^{\infty}(x-E(X))^2 f(x)dx $$4. 连续型随机变量方差相关公式4.1 方差的性质连续型随机变量的方差具有以下性质：- 对于任意常数c，有Var(cX)=c^2Var(X)。

- 对于任意随机变量X和Y，Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)，其中Cov(X,Y)为X和Y的协方差。

4.2 使用方差的性质计算方差可以利用方差的性质来简化计算：- 如果X是一个连续型随机变量，那么Var(aX+b)=a^2Var(X)，其中a和b都是常数。

- 如果X和Y是正交的随机变量（即Cov(X,Y)=0），那么Var(X+Y)=Var(X)+Var(Y)。

方差__随机变量的数字特征.


>0, 不等式P{| X | } 2 / 2成立，
或
P{| X | } 1 2 / 2
证明：（只证 X 是连续型）
P{| X
|
}
f
|x|
( x)dx
|x|
|
x
2
|2
f (x)dx
1
2
(x
)2
f
(x)dx
DX
2
2
2
。
返回主目录
第四章 随机变量的数字特征 §2 方差
这个不等式给出了随机变量 X 的分布未知情 况下，事件{| X | } 的概率的一种估计方法。
§2 方差
引言
随机变量的数学期望体现了随机变量所有可能取值的加权
平均．
离散型： 若级数
k 1
xk
pk
绝对收敛，则
E(X )
k 1
xk
pk
连续型： 若积分 xf ( x)dx 绝对收敛，则
E( X ) xf ( x)dx
§2 方差
设有一批灯泡寿命为：一半约950小时，另一半约1050小时→平均寿命为1000小时； 另一批灯泡寿命为： 一半约1300小时，另一半约700小时→平均寿命为1000小时；
方差D(X ) 2
0，记X *
X
证明：E( X *) 0，D( X *) 1，称X *为X的标准化变量
例2：设随机变量X具有0-1分布，其分布律为：
P( X 0) 1 p，P( X 1) p，求D( X )。
解：
E(X ) 0 (1 p) 1 p p E( X 2 ) 02 (1 p) 12 p p
返回主目录
例 已知正常男性成人血液中，每一毫升白细胞数平均

随机变量的方差和标准差


P|
x
EX
|
f
|xEX |
( x)dx
1
2
(x
EX
)2
f
(x)dx
DX
2
例4.11 设随机变量X的数学期望为μ，方差为 ，2 则由切
贝绍夫不等式，有
P 3 X 3 P X 3 1 1 0.89 9 然而，假如 X ~ N(, 2 ) 则利用附表1，可得
P
3
X
3
P|
X
|
3
一、随机变量的方差和标准差的 概念和性质
1、方差和标准差的定义 X－EX表示随机变量 X 对数学期 望 EX 的离差；为避免离差符号的影响，人们常使用X 对数 学期望 EX 的平方离差 (X EX )2 它显然也是随机变量；称 (X EX )2 的数学期望
DX E(X EX )2 EX 2 (EX )2
二、切贝绍夫不等式
设随机变量X的数学期望和方差都存在，则对于任意ε>0， 事件{|X－EX|≥ε}的概率有如下估计式——切贝绍夫不等式：
P
X
EX
DX
2
或
P X EX
1
DX
2
证明 (1) 设X是非负离散型随机变量，其一切可能值为{Xi}，
则对于任意ε>0，有
P X EX PX xi
xi EX
1
2 xi EX
( X EX )2 P
X xi
1
2
xi
(X
EX )2 PX
xi
DX
2
,
其中前两个和式∑表示对于满足| xi －EX|≥ε的X 的一切可能 值xi求和，后一个和式∑表示对于X 的一切可能值xi求和．

离散型随机变量期望和方差

1.期望：若离散型随机变量ξ，当ξ=x i的概率为P（ξ=x i）=P i（i=1，2，…，n，…），则称Eξ=∑x i p i为ξ的数学期望，反映了ξ的平均值.期望是算术平均值概念的推广，是概率意义下的平均.Eξ由ξ的分布列唯一确定.2.方差：称Dξ=∑（x i－Eξ）2p i为随机变量ξ的均方差，简称方差.D叫标准差，反映了ξ的离散程度.3.性质：（1）E（aξ+b）=aEξ+b，D（aξ+b）=a2Dξ（a、b为常数）.（2）二项分布的期望与方差：若ξ～B（n，p），则Eξ=np，Dξ=npq（q=1－p）.Dξ表示ξ对Eξ的平均偏离程度，Dξ越大表示平均偏离程度越大，说明ξ的取值越分散.1．（2013•广东）已知离散型随机变量X的分布列为X 1 2 3P则X的数学期望E（X）=（）A．B． 2 C．D． 32．（2010•宁夏）某种种子每粒发芽的概率都为0.9，现播种了1000粒，对于没有发芽的种子，每粒需再补种2粒，补种的种子数记为X，则X的数学期望为（）A． 100 B． 200 C． 300 D． 4003．（2007•四川）某商场买来一车苹果，从中随机抽取了10个苹果，其重量（单位：克）分别为：150，152，153，149，148，146，151，150，152，147，由此估计这车苹果单个重量的期望值是（）A．150.2克B．149.8克C．149.4克D．147.8克4．（2014•浙江二模）李先生居住在城镇的A处，准备开车到单位B处上班，途中（不绕行）共要经过6个交叉路口，假设每个交叉路口发生堵车事件的概率均为，则李先生在一次上班途中会遇到堵车次数ξ的期望值Eξ是（）A．B． 1 C．6×（）6D． 6×（）6 5．从装有颜色外完全相同的3个白球和m个黑球的布袋中随机摸取一球，有放回的摸取5次，设摸得白球数为X，已知E（X）=3，则D（X）=（）A．B．C．D．6．有10件产品，其中3件是次品，从中任取两件，若ξ表示取到次品的个数，则Eξ等于（）A．B．C．D． 17．某射手射击击中目标的概率为0.8，从开始射击到击中目标所需的射击次数为ξ，则Eξ等于（）A．B．C．D．58．某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者，若用随机变量ξ表示选出的志愿者中女生的人数，则数学期望Eξ_________（结果用最简分数表示）．9．设离散型随机变量ξ可能取的值为1，2，3，4．P（ξ=k）=ak+b（k=1，2，3，4），又ξ的数学期望Eξ=3，则a+b= _________．10．同时抛掷两枚相同的均匀硬币，随机变量ξ=1表示结果中有正面向上，ξ=0表示结果中没有正面向上，则Eξ=_________．11．一个袋子里装有大小相同的3个红球和2个黄球，从中同时取出2个球，则其中含红球个数的数学期望是_________．12．（2014•温州一模）现有三个小球全部随机放入三个盒子中，设随机变量ξ为三个盒子中含球最多的盒子里的球数，则ξ的数学期望Eξ为_________．13．从1，2，3，…，n﹣1，n这n个数中任取两个数，设这两个数之积的数学期望为Eξ，则Eξ=_________．14．（2013•闸北区二模）一个袋中装有大小相同的黑球、白球和红球共10个．已知从袋中任意摸出1个球，得到黑球的概率是；从袋中任意摸出2个球，至少得到1个白球的概率是．从袋中任意摸出2个球，记得到白球的个数为ξ，则随机变量ξ的数学期望Eξ=_________．15．某班从4名男生、2名女生中选出3人参加志愿者服务，若选出的男生人数为ξ，则ξ的方差Dξ=_________．16．（2013•嘉兴一模）一盒中有6个小球，其中4个白球，2个黑球•从盒中一次任取3个球，若为黑球则放回盒中，若为白球则涂黑后再放回盒中．此时盒中黑球个数X的均值E（X）=_________．17．（2013•虹口区二模）从集合的所有非空子集中，等可能地取出一个，记取出的非空子集中元素个数为ξ，则ξ的数学期望Eξ=_________．18．（2012•台州一模）把2对孪生兄弟共4人随机排成一排，记随机变量ξ为这一排中孪生兄弟相邻的对数，则随机变量ξ的期望Eξ=_________．19．（2012•杭州二模）（理）设整数m是从不等式x2﹣2x﹣8≤0的整数解的集合S中随机抽取的一个元素，记随机变量ξ=m2，则ξ的数学期望Eξ=_________．20．（2011•温州二模）甲、乙两个同学每人有两本书，把四本书混放在一起，每人随机从中拿回两本，记甲同学拿到自己书的本数为ξ，则Eξ=_________．21．一个人随机的将编号为1，2，3，4的四个小球放入编号为1，2，3，4的四个盒子，每个盒子放一个小球，球的编号与盒子的编号相同时叫做放对了，否则叫做放错了．设放对的个数记为ξ，则ξ的期望Eξ=_________．22．设口袋中有黑球、白球共9个球，从中任取2个球，若取到白球个数的数学期望为，则口袋中白球的个数为_________．23．（2011•嘉定区三模）某班从5名班干部（其中男生3人，女生2人）中选3人参加学校学生会的干部竞选．设所选3人中女生人数为ξ，则随机变量ξ的方差Dξ=_________．24．（2012•重庆）甲、乙两人轮流投篮，每人每次投一球．约定甲先投且先投中者获胜，一直到有人获胜或每人都已投球3次时投篮结束．设甲每次投篮投中的概率为，乙每次投篮投中的概率为，且各次投篮互不影响．（Ⅰ）求甲获胜的概率；（Ⅱ）求投篮结束时甲的投篮次数ξ的分布列与期望．25．（2012•四川）某居民小区有两个相互独立的安全防范系统（简称系统）A和B，系统A和B在任意时刻发生故障的概率分别为和p．（Ⅰ）若在任意时刻至少有一个系统不发生故障的概率为，求p的值；（Ⅱ）设系统A在3次相互独立的检测中不发生故障的次数为随机变量ξ，求ξ的概率分布列及数学期望Eξ．26．（2012•山东）现有甲、乙两个靶．某射手向甲靶射击一次，命中的概率为，命中得1分，没有命中得0分；向乙靶射击两次，每次命中的概率为，每命中一次得2分，没有命中得0分．该射手每次射击的结果相互独立．假设该射手完成以上三次射击．（Ⅰ）求该射手恰好命中一次得的概率；（Ⅱ）求该射手的总得分X的分布列及数学期望EX．27．甲、乙两个篮球运动员互不影响地在同一位置投球，命中率分别为与p，且乙投球2次均未命中的概率为．（Ⅰ）求乙投球的命中率p；（Ⅱ）若甲投球1次，乙投球2次，两人共命中的次数记为ξ，求ξ的分布列和数学期望．28．甲、乙俩人各进行3次射击，甲每次击中目标的概率为，乙每次击中目标的概率为．（Ⅰ）记甲击中目标的次数为ξ，求ξ的概率分布及数学期望Eξ；（Ⅱ）求乙至多击中目标2次的概率；（Ⅲ）求甲恰好比乙多击中目标2次的概率．29．一接待中心有A、B、C、D四部热线电话，已知某一时刻电话A、B占线的概率均为0.5，电话C、D占线的概率均为0.4，各部电话是否占线相互之间没有影响．假设该时刻有ξ部电话占线．试求随机变量ξ的概率分布和它的期望．30．（2014•淄博三模）一个袋子装有大小形状完全相同的9个球，其中5个红球编号分别为1，2，3，4，5，4个白球编号分剐为1，2，3，4，从袋中任意取出3个球．（Ⅰ）求取出的3个球编号都不相同的概率；（Ⅱ）记X为取出的3个球中编号的最小值，求X的分布列与数学期望．。

4.2随机变量的方差




例3 设X1, X2, …, Xn相互独立，有共同的期
望 和方差 2 ， 则: 证明:
n 1 n 1 1 n E ( X i ) E ( X i ) E ( X i ) , n i 1 n i 1 n i 1 n 1 n 1 1 n 1 2 D( X i ) 2 D( X i ) 2 D( X i ) . n i 1 n n i 1 n i 1
D(X)=D(X1+X2+…+Xn) =D(X1)+D(X2)+…+D(Xn)= npq.
设随机变量 X 的期望E(X )、方差D(X )都 存在, 且D(X ) 0, 则称
X

X E( X ) D( X )
为 X 的标准化随机变量. 显然，
E ( X ) 0, D( X ) 1
1 n E( X i ) , n i 1
1 n 1 2 D( X i ) . n i 1 n
例4 已知随机变量X1,X2,…,Xn相互独立，且 每个Xi的期望都是0，方差都是1，令Y= X1+X2+…+Xn .求 E(Y2). 解：由已知，则有
E (Y ) E (Y1 ) E (Y2 ) E (Yn ) 0 D(Y ) D(Y1 ) D(Y2 ) D(Yn ) n
若X的取值比较集中，则方差较小； 若X的取值比较分散，则方差较大.
1) D(X)0，即方差是一个非负实数. 2）当X 服从某分布时，我们也称某分布的方差 为D(X). 3) 方差是刻划随机变量取值的分散程度的一个 特征.
(1)若 X 为离散型，概率分布为
P X xk pk , k 1, 2,
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

σ 0, x .
先求标准正态变量 Z x μ 的数学期望和方差. σ
Z的概率密度为 (t) 1 et2 2,
2π
于是 E(Z ) 1 tet2 2 d t 1 et2 2 0，
2π
2π
D(Z ) E(Z 2 )
1 t 2et2 2 d t
2π
1 tet2 2 1 et2 2 d t
求D( X ).
解 E( X ) 0 (1 p) 1 p p, E( X 2 ) 02 (1 p) 12 p p,
由(2.4)式 D( X ) E( X 2 ) [E( X )]2 p p2 p(1 p).
例3 设 X ~ π( ), 求D( X ).
解 X 的分布律为
2π
2π
1，
因 X Z,
即得 E( X ) E( Z ) μ.
D( X ) D( Z ) D(Z ) 2D(Z ) σ 2.
正态分布的期望和方差分别为两个参数 μ 和 σ2.
若X i
~
N
(
i
,
2 i
),
i
1,2,
, n,
且它们相互独
立，则它们的线性组合：C1 X1 C2 X2 Cn Xn
D( X C ) E{[X C E( X C)]2} E{[X E( X )]2} D( X ).
3 设 X ,Y 是两个随机变量，则有 D( X Y ) D( X ) D(Y ) 2E{(X E( X ))(X E(Y ))}.
若 X ,Y 相互独立, 则有 D( X Y ) D( X ) D(Y ).
第二节 方 差
一、随机变量方差的概念及性质 二、重要概率分布的方差 三、例题讲解 四、小结
一、随机变量方差的概念及性质
1. 概念的引入
方差是一个常用来体现随机变量取值分散程度 的量. 实例 有两批灯泡,其平均寿命都是 E(X)=1000小时.
•
• • • • • •• • •
O
1000
x
• •• • •
2E{(X E( X ))(X E(Y ))} 2E{XY XE(Y ) YE( X ) E( X )E(Y )}
2{E( XY ) E( X )E(Y ) E(Y )E( X ) E( X )E(Y )}
2{E( XY ) E( X )E(Y )}.
若 X ,Y 相互独立,由数学期望的性质4 知道上 式右端为0，于是
E
X
2
1
2 E[( X
)2]
2 2
1.
X X ,
则 E( X ) 1 E( X ) 1 [E( X ) ] 0;
D( X ) E( X 2 ) [E( X )]2
E
X
2
1
2 E[( X
)2]
2 2
1.
例2 设随机变量X 具有(0 1)分布,其分布律为 P{X 0} 1 p, P{X 1} p.
D( X Y ) D( X ) D(Y ). 这一性质可以推广到任意有限多个相互独立的随 机变量之和的情况.
推广 若 X1, X2, , Xn 相互独立, 则有
D( X1 X2 Xn )D( X1) D( X2 ) D( Xn ).
(4) D( X ) 0 的充要条件是 X 以概率1 取常数 C,
(n2 n) p2 np (np)2
np(1 p).
3. 泊松分布
设 X ~ π( ), 且分布律为
P{X k} k e , k 0,1,2, , 0.
k! 则有
E(X
)
k
k0
k
k!
e
e
k 1
k1 (k 1)!
e e .
E( X 2 ) E[ X ( X 1) X ]
3. 方差的意义
按定义, 随机变量 X 的方差表达了X 的取值与 其数学期望的偏离程度. 若 D( X )较小意味着X 的 取值比较集中在E( X )的附近, 反之, 若 D( X )较大 则表示 X 的取值较分散. 因此, D( X )是刻画X 取 值分散程度的一个量,它是衡量X 取值分散程度 的一个尺度.
a
2
b
2
(b a)2 . 12
例5 设随机变量 X 服从指数分布, 其概率密度为
1 ex θ , x 0,
f (x) θ
0,
x 0.
其中θ 0, 求E( X ), D( X ).
解 E( X ) xf ( x)d x x 1 ex θ d x
0θ
xex θ ex θ d x θ. 00
设随机变量 X 服从指数分布,其概率密度为
则有
1 ex θ , x 0,
f (x) θ
0,
x 0.
E( X ) xf ( x)d x x 1 ex θ d x
0θ
xe x θ 0
ex θ d x θ.
0
E( X 2 ) x2 f ( x)d x
x2 1 e x θ d x
(2) 利用公式计算
D( X ) E( X 2 ) [E( X )]2. 证 D( X ) E{[X E( X )]2}
E{X 2 2XE( X ) [E( X )]2} E( X 2 ) 2E( X )E( X ) [E( X )]2 E( X 2 ) [E( X )]2
泊松分布的期望和方差相等, 都等于参数 .
例4 设 X ~ U (a,b), 求( X ).
解 X 的概率密度为
f (x)
1, ba
0,
a x b, 其他.
上节例7已算得 E( X ) a b , 方差为 2
D( X ) E( X 2 ) [E( X )]2
b a
x
2
b
1
a
d
x
E[X ( X 1)] E( X )
k(k 1) k e
k0
k!
2e
k 2
k2 (k 2)!
2e e
2
.
所以 D( X ) E( X 2 ) [E( X )]2 2 2 .
泊松分布的期望和方差都等于参数 .
4. 均匀分布
设 X ~ U(a,b), 其概率密度为
5. 方差的性质
1 设 C 是常数，则D(C ) 0.
证 D(C) E{[C E(C)]2} 0. 2 设 X 是一个随机变量，C是常数，则有 D(CX ) C 2D( X )， D( X C) D( X ).
证 D(CX ) E{[CX E(CX )]2} C 2E{[X E( X )]2} C 2D( X ).
k0
n
n k(k 1)n!pk (1 p)nk np
k0 k!(n k)!
n
n(n 1) p2
(n 2)! pk2 (1 p)(n2)(k2)
k2 (n k)!(k 2)!
np
n(n 1) p2[ p (1 p)]n2 np
(n2 n) p2 np.
D( X ) E( X 2 ) [E( X )]2
E( X 2 ) x2 f ( x)d x x2 1 ex θ d x
0
θ
x2e x θ 2 xe x θ d x θ 2 . 00
于是 D( X ) E( X 2 ) [E( X )]2 2θ2 θ2 θ2 .
即有 E( X ) θ, D( X ) θ2 .
例6 设 X ~ b(n, p), 求E( X ), D( X ).
解 由二项分布的定义知,随机变量X 是 n重伯 努利试验中事件A发生的次数, 且在每次试验中A 发生的概率为p . 引入随机变量
Xk
1, 0，
A在第k次试验发生， k A在第k次试验不发生，
1,2,
4. 随机变量方差的计算
(1) 利用定义计算
对于离散型随机变量
D( X ) [ xk E( X )]2 pk ,
k 1
其中 P{X xk } pk , k 1,2, 是 X 的分布律. 对于连续型随机变量
D( X ) [ x E( X )]2 f ( x)d x,
其中 f ( x) 为X的概率密度.
0
θ
x2e x θ 2 xe x θ d x
0
0
θ2.
D( X ) E( X 2 ) [E( X )]2 2θ2 θ2 θ2 .
指数分布的期望和方差分别为θ 和 θ2.
6. 正态分布
设 X ~ N ( μ,σ2 ), 其概率密度为
f (x)
1 e ,
(
x μ 2σ2
)2
2πσ
E(Z ) 2 1 3 2 4, D(Z ) D(2X 3Y ) 4D( X ) 9D(Y ) 48.
故有Z ~ N (4,48).
分布 两点分布 二项分布
泊松分布 均匀分布 指数分布 正态分布
参数
0 p1 n 1,
0 p1
0
ab
θ0 μ,σ 0
数学期望 方差
p
p(1 p)
证 D( X Y ) E{[(X Y ) E( X Y )]2} E{[X E( X )] [Y E(Y )]}2 E[X E( X )]2 E[Y E(Y )]2
2E{[X E( X )][Y E(Y )]} D( X ) D(Y ) 2E{(X E( X ))(X E(Y ))}. 上式右端第三项:
f (x)
1, ba
0,
a x b, 其他.
则有E( X )
b1
xf ( x)d x
xd x
aba
1 (a b). 2
结论 均匀分布的数学期望位于区间的中点.
D( X ) E( X 2 ) [E( X )]2