下载文档原格式
复杂反应 ------ 丙酮碘化反应实验目的1. 采用分光光度法测定用酸作催化剂时丙酮碘化反应的速率系数、反应级数和活化能。
2. 通过本实验加深对复合反应特征的理解。
3. 熟练掌握分光光度计的原理和使用方法。
实验原理只有少数化学反应是由一个基元反应组成的简单反应，大多数化学反应并不是简单反应，而是由若干个基元反应组成的复合反应。
大多数复合反应的反应速率和反应物浓度间的关系，不能用质量作用定律表示。
因此用实验测定反应速率与反应物或产物浓度间的关系，即测定反应对各组分的分级数，从而得到复合反应的速率方程，乃是研究反应动力学的重要内容。
对于复合反应，当知道反应速率方程的形式后，就可以对反应机理进行某些推测。
如该反应究竟由哪些步骤完成，各个步骤的特征和相互联系如何等等。
实验测定表明，丙酮与碘在稀薄的中性水溶液中反应是很慢的。
在强酸（如盐酸）条件下，该反应进行得相当快。
但强酸的中性盐不增加该反应的反应速率。
在弱酸（如醋酸）条件下，对加快反应速率的影响不如强酸（如盐酸）。
酸性溶液中，丙酮碘化反应是一个复合反应，其反应式为：+H+32332(CH )CO+I CH COCH I+H +2I −−→－－ （1） 该反应由H +催化，而反应本身又能生成H +，所以这是一个H +自催化反应，其速率方程为：()()()()()()3αβδ+3-dc I -dc A dc E r ====kc A c I c H dt dt dt－－ （2）式中：r —反应速率；k —速率系数；()c A 、()3c I －、()+c H 、()c E —分别为丙酮、碘、氢离子、碘化丙酮的浓度，-3mol dm ；α、β、γ—分别为反应对丙酮、碘、氢离子的分级数。
反应速率、速率系数及反应级数均可由实验测定。
丙酮碘化对动力学的研究是一个特别合适而且有趣的反应。
因为3I －在可见光区有一个比较宽的吸收带，而在这个吸收带中，盐酸和丙酮没有明显的吸收，所以可以采用分光光度计测定光密度的变化（也就是3I －浓度的变化）来跟踪反应过程。
关于“复合反应速率近似处理法”的解析作者：贺晓凌来源：《新一代》2019年第22期摘要：物理化学课程中，化学动力学部分通过反应机理推导复合反应速率方程，是较难掌握的知识点，本文结合实例，对“复合反应速率近似处理法”进行解析。
关键词：物理化学;化学动力学;复合反应速率;近似处理法物理化学是高等院校化学化工类专业非常重要的基础理论课，理论性强、概念抽象、公式繁多，学生学习感觉困难较大，其中化学动力学部分通过反应机理推导复合反应速率方程，是较难掌握的知识点，本文就“复合反应速率近似处理法”进行解析。
一、复合反應速率近似处理法介绍化学动力学部分，研究的重点是反应速率、速率方程以及相关定律、理论。
对于基元反应的速率方程，可以依据质量作用定律，根据反应方程式直接写出，但对于非基元反应，则需要通过机理推导速率方程。
非基元反应由一系列基元反应组成，如果按数学方法处理，每个基元反应可以列一个微分方程，需要解微分方程组进行求解，这样求解复杂程度加剧，甚至有的反应无法求解，因此，采用近似处理法相当必要，可以使问题大大简化，而且得出正确的结果。
复合反应速率近似处理法包括三种方法[1]：（1）速率控制步骤法：连串反应由一连串基元反应组成，每一个基元反应都有一个反应速率，但总反应的反应速率由最慢一步反应的反应速率决定，因此总反应的反应速率近似等于最慢反应的反应速率。
（2）平衡态近似法：机理为A+B; C→D的复合反应，前边为一快平衡，后边为一慢反应，求其速率方程可用平衡态近似法。
平衡态近似法的解题思路为：根据慢步骤，依据质量作用定律，写出速率方程，但此时速率方程中往往含有中间产物的浓度项，再通过前边的快平衡，利用平衡常数和各反应组分浓度的关系，将中间产物的浓度求出，代入慢步骤的速率方程，进行数学整理，最后得到总反应的速率方程。
（3）稳态近似法：连串反应中，若中间产物非常活泼，一旦生成，立即经后续反应反应掉，因此其浓度没有积累，不随时间变化，即dCB/dt=0，式中CB为中间产物浓度，t为反应时间。
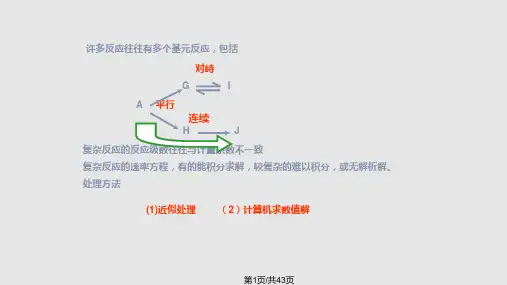
§10.2 复合反应近似处理方法前节讨论的典型复合反应是几种最简单的复合反应类型。
对峙反应中除正、逆向都是一级反应的1-1级外，还有1-2级、2-1级、2-2级等，平行反应和连串反应中也有多级数的反应，此外，很多复合反应往往同时包含对峙反应、平行反应或连串反应等。
对于这些复杂的复合反应，如果试图通过严格求解微分方程从而找出各物质的浓度随时间的变化关系，往往十分困难，有时甚至是难以办到的。
为此，化学动力学中经常采用一些近似方法来处理这些复杂的复合反应。
前节提到的“速率控制步骤”就是一种近似处理方法。
此外，常用的近似方法还有稳态近似法和平衡态近似法。
(1) 稳态近似法以最简单的连串反应为例：AC k 1k 2所谓稳态，严格而论，应该是A 、B 、C 的浓度均不随时间而变化的状态。
显然，这只有在不断引入A 移走C 的开放流动系统中方可能实现。
对于封闭的反应系统，A 和C 都不可能达到稳态，除非反应实际上没有进行。
但是，反应进行一段时间后，中间产物B 有可能达到近似的稳态，即物质B 的生成速率和消耗速率相差甚微，[B]随时间的变化几乎可以忽略不计。
即12[B][A][B]0d k k dt=-≈ 由此可以比较方便地求出物质B 达到稳态时的浓度：1ss 2[B][A]kk = （10.17）[B]ss 表示物质B 的稳态浓度。
将1[A]e k t a -=，即(10.15a)式代入上式，则11ss 2[B]e k t ka k -= （10.18）前节通过严格求解微分方程，得到[B]的表示式即(10.15b)式为121()121[B]e [1e ]k t k k t k a k k ---=--不难看出，当k 2>>k 1时，该式即可化简为(10.18)式的形式。
假设中间产物的生成速率和消耗速率近似相等的处理方法称为“稳态近似法”。
对于不同的反应机理，稳态近似法的适用条件是不同的。
通常，当中间产物非常活泼并因而以极小浓度存在时，运用稳态近似法是适宜的。
