有限单元法作业非线性分析+程序

轨道结构的非线性有限元分析姜建华 练松良摘 要 实际轨道结构受载时的力学行为,属于典型的非线性力学问题。

钢轨垫层刚度、钢轨抗扭刚度和扣件扣压力的大小是影响轨距扩大的主要因素。

根据非线性有限元接触理论,建立了能准确反映扣件、钢轨与垫层的拧紧接触,以及受载车轮与钢轨侧向滑动接触的力学计算模型;并研究计算了不同扣件压力下,由于受载车轮与钢轨侧向滑动接触引起的轨距扩大问题。

关键词 轮轨关系,扣件压力,非线性弹性力学,有限元分析1 引言实际工程中常见的非线性问题一般可以归纳为三类:材料非线性、几何非线性以及边界条件非线性。

材料非线性问题是由于材料的非线性本构关系所引起的,例如材料的弹塑性变形,材料的屈服和硬化等;几何非线性问题是由于结构的位移或变形相当大,以至必须按照变形后的几何位置来建立平衡方程;边界条件非线性问题是指边界条件随位移变化所引起的非线性问题。

通常情况下,我们所遇到的非线性问题多数是上述三类非线性问题的组合[1,2]。

实际轨道结构受载时的力学行为,属于典型的非线性力学问题。

比如基于轮轨接触的材料非线性、几何非线性及边界条件非线性问题,以及扣件、钢轨、垫层三者间相互作用时所表现的边界条件非线性行为等。

所以,机车车辆在轨道结构上行驶时引起的力学现象是相当复杂的。

以往在研究轨道各部分应力应变分布规律时,通常采用连续弹性基础梁理论或连续点支承,偶尔简单考虑扣件的作用和弹性垫层的使用。

不管用哪一种支承方式建立模型,都由于这样那样的假设而带有一定程度的近似性。

所以,如何利用现代力学理论的最新成果以及日益发展的计算机技术,根据轨道结构的具体情况,建立更为完整更为准确的轨道结构计算模型,为轨道设计部门提供更加可靠的设计依据或研究思路,已十分必要。

本文提出了用非线性有限元理论研究轮轨系统和轨道结构的思路。

作为算例之一,本文将根据非线性有限元理论,建立能准确反映扣件、钢轨与垫层的拧紧接触,以及受载车轮与钢轨侧向滑动接触的力学计算模型。

第八章 几何非线性问题的有限元法8.1 引言前面各章所讨论的问题都是在小变形假设的前提下进行的，即假定物体所发生的位移远小于物体自身的几何尺寸，应变远小于1。

在此前提下，建立物体或微元体的平衡条件时可以不考虑物体的位置和形状（简称位形）的变化，因此在分析中不必区别变形前后位形的差别，且应变可用一阶无穷小的线性应变表达。

实际上，上述假设有时是不成立的。

即使实际应变可能是小的，且不超过材料的弹性极限，但如果需要精确地确定位移，就必须考虑几何非线性，即平衡方程应该相对于变形后的位置得出，而几何关系应该计及二次项。

例如平板大挠度理论中，由于考虑了中面内的薄膜应力，求得的挠度比小挠度理论的结果有显著的减低。

再如在结构稳定性问题中，当载荷达到一定数值后，挠度比线性解答予示的结果更剧烈地增加，并且确实存在承载能力随继续变形而减低的现象。

在冷却塔、薄壁结构及其它比较细长的结构中，几何非线性分析都显得十分重要。

几何非线性问题可以分为以下几种类型：（1）大位移小应变问题。

一般工程结构所遇到的几何非线性问题大多属于这一类。

例如高层建筑或高耸构筑物以及大跨度网壳等结构的分析常需要考虑到结构大位移的影响。

（2）大位移大应变问题，如金属压力加工中所遇到的问题就属于这一类型。

（3）结构的变形引起外载荷大小、方向或边界支承条件的变化等。

结构的平衡实际上是在结构发生变形之后达到的，对于几何非线性问题来说，平衡方程必须建立在结构变形之后的状态上。

为了描述结构的变形需要设置一定的参考系统。

一种做法是让单元的局部坐标系始终固定在结构发生变形之前的位置，以结构变形前的原始位形作为基本的参考位形，这种分析方法称作总体的拉格朗日（Ｌagrange ）列式法；另一种做法是让单元的局部坐标系跟随结构一起发生变位，分析过程中参考位形是不断被更新的，这种分析方法称作更新的拉格朗日列式法。

本章首先对几何非线性问题作一般性讨论，从中导出经典的线性屈曲问题的公式；然后建立平板大挠度问题和壳体的大位移（及大转动）分析的有限方法公式；接着还给出了大应变及大位移的一般公式，最后还详细讨论了杆系结构几何非线性问题的有关公式。

非线性问题的类型和求解特点1 非线性问题的类型1. 1 线性分析的含义在有限元分析中的线性假设包含下列含义：即结点位移为无限小量，材料为线弹性，加载时边界条件的性质保持不变。

于是，静力平衡方程可以表示为：[]{}{}R U K = (2.1)其中，[]K 为刚度矩阵，{}R 为荷载矢量。

由于[]K 和{}R 的元素为常数，故位移响应{}U 是荷载矢量{}R 的线性函数。

也就是说，如果{}R 变为{}R α，则{}U 变为{}U α，其中，α为常数。

这就是所谓的线性有限元分析。

如果上述假设中的任何一条不能得到满足，那么就属于非线性有限元分析。

1. 2 非线性分析的必要性结构力学问题，从本质上讲都是非线性的，线性假设只是实际工程问题的一种简化。

当然，任何实际工程问题的求解都避免不了适当地简化，简化是否合理主要应根据求解效果和实际经验来判断。

对于目前工程实际中的很多问题，如地震作用下结构的弹塑性动力响应，高层建筑抗风，大跨度网壳结构动力稳定性，索膜结构找形荷载与裁减分析，大型桥梁风致振动等问题的研究，仅仅假设为线性问题是很不够的，常常需要进一步考虑为非线性问题。

因此，对各种工程结构的非线性分析就是必不可少且日趋重要了。

对于结构力学的非线性问题来说，有限单元法是最为有效的数值分析方法。

1. 3 非线性问题的类型通常，把非线性问题分为两大类，即分为几何非线性和材料非线性。

但从建立基本方程和程序设计的方便出发，又可分为三种类型：1．材料非线性：非线性效应仅由应力应变关系的非线性引起，位移分量仍假设为无限小量，故仍可采用工程应力和工程应变来描述，即仅材料为非线性。

非线性的应力应变关系是结构非线性的常见原因，许多因素都可以影响材料的应力应变性质，包括加载历史（如在弹塑性响应状况下），环境状况（如温度），加载的时间总量（如在蠕变响应状况下）等。

2．几何非线性：如果结构经受大变形，则变化了的几何形状可能会引起结构的非线性响应，这又可以分为两种情形：第一种情形，大位移小应变。

第9章非线性问题的有限单元法9.1 非线性问题概述前面章节讨论的都是线性问题，但在很多实际问题中，线弹性力学中的基本方程已不能满足，需要用非线性有限单元法。

非线性问题的基本特征是变化的结构刚度，它可以分为三大类：材料非线性、几何非线性、状态非线性。

1. 材料非线性(塑性, 超弹性, 蠕变)材料非线性指的是材料的物理定律是非线性的。

它又可分为非线性弹性问题和非线性弹塑性问题两大类。

例如在结构的形状有不连续变化（如缺口、裂纹等）的部位存在应力集中，当外载荷到达一定数值时该部位首先进入塑性，这时在该部位线弹性的应力应变关系不再适用，虽然结构的其他大部分区域仍保持弹性。

2. 几何非线性(大应变, 大挠度, 应力刚化)几何非线性是有结构变形的大位移引起的。

例如钓鱼杆，在轻微的垂向载荷作用下，会产生很大的变形。

随着垂向载荷的增加，杆不断的弯曲，以至于动力臂明显减少，结构刚度增加。

3. 状态非线性(接触, 单元死活)状态非线性是一种与状态相关的非线性行为。

例如，只承受张力的电缆的松弛与张紧；轴承与轴承套的接触与脱开；冻土的冻结与融化。

这些系统的刚度随着它们状态的变化而发生显著变化。

9.2 非线性有限元问题的求解方法对于线性方程组，由于刚度方程是常数矩阵，可以直接求解，但对于非线性方程组，由于刚度方程是某个未知量的函数则不能直接求解。

以下将简要介绍借助于重复求解线性方程组以得到非线性方程组解答的一些常用方法。

1.迭代法迭代法与直接法不同，它不是求方程组的直接解，而是用某一近似值代人，逐步迭代，使近似值逐渐逼近，当达到允许的规定误差时，就取这些近似值为方程组的解。

与直接法相比，迭代法的计算程序较简单，但迭代法耗用的机时较直接法长。

它不必存贮带宽以内的零元素，因此存贮量大大减少，且计算中舍入误差的积累也较小。

以平面问题为例，迭代法的存贮量一般只需直接法的14左右。

在求解非线性方程组时，一般采用迭代法。

2. 牛顿—拉斐逊方法ANSYS程序的方程求解器计算一系列的联立线性方程来预测工程系统的响应。

非线性有限元分析1 概述在科学技术领域内，对于许多力学问题和物理问题，人们已经得到了它们所应遵循的基本方程（常微分方程或偏微分方程）和相应的定解条件（边界条件）。

但能够用解析方法求出精确解的只是少数方程性质比较简单，并且几何形状相当规则的问题。

对于大多数工程实际问题，由于方程的某些特征的非线性性质，或由于求解区域的几何形状比较复杂，则不能得到解析的答案。

这类问题的解决通常有两种途径。

一是引入简化假设，将方程和几何边界简化为能够处理的情况，从而得到问题在简化状态下的解答。

但是这种方法只是在有限的情况下是可行的，因为过多的简化可能导致误差很大甚至是错误的解答。

因此人们多年来一直在致力于寻找和发展另一种求解途径和方法——数值解法。

特别是五十多年来，随着电子计算机的飞速发展和广泛应用，数值分析方法已成为求解科学技术问题的主要工具。

已经发展的数值分析方法可以分为两大类。

一类以有限差分法为代表，主要特点是直接求解基本方程和相应定解条件的近似解。

其具体解法是将求解区域划分为网格，然后在网格的结点上用差分方程来近似微分方程，当采用较多结点时，近似解的精度可以得到改善。

但是当用于求解几何形状复杂的问题时，有限差分法的精度将降低，甚至发生困难。

另一类数值分析方法是首先建立和原问题基本方程及相应定解条件相等效的积分提法，然后再建立近似解法并求解。

如果原问题的方程具有某些特定的性质，则它的等效积分提法可以归结为某个泛函的变分，相应的近似解法实际上就是求解泛函的驻值问题。

诸如里兹法，配点法，最小二乘法，伽辽金法，力矩法等都属于这一类方法。

但此类方法也只能局限于几何形状规则的问题，原因在于它们都是在整个求解区域上假设近似函数，因此，对于几何形状复杂的问题，不可能建立合乎要求的近似函数。

1960年，R.W.CLOUGH发表了有限单元法的第一篇文献“The Finite Element Method in Plane Stress Analysis”，这同时也标志着有限单元法（FEM）的问世。

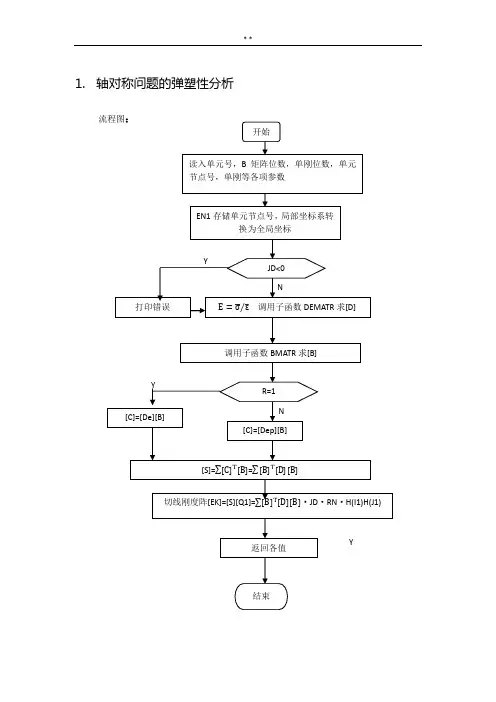
1.轴对称问题的弹塑性分析解析解。

厚壁筒受内压，采用Mises 屈服准则σθ−σγ=√3s(1)经计算知，当t=12.5（12.91）时，材料处于弹塑性交界面。

弹性区为:t ≤r ≤bσr=t 2σs √3b 2(b 2r 2−1) (2)σθ=t 2σs √3b 2(b 2r 2+1) (3)塑性区：a ≤r ≤tσr=3sln ra −P (4) σθ=3s(1+ln ra)−P (5)交界处有：r =t ，σre =σrpP =σs√3−t 2b +2ln ta ) (6) 最后解得残余应力为：σr r=√3sln ra−b 2P b 2−a 2(1−a 2r 2) ，a ≤r ≤t (7a) σr r =(σs t 2√3b2a 2Pb 2−a 2)(1−a 2r2) ，t ≤r ≤b (7b) σθr=3s (1+ln ra )−b 2Pb 2−a 2(1+a 2r 2) ，a ≤r ≤t (8a) σθr =(σst 2√3b2a 2P b 2−a 2)(1+a 2r2) ，a ≤r ≤t (8b)有限元网格信息图：图1 有限元网格输入数据文件内容(详细信息见附件):DATA(1)NNODE MELEM IFU IFW IPF IPR NPP NRM HAC MSF NULOAD EXPNM(1-MELEM) NNNN(1-NNODE) R ZNFU(1-IFU) FUNFW(1-IFW) FWMPQ(1-IPF) NPQ*PQNPRNRZ(1-IPR) PRNRZE EMU SSS HH UNLOAD对理想塑性材料厚壁筒，从初始状态开始，历经加载后完全卸载。

这一过程中，厚壁筒内会产生残余应力。

沿径向R的残余应力如图2-3所示。

-1.6-1.4-1.2-1-0.8-0.6-0.4-0.2101214161820R a d i a l s t r e s sRadius R图2 径向残余应力-半径曲线-15-10-55101214161820T a n g e n t i a l s t r e s sRadius R图3 切向残余应力-半径曲线图2-3中分别给出了径向残余应力和切向残余应力随半径的变化，并且和解析解进行了比较。

非线性有限元之非线性求解方法平衡回顾✧静态平衡是内力I和外载P力量平衡；✧在非线性问题中，模型的内力I可以是以下量的非线性函数；✧在非线性问题中，模型的外力P也可以是某些量的非线性函数，如位移u和时间t。

非线性求解方法1.已知一个分析，知道结构总载荷和初始刚度，目的是找到最后的位移。

线性分析中，一次计算就能求解出最终位移；非线性问题中不可能，因为结构刚度随着结构变形而改变。

2.求解这类非线性问题需要的是一种增量\迭代技术，获得的解是非线性问题准确的近似。

这些方程通常没有精确解。

3.Abaqus使用迭代求解该方程：使用牛顿拉普森方法求解近似解，使误差最小。

4.Abaqus用法：1）载荷历史被拆解为一系列的分析步；每个分析步拆解为一系列增量步；用户为初始时间增量猜测一个值；Abaqus使用自动增量算法确定其他的增量步。

在每个增量步结束时，Abaqus根据载荷与时间关系计算当前负载大小2）使用牛顿拉普森程序迭代求解每个增量结束时的解；根据收敛容差判断牛顿拉普森程序的收敛；如果迭代不收敛，减少增量步的大小；然后使用小增量步重新进行计算。

5.分析步、增量步、迭代步1）分析步仿真载荷历程含有一个或多个分析步。

2）增量步是分析步的一部分；在静态问题中，总载荷被分成很小的增量步。

以便可以沿着非线性路径求解。

3）迭代步迭代步是增量步中寻找平衡解得一次计算尝试。

5.牛顿拉普森方法Abaqus/Standard 基于牛顿拉普森方法的增量迭代求解技术，该方法是无条件稳定（任何大小的增量步都可以）。

增量步大小影响动态分析精度，每个增量步通常要求多次迭代才能满足收敛要求，每个分析步通常有多个增量步，牛顿拉普森定义了一个残差为0位移曲线。

6.牛顿拉普森方法基础。

平衡是u的非线性方程，牛顿拉普森迭代求解在Cu 处的线性方程，Cu是位移u的修正量。

7.残差定义为了得到线性方程组，重写一下平衡方程，R（u）是u的残差。

这个残差表示的是位移u处不平衡力。

工程结构分析专业毕业设计论文：基于有限元法的复杂结构非线性分析模型建立结构非线性分析模型建立摘要：随着工程结构的复杂性和不确定性增加，有限元法在结构分析中变得越来越重要。

本文旨在建立基于有限元法的复杂结构非线性分析模型，以提高对复杂结构的行为和响应的准确理解。

本文的研究内容主要包括研究背景、意义、目的、方法、步骤、未来发展方向、结果和结论等。

1. 研究背景和意义有限元法是一种广泛应用于工程结构分析的数值计算方法，它可以将一个连续的求解域离散成有限个小的子域，即“有限元”，从而将连续的偏微分方程转化为离散的线性方程组进行求解。

在处理复杂的结构形式、非线性的材料行为以及复杂边界条件等方面，有限元法具有显著的优势。

然而，有限元法的应用面临一些挑战，特别是在处理复杂结构时。

首先，有限元模型的建立过程较为繁琐，需要对结构的几何形状、材料属性、边界条件等进行精细的建模。

其次，由于模型的复杂性和非线性，往往需要采用更高级的有限元方法和计算工具进行求解，增加了计算成本和难度。

因此，本文的研究旨在建立基于有限元法的复杂结构非线性分析模型，为准确评估复杂结构的行为和响应提供有效的方法和工具。

2. 研究目的本文的研究目的主要包括以下几点：（1）探讨基于有限元法的复杂结构非线性分析模型建立的方法和流程；（2）分析有限元模型在复杂结构分析中的优势和存在的问题；（3）验证有限元模型的准确性和可靠性；（4）提出未来在工程结构分析中应用有限元法的发展方向。

3. 研究方法本文的研究方法主要包括理论分析、实验研究和数值模拟等。

首先，基于有限元法的基本原理，建立复杂结构非线性分析模型；然后，利用实验和数值模拟方法对模型进行验证和修正；最后，对模型进行实际应用和测试。

4. 研究步骤本文的研究步骤如下：（1）了解和掌握有限元法的基本原理和方法；（2）分析复杂结构的特点和非线性行为，确定模型的关键要素；（3）基于有限元法建立复杂结构非线性分析模型；（4）设计实验方案，采集结构的响应数据；（5）利用数值模拟方法对模型进行求解和验证；（6）将模型应用于实际工程结构，进行评估和测试；（7）总结研究成果，撰写毕业设计论文。

土体非线性有限元程序说明一、程序功能和特点:1.本程序为平面变形问题非线性有限元程序,可用于计算土坝、地基、•挡土墙或地下结构的应力和变形。

2.土的非线性应力--应变关系采用邓肯双曲线模式另一个弹性常数可有两种选择:(a)切线泊松比:(b)切线体积模量:3.解题方法为中点增量法,•考虑到每级加荷的两次计算所得的弹性常数对某些单元可能相差较大,而实际可能处于这两者之间,因此取两者的某种加权平均值作为修正的计算弹性常数,其中初始弹性常数取权为1/4,中点弹性常数取权为3/4,•以反映平均结果接近中点弹性常数。

4.网格为任意四边形等参数单元。

5.程序中包含了一维的Goodman接触单元。

6.蓄水引起的湿化,由干、湿两种状态下不同的非线性参数进行计算。

7.可模拟施工过程逐级加荷。

8.坐标方向:y坐标以向上为正,x坐标以向下游为正。

二、输入数据1.九个控制数据NNN----结点总数;NEE----非接触单元总数(不包括接触单元数);NJJ----接触单元总数(若无接触单元,填0);NX-----X向位移为0的结点数;NY-----Y向位移为0的结点数;NPP----加荷级数;NMT----材料类型数,接触单元材料类型也计入其中;III----参数(0--弹性常数用E,μ; 1--弹性常数为E,B);IA-----参数(0--不打印输入输出数据中的长数组; 1--打印输入输出数据中的长数组);2.IX-----X向位移为0的结点号,共NX个数;3.IY-----Y向位移为0的结点号,共NY个数;4.x,y----各结点的x,y坐标,每个结点两个数,5个结点的10个数为一行(也可按需要进行修改);结点编号顺序根据网格情况而定,可以横向为序编号,也可以竖向编号,以带宽小为准则;5.ME和MTME为各单元的四个结点号,逆时针为序,若为过渡单元,只有三个结点,则第四个点重复第三点号;MT为单元材料类型号,材料各类型排列顺序须按数组CT中的次序。

几何非线性大作业荷载增量法和弧长法程序设计一、几何非线性大作业（Newton-Raphson法）用荷载增量法（Newton-Raphson法）编写几何非线性程序：（1）用平面梁单元，可分析平面杆系（2）算例：悬臂端作用弯矩。

悬臂梁最终变形形成周长为悬臂梁长度的圆。

1.1 Newton-Raphson算法基本思想图1.1 Newton-Raphson算法基本思想1.2 悬臂梁参数基本参数：L=2m, D=0.03m, A=7.069E-4m2, I=3.976E-08m4 ,E=2.0E11N/m2图1.2 悬臂梁单元信息将悬臂梁分成10个单元，如图1.2所示2.1 MATLAB输入信息材料信息单元信息约束信息（0为约束，1为放松）荷载信息（FX,FY,M）节点信息2.2 求解过程梁弯成圆形：理论弯矩M=EIY"=24981.944N.m ,直径为0.642m 运用ABAQUS和MATLAB进行求解对比：图1.3 加载图图1.4 ABAQUS变形图图1.5 MATLAB变形曲线ABAQUS和MATLAB变形对比，最终在理论荷载作用下都弯成了一个圆，其直径为0.64716m，与理论值相对比值为：（0.64716-0.642）/0.642=0.00804.非常接近。

2.3 加载点荷载位移曲线图1.5 加载点Y方向的荷载位移曲线加载点的最大竖向位移分别为1.4525m和1.45246m，相对比值（1.4525-1.45246）/1.45246=2.75395E-05。

完全相同，说明MATLAB的计算结果很好。

二、几何非线性大作业（弧长法）用弧长法编写几何非线性程序，分析荷载位移全过程曲线：1) 用平面梁单元，可分析平面杆系结构2) 算例(1)受集中荷载的拱：考察拱的矢跨比、荷载位置对荷载位移曲线的影响。

(2)其他有复杂平衡路径的结构3) 将结果与相关文献进行对比1.1 弧长法基本思想图2.1 弧长法基本思想1.2 拱基本参数拱参数：L=100m, A=0.32m2,I=1m4 ,E=1.0e7N/m2，F=-5000N，拱曲线y=5×sin(3.1415926*x/L)将拱结构分成25个单元，如图2所示图2.2拱单元信息2.1 MATLAB输入信息材料信息单元信息约束信息（0为约束，1为放松）荷载信息（FX,FY,M）节点信息2.2运用ANSYS和MATLAB进行求解对比（两端铰接）ANSYS中模型:图2.3 ANSYS模型图2.4 MA TLAB和ANSYS变形图2.3 加载点荷载位移曲线图2.5 加载点荷载位移曲线ANSYS求得的极限承载力3042.53,对应位移3.00142MATLAB求得的极限承载力3043.8, 对应位移3.0768相对误差分别为0.0417%,2.45%，模拟效果比较好。

非线性有限元方法及实例分析梁军河海大学水利水电工程学院，南京（210098）摘 要：对在地下工程稳定性分析中常用的非线性方程组的求解方法进行研究，讨论了非线性计算的迭代收敛准则，并利用非线性有限元方法分析了一个钢棒单轴拉伸的实例。

关键词：非线性有限元，方程组求解，实例分析1引 言有限单元法已成为一种强有力的数值解法来解决工程中遇到的大量问题，其应用范围从固体到流体，从静力到动力，从力学问题到非力学问题。

有限元的线性分析已经设计工具被广泛采用。

但对于绝大多数水利工程中遇到的实际问题如地下洞室等，将其作为非线性问题加以考虑更符合实际情况。

根据产生非线性的原因，非线性问题主要有3种类型[1]：1．材料非线性问题（简称材料非线性或物理非线性） 2．几何非线性问题3．接触非线性问题（简称接触非线性或边界非线性）2 非线性方程组的求解在非线性力学中，无论是哪一类非线性问题，经过有限元离散后，它们都归结为求解一个非线性代数方程组[2]：()()()00021212211=……==n n n n δδδψδδδψδδδψΛΛΛ （1.1）其中n δδδ,,,21Λ是未知量，n ψψψ,,,21Λ是n δδδ,,,21Λ的非线性函数，引用矢量记号[]T n δδδδΛ21＝ （1.2） []T n ψψψψΛ21= （1.3）上述方程组（1.1）可表示为()0=δψ （1.4）可以将它改写为()()()0=−≡−≡R K R F δδδδψ （1.5）其中()δK 是一个的矩阵，其元素是矢量的函数，n n ×ijk R 为已知矢量。

在位移有限元中，δ代表未知的结点位移，()δF 是等效结点力，R 为等效结点荷载，方程()0=δψ表示结点平衡方程。

在线弹性有限元中，线性方程组0＝－R K δ （1.6）可以毫无困难地求解，但对线性方程组()0=δψ则不行。

一般来说，难以求得其精确解，通常采用数值解法，把非线性问题转化为一系列线性问题。

专题3 非线性问题的有限单元法第七章几何非线性问题一、非线性问题前面各章所讨论的都是属于弹性力学中的线性问题，它最后导出了如下一个关于各节点平衡的线性代数方程组：[]{}{}Rδ (7-1)K=其中[]K是一个和{}δ无关的常系数矩阵，仅和结构的离散情况，结构变形前的几何及物理特性有关。

当然，严格地说。

固体力学中的所有现象均是非线性。

然而，对于解决许多工程问题，近似地用线性理论来处理可以使计算简单切实可行，并能符合工程上的精度要求。

但是许多问题，用线性理论却是完全不适合的，它必须用非线性理论来解决。

1.分类非线性问题主要可以分成二大类。

第一类为几何非线性，第二类为材料非线性。

几何非线性问题指的是大位移问题。

对于几何非线性问题，由于问题本身的特征及解的精度，平衡方程必须相对于预先未知的变形后的几何位置写出。

严格地说，所有问题都要用已变形位置写出它的平衡方程，但是若问题的基本特征不因变形而改变，精度也满足要求，它就可以用变形前的几何位置来描述。

这正是我们以前处理问题的方法。

然而，对于有些问题就不能这样处理；例如图7-1a所示结构中B点的平衡方程就要由变形后的几何位置写出，如图7-16所示。

又例如压杆失稳后的变形研究，平板大挠度问题均属于几何非线性问题。

图7-1 非线性桁架的问题在极大多数的大位移问题中，结构内部的应变是微小的，事实上，只有在材料出现塑性变形时，以及在工程上很少应用的类似于橡皮的材料中才会遇到大的应变。

本章所讨论的几何非线性问题将限于大位移小应变问题，这时材料的应力应变关系是线性，这将使问题得到一些简化。

至于材料非线性问题，则是指材料的本构关系，即应力应变关系的非线性问题，当结构采用非金属材料，或采用金属材料但发生塑性变形时，属于这类问题。

这类问题一般仅限于讨论小变形材料非线问题。

这将于下章讨论。

对于更加复杂的几何非线性及材料非线性复合问题，如金属的塑性加工等，也将于下一章作简单讨论。

高空作业半拄车状态非线性有限元分析的线性化处理
近年来，由于国内经济和科技的迅猛发展，随之而来的是越来越多的高空作业需求，特别是半拄车钢结构作业以及细长物体起重，使得研究高空作业半拄车状态的非线性分析显得尤为重要。

有限元分析是用来分析结构的常用方法，但其本质是一种非线性结构分析，在实际应用中不易处理，并且易出现数值不稳定的问题。

为了解决上述问题，本文提出了一种用于高空作业半拄车状态非线性有限元分析的线性化处理方法。

首先，建立了一种基于有限元分析的非线性模型，考虑了响应应力和变形特性，以及半拄车作业的特定场景。

其次，基于有限元分析，对模型进行重新编码并进行相应参数调整，找到非线性有限元分析可用的线性化方程。

最后，考虑了各种不同工况条件，采用数值方法对所提出的线性化方程进行了求解，进行了静力和动力仿真，并对比了正确性。

实验结果表明，本文提出的线性化处理方法不仅可以有效降低计算复杂度，而且可以保证计算的正确性。

因此，本文提出的线性化处理方法在高空作业半拄车分析中具有较好的应用前景。

基于此，未来有必要进一步深入研究有限元分析，探索更为优化的处理方法，以实现结构响应分析更精准的结果。

综上所述，本文针对高空作业半拄车状态的非线性有限元分析，提出了一种新的线性化处理方法，具有正确性及计算复杂度低的特点，可以为设计者提供良好的参考。

- 1 -。

有限元非线性分析作业一
按照练习1的内容，分别采用：
Beam单元：188
shell单元: 181
Solid单元：185
进行非线性和线性分析，求解梁中部的最大位移。

并比较采用三种不同单元时“浅拱形梁”的线性和非线性分析结果。

beam单元：188
模型
网格划分
节点数
施加边界条件和载荷
求解线性分析
垂直位移
非线性分析求解
建模
网格划分
提交作业要求：
1.给出采用三种不同单元分析时的有限元模型，包括：网格划分
（图），单元数，节点数，所施加的边界条件、载荷等。

2.给出六种情况下梁受力后的垂直位移云图。

3.按下表给出计算结果
分析类型线性非线性
梁的最大位移Shell 181
Beam 188 2.958mm 3.281mm solid 185
4. 计算结果分析。