大连理工大学非线性分析报告第三次作业

第三章 逐次逼近法1.1内容提要1、一元迭代法x n+1=φ(x n )收敛条件为：1）映内性x ∈[a,b]，φ(x) ∈[a,b] 2）压缩性∣φ(x) -φ(y)∣≤L ∣x-y ∣其中L ＜1，此时φ为压缩算子，在不断的迭代中，就可以得到最终的不动点集。

由微分中值定理，如果∣φ’∣≤L ＜1，显然它一定满足压缩性条件。

2、多元迭代法x n+1=φ(x n )收敛条件为：1）映内性x n ∈Ω，φ(x n ) ∈Ω 2）压缩性ρ（▽φ）＜1，其中▽φ为x n 处的梯度矩阵，此时φ为压缩算子，在不断的迭代中，就可以得到最终的不动点集。

3、当φ(x )= Bx+f 时，收敛条件为，ρ（B ）＜1，此时x n+1= Bx n +f ，在不断的迭代中，就可以得到线性方程组的解。

4、线性方程组的迭代解法，先作矩阵变换 U L D A --= Jacobi 迭代公式的矩阵形式 f Bx b D x U L D x n n n +=++=--+111)(Gauss-Seidel 迭代公式的矩阵形式 f Bx b L D Ux L D x n n n +=-+-=--+111)()( 超松弛迭代法公式的矩阵形式f Bx b L D x U D L D x k k k +=-++--=--+ωωωωω111)(])1[()(三种迭代方法当1)(<B ρ时都收敛。

5、线性方程组的迭代解法，如果A 严格对角占优，则Jacob 法和Gauss-Seidel 法都收敛。

6、线性方程组的迭代解法，如果A 不可约对角占优，则Gauss-Seidel 法收敛。

7、Newton 迭代法，单根为二阶收敛 2211'''21lim)(2)(lim---∞→+∞→--=-==--k k k k k k k k x x x x f f c x x ξξαα8、Newton 法迭代时，遇到重根，迭代变成线性收敛，如果知道重数m ， )()('1k k k k x f x f m x x -=+仍为二阶收敛 9、弦割法)()())((111--+---=k k k k k k k x f x f x x x f x x 的收敛阶为1.618，分半法的收敛速度为（b-a ）/2n-110、Aitken 加速公式11211112)(),(),(+----+-+--+---+---===k k k k k k k k k k k x x x x x x x x x x x ϕϕ1.2 典型例题分析1、证明如果A 严格对角占优，则Jacob 法和Gauss-Seidel 法都收敛。

大连理工大学本科实验报告课程名称：自动控制原理实验A 学部：电子信息与电气工程专业：自动化辅修班级：学号：学生姓名：2017年 3 月9 日实验项目列表大连理工大学实验预习报告学院（系）：专业：班级：姓名：学号：组：___ 实验时间：实验室：实验台：指导教师签字：成绩：典型线性环节的模拟一、实验目的和要求二、实验原理和内容三、实验步骤1．比例环节模拟电路图及参数计算方法2．积分环节模拟电路图及参数计算方法3．比例积分环节模拟电路图及参数计算方法4．比例微分环节模拟电路图及参数计算方法5．微分环节的模拟电路图及参数计算方法6．比例积分微分环节模拟电路图及参数计算方法7．一阶惯性环节模拟电路图及参数计算方法四、实验数据记录表格1．比例环节2．积分环节3．比例积分环节4．比例微分环节5．比例微分积分环节6．一阶惯性环节大连理工大学实验报告学院（系）：专业：班级：姓名：学号：组：___ 实验时间：实验室：实验台：指导教师签字：成绩：典型线性环节的模拟一、实验目的和要求见预习报告二、实验原理和内容见预习报告三、主要仪器设备四、实验步骤与操作方法五、实验数据记录和处理1．比例环节的阶跃响应曲线2．积分环节的阶跃响应曲线3．比例积分环节的阶跃响应曲线4．比例微分环节的阶跃响应曲线5．微分环节的阶跃响应曲线6．比例积分微分环节的阶跃响应曲线7．惯性环节的阶跃响应曲线六、实验结果与分析七．思考题八、讨论、建议、质疑大连理工大学实验预习报告学院（系）：专业：班级：姓名：学号：组：___实验时间：实验室：实验台：指导教师签字：成绩：二阶系统的阶跃响应一、实验目的和要求二、实验原理和内容画出二阶系统的模拟电路图，如何通过改变电路中的阻、容值来改变二阶系统的参数？三、实验步骤1．在学习机上模拟二阶系统，仔细连线，不要发生错误2．取二阶系统的阻尼比ζ=0.2，时间常数T=0.47秒，求二阶系统的单位阶跃响应3．取二阶系统的阻尼比ζ=0.2，时间常数T=1.47秒，求二阶系统的单位阶跃响应4．取二阶系统的阻尼比ζ=0.2，时间常数T=1.0秒，求二阶系统的单位阶跃响应5．取二阶系统的阻尼比ζ=0.4，时间常数T=1.0秒，求二阶系统的单位阶跃响应6．取二阶系统的阻尼比ζ=0.7，时间常数T=1.0，求二阶系统的单位阶跃响应7．取二阶系统的阻尼比ζ=1，时间常数T=1.0，求二阶系统的单位阶跃响应四、实验数据记录大连理工大学实验报告学院（系）：专业：班级：姓名：学号：组：___ 实验时间：实验室：实验台：指导教师签字：成绩：二阶系统的阶跃响应一、实验目的和要求见预习报告二、实验原理和内容见预习报告三、主要仪器设备四、实验步骤与操作方法五、实验数据记录和处理标示出每条曲线的峰值、峰值时间、调整时间，计算最大超调量。

非线性环节实验报告引言非线性系统在现实生活中的广泛应用引起了研究者们的极大关注。

非线性环节作为其中的重要组成部分，对系统的稳定性和性能起着至关重要的作用。

本实验通过建立一个非线性环节的模型，探究其对系统行为的影响，并分析非线性环节的性能和稳定性特性。

实验目的1. 建立一个非线性环节的数学模型；2. 分析非线性环节对系统行为的影响；3. 考察非线性环节的性能和稳定性特性。

实验原理非线性环节是指输入与输出之间不满足线性关系的部分。

在控制系统中，非线性环节可能会导致系统产生不确定性和非稳定的行为。

为了研究非线性环节的特性，本实验使用了一个常见的非线性函数作为实验模型，即sigmoid函数。

Sigmoid函数定义如下：f(x) = \frac{1}{{1+e^{-ax}}}其中，x代表输入，a代表一个可调节的参数，f(x)代表经过非线性环节后的输出。

实验步骤1. 首先，我们需要选择合适的参数a值来控制sigmoid函数的形状。

较小的a 值将导致sigmoid函数的输出变化更缓慢，而较大的a值则会使函数的曲线更陡峭。

本次实验选择a=2作为sigmoid函数的参数。

2. 在Matlab或Python等工具中编写代码，根据sigmoid函数的表达式计算输入x对应的输出f(x)。

3. 绘制x与f(x)之间的关系曲线，观察并分析非线性环节对系统行为的影响。

实验结果根据实验步骤所给出的sigmoid函数表达式和参数，我们得到了如下结果：import numpy as npdef sigmoid(x, a):return 1 / (1 + np.exp(-a * x))x = np.linspace(-10, 10, 100)a = 2y = sigmoid(x, a)import matplotlib.pyplot as pltplt.plot(x, y)plt.xlabel('Input (x)')plt.ylabel('Output (f(x))')plt.title('Nonlinear Link Function')plt.grid(True)plt.show()如上所示的代码及其运行结果，绘制了sigmoid函数的输入和输出之间的关系曲线。

第一章 非线性分析绪论
一.分析数学的发展历程：
1.初创 现代分析数学的发展应该起源于微积分的
发明和极限理论的建立。即使仅仅是对“数 “的理论的完善也归功于极限论的建立。
经过16世纪中叶到17世纪初的酝酿，牛顿 （1642——1727）和莱布尼茨（1646—— 1716）终于在17世纪下半叶创立了微积分。
梅莱，海涅，康托把无理数看成柯西列。 戴德金采用对有理数分割的办法，建立 了不依赖于极限论的实数理论。
4. 20世纪分析学的发展
勒贝格（1875-1941）——创立可列可加 测度的积分论，形成实变函数论。
以实分析为基础的概率论和随机过程， 称为现代分析。
复变函数论的发展，形成复分析。 以函数空间为背景的泛函和算子理论— —泛函分析。 此外还有傅立叶分析等。
在此之前，通过略去高次项（即忽略高阶 无穷小量）。帕斯卡，费马，沃利斯，巴罗等 著名学者使微积分学产生萌芽。
牛顿的流数术（微积分）是他一生三大发 明之一。
流数术：
给定函数y x2 0
时间的刹那用o表示（即dt）
x, y 的刹那用xo和yo表示
（即dx dx dt, dy dy dt）
社,1989
理论教学：32学时
学分：
2学分
课程代码：000250
课程类型：学位课
课程性质：专业基础课
考试方法
1. 期终考试占70%;
2. 平时成绩占20％，包括作业和 课堂回答问题； 3. 创新成绩占10％，根据课堂内 容所进行的创新活动，如科技小论 文、心得体会、对课程改革的建议 等，以读书报告的形式提交两次.
dt
dt
以x xo及y yo代替 x, y代入 方程得到
y yo - (x2 2xxo x2o2 ) 0 由于y - x2 0,故有

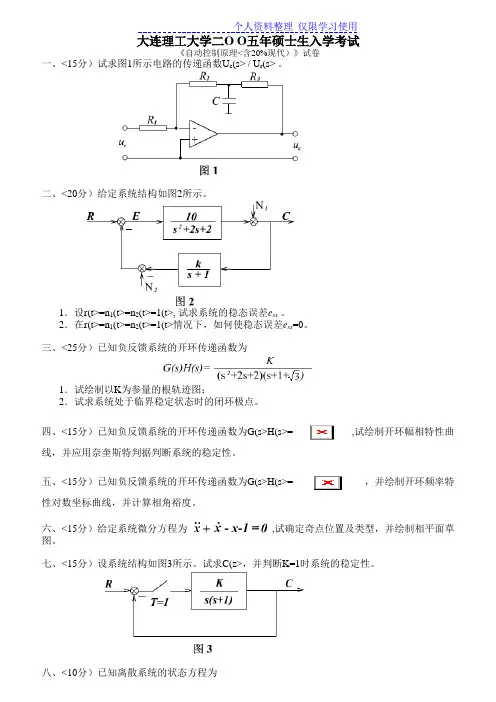
大连理工大学二O O五年硕士生入学考试《自动控制原理<含20%现代）》试卷一、<15分）试求图1所示电路的传递函数U c(s> / U r(s> 。

二、<20分）给定系统结构如图2所示。

1．设r(t>=n1(t>=n2(t>=1(t>, 试求系统的稳态误差e ss。

2．在r(t>=n1(t>=n2(t>=1(t>情况下，如何使稳态误差e ss=0。

三、<25分）已知负反馈系统的开环传递函数为1．试绘制以K为参量的根轨迹图；2．试求系统处于临界稳定状态时的闭环极点。

四、<15分）已知负反馈系统的开环传递函数为G(s>H(s>=,试绘制开环幅相特性曲线，并应用奈奎斯特判据判断系统的稳定性。

五、<15分）已知负反馈系统的开环传递函数为G(s>H(s>=，并绘制开环频率特性对数坐标曲线，并计算相角裕度。

六、<15分）给定系统微分方程为,试确定奇点位置及类型，并绘制相平面草图。

七、<15分）设系统结构如图3所示。

试求C(z>，并判断K=1时系统的稳定性。

八、<10分）已知离散系统的状态方程为a>0，试用李雅普诺夫第二方法确定使平衡点渐进稳定的a取值范围。

九、<20分）给定系统结构如图4所示。

1．试建立系统的状态空间描述；2．试设计状态反馈阵，使系统闭环极点位于-2，-2处；3．K是否可以取为0.5，为什么？大连理工大学二O O四年硕士生入学考试《自动控制原理<含30%现代）》试卷一、<15分）试求图1所示电路的结构图和传递函数。

二、<10分）已知系统的特征方程为：s4+2.5s3+2.5s2+10s -6 = 0试求特征根在S平面上的分布。

三、<10分）试求系统的单位脉冲响应。

四、<20分）设系统的开环传递函数为：1.试绘制根轨迹图<可能的分离点为：-1.2、-1.6、-2.6、-2.9、-3.5）；2.试求出分离点处的K值。

-03cos 2lnlim 0=+=®xx （10分）四、解：(1)0)cos )((lim 00sin )(lim 00=-¢=÷øöçèæ-=®®x x g x x x g a x x （4分）(2)200sin )(lim )0()(lim )0(x xx g x f x f f x x-=-=¢®® =12)0(2sin )(lim 2cos )(lim 00=¢¢=+¢¢=-¢®®g x x g x x x g x x∴ ïîïíì=¹---¢=¢时时010,)sin )(()cos )(()(2x x x x x g x x g x x f （8分） （3）200)sin )(()cos )((lim )(lim x x x g x x g x x f x x ---¢=¢®® =xx x g x x g x x x g x 2)cos )(()sin )((cos )(lim 0-¢-+¢¢+-¢® =)0(12)0(f g ¢==¢¢，因此)(x f ¢在(-∞，+∞+∞))连续。

连续。

（10分）五、解五、解:: 设x x x f ln)(=，由2ln 1)('xxx f -=，可知,当e x >时)(x f 单调减少单调减少 （5分）若e a b >>，则有b b a a ln ln >，推出a b b a ln ln >，即有a b b a > 2011201220122011> （10分）分）所以六、解：2)()()(x x f x f x x x f -¢=¢÷øöçèæ（4分）分） 令)()()(x f x f x x g -¢=，)()(x f x x g ¢¢=¢，令0)(=¢x g ，得0=x （唯一驻点），当0<x 时，0)(<¢x g ，当0>x 时，0)(>¢x g ，故)0(g 为最小值，故0)0()0()(>-=³f g x g ，∴0)(>¢÷øöçèæx x f ，即x x f )(单调增加。

6.2 波形畸变的基本概念
《电能质量分析与控制》
• 无功功率
正弦电路：若
u 2U sin t
i 2I sin(t ) i p iq
有功功率：
P UI cos
平均功率
无功功率：
Q UI sin
大连理工大学电气工程学院
6.2 波形畸变的基本概念 非正弦电路：
畸变功率：D S P Q U
仅有同频率的电压和电 流才构成有功功率； 对称三相系统电压、电 流的各次谐波具有不同的 相序特性； 不同频率的无功功率是 不可能互相抵消或补偿的。 不对称三相系统各次谐 波的相序和对称时不同， 各次谐波都可能不对称， 可用对称分量法分解。
I1 I1 1 DPF cos 1 = cos 1 功率因数： PF 2 I I 1+THDI
电压和电流的有效值： U


《电能质量分析与控制》
U
n 1
2 n
I
2 I n n 1
有功功率：
P U n I n cos n
n 1

视在功率： 无功功率：
2
S
U
n 1
2 n

I
n 1

2 n
Q S 2 P2
2 2 2 f 2 2 I n n2
发电机
（1）发电机磁饱和非线性产生的谐波
磁极磁场并非完全 按正弦分布
定子绕组出现的负序电流引起，转 子侧偶次，定子侧齐次
大连理工大学电气工程学院
6.3供用电系统典型谐波源
《电能质量分析与控制》
变压器与电抗器
铁磁 饱和
计及磁滞影响
电压与磁通为正 弦波 电流为正弦波 一般小于额定满载 电流的 1%

２ １ 方 法的力 学解 释 ． 该方 法 的力学解 释如 下 ：
余位移的存在， 构的平衡位 置会 发生变化。在地震 结 作用 下 的很 多 时刻 ， 结构 的基 底 剪 力 为零 。可 以近 似
认为 ， 当结构的基底剪力为零时 ， 结构处在平衡 位置。 本文将相邻 的平衡位置出现时刻之间的过程称为一个
分析中考虑应变率效应 的有效 方法 。 关键词 ：非线性 时程分 析 ； 应变率 ；／ 环 ； １４循 平均应变率
中 图分 类 号 ：Ｔ ３ ５ Ｕ ７ 文 献标 识 码 ：Ａ
Ａ ｎ ｉ ｅ ｒ ｔｍ ｅ ｈ ｓｏ ｙ ａ ｌ ｓｓ ｍ ｅ ｈｏ ｆ ｓｒ ｔ ｒ ｓ ｃ ｎ ｉ ｒｎｇ ｓｒ ｉ ａ ｅ ｅ ｅ ｔ ｎｏ ｌｎ ａ ｉ ・ ｉｔ ｒ ｎａ ｙ ｉ ｔ ｄ ｏ ｔ ｕｃ ｕ ｅ ｏ ｓｄｅ ｉ ｔ ａ ｎ ｒ ｔ ｆ ｃ ＷＡＮＧ ｎ ｒ ｉｇ ．Ｌ ｎ 一 Ｗｅ — ｎ ｕ ＩＨｏ ｇ
一
变率 下 的本 构 关 系 ， 用 平 均 应 变 率 下 的本 构 关 系 是 采 较 为合理 的 。 （ ） 根据控 制截 面一些 位 置 的平 均应 变率 对 整个 ３ 构件 的本 构 关 系进 行 修 正是 合 理 的 。在 地 震 作 用 下 ， 构件 的 非 线 性 变 形 集 中于 局 部 ， 他 部 位 保 持 弹 性 。 其 对 于处 于弹性 阶段 的部 位 ， 管 采 用 多 大 应 变 率 下 的 不 本构 关 系 ， 都不 会对 计算 得到 的结 构 响应 产 生 影 响 （ 在 不 同的应 变率 下 ， 以认 为 材 料 的弹 性 模 量 和 泊 松 比 可
（ ａｕｔ ｏ ｆ ｓ ｕｔｒ Ｅ ｇｎｅ ｎ ， ａａ ｎ ｅｓｙｏ ｅｈ ｏ ｇ ， ａａ １０ ４ Ｃ ｉａ Ｆｃｌ ｆ ｎ ａｔ ｃ ｅ ｎｉｅｒ ｇ Ｄ ｌ ｎＵ ｉ ｒ ｔ ｆ ｃｎｌ ｙ Ｄ ｌ ｎｌ６ ２ ， ｈｎ ） ｙ Ｉｒ ｒ ｕ ｉ ｉ ｖ ｉ Ｔ ｏ ｉ

非线性实验报告非线性实验报告摘要：本实验旨在研究非线性系统的特性，并通过实验验证非线性系统的存在和影响。

实验过程中，我们采用了不同的实验方法和工具，包括数学模型、实验仪器和数据分析软件。

通过实验结果的分析和对比，我们得出了一些关于非线性系统的结论，并对实验中可能存在的误差和限制进行了讨论。

引言：非线性系统是指其输入与输出之间的关系不符合线性关系的系统。

在现实世界中，非线性系统无处不在，如生物系统、电子电路、经济系统等。

了解和研究非线性系统的特性对于我们理解和应用这些系统具有重要意义。

本实验旨在通过实际操作和数据分析，探索非线性系统的行为和特性。

实验方法：我们选择了一种简单的非线性系统作为研究对象，即二次函数。

通过调整二次函数的系数和参数，我们可以观察到不同的非线性行为。

在实验中，我们使用了一台计算机和数据采集卡作为实验仪器，利用数学建模和数据分析软件进行数据处理。

实验步骤：1. 设计二次函数模型：我们首先根据实验要求设计了一个二次函数模型，包括系数和参数的选择。

这个模型可以模拟实际系统中的非线性行为。

2. 数据采集：我们通过计算机和数据采集卡采集了一系列输入和输出数据。

输入数据是实验中施加在系统上的不同信号，输出数据是系统对这些信号的响应。

3. 数据处理和分析：我们使用数据分析软件对采集到的数据进行处理和分析。

首先，我们绘制了输入-输出曲线，以观察系统的非线性特性。

然后，我们对数据进行了拟合和回归分析，以确定二次函数的系数和参数。

实验结果：通过实验和数据分析，我们得到了以下结果：1. 非线性特性的存在：我们观察到系统的输入-输出曲线不是一条直线，而是呈现出弯曲的形状。

这表明系统存在非线性特性。

2. 参数对系统行为的影响：我们发现，调整二次函数的系数和参数可以改变系统的响应。

例如，增加二次项的系数可以使曲线更加陡峭，而增加线性项的系数可以使曲线更加平缓。

3. 非线性现象的局限性：我们也观察到，在一定范围内，系统的响应是线性的。

大连理工大学22春“计算机科学与技术”《数据结构》作业考核题库高频考点版（参考答案）一.综合考核(共50题)1.n个结点的完全有向图含有边的数目()。

A.n*nB.n(n+1)C.n/2D.n*(n-l)参考答案：D2.队列是只允许在表的一端进行插入，而在另一端删除元素的线性表。

()A.正确B.错误参考答案：A3.从19个记录中查找其中的某个记录，最多进行4次关键字的比较，则采用的查找方法只可能是()。

A.顺序查找B.折半查找C.哈希查找D.二叉排序树查找参考答案：C4.查找效率最高的二叉排序树是()。

A.所有结点的左子树都为空的二叉排序树B.所有结点的右子树都为空的二叉排序树C.平衡二叉树D.没有左子树的二叉排序数参考答案：C算法中语句执行的频度就是算法的时间复杂度。

()A.正确B.错误参考答案：B6.归并排序是原地排序。

()A.正确B.错误参考答案：B7.下述哪一条是顺序存储结构的优点?()A.存储密度大B.插入运算方便C.删除运算方便D.可方便地用于各种逻辑结构的存储表示参考答案：A8.数据元素是数据的最小单位()。

A.正确B.错误参考答案：B9.算法的有穷性是指一个算法必须总是(对任何合法的输入)在执行有穷步之后结束，且每一步都可在有穷时间内完成。

()A.正确B.错误10.树的后根遍历序列等同于该树对应的二叉树的()。

A.先序序列B.中序序列C.后序序列D.以上都不对参考答案：B11.一个栈的输入序列为123...n，若输出序列的第一个元素是n，输出第i(1=i=n)个元素是()。

A.不确定B.n-i+1C.iD.n-i参考答案：B12.在下列存储形式中，哪一个不是树的存储形式?()A.双亲表示法B.孩子链表表示法C.孩子兄弟表示法D.顺序存储表示法参考答案：D13.下述文件中适合于磁带存储的是()。

A.顺序文件B.索引文件C.散列文件D.多关键字文件参考答案：A折半查找所对应的判定树是一棵理想平衡树。

大连理工大学应用数学系数学分析2001——2005（2005有答案）高等代数2000——2005、2007（2005有答案）物理系数学物理方法2000——2005量子力学2000，2002——2005热力学与统计物理2000，2002——2005电动力学2000，2002——2005普通物理2000——2005光学（几何光学与波动光学）2000晶体管原理2000半导体材料2004——2005半导体器件2004——2005半导体物理2001——2002，2004——2005神经科学基础2004——2005生物统计学2004——2005生物物理学2004——2005工程光学2005微电子技术2003——2005离散数学及应用2000——2001（2000有答案）离散数学与数据结构2002——2005模拟电子技术2001——2005工程力学系材料力学1999——2001，2003——2005，2010（2010为回忆版）理论力学1995，1999——2001，2003——2005理论力学（土）2000土力学1999——2005自动控制原理(含现代20%) 1999——2005杆系结构静力学1998，2000弹性力学（不含板壳）1999——2004流体力学1999——2005流体力学（土）2004——2005流体力学基础2002——2005岩石力学1999——2000钢筋混凝土结构1999——2000工程流体力学2001，2004——2005水力学1999——2000，2002，2004——2005机械工程学院机械设计2001——2005（2001——2005有答案）机械原理1999——2000，2003——2005画法几何及机械制图2003——2005控制工程基础2001，2003——2005微机原理及应用（8086）1999——2000微机原理及应用（机）2004——2005微机接口与通讯及程序设计1999——2000模拟电子技术2001——2005离散数学及应用2000——2001（2000有答案）离散数学与数据结构2002——2005过程控制（含计算机控制）2000杆系结构静力学1998，2000微电子技术2003——2005系统工程概论1999——2002晶体管原理2000系统工程概论1999——2005管理基础知识1999——2001，2003——2005（2003——2005有答案）计算机组成原理（软）2005管理学基础2004——2005（2004——2005有答案）管理学2010（回忆版）材料力学1999——2001，2003——2005，2010（2010为回忆版）自动控制原理(含现代20%) 1999——2005材料科学与工程学院材料科学基础2003——2005，2010（2010为回忆版）机械设计2001——2005（2001——2005有答案）模拟电子技术2001——2005微电子技术2003——2005物理化学2004物理化学及物理化学实验1991——1993，2000，2002——2005（2002——2004有答案）胶凝材料学2001——2005硅酸盐物理化学2001——2002，2005杆系结构静力学1998，2000金属学2000金属热处理原理2000金属材料学2000钢筋混凝土结构1999——2000晶体管原理2000土木水利学院材料力学（土）2000，2003——2005材料力学1999——2001，2003——2005，2010（2010为回忆版）土力学1999——2005结构力学2000——2001，2003——2005水力学1999——2000，2002，2004——2005杆系结构静力学1998，2000理论力学（土）2000弹性力学（不含板壳）1999——2004流体力学1999——2005流体力学（土）2004——2005流体力学基础2002——2005岩石力学1999——2000钢筋混凝土结构1999——2000工程流体力学2001，2004——2005系统工程概论1999——2005工程经济学2004——2005无机化学2003——2005传热学2002，2004——2005工程力学2004——2005工程项目管理2004——2005建筑材料2005工程热力学2001——2002，2004——2005热工基础（含工程热力学和传热学）2003化工学院无机化学2003——2005物理化学2004物理化学及物理化学实验1991——1993，2000，2002——2005（2002——2004有答案）有机化学及实验2001，2003——2005高分子化学及物理2002——2005化工原理及化工原理实验2001——2005材料力学1999——2001，2003——2005，2010（2010为回忆版）工程流体力学2001，2004——2005硅酸盐物理化学2001——2002，2005热力学基础2005天然药物化学2005药剂学2005生物化学及生物化学实验1999——2005船舶工程学院船舶动力装置2002——2005船舶设计原理2001——2005水声学原理2002——2005船舶静力学2001——2005杆系结构静力学1998，2000电子与信息工程学院模拟电子技术2001——2005信号与系统（含随机信号20%）1999——2005 自动控制原理(含现代20%) 1999——2005工程光学2005通信原理2004——2005离散数学及应用2000——2001（2000有答案）离散数学与数据结构2002——2005离散数学与计算机组成原理2005离散数学与数据库原理2004——2005数据结构与计算机组成原理2004——2005计算机组成原理与计算机体系结构2004——2005 计算机组成原理与数字逻辑2000计算机组成原理（软）2005编译方法1999——2000操作系统1999——2001高等代数2000——2005过程控制（含计算机控制）2000微电子技术2003——2005微机接口与通讯及程序设计1999——2000系统工程概论1999——2005晶体管原理2000能源与动力学院汽车理论2000——2005机械原理1999——2000，2003——2005自动控制原理(含现代20%) 1999——2005化工原理及化工原理实验2001——2005普通物理2000高等代数2000——2005离散数学及应用2000——2001（2000有答案）离散数学与数据结构2002——2005运筹学基础及应用2004——2005计算机信息管理1999——2001，2004——2005 微电子技术2003——2005杆系结构静力学1998，2000系统工程概论1999——2005晶体管原理2000信息管理与信息系统2010（回忆版）管理学院计算机信息管理1999——2001，2004——2005 运筹学基础及应用2004——2005离散数学及应用2000——2001（2000有答案）离散数学与数据结构2002——2005公共经济学基础2004——2005，2010（2010为回忆版）过程控制（含计算机控制）2000微电子技术2003——2005系统工程概论1999——2002政治学原理2004——2005行政管理学2004——2005，2010（2010为回忆版）经济学基础2001——2005（2001——2005有答案）运筹学基础及应用2004——2005公共管理学2005社会保障学2004——2005管理学2010（回忆版）信息管理与信息系统2010（回忆版）人文社会科学学院经济学基础2001——2005（2001——2005有答案）管理基础知识1999——2001，2003——2005（2003——2005有答案）管理学基础2004——2005（2004——2005有答案）管理学2010（回忆版）系统工程概论1999——2002现代科学技术基础知识1999——2000，2004——2005思想政治教育学2004——2005马克思主义哲学原理2004——2005马克思主义哲学2001——2002西方哲学史2005哲学概论2004——2005科学技术史（含命题作文）2004——2005科学史、技术史、命题作文2001——2003政治学原理2004——2005行政管理学2004——2005，2010（2010为回忆版）传播学2004——2005新闻传播实务2004——2005民法学2004——2005法理学与商法总论2004——2005政治学2004——2005中外教育史2004——2005教育学2005中国近现代史2004——2005世界近现代史2004——2005电气工程及应用电子技术系电路理论2002——2005自动控制原理(含现代20%) 1999——2005过程控制（含计算机控制）2000微电子技术2003——2005系统工程概论1999——2005晶体管原理2000外国语学院二外德语2002，2004二外俄语2002——2004二外法语2004——2005二外日语2002——2004专业基础英语2003英汉翻译2003，2005英汉翻译与写作2004英语水平测试2004——2005二外英语2002——2005日语水平测试2004——2005翻译与写作（日）2004——2005专业基础日语2002——2003外国语言学与应用语言学（日语）专业综合能力测试2002——2003体育教学部运动生物力学2005人体测量与评价2004——2005生物学基础2005体质学2004——2005建筑艺术学院建筑设计（8小时）2000，2004——2005建筑设计原理1999——2000，2003建筑设计理论综合2004——2005城市建设史2002——2003中国与外国建筑史2000建筑构造与建筑结构1999——2000城市规划历史与理论2004——2005城市规划原理2003城市设计2002规划设计(8小时)2004-2005素描(8小时)2005泥塑(8小时)2005色彩(4小时)2005软件学院离散数学及应用2000——2001（2000有答案）离散数学与数据结构2002——2005离散数学与计算机组成原理2005离散数学与数据库原理2004——2005数据结构与计算机组成原理2004——2005计算机组成原理与计算机体系结构2004——2005计算机组成原理与数字逻辑2000计算机组成原理（软）2005编译方法1999——2000操作系统1999——2001环境与生命学院物理化学2004物理化学及物理化学实验1991——1993，2000，2002——2005（2002——2004有答案）化工原理及化工原理实验2001——2005硅酸盐物理化学2001——2002，2005基因工程原理2004——2005微生物学2004——2005细胞生物学2005环境化学2004——2005环境工程原理2004——2005，2010（2010为回忆版）分子遗传学2004——2005环境微生物2002经济系经济学基础2001——2005（2001——2005有答案）公共经济学基础2004——2005，2010（2010为回忆版）高科技研究院数学分析2001——2005（2005有答案）高等代数2000——2005数学物理方法2000——2005量子力学2000，2002——2005热力学与统计物理2000，2002——2005电动力学2000，2002——2005物理化学2004物理化学及物理化学实验1991——1993，2000，2002——2005（2002——2004有答案）硅酸盐物理化学2001——2002，2005微电子技术2003——2005。

请在左侧装订成册大连理工大学Array本科实验报告课程名称：电工学实验A/B（一）学院（系）：专业：班级：学号：学生姓名：联系电话：2013 年~ 2014 年第1 学期实验项目列表姓名：学号：注意：3 学时实验请按下面时间上课（其他学时实验仍按教务处规定时间上课）第一节：（1.2节课）7：30 第二节：（3.4节课）10：05 第三节：（5.6节课）13：00 第四节：（7.8节课）15：30 第五节：（9.10节课）17：50 第六节：(11.12节课）20：00电工学实验须知一、选课要求实验选课前需确认在教务选课系统中选择该课程。

电工学实验实行网上选课，选课网址：http://58.155.210.208，请按选课时间上课，有特殊情况需事先请假，无故选课不上者按旷课处理，不给补做，缺实验者不给成绩。

二、预习要求1.课前认真阅读实验教程，复习相关理论知识，学习本节实验预备知识，回答相关问题。

按要求写好预习报告，注意实验内容有必做实验和选做实验；2.课前在实验报告中绘制电路原理图及实验数据表格（用铅笔、尺作图）；3.课前在实验报告中列出所用实验设备及用途、注意事项（设备型号课后填写）；4.设计性实验和综合性实验要求课前完成必要的电路设计和实验方案设计；5.没有预习报告或预习报告不合格者不允许做实验。

三、实验课上要求1.每个实验均须独立完成，抄袭他人数据记0分；2.认真完成实验操作和观测；3.所有实验记录均需指导教师确认（盖印），否则无效；4.请遵守《电工实验安全规则》。

四、实验报告1.请按实验教材中的要求提交预习报告；2.所有绘图必须用坐标纸绘图，并自行粘贴在报告上；3.没有按要求提交报告者不给成绩；4.抄袭报告记0分。

五、实验成绩评定（满分100分）1．实验课的考核方式：平时实验成绩70%+期末考核成绩30%。

平时成绩：完成必做实验任务满分记良好，完成必做实验任务和选做实验任务满分记优秀。

2．实验课考核成绩确定：平时实验成绩：预习20%+实际操作50%+实验总结+实验总结30%期末考核成绩：笔试40%+独立操作60%实验结束提交实验心得体会。

#define OVERFLOW -2
typedef int ElemType;
typedef int Status;
#define LIST_INIT_SIZE 100
#define LISTTINCREMENT 10
typedef struct{
ElemType *elem;
int length;
for(i=0;i<n;i++)
{
printf("input elem:");
scanf("%d",&L.elem[i]);
}
}
//输出顺序表中的元素
void ListOutput_Sq(SqList L){
int i,n;
n=L.length;
for(i=0;i<n;i++)
printf("%2d",L.elem[i]);
else
return -2;
}//优先级比较
void transform(char suffix[], char exp[])
{
char *p, ch, c;
p = exp;
ch = *p;
SqStack S;
InitStack (S);
Push (S, '#');
while(!StackEmpty(S))
}
}
}
void DeleteList(LinkList &L,ElemType mink,ElemType maxk){
LNode *p=L,*q;
while(p->next&&p->next->data<=mink)

The coordinate (x,y,z) has a relationship with the coordinate (x’,y’,z’) in the rotating system
Then
So
Thus
(b)
Then
Then
6.2 Small Particle in Bowl (Stony Brook) A small particle of mass m slides without
, the physically meaningful solution of
makes sense----if the cylinder is massless, it will immediately shoot to the left once we tap the block, and the block will lose contact with the cylinder.
at which the block loses contact with the cylinder, set
; this
results in the following cubic equation for
For
, we recover the result so that
which we had obtained for the immobile cylinder. If is . This
Where
. We also have
Using the equations above
Solving the equation for
Expressing the result completely in terms of

两种拉格朗日法T.L和U.L.几何非线性计算对比分析作者：张凯庆李永刘张璇赖建聪来源：《科技创新与应用》2016年第19期摘要：文章针对材料几何非线性特性，选取周边固支受均布载荷作用的圆板，分别利用两种拉格朗日法T.L和U.L.进行计算，最后进行对比分析。

通过对比发现，两种计算方法相差很小。

关键词：几何非线性拉格朗日法；TL法；UL法1 计算工况周边固支受均布载荷作用的圆板，其几何参数为：R=50.0cm，h=1cm，E=2.0E6kg/cm2（或2.56E6kg/cm2），v=0.3，？滓s=17.32kg/cm2，圆板大挠度理论解公式：wc/h+A（wc/h）3=Bq（a/h）4/E，将计算模型划分为15个单元，按15个等增量步计算中心点的载荷-位移曲线。

2 数值解计算与对比划分模型如图1所示。

单元划分及节点信息单元划分：径向划分15个8结点等参单元；结点总数：78；R向位移约束数：6；Z向位移约束数：3；均布力数：15。

边界条件：上边界作用均布力15；下边界自由；左边界简支；右边界固支根据几何非线性程序计算，可以得到TL和UL两种方法的中心点载荷位移曲线。

TL法结果如表1所示，UL方法结果如表2所示。

两种方法所得到的位移曲线比较如图2所示。

参考文献[1]李元媛，淡勇，蔡睿贤.理想塑性轴对称平面问题的解析解[J].机械工程学报，2009，7：270-273+277.[2]张年文，童根树.平面框架几何非线性分析的修正拉格朗日-协同转动联合法[J].工程力学，2009，8：100-106+130.[3]J.E.Barradas Cardoso，Nuno M.B. Benedito，Aníbal J.J. Valido.考虑翘曲变形的复合材料叠合梁几何非线性的有限元分析[J].钢结构，2009，10：82-83.[4]周凌远，李乔.基于UL法的CR列式三维梁单元计算方法[J].西南交通大学学报，2006，6：690-695.。