位移计算的一般公式(力学)

理论力学公式理论力学是物理学中重要的分支之一，它研究的是物质运动的规律以及力对物体运动的影响。

在理论力学中有很多重要的公式，下面将介绍一些较为常用的公式。

1.速度与位移的关系：速度（v）是一个物体在单位时间内所经过的位移（s）的变化率。

速度的公式可以表示为：v = ds/dt其中，v代表速度，s代表位移，t代表时间。

这个公式表明，速度等于位移的导数。

2.加速度和速度的关系：加速度（a）是一个物体在单位时间内速度（v）的变化率。

加速度的公式可以表示为：a = dv/dt其中，a代表加速度，v代表速度，t代表时间。

这个公式表明，加速度等于速度的导数。

3.牛顿第二定律：牛顿第二定律描述了力对物体运动的影响。

牛顿第二定律可以表示为：F = ma其中，F代表力，m代表物体的质量，a代表物体的加速度。

这个公式表明，物体受到的力等于其质量乘以加速度。

4.动能和功的关系：动能（K）是物体运动时所具有的能量。

根据定义，动能等于物体的质量乘以速度的平方的一半，即：K = (1/2)mv^2其中，K代表动能，m代表物体的质量，v代表物体的速度。

功（W）则描述了力对物体运动所做的功。

功的公式可以表示为：W = F·s·cosθ其中，W代表功，F代表力，s代表位移，θ代表力在位移方向上与位移的夹角。

这个公式表明，功等于力乘以位移乘以力在位移方向上的投影。

5.势能和力的关系：势能（U）是力学系统中保持的一种能量形式。

势能的公式可以表示为：U = -∫F·ds其中，U代表势能，F代表力，s代表位移。

这个公式表明，势能等于力对位移的负积分。

6.角动量和力矩的关系：角动量（L）是一个物体围绕一些点旋转时所具有的动量。

L=r×p其中，L代表角动量，r代表与旋转点的矢量距离，p代表物体的动量。

这个公式表明，角动量等于与旋转点的矢量距离与动量的叉乘。

力矩（τ）则描述了力对物体旋转的影响。

力矩的公式可以表示为：τ=r×F其中，τ代表力矩，r代表与旋转点的矢量距离，F代表力。

简支梁位移计算公式
简支梁的位移计算公式可以通过梁的弯曲理论来推导。

在简支
梁的情况下，当集中力作用于梁上时，梁会发生弯曲变形，导致梁
的位移。

位移计算公式可以通过弯曲理论和梁的几何特征来推导。

首先，我们可以使用弹性力学理论中的梁弯曲方程来描述梁的
位移。

对于简支梁而言，可以使用Euler-Bernoulli梁理论来进行
分析。

根据这个理论，简支梁在受到集中力作用时的最大位移可以
通过以下公式来计算：
δ = (F L^3) / (3 E I)。

在这个公式中，δ代表梁的最大位移，F代表作用在梁上的力
的大小，L代表梁的长度，E代表梁的弹性模量，I代表梁的惯性矩。

这个公式适用于简支梁在受到集中力作用时的情况。

另外，如果梁上分布有均匀载荷，则可以使用不同的公式来计
算梁的位移。

对于简支梁在均匀载荷作用下的位移，可以使用以下
公式：
δ = (5 w L^4) / (384 E I)。

在这个公式中，δ代表梁的最大位移，w代表均匀分布载荷的大小，L代表梁的长度，E代表梁的弹性模量，I代表梁的惯性矩。

需要注意的是，以上提到的公式都是针对简支梁在弹性范围内的情况下推导得出的。

在实际工程中，还需要考虑许多其他因素，例如梁的材料特性、截面形状等，因此在使用这些公式进行位移计算时，需要结合具体情况进行综合考虑。

力学中各种公式的计算力学是物理学的一个重要分支，研究物体受力的规律及其运动状态。

在力学中，有许多重要的公式用于计算各种物理量。

在本文中，我将为您介绍力学中一些常用的公式，并提供相应的计算方法。

1. 力的公式（F=ma）：力（F）等于物体的质量（m）乘以物体的加速度（a）。

这个公式用于计算物体所受的力。

如果已知物体的质量和加速度，可以通过乘法运算得到物体所受的力。

2. 动能的公式（K=½mv²）：动能（K）等于物体的质量（m）乘以物体的速度的平方（v²）再除以2、这个公式用于计算物体的动能。

如果已知物体的质量和速度，可以通过乘法和除法运算得到物体的动能。

3. 动量的公式（p=mv）：动量（p）等于物体的质量（m）乘以物体的速度（v）。

这个公式用于计算物体的动量。

如果已知物体的质量和速度，可以通过乘法运算得到物体的动量。

4.力与位移的公式（W=Fs）：力（F）等于物体所受的作用力，位移（s）是物体移动的距离。

这个公式用于计算力对物体进行的位移所做的功（W）。

如果已知力和位移，可以通过乘法运算得到功。

5.功率的公式（P=W/t）：功率（P）等于做功（W）的速率。

这个公式用于计算物体的功率。

如果已知做功和时间，可以通过除法运算得到功率。

6.动能定理（W=ΔK）：根据动能定理，当物体受到合力的作用时，物体的动能会发生变化，动能的变化等于合外力（W）对物体所做的功。

这个公式用于计算物体动能的变化。

如果已知外力和动能的变化，可以通过等式计算功。

7. 运动学方程（v=u+at）：当物体的初速度（u）、加速度（a）和时间（t）已知时，可以使用运动学方程计算物体的末速度（v）。

根据公式，最终速度等于初速度加上加速度乘以时间。

8. 自由落体公式（h=½gt²）：自由落体公式用于计算自由落体运动中物体的下落距离（h）。

根据公式，下落距离等于重力加速度（g）的一半乘以时间的平方。

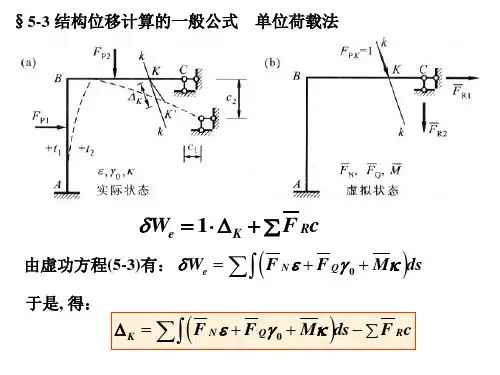
结构力学位移计算结构力学是研究结构在外力作用下产生的应变和变形的学科。

位移计算是结构力学中非常重要的内容之一，通过计算结构的位移可以确定结构的稳定性、刚度和形态等信息。

本文将从基本概念、位移计算的方法和实例等方面进行详细介绍。

一、基本概念1.结构位移：结构在受到外力作用后，发生变形产生的位移称为结构位移。

结构位移是结构变形的主要表征，通过位移计算可以得到结构中各个点的位移量。

2.位移与应变关系：根据材料力学的基本原理，结构的位移与结构中各个点的应变密切相关。

通常使用应变平衡方程来建立位移与应变之间的关系。

3.位移计算方法：位移计算主要分为两类方法，即解析解法和数值解法。

解析解法通过解析求解结构的位移方程，得到精确的位移结果。

数值解法通过离散化结构、建立结构的数值模型，并采用数值算法求解位移方程，得到近似的位移结果。

二、位移计算的方法1.解析解法：解析解法常用于简单结构或具有对称性的结构，通过假设结构的位移形式和边界条件，建立结构的位移方程，然后求解解析解。

2.数值解法：数值解法常用于复杂结构或无法采用解析解法求解的情况。

主要包括有限元法、有限差分法和边界元法等。

这些方法通过将结构离散化成若干个单元，建立数值模型，并采用近似的数值算法求解结构的位移方程。

三、位移计算的实例以简支梁的位移计算为例，介绍位移计算的具体过程。

1.简支梁位移计算的基本假设：（1）结构为理想化的一维结构；（2）结构之间没有弯矩和剪力的连梁或折线等连接形式；（3）结构在垂直于横截面方向上没有刚度差异。

2.简支梁的位移计算步骤：（1）根据梁的边界条件和受力情况，建立梁的位移方程；（2）求解梁的位移方程，得到梁在各个截面上的位移表达式；（3）根据边界条件，确定梁的位移常数；（4）结合位移表达式和位移常数，求解梁在各个截面上的位移。

3.简支梁的位移计算具体公式：（1）若梁在x轴方向上的长度为L，截面x处的位移为y(x)，则梁的位移方程可表示为：d²y/dx²=-M(x)/EI，其中M(x)为梁在x处的弯矩，E为梁的弹性模量，I为梁的截面矩。