常微分方程(王高雄)第三版 3.3
- 格式:ppt
- 大小:1.60 MB
- 文档页数:24




常微分方程(第三版)王高雄著课后习题答案.d o c(总86页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习题1.dxdy =2xy,并满足初始条件:x=0,y=1的特解。
解:ydy =2xdx 两边积分有:ln|y|=x 2+c y=e 2x +e c =cex 2另外y=0也是原方程的解,c=0时,y=0原方程的通解为y= cex 2,x=0 y=1时 c=1特解为y= e 2x .2. y 2dx+(x+1)dy=0 并求满足初始条件:x=0,y=1的特解。
解:y 2dx=-(x+1)dy 2y dy dy=-11+x dx 两边积分: -y1=-ln|x+1|+ln|c| y=|)1(|ln 1+x c 另外y=0,x=-1也是原方程的解 x=0,y=1时 c=e特解:y=|)1(|ln 1+x c 3.dx dy =yx xy y 321++ 解:原方程为:dx dy =y y 21+31x x + yy 21+dy=31x x +dx 两边积分:x(1+x 2)(1+y 2)=cx 24. (1+x)ydx+(1-y)xdy=0解:原方程为: yy -1dy=-x x 1+dx 两边积分:ln|xy|+x-y=c另外 x=0,y=0也是原方程的解。
5.(y+x )dy+(x-y)dx=0解:原方程为:dx dy =-yx y x +- 令xy =u 则dx dy =u+x dx du 代入有: -112++u u du=x 1dx ln(u 2+1)x 2=c-2arctgu即 ln(y 2+x 2)=c-2arctg2x y . 6. x dxdy -y+22y x -=0 解:原方程为:dx dy =x y +x x ||-2)(1x y - 则令xy =u dx dy =u+ x dx du 211u - du=sgnx x 1dx arcsin xy =sgnx ln|x|+c 7. tgydx-ctgxdy=0解:原方程为:tgy dy =ctgxdx 两边积分:ln|siny|=-ln|cosx|-ln|c| siny=x c cos 1=xc cos 另外y=0也是原方程的解,而c=0时,y=0. 所以原方程的通解为sinycosx=c. 8 dx dy +y e x y 32+=0解:原方程为:dx dy =ye y 2e x 3 2 e x 3-3e 2y -=c.(lnx-lny)dy-ydx=0解:原方程为:dx dy =x y ln xy 令xy =u ,则dx dy =u+ x dx duu+ xdxdu =ulnu ln(lnu-1)=-ln|cx| 1+ln xy =cy. 10. dxdy =e y x - 解:原方程为:dx dy =e x e y - e y =ce x 11 dxdy =(x+y)2 解:令x+y=u,则dx dy =dx du -1 dxdu -1=u 2 211u+du=dx arctgu=x+carctg(x+y)=x+c 12. dx dy =2)(1y x + 解:令x+y=u,则dx dy =dx du -1 dx du -1=21uu-arctgu=x+cy-arctg(x+y)=c. 13. dx dy =1212+-+-y x y x 解: 原方程为:(x-2y+1)dy=(2x-y+1)dxxdy+ydx-(2y-1)dy-(2x+1)dx=0dxy-d(y 2-y)-dx 2+x=cxy-y 2+y-x 2-x=c 14: dx dy =25--+-y x y x 解:原方程为:(x-y-2)dy=(x-y+5)dxxdy+ydx-(y+2)dy-(x+5)dx=0 dxy-d(21y 2+2y)-d(21x 2+5x)=0y 2+4y+x 2+10x-2xy=c. 15:dxdy =(x+1) 2+(4y+1) 2+8xy 1+ 解:原方程为:dxdy =(x+4y )2+3 令x+4y=u 则dx dy =41dx du -41 41dx du -41=u 2+3 dxdu =4 u 2+13 u=23tg(6x+c)-1 tg(6x+c)=32(x+4y+1). 16:证明方程y x dx dy =f(xy),经变换xy=u 可化为变量分离方程,并由此求下列方程: 1) y(1+x 2y 2)dx=xdy2) y x dx dy =2222x -2 y x 2y + 证明: 令xy=u,则xdx dy +y=dxdu 则dx dy =x 1dx du -2x u ,有: u x dx du =f(u)+1 )1)((1+u f u du=x 1dx 所以原方程可化为变量分离方程。

1常微分方程习题答案2.11.xy dx dy2=,并求满足初始条件:x=0,y=1的特解.解:对原式进行变量分离得。
故它的特解为代入得把即两边同时积分得:e e xx y c y x x c y c y xdx dy y22,11,0,ln ,212=====+==,0)1(.22=++dy x dx y 并求满足初始条件:x=0,y=1的特解.解:对原式进行变量分离得:。
故特解是时,代入式子得。
当时显然也是原方程的解当即时,两边同时积分得;当xy c y x y x c y c y x y dy dx x y++=====++=+=+≠=+-1ln 11,11,001ln 1,11ln 0,11123.yxy dx dy x y 321++=解:原式可化为:x x y xxyxyx yyxyc c c c x dx x dy y yx ydxdy2222222232232)1(1)1)(1(),0(ln 1ln 21ln 1ln 2111,0111=++=++≠++-=++=+≠+∙+=+)故原方程的解为(即两边积分得故分离变量得显然.0;0;ln ,ln ,ln ln 0110000)1()1(4===-==-+=-++=-=+≠===-++x y c y x xy c y x xy c y y x x dy y y dx x x xy x y xdy y ydx x 故原方程的解为即两边积分时,变量分离是方程的解,当或解:由:10ln 1ln ln 1ln 1,0ln 0)ln (ln :931:8.cos ln sin ln 07ln sgn arcsin ln sgn arcsin 1sgn 11,)1(,,,6ln )1ln(21111,11,,,0)()(:53322222222222c dxdy dx dy xycy ud uudx x x y u dx xydy x y ydx dy y x x c dy yy yydxdy c x y tgxdx ctgydy ctgxdy tgydx cx x xycx x u dxx x du xdxdudxdux u dx dy ux y u x y y dx dy xc x arctgu dx x du u u u dx du x u dxdu xu dx dy ux y u x y x y x y dx dy dx x y dy x y ee ee ee eexy uu xy x uu xyxyyx xx+===+=+-===-∙-=--+-=-=+-===-=+∙=+∙=∙=--=+===-+=+-=++=++-++=++===+-==-++-+--两边积分解:变量分离:。



目录第三章一阶微分方程的解的存在定理 (I)内容提要及其它 (1)3.1 解的存在唯一性定理与逐步逼近法 (3)3.1.1 存在唯一性定理 (3)3.1.1.1 特殊情况 (3)1、等价积分方程 (4)2、逐步逼近法 (4)3、引理 (4)3.1.1.2 一般情况 (8)3.1.2 近似计算和误差估计 (9)3.2 解的延拓 (11)3.2.1 局部的利普希茨条件 (11)3.2.2 解的延拓 (11)3.2.3 饱和解 (12)3.2.4 解的延拓定理 (13)3.2.5 解延拓定理的应用 (13)3.3 解对初值的连续性和可微性定理 (15)3.3.1 引言 (15)3.3.2 解关于初值的对称性 (15)3.3.3 引理 (15)3.3.4 解对初值的连续依赖定理 (15)3.3.5 解对初值和参数的连续依赖定理 (16)3.3.6 解对初值得可微性 (17)3.4 奇解 (20)3.4.1 包络和奇解 (20)3.4.2 C-判别曲线法 (20)3.4.3 P-判别曲线 (22)第五节内容提要及其它 (24)3.5 数值解 (25)主要内容 (25)具体内容 (25)主题 (25)3.5.1 欧拉公式 (26)3.5.1.1 基本方法 (26)3.5.1.2 格式 (26)3.5.1.3 局部截断误差和精度 (26)3.5.1.4 隐式欧拉公式 (26)3.5.1.5两步欧拉公式 (27)3.5.1.6应用 (27)3.5.2 改进的欧拉方法 (28)3.5.2.1 梯形格式 (28)3.5.2.2 改进的欧拉格式 (28)3.5.2.3 例题分析(p101-102) (29)3.5.3 龙格-库塔方法 (31)3.5.3.1 设计思想 (31)3.5.3.2二阶Runge-Kutta (32)3.5.3.3 三阶Runge-Kutta (33)3.5.4 收敛性和稳定性 (35)3.5.4.1 收敛性问题 (35)3.5.4.2 稳定性 (35)本章小结及其它 (37)第三章一阶微分方程的解的存在定理内容提要及其它授课题目(章、节)第三章:一阶微分方程的解的存在定理教材及主要参考书(注明页数)教材:常微分方程(第三版),王高雄等,高等教育出版社,2006年,p75-119主要参考书:[1]常微分方程,东北师范大学微分方程教研室编,高等教育出版社,2005,p71-115[2]数学分析(下)(第二版),华东师范大学数学系编,高等教育出版社,1998,p33-46[3]常微分方程习题解,庄万主编,山东科学技术出版社,2003,p170-224[4]差分方程和常微分方程,阮炯编著,复旦大学出版社,2002,p149-164目的与要求:掌握一阶常微分方程初值问题的解的存在唯一性定理及其证明方法,理解常微分方程初值问题的解的延拓和解对初值以及参数的连续依赖性和可微性定理.了解一阶常微分方程奇解和包络的概念以及求奇解的方法.教学内容与时间安排、教学方法、教学手段:教学内容:第1节解的存在唯一性定理;第2节解的延拓;第3节解对初值的连续性和可微性;第4节奇解;(数学与应用数学专业)第5节数值解。

常微分方程1.xy dxdy2=,并求满足初始条件:x=0,y=1的特解. 解:对原式进行变量分离得。
故它的特解为代入得把即两边同时积分得:e e xx y c y x x c y c y xdx dy y22,11,0,ln ,212=====+==,0)1(.22=++dy x dx y 并求满足初始条件:x=0,y=1的特解.解:对原式进行变量分离得:。
故特解是时,代入式子得。
当时显然也是原方程的解当即时,两边同时积分得;当xy c y x y x c y c y x y dy dx x y++=====++=+=+≠=+-1ln 11,11,001ln 1,11ln 0,11123yxy dx dy x y 321++=解:原式可化为:x x y x x yx yx yyxyc c c c x dx x dy y yx ydxdy 2222222232232)1(1)1)(1(),0(ln 1ln 21ln 1ln 2111,0111=++=++≠++-=++=+≠+•+=+)故原方程的解为(即两边积分得故分离变量得显然.0;0;ln ,ln ,ln ln 0110000)1()1(4===-==-+=-++=-=+≠===-++x y c y x xy c y x xy c y y x x dy y y dx x x xy x y xdy y ydx x 故原方程的解为即两边积分时,变量分离是方程的解,当或解:由:10ln 1ln ln 1ln 1,0ln 0)ln (ln :931:8.cos ln sin ln 07ln sgn arcsin ln sgn arcsin 1sgn 11,)1(,,,6ln )1ln(21111,11,,,0)()(:53322222222222c dx dy dx dy xycy ud uu dx x x y u dx xydy x y ydx dy y x x c dy yy yydx dy c x y tgxdx ctgydy ctgxdy tgydx cx x xycx x u dxx x du xdxdu dxdux u dx dy ux y u x y y dx dy xc x arctgu dxx du u u u dx du x u dxdu xu dx dy ux y u x y x y x y dx dy dx x y dy x y e e e e e e ee x y uu xy x u u x yxyy x xx+===+=+-===-•-=--+-=-=+-===-=+•=+•=•=--=+===-+=+-=++=++-++=++===+-==-++-+--两边积分解:变量分离:。

第一章 绪论微分方程: 联系自变量、未知函数以及它的导数间的关系式。
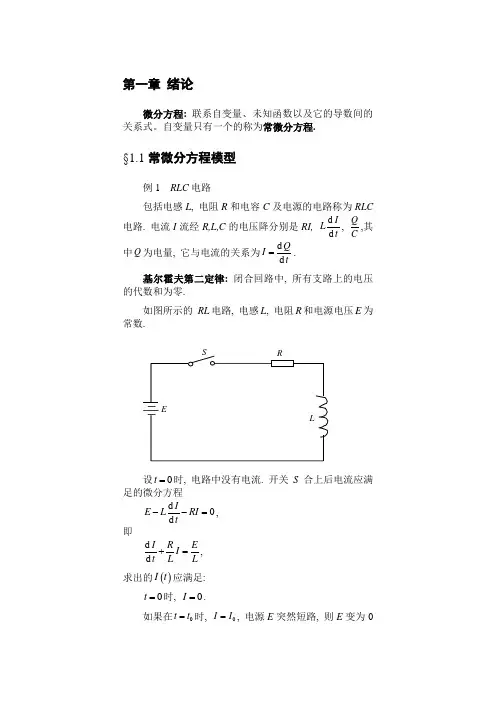
自变量只有一个的称为常微分方程.§1.1 常微分方程模型例1 RLC 电路包括电感L , 电阻R 和电容C 及电源的电路称为RLC电路. 电流I 流经R,L,C 的电压降分别是RI, d d I Lt , Q C,其中Q 为电量, 它与电流的关系为d d QI t =. 基尔霍夫第二定律: 闭合回路中, 所有支路上的电压的代数和为零.如图所示的 RL 电路, 电感L , 电阻R 和电源电压E 为常数.设0t =时, 电路中没有电流. 开关S 合上后电流应满足的微分方程d 0d I E L RI t--=, 即d d I R E I t L L +=, 求出的()I t 应满足: 0t =时, 0I =.如果在0t t =时, 0I I =, 电源E 突然短路, 则E 变为0并且此后一直保持为0, 则电流I 满足方程d 0d I RI t L +=, 及条件0t t =时, 0I I =.再看如图所示的RLC 电路, 电阻R, 电感L 和电容C 都是常数. 电源()e t 是时间t 的已知函数.开关S 合上后, 电流I 应满足的微分方程()d d I Qe t L RI t C=++, 微分上式可得()22d d d 1d d d e t I R I I t L t LC L t++=, 如果()e t =常数, 则有22d d 10d d I R I t L t LC++=. 如果电阻R =0, 则有22d 10d I t LC+= 例2 数学摆解 设摆在铅垂线右边时所成夹角ϕ为正. 质点M 沿圆周切向速度v 可表示为d d v l tϕ=. 重力mg 沿圆周切向的分力为MP, 数值为sin mg ϕ-, 于是摆的运动方程为 d sin d vmmg tϕ=-, 即22d sin d gt l ϕϕ=-. 如果是微小振动, 即ϕ比较小时, 可取sin ϕϕ≈, 于是微小振动方程为22d 0d gt lϕϕ+=. 如果摆在一个粘性介质中运动, 设阻力系数为μ, 则摆的运动方程为22d d 0d d gt m t lϕμϕϕ++=. 如果沿摆的运动方向恒有一个外力()F t 作用于它, 则称受迫微小振动, 方程为()22d d 1d d g F t t m t l mlϕμϕϕ++=.摆的初始条件为0t =时, 0ϕϕ=,0d d tϕω=. 例3 人口模型Malthus 假定: 人口出生率是常数r , 则从t 到t t +∆这段时间人口数量()N t 的增长量为()()()N t t N t rN t t +∆-=∆于是人口数量满足d d NrN t = 改写为d d Nr t N= 两边积分可得ln N rt c =+ 这里c 为任意常数, 上式又可变形为rt N ce =这里c c e =, 注意0N =也是解, 所以c 可以是任意常数. 如果设初值条件为0t t =时, ()0N t N =代入上式可得00rt c N e -=, 即方程满足此初始条件的解为()()00r t t N t N e -=.Logistic 模型: 引入环境最大容纳量m N , 假定净相对增长率为()1m N t r N ⎛⎫- ⎪⎝⎭, 则人口模型变为d 1d m N N r N t N ⎛⎫=- ⎪⎝⎭. 例4 传染病模型设某地区在某种传染病传播期间总人数保持不变, 为常数n . 开始感染人数为0x , 在t 时刻的健康人数为()y t ,染病人数为()x t , 则有()()x t y t n +=设单位时间内一个病人能传染的人数和当时健康人数成正比, 比例常数为k , 称之为传染系数, 于是()()()d d x t ky t x t t= 注意到总人数不变, 可得()()0d ,0d xkx n x x x t=-= 此模型称为SI 模型, 即Susceptible, Infective.对无免疫性的疾病, 病人治愈后会再次感染. 设单位时间治愈率为μ, 则SI 模型应修正为 ()()()()()0d ,0d x t ky t x t x t x x tμ=-=, 即()()0d 1,0d x kx n x x kx n x x x t μσ⎛⎫=--=--= ⎪⎝⎭这个称为SIS 模型. 其中1μ是这个传染病的平均传染期,kσμ=是整个传染期内每个病人有效接触的平均人数(接触数).对于免疫性很强的疾病, 病人治愈后不会再被感染, 即在t 时刻的治愈后免疫人数为()r t , 称为移除者(Removed), 设治愈率l 为常数, 即()()d d r t lx t t= 注意到总人口不变, ()()()x t y t r t n ++=, 我们得到d d d d xkxy lx ty kxy t⎧=-⎪⎪⎨⎪=-⎪⎩这个模型称为SIR 模型.例5 两生物种群生态模型某环境中有两种鱼: 被食鱼与捕食鱼. 设t 时刻被食鱼的总数为()x t , 捕食鱼的总数为()y t , 如果没用捕食鱼, 则被食鱼的增长规律为d d xax t=, 设捕食率为b , 则有d d xax bxy t=- 而捕食鱼有一个自然减少率c , 被食鱼供养捕食鱼的能力为d , 则有d d ycy dxy t=-+ 这个称之为Volterra 捕食-被捕食模型.其更一般的模型为()()d d d d d xx a bx cy ty y ex fy t⎧=++⎪⎪⎨⎪=++⎪⎩ 从数学的角度归类:d d I R E I t L L +=, d d N rN t =可以写为d d yay c t+=. 而 ()22d d d 11d d d e t I R I t L t LC L t++= 和()22d d 1d d g F t t m t l ml ϕμϕϕ++= 可以写为()22d d d d y yb cy f t t t++=.§1.2 基本概念和常微分方程的发展历史1.2.1 常微分方程的基本概念(1) 常微分方程和偏微分方程如果在微分方程中自变量的个数只有一个, 则称为常微分方程; 自变量的个数多于一个的微分方程则称为偏微分方程.第一节中的例子都是常微分方程. 以下是偏微分方程2222220T T Tx y z ∂∂∂++=∂∂∂,224T Tx t∂∂=∂∂. 阶数: 微分方程中出现的最高阶导数的阶数称为微分方程的阶数. 一般的n 阶常微分方程具有如下形式:d d ,,,,0d d n n y y F x y x x ⎛⎫= ⎪⎝⎭ ,这里F 是d d ,,,,d d n n y y x y x x 的表达式, 且必含有d d n n yx, y 是未知函数, x 是自变量.此书中常微分方程也简称为微分方程或方程. (2) 线性和非线性如果方程d d ,,,,0d d n n y y F x y x x ⎛⎫= ⎪⎝⎭ 左端为y 及d d ,,d d n n y yx x的一次有理整式, 则称方程为n 阶线性微分方程. 一般n 阶线性微分方程的形式为()()()()1111d d d d d d n n n n n n y y ya x a x a x y f x x x x---++++= , 这里()()()1,,,n a x a x f x 是x 的已知函数.不是线性方程的方程统称为非线性方程. 例如22d sin d gt lϕϕ=- 是二阶非线性方程.(3) 解和隐式解如果函数()y x ϕ=代入方程d d ,,,,0d d n n y y F x y x x ⎛⎫= ⎪⎝⎭ 后能使它变为恒等式, 则称()y x ϕ=为方程的解. 如果关系式(),0x y Φ=决定的隐函数()y x ϕ=是方程的解, 则称(),0x y Φ=为方程的隐式解.例: 一阶微分方程d d y xx y=-的有解y =y =则关系式221x y +=就是此方程的隐式解.解和隐式解统称为方程的解而不加以区别. (4) 通解和特解含有n 个独立的任意常数12,,,n c c c 的解()12,,,,n y x c c c ϕ=称为方程d d ,,,,0d d n n y y F x y x x ⎛⎫= ⎪⎝⎭ 的通解. 同样可定义隐式通解. 它们统称为方程的通解而不加以区分. 为了确定微分方程一个特解所需的条件称为定解条件. 常见的定解条件是初始条件, 方程d d ,,,,0d d n n y y F x y x x ⎛⎫= ⎪⎝⎭ 的初始条件是指当0x x =时, ()()1110001d d ,,,d d n n n y y y y y y x x---=== ,()()110000,,,,n x y y y - 是给定的n +1个常数.求微分方程满足定解条件的解, 就是定解问题. 当定解条件为初始条件时, 称为初值问题, 这也是本书讨论的主要内容.满足初始条件的解称为微分方程的特解. 初始条件不同, 特解也不同.例: 人口模型的解rt N ce =含有一个任意常数c , 所以是d d NrN t=的通解, 而()()00r t t N t N e -=就是满足初始条件0t t =时, ()0N t N =的特解, 它可在通解中令00rt c N e-=得到.例: 二阶微分方程22d d 540d d y yy x x++= 的通解为412x x y c e c e --=+,这里12,c c 是任意常数, 满足初始条件()()d 002,1d y y x== 的特解为43x x y e e --=-. 5) 积分曲线和方向场 一阶微分方程()d ,d yf x y x= 的解()y x ϕ=代表xy 平面上一条曲线, 称为微分方程的积分曲线. 而通解(),y x c ϕ=则对应一族曲线, 称为积分曲线族.满足初始条件()00y x y =的解就是过点()00,x y 的积分曲线. 积分曲线上每一点(),x y 的切线斜率正好就是(),f x y . 反之, 如果有某条曲线, 它在点(),x y 的切线斜率是(),f x y , 则它就是一条积分曲线.方向场: 设(),f x y 的定义域为D , 在每个(),x y D ∈上画一个方向, 此方向的斜率等于(),f x y , 这种带有方向的区域称为方程()d ,d yf x y x=确定的方向场. 等斜线: 在方向场中, 方向相同的点的轨迹称为等斜线. ()d ,d yf x y x =的等斜线方程为(),f x y k =,其中k 是参数.例 d 1d yxy x=+. 利用Maple 模拟出的此方程的方向场:6) 微分方程组用两个及两个以上的关系式表示的涉及多个函数的导数的微分方程称为微分方程组.第二章 一阶微分方程的初等解法初等解法: 即将微分方程的求解问题转化为积分问题 注1 不一定要求用初等函数表示积分.注2 并不是所有的微分方程都有初等解法. §2.1 变量分离方程与变量变换2.1.1 变量分离方程形如()()d d y f x y x ϕ= 的方程, 称为变量分离方程, 这里()f x 和()y ϕ分别是x,y 的连续函数.解法: 如果()0y ϕ≠, 则方程可改写为()()d d y f x x y ϕ=, 两边积分, 得到()()d d y f x x c y ϕ=+⎰⎰,其中c 是任意常数, 而()d y y ϕ⎰和()d f x x ⎰则分别表示()1y ϕ和()f x 的一个原函数. 容易验证方程()()d d y f x x c y ϕ=+⎰⎰所确定的隐函数(),y y x c =就是原微分方程的通解.如果存在0y 使得()00y ϕ=, 则0y y =也是原方程的解, 它不包含的通解中, 须补上.例1 求解方程d d y x x y=-. 解 分离变量, 可得d d y y x x =-,两边积分 2222y x c =-+, 化简可得通解为22x y c +=.例2 求解两种群模型 ()()d d d y c x y x x a by -+=-, 0,0x y ≥≥. 解 分离变量 d d d c a x b y x y ⎛⎫⎛⎫-=-+ ⎪ ⎪⎝⎭⎝⎭, 积分得 ln ln c x dx a y by k -=-++化简为d c x a by xe y e k --=±考虑条件0,0x y ≥≥以及0y =是解, 可得方程的通解为 d c x a by x e y e k --=这里0k ≥是任意常数.例3 求解Logistic 模型 ()()00d 1,,0d m N N r N N t N N t t N ⎛⎫=-=≥ ⎪⎝⎭. 解 分离变量()d d d d m m m N N N N r t N N N N N N ==+--积分可得()ln ln m rt c N N N +=-- 其中c 为任意常数, 化简 ()1rt c m N e N-+=- 即 1m rtN N ce -=+ 这里c c e -=, 代入初值得 001rt m N ce N -=- 最后得到 ()()0011mN r t t mN N N e --=+-.例4 求方程()d d y P x y x=的通解, 其中()P x 是x 的连续函数. 解 分离变量 ()d d y P x x y=, 两边积分()ln d y P x x c =+⎰ , 即()d P x x c y e +⎰= , 于是()d P x x c y e e ⎰=±⋅ ,令c c e =± , 于是()d P x x y ce ⎰=. 此外0y =也是方程的解, 但它已包括在上述解中. 故通解为()d P x x y ce ⎰=, 其中c 为任意常数.2.1.2 可化为变量分离方程的类型介绍两种简单情形:1) 形如 d d y y g x x ⎛⎫= ⎪⎝⎭的方程称为齐次方程, 这里()g u 是u 的连续函数.求解方法: 作变量变换 y u x= 于是 d d d d y u x u x x=+, 将上两式代入原方程可得 ()d d u x u g u x+=, 整理后可得 ()d d g u u u x x-=, 这是一个关于u,x 的变量分离方程, 可求解, 再代回原来的变量即可.例5 求解方程d tan d y y y x x x=+. 解 这是齐次方程, 令y u x =, d d d d y u x u x x =+, 代入原方程d tan d u x u u u x +=+, 即d tan d u u x x=, 分离变量 d cot d x u u x=, 两边积分 ln sin ln u x c=+ , c 是任意常数, 整理可得sin c u e x =±⋅ ,令c c e =± , 可得sin u cx =, 此外方程还有解tan 0u =, 此解已包括在上式中, 故通解为sin u cx =, c 是任意常数, 代回原来的变量可得到原方程的通解为 sin y cx x=, c 是任意常数. 例6求解方程()d 0d y x y x x+=<. 解 将方程改写为d d y y x x= ()0x <, 这是齐次方程, 令y u x =, d d d d y u x u x x =+, 代入原方程得d d u xx=分离变量d x x =, 两边积分()ln x c =-+, 即()()()2ln ln 0u x c x c =-+-+>⎡⎤⎣⎦,这里c 是任意常数, 此外0u =也是方程的解, 它不包括在通解中.代回原来的变量, 得到原方程的通解为()()()2ln ln 0y x x c x c =-+-+>⎡⎤⎣⎦及0y =.或者也可将方程的解表示为 ()()()2ln ,ln 0,0,ln 0.x x c x c y x c ⎧-+-+>⎡⎤⎪⎣⎦=⎨-+≤⎪⎩2) 形如111222d x a x b y c =++ 的方程也可化为变量分离方程. 分三种情形讨论.(1) 120c c ==的情形此时方程可化为 11112222d d yx y x a b a x b y y y g x a x b y x a b ++⎛⎫=== ⎪++⎝⎭ , 从而变为一个齐次方程求解. (2) 11220a b a b =, 即1122a b a b =的情形. 设上面的比值为k , 即1122a b k a b ==, 则方程可写为 ()()22122222d d k a x b y c y f a x b y x a x b y c ++==+++, 令22a x b y u +=, 则有()22d d u a b f u x=+, 这是一个关于u , x 的变量分离方程, 可求解. (3) 11220a b a b ≠, 及1c , 2c 不全为零的情形. 此时方程组11122200a x b y c a x b y c ++=⎧⎨++=⎩ 有解, 设解为(),αβ. 显然()(),0,0αβ≠, 否则与1c , 2c 不全为零矛盾.可通过坐标平移将原点移至(),αβ, 可令,X x Y y αβ=-⎧⎨=-⎩, 从而原方程化为1122d X a X b Y=+, 又转化为情形(1). 对于方程111222d d a x b y c y f x a x b y c ⎛⎫++= ⎪++⎝⎭, 也可用同样方法求解.此外, 下面各种方程也可通过适当的变量变换化为变量分离方程求解.()d d y f ax by c x =++ 令ax by c u ++=. 则()d d d d u y a b a bf u x x=+=+ ()()d d 0yf xy x xg xy y +=令xy u =, 则 ()()()()d d 11d d f u f u u y u y x y x x g u x g u ⎛⎫⎛⎫=+=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭. ()2d d y x f xy x= 令xy u =, 则 ()()()d d 11d d u y y x y f u u f u x x x x=+=+=+. 2d d y y xf x x ⎛⎫= ⎪⎝⎭令2y u x =. ()2d d 2d d y u xu x xf u x x=+=, 方程变为()2d d f u u u x x-= ()()()(),d d ,d d 0M x y x x y y N x y x y y x ++-=, 其中M, N 为x, y 的齐次函数. 令y u x =. d d d d y u u x x x=+,方程变为12d d 10d d y y y y y y g g x x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫++-= ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭, 代入可得()()12d d 10d d u u g u u u x g u u x u x x ⎛⎫⎛⎫⎛⎫++++-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 整理可得()()()()()21121d d u g u u x x ug u g u +=-+ 例7 求解方程d 1d 3y x y x x y -+=+-. 解 解方程组1030x y x y -+=⎧⎨+-=⎩, 解得1,2x y ==, 令12X x Y y =-⎧⎨=-⎩原方程变为 d d Y X Y X X Y-=+ 再令 Y u X=, 即 Y uX = 方程又变为 d 1d 1u u u X X u-+=+, 分离变量得 2d 1d 12X u u X u u+=-- 两边积分 22ln ln 21X u u c=-+-+ 整理得 ()2221c X u u e +-=±令1c c e =± , 则有()22121X u u c +-=代回原变量2212Y XY X c +-=, ()()()()22122121y x y x c -+----= 又2210u u +-=也是原方程的解, 故整理上式可得原方程的通解为22262y xy x y x c +---=这里c 为任意常数.2.1.3 应用举例例7 电容器的充电和放电如图所示的R-C 电路, 开始电容C 没有电荷, 其两端电压为零, 开关合上1后, 电容开始充电, 电压逐渐升高, 充电完毕后, 合上开关2, 电容开始放电, 求充放电过程中电容C 两端的电压c u 随时间t 的变化规律.解 对充电过程, 由基尔霍夫第二定律c u RI E +=,由于c Q Cu =, 微分得到 d d d d c u Q I C t t==, 代入可得d d c c u RC u E t+=, 这是c u 满足的微分方程, 分离变量 d d c c u t u E RC=-- 两边积分 11ln c u E t c RC-=-+ 即 1112RC RC t t c c u E e e c e ---=±=,代入初始条件0,0c t u ==可得2c E =-, 于是 ()11RC t c u E e -=-.函数图象如下放电过程类似可讨论.例8 探照灯反射镜面的形状.探照灯要求将点光源射出的光线平行反射出, 求反射镜面的形状.解 将点光源设为坐标原点, 设所求曲面为曲线 ()0y f x z =⎧⎪⎨=⎪⎩绕x 轴旋转而成的. 下面求曲线()f x , 如图.过曲线()y f x =上任一点(),M x y 做切线NT , 由反射定律可得12αα=从而 OM ON =切线斜率为 2d tan d y MP x NPα==,又OP x =, MP y =, OM =可得()y f x =满足的微分方程d d y x = 此为齐次方程, 可令y u x =进行求解. 此外, 齐次方程还可令x v y=, 此时x yv =, 微分可得d d d d x v v y y y=+ 代入方程得到d sgn d v v y v y y+=+整理可得d sgn y y y =ln x c ⎛⎫=+ ⎪⎝⎭ 注意到0y >, 可解得(y c v = 代入x v y =可得2y cx =+,整理得 ()22y c c x =+, c 为任意常数.此曲线为抛物线, 反射镜面即为旋转抛物面()222y z c c x +=+.§2.2 线性方程与常数变易法一阶线性微分方程()()()d 0d y a x b x y c x x ++= 当()0a x ≠时可写为 ()()d d y P x y Q x x=+, 下面主要讨论这种形式, 这里()P x 和()Q x 都是连续函数.当()0Q x =时, 方程 ()d d y P x y x= 称为一阶齐线性方程. 若()0Q x ≠称为一阶非齐线性方程.一阶齐线性方程为变量分离方程, 上节例3已求得其通解为()d P x x y ce ⎰=, 其中c 为任意常数.下面讨论一阶非齐线性方程的求解问题. 设想两种方程( 齐次与非齐次) 的解必有某种联系或者形式上的相似. 但是()d P x x y ce ⎰=必不可能是一阶非齐线性方程的解. 设想c 不是常数, 而是一个关于x 的函数()c x , 这是一个待定的函数. 于是, 将()()d P x x y c x e ⎰=代入到一阶非齐线性方程: ()()()()()()()()()d d d d d P x x P x x P x x c x e c x P x e P x c x e Q x x⎰⎰⎰+=+ 即()()()d d d P x x c x Q x e x-⎰= 积分后可得()()()d d P x x c x Q x e x c -⎰=+⎰ 代入得到()()()d d d P x x P x x y e Q x e x c -⎛⎫⎰⎰=+ ⎪⎝⎭⎰ 这就是非齐线性方程的通解. 此法称为常数变易法.例1 求方程()()1d 11d n x y x ny e x x++-=+的通解, 其中n 为常数.解 将方程改写为 ()d 1d 1n x y n y e x x x =+++, 先求对应的齐次方程 d d 1y n y x x =+ 的通解, 由公式可知通解为()1n y c x =+.下面应用常数变易法, 令 ()()1n y c x x =+ 微分之可得()()()()1d d 11d d n n c x y x n x c x x x-=+++ 代入原方程()d d x c x e x= 积分可得()x c x e c=+ 因此非齐次方程的通解为()()1n x y x e c =++ 其中c为任意常数. 例2 求方程2d d 2y y x x y =-的通解. 解 将方程改写为 d 2d x x y y y=-, 这是一个关于未知函数x 的非齐线性方程.其对应的齐次方程 d 2d x x y y= 的通解是2x cy =.应用常数变易法, 令()2x c y y =并代入方程可得 ()d 1d c y y y=- 积分可得()ln c y y c=-+ 从而原方程的通解为()2ln x y c y =- 这里c是任意常数. 伯努利方程:()()d d n y P x y Q x y x=+ 这里()(),P x Q x 都是连续函数, 且0,1n ≠.可以利用变量变换将伯努利方程化为线性方程. 当0y ≠时, 用n y -乘方程两边()()1d d n n y y y P x Q x x --=+, 令1n z y -=可得 ()d d 1d d n z y n y x x-=- 于是原方程化为 ()()()()d 11d z n P x z n Q x x=-+- 这是一个关于z,x 的线性方程, 可求通解. 此外方程还有解0y =.例3 求方程2d 6d y y xy x x=-的通解. 解 这是2n =时的伯努利方程. 令1z y -=可得 2d d d d z y y x x-=- 代入原方程 d 6d z z x x x=-+, 这是线性方程, 它的通解为 268c x z x =+ 代回原变量y 得到2618c x y x =+ 或688x x c y -= 这里c 是任意常数, 此外方程还有解0y =.§2.3 恰当方程与积分因子2.3.1 恰当方程将一阶方程 ()d ,d y f x y x= 写成微分形式(),d d 0f x y x y -=或写成具有对称形式的一阶微分方程()(),d ,d 0M x y x N x y y +=, 这里假设M, N 是x, y 的连续函数, 且具有连续的一阶偏导数.如果方程左端恰好是某个二元函数(),u x y 的全微分, 即()()(),d ,d d ,d d u u M x y x N x y y u x y x y x y ∂∂+≡≡+∂∂ 则称为恰当方程.恰当方程的通解是(),u x y c =, c 是任意常数.下面将解决两个问题(1) 如何判定方程是恰当方程?(2) 如果方程是恰当方程, 如何求出函数(),u x y ? 分析:如果()(),d ,d 0M x y x N x y y +=是恰当方程, 则有 ,u u M N x y ∂∂==∂∂,上两式对y, x 分别再求偏导 22,u M u N y x y x y x∂∂∂∂==∂∂∂∂∂∂ 由假设上面的混合偏导相等, 于是 M N y x∂∂=∂∂ 这是恰当方程的必要条件. 下证这也是恰当方程的充分条件, 即证明当方程满足此条件时能找到函数(),u x y 满足 ,u u M N x y∂∂==∂∂. 首先积分u M x ∂=∂, 得到 ()(),d u M x y x y ϕ=+⎰这里()y ϕ是y 的任意可微函数, 现在选择()y ϕ使u 能满足u N y∂=∂, 即 ()()d ,d d y M x y x N y yϕ∂+=∂⎰, 所以 ()()d ,d d y N M x y x y yϕ∂=-∂⎰. 上式右端与x 无关, 事实上右端对x 的偏导数()()(),d ,d ,d 0N N M x y x M x y x x y x x y N M x y x x y x N M x y ⎡⎤⎡⎤∂∂∂∂∂-=-⎢⎥⎢⎥∂∂∂∂∂⎣⎦⎣⎦∂∂∂⎡⎤=-⎢⎥∂∂∂⎣⎦∂∂=-≡∂∂⎰⎰⎰ 这样()y ϕ就可以积分得到()(),d d y N M x y x y y ϕ⎡⎤∂=-⎢⎥∂⎣⎦⎰⎰ 即求得()(),d ,d d u M x y x N M x y x y y ⎡⎤∂=+-⎢⎥∂⎣⎦⎰⎰⎰, 于是恰当方程的通解即为()(),d ,d d M x y x N M x y x y c y ⎡⎤∂+-=⎢⎥∂⎣⎦⎰⎰⎰ 这里c 是任意常数.例1 求()()222336d 64d 0x xy x x y y y +++=的通解.解 这里2236M x xy =+, 2364N x y y =+ 12,12M N xy xy y x∂∂==∂∂ 所以这是一个恰当方程.现求u 使得它同时满足 2236u x xy x∂=+∂ 和 2364u x y y y ∂=+∂ 积分上面第一式可得()3223u x x y y ϕ=++再对y 求导 ()223d 664d y u x y x y y y yϕ∂=+=+∂ 所以()3d 4d y y y ϕ= 积分可得()4y y ϕ=所以得到32243u x x y y =++ 方程的通解为32243x x y y c ++=,这里c 是任意常数.恰当方程可以采用”分项组合”的方法. 此法须熟记一些已知的二元函数的全微分, 如()d d d y x x y xy += 2d d d y x x y x y y ⎛⎫-= ⎪⎝⎭2d d d y x x y y x x -+⎛⎫= ⎪⎝⎭ d d d ln y x x y x xy y ⎛⎫-= ⎪⎝⎭22d d d arctan y x x y x x y y ⎛⎫-= ⎪+⎝⎭ 22d d 1d ln 2y x x y x y x y x y ⎛⎫--= ⎪-+⎝⎭例2 用”分项组合”的办法求例1. 解 分组23223d 4d 6d 6d 0x x y y xy x x y y +++= 即342222d d 3d 3d 0x y y x x y +++=再写成()3422d 30x y x y ++= 于是通解为34223x y x y c ++= 这里c 是任意常数.例3 求解方程211cos d d 0x x x y y y y ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭. 解 因为2211,M N y y x y ∂∂=-=-∂∂, 故方程是恰当方程, 分项组合:211cos d d d d 0x x x y x y y y y ⎛⎫++-= ⎪⎝⎭ 即2d d dsin d ln 0y x x y x y y -++= 或 d sin ln 0x x y y ⎛⎫++= ⎪⎝⎭ 所以方程的通解是 sin ln x x y c y ++= 这里c 是任意常数.2.3.2 积分因子这一部分介绍如何将一个非恰当方程转化为恰当方程.如果存在连续可微的函数(),0x y μ≠使得()()()(),,d ,,d 0x y M x y x x y N x y y μμ+= 成为一个恰当方程, 则称(),x y μ为方程()(),d ,d 0M x y x N x y y +=的积分因子.注: 理论上微分方程有解必存在积分因子且不唯一, 从而通解也可能有不同形式.(),x y μ成为方程()(),d ,d 0M x y x N xy y +=的积分因子的充要条件是()()M N y xμμ∂∂=∂∂ 即 M N N M x y y x μμμ⎛⎫∂∂∂∂-=- ⎪∂∂∂∂⎝⎭这是一个关于μ的一阶线性偏微分方程, 事实上, 解这个方程可能会比解原方程更困难. 但对于特殊形式的μ求解会相对容易许多.如果方程存在只与x 有关的积分因子()x μμ=, 则0yμ∂=∂, 这时上述关于μ的一阶线性偏微分方程变为d d M N N x y x μμ⎛⎫∂∂=- ⎪∂∂⎝⎭ 即 d d M N y x x Nμμ⎛⎫∂∂- ⎪∂∂⎝⎭= 于是方程有只与x 有关的积分因子的充要条件是 ()M N y x x Nψ∂∂-∂∂= 这里()x ψ是仅为x 的函数, 如果此条件成立, 则可积分求得方程的一个只与x 有关的积分因子()d x x e ψμ⎰=.同样, 方程有只与y 有关的积分因子的充要条件是 ()M N y x y Mϕ∂∂-∂∂=- 积分可求得方程的一个只与y 有关的积分因子 ()d y y e ϕμ⎰=.例4 试用积分因子法解一阶线性方程.解 将一阶线性方程改写为()()d d 0P x y Q x x y +-=⎡⎤⎣⎦设()()(),M x y P x y Q x =+, (),1N x y =-, 计算可得()M N y x P x N ∂∂-∂∂=- 因此方程有只与x 有关的积分因子()d P x x e μ-⎰=, 用它乘以方程两边得()()()()()d d d d d d 0P x x P x x P x x P x e y x e y Q x e x ---⎰⎰⎰-+= 即()()()()d d d d d d 0P x x P x x P x x y e e y Q x e x ---⎰⎰⎰+-=或()()()d d d 0P x x P x x ye Q x e --⎛⎫⎰⎰-= ⎪⎝⎭⎰ 故通解为()()()d d d P x x P x x ye Q x e x c --⎰⎰-=⎰或改写为()()()d d d P x x P x x y e Q x e x c -⎛⎫⎰⎰=+ ⎪⎝⎭⎰. 例5求解方程d d y x x y =-+()0y >.解 改写方程d d x x y y x +=即 ()221d 2x y x +=容易看出此方程有积分因子μ=, 用它乘以方程两边22d d x y x +=或写为d x =故通解为x c =+ 或()22y c c x =+.例6 求解方程()d d 0y x y x y +-=解 设M y =, N y x =-,1M y ∂=∂, 1N x ∂=-∂, 此方程不是恰当方程.方法1 因为2M N y x M y∂∂-∂∂=--, 故方程有只与y 有关的积分因子 ()2d 2ln 21y y y e e y μ--⎰=== 用它乘以方程的两边得到211d d d 0x x y y y y y+-= 或 2d d d 0y x x y y y y -+= 故通解为 ln x y c y+=. 方法2 将方程改写为d d d y x x y y y -=-由公式知左端有多种积分因子, 其中只和y 有关的积分因子有21y μ=, 用它乘以方程两边可得同样结果. 方法3 改写方程为 d d y y x x y=- 这是一个齐次方程, 令y u x =可求解. 方法4 改写方程为 d 1d x x y y=-这是一个x 作为未知函数的线性方程, 直接用公式可求解. §2.4 一阶隐方程与参数表示一阶隐微分方程的一般形式(),,0F x y y '=如果能够解出y ', 则方程可以采用前面介绍的方法处理. 如果不能解出y '或者解出后形式太复杂, 则可考虑利用变量变换将其变为导数解出的方程. 本节主要介绍一下四种类型1) (),y f x y '= 2) (),x f y y '= 3) (),0F x y '= 4) (),0F y y '=.2.4.1 可以解出y (或x )的方程1) 先讨论形如 d ,d y y f x x ⎛⎫= ⎪⎝⎭的方程, 假设f 有连续偏导数. 引进参数d d y p x =, 则方程变为 (),y f x p =两边对x 求导可得 d d f f p p x p x∂∂=+∂∂ 这是关于p 的导数解出的方程, 若已求得其通解为 (),p x c ϕ=则原方程的通解为()(),,y f x x c ϕ=.若求得通解为 (),x p c ψ=,则原方程的通解为如下参数形式()()(),,,x p c y f p c p ψψ=⎧⎪⎨=⎪⎩若求得通解为(),,0x p c Φ=,则原方程的通解为()(),,0,x p c y f x p Φ=⎧⎪⎨=⎪⎩ 其中p 是参数, c 是任意常数.例1 求方程3d d 20d d y y x y x x ⎛⎫+-= ⎪⎝⎭的解. 解 解出y , 并令d d y p x =, 得到 32y p xp =+两边对x 求导 2d d 322d d p p p p x p x x=++ 整理得23d 2d d 0p p x p p x ++=当0p ≠时, 用p 乘以方程两边3223d d d 0p p x p p x ++=即 423d 04p xp ⎛⎫+= ⎪⎝⎭ 故通解为 4234p xp c += 解出x 并代入32y p xp =+可得 ()43342c p y p p -=+ 因此原方程的参数式的通解为22334212c x p p c y p p ⎧=-⎪⎪⎨⎪=-⎪⎩ 0p ≠ 当0p =时, 直接计算可知0y =也是原方程的解.例2 求方程22d d d d 2y y x y x x x ⎛⎫=-+ ⎪⎝⎭的解. 解 令d d y p x =, 得到 222x y p xp =-+ 两边对x 求导 d d 2d d p p p p x p x x x=--+ 即()d 120d p p x x ⎛⎫--= ⎪⎝⎭ 由d 10d p x-= 解得p x c =+, 并得到原方程的通解 222x y cx c =++ 又20p x -=可解得2x p =, 代入后可解得原方程的另一个解 24x y = 此解和通解中每一条曲线相切, 称之为奇解, 下一章将详细介绍.2) 形如 d ,d y x f y x ⎛⎫= ⎪⎝⎭的方程解法与1)类似. 引入参数d d y p x =, 方程变为 (),x f y p =两边对y 求导再以d 1d x y p=代入得 1d d f f p p y p y∂∂=+∂∂ 此为关于p 的导数解出方程, 可求解, 设通解为 (),,0y p c Φ=则原方程的通解为()(),,,0x f y p y p c =⎧⎪⎨Φ=⎪⎩ 例3 求解例1中的方程3d d 20d d y y x y x x ⎛⎫+-= ⎪⎝⎭. 解 解出x , 并以d d y p x =代入 ()3,02y p x p p-=≠ 两边对y 求导()()232d d d d 1312p p y y p p y p p p ---= 即3d d 2d 0p y y p p p ++=积分可得42yp p c +=因而 42c p y p-= 代入得 4234c p x p -=, 于是原方程的通解为424342c p x p c p y p ⎧-=⎪⎪⎨-⎪=⎪⎩ 此外还有0y =.2.4.2 不显含y (或x )的方程3) 形如(),0F x y '=的方程, 可令d d y p y x'==, 则(),0F x p =代表xp 平面上一条曲线, 设这条曲线有参数式 ()(),x t p t ϕψ==因为d d y p x =, 代入上面的参数式可得()()d d y t t t ψϕ'=积分可得()()d y t t t c ψϕ'=+⎰ 于是原方程的参数式通解为()()(),d .x t y t t t c ϕψϕ=⎧⎪⎨'=+⎪⎩⎰ 例4 求解方程3330x y xy ''+-=.解 令y p tx '==, 方程变为333230x t x x t +-=可得 331t x t =+ 从而2331t p t =+ 于是()()3233912d d d 1t t y tx x t t -==+积分可得()32331421t y c t +=++ 因此原方程的通解为 ()332331314.21t x t t y c t ⎧=⎪+⎪⎨+=+⎪⎪+⎩4) 形如(),0F y y '=可采用同样方法求解. 令p y '=, 将(),0F y p =表示为参数式()(),y t p t ϕψ==由d d y p x =可得()()d d t t t x ϕψ'=, 所以()()d d t x t t ϕψ'=积分得()()d t x t c t ϕψ'=+⎰于是原方程的通解为()()()d .t x t c t y t ϕψϕ'⎧=+⎪⎨⎪=⎩⎰ 此外若(),00F y =有实根y k =, 则y k =亦是原方程的解.例5 求解方程()()2212y y y ''-=-. 解 令2y yt '-=, 代入原方程得 ()2221y yt y t -=即 1y t t=+故21y t '=-所以2d 1d d y x t y t==-', 积分得1x c t=+于是原方程的通解为11x c ty t t ⎧=+⎪⎪⎨⎪=+⎪⎩此外0y '=时原方程变为24y =, 所以2y =±也是原方程的解.§2.5 习题选讲1. 求下列方程的解(1) d sin cos 1d yy x x x+= 解 方程变形为sin d cos d d y x x x y x +=, 左端寻找只和x 有关的积分因子2cos x -, 积分可得2cos d tan cos yx x c x c x-=+=+⎰. (2) 2d d d y x x y x y y -=. 解 方程两边同乘以21x , 可得 2d d d y x x yy y x -=,即d d y y y x ⎛⎫-= ⎪⎝⎭, 通解为212y y c x +=. (3)d 4sin 1d y ye x x-=- 解 方程变为()4sin d d 0y yx e x e y --=, 因为1M Ny x N∂∂-∂∂= 故方程有积分因子x e , 用x e 乘以方程两边可得4sin d d d 0x y x x y e x x e e x e e y --=,即 4sin d x y xe e e x x c =+⎰,所以通解为()2sin cos y x e x x ce -=-+.(5) 22d d 0xxy y xye y x x e y ⎛⎫+-= ⎪⎝⎭解 方程可变形为齐次方程22d d xyxyy xye y x x e+=. 令x u y=, 则x uy =, d d d d x u u y y y =+,代入方程可得2d d 1u uu u e u y y ue +=+, 化简并且变量分离1d d u y e u u y ⎛⎫+=- ⎪⎝⎭, 两边积分可得 ln ln uu e y c +=-+代入原来的变量ln x yex c +=.(6) ()1d d 0xy y x x y +-= 解 方程改写为2d d d xy x x y y x =-容易看出有积分因子2y -.(7) ()()221d 2d 0x y x x y y +-++-= 解 令u x y =+d d d u x y =+, 方程化为()()()()()()()21d 2d 21d 2d d 1d 2d 0u x u yu x u u x u x u u -+-=-+--=++-= 当1u ≠-时, 变量分离可得2d d 1u u x u -=-+, 积分可得3ln 1u u x c -+=-+, ()31u x c e u +-=+代入u 得到方程通解()321x y x y ce +++=,另外1u =-即1x y +=-也是解, 包含于通解中.(8) 23d d y y y x x x=+(伯努利方程)(9)d 32d yy x x=+-(线性方程) (10) 2d d 1d d y y x x x ⎛⎫=+ ⎪⎝⎭(x 可解出的隐方程) (11)2d 1d 3y x y x x y -+=++ 解 方程化为()()21d 3d 0x y x x y y -+-++=,可验证M Ny x∂∂=∂∂, 此为恰当方程. (12) d 1d y x y e xe x -⎛⎫+=⎪⎝⎭解 方程变形为d d d y y xe x e x xe x --+=容易看出方程有积分因子x e -.(13) ()22d 2d 0x y x xy y +-=(14)d 1d yx y x=++ (15) d d yx y y e x x=+(16) ()d 112d y yx e x-++= 解 方程变形为()()12d 1d 0ye x x y --++=方程有只和y 有关的积分因子.(17) ()()2d 1d 0x y x y x y -++=解 方程改写为1d 1d 11y x y y x x x -=-++ 此为1n =-的伯努利方程.(18) ()2234d 21d 0x y x x y y +-=提示: 寻找只和y 有关的积分因子.22M Nx y y x∂∂-=∂∂, 12M Ny x M y∂∂-∂∂=--,方程有积分因子12y -.(19) 2d d 240d d y y x y x x x ⎛⎫⎛⎫-+= ⎪ ⎪⎝⎭⎝⎭. (20) 22d 11d y y x ⎡⎤⎛⎫-=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦解 令sin y p t '==, 代入得sec y t =±, 由d sin d yt x=可得 sec tan d sin d t t t t x ±=, 整理得2sec d d t t x ±=, 积分得tan x t c =±+消去参数可得()221y x c =++, 此外还有解1y =±.第三章 一阶微分方程的解的存在定理在实际应用当中, 如果能够找出方程的通解表达式, 则可以通过它了解和掌握所研究对象的性质. 但是, 很多一阶方程并不能用初等解法求出通解, 而且实际问题中很多情况下都是要求满足初始条件的解, 因此研究初值问题的解的存在和唯一性具有重要的地位.反例 解存在而不唯一的例子, 方程d d yx=()0,0的解不止一个,0y =和2y x =都是解.解的存在唯一性的意义: 在解的近似计算中提供的理论依据. 在初值问题中对初值测量偏差所产生的影响.§3.1 解的存在唯一性定理与逐步逼近法3.1.1 存在唯一性定理1) 先考虑导数解出的一阶微分方程()d ,d yf x y x= 这里(),f x y 定义在矩形域00:,R x x a y y b -≤-≤上的连续函数.利普希兹条件 如果存在常数0L >使得不等式()()1212,,f x y f x y L y y -≤-对所有()()12,,,x y x y R ∈都成立, 则称函数(),f x y 在R 上满足利普希兹条件, L 成为利普希兹常数.定理1 如果(),f x y 在R 上连续且关于y 满足利普希兹条件, 则方程()d ,d yf x y x=存在唯一的解()y x ϕ=, 定义于区间0x x h -≤上, 连续且满足初始条件()00x y ϕ=这里()(),min ,,max ,x y Rbh a M f x y M∈⎛⎫== ⎪⎝⎭. 证明思路 皮卡逐步逼近法 首先将为微分方程转化为积分方程()00,d xx y y f x y x =+⎰再任取一个连续函数()0x ϕ代入上面积分方程右端的y , 得到()()()0100,d xx x y f x x x ϕϕ≡+⎰,则()1x ϕ也是连续函数, 如果()()10x x ϕϕ≡, 则()0x ϕ就是积分方程的解, 否则继续把()1x ϕ代入积分方程右端的y ,()()()0201,d xx x y f x x x ϕϕ≡+⎰如果()()21x x ϕϕ≡, 则()2x ϕ就是积分方程的解, 否则可以继续此步骤从而得到一个连续函数列()()()01,,,,n x x x ϕϕϕ可以证明上面的函数列有极限函数()x ϕ, 而它正是积分方程的解. 函数列中的第n 项称为n 次近似解.命题 1 设()y x ϕ=是方程()d ,d yf x y x=的定义于区间00x x x h ≤≤+上, 且满足初始条件()00x y ϕ=的解, 则()y x ϕ=是积分方程()00,d xx y y f x y x =+⎰定义于区间00x x x h ≤≤+上的连续解, 反之亦然.取()00x y ϕ=, 构造皮卡逐项逼近函数列()()()()00001,d x nn x x y x y f ϕϕξϕξξ-⎧=⎪⎨=+⎪⎩⎰ 命题 2 对所有的n , 上式中的()n x ϕ在[]00,x x h +上有定义、连续且满足不等式()0n x y b ϕ-≤.命题3 函数列(){}n x ϕ在[]00,x x h +上是一致收敛的.设()()lim n n x x ϕϕ→∞=, 则()x ϕ连续且()0x y b ϕ-≤. 命题 4 ()x ϕ是积分方程()00,d xx y y f x y x =+⎰定义于[]00,x x h +上的连续解.命题 5 设()x ψ是积分方程()00,d xx y y f x y x =+⎰定义于[]00,x x h +上的一个连续解, 则()()x x ϕψ≡.命题1——5即为定理1的证明.注1 利普希兹条件常用(),f x y 在R 上有对y 的连续偏导代替. 此时, 在R 上,fL y∂≤∂,()()()()212121212,,,f x y y y f x y f x y y y yL y y θ∂+--=-∂≤-注 2 对于线性方程()()d d yP x y Q x x=+, 当()P x 和()Q x 都连续时, 则定理条件就能满足.2) 现在考虑一阶隐方程(),,0F x y y '=根据隐函数定理, 如果在()000,,x y y '的某一邻域内F连续且()000,,0F x y y '=, 而0Fy∂≠'∂, 则y '必可唯一的看成是x, y 的函数(),y f x y '=且导数f FFy y y∂∂∂=-'∂∂∂ 也是连续有界的, 这样(),f x y 即满足利普希兹条件, 于是可得到下面定理.定理2 如果在()000,,x y y '的某一邻域中: 1. (),,F x y y '对所有变元连续, 且存在连续偏导数;2. ()000,,0F x y y '=;3.()000,,0F x y y y '∂≠'∂ 则方程(),,0F x y y '=存在唯一解()0,y y x x x h =-≤满足初始条件()()0000,y x y y x y ''==. 3.1.2 近似计算和误差估计§3.2 解的延拓上节中解的存在唯一性定理是局部性的, 即解只在初值附近较小领域存在. 本节讨论如何延拓解的区间至最大范围.解的延拓定理 如果方程()d ,d yf x y x=右端的函数(),f x y 在有界区域G 中连续, 且在G 内关于y 满足局部利普希兹条件, 那么此方程通过G 内任何一点()00,x y 的解()y x ϕ=可以延拓, 直到点()(),x x ϕ任意接近区域G 的边界.推论 如果G 是无界区域, 在上面解的延拓定理的条件下, 方程通过点()00,x y 的解()y x ϕ=可以延拓, 以向x 增大的方向来说, 有两种情况: (1) 解()y x ϕ=可以延拓到区间0[,)x +∞;(2) 解()y x ϕ=只可以延拓到区间0[,)x m , m 为有限数,则当x 趋向于m 时, 或者y 无界, 或者()(),x x ϕ趋向于区域的边界.如果函数(),f x y 在整个xy 平面上定义、连续且有界, 同时存在关于y 的一阶连续偏导数, 则方程()d ,d yf x y x=的任一解可以延拓到区间x -∞<<+∞.§3.3 解对初值的连续性和可微性方程()d ,d yf x y x=的解经过初值()00,x y 是唯一的,当初值()00,x y 变化时,解也随之变化. 因此可以把方程的解看成是三元函数()00,,y x x y ϕ=满足()0000,,y x x y ϕ=.解关于初值的对称性 设方程()d ,d yf x y x=的经过初值()00,x y 的解是唯一的, 记为()00,,y x x y ϕ=, 则此表达式中(),x y 和()00,x y 可以对调位置, 即成立()00,,y x x y ϕ=。
常微分方程王高雄第三版答案_百度文库百度首页 | 百度知道 | 百度文库首页 | 手机文库 | 注册 | 登录新闻网页贴吧知道MP3 图片视频百科文库帮助全部 DOC PDF PPT XLS TXT百度文库 > 高等教育下载收藏分享加入文辑常微分方程王高雄第三版答案高等教育出版社《常微分方程》王高雄第三版答案高等教育出版社《常微分方程》王高雄第三版答案<<隐藏下载本文档需要登录,并付出相应财富值。
如何获取财富值?大小: 638.1KB所需财富值: 20喜欢此文档的人还喜欢4268人阅读常微分方程第三版答案(王高雄) 19829人阅读常微分方程王高雄第三版答案6103人阅读常微分方程(第三版)课后答案 1570人阅读常微分方程第三版——答案 1192人阅读第三版常微分方程答案.doc 文库书店等你来逛点击进入书店 prevnext当前文档信息4.5已有160人评价浏览:10591次下载:1285次贡献时间:2010-02-13贡献者: dengliang19854 手不释卷四级文档关键词文档关键词暂无收录此文档的文辑信息与计算科学专业电子资...创建者:某某丙哥收藏量:2常微分,微分几何,数学建模...创建者:nazai娜收藏量:0家教创建者:gaojunzi0830 收藏量:0更多相关推荐文档常微分方程答案4.114人评 2页常微分方程08秋重修11人评 4页常微分方程答案 4.212人评 6页常微分方程试题参考答案计分...5人评 5页高雄餐旅大学发展5人评 1页更多同分类热门文档政治无敌笔记43139人评 27页处理人际关系的55个绝招37631人评 9页新东方美文背诵30篇38598人评 25页16天记住7000考研单词18523人评 30页Excel的使用方法与技巧49012人评 68页如要投诉或提出意见建议,请到百度文库投诉吧反馈。
©2011 Baidu使用百度前必读文库协议iPhone2.0震撼升级文库iPhone华丽升级2.0,超逼真3D翻页,支持多格式、原文档下载,享受原汁原味的文档盛宴…马上体验。
习题1.21.dxdy=2xy,并满足初始条件:x=0,y=1的特解。
解:ydy =2xdx 两边积分有:ln|y|=x 2+c y=e2x +e c =cex2另外y=0也是原方程的解,c=0时,y=0原方程的通解为y= cex 2,x=0 y=1时 c=1 特解为y= e 2x .2. y 2dx+(x+1)dy=0 并求满足初始条件:x=0,y=1的特解。
解:y 2dx=-(x+1)dy2ydy dy=-11+x dx 两边积分: -y 1=-ln|x+1|+ln|c| y=|)1(|ln 1+x c 另外y=0,x=-1也是原方程的解 x=0,y=1时 c=e 特解:y=|)1(|ln 1+x c3.dx dy =yx xy y 321++解:原方程为:dx dy =y y 21+31xx + y y 21+dy=31x x +dx 两边积分:x(1+x 2)(1+y 2)=cx 24. (1+x)ydx+(1-y)xdy=0 解:原方程为:y y −1dy=-xx 1+dx两边积分:ln|xy|+x-y=c另外 x=0,y=0也是原方程的解。
5.(y+x )dy+(x-y)dx=0解:原方程为:dx dy =-yx yx +− 令x y =u 则dx dy =u+x dx du 代入有: -112++u u du=x 1dxln(u 2+1)x 2=c-2arctgu 即 ln(y 2+x 2)=c-2arctg 2x y. 6. xdxdy -y+22y x −=0 解:原方程为:dx dy =x y +x x ||-2)(1xy − 则令x y =u dx dy =u+ x dxdu 211u − du=sgnxx1dx arcsinxy=sgnx ln|x|+c 7. tgydx-ctgxdy=0 解:原方程为:tgy dy =ctgxdx 两边积分:ln|siny|=-ln|cosx|-ln|c| siny=x c cos 1=xccos 另外y=0也是原方程的解,而c=0时,y=0.所以原方程的通解为sinycosx=c.8 dx dy +ye xy 32+=0 解:原方程为:dx dy =ye y 2e x 32 ex3-3e2y −=c.9.x(lnx-lny)dy-ydx=0 解:原方程为:dx dy =x y ln xy令x y =u ,则dx dy =u+ x dx duu+ xdx du=ulnu ln(lnu-1)=-ln|cx| 1+lnxy =cy. 10.dxdy =e yx − 解:原方程为:dxdy =e x e y− e y=ce x11dxdy =(x+y)2解:令x+y=u,则dx dy =dxdu -1 dx du -1=u 2211u+du=dx arctgu=x+c arctg(x+y)=x+c12.dx dy =2)(1y x + 解:令x+y=u,则dx dy =dxdu -1dx du-1=21uu-arctgu=x+c y-arctg(x+y)=c. 13.dx dy =1212+−+−y x y x 解: 原方程为:(x-2y+1)dy=(2x-y+1)dx xdy+ydx-(2y-1)dy-(2x+1)dx=0 dxy-d(y 2-y)-dx 2+x=cxy-y 2+y-x 2-x=c14:dx dy =25−−+−y x y x 解:原方程为:(x-y-2)dy=(x-y+5)dx xdy+ydx-(y+2)dy-(x+5)dx=0dxy-d(21y 2+2y)-d(21x 2+5x)=0 y 2+4y+x 2+10x-2xy=c. 15:dxdy =(x+1) 2+(4y+1) 2+8xy 1+ 解:原方程为:dxdy =(x+4y )2+3令x+4y=u 则dx dy =41dx du -4141dx du -41=u 2+3 dx du =4 u 2+13 u=23tg(6x+c)-1 tg(6x+c)=32(x+4y+1).16:证明方程y x dxdy=f(xy),经变换xy=u 可化为变量分离方程,并由此求下列方程: 1) y(1+x 2y 2)dx=xdy2) y x dx dy =2222x -2y x 2y + 证明: 令xy=u,则x dx dy +y=dxdu 则dx dy =x 1dx du -2x u,有:u x dxdu=f(u)+1)1)((1+u f u du=x1dx所以原方程可化为变量分离方程。
第二章目录内容提要及其它 (1)第二章一阶微分方程的初等解法(初等积分) (2)第一节变量分离方程与变量变换 (2)一、变量分离方程 (2)二、可化为变量分离方程的类型 (6)1、齐次方程 (6)2、可化为变量分离方程 (7)三、应用例题选讲 (10)第二节线性方程与常数变易法 (11)第三节恰当方程与积分因子 (15)一、恰当方程 (15)二、积分因子 (20)第四节一阶隐含方程与参数表示 (23)一、可以解出y(或x)的方程 (24)二、不显含y(或x)的方程 (25)本章小结及其它 (27)内容提要及其它授课题目(章、节)第二章:一阶微分方程的初等解法教材及主要参考书(注明页数)教材:常微分方程(第三版),王高雄等,高等教育出版社,2006年,p30-74主要参考书:[1]常微分方程,东北师范大学微分方程教研室编,高等教育出版社,2005,p1-70[2]常微分方程教程,丁同仁等编,高等教育出版社,1991,p1-20[3]偏微分方程数值解法(第2版),陆金甫关治,清华大学出版社,2004,p1-12[4]常微分方程习题解,庄万主编,山东科学技术出版社,2003,p28-169[5]微分方程模型与混沌,王树禾编著,中国科学技术大学出版社,1999,p15-158[6]差分方程和常微分方程,阮炯编著,复旦大学出版社,2002,p38-124目的与要求:掌握变量分离方程、齐次方程、线性方程、伯努利方程和恰当方程的解法.理解变量变换思想方法和积分因子方法,并能应用于求解一些特殊的常微分方程.掌握四类典型的一阶隐方程的解法.能熟练求解变量分离方程、齐次方程、线性方程、伯努利方程、恰当方程和四类典型的一阶隐方程.领会变量变换思想方法和积分因子方法,并能应用于求解一些特殊的常微分方程.教学内容与时间安排、教学方法、教学手段:教学内容:第1节变量分离方程与变量变换;第2节线性方程与常数变易法;第3节恰当方程与积分因子;第4节一阶隐方程与参数表示:可以解出(或y x)的方程、不显含(或y x)的方程.时间安排:8学时教学方法:讲解方法教学手段:传统教学方法与多媒体教学相结合。