高一数学课件 二次函数在闭区间上的最值
- 格式:ppt
- 大小:1.60 MB
- 文档页数:26
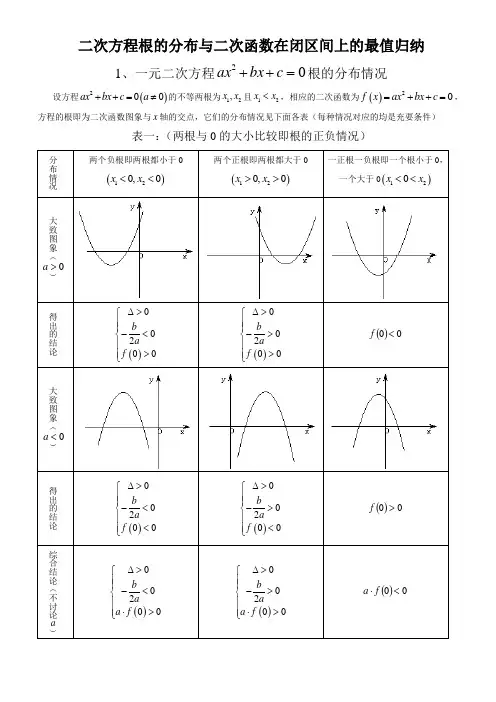
二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程02=++c bx ax 根的分布情况 设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=,方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与0的大小比较即根的正负情况)k k k根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)需满足的条件是(1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,内有以下特殊情况:1︒ 若()0f m =或()0f n =,则此时()()0f m f n <不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,内,从而可以求出参数的值。
如方程()2220mx m x -++=在区间()1,3上有一根,因为()10f =,所以()()()22212mx m x x mx -++=--,另一根为2m,由213m <<得223m <<即为所求; 2︒ 方程有且只有一根,且这个根在区间()n m ,内,即0∆=,此时由0∆=可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数。
如方程24260x mx m -++=有且一根在区间()3,0-内,求m 的取值范围。
分析:①由()()300f f -<即()()141530m m ++<得出15314m -<<-;②由0∆=即()2164260m m -+=得出1m =-或32m =,当1m =-时,根()23,0x =-∈-,即1m =-满足题意;当32m =时,根()33,0x =∉-,故32m =不满足题意;综上分析,得出15314m -<<-或1m =-根的分布练习题例1、已知二次方程()()221210m x mx m +-+-=有一正根和一负根,求实数m 的取值范围。

二次函数在闭区间上的最值一、知识要点:一元二次函数的区间最值问题,核心是函数对称轴与给定区间的相对位置关系的讨论。
一般分为:对称轴在区间的左边,中间,右边三种情况.设,求在上的最大值与最小值。
分析:将配方,得顶点为、对称轴为当时,它的图象是开口向上的抛物线,数形结合可得在[m,n]上的最值:(1)当时,的最小值是的最大值是中的较大者。
(2)当时若,由在上是增函数则的最小值是,最大值是若,由在上是减函数则的最大值是,最小值是当时,可类比得结论。
二、例题分析归类:(一)、正向型是指已知二次函数和定义域区间,求其最值。
对称轴与定义域区间的相互位置关系的讨论往往成为解决这类问题的关键。
此类问题包括以下四种情形:(1)轴定,区间定;(2)轴定,区间变;(3)轴变,区间定;(4)轴变,区间变。
1. 轴定区间定二次函数是给定的,给出的定义域区间也是固定的,我们称这种情况是“定二次函数在定区间上的最值”。
例1.函数在区间[0,3]上的最大值是_________,最小值是_______。
解:函数是定义在区间[0,3]上的二次函数,其对称轴方程是,顶点坐标为(2,2),且其图象开口向下,显然其顶点横坐标在[0,3]上,如图1所示。
函数的最大值为,最小值为。
图1练习. 已知,求函数的最值。
解:由已知,可得,即函数是定义在区间上的二次函数。
将二次函数配方得,其对称轴方程,顶点坐标,且图象开口向上。
显然其顶点横坐标不在区间内,如图2所示。
函数的最小值为,最大值为。
图22、轴定区间变二次函数是确定的,但它的定义域区间是随参数而变化的,我们称这种情况是“定函数在动区间上的最值”。
例2. 如果函数定义在区间上,求的最小值。
解:函数,其对称轴方程为,顶点坐标为(1,1),图象开口向上。
如图1所示,若顶点横坐标在区间左侧时,有,此时,当时,函数取得最小值。
图1如图2所示,若顶点横坐标在区间上时,有,即。
当时,函数取得最小值。
图2如图3所示,若顶点横坐标在区间右侧时,有,即。

第三讲 二次函数在闭区间上的最值问题 一.知识点介绍1.区间的概念设a 、b 是两个实数,且a<b ,规定:说明:① 对于[a,b],(a,b),[a,b),(a,b]都称数a 和数b 为区间的端点,其中a 为左端点,b 为右端点,称b-a 为区间长度;②在数轴上,这些区间都可以用一条以a 和b 为端点的线段来表示,在图中,用实心点表示包括在区间内的端点,用空心点表示不包括在区间内的端点;③实数集R 也可以用区间表示为(-∞,+∞),“∞”读作“无穷大”,“-∞”读作“负无穷大”,“+∞”读作“正无穷大”,还可以把满足x ≥a, x>a, x ≤b, x<b 的实数x 的全体分别表示为[a,+∞)、(a,+∞)、(-∞,b]、(-∞,b)。
我们把以上区间记为A ,若x 是A 中的一个数,就说x 属于A ,记作x ∈A 。
否则就说x 不属于A ,记作x ∉A 。
2. 二次函数f(x)=ax 2+bx+c(a≠0)在x ∈[α,β]上的最值: 当a>0时,有三种情况:从上述a>0的三种情况可得结论:(1)若[,]2baαβ-∈,则当2b x a =-时,2min4()24b ac b y f a a-=-=,它的最大值为()f α与()f β中较大的一个。
(2) 若[,]2baαβ-∉,则最大值为()f α与()f β中较大的一个,另一个即为最小值。
当a<0可作同样处理。
二.例题讲解:类型一“轴定区间定”例1:已知f(x)=x 2-x+2,当x 在以下区间内取值时,求f(x)的最大值与最小值。
(1) x ∈[-1,0] (2) x ∈[0,1] (3) x ∈[1,2]变式1:求y =的最值。
变式2:已知0≤x≤1,求y =的最值。
变式3:求函数y x =+的最小值。
类型二“轴变区间定”例2:求函数f(x)=2x 2-2ax+3在区间[-1,1]上的最小值。

二次函数在闭区间上的最值问题
最值问题是函数的基本概念之一,它旨在求出函数在定义域中的最大值和最小值。
函数的最值问题也是极其重要的问题,其研究可以帮助我们求出目标函数的最优解,从而获得最佳的求解结果。
在闭区间上的二次函数最值问题中,其对应的函数形式为:
$f(x)=ax^2+bx+c$
其中,a,b,c为常量。
问题要求给定区间[a,b],求出f(x)在这个区间内的最大值和最小值。
一、求二次函数在闭区间上的最值
二、最值求解:
最终,我们就可以得出该函数在指定的闭区间上的最大值和最小值。



二次函数闭区间上的最值问题与根的分布一、二次函数闭区间上的最值问题一元二次函数的区间最值问题,核心是对函数对称轴与给定区间的相对位置关系的讨论。
一般分为:对称轴在区间的左边,中间,右边三种情况.设2()(0)f x a x b x c a =++≠,求f x ()在[]x m n ∈,上的最大值与最小值。
分析:将f x ()配方,得对称轴方程x b a=-2当a >0时,抛物线开口向上 若-∈b am n 2[],必在顶点取得最小值,离对称轴较远端点处取得最大值; 若-∉b am n 2[], 当a >0时,抛物线开口向上,此时函数在[]m n ,上具有单调性,故在离对称轴x b a=-2较远端点处取得最大值,较近端点处取得最小值。
当a <0时,如上,作图可得结论,对二次函数的区间最值结合函数图象总结如下: 当a >0时m a x121()()()22()1()()()22b f m m n a f x b f n m n a ⎧-≥+⎪⎪=⎨⎪-<+⎪⎩如图如图,,f x f n b a n f b a m b a n f m b a m ()()()()()()()m in=->-≤-≤-<⎧⎨⎪⎪⎪⎩⎪⎪⎪,,,如图如图如图2222345当a <0时f x f n b a n f b a m b a n f m b a m ()()()()()()()m ax=->-≤-≤-<⎧⎨⎪⎪⎪⎩⎪⎪⎪,,,如图如图如图2222678m i n 9101()()()22()1()()()22b f m m n a f x b f n m n a ⎧-≥+⎪⎪=⎨⎪-<+⎪⎩如图如图,,1. 定二次函数在定区间上的最值二次函数是给定的,给出的定义域区间也是固定的,我们称这种情况是“定二次函数在定区间上的最值”。
例1. 函数y x x =-+-242在区间[]03,上的最大值是_________,最小值是_______。




二次函数在闭区间上的最值一.知识点精讲1 二次函数的三种形式(1)一般式 c bx ax x f ++=2)(; (2)交点式))(()(21x x x x a x f --=; (3)顶点式k h x a x f +-=2)()( 2.二次函数的基本性质(1)开口方向 0>a 时,开口向上, 0<a 时,开口向上,(2)对称轴方程ab x 2-= (3)02=++c bx ax 根的判别式 ac b 42-=∆(4)02=++c bx ax 的求根公式 aac b b x 2422,1-±-=(5)02=++c bx ax 两根和,两根积 a b x x -=+21 ac x x =21 3 解决二次函数问题的常用方法——数形结合法二次函数()0)(2≠++=a cbx ax x f 的图像为抛物线,具有许多优美的性质,如对称性、单调性、凹凸性等。
结合这些图像特征解决有关二次函数的问题,可以化难为易,形象直观。
因为二次函数()0)(2≠++=a cbx ax x f 在区间]2,(a b --∞和区间),2[+∞-ab上分别单调,所以函数()x f 在闭区间上的最大值、最小值必在区间端点或顶点处取得;函数)(x f 在闭区间上的最大值必在区间端点或顶点处取得。
4 二次函数c bx ax x f ++=2)(在区间[p ,q ]上的值域求法方法:讨论或分析对称轴和区间的位置关系。
由于二次函数的解析式简捷明了,易于变形(一般式、顶点式、零点式等),所以,在解决二次函数的问题时,常常借助其解析式,通过纯代数推理,进而导出二次函数的有关性质。
二 典型例题1 求函数22)(2+-=x x x f 在]1,[+m m 上的最小值 解析:二次函数的对称轴为1=x ,(1)当11<+m 时,即0<m ,12m in +=m y(2)当1>m 时,1)1(2m in +-=m y (3)当10≤≤m 时,1m in =y变式1:求函数22)(2+-=x x x f 在]1,[+m m 上的最大值 解析:(1)当21≤m 时,1)1(2m ax +-=m y (2)当21>m 时,12max +=m y变式2 求函数22)(2+-=ax x x f 在]1,1[-上的最小值 解析:二次函数的对称轴为a x =, (1)当1-<a 时, 12m in +=a y (2)当1>a 时,1)1(2m in +-=a y (3)当10≤≤a 时,1m in =y变式3:求函数22)(2+-=ax x x f 在]1,1[-上的最大值 解析:(1)当0≤a 时, a y 24m ax -=(2)当0>a 时,a y 24m ax +=二次函数是个筐,什么东西都能往里装变式4求124)(1+-=+x xx f ,]2,1[-∈x 的值域解析:xt 2=]4,21[∈t ,22)1(12)(-=+-=t t t t g ,当1=t 时,即0=x ,0)(m in =t g 当4=t 时,即2=x ,9)(m ax =t g ,∴]9,0[)(∈t g 即]9,0[∈y变式5 求1log log )(222++=x x x f ]2,81(∈x 的值域 注意:22)(log log x x a a =解析:x t 2log =,]1,3(-∈t ,43)21(1)(22++=++=t t t t g ,当21-=t 时,即22=x 时,43)(min =t g 当3-=t 时,即81=x ,7)(m ax =t g ,∴]7,43()(∈t g 即]9,0[∈y 当4=t 时,即2=x ,9)(m ax =t g ,∴]9,0[)(∈t g 即]7,43[∈y变式6 (2009福建理)函数2()(0)f x ax bx c a =++≠的图象关于直线2bx a=-对称。
【最新整理,下载后即可编辑】二次函数在闭区间上的最值一、 知识要点:一元二次函数的区间最值问题,核心是函数对称轴与给定区间的相对位置关系的讨论。
一般分为:对称轴在区间的左边,中间,右边三种情况. 设f x ax bx c a ()()=++≠20,求f x ()在x m n ∈[],上的最大值与最小值。
分析:将f x ()配方,得顶点为--⎛⎝ ⎫⎭⎪b aac b a 2442,、对称轴为x ba =-2当a >0时,它的图象是开口向上的抛物线,数形结合可得在[m ,n]上f x ()的最值:(1)当[]-∈bam n2,时,f x ()的最小值是f b a ac b af x -⎛⎝ ⎫⎭⎪=-2442,()的最大值是f m f n ()()、中的较大者。
(2)当[]-∉bam n 2,时若-<bam 2,由f x ()在[]m n ,上是增函数则f x ()的最小值是f m (),最大值是f n ()若n ba<-2,由f x ()在[]m n ,上是减函数则f x ()的最大值是f m (),最小值是f n ()当a <0时,可类比得结论。
二、例题分析归类: (一)、正向型是指已知二次函数和定义域区间,求其最值。
对称轴与定义域区间的相互位置关系的讨论往往成为解决这类问题的关键。
此类问题包括以下四种情形:(1)轴定,区间定;(2)轴定,区间变;(3)轴变,区间定;(4)轴变,区间变。
1. 轴定区间定二次函数是给定的,给出的定义域区间也是固定的,我们称这种情况是“定二次函数在定区间上的最值”。
例1. 函数y x x =-+-242在区间[0,3]上的最大值是_________,最小值是_______。
练习. 已知232x x ≤,求函数f x x x ()=++21的最值。
2、轴定区间变二次函数是确定的,但它的定义域区间是随参数而变化的,我们称这种情况是“定函数在动区间上的最值”。